Alignment Error Modelling, Analysis and Experiment of the Deep-Water Bolt Flange Automatic Connection Tool
Abstract
:1. Introduction
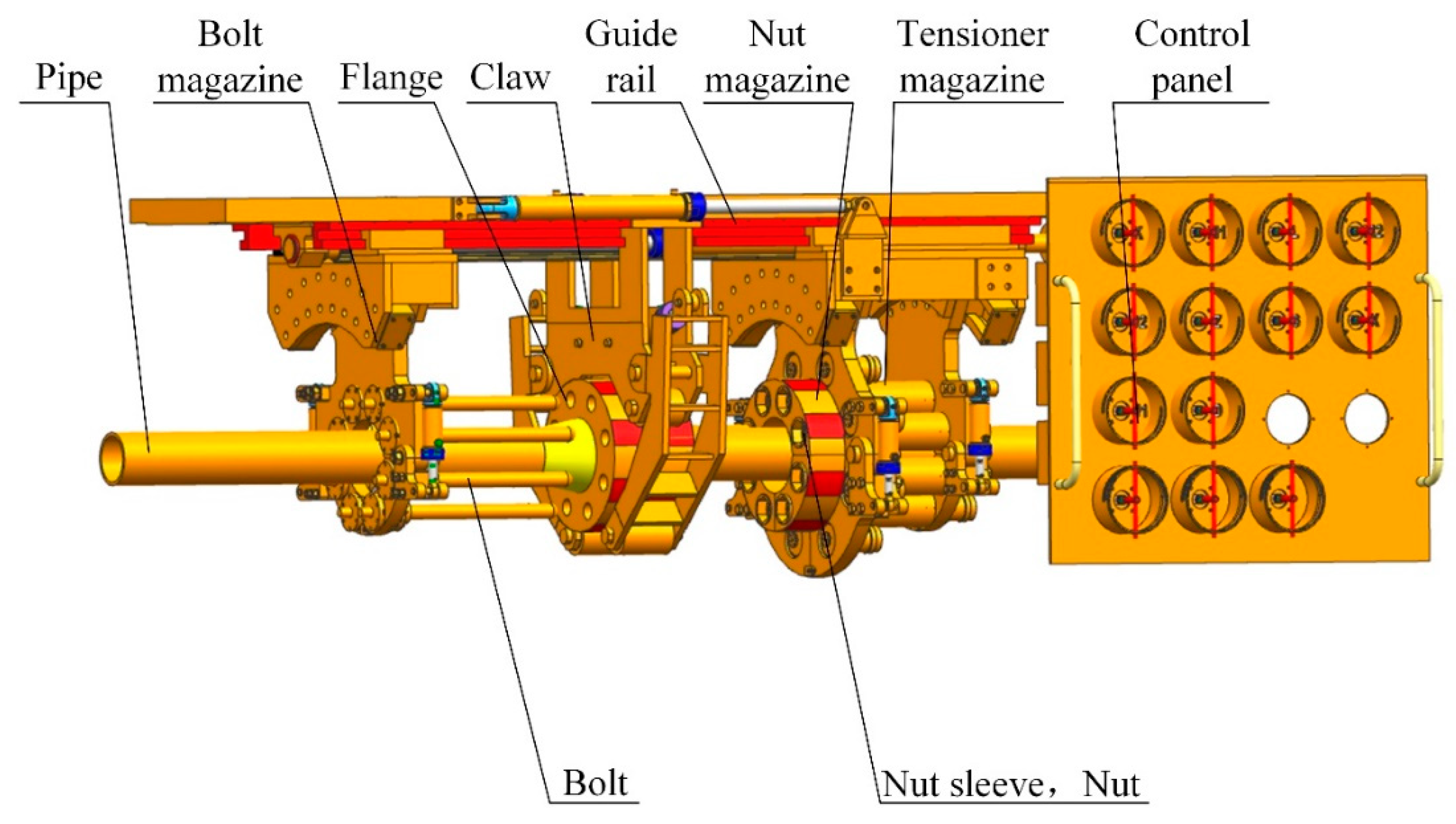
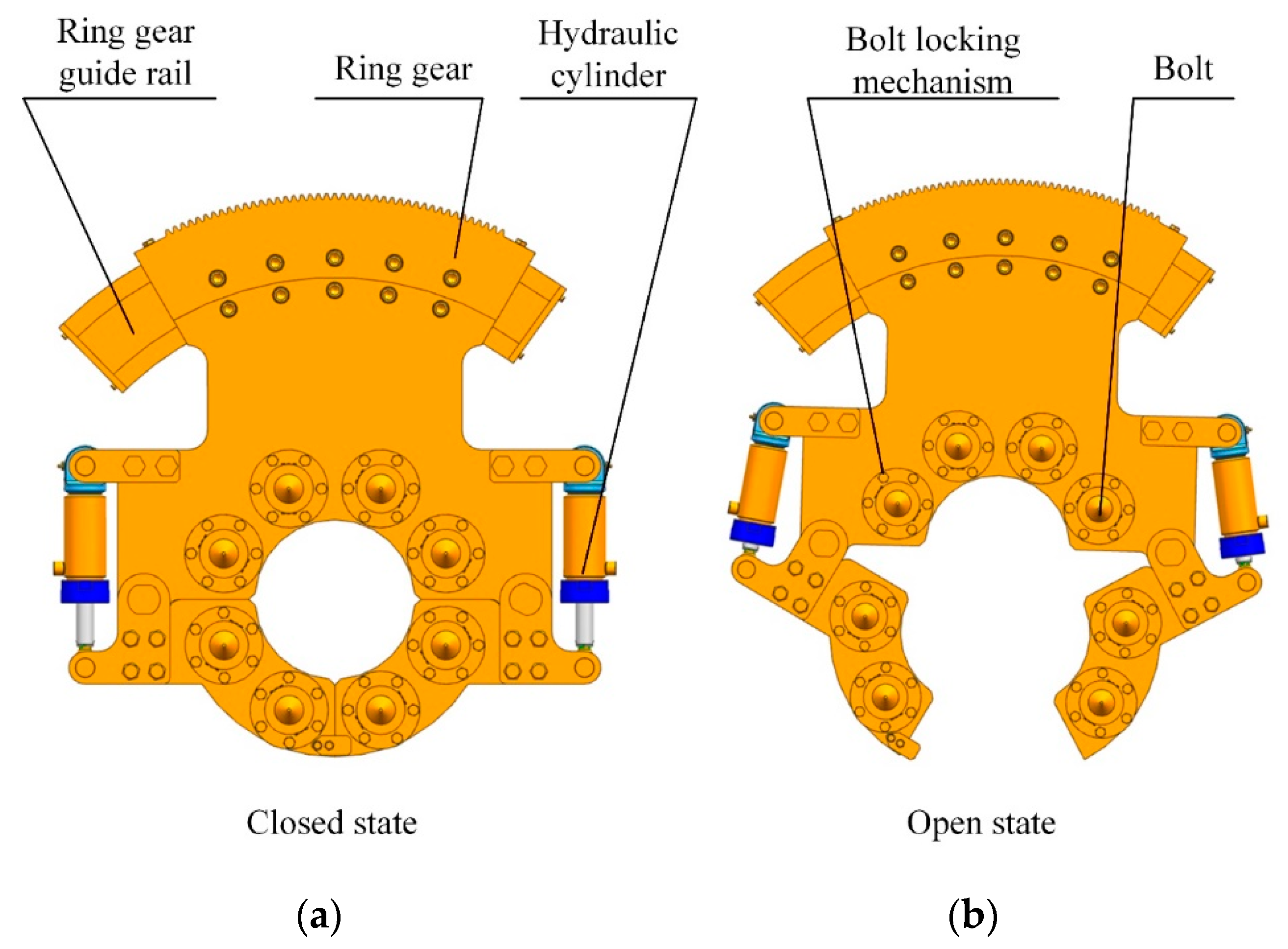
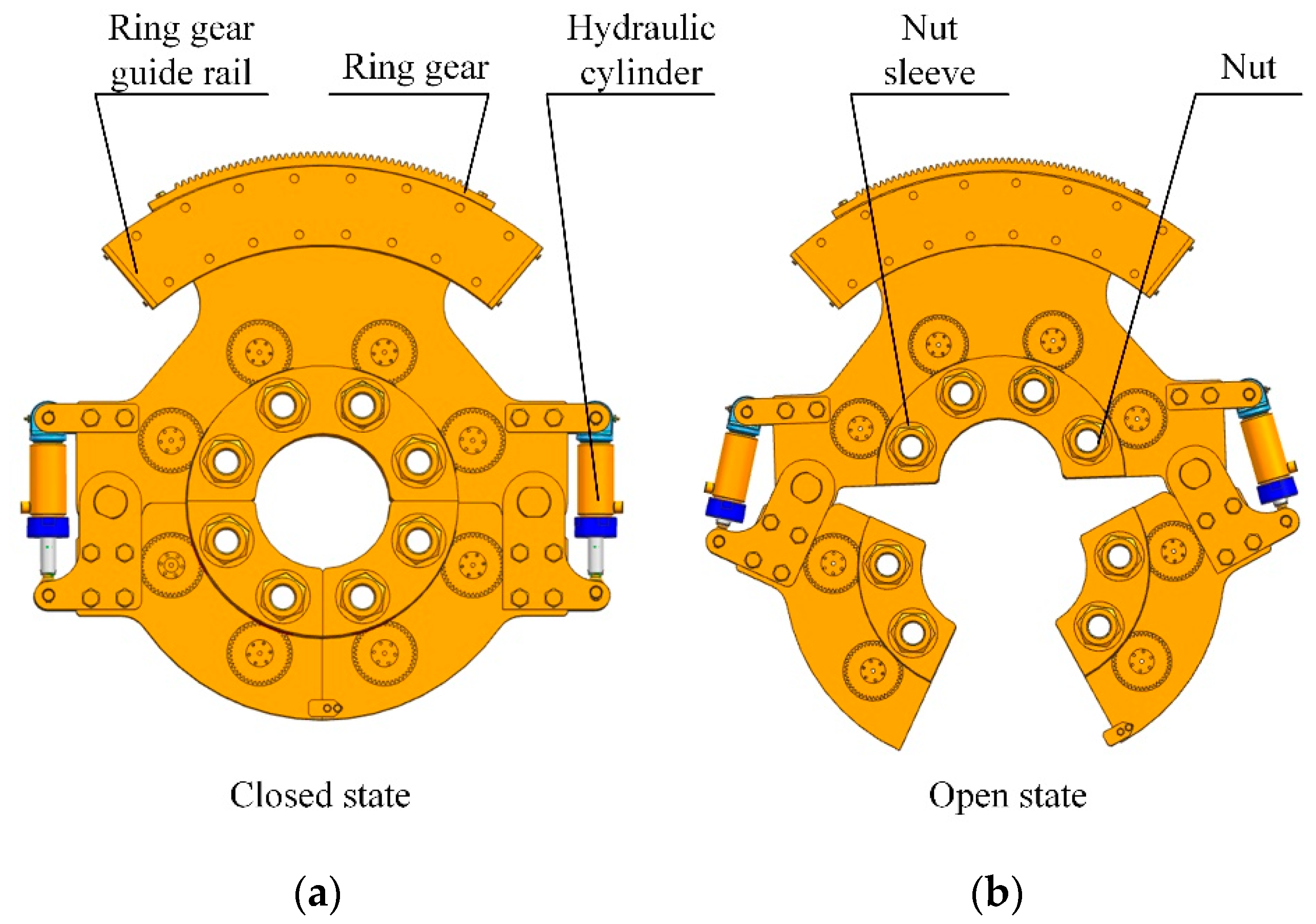
2. Error Model of Deep-Water Bolt Flange Automatic Connection Tool
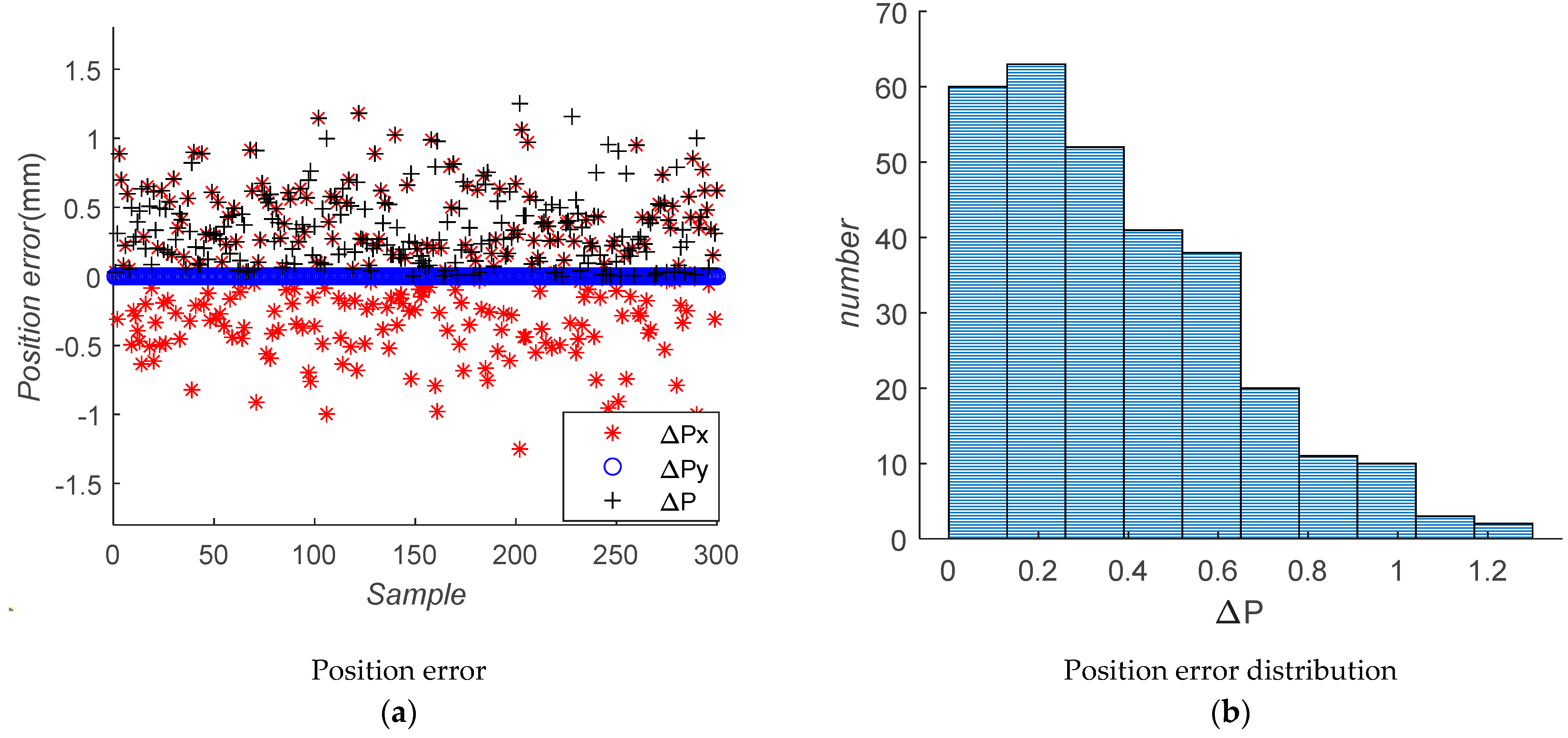
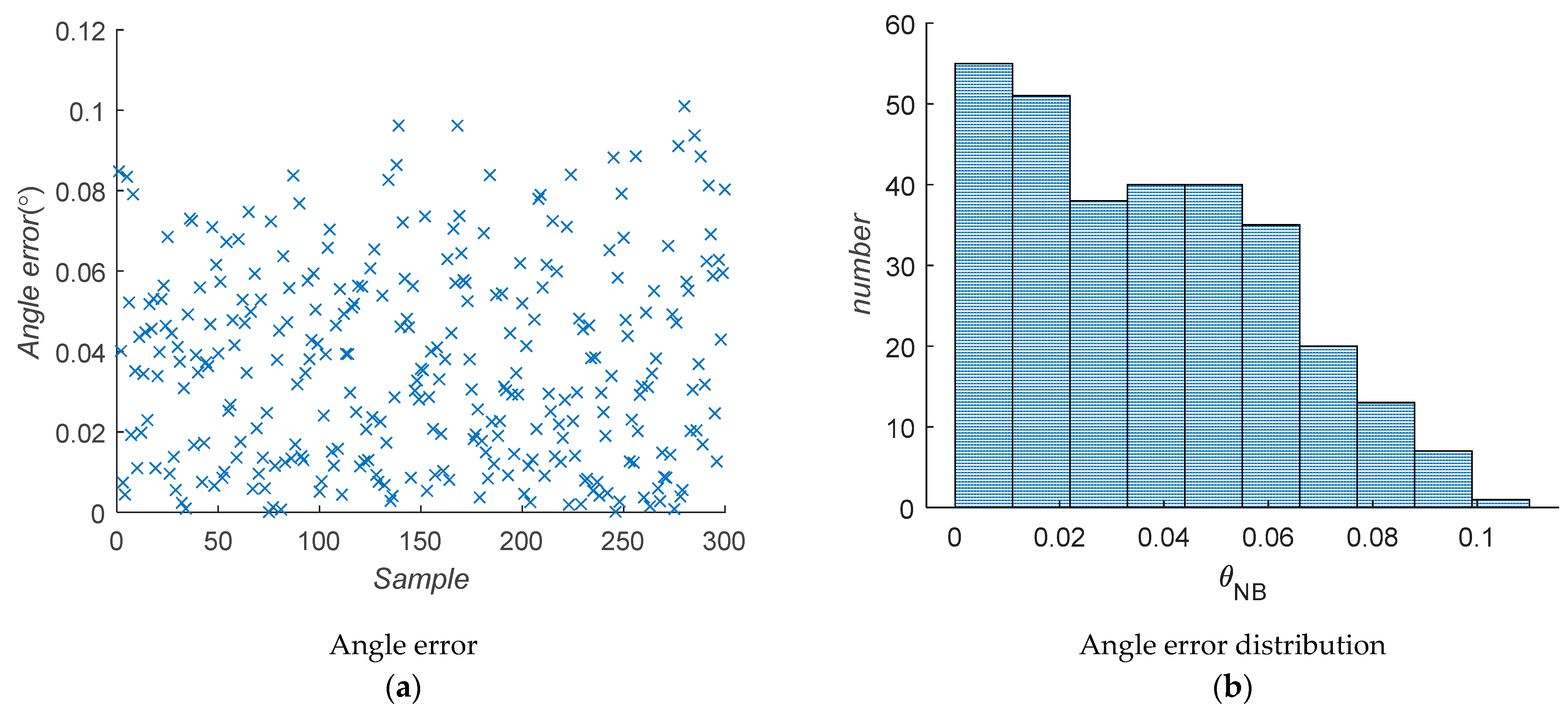
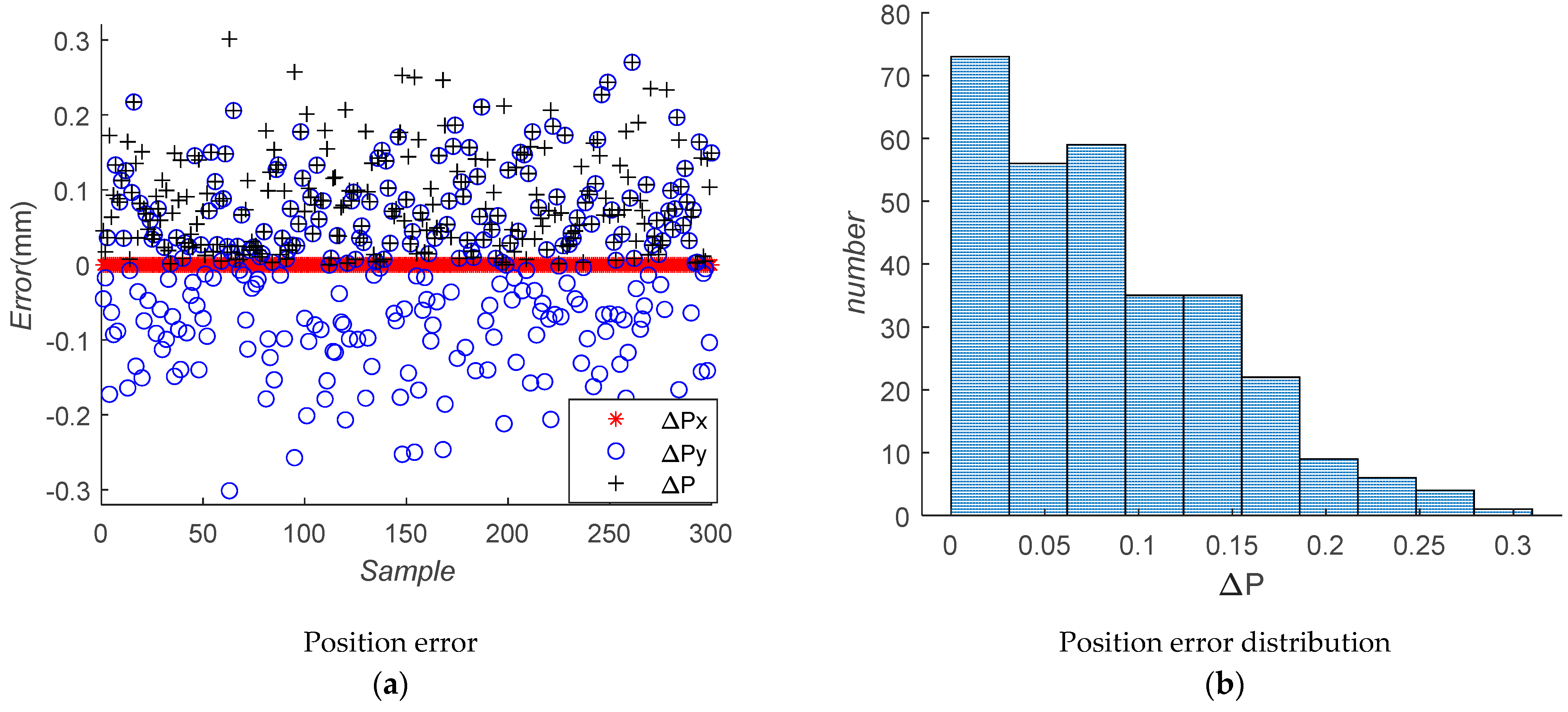
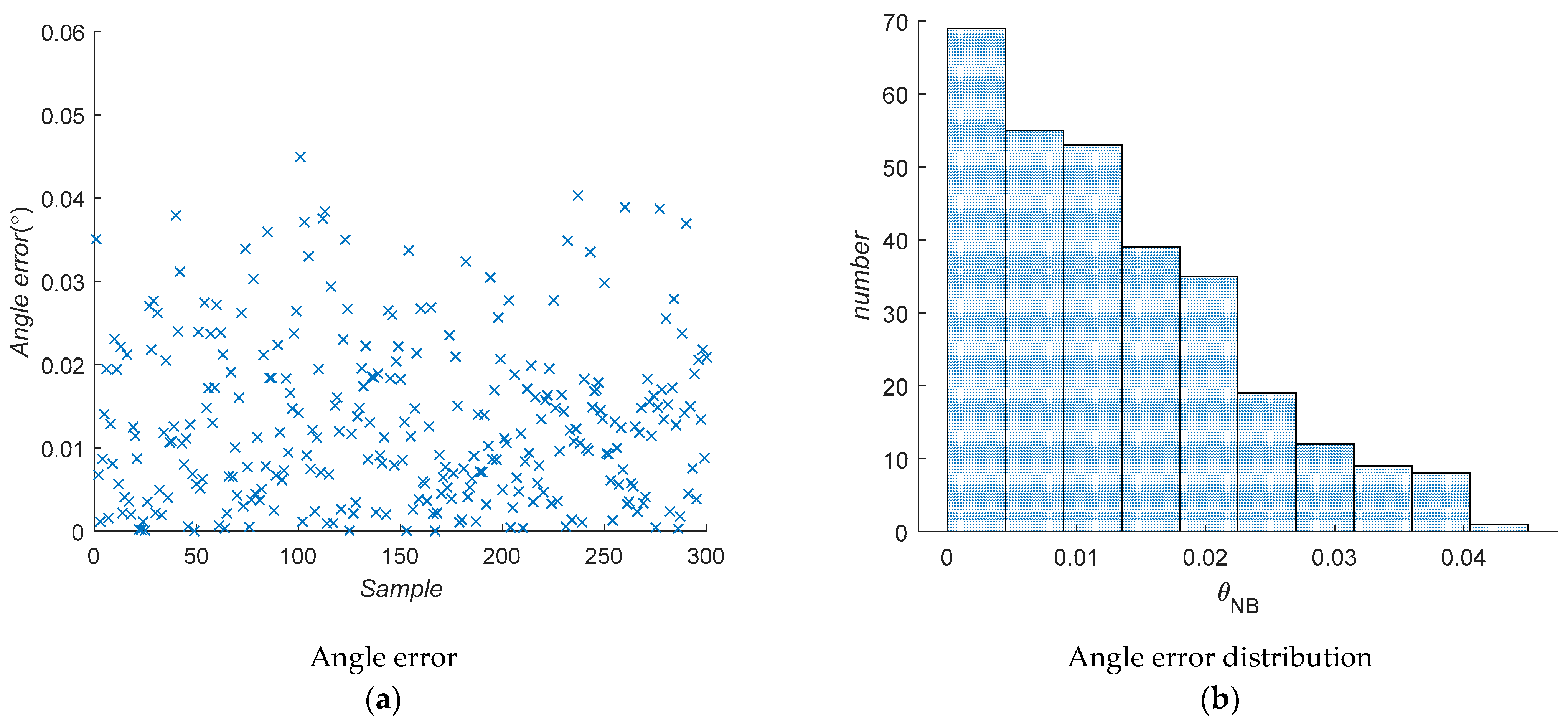
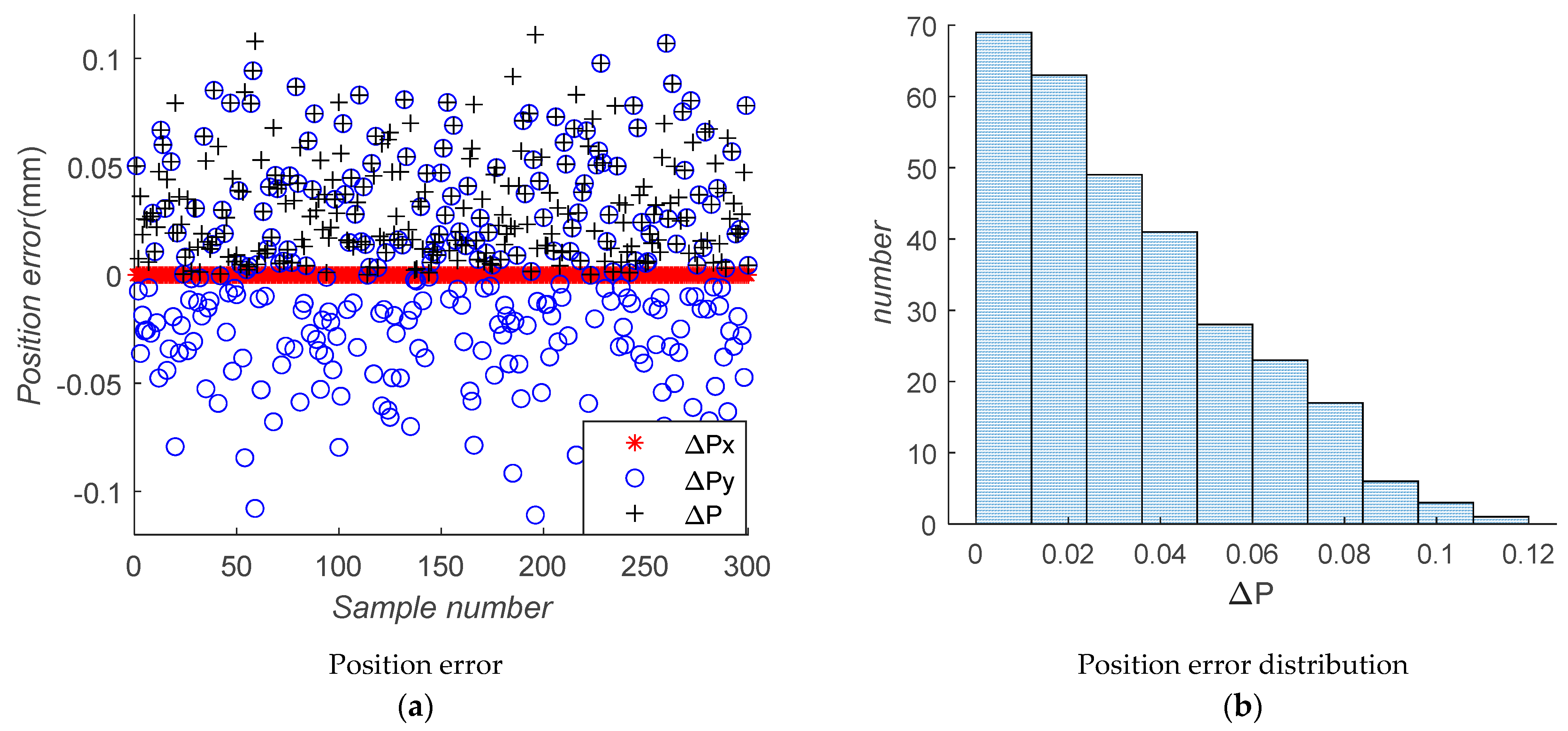
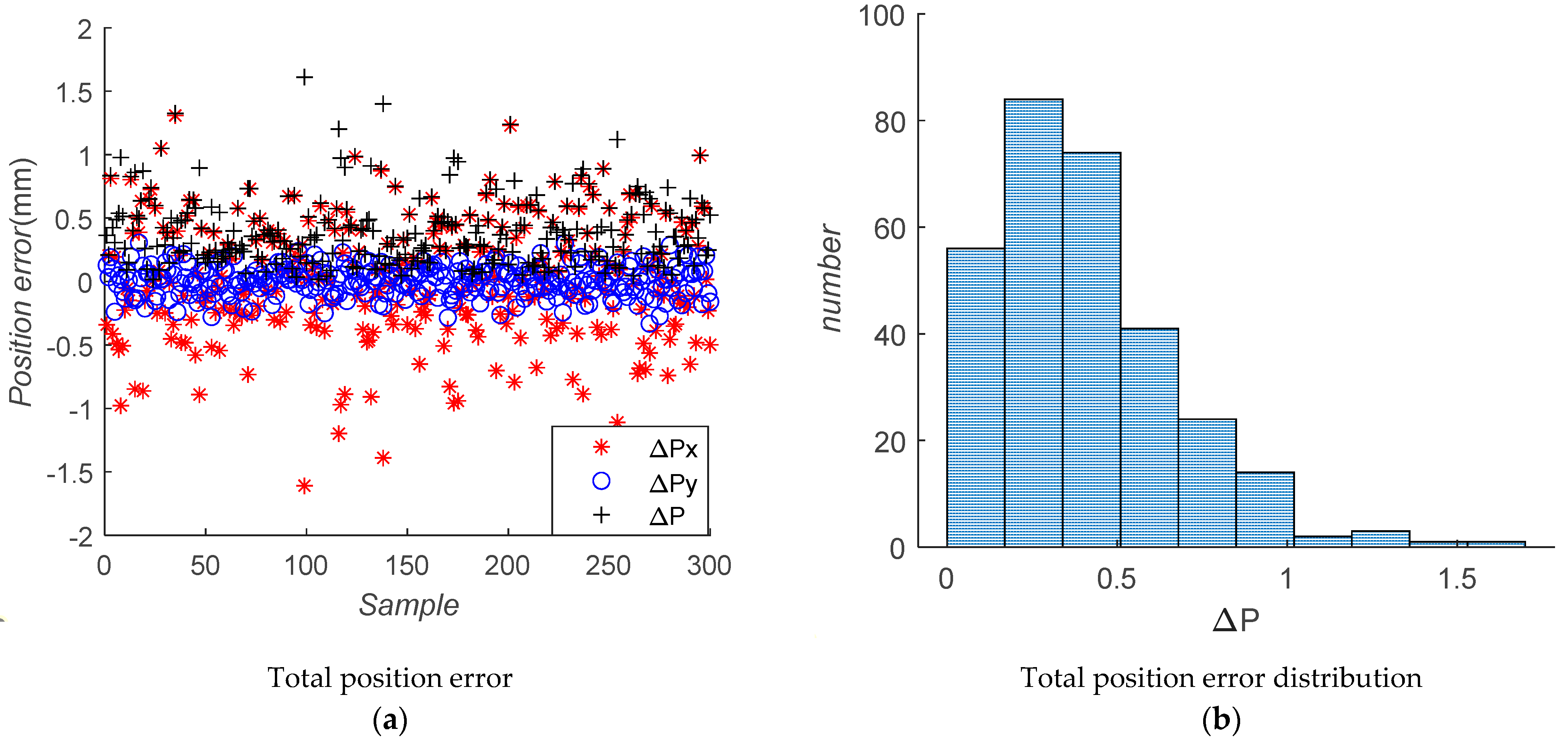
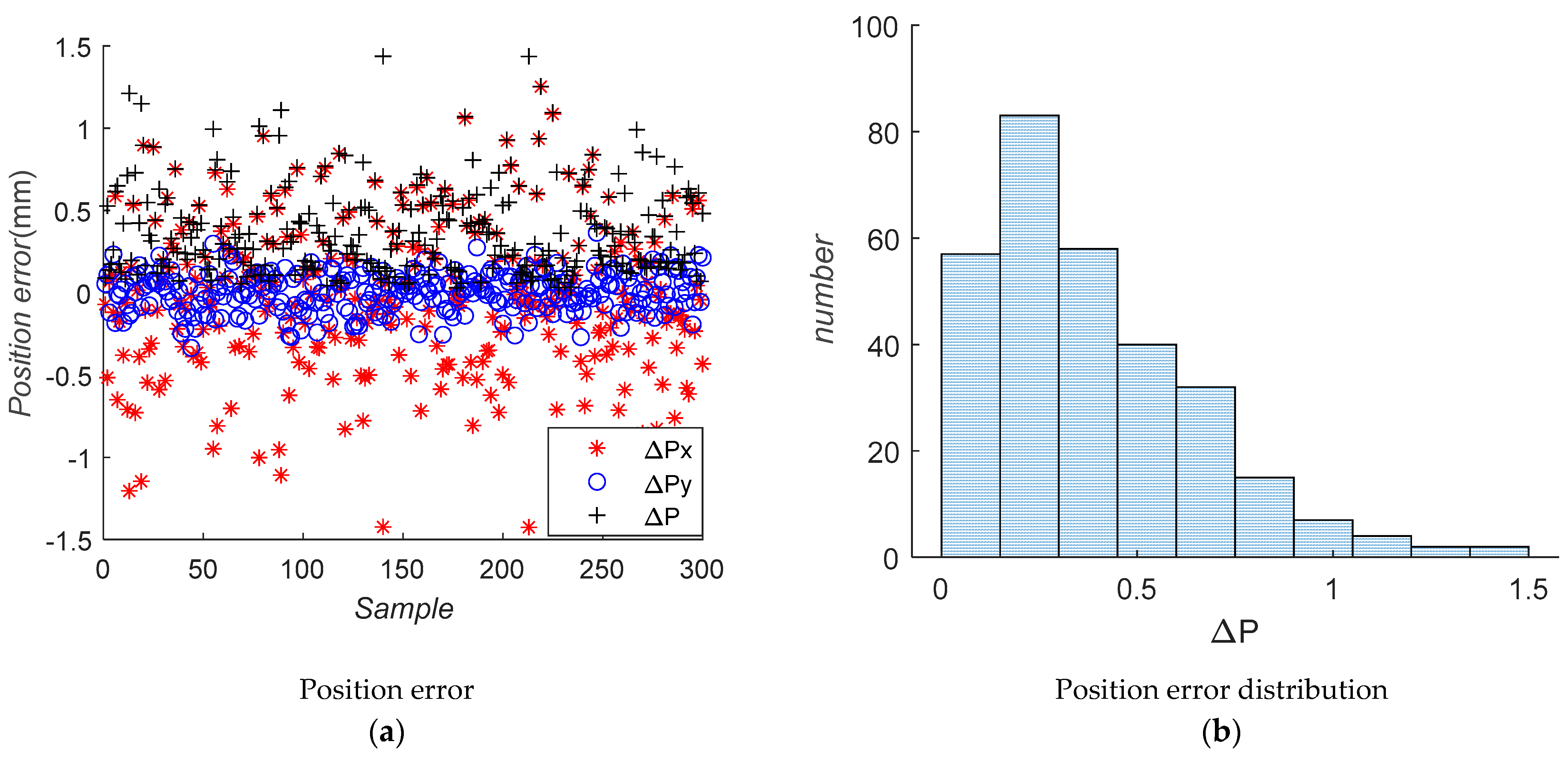
3. Error Analysis
4. Tolerance Assignment
5. Experiment and Verification
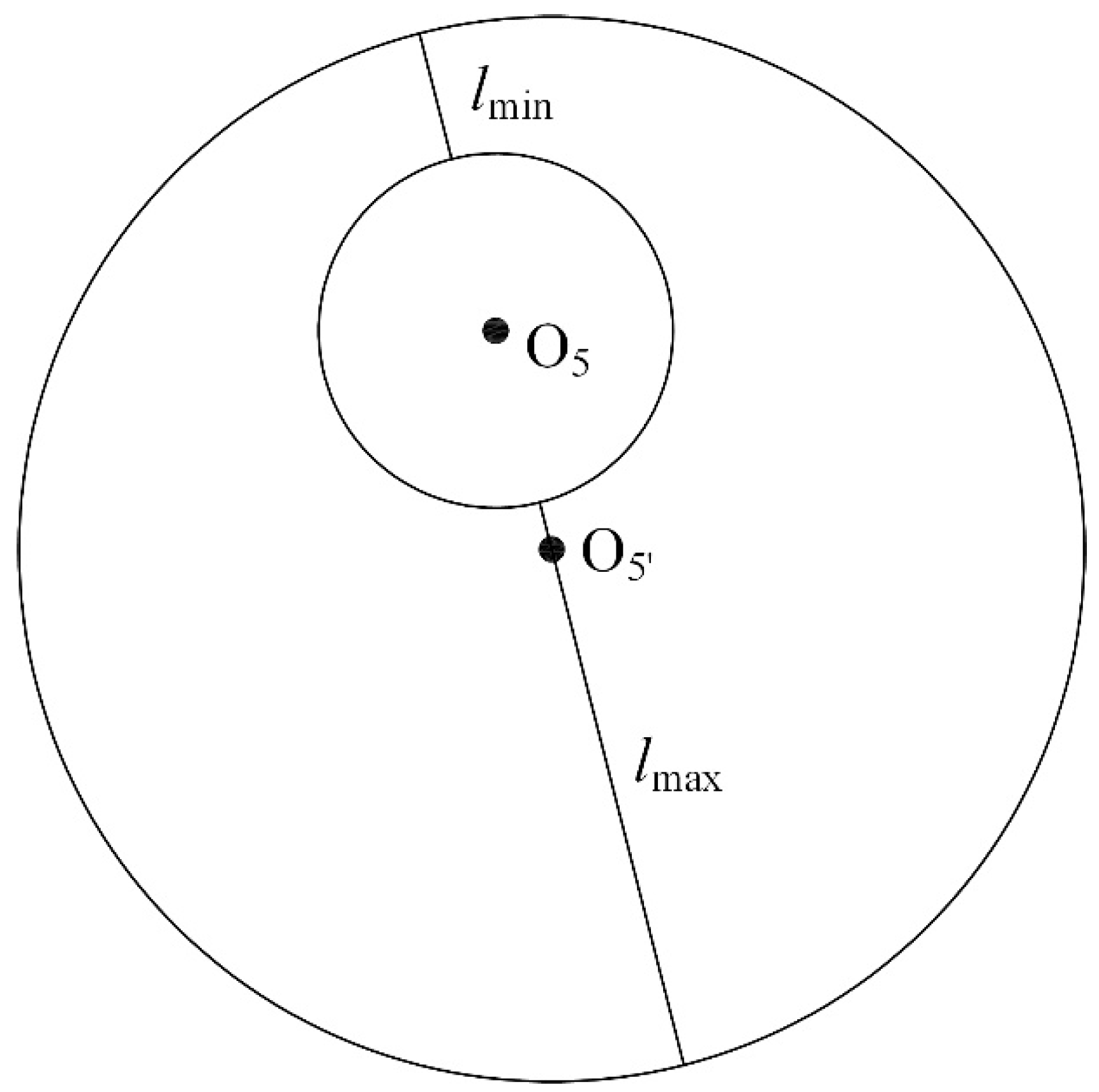
- Fix the micrometer on the outer edge of the nut sleeve;
- The micrometer rotates around the bolt;
- Record the maximum and minimum readings of the micrometer as lmax and lmin, respectively.
- Assemble the deep-water bolt flange automatic connection tool on land;
- Use the crane to put the deep-water bolt flange automatic connection tool into the pool, as shown in Figure 18a;
- Close the claw to hold the flange;
- Close the bolt magazine, nut magazine and tensioner magazine, as shown in Figure 18b;
- Adjust the position of the bolt magazine and the nut magazine to align the bolts and holes;
- Move the bolt magazine forward and make the bolts go through the flange bolt holes, as shown in Figure 18c;
- After the bolt magazine moves to the position, the nut magazine moves forward with the nut until the nuts contact the bolts; then, the motors rotate to tighten up the nuts, as shown in Figure 18d;
- Open the claw, bolt magazine, nut magazine and tensioner magazine; lift up the deep-water bolt flange automatic connection tool back to land by crane and the test is complete;
- Redo steps 1 to 8 10 times and record the results.
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Joint Number | Length Tolerance (mm) | Assembly Tolerance (mm) | Coaxiality Tolerance/Parallelism Tolerance (mm) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Grade of Tolerance | Grade of Tolerance | Grade of Tolerance | ||||||||
| f | m | IT5 | IT6 | IT7 | IT8 | IT5 | IT6 | IT7 | IT8 | |
| 1 | 0.600 | 1.600 | 0.050 | 0.080 | 0.120 | 0.200 | ||||
| 2 | 0.600 | 1.600 | 0.055 | 0.078 | 0.125 | 0.195 | 0.040 | 0.060 | 0.100 | 0.150 |
| 3 | 0.400 | 1.000 | 0.009 | 0.013 | 0.021 | 0.033 | 0.030 | 0.050 | 0.080 | 0.120 |
| 4 | 0.400 | 1.000 | 0.013 | 0.019 | 0.030 | 0.046 | 0.030 | 0.050 | 0.080 | 0.120 |
| 5 | 0.600 | 1.600 | 0.020 | 0.030 | 0.050 | 0.080 | ||||
| 1′ | 0.600 | 1.600 | 0.040 | 0.060 | 0.100 | 0.150 | ||||
| 2′ | 0.600 | 1.600 | 0.055 | 0.078 | 0.125 | 0.195 | 0.040 | 0.060 | 0.100 | 0.150 |
| 3′ | 0.400 | 1.000 | 0.011 | 0.016 | 0.025 | 0.039 | 0.030 | 0.050 | 0.080 | 0.120 |
| 4′ | 0.400 | 1.000 | 0.015 | 0.022 | 0.035 | 0.054 | 0.030 | 0.050 | 0.080 | 0.120 |
| 5′ | 0.300 | 0.600 | 0.010 | 0.015 | 0.025 | 0.040 | ||||
| Joint Number | Δdi (10−2 mm) | Δai (10−3 mm) | Δαi (10−6°) | Δθi (10−6°) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Grade of Tolerance | Grade of Tolerance | Grade of Tolerance | Grade of Tolerance | |||||||||||
| f | m | IT5 | IT6 | IT7 | IT8 | IT5 | IT6 | IT7 | IT8 | IT5 | IT6 | IT7 | IT8 | |
| 1 | 60 | 160 | 50 | 80 | 120 | 200 | 77 | 123 | 185 | 308 | 77 | 123 | 185 | 308 |
| 2 | 60 | 160 | 95 | 138 | 225 | 345 | 65 | 97 | 161 | 242 | 65 | 97 | 161 | 242 |
| 3 | 40 | 100 | 39 | 63 | 101 | 153 | 103 | 171 | 274 | 411 | 103 | 171 | 274 | 411 |
| 4 | 40 | 100 | 43 | 69 | 110 | 166 | 107 | 179 | 286 | 429 | 107 | 179 | 286 | 429 |
| 5 | 60 | 160 | 20 | 30 | 50 | 80 | 37 | 56 | 93 | 148 | 37 | 56 | 93 | 148 |
| 1′ | 60 | 160 | 40 | 60 | 100 | 150 | 80 | 120 | 200 | 300 | 80 | 120 | 200 | 300 |
| 2′ | 60 | 160 | 95 | 138 | 225 | 345 | 65 | 97 | 161 | 242 | 65 | 97 | 161 | 242 |
| 3′ | 40 | 100 | 41 | 66 | 105 | 159 | 80 | 133 | 213 | 320 | 80 | 133 | 213 | 320 |
| 4′ | 40 | 100 | 45 | 72 | 115 | 174 | 80 | 132 | 212 | 317 | 80 | 132 | 212 | 317 |
| 5′ | 30 | 60 | 10 | 15 | 25 | 40 | 83 | 125 | 209 | 333 | 83 | 125 | 209 | 333 |
References
- Wang, L.; Wei, Z.; Yao, S.; Guan, Y.; Li, S. Sealing Performance and Optimization of a Subsea Pipeline Mechanical Connector. Chin. J. Mech. Eng. 2018, 31, 1–14. [Google Scholar] [CrossRef]
- Yun, F.; Wang, G.; Yan, Z.; Jia, P.; Xu, X.; Wang, L.; Sun, H.; Liu, W. Analysis of Sealing and Leakage Performance of the Subsea Collet Connector with Lens-Type Sealing Structure. J. Mar. Sci. Eng. 2020, 8, 444. [Google Scholar] [CrossRef]
- Zhang, L.; Zhao, C.; Liu, M.; Ru, C.; Zhu, Z.; Wang, L.; Liu, H. Mechanics analysis and performance research of hermetic rubber barrel for large diameter submarine pipeline stopper used in deepwater environment. Polym. Test. 2019, 79, 106014. [Google Scholar] [CrossRef]
- Li, Z.; Lin, Q.; Zhao, D.; Wang, L. The structural design and optimization for the inner-frame of subsea flange connection tool. Key Eng. Mater. 2009, 419, 197–200. [Google Scholar] [CrossRef]
- Shang, Z.; Ruan, W.; Qiao, H.; Bai, Y. Study on risk assessment and numerical simulation method of subsea manifold system. Ships. Offshore Struct. 2021, 16, 245–255. [Google Scholar] [CrossRef]
- Bouchonneau, N.; Sauvant-Moynot, V.; Choqueuse, D.; Grosjean, F.; Poncet, E.; Perreux, D. Experimental testing and modelling of an industrial insulated pipeline for deep sea application. J. Pet. Sci. Eng. 2010, 73, 111–112. [Google Scholar] [CrossRef]
- Wang, L.; Wang, W.; He, N.; Li, W.; Lin, Q. Design and simulation analysis of deep-sea flange connection tool. J. Harbin Eng. Univ. 2010, 31, 559–563. [Google Scholar] [CrossRef]
- Alliot, V.; Frazer, I. Tie-in system uses low-cost flanges on deepwater Girassol development. Oil Gas J. 2002, 10, 96–104. [Google Scholar] [CrossRef]
- Jia, Z.; Ma, J.; Song, D.; Wang, F.; Liu, W. A review of contouring-error reduction method in multi-axis CNC machining. Int. J. Mach. Tools Manuf. 2018, 125, 34–54. [Google Scholar] [CrossRef]
- Zhang, J.; Ding, J.; Li, Q.; Jiang, Z.; Ding, Q.; Du, L.; Wang, W. A new contouring error estimation for the high form accuracy of a multi-axis CNC machine tool. Int. J. Adv. Manuf. Technol. 2019, 101, 1403–1421. [Google Scholar] [CrossRef]
- Yang, X.; Seethaler, R.; Zhan, C.; Lu, D.; Zhao, W. A Novel Contouring Error Estimation Method for Contouring Control. Mechatronics. IEEE/ASME Trans. Mechatron. 2019, 24, 1902–1907. [Google Scholar] [CrossRef]
- Yang, J.; Rao, P.; Chen, B.; Ding, H.; Ai, W. Form error on-line estimation and compensation for non-circular turning process. Int. J. Mech. Sci. 2020, 184, 105847. [Google Scholar] [CrossRef]
- Liu, Z.; Dong, J.; Wang, T.; Ren, C.; Guo, J. Real-time exact contour error calculation of NURBS tool path for contour control. Int. J. Adv. Manuf. Technol. 2020, 108, 2803–2821. [Google Scholar] [CrossRef]
- Zhang, D.; Chen, H.; Wang, Z.; Zhao, H.; Ding, H. Variable-parameter-model-based iterative pre-compensation method of the tracking error. Mech. Syst. Signal. Proc. 2021, 156, 107687. [Google Scholar] [CrossRef]
- Denavit, J.; Hartenberg, R. A kinematic notation for lower-pair mechanisms based on matrices. ASME J. Appl. Mech. 1955, 23, 215–221. [Google Scholar] [CrossRef]
- Zheng, D.; Fei, Y.; Hu, Y.; Yang, R. Research on the Spatial Error Distribution Model of Flexible Coordinate Measuring Machines Based on Support Vector Regression. Adv. Mater. Res. 2011, 201–203, 2058–2062. [Google Scholar] [CrossRef]
- Zheng, D. Research on spatial error model of flexible coordinate measuring machine. J Mech. Eng. 2010, 46, 19–25. [Google Scholar] [CrossRef]
- Cheng, D. Limit and fit. In Handbook of Mechanical Design, 5th ed.; Chemical Industry Press: Beijing, China, 2007; Volume 1, pp. 92–154. [Google Scholar]
- Gafurov, A.; Jeong, J.; Park, P.; Kim, I.; Phung, T.; Kim, H.C.; Kang, D.; Oh, D.; Lee, T. Registration error analysis and compensation of roll-to-roll screen printing system for flexible electronics. Flex. Print. Electron. 2021, 6, 024003. [Google Scholar] [CrossRef]
- Qi, X.; Peng, Q.; Zhao, C. A new method based on attitude quaternion matching for transfer alignment. J. Astronaut. 2011, 32, 81–87. [Google Scholar] [CrossRef]
- Shi, H.; Zhao, Y. Error correction design. In New Idea and Methods of Error Design; Science Press: Beijing, China, 2007; pp. 112–113. [Google Scholar]
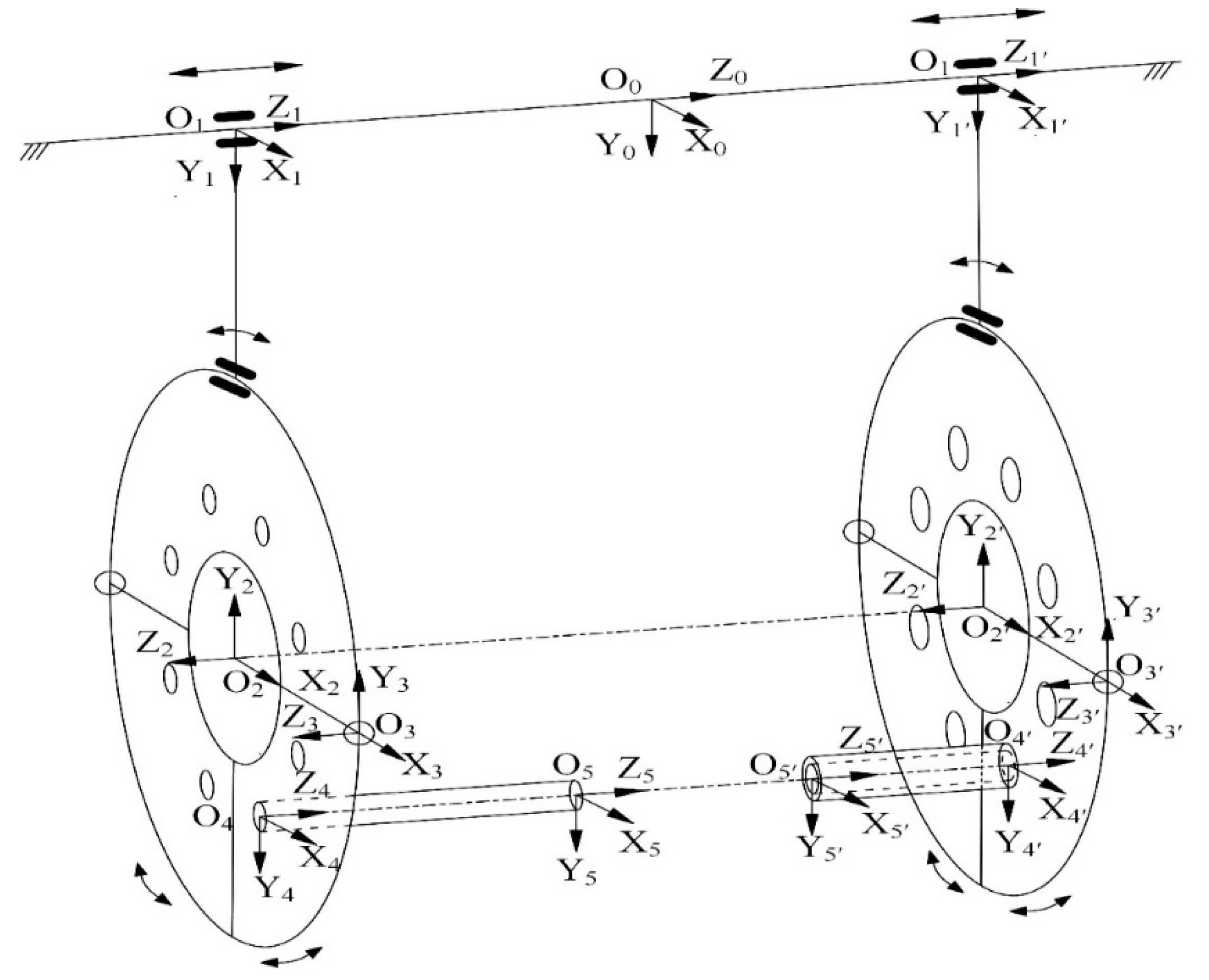
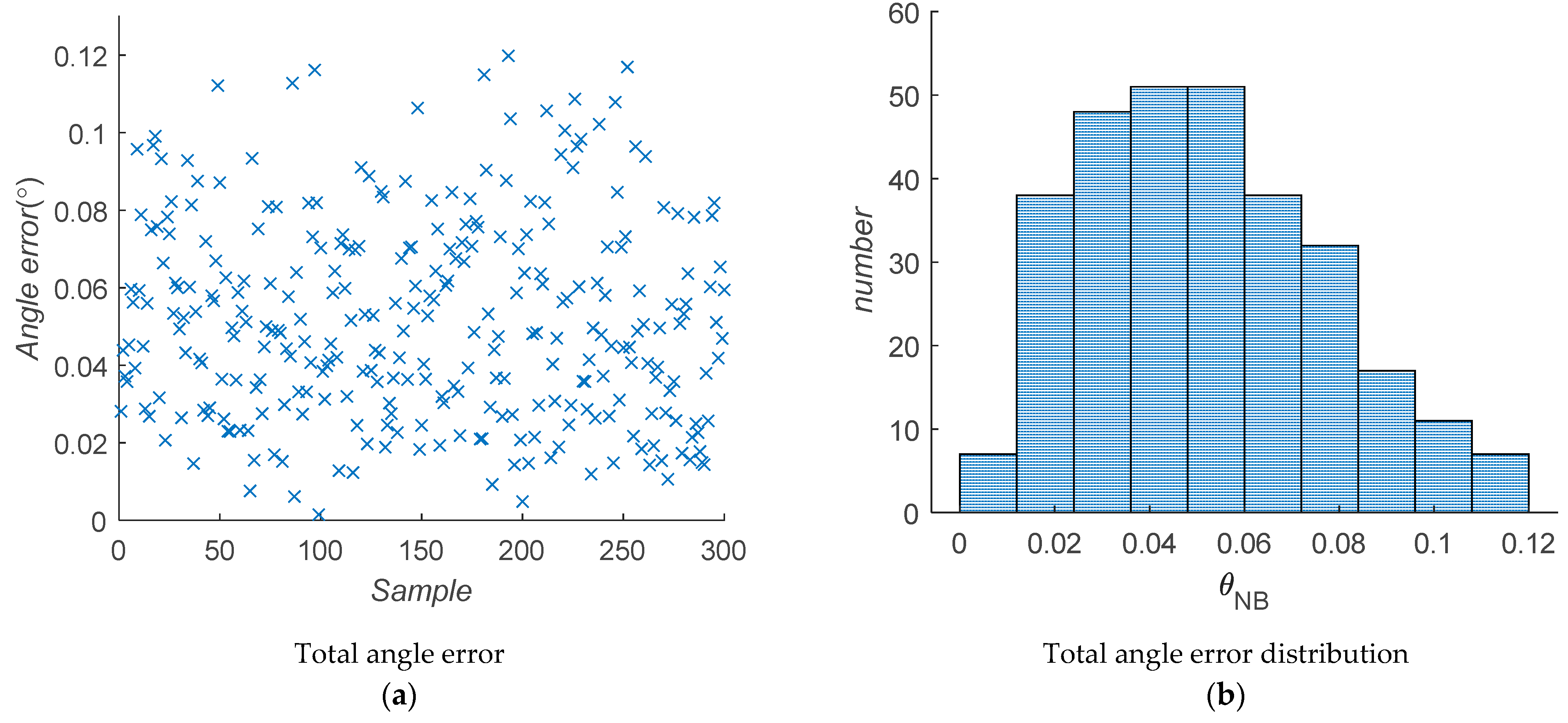








| i | ai (mm) | di (mm) | αi (°) | θi (°) |
|---|---|---|---|---|
| 1 | 0 | 650 | 0 | 0 |
| 2 | 0 | 0 | 180 | 0 |
| 3 | 292 | 0 | 0 | 0 |
| 4 | −222 | 0 | 180 | 0 |
| 5 | 0 | −540 | 0 | 0 |
| 1′ | 0 | −500 | 0 | 0 |
| 2′ | 0 | 0 | 180 | 0 |
| 3′ | 375 | 0 | 0 | 0 |
| 4′ | −305 | 0 | 180 | 0 |
| 5′ | 0 | 120 | 0 | 0 |
| Joint Number | Grade of Tolerance of Δdi | Grade of Tolerance of Δai | Grade of Tolerance of Δαi | Grade of Tolerance of Δθi |
|---|---|---|---|---|
| 1 | m | IT7 | IT 7 | IT 7 |
| 2 | m | IT 5 | IT 6 | IT6 |
| 3 | m | IT 5 | IT 6 | IT 6 |
| 4 | m | IT 5 | IT 6 | IT 6 |
| 5 | m | IT 5 | IT 6 | IT 6 |
| 1′ | m | IT 7 | IT 7 | IT 7 |
| 2′ | m | IT 5 | IT 6 | IT 6 |
| 3′ | m | IT 5 | IT 6 | IT 6 |
| 4′ | m | IT 5 | IT 6 | IT 6 |
| 5′ | m | IT 5 | IT 6 | IT 6 |
| Test No. | lmax (mm) | lmin (mm) | ΔP (mm) |
|---|---|---|---|
| 1 | 46.552 | 44.448 | 1.052 |
| 2 | 46.453 | 44.547 | 0.953 |
| 3 | 46.445 | 44.555 | 0.945 |
| 4 | 46.451 | 44.549 | 0.951 |
| 5 | 46.454 | 44.546 | 0.954 |
| 6 | 46.526 | 44.474 | 1.026 |
| 7 | 46.522 | 44.478 | 1.022 |
| 8 | 46.465 | 44.535 | 0.965 |
| 9 | 46.456 | 44.544 | 0.956 |
| 10 | 46.483 | 44.517 | 0.983 |
| 11 | 46.492 | 44.508 | 0.992 |
| 12 | 46.502 | 44.498 | 1.002 |
| 13 | 46.563 | 44.437 | 1.063 |
| 14 | 46.425 | 44.575 | 0.925 |
| 15 | 46.463 | 44.537 | 0.963 |
| 16 | 46.525 | 44.475 | 1.025 |
| 17 | 46.568 | 44.432 | 1.068 |
| 18 | 46.462 | 44.538 | 0.962 |
| 19 | 46.412 | 44.588 | 0.912 |
| 20 | 46.469 | 44.531 | 0.969 |
| Test Name | Test Times | Success Times | Success Rate |
|---|---|---|---|
| Land test | 20 | 20 | 100% |
| Pool test | 10 | 10 | 100% |
| Sea test | 1 | 1 | 100% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, P.; Gong, H.; Wang, L.; Yun, F.; Nan, Y.; Ju, M.; Li, C.; Wang, H.; Xu, K. Alignment Error Modelling, Analysis and Experiment of the Deep-Water Bolt Flange Automatic Connection Tool. J. Mar. Sci. Eng. 2022, 10, 64. https://doi.org/10.3390/jmse10010064
Wang P, Gong H, Wang L, Yun F, Nan Y, Ju M, Li C, Wang H, Xu K. Alignment Error Modelling, Analysis and Experiment of the Deep-Water Bolt Flange Automatic Connection Tool. Journal of Marine Science and Engineering. 2022; 10(1):64. https://doi.org/10.3390/jmse10010064
Chicago/Turabian StyleWang, Pengpeng, Haixia Gong, Liquan Wang, Feihong Yun, Yibo Nan, Ming Ju, Chao Li, Honghai Wang, and Kai Xu. 2022. "Alignment Error Modelling, Analysis and Experiment of the Deep-Water Bolt Flange Automatic Connection Tool" Journal of Marine Science and Engineering 10, no. 1: 64. https://doi.org/10.3390/jmse10010064
APA StyleWang, P., Gong, H., Wang, L., Yun, F., Nan, Y., Ju, M., Li, C., Wang, H., & Xu, K. (2022). Alignment Error Modelling, Analysis and Experiment of the Deep-Water Bolt Flange Automatic Connection Tool. Journal of Marine Science and Engineering, 10(1), 64. https://doi.org/10.3390/jmse10010064






