Generation of Gravity-Capillary Wind Waves by Instability of a Coupled Shear-Flow

Abstract

The theory of surface wave generation, in viscous flows, is modified by replacing the linear-logarithmic shear velocity profile, in the air, with a model which links smoothly the linear and logarithmic layers through the buffer layer. This profile includes the effects of air flow turbulence using a damped mixing-length model. In the water, an exponential shear velocity profile is used. It is shown that this modified and coupled shear-velocity profile gives a better agreement with experimental data than the coupled linear-logarithmic, non smooth profile, (in the air)–exponential profile (in the water), widely used in the literature. We also give new insights on retrograde modes that are Doppler shifted by the surface velocity at the air-sea interface, namely on the threshold value of the surface current for the occurrence of a second unstable mode.

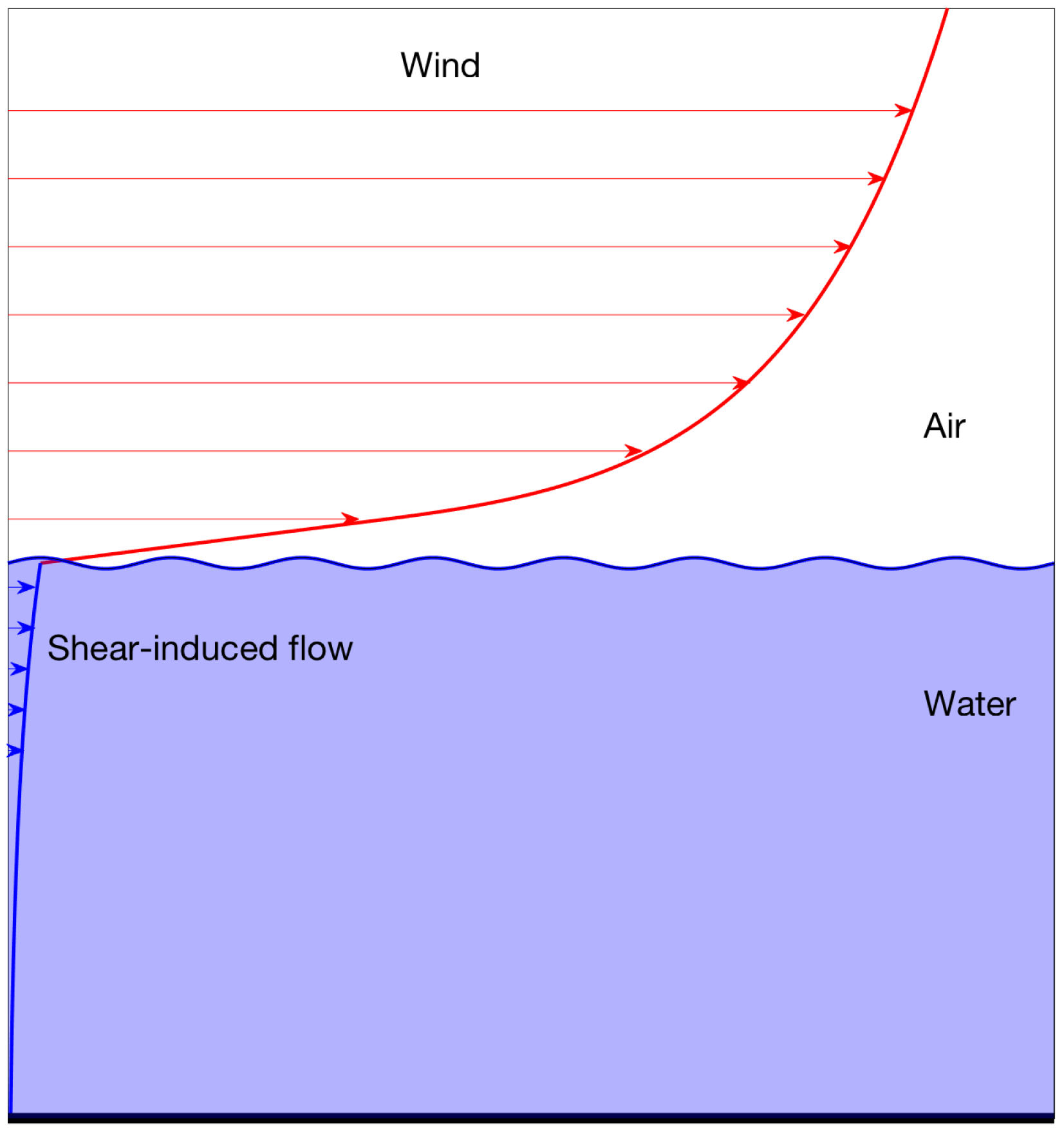
1. Introduction

An important literature has been devoted to the generation of gravity-capillary waves at the sea surface under the action of a turbulent wind. The occurrence of gravity-capillary waves has been considered theoretically as the stability of a viscous parallel shear flow of air over water. Note that several studies have considered inviscid fluids, too. For a review on can refer to the paper by [1]. In the present paper we focus attention on viscous fluids and take into account the shear-induced flow (Figure 1). Ref. [2] investigated the energy transfer from wind to short water waves through the viscous stress in the vicinity of the surface and neglected the shear flow in the water. He suggested that the generation of the short waves is due to a resonance mechanism between the water waves and the Tollmien-Schlichting waves occurring in the air shear flow. Within the framework of the Orr-Sommerfeld equation, ref. [3] investigated numerically the linear stability of the basic state composed of lin-log profiles in the water and in the air. He showed that the initial growth of the gravity-capillary wind waves is due to the linear instability of the parallel shear flow and that the water shear flow cannot be ignored. He found that the uncoupled model of Miles underestimates and overestimates the growth rate of waves of small and large wavenumbers, respectively. Ref. [4] carried out experimentally and numerically the study of the same problem. He found that the frequency and the growth rate of the gravity-capillary waves depend on the air friction velocity and do not depend on the fetch. The basic coupled shear flow, composed of the lin-log profile in the air and an analytic functional form for the velocity profile in the water initially proposed by [5], was investigated numerically by using the Orr-Sommerfeld equation. He claimed that the amplification of infinitesimal disturbances inevitably present in the flow is due the instability of the basic state. Ref. [6] used microwave backscatter based on the resonant Bragg scattering mechanism to measure experimentally at fixed fetch the growth rates of wind induced gravity-capillary waves. They found the growth rate does not depend on fetch. Furthermore, they proposed a power law for the growth rate depending only the wavenumber of the water waves and the friction velocity. Ref. [7] tackled the problem of the linear stability of the basic state using asymptotic methods to solve the Orr-Sommerfeld equation. They considered the lin-log velocity profile in the air and an exponential velocity profile in the water. They showed that the maximum growth rate is proportional to $u_{*a}^3$ where $u_{*a}$ is the air friction velocity. Note that [4] found that the maximum growth rate depends on $u_{*a}^{3.5}$. They concluded that the wave growth is mainly due to pressure work resulting from normal pressure perturbation of the air on the surface. Ref. [8] used a compound matrix method to integrate the Orr-Sommerfeld equation. To avoid the unphysical discontinuity of the second derivative of the velocity profile in the air existing in the previous models, they considered a velocity profile in the air with a smooth variation of the second derivative and an exponential velocity profile in the water. Note that the presence of discontinuities in the velocity profile in the air may be troublesome computationally. They emphasized the influence of the second derivative of the velocity profile in the air on the growth rate. As [7] they found that the growth rate of the gravity-capillary waves increases as $u_{*a}^3$. Ref. [9] extended numerically the stability of the coupled air-water shear flow investigated analytically by [7]. They used a lin-log velocity profile in the air and an exponential velocity profile in the water. Ref. [10] investigated numerically the temporal and spatial growth rates of short waves. They extended the results of previous studies to larger wavelengths (up to 20 cm) and stronger winds (up to $u_{*a}\sim 1 \mathrm{m}·{\mathrm{s}}^{-1}$). Their main finding is the occurrence of a second unstable mode when $u_{*a}>0.5 \mathrm{m}·{\mathrm{s}}^{-1}$. Our main purpose focuses on the occurrence condition of the second unstable mode discovered by [10]. In the present study, the theory of surface wave generation, in viscous flows, is modified by replacing the linear-logarithmic shear velocity profile, in the air, with the model proposed by [11] which links smoothly the linear and logarithmic layers through the buffer layer. This profile includes the effects of air flow turbulence using a damped mixing-length model. In the water, an exponential shear velocity profile is used. Note that [12] used the model proposed by van Driest to study wave generation by wind, but in the context of Miles’ theory, i.e. with inviscid flows and no current in the water. The paper is organized as follows. The mathematical model is presented in Section 2. Section 3 is devoted to the presentation of the velocity profiles in the air and in the water. A particular attention is paid to the velocity profile introduced by [11]. The developed numerical method and its validation are presented in Section 4. Finally, we present our main results in Section 5 and our conclusions are given in Section 6.

2. Mathematical Model

We consider the stability of a basic state $(U_0\left(z\right),P_0\left(z\right))$ to small perturbations $\mathbf{u}(x,z,t)=(u,w)$ and $p(x,z,t)$ where $U_0\left(z\right)$ is the mean velocity profile, $P_0\left(z\right)$ the static pressure, t the time, x and z the horizontal and vertical coordinates, respectively.

The continuity equation and the linearized Navier-Stokes equation read

$$\begin{array}{c}\hfill \frac{\partial u}{\partial x}+\frac{\partial w}{\partial z}=0\end{array}$$

(1)

$$\begin{array}{c}\hfill \frac{\partial u}{\partial t}+U_0\frac{\partial u}{\partial x}+w\frac{\partial U_0}{\partial z}=-\frac{1}{\rho }\frac{\partial p}{\partial x}+\nu (\frac{{\partial }^{2}u}{\partial x^2}+\frac{{\partial }^{2}u}{\partial z^2})\end{array}$$

(2)

$$\begin{array}{c}\hfill \frac{\partial w}{\partial t}+U_0\frac{\partial w}{\partial x}=-\frac{1}{\rho }\frac{\partial p}{\partial z}+\nu (\frac{{\partial }^{2}w}{\partial x^2}+\frac{{\partial }^{2}w}{\partial z^2})\end{array}$$

(3)

where $\rho$ and $\nu$ are the density and kinematic viscosity, respectively.

The solutions of the linearized problem are sought in the form

$$(u,w,p)=(u_1\left(z\right),w_1\left(z\right),p_1\left(z\right))exp\left[ik(x-ct)\right]$$

where k is the wavenumber of the perturbation and c its complex velocity. Note that the growth rate of the perturbation is ${\omega }_i=\Im \left(kc\right)$ and the energy growth rate is $\beta =2{\omega }_i$.

The system of Equations (1)–(3) gives

$$\begin{array}{c}\hfill ik{u}_1+\frac{d{w}_1}{dz}=0\end{array}$$

(4)

$$\begin{array}{c}\hfill ikW{u}_1+w_1\frac{dW}{dz}=-\frac{ik{p}_1}{\rho }+\nu (\frac{d^2{u}_1}{d{z}^2}-k^2{u}_1)\end{array}$$

(5)

$$\begin{array}{c}\hfill ikW{w}_1=-\frac{1}{\rho }\frac{d{p}_1}{dz}+\nu (\frac{d^2{w}_1}{d{z}^2}-k^2{w}_1)\end{array}$$

(6)

where $W=U_0\left(z\right)-c$.

After simple algebraic calculations the system of Equations (4)–(6) reduces to the following differential equation (Orr-Sommerfeld equation)

$$iW(\frac{d^2}{d{z}^2}-k^2)w_1-i\frac{d^{2}W}{d{z}^2}{w}_1=\frac{\nu }{k}\frac{d^4{w}_1}{d{z}^4}-2\nu k\frac{d^2{w}_1}{d{z}^2}+\nu k^3{w}_1$$

(7)

Note that the left-hand side of Equation (7) corresponds to the Rayleigh equation.

The system of differential equations to sove is

$$\begin{array}{c}\hfill \frac{{\nu }_a}{k}{(\frac{d^2}{d{z}^2}-k^2)}^2{w}_1=iW(\frac{d^2}{d{z}^2}-k^2)w_1-i\frac{d^{2}W}{d{z}^2}{w}_1\end{array}$$

(8)

$$\begin{array}{c}\hfill \frac{{\nu }_w}{k}{(\frac{d^2}{d{z}^2}-k^2)}^2{w}_1=iW(\frac{d^2}{d{z}^2}-k^2)w_1-i\frac{d^{2}W}{d{z}^2}{w}_1\end{array}$$

(9)

where the subscripts a and w refer to the air and water, respectively.

At frst-order, the amplitude $p_1$ of the wave pressure can be derived from the horizontal component of the linearized Navier-Stokes equation

$$p_1=\frac{\rho }{ik}(W\frac{d{w}_1}{dz}-w_1\frac{dW}{dz})+\frac{\mu }{k^2}(\frac{d^3{w}_1}{d{z}^3}-k^2\frac{d{w}_1}{dz})$$

(10)

where $\mu =\rho \nu$ is the dynamic viscosity.

Using a Taylor expansion about $z=0$, the first-order continuity condition for the normal stress at the interface $\eta (x,t)={\eta }_{1}exp\left[ik(x-ct)\right]$ reads

$$p(x,0+,t)-p(x,0-,t)=2{\mu }_a\frac{\partial w}{\partial z}(x,0+,t)-2{\mu }_w\frac{\partial w}{\partial z}(x,0-,t)+T\frac{{\partial }^2\eta }{\partial x^2}+({\rho }_a-{\rho }_w)g\eta$$

(11)

where T is the surface tension, g the acceleration due to gravity, ${\mu }_a={\rho }_a{\nu }_a$ and ${\mu }_w={\rho }_w{\nu }_w$.

The linearized kinematic boundary condition about $z=0$ is

$$(\frac{\partial }{\partial t}+U_s\frac{\partial }{\partial x})\eta =w$$

where $U_s=U_0\left(0\right)$.

From this equation one can derive

$${\eta }_1=\frac{w_1\left(0\right)}{ikW\left(0\right)}$$

(12)

with $W\left(0\right)=U_s-c$.

Combining Equations (10)–(12) gives in fine the first-order continuity condition for the normal stress at the interface

$${\rho }_a\left\{W\left(0\right)\left(W\left(0\right)w_1^{\prime }(0+)-W^{\prime }(0+)w_1\left(0\right)\right)+i{\nu }_a\frac{W\left(0\right)}{k}\left(w_1^{\prime \prime \prime }(0+)-3k^2{w}_1^{\prime }(0+)\right)-g{w}_1\left(0\right)\right\}=$$

$${\rho }_w\left\{W\left(0\right)\left(W\left(0\right)w_1^{\prime }(0-)-W^{\prime }(0-)w_1\left(0\right)\right)+i{\nu }_w\frac{W\left(0\right)}{k}\left(w_1^{\prime \prime \prime }(0-)-3k^2{w}_1^{\prime }(0-)\right)-G{w}_1\left(0\right)\right\}.$$

(13)

The prime denotes $d/dz$ and $G=g+T{k}^2$. Note that we can use $w_1\left(0\right)=ikW\left(0\right){\eta }_1$.

Using a Taylor expansion about $z=0$, the first-order continuity condition for the tangential stress at the interface reads

$${\mu }_a\left\{\frac{\partial w}{\partial x}(x,0+,t)+\frac{\partial }{\partial z}(u+\eta W^{\prime })(x,0+,t)\right\}={\mu }_w\left\{\frac{\partial w}{\partial x}(x,0-,t)+\frac{\partial }{\partial z}(u+\eta W^{\prime })(x,0-,t)\right\}$$

(14)

Using $u_1^{\prime }=-w_1^{\prime \prime }/\left(ik\right)$ the boundary condition at the interface for the tangentiel stress becomes

$${\mu }_a\left\{w_1\left(0\right)W^{\prime \prime }(0+)-W\left(0\right)\left(w_1^{\prime \prime }(0+)+k^2{w}_1\left(0\right)\right)\right\}=$$

$${\mu }_w\left\{w_1\left(0\right)W^{\prime \prime }(0-)-W\left(0\right)\left(w_1^{\prime \prime }(0-)+k^2{w}_1\left(0\right)\right)\right\}$$

(15)

The continuity of the vertical and horizontal components of fluid velocity at the interface reads

$$\begin{array}{c}\hfill w(x,0+,t)=w(x,0-,t)\\ \hfill u(x,0+,t)+\eta W^{\prime }(0+)=u(x,0-,t)+\eta W^{\prime }(0-)\end{array}$$

Using $u_1=-w_1^{\prime }/\left(ik\right)$ the fluid velocity continuity at the interface becomes

$$\begin{array}{c}\hfill w_1(0+)=w_1(0-)=w_1\left(0\right)\end{array}$$

(16)

$$\begin{array}{c}\hfill w_1^{\prime }(0+)W\left(0\right)-w_1\left(0\right)W^{\prime }(0+)=w_1^{\prime }(0-)W\left(0\right)-w_1\left(0\right)W^{\prime }(0-)\end{array}$$

(17)

Far from the interface all perturbations should vanish. Therefore

$$\underset{z\to \pm \infty }{lim}{w}_1\left(z\right)=0.$$

(18)

3. Velocity Profiles

The theoretical study of the generation of water waves by wind relies on the hypothesis that the mean velocities in the turbulent boundary layers (in the air and in the water) may be regarded as parallel shear flows (Figure 1). It is also well known that the results of instability studies are sensitive to the velocity profile shape. In this section, details concerning the mean flows used, herein, in the air and in the water are given.

3.1. Air Profiles

The exact mean turbulent profile above water waves is not well known. As infinitesimal waves are studied, it is a good approximation to consider mean flow profiles above flat plates. Two profiles have retained our attention, the lin-log profile and the damped mixing-length profile.

3.1.1. The Lin-Log Profile

The widely used velocity profile, for water wave generation by wind, is called the lin-log profile. It is linear in a viscous sublayer and is asymptotically logarithmic far from the interface. The lin-log velocity profile, used in previous studies, reads ([10]):

$$U_a=\left\{\begin{array}{cc}{U}_s+\frac{u_{*}^2}{{\nu }_a}z,\hfill & 0\le z\le z_1,\hfill \\ U_s+m{u}_{*}+\frac{u_{*}}{\kappa }\left[\alpha -tanh\left(\frac{\alpha }{2}\right)\right],\hfill & z\ge z_1\hfill \end{array}\right.$$

(19)

$$\alpha ={sinh}^{-1}\left(\beta \right),\beta =\frac{2\kappa u_{*}}{{\nu }_a}\left(z-z_1\right),z_1=\frac{m{\nu }_a}{u_{*}},U_s=B{u}_{*},m=5,B=0.5.$$

(20)

3.1.2. The Mixing-Length Profile

For a boundary layer in the air, according to the Prandtl mixing length hypothesis, the total shear stress near the air-sea interface is

$$\frac{{\tau }_a\left(z\right)}{{\rho }_a}={\nu }_a\frac{\partial U_a}{\partial z}+{\nu }_T\frac{\partial U_a}{\partial z},$$

(21)

where ${\nu }_T$ is the turbulent viscosity given by ${\nu }_T={\ell }_m\partial U_a/\partial z$ and ${\ell }_m\left(z\right)$ is the mixing length. Using the following normalisations:

$$U_a^{+}=U_a/u_{*},z^{+}=u_{*}z/{\nu }_a{\tau }^{+}={\tau }_a/\left({\rho }_a{u}_{*}^2\right),{\ell }_m^{+}=u_{*}{\ell }_m/{\nu }_a,$$

(22)

the total shear stress reads

$$\frac{{\tau }_a\left(z\right)}{{\tau }_a^{+}}=\frac{\partial U_a^{+}}{\partial z^{+}}+{\left({\ell }_m\frac{\partial U_a^{+}}{\partial z^{+}}\right)}^2.$$

(23)

The solution of this quadratic equation for $\partial U_a^{+}/\partial z^{+}$ is

$$\frac{\partial U_a^{+}}{\partial z^{+}}=\frac{2{\tau }_a/{\tau }_a^{+}}{1+{[1+(4{\tau }_a/{\tau }_a^{+}){\left({\ell }_m^{+}\right)}^2]}^{(1/2)}}.$$

(24)

Near the air-sea interface, the ratio ${\tau }_a\left(z\right)/{\tau }_a^{+}$ is practically unity so that

$$U_a^{+}\left(z^{+}\right)={\int }_0^{z^{+}}\frac{2}{1+\sqrt{1+4{\ell }_m^{+}{\left(z^{\prime }\right)}^2}}d{z}^{\prime }.$$

(25)

For large $z^{+}$, where viscosity effect is small, the mixing length is ${\ell }_m^{+}=\kappa z^{+}$ and the log law is recovered when constant terms in the integrand denominator are neglected in the limit $z^{+}⟶+\infty$. If the same specification for the mixing length is used near the air-sea interface (in the viscous sublayer) considered as rigid (a wall), the resulting turbulent stress ${\nu }_T\partial U_a/\partial z$ will increase as $z^2$, whereas the Reynolds stress $-\langle uw\rangle$ increases more slowly, as $z^3$ ([13]). Therefore, the specification ${\ell }_m=\kappa z$ needs to be damped near the interface and [11] proposed

$${\ell }_m^{+}\left(z^{+}\right)=\kappa \left[1-exp(-z^{+}/A^{+})\right],$$

(26)

where $A^{+}$ is a constant attributed the value $A^{+}=26$.

The van Driest and the lin-log velocity profiles are compared in Figure 2 together with experimental data from [14] and direct numerical-simulation results from [15]. The law of the wall is also shown. Normalised coordinate $z^{+}$ and velocity $U_a+$ are used. The different profiles are practically undistinguishable for $z^{+}\le 10$. However, It is clear that the van Driest profile fits better with experimental data and numerical simulations than the lin-log profile for $z^{+}>10$. Furthermore, the main advantage of the van Driest profile is the fact that it is infinitely derivable, i.e., ${\mathcal{C}}^{\infty }$, contrarily to the lin-log profile who is piecewise defined and hence not infinitely derivable. This is shown in Figure 3.

3.2. Water Profile

Many velocity profiles have been used in the water, in previous studies, and are reported in Figure 1 of [7]. Among them the exponential profile has retained our attention because it resembles experimental observations ([4]) and because it allows for exact solution of the Rayleigh equation that will be used below to compute sheared gravity-capillary wave speeds. In the water, the current profile is ([10])

$$U_w\left(z\right)=U_{s}exp\left(\frac{{\rho }_a{u}_{*}^2}{U_s{\mu }_w}z\right),z<0.$$

(27)

4. Numerical Method and Validation

The differential Equation (7) and boundary conditions (13) and (15)–(18) are transformed into an algebraic system of equations using a spectral Tau approximation method [16]. This algebraic system of equations is solved numerically for $w_1$ and c for a given wavenumber k. Note that the algebraic system is nonlinear in c due to the boundary condition (13). Therefore, the Levenberg-Marquardt method [17] is used and computations are stopped when the residual is $O\left({10}^{-12}\right)$. We also used the Broyden method [18]. The boundary conditions at infinity are enforced at $z_{\pm \infty }=\pm 1.6\lambda$ where $\lambda =2\pi /k$ is the reference wavelength [10]. This choice corresponds to $k{z}_{\pm \infty }\simeq \pm 10$. We have checked that doubling $z_{\pm \infty }$ does not affect significantly the results. The obtained results are validated by (a) the self consistency of the results from Levenberg-Marquardt and Broyden methods and (b) by comparisons with already published results in the literature obtained with the lin-log velocity profile in the air. The sum up of these comparisons is given in Figure 4.

5. Results

5.1. Prograde Unstable Modes

Using the above described Orr-Sommerfeld equations, and the appropriate boundary conditions, we have computed the maximum energy growth rate, $\beta$, for wavenumbers in the range $1<k<9 \left({\mathrm{cm}}^{-1}\right)$, and for different values of the friction velocity $u_{*}$. In this paragraph waves travelling with the wind (waves with positive intrinsic phase speeds) are considered. The results are presented in Figure 5 for the lin-log profile and the van Driest profile in the air and exponential profile in the water. The results from [4] are also reported. The agreement using the van Driest profile is better than that obtained with the lin-log profile. This fact could be justified by inspection of the comparison of the different velocity profiles presented in Figure 2. Indeed, the lin-log profile departs from the other profiles far from the air-water interface. Besides, the van Driest profile is infinitely derivable and this fact is an advantage for numerical computations.

5.2. Retrograde Unstable Modes (Second Mode)

Ref. [1] have pointed out the existence of a second unstable mode, called rippling mode, in the context of inviscid fluids (using the Rayleigh equations). The maximum growth rate they obtained is $O(1 {\mathrm{s}}^{-1})$ for $k=O(4 {\mathrm{cm}}^{-1})$. Noting that for these values ${\nu }_a{k}^2=O(2.4 {\mathrm{s}}^{-1})$, the second mode will be obviously damped by viscosity in the context of Orr-Sommerfeld equations. Ref. [10] have also discovered a second mode in the context of viscous flows when the air friction velocity is larger than 50 cm ${\mathrm{s}}^{-1}$. In both cases, the second modes are retrograde modes (waves with negative intrinsic phase velocity) that are Doppler shifted by the surface velocity $U_s$ in the wind direction (positive phase velocity). Therefore, a necessary condition for their occurrence is

$$c_0\ge 0\mathrm{and}{c}_0-U_s\le 0,$$

(28)

where $c_0$ should be the sheared gravity-capillary wave speed in the laboratory frame. Ref. [10] have found a minimum value $u_{*}\simeq$50 cm ${\mathrm{s}}^{-1}$ corresponding to $\lambda \simeq 3$ cm for the occurrence of the second mode. However, they used the gravity-capillary wave speed

$$c_0=U_s\pm \sqrt{\frac{g}{k}+\gamma k},\gamma =\frac{T}{{\rho }_a},$$

(29)

and not the sheared gravity-capillary one, as it should be, to justify these values (in their Figure 13). Retrograde waves correspond to the minus sign before the square root. In the present study, we use the sheared gravity-capillary wave speed given by Equation (6.3) of [1] to predict the critical values. Note that this equation presents a typo that we have corrected. The corrected equation reads (with $U_s>0$ as it is the wind-induced surface drift),

$$c_0=U_s\left[1-\frac{1}{2\sqrt{1+{\left(h_{w}k\right)}^2}}\pm \sqrt{\frac{\left(g{h}_w\right)/U_s^2+(\gamma /{\left(h_w{U}_s\right)}^2){\left(h_{w}k\right)}^2}{\sqrt{1+{\left(h_{w}k\right)}^2}}+\frac{1}{4(1+{\left(h_{w}k\right)}^2)}}\right],$$

(30)

and it is valid for gravity-capillary waves propagating on an exponential velocity profile in the water of the form $exp(z/h_w)$, where $h_w$ is the characteristic shear length. In the present study the characteristic shear length depends on air density, friction velocity (or equivalently on the surface velocity $U_s$) and water viscosity. By inspection of Equation (27) we have

$$h_w\left(U_s\right)=\frac{{\mu }_w}{4{\rho }_a{U}_s}.$$

Therefore, we obtain the following implicit equation for $U_s$ to satisfy the necessary condition of the occurrence of the second mode:

$$U_s=\sqrt{\left(\frac{g}{k}+\gamma k\right)\left(\frac{4({\rho }_a/{\rho }_w)U_s}{{\nu }_{w}k}+\sqrt{\left(1+{\left(\frac{4({\rho }_a/{\rho }_w)U_s}{{\nu }_{w}k}\right)}^2\right)}\right)},$$

(31)

and the corresponding friction velocity is

$$u_{*}=2U_s,$$

with in cgs units: $g=981;\gamma =75;{\mu }_w={10}^{-2};$${\rho }_a=1.23{10}^{-3}$. The Newton method is used to solve the implicit Equation (31) and the results are given in Figure 6 using $\lambda =2\pi /k$ where $\lambda$ is the wavelength. By inspection of this figure, the minimum friction velocity for the occurrence of the second mode is $u_{*}\simeq 160$ cm ${\mathrm{s}}^{-1}$ corresponding to $\lambda \simeq 0.35$ cm. Indeed, using the van Driest velocity profile in the air and the exponential profile in the water, we have found no second mode for as high values of $u_{*}$ as 124 cm ${\mathrm{s}}^{-1}$ (the highest value studied experimentally by [6]). Ref. [8] have emphasized the sensitivity of the growth rate to the curvature of the air velocity profile. Note that this fact does not call into question the existence of the second mode.

6. Conclusions

We studied surface wave generation by wind in viscous flows. We focused on gravity-capillary waves. Our main purpose was to use air velocity profile that avoids the inherent discontinuity of the second derivative of the lin-log profile. That is why we have considered the van Driest profile which links smoothly through the buffer layer the linear and logarithmic layers. Our numerical computations of the rate of growth of the gravity-capillary waves, with the van Driest profile, are in better agreement with the experimental data of [4] than those calculated with the lin-log profile.

Besides the unstable mode which occurs whatever the investigated values of the air friction velocity, ref. [10] discovered a new additional unstable mode for strong winds when the air friction velocity is larger than approximately 50 cm ${\mathrm{s}}^{-1}$. We have developed eigenvalue computations until 124 cm ${\mathrm{s}}^{-1}$ (the highest value studied experimentally by [6] and did not find second mode instability using the van Driest profile. A theoretical approach, based on the linear dispersion relation of gravity-capillary waves travelling on an exponential current, showed that the threshold value is close to 160 cm ${\mathrm{s}}^{-1}$ whereas it is close to 50 cm ${\mathrm{s}}^{-1}$ for a constant current. This gap is probably due to the sensitivity of the growth rate to the profiles used as mentioned by previous authors.