Automating the Acoustic Detection and Characterization of Sea Ice and Surface Waves
Abstract
:1. Introduction
1.1. Overview and Rationale
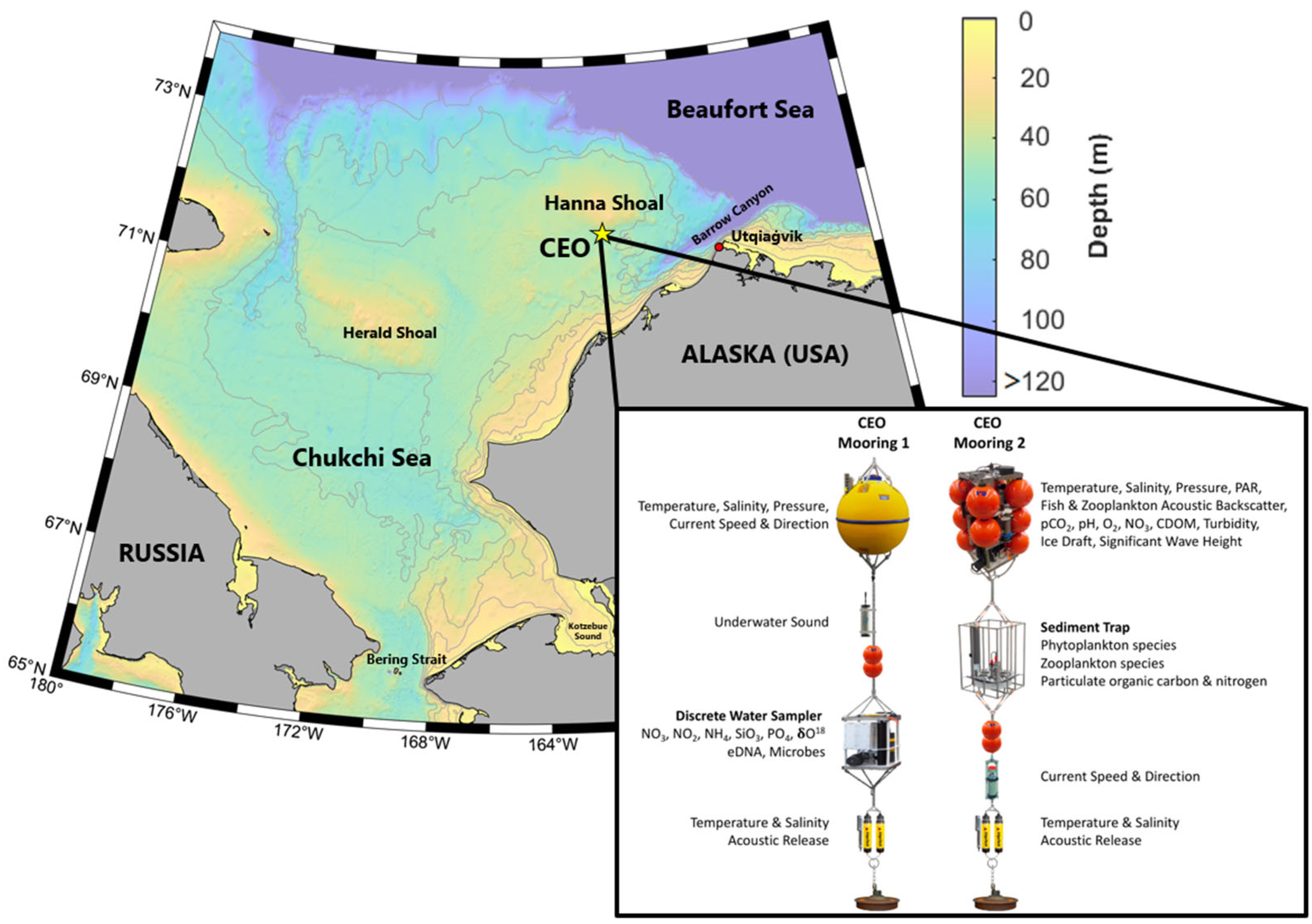
1.2. Environmental Setting
1.3. Acoustic Detection of Sea Ice from Below
2. Materials and Methods
2.1. Data
2.2. Locating the Acoustic Reflection

2.3. Self-Organizing Map
2.4. Automating the Construction of
3. Results
3.1. Acoustic Reflection Characteristics
3.2. Statistics of the Return Echoes
3.3. Delineating Sea Ice and Open Water with SOM Analysis





3.4. The Surface Wave Field

4. Discussion

5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pachauri, R.K.; Allen, M.R.; Barros, V.R.; Broome, J.; Cramer, W.; Christ, R.; Church, J.A.; Clarke, L.; Dahe, Q.; Dasgupta, P.; et al. Climate Change 2014: Synthesis Report; Contribution of Working Groups I, II and III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change/R; Pachauri, R.K., Meyer, L., Eds.; IPCC: Geneva, Switzerland, 2014; 151p, ISBN 978-92-9169-143-2. [Google Scholar]
- Woodgate, R.A.; Weingartner, T.; Lindsay, R. The 2007 Bering Strait oceanic heat flux and anomalous Arctic sea-ice retreat. Geophys. Res. Lett. 2010, 37, L01602. [Google Scholar] [CrossRef] [Green Version]
- Carmack, E.C.; Yamamoto-Kawai, M.; Haine, T.W.; Bacon, S.; Bluhm, B.A.; Lique, C.; Melling, H.; Polyakov, I.V.; Straneo, F.; Timmermans, M.L.; et al. Freshwater and its role in the Arctic Marine System: Sources, disposition, storage, export, and physical and biogeochemical consequences in the Arctic and global oceans. J. Geophys. Res. Biogeosci. 2016, 121, 675–717. [Google Scholar] [CrossRef] [Green Version]
- Meier, W.N.; Hovelsrud, G.K.; Van Oort, B.E.H.; Key, J.R.; Kovacs, K.M.; Michel, C.; Haas, C.; Granskog, M.A.; Gerland, S.; Perovich, D.K.; et al. Arctic sea ice in transformation: A review of recent observed changes and impacts on biology and human activity. Rev. Geophys. 2014, 51, 185–217. [Google Scholar] [CrossRef]
- Stroeve, J.C.; Serreze, M.C.; Holland, M.M.; Kay, J.E.; Malanik, J.; Barrett, A.P. The Arctic’s rapidly shrinking sea ice cover: A research synthesis. Clim. Chang. 2012, 110, 1005–1027. [Google Scholar] [CrossRef] [Green Version]
- Grebmeier, J.M.; Cooper, L.W.; Feder, H.M.; Sirenko, B.I. Ecosystem dynamics of the Pacific-influenced Northern Bering and Chukchi Seas in the Amerasian Arctic. Prog. Oceanogr. 2006, 71, 331–361. [Google Scholar] [CrossRef]
- Danielson, S.L.; Ahkinga, O.; Ashjian, C.; Basyuk, E.; Cooper, L.W.; Eisner, L.; Farley, E.; Iken, K.B.; Grebmeier, J.M.; Juranek, L.; et al. Manifestation and consequences of warming and altered heat fluxes over the Bering and Chukchi Sea continental shelves. Deep-Sea Res. Part II Top. Stud. Oceanogr. 2020, 177, 104781. [Google Scholar] [CrossRef]
- Woodgate, R.A.; Aagaard, K.; Weingartner, T.J. A year in the physical oceanography of the Chukchi Sea: Moored measurements from autumn 1990–1991. Deep-Sea Res. Part II Top. Stud. Oceanogr. 2005, 52, 3116–3149. [Google Scholar] [CrossRef]
- Lu, K.; Danielson, S.; Hedstrom, K.; Weingartner, T. Assessing the role of oceanic heat fluxes on ice ablation of the central Chukchi Sea shelf. Prog. Oceanogr. 2020, 184, 102313. [Google Scholar] [CrossRef]
- Fang, Y.C.; Weingartner, T.J.; Dobbins, E.L.; Winsor, P.; Statscewich, H.; Potter, R.A.; Mudge, T.D.; Stoudt, C.A.; Borg, K. Circulation and thermohaline variability of the Hanna Shoal region on the northeastern Chukchi Sea shelf. J. Geophys. Res. Oceans 2020, 125, e2019JC015639. [Google Scholar] [CrossRef]
- Carmack, E.; Wassmann, P. Food webs and physical-biological coupling on pan-Arctic shelves: Unifying concepts and comprehensive perspectives. Prog. Oceanogr. 2006, 71, 446–477. [Google Scholar] [CrossRef]
- Weingartner, T.; Aagaard, K.; Woodgate, R.; Danielson, S.; Sasaki, Y.; Cavalieri, D. Circulation on the north central Chukchi Sea shelf. Deep-Sea Res. Part II Top. Stud. Oceanogr. 2005, 52, 3150–3174. [Google Scholar] [CrossRef]
- Walsh, J.J.; McRoy, C.P.; Coachman, L.K.; Goering, J.J.; Nihoul, J.J.; Whitledge, T.E.; Blackburn, T.H.; Parker, P.L.; Wirick, C.D.; Shuert, P.G.; et al. Carbon and nitrogen cycling within the Bering/Chukchi Seas: Source regions for organic matter effecting AOU demands of the Arctic Ocean. Prog. Oceanogr. 1989, 22, 277–359. [Google Scholar] [CrossRef]
- Hennon, T.D.; Danielson, S.L.; Woodgate, R.; Irving, B.; Stockwell, D.; Mordy, C. Mooring measurements of Anadyr Current nitrate, phosphate, and silicate enable updated Bering Strait nutrient flux estimates. Geophys. Res. Lett. 2022, 49, e2022GL098908. [Google Scholar] [CrossRef]
- Grebmeier, J.M.; McRoy, C.P.; Feder, H.M. Pelagic-benthic coupling on the shelf of the northern Bering and Chukchi Seas. I. Food supply source and benthic biomass. Mar. Ecol. Prog. Ser. 1988, 48, 57–67. [Google Scholar] [CrossRef]
- Codispoti, L.A.; Flagg, C.; Kelly, V.; Swift, J.H. Hydrographic conditions during the 2002 SBI process experiments. Deep-Sea Res. Part II Top. Stud. Oceanogr. 2005, 52, 3199–3226. [Google Scholar] [CrossRef]
- Mahoney, A.R.; Eicken, H.; Fukamachi, Y.; Ohshima, K.I.; Simizu, D.; Kambhamettu, C.; Rohith, M.V.; Hendricks, S.; Jones, J. Taking a look at both sides of the ice: Comparison of ice thickness and drift speed as observed from moored, airborne and shore-based instruments near Barrow. Alaska Ann. Glaciol. 2015, 56, 363–372. [Google Scholar] [CrossRef] [Green Version]
- Fukamachi, Y.; Simizu, D.; Ohshima, K.I.; Eicken, H.; Mahoney, A.R.; Iwamoto, K.; Moriya, E.; Nihashi, S. Sea-ice thickness in the coastal northeastern Chukchi Sea from moored ice-profiling sonar. J. Glaciol. 2017, 63, 888–898. [Google Scholar] [CrossRef] [Green Version]
- Barrett, S.A.; Stringer, W.J. Growth Mechanisms of “Katie’s Floeberg”. Arct. Alp. Res. 1978, 10, 775–783. [Google Scholar] [CrossRef]
- Grebmeier, J.M.; Bluhm, B.A.; Cooper, L.W.; Danielson, S.L.; Arrigo, K.R.; Blanchard, A.L.; Clarke, J.T.; Day, R.H.; Frey, K.E.; Gradinger, R.R.; et al. Ecosystem characteristics and processes facilitating persistent microbenthic biomass hotspots and associated benthivory in the Pacific Arctic. Prog. Oceanogr. 2015, 136, 92–114. [Google Scholar] [CrossRef]
- Jay, C.V.; Fischbach, A.S.; Kochnev, A.A. Walrus areas of use in the Chukchi Sea during sparse sea ice cover. Mar. Ecol. Prog. Ser. 2012, 468, 1–13. [Google Scholar] [CrossRef]
- Iken, K.; Mueter, F.; Grebmeier, J.M.; Cooper, L.W.; Danielson, S.L.; Bluhm, B.A. Developing an observational design for epibenthos and fish assemblages in the Chukchi Sea. Deep-Sea Res. Part II Top. Stud. Oceanogr. 2019, 162, 180–190. [Google Scholar] [CrossRef]
- Danielson, S.L.; Iken, K.; Hauri, C.; Hopcroft, R.R.; McDonnell, A.M.P.; Winsor, P.; Lalande, C.; Grebmeier, J.M.; Cooper, L.W.; Horne, J.K.; et al. Collaborative approaches to multi-disciplinary monitoring of the Chukchi shelf marine ecosystem: Networks of networks for maintaining long-term Arctic observations. In Proceedings of the Oceans 2017—Anchorage, Anchorage, AK, USA, 18–21 September 2017. [Google Scholar]
- Hauri, C.; Danielson, S.; McDonnell, A.M.P.; Hopcroft, R.R.; Winsor, P.; Shipton, P.; Lalande, C.; Stafford, K.M.; Horne, J.K.; Cooper, L.W.; et al. From sea ice to seals: A moored marine ecosystem observatory in the Arctic. Ocean Sci. 2018, 14, 1423–1433. [Google Scholar] [CrossRef] [Green Version]
- McCammon, M. Arctic Build-Out Plan 2013, Alaska Ocean Observing System; Alaska Ocean Observing System: Anchorage, AK, USA, 2013; 8p.
- Lalande, C.; Grebmeier, J.M.; Hopcroft, R.R.; Danielson, S.L. Annual cycle of export fluxes of biogenic matter near Hanna Shoal in the northeast Chukchi Sea. Deep-Sea Res. Part II Top. Stud. Oceanogr. 2020, 177, 104730. [Google Scholar] [CrossRef]
- Birch, R.; Fissel, D.; Melling, H.; Vaudrey, K.; Lamb, W.; Schaudt, K.; Heideman, J. Ice-profiling sonar. Sea Technol. 2000, 41, 48–54. [Google Scholar]
- Melling, H.; Johnston, P.H.; Riedel, D.A. Measurements of the underside topography of sea ice by moored subsea sonar. J. Atmos. Ocean. Technol. 1995, 12, 589–602. [Google Scholar] [CrossRef]
- Strass, V.H. Measuring sea ice draft and coverage with moored upward looking sonars. Deep-Sea Res. Part I 1998, 45, 795–818. [Google Scholar] [CrossRef]
- Kvambekk, Å.S.; Vinje, T. Ice Draft Recordings from Upward Looking Sonars (ULSs) in the Fram Strait and the Barents Sea in 1987/88 and 1990/91; Norsk Polarinstitutt Rapportse; Norwegian Polar Research Institute: Oslo, Norway, 1992; Volume 79. [Google Scholar]
- Krishfield, R.A.; Proshutinsky, A.; Tateyama, K.; Williams, W.J.; Carmack, E.C.; McLaughlin, F.A.; Timmermans, M.-L. Deterioration of perennial sea ice in the Beaufort Gyre from 2003 to 2012 and its impact on the oceanic freshwater cycle. J. Geophys. Res. Oceans 2014, 119, 1271–1305. [Google Scholar] [CrossRef]
- Melling, H. Sound scattering from sea ice: Aspects relevant to ice-draft profiling by sonar. J. Atmos. Ocean Technol. 1998, 15, 1023–1034. [Google Scholar] [CrossRef]
- Jezek, K.C.; Stanton, T.K.; Gow, A.J.; Lange, M.A. Influence of environmental conditions on acoustical properties of sea ice. J. Acoust. Soc. 1990, 88, 1903–1912. [Google Scholar] [CrossRef]
- Light, B.; Maykut, G.A.; Grenfell, T.C. Effects of temperature on the microstructure of first-year Arctic sea ice. J. Geophys. Res. 2003, 108, 3051. [Google Scholar] [CrossRef]
- Onana, V.; Kurtz, N.T.; Farrell, S.L.; Koenig, L.S.; Studinger, M.; Harbeck, J.P. A sea-ice lead detection algorithm for use with high-resolution airborne visible imagery. IEEE Trans. Geosci. Remote Sens. 2013, 51, 38–56. [Google Scholar] [CrossRef]
- Hutter, N.; Zampieri, L.; Losch, M. Leads and ridges in Arctic sea ice from RGPS data and a new tracking algorithm. Cryosphere 2019, 13, 627–645. [Google Scholar] [CrossRef] [Green Version]
- Behrendt, A.; Dierking, W.; Fahrbach, E.; Witte, H. Sea ice draft in the Weddell Sea, measured by upward looking sonars. Earth Syst. Sci. Data 2013, 5, 209–226. [Google Scholar] [CrossRef] [Green Version]
- Gonzalez, S.; Horne, J.K.; Danielson, S.L. Multi-scale temporal variability in biological-physical associations in the NE Chukchi Sea. Polar Biol. 2021, 44, 837–855. [Google Scholar] [CrossRef]
- Skyllingstad, E.D.; Paulson, C.A.; Pegau, W.S.; McPhee, M.G.; Stanton, T. Effects of keels on ice bottom turbulence exchange. J. Geophys. Res. 2003, 108, 3372. [Google Scholar] [CrossRef] [Green Version]
- Pawlowicz, R.; Beardsley, B.; Lentz, S. Classical tidal harmonic analysis including error estimates in MATLAB using T_TIDE. Comput. Geosci. 2002, 28, 929–937. [Google Scholar] [CrossRef]
- Kohonen, T. The self-organizing map. Neurocomputing 1998, 21, 1–6. [Google Scholar] [CrossRef]
- Richardson, A.J.; Risien, C.; Shillington, F.A. Using self-organizing maps to identify patterns in satellite imagery. Prog. Oceanogr. 2003, 59, 223–239. [Google Scholar] [CrossRef]
- Liu, Y.; Weisberg, R.H.; Mooers, C.N.K. Performance evaluation of the self-organizing map for feature extraction. J. Geophys. Res. 2006, 3, C05018. [Google Scholar] [CrossRef]
- Mihanović, H.; Cosoli, S.; Vilibić, I.; Ivanković, D.; Dadić, V.; Gačić, M. Surface current patterns in the northern Adriatic extracted from high-frequency radar data using self-organizing map analysis. J. Geophys. Res. 2011, 116, C08033. [Google Scholar] [CrossRef] [Green Version]
- Kohonen, T. Self-organized formation of topologically correct feature maps. Biol. Cybern. 1982, 43, 59–69. [Google Scholar] [CrossRef]
- Maslanik, J.; Stroeve, J. Near-Real-Time DMSP SSMIS Daily Polar Gridded Sea Ice Concentrations, Version 1; electronic dataset; NASA National Snow and Ice Data Center Distributed Active Archive Center: Boulder, CO, USA, 1999.
- Gloersen, P. Nimbus-7 SMMR Polar Gridded Radiances and Sea Ice Concentrations, Version 1; electronic dataset; NASA National Snow and Ice Data Center Distributed Active Archive Center: Boulder, CO, USA, 2006.
- Stanton, T.J.; Jezek, K.C.; Gow, A.J. Acoustical reflection and scattering from the underside of laboratory grown sea ice: Measurements and predictions. J. Acoust. Soc. 1986, 80, 1486–1494. [Google Scholar] [CrossRef] [Green Version]
- Rolph, R.J.; Mahoney, A.R.; Walsh, J.; Loring, P.A. Impacts of a lengthening open water season on Alaskan coastal communities: Deriving locally relevant indices from large-scale datasets and community observations. Cryosphere 2018, 12, 1779–1790. [Google Scholar] [CrossRef] [Green Version]
- Baxevani, A.; Caires, S.; Rychlik, I. Spatio-temporal statistical modelling of significant wave height. Environmetrics 2008, 20, 14–31. [Google Scholar] [CrossRef]
- Felizardo, F.C.; Melville, W.K. Correlations between ambient noise and the ocean surface wave field. J. Phys. Oceanogr. 1995, 25, 513–532. [Google Scholar] [CrossRef]
- Ahn, S. Modeling mean relation between peak period and energy period of ocean surface wave systems. Ocean Eng. 2021, 228, 108937. [Google Scholar] [CrossRef]
- Eisen, O.; Kottmeier, C. On the importance of leads in sea ice to the energy balance and ice formation in the Weddell Sea. J. Geophys. Res. 2000, 105, 14045–14060. [Google Scholar] [CrossRef]
- Lüpkes, C.; Vihma, T.; Birnbaum, G.; Wacker, U. Influence of leads in sea ice on the temperature of the atmospheric boundary layer during polar night. Geophys. Res. Lett. 2008, 35, L03805. [Google Scholar] [CrossRef] [Green Version]
- Stigebrandt, A. A model for the thickness and salinity of the upper layer in the Arctic Ocean and the relationship between the ice thickness and some external parameters. J. Phys. Oceanogr. 1981, 11, 1407–1422. [Google Scholar] [CrossRef]
- Maykut, G.A. Large-scale heat exchange and ice production in the central Arctic. J. Geophys. Res. 1982, 87, 7971–7984. [Google Scholar] [CrossRef]
- Mahoney, A.R.; Hutchings, J.K.; Eicken, H.; Haas, C. Changes in the thickness and circulation of multiyear ice in the Beaufort Gyre determined from pseudo-Lagrangian methods from 2003–2015. J. Geophys. Res. Oceans 2019, 124, 5618–5633. [Google Scholar] [CrossRef]
- Norton, D.W.; Gaylord, A.G. Drift velocities of ice floes in Alaska’s northern Chukchi Sea flaw zone: Determinants of success by spring subsistence whalers in 2000 and 2001. Arctic 2004, 57, 347–362. [Google Scholar] [CrossRef] [Green Version]
- Kwok, R.; Spreen, G.; Pang, S. Arctic sea ice circulation and drift speed: Decadal trends and ocean currents. J. Geophys. Res. Oceans 2013, 118, 2408–2425. [Google Scholar] [CrossRef]








| Deployment Years | Start Date and Time (GMT) | Target Depth (m) | Bin Size (m) | Ping Interval (s) | Samples per Ping | CTD Offset (m) |
|---|---|---|---|---|---|---|
| 2014–2015 | 20 September 2014 22:48:00 | 28 | 0.0113 | 15 | 3384 | 0.38 |
| 2015–2016 | 20 August 2015 16:53:00 | 33 | 0.0340 | 10 | 1176 | 0.84 |
| 2016–2017 | 4 August 2016 4:33:00 | 33 | 0.0113 | 20 | 3528 | 0.84 |
| 2017–2018 | 15 August 2017 1:03:00 | 33 | 0.0113 | 20 | 3528 | 0.84 |
| 2018–2019 | 6 August 2018 5:00:00 | 33 | 0.0340 | 15 | 1176 | 0.98 |
| 2019–2020 | 19 August 2019 16:03:00 | 33 | 0.0113 | 20 | 3529 | 0.84 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sandy, S.J.; Danielson, S.L.; Mahoney, A.R. Automating the Acoustic Detection and Characterization of Sea Ice and Surface Waves. J. Mar. Sci. Eng. 2022, 10, 1577. https://doi.org/10.3390/jmse10111577
Sandy SJ, Danielson SL, Mahoney AR. Automating the Acoustic Detection and Characterization of Sea Ice and Surface Waves. Journal of Marine Science and Engineering. 2022; 10(11):1577. https://doi.org/10.3390/jmse10111577
Chicago/Turabian StyleSandy, Savannah J., Seth L. Danielson, and Andrew R. Mahoney. 2022. "Automating the Acoustic Detection and Characterization of Sea Ice and Surface Waves" Journal of Marine Science and Engineering 10, no. 11: 1577. https://doi.org/10.3390/jmse10111577
APA StyleSandy, S. J., Danielson, S. L., & Mahoney, A. R. (2022). Automating the Acoustic Detection and Characterization of Sea Ice and Surface Waves. Journal of Marine Science and Engineering, 10(11), 1577. https://doi.org/10.3390/jmse10111577





