Research on an All-Flow Velocity Control Strategy for a 120 kW Variable-Pitch Horizontal Axis Tidal Current Turbine
Abstract
:1. Introduction
2. Tidal Current Generation System
3. Computational Model
3.1. Dynamic Model
3.2. Simulation Model of the Turbine
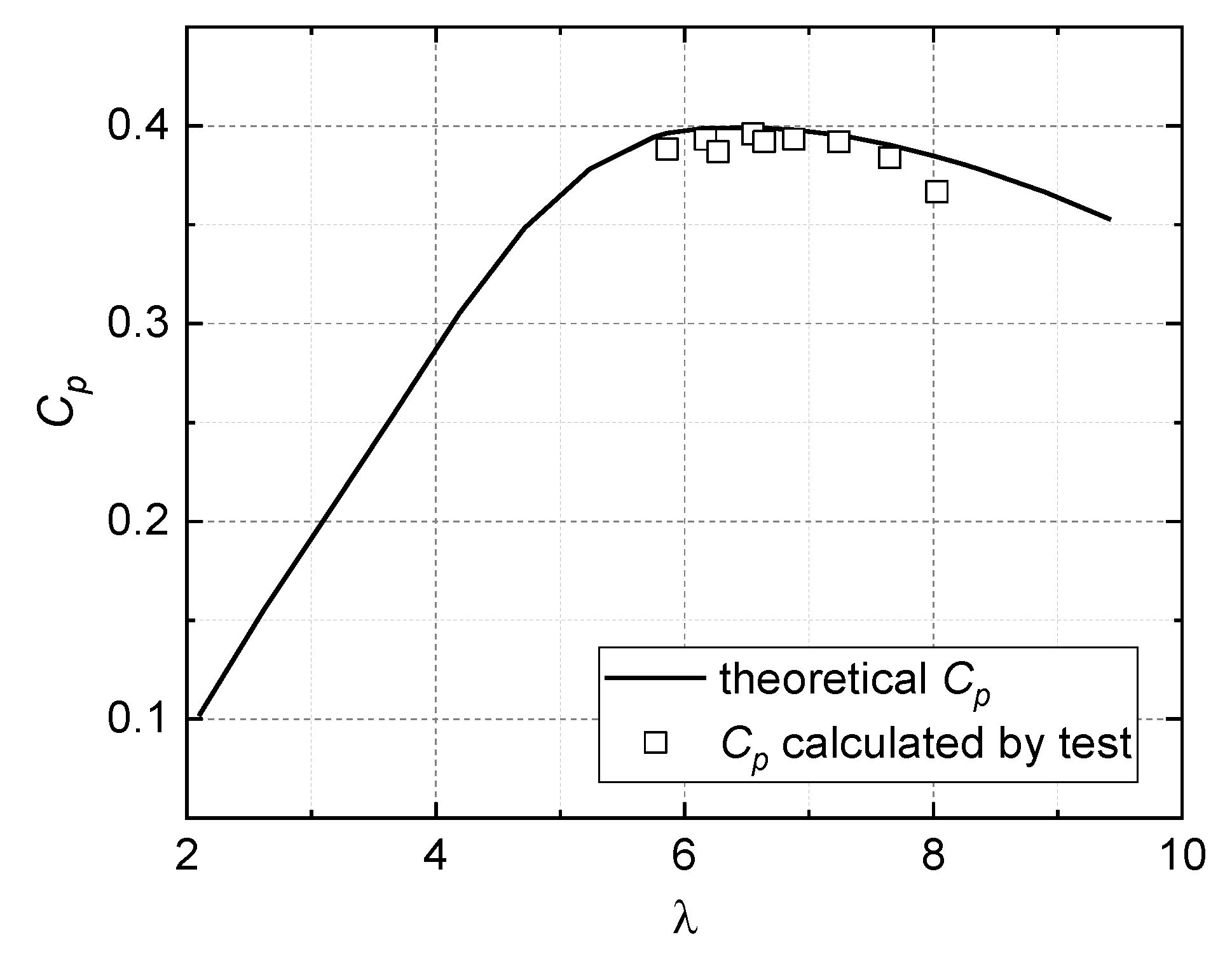
3.3. Experimental Verification
3.4. Generator Characteristics
4. Control Characteristic Analysis
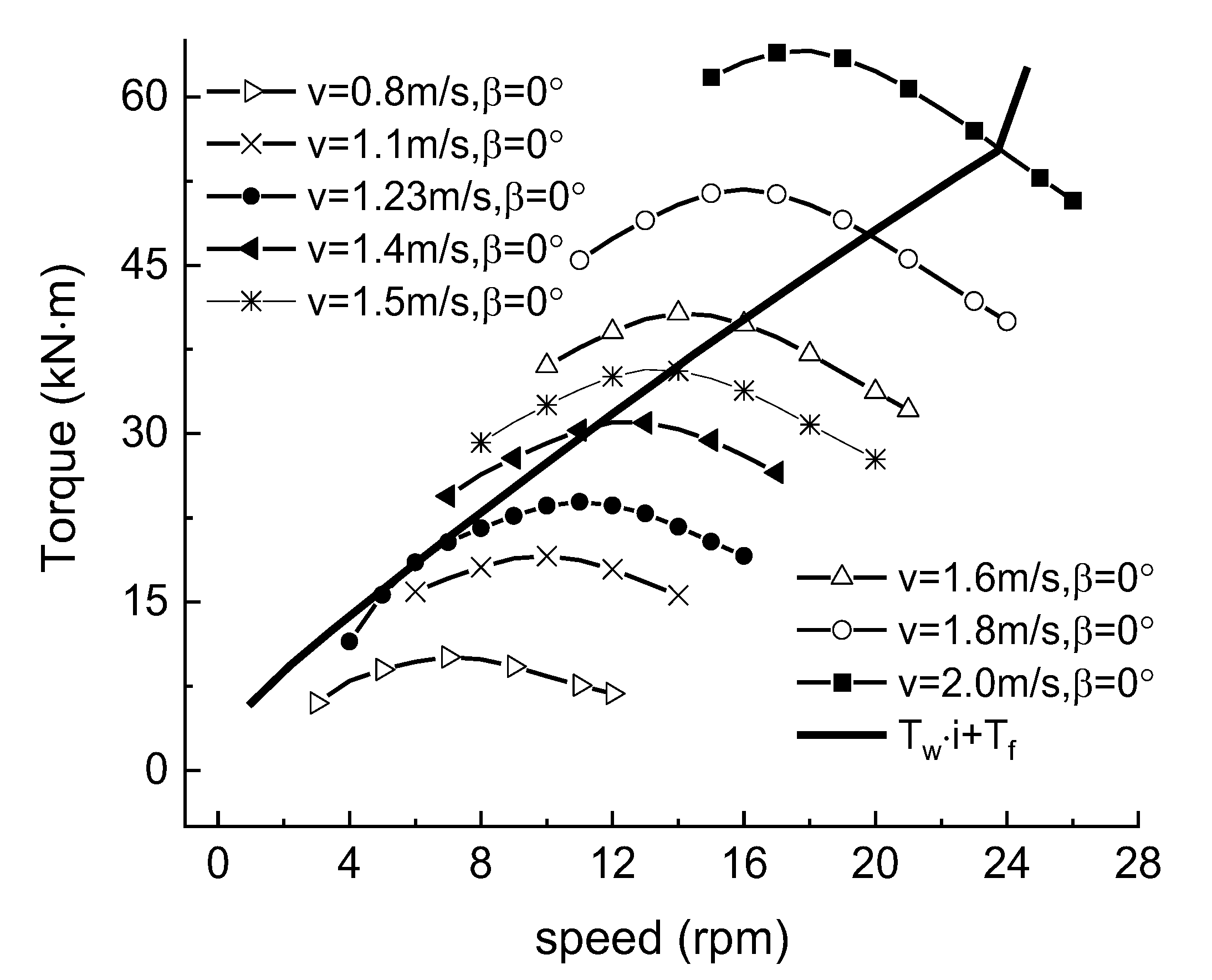
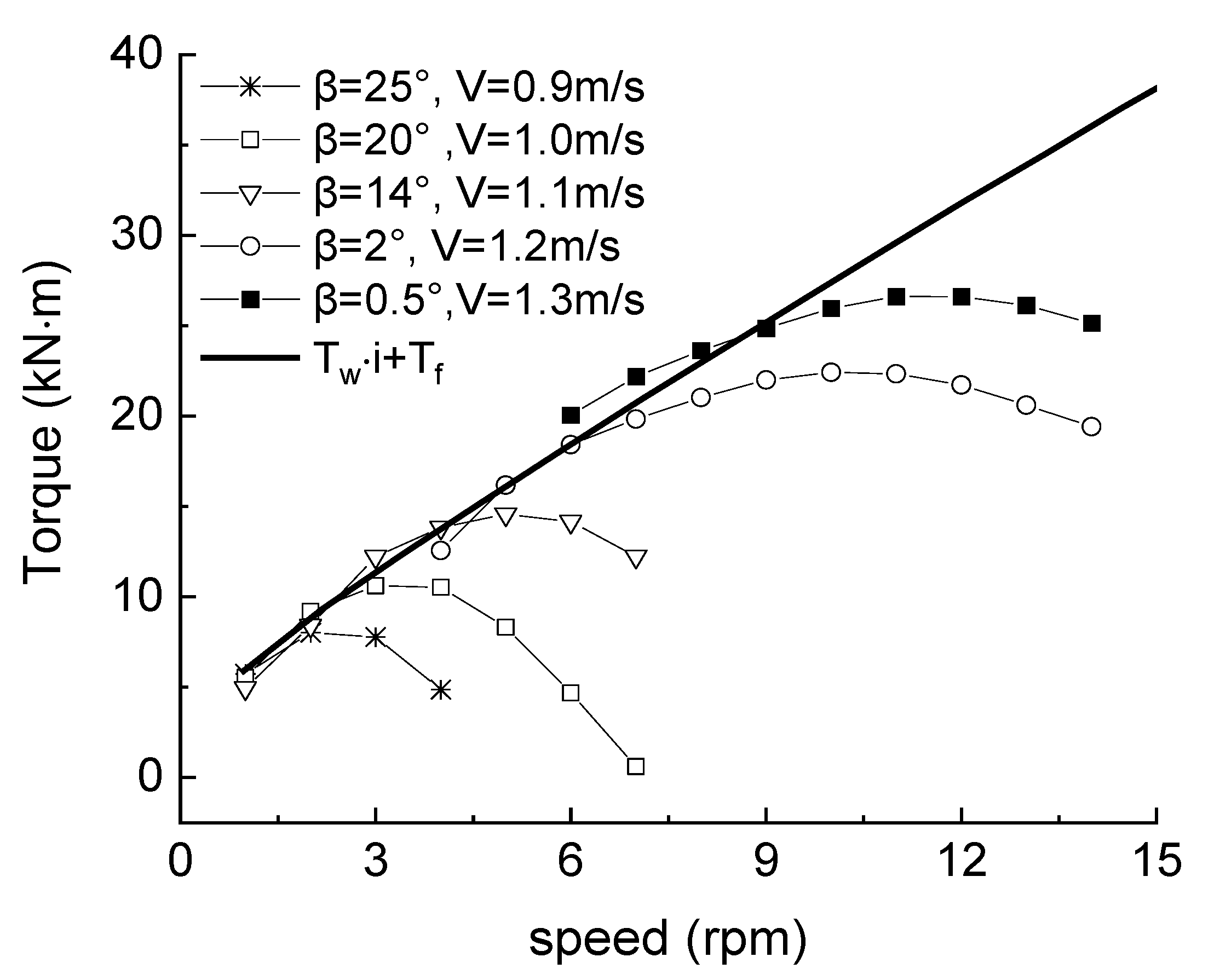
4.1. Control Strategy for Low-Flow Stage
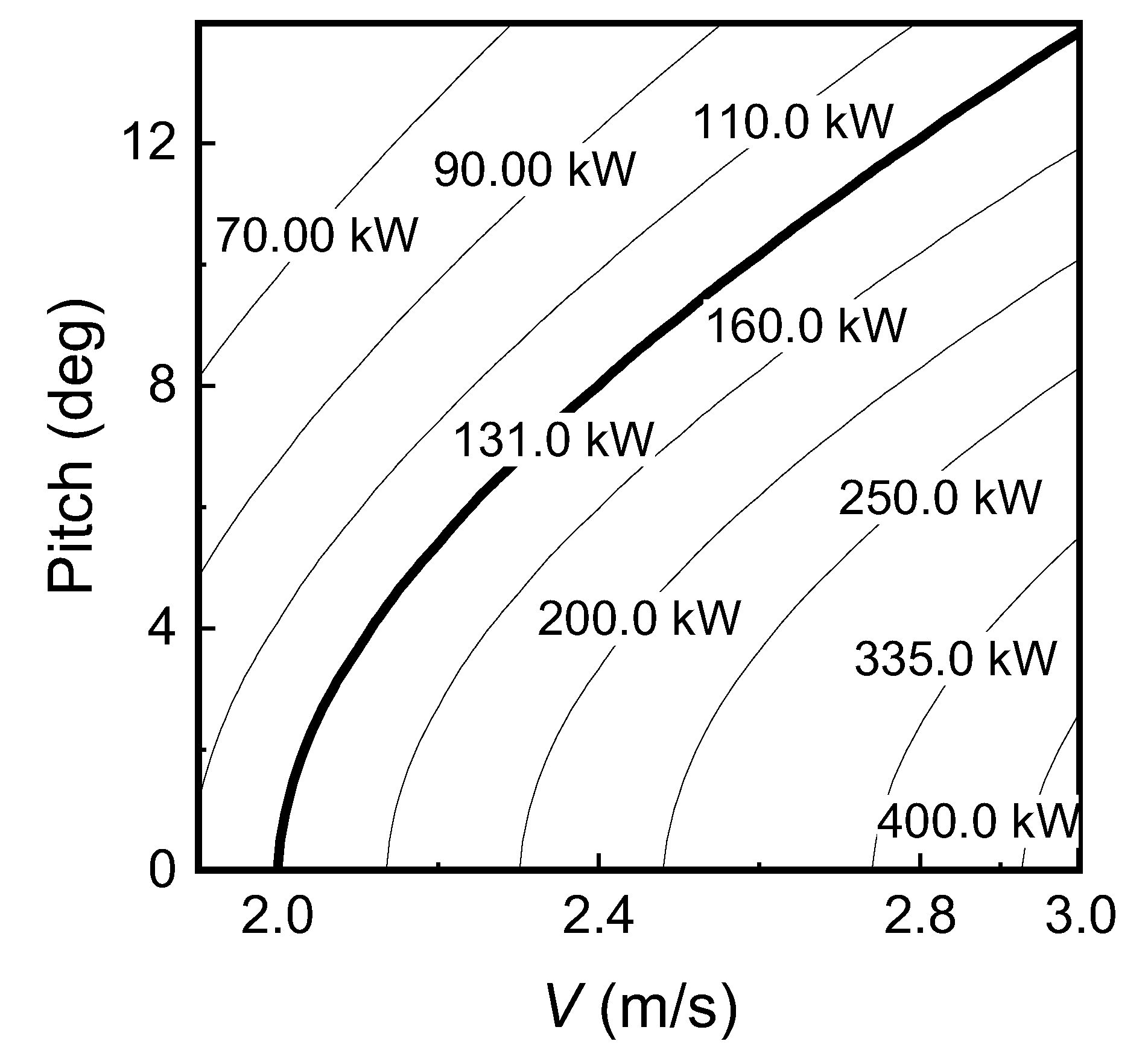
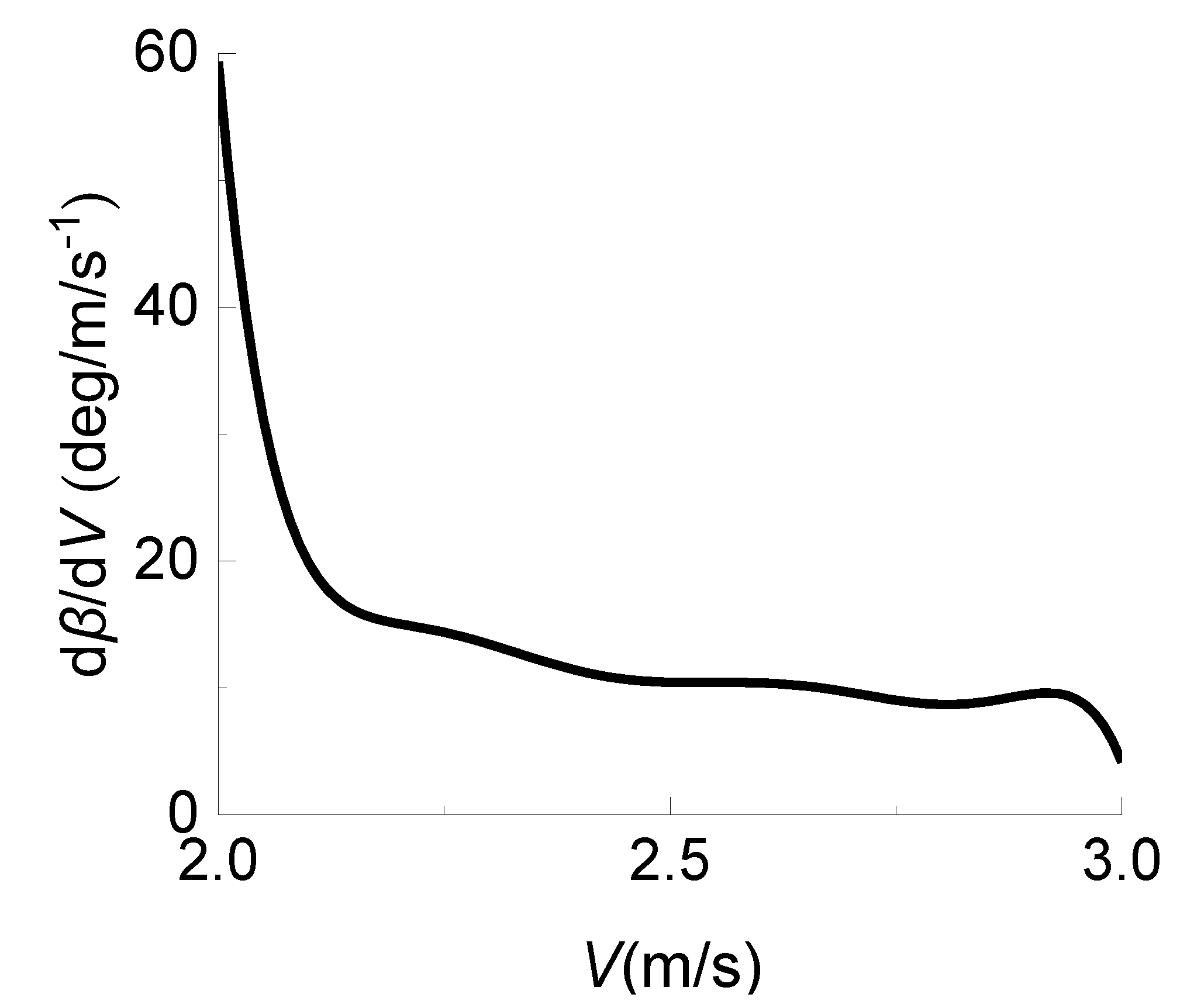
4.2. Power Limit Control and Working Limit Point
4.2.1. Power Limit Control Strategy
4.2.2. Limit Working Point
4.3. Overcurrent Protection
4.3.1. Dynamic Characteristics of Turbine with Large Pitch Angle under High Flow Velocity
4.3.2. Overcurrent Protection Strategy
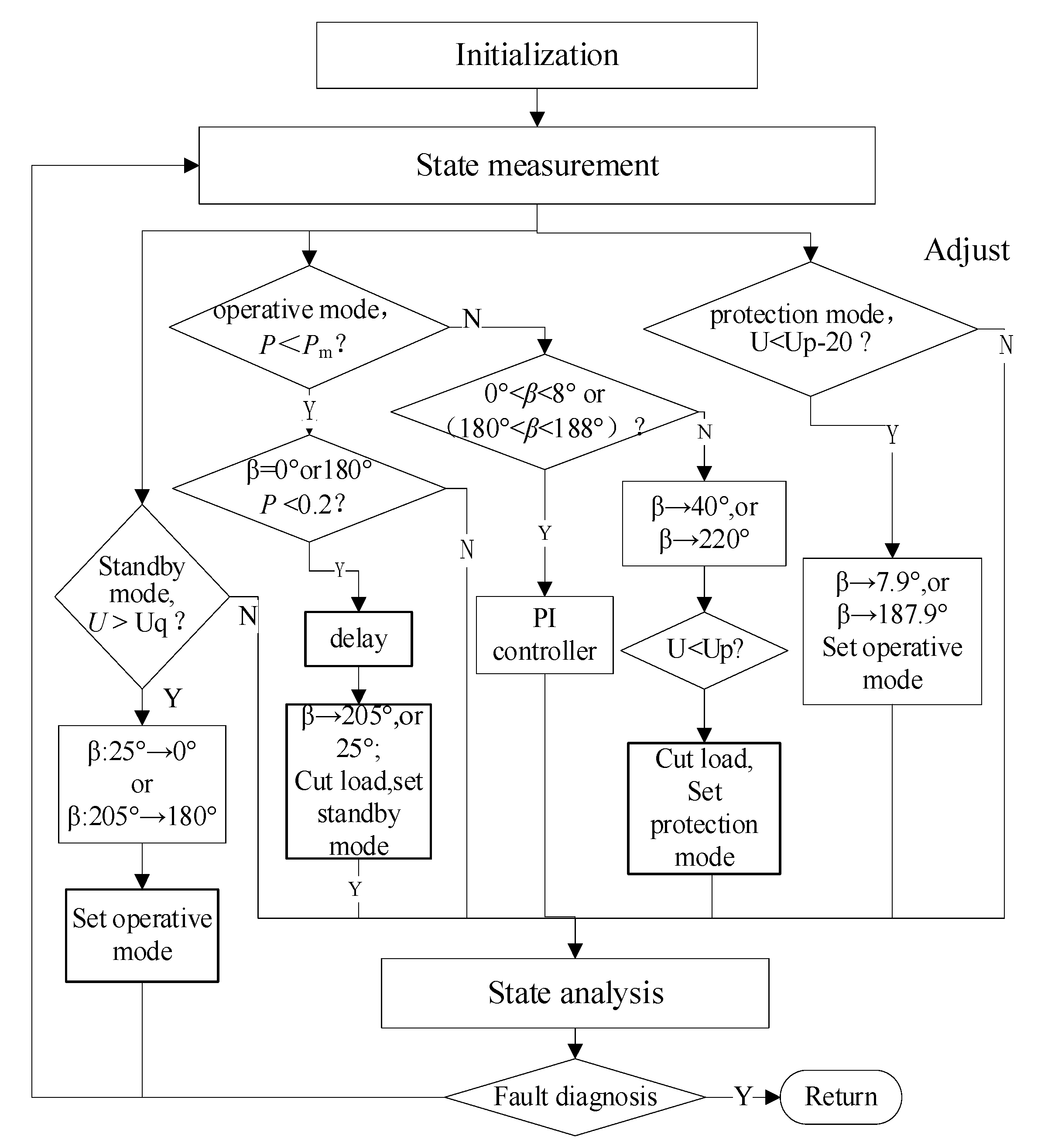
5. Control Process Design
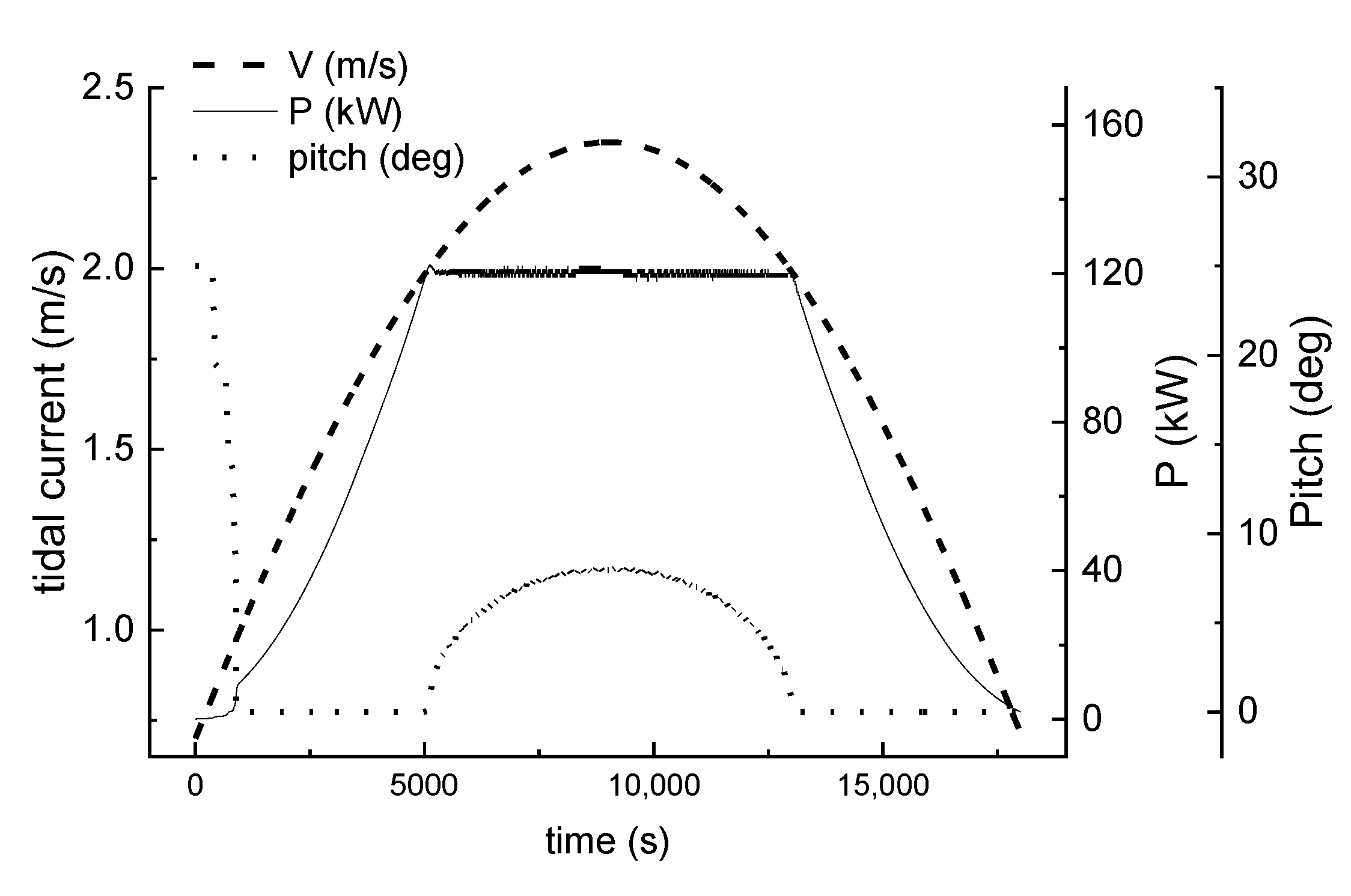
6. Control Process Simulation Analysis
6.1. Tidal Current Calculation Model
6.2. Power Generation Process Simulation
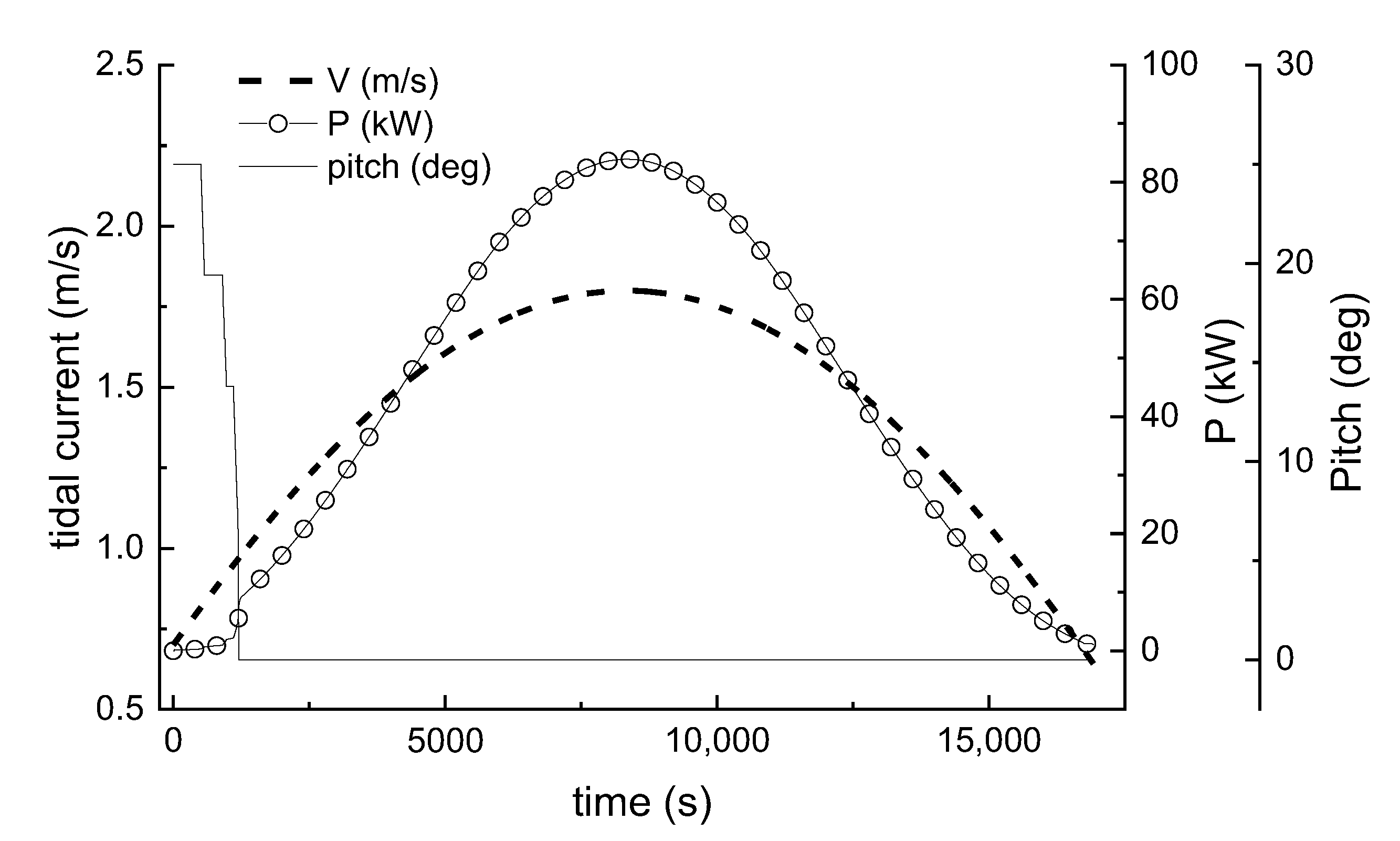
6.2.1. Power Generation at Low Flow Rate
6.2.2. Power Generation at High Flow Rate
6.2.3. Maximum Flow Rate Exceeding the Limit Value
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| TCT | Tidal current turbine |
| HATCT | Horizontal axis tidal current turbine |
| BEMT | Blade element momentum theory |
| MPPT | Maximum power point tracking |
| VSVP | Variable-speed, variable-pitch |
| DFIG | Doubly fed induction generator |
| IOPI | Integer-order PI |
| ADCP | Acoustic Doppler current profiler |
| J | Moment of inertia of the unit (kg*m2) |
| ε | Angular acceleration of the rotor |
| T | Torque of the turbine (Nm) |
| Tz | Resistance torque (Nm) |
| Tf | Friction torque of the transmission system (Nm) |
| Tw | Effective resistance torque from the generator (Nm) |
| Tw’ | Corrected working resistance torque (Nm) |
| n | Rotation speed of the impeller (rpm) |
| ng | Rotation speed of the generator (rpm) |
| i | Speed ratio of the gearbox |
| Ja | Added mass of the blade (kg*m2) |
| a, b | Axial and tangential flow induction factors, respectively |
| φ | Inflow angle (degree) |
| θ | Mounting angle of the leaf element (degree) |
| β | Pitch angle of the blade (degree) |
| V | Tidal current speed (m/s) |
| F | Loss coefficient |
| B | Number of blades |
| r | Radius of the local blade element (m) |
| R | Rotor radius (m) |
| σr | Local solidity |
| c | Chord length of the local blade (m) |
| CL, CD | Lift and drag coefficient |
| Cp | Power coefficient |
| λ | Tip speed ratio (TSR) |
| λr | Local tip speed ratio |
| ρ | Seawater density (kg/m3) |
| sj (=cj∙dr) | Local area of the blade element |
| Vo | Voltage with load of the generator (V) |
| Vo’ | Floating voltage of the generator (V) |
| η | Working efficiency of the generator |
| P, Pe | Output power and limited power of the unit (kW) |
| DI, D0 | Duty cycle coefficient and initial value of the duty cycle, respectively |
| Uup | Upper-limit voltage (V) |
| Uq | Starting voltage of the unit (V) |
| Kp, KI | Proportional control factor and integral coefficient, respectively |
| Pi, Pi-k | Current output power and output power at the adjacent k-th sampling time (kW), respectively |
| Tc | Tidal period |
| Vm | Maximum flow velocity in the tidal cycle (m/s) |
References
- Chu, S.; Majumdar, A. Opportunities and challenges for a sustainable energy future. Nature 2012, 488, 294–303. [Google Scholar] [CrossRef] [PubMed]
- Gielen, D.; Boshell, F.; Saygin, D.; Bazilian, M.D.; Wagner, N.; Gorini, R. The role of renewable energy in the global energy transformation. Energy Strategy Rev. 2019, 24, 38–50. [Google Scholar] [CrossRef]
- Ng, K.W.; Lam, W.-H.; Ng, K.C. 2002–2012: 10 Years of Research Progress in Horizontal-Axis Marine Current Turbines. Energies 2013, 6, 1497–1526. [Google Scholar] [CrossRef] [Green Version]
- Chowdhury, M.S.; Rahman, K.S.; Selvanathan, V.; Nuthammachot, N.; Suklueng, M.; Mostafaeipour, A.; Habib, A.; Akhtaruzzaman, M.; Amin, N.; Techato, K. Current trends and prospects of tidal energy technology. Environ. Dev. Sustain. 2020, 23, 8179–8194. [Google Scholar] [CrossRef]
- Bahaj, A.S. Generating electricity from the oceans. Renew. Sustain. Energy Rev. 2011, 15, 3399–3416. [Google Scholar] [CrossRef]
- Ben Elghali, S.; Benbouzid, M.E.H.; Charpentier, J.F. Marine Tidal Current Electric Power Generation Technology: State of the Art and Current Status. In Proceedings of the 2007 IEEE International Electric Machines & Drives Conference, Antalya, Turkey, 16 July 2007; pp. 1407–1412. [Google Scholar]
- Chen, H.; Tang, T.-h.; Aït-Ahmed, N.; Benbouzid, M.E.H.; Machmoum, M.; Zaïm, M.E. Attraction, Challenge and Current Status of Marine Current Energy. IEEE Access 2018, 6, 12665–12685. [Google Scholar] [CrossRef]
- Melikoğlu, M. Current status and future of ocean energy sources: A global review. Ocean Eng. 2018, 148, 563–573. [Google Scholar] [CrossRef]
- Liu, X.; Chen, Z.; Si, Y.; Qian, P.-F.; Wu, H.; Cui, L.; Zhang, D. A review of tidal current energy resource assessment in China. Renew. Sustain. Energy Rev. 2021, 145, 111012. [Google Scholar] [CrossRef]
- Tawil, T.E.; Charpentier, J.F.; Benbouzid, M.E.H. Tidal energy site characterization for marine turbine optimal installation: Case of the Ouessant Island in France. Int. J. Mar. Energy 2017, 18, 57–64. [Google Scholar] [CrossRef]
- Benbouzid, M.E.H.; Astolfi, J.A.; Bacha, S.; Charpentier, J.F.; Machmoum, M.; Maître, T.; Roye, D. Concepts, Modeling and Control of Tidal Turbines; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Khan, M.Z.A.; Khan, H.A.; Aziz, M. Harvesting Energy from Ocean: Technologies and Perspectives. Energies 2022, 15, 3456. [Google Scholar] [CrossRef]
- Roberts, A.K.; Thomas, B.M.; Sewell, P.; Khan, Z.A.; Balmain, S.; Gillman, J. Current tidal power technologies and their suitability for applications in coastal and marine areas. J. Ocean. Eng. Mar. Energy 2016, 2, 227–245. [Google Scholar] [CrossRef] [Green Version]
- Xu, Q.; Li, W.; Lin, Y.; Liu, H.; Gu, Y.-j. Investigation of the performance of a stand-alone horizontal axis tidal current turbine based on in situ experiment. Ocean Eng. 2016, 113, 111–120. [Google Scholar] [CrossRef]
- Zhang, J.; Moreau, L.; Machmoum, M.; Guillerm, P.E. State of the art in tidal current energy extracting technologies. In Proceedings of the First International Conference on Green Energy ICGE, Sfax, Tunisia, 25–27 March 2014; pp. 1–7. [Google Scholar]
- Ghefiri, K.; Bouallègue, S.; Garrido, I.; Garrido, A.J.; Haggège, J. Complementary Power Control for Doubly Fed Induction Generator-Based Tidal Stream Turbine Generation Plants. Energies 2017, 10, 862. [Google Scholar] [CrossRef] [Green Version]
- Gu, Y.-j.; Liu, H.; Li, W.; Lin, Y.; Yangjian, L. Integrated design and implementation of 120-kW horizontal-axis tidal current energy conversion system. Ocean Eng. 2018, 158, 338–349. [Google Scholar] [CrossRef]
- Wang, Y.; Wei, X.; Zhu, W.; Chen, J.; Dong, Y.; Guo, J. Research on Maximum Power Tracking Control of Tidal Power Generation System. In Proceedings of the 12th International Conference on Measuring Technology and Mechatronics Automation (ICMTMA), Phuket, Thailand, 28–29 February 2020; pp. 450–454. [Google Scholar]
- Saihi, L.; Boutera, A. Robust Control of a Variable-Speed Wind Turbine with Fixed Pitch Angle and Strategy MPPT Control Associated on a PMSG. In Proceedings of the 8th International Conference on Modelling, Identification and Control (ICMIC), Algiers, Algeria, 5 January 2017; pp. 326–331. [Google Scholar]
- Boukhezzar, B.; Lupu, L.; Siguerdidjane, H.; Hand, M.M. Multivariable control strategy for variable speed, variable pitch wind turbines. Renew. Energy 2007, 32, 1273–1287. [Google Scholar] [CrossRef]
- Qian, P.; Feng, B.; Liu, H.; Tian, X.; Si, Y.; Zhang, D. Review on configuration and control methods of tidal current turbines. Renew. Sustain. Energy Rev. 2019, 108, 125–139. [Google Scholar] [CrossRef]
- Whitby, B.; Ugalde-Loo, C.E. Performance of Pitch and Stall Regulated Tidal Stream Turbines. IEEE Trans. Sustain. Energy 2014, 5, 64–72. [Google Scholar] [CrossRef]
- Zhen, C.; Shukai, C.; Ming, L.; Jianguo, W. Design and Implementation of the Pitch Control System for Horizontal Axis Tidal Turbines. In Proceedings of the 27th Chinese Control and Decision Conference (2015 CCDC), Qingdao, China, 20 July 2015; pp. 4078–4082. [Google Scholar]
- Chen, H.; Xie, W.; Chen, X.; Han, J.; Aït-Ahmed, N.; Zhou, Z.; Tang, T.-h.; Benbouzid, M.E.H. Fractional-Order PI Control of DFIG-Based Tidal Stream Turbine. J. Mar. Sci. Eng. 2020, 8, 309. [Google Scholar] [CrossRef]
- Alipour, R.; Alipour, R.; Fardian, F.; Hossein Tahan, M. Optimum performance of a horizontal axis tidal current turbine: A numerical parametric study and experimental validation. Energy Convers. Manag. 2022, 258, 115533. [Google Scholar] [CrossRef]
- Moon, S.-H.; Park, B.-G.; Kim, J.-W.; Kim, J.-M. Maximum Power-Point Tracking Control Using Perturb and Observe Algorithm for Tidal Current Generation System. Int. J. Precis. Eng. Manuf. Green Technol. 2019, 7, 849–858. [Google Scholar] [CrossRef]
- Thomson, J.; Polagye, B.L.; Durgesh, V.; Richmond, M.C. Measurements of Turbulence at Two Tidal Energy Sites in Puget Sound, WA. IEEE J. Ocean. Eng. 2012, 37, 363–374. [Google Scholar] [CrossRef]
- Gu, Y.-j.; Lin, Y.; Xu, Q.; Liu, H.; Li, W. Blade-pitch system for tidal current turbines with reduced variation pitch control strategy based on tidal current velocity preview. Renew. Energy 2018, 115, 149–158. [Google Scholar] [CrossRef]
- Bir, G.S.; Lawson, M.J.; Li, Y. Structural Design of a Horizontal-Axis Tidal Current Turbine Composite Blade. In Proceedings of the ASME 2011 30th International Conference on Ocean, Offshore and Arctic Engineering, Rotterdam, The Netherlands, 19–24 June 2011. [Google Scholar]
- Ledoux, J.; Riffo, S.; Salomon, J. Analysis of the Blade Element Momentum Theory. SIAM J. Appl. Math. 2021, 81, 2596–2621. [Google Scholar] [CrossRef]
- Porate, D.K.; Gawande, S.P.; Porate, K.B.; Nagpure, R.N.; Waghmare, M.A.; Kadwane, S.G. Performance of PMSG Based Variable Speed WECS with Parallel Back-to-Back Converters Using Separate Zero d-axis Current Control. In Proceedings of the 2018 IEEE International Conference on Power Electronics, Drives and Energy Systems (PEDES), Chennai, India, 18–21 December 2018; pp. 1–6. [Google Scholar]
- Zheng, Z. The Estimation of Ocean Tidal Current Energy. Mar. Sci. Bull. 1987, 6, 70–75. [Google Scholar]

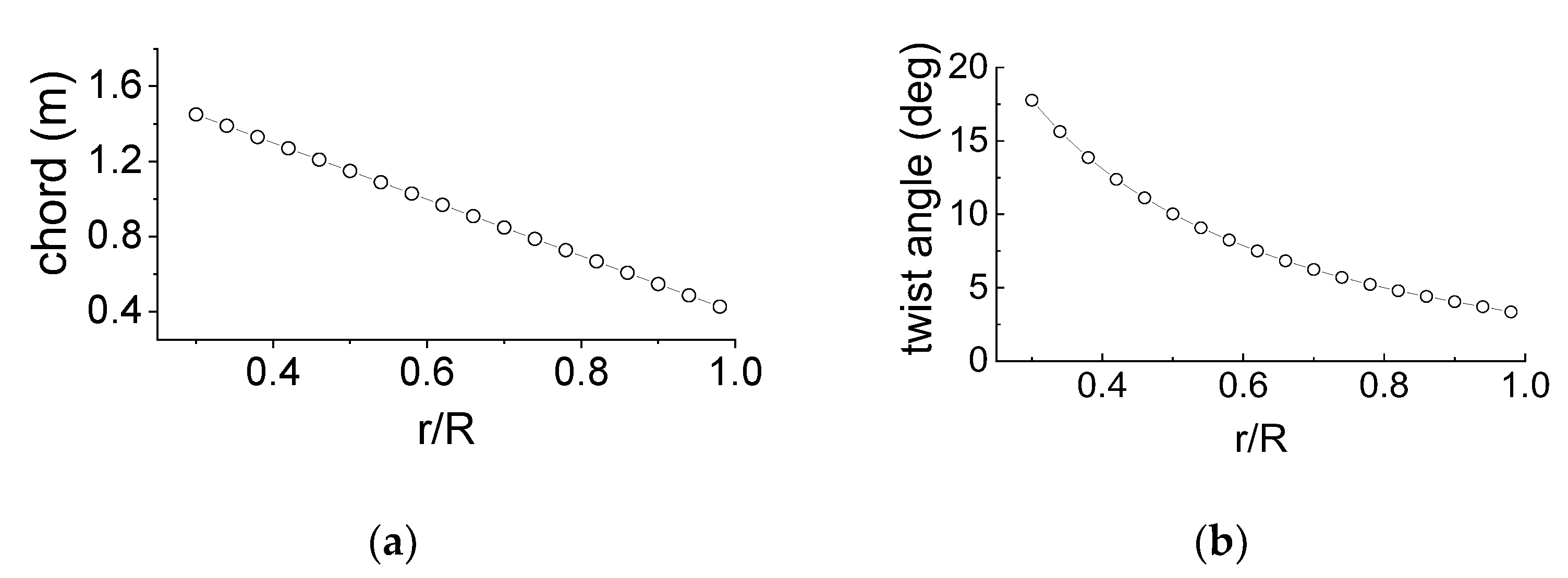






Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, B.; Ke, W.; Zhang, Y.; Duan, Y. Research on an All-Flow Velocity Control Strategy for a 120 kW Variable-Pitch Horizontal Axis Tidal Current Turbine. J. Mar. Sci. Eng. 2022, 10, 1578. https://doi.org/10.3390/jmse10111578
Wang B, Ke W, Zhang Y, Duan Y. Research on an All-Flow Velocity Control Strategy for a 120 kW Variable-Pitch Horizontal Axis Tidal Current Turbine. Journal of Marine Science and Engineering. 2022; 10(11):1578. https://doi.org/10.3390/jmse10111578
Chicago/Turabian StyleWang, Bingzhen, Wei Ke, Yuanfei Zhang, and Yunqi Duan. 2022. "Research on an All-Flow Velocity Control Strategy for a 120 kW Variable-Pitch Horizontal Axis Tidal Current Turbine" Journal of Marine Science and Engineering 10, no. 11: 1578. https://doi.org/10.3390/jmse10111578
APA StyleWang, B., Ke, W., Zhang, Y., & Duan, Y. (2022). Research on an All-Flow Velocity Control Strategy for a 120 kW Variable-Pitch Horizontal Axis Tidal Current Turbine. Journal of Marine Science and Engineering, 10(11), 1578. https://doi.org/10.3390/jmse10111578





