Crisis Ocean Modelling with a Relocatable Operational Forecasting System and Its Application to the Lakshadweep Sea (Indian Ocean)
Abstract
:1. Introduction
2. Data and Methods
2.1. NEMO Model
2.2. External Data
2.3. Data Assimilation
2.4. Workflow Engine
3. Results
3.1. The effect of Data Assimilation
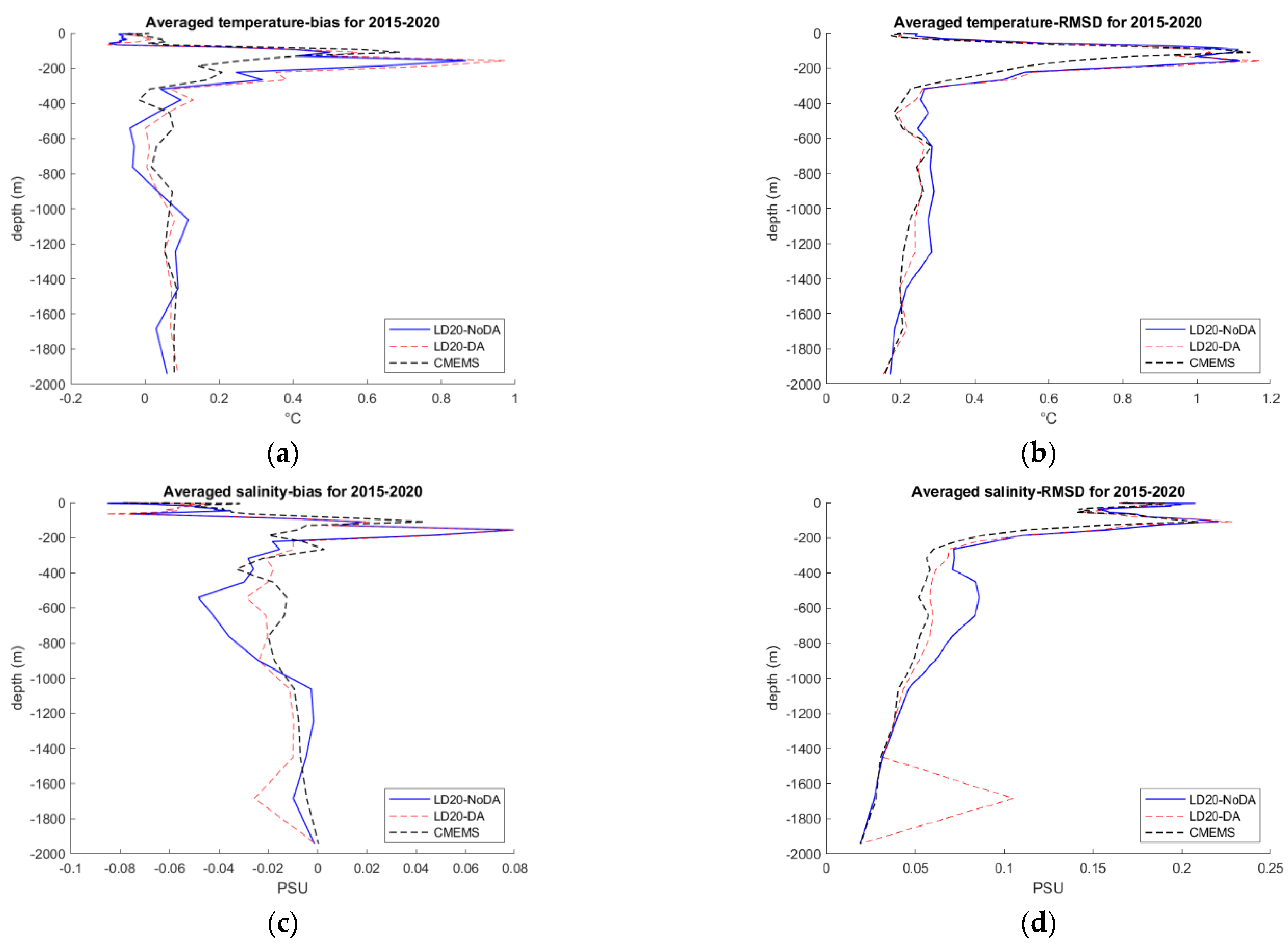
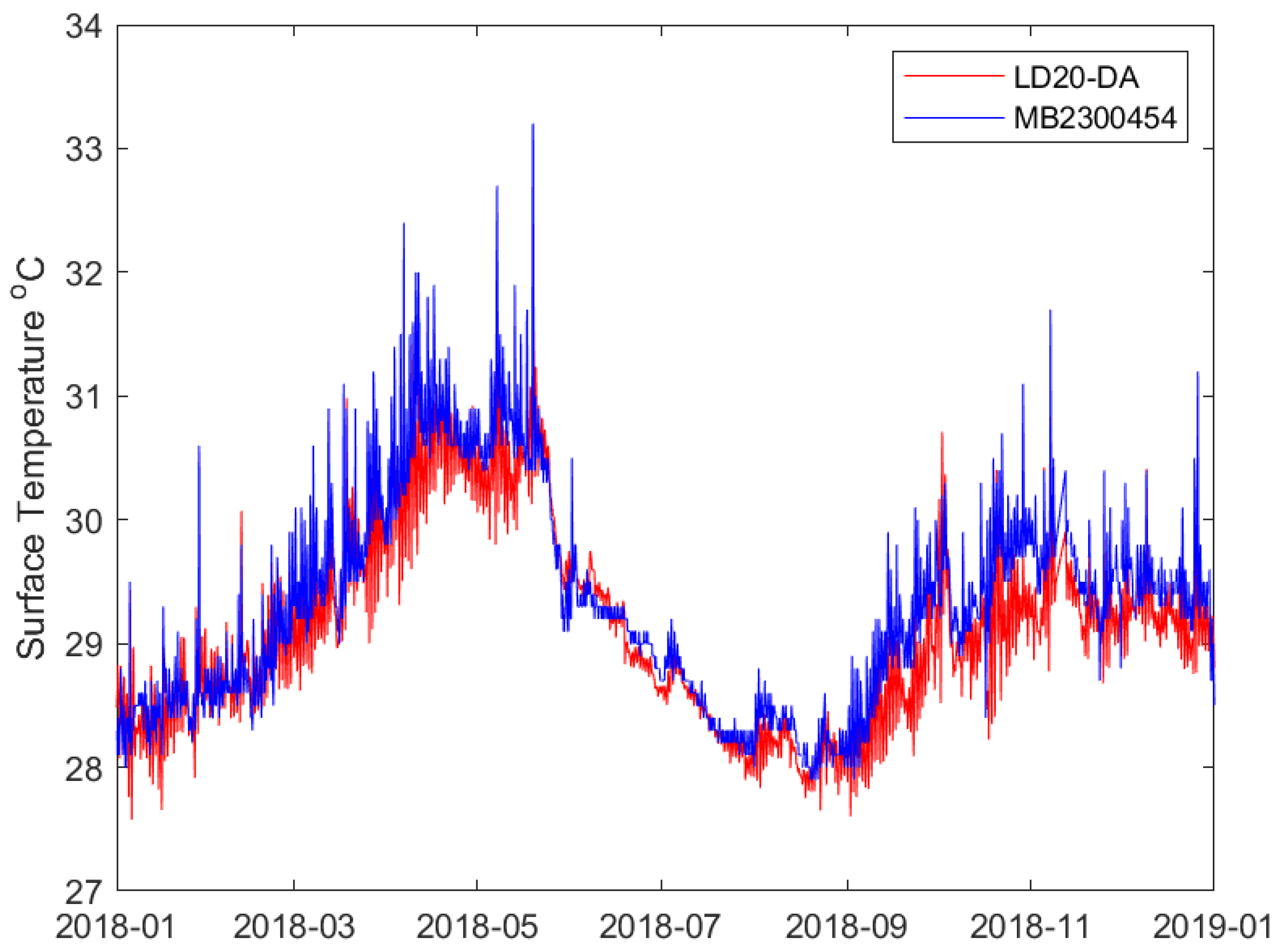
3.2. Model Validation
3.3. Higher Resolution Models
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- DITTO-2021. Available online: https://www.oceandecade.org/actions/digital-twins-of-the-ocean-ditto/ (accessed on 1 May 2022).
- CMEMS. 2022. Available online: https://marine.copernicus.eu/ (accessed on 1 May 2022).
- Lorente, P.; García-Sotillo, M.; Amo-Baladrón, A.; Aznar, R.; Levier, B.; Sánchez-Garrido, J.C.; Sammartino, S.; Reffray, G.; Toledano, C.; Álvarez-Fanjul, E. Skill assessment of global, regional, and coastal circulation forecast models: Evaluating the benefits of dynamical downscaling in IBI (Iberia–Biscay–Ireland) surface waters. Ocean Sci. 2019, 5, 967–996. [Google Scholar] [CrossRef] [Green Version]
- Onken, R.; Baschek, B.; Angel-Benavides, I.M. Very high-resolution modelling of submesoscale turbulent patterns and processes in the Baltic Sea. Ocean Sci. 2020, 16, 657–684. [Google Scholar] [CrossRef]
- Liu, Y.; MacCready, P.; Hickey, B.M.; Dever, E.P.; Kosro, P.M.; Banas, N.S. Evaluation of a coastal ocean circulation model for the Columbia River plume in summer 2004. J. Geophys. Res. Ocean. 2009, 114. [Google Scholar] [CrossRef] [Green Version]
- Aguiar, E.; Mourre, B.; Juza, M.; Reyes, E.; Hernández-Lasheras, J.; Cutolo, E.; Mason, E.; Tintoré, J. Multi-platform model assessment in the Western Mediterranean Sea: Impact of downscaling on the surface circulation and mesoscale activity. Ocean Dyn. 2020, 70, 273–288. [Google Scholar] [CrossRef] [Green Version]
- CAM. 2022. Available online: https://www.metoffice.gov.uk/research/approach/modelling-systems/unified-model/weather-forecasting (accessed on 1 May 2022).
- Shapiro, G.I.; Gonzalez-Ondina, J.M. An Efficient Method for Nested High-Resolution Ocean Modelling Incorporating a Data Assimilation Technique. J. Mar. Sci. Eng. 2022, 10, 432. [Google Scholar] [CrossRef]
- Bendoni, M.; Fattorini, M.; Taddei, S.; Brandini, C. High-resolution downscaling of CMEMS oceanographic reanalysis in the area of the Tuscany Archipelago (Italy). Ocean Dyn. 2022, 72, 295–312. [Google Scholar] [CrossRef]
- NEMO. 2021. Available online: https://www.nemo-ocean.eu/ (accessed on 16 June 2021).
- Rose. 2022. Available online: https://www.metoffice.gov.uk/research/approach/modelling-systems/rose (accessed on 10 June 2022).
- Madec, G.; Bourdallé-Badie, R.; Bouttier, P.-A.; Bricaud, C.; Bruciaferri, D.; Calvert, D.; Chanut, J.; Clementi, E.; Coward, A.; Delrosso, D.; et al. NEMO Ocean Engine. 2017. Available online: https://www.earth-prints.org/handle/2122/13309 (accessed on 10 September 2022).
- Bruciaferri, D.; Shapiro, G.; Stanichny, S.; Zatsepin, A.; Ezer, T.; Wobus, F.; Francis, X.; Hilton, D. The development of a 3D computational mesh to improve the representation of dynamic processes: The Black Sea test case. Ocean Model. 2020, 146, 101534. [Google Scholar] [CrossRef]
- Madec, G.; NEMO Team. 2016. NEMO Ocean Engine, ISSN No 1288–1619. Available online: https://zenodo.org/record/3248739#.Yx8zIdfMKUk (accessed on 10 September 2022).
- GEBCO. 2014: The GEBCO_2014 Grid, Version 20150318. Available online: https://www.gebco.net/ (accessed on 6 July 2020).
- Arnold, A. The Sensitivity of AMM15 Ocean Model Sea Surface Temperature to Shortwave Radiation Forcing. Forecasting Research Technical Report No: 627. 2018. Available online: https://digital.nmla.metoffice.gov.uk/download/file/IO_d5348b81-ccf4-4e8a-aff0-6174d69dcb1c (accessed on 10 September 2022).
- Egbert, G.D.; Erofeeva, S.Y. Efficient inverse modeling of barotropic ocean tides. J. Atmos. Ocean. Technol. 2002, 19, 183–204. [Google Scholar] [CrossRef]
- OSTIA. 2022. The Operational Sea Surface Temperature and Ice Analysis. Available online: https://ghrsst-pp.metoffice.gov.uk/ostia-website/index.html#:~:text=The%20Operational%20Sea%20Surface%20Temperature,satellite%20and%20and%20insitu%20data (accessed on 10 February 2022).
- GHRSST-MUR. 2022. Available online: https://www.ghrsst.org/ (accessed on 10 February 2022).
- ARGO. 2022. Available online: https://www.aoml.noaa.gov/phod/argo/ (accessed on 10 February 2022).
- Kalnay, E. Atmospheric Modeling, Data Assimilation and Predictability; Cambridge University Press: Cambridge, UK, 2003; 369p. [Google Scholar]
- Valler, V.; Franke, J.; Brönnimann, S. Impact of different estimations of the background-error covariance matrix on climate reconstructions based on data assimilation. Clim. Past 2019, 15, 1427–1441. [Google Scholar] [CrossRef] [Green Version]
- Carrassi, A.; Bocquet, M.; Bertino, L.; Evensen, G. Data assimilation in the geosciences: An overview of methods, issues, and perspectives. WIREs Clim. Change 2018, 9, e535. [Google Scholar] [CrossRef]
- Polavarapu, S.; Ren, S.; Rochon, Y.; Sankey, D.; Ek, N.; Koshyk, J.; Tarasick, D. Data assimilation with the Canadian middle atmosphere model. Atmos. Ocean 2005, 43, 77–100. [Google Scholar] [CrossRef]
- Hollingsworth, A.; Lönnberg, P. The statistical structure of short-range forecast errors as determined from radiosonde data, Part 1: The wind field. Tellus A 1986, 38, 111–136. [Google Scholar] [CrossRef] [Green Version]
- Rutherford, I.D. Data assimilation by statistical interpolation of forecast error fields. J. Atmos. Sci. 1972, 29, 809–815. [Google Scholar] [CrossRef]
- Shapiro, G.I.; Gonzalez-Ondina, J.M.; Belokopytov, V.N. High-resolution stochastic downscaling method for ocean forecasting models and its application to the Red Sea dynamics. Ocean Sci. 2021, 17, 891–907. [Google Scholar] [CrossRef]
- Moser, W.R. Linear Models: A Mean Model Approach; Elsevier: Amsterdam, The Netherlands, 1996. [Google Scholar] [CrossRef]
- Gandin, L.S. The Problem of Optimal Interpolation; Scientific papers; Main Geophysical Observatory: Saint Petersburg, Russia, 1959; Volume 99, pp. 67–75. [Google Scholar]
- Weaver, A.T.; Mirouze, I. On the diffusion equation and its application to isotropic and anisotropic correlation modelling in variational assimilation. Quart. J. R. Meteor. Soc. 2013, 139, 242–260. [Google Scholar] [CrossRef]
- Mirouze, I.; Blockley, E.W.; Lea, D.J.; Martin, M.J.; Bell, M.J. A multiple length scale correlation operator for ocean data assimilation. Tellus A Dyn. Meteorol. Oceanogr. 2016, 68, 29744. [Google Scholar] [CrossRef] [Green Version]
- Polonskii, A.B.; Shokurova, I.G. Statistical structure of the large-scale fields of temperature and salinity in the Black Sea. Phys. Oceanogr. 2008, 18, 38–51. [Google Scholar] [CrossRef]
- Bouttier, F.; Courtier, P. Data Assimilation Concepts and Methods. 1999. Available online: https://www.ecmwf.int/en/elibrary/16928-data-assimilation-concepts-and-methods (accessed on 5 August 2021).
- FCM. 2022. Available online: https://www.metoffice.gov.uk/research/weather/weather-science-it/fcm (accessed on 13 September 2022).
- Zingerlea, C.; Nurmib, P. Monitoring and verifying cloud forecasts originating from operational numerical models. Meteorol. Appl. 2008, 15, 325–330. [Google Scholar] [CrossRef]
- MetOffice. 20 Years of UM and NWP at the Interdisciplinary Centre for Mathematical and Computational Modelling. 2017. Available online: https://www.metoffice.gov.uk/research/news/2017/20-years-of-um-use-at-icm (accessed on 10 February 2022).
- Donlon, C.J.; Martin, M.; Stark, J.; Roberts-Jones, J.; Fiedler, E.; Wimmer, W. The operational sea surface temperature and sea ice analysis (OSTIA) system. Remote Sens. Environ. 2012, 116, 140–158. [Google Scholar] [CrossRef]
- Willmott, C.J. On the validation of models. Phys. Geogr. 1981, 2, 184–194. [Google Scholar] [CrossRef]
- Wei, E.; Zhang, A. The Tampa Bay Operational Forecast System (TBOFS): Model Development and Skill Assessment. NOAA Technical Report NOS CS 30. 2011. Available online: https://tidesandcurrents.noaa.gov/ofs/publications/TBOFS_TechReport.pdf (accessed on 10 February 2022).
- CORIOLIS. 2022. Available online: https://www.coriolis.eu.org/Data-Products/Data-selection (accessed on 10 August 2022).
- Onken, R. Validation of an ocean shelf model for the prediction of mixed-layer properties in the Mediterranean Sea west of Sardinia. Ocean Sci. 2017, 13, 235–257. [Google Scholar] [CrossRef] [Green Version]
- Onken, R.; Robinson, A.R.; Kantha, L.; Lozano, C.J.; Haley, P.J.; Carniel, S. A rapid response nowcast/forecast system using multiply nested ocean models and distributed data systems. J. Mar. Syst. 2005, 56, 45–66. [Google Scholar] [CrossRef]
- Mourre, B.; Aguiar, E.; Juza, M.; Hernandez-Lasheras, J.; Reyes, E.; Heslop, E.; Escudier, R.; Cutolo, E.; Ruiz, S.; Pascual, A.; et al. Assesment of High-Resolution Regional Ocean Prediction Systems Using Multiplatform Observations: Illustrations in the Western Mediterranean Sea. In New Frontiers in Operational Oceanography; 2018; Volume 663–694, GODAE Ocean View; Available online: https://doi.org/10.17125/gov2018 (accessed on 12 July 2022).
- Lynch, P.; Huang, X.Y. Initialization of the HIRLAM model using a digital filter. Mon. Weather. Rev. 1992, 120, 1019–1034. [Google Scholar] [CrossRef]
- Hastermann, G.; Reinhardt, M.; Klein, R.; Reich, S. Balanced data assimilation for highly oscillatory mechanical systems. Commun. Appl. Math. Comput. Sci. 2021, 16, 119–154. [Google Scholar] [CrossRef]

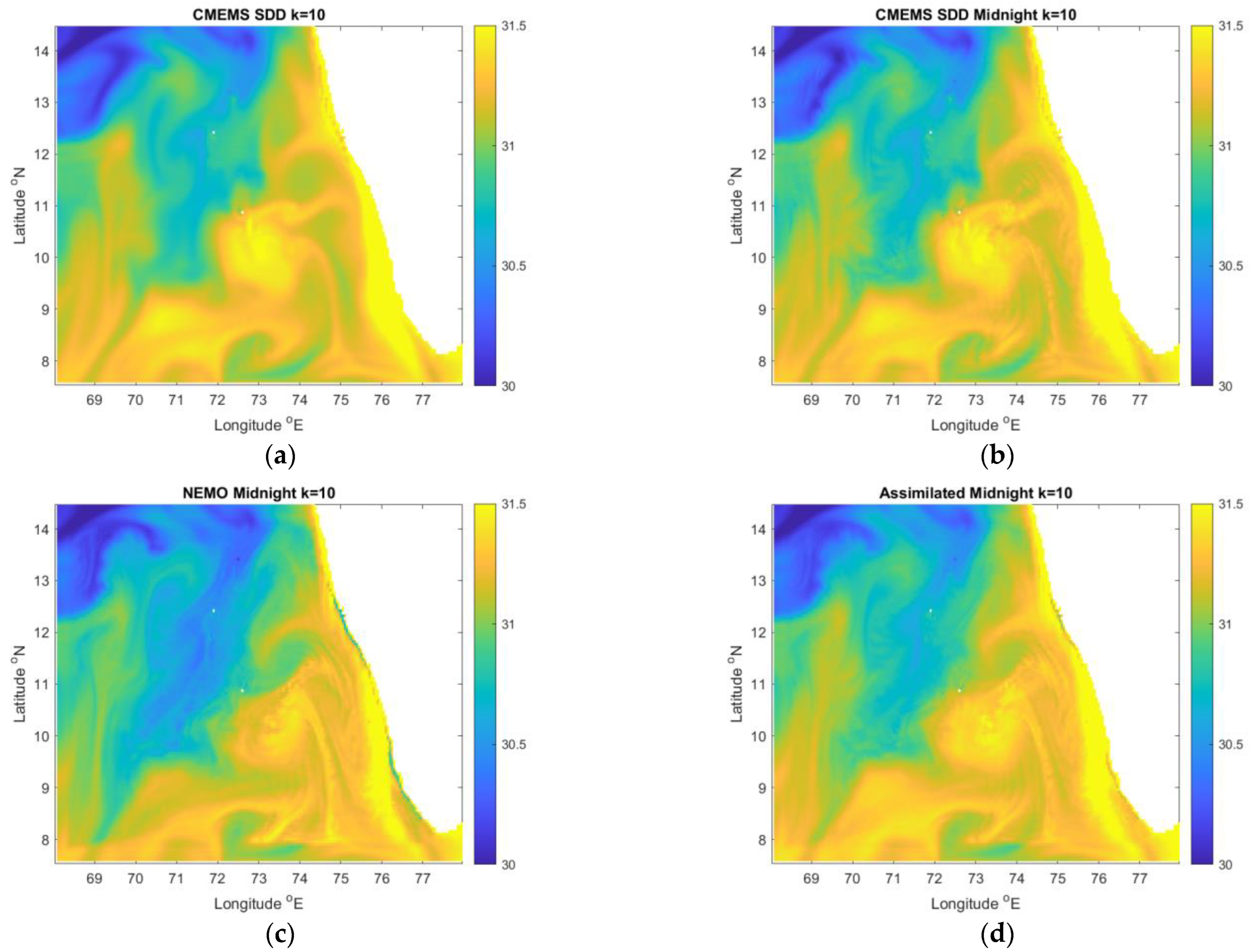
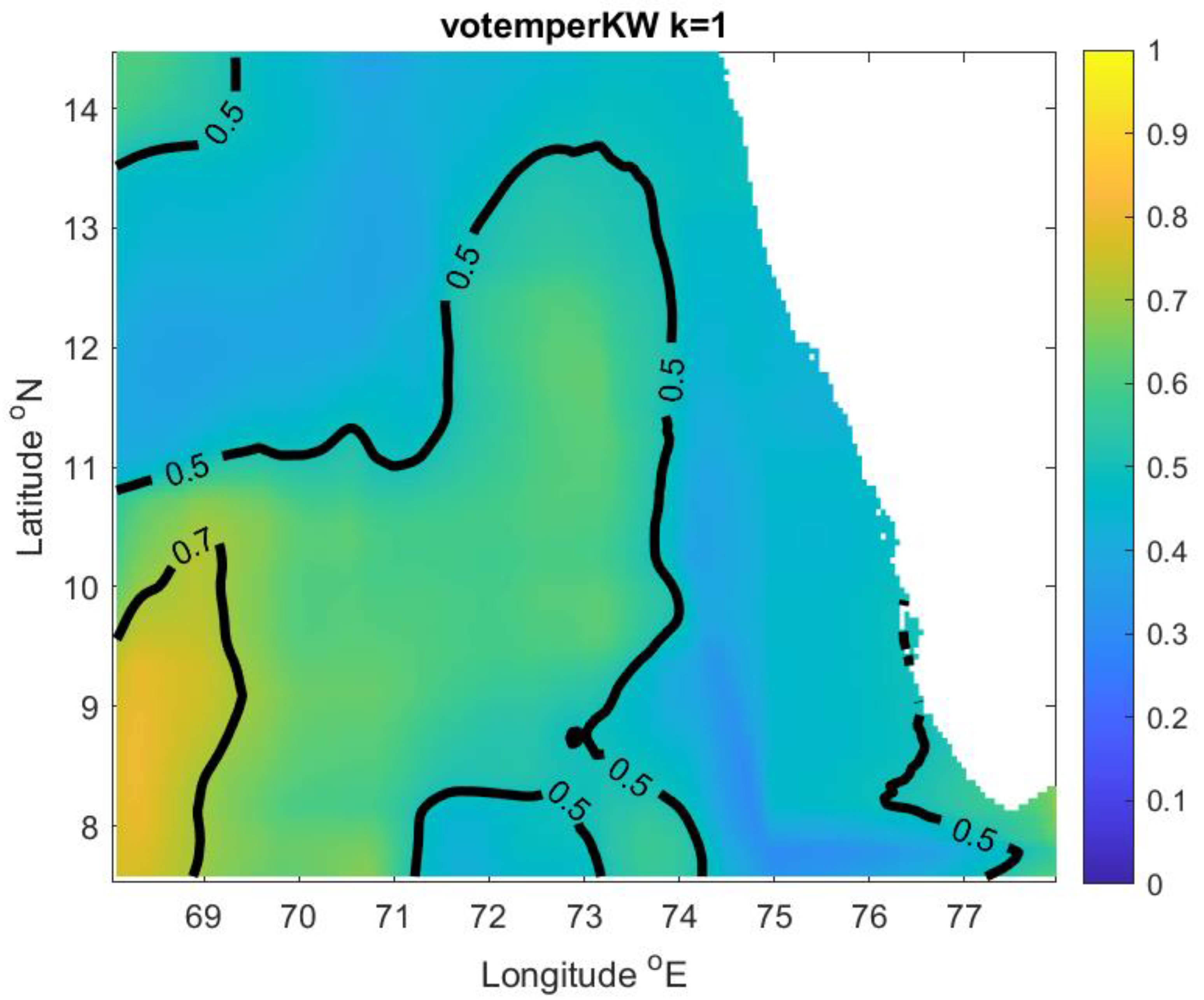

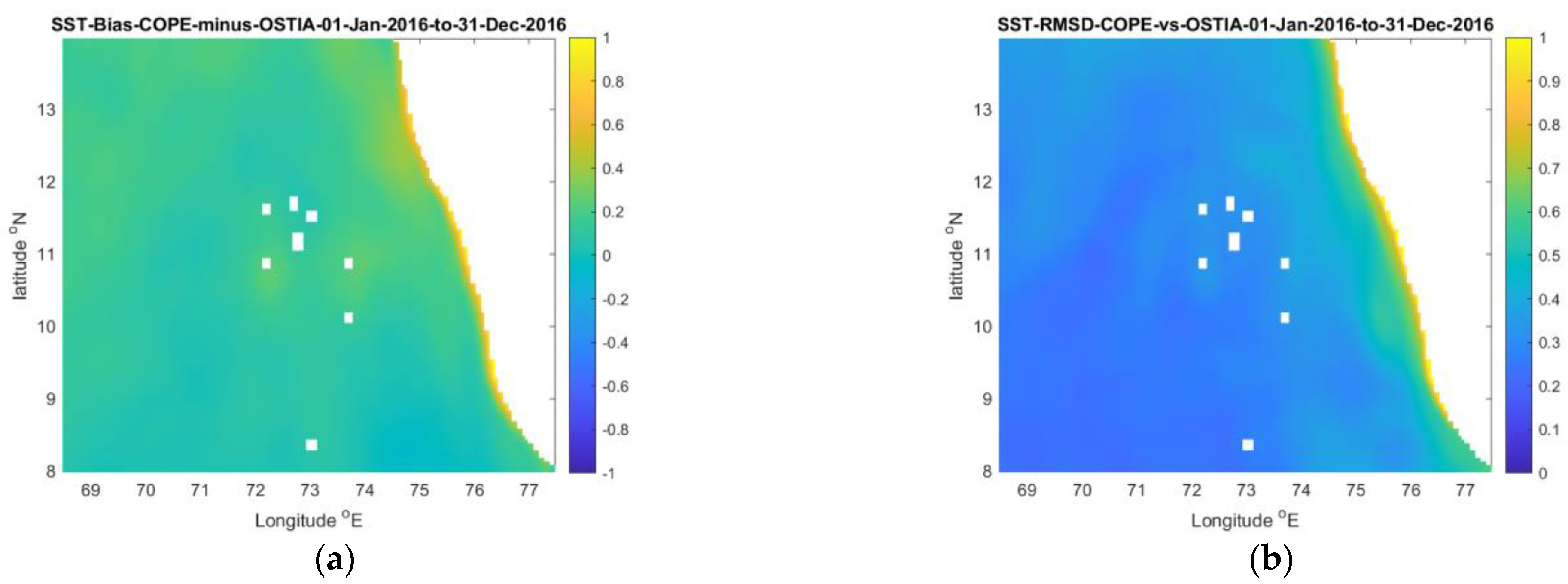
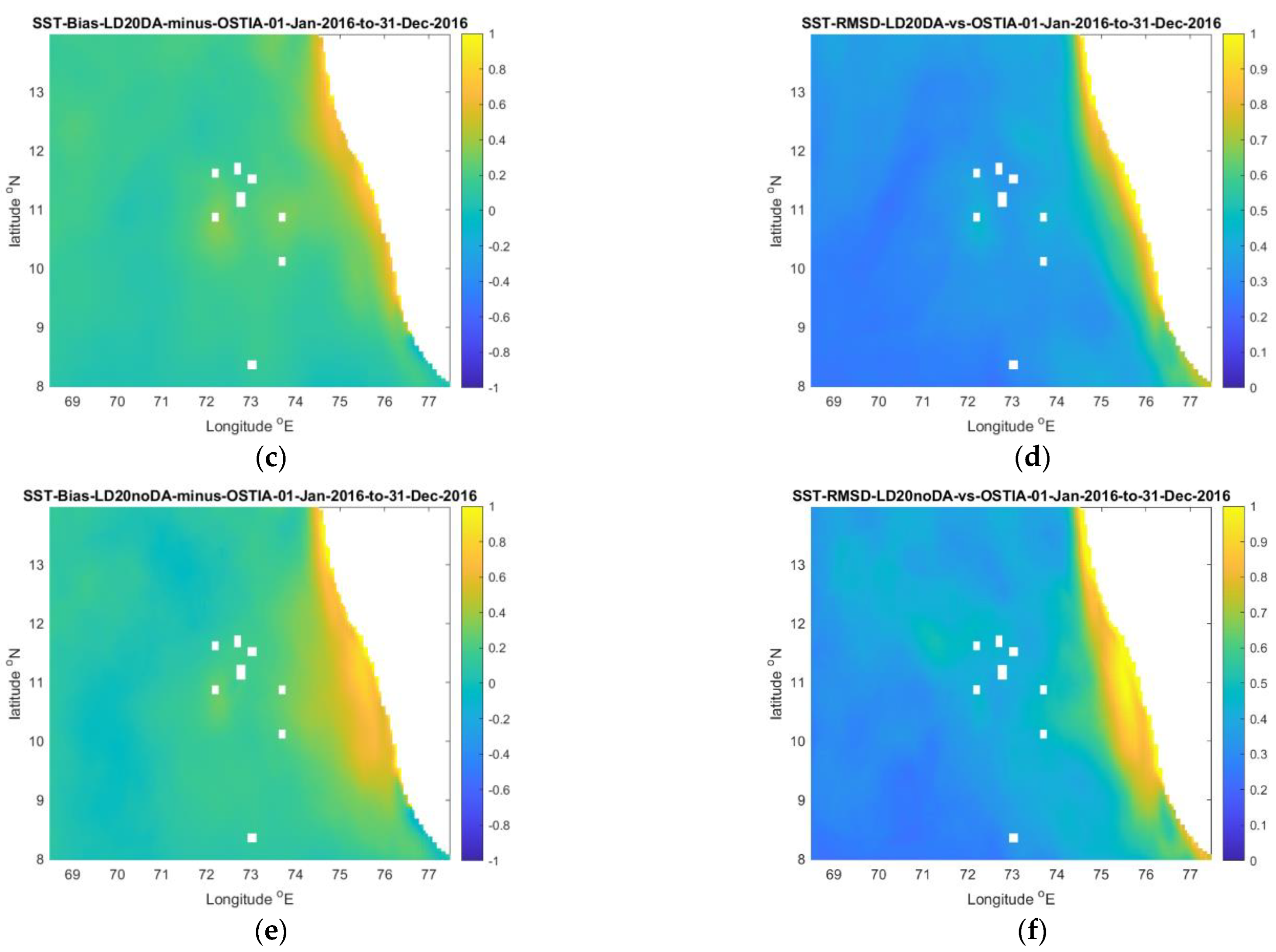
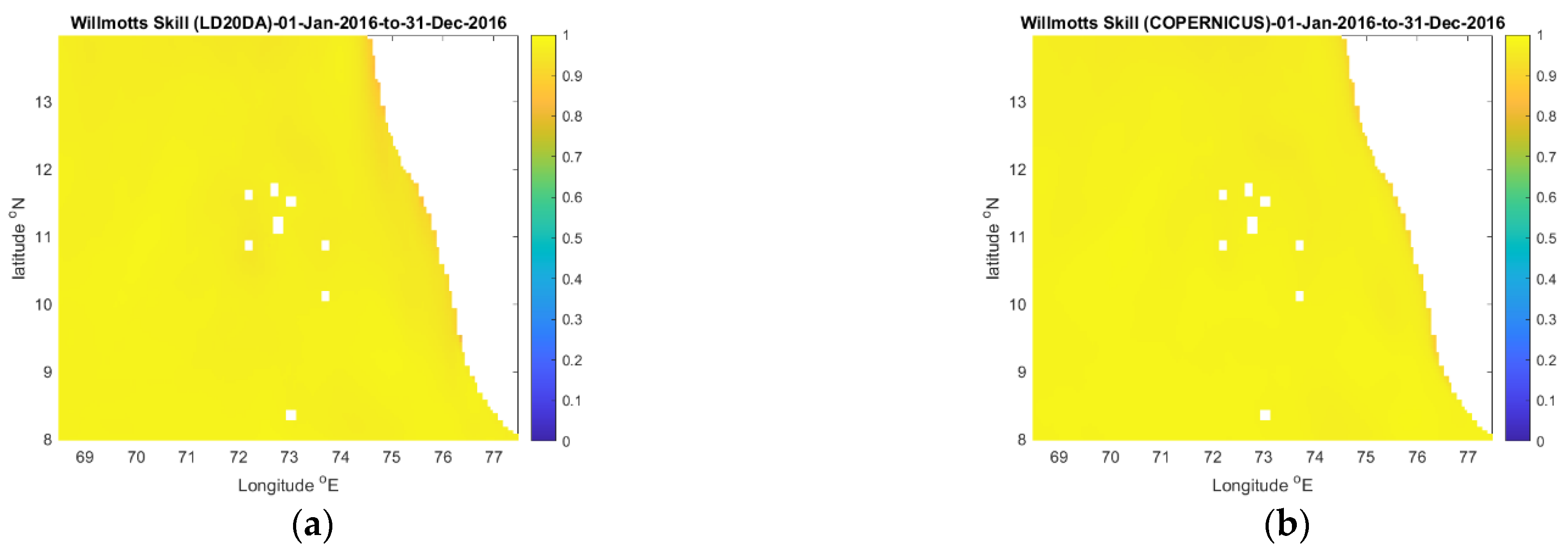
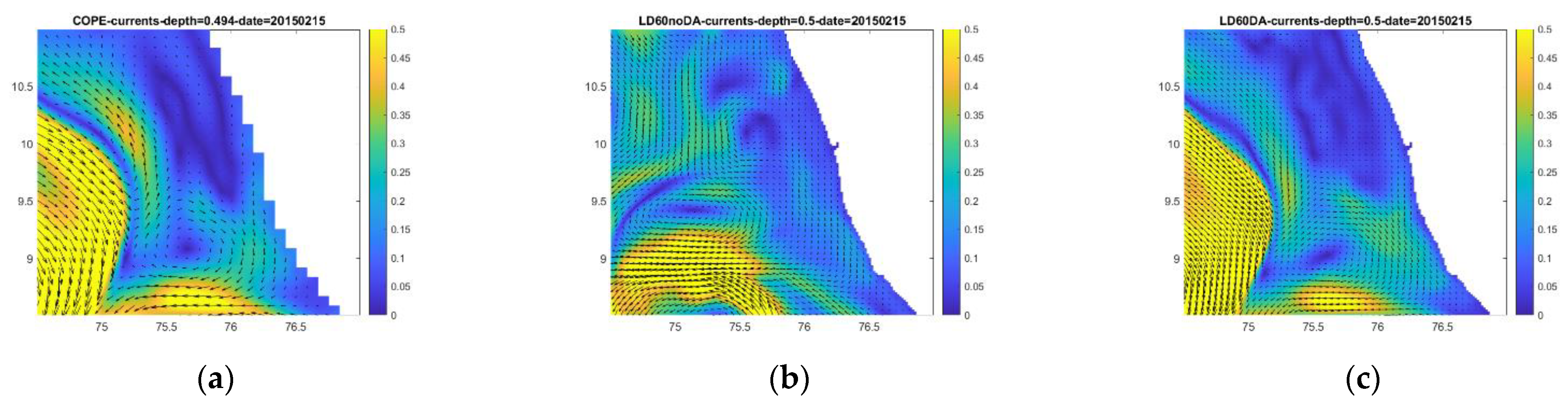
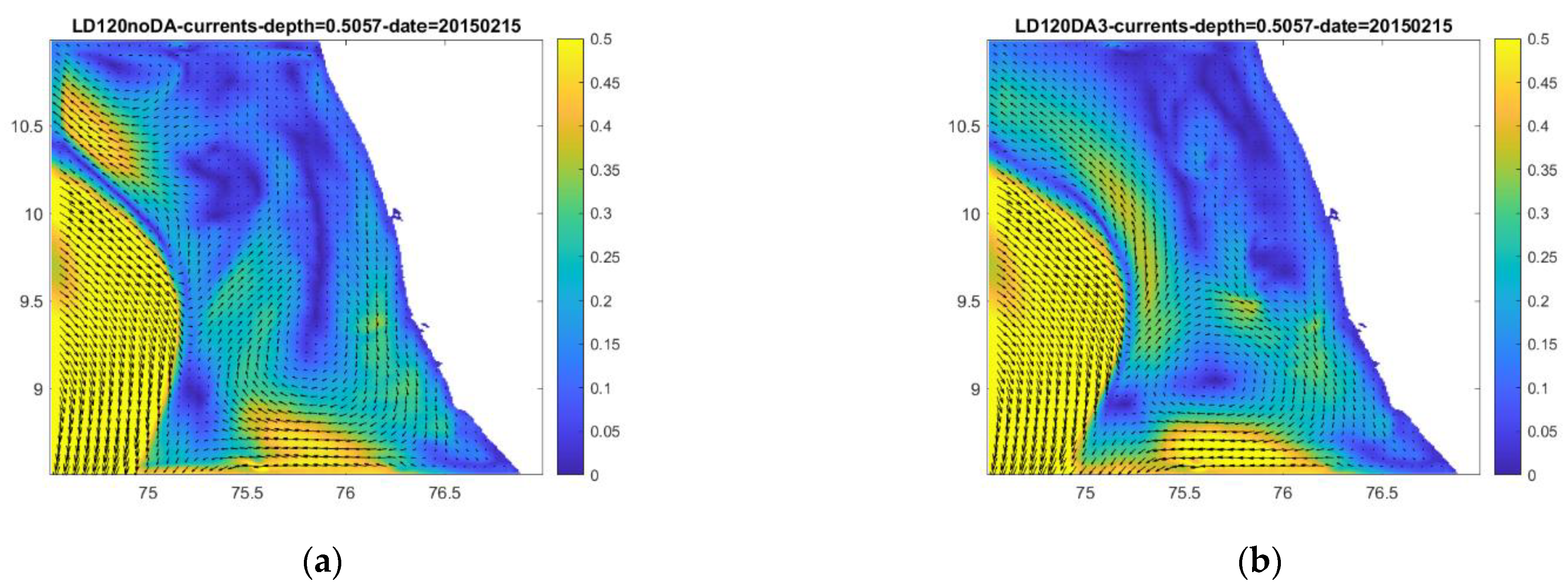
| Variable | (Depth Level)/Depth | Model Output Pairs—All at 24:00GMT on 4 May 2016 | |||
|---|---|---|---|---|---|
| CMEMS vs. LD20_DA (after DA Cycle) | CMEMS vs. LD20_noDA | LD20_noDA vs. LD20_DA (after DA Cycle) | LD20_DA before vs. LD20_DA after DA Cycle | ||
| Temperature | Surface | 0.07 | 0.25 | 0.23 | 0.09 |
| (k = 10) 9.5 m | 0.08 | 0.27 | 0.24 | 0.08 | |
| (k = 20) 53 m | 0.11 | 0.40 | 0.38 | 0.09 | |
| (k = 25) 449 m | 0.04 | 0.20 | 0.20 | 0.03 | |
| Salinity | Surface | 0.10 | 0.33 | 0.31 | 0.08 |
| (k = 10) 9.5 m | 0.10 | 0.32 | 0.30 | 0.08 | |
| (k = 20) 53 m | 0.06 | 0.24 | 0.24 | 0.05 | |
| (k = 25) 449 m | 0.01 | 0.05 | 0.05 | 0.01 | |
| Ref. Data OSTIA | LD20_DA | CMEMS | GHR-MUR | LD20_noDA | |
|---|---|---|---|---|---|
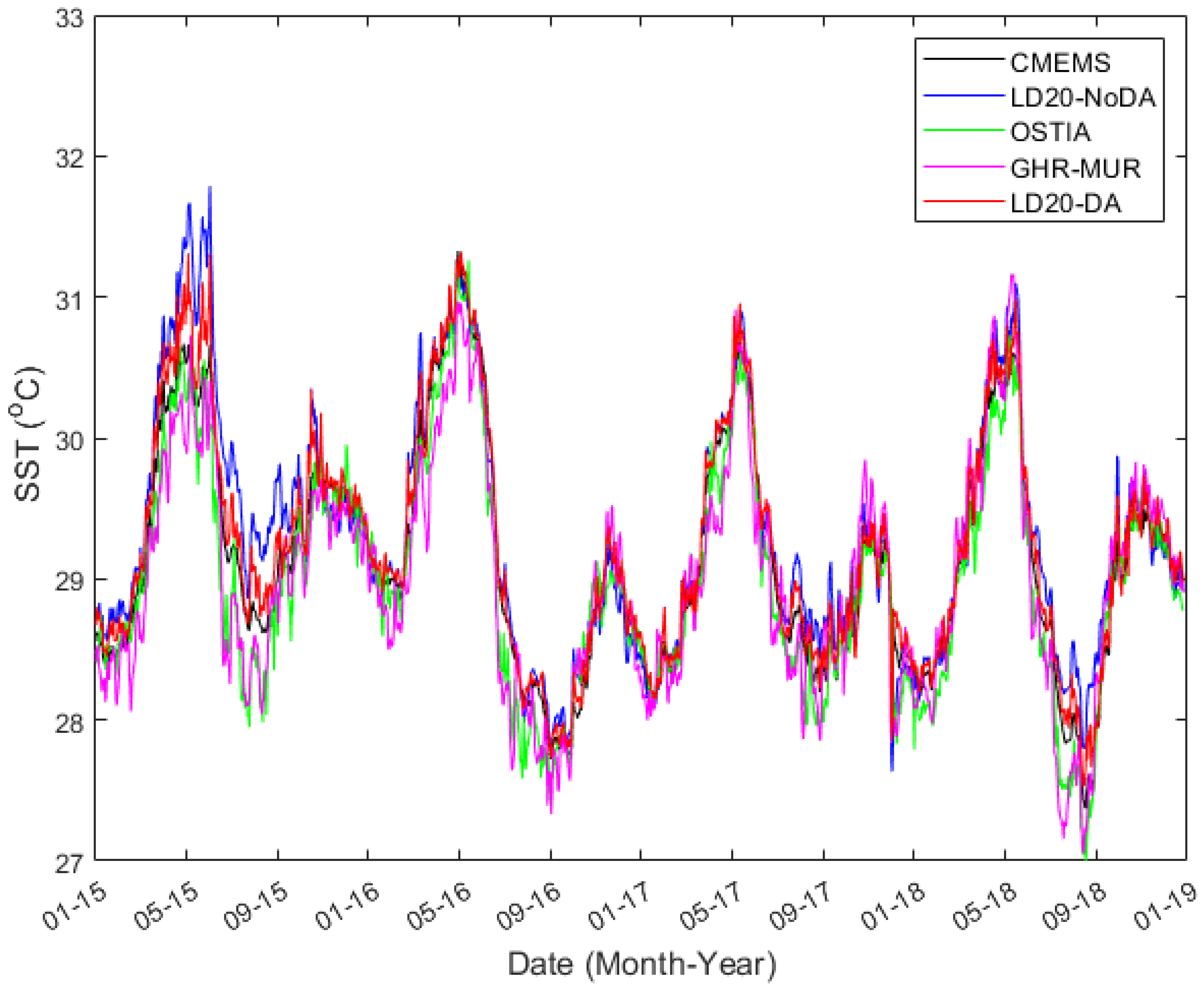
| Average over year 2015–2018 | RMSD, °C | 0.42 | 0.35 | 0.38 | 0.53 |
| BIAS, °C | 0.23 | 0.14 | 0.01 | 0.31 | |
| Corr. | 0.61 | 0.65 | 0.67 | 0.53 |
| Buoy ID | Latitude, °N | Longitude, °E | Period | Bias, °C | RMSD, °C |
|---|---|---|---|---|---|
| MB2300454 | 10.32 | 72.59 | 27 October 2016 to 31 December 2020 | −0.08 | 0.29 |
| MB2300492 | 10.87 | 72.21 | 23 May 2016 to 31 December 2020 | 0.22 | 0.44 |
| MB2300497 | 10.61 | 72.30 | 23 May 2016 to 31 December 2020 | 0.07 | 0.44 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shapiro, G.I.; Gonzalez-Ondina, J.M.; Salim, M.; Tu, J.; Asif, M. Crisis Ocean Modelling with a Relocatable Operational Forecasting System and Its Application to the Lakshadweep Sea (Indian Ocean). J. Mar. Sci. Eng. 2022, 10, 1579. https://doi.org/10.3390/jmse10111579
Shapiro GI, Gonzalez-Ondina JM, Salim M, Tu J, Asif M. Crisis Ocean Modelling with a Relocatable Operational Forecasting System and Its Application to the Lakshadweep Sea (Indian Ocean). Journal of Marine Science and Engineering. 2022; 10(11):1579. https://doi.org/10.3390/jmse10111579
Chicago/Turabian StyleShapiro, Georgy I., Jose M. Gonzalez-Ondina, Mohammed Salim, Jiada Tu, and Muhammad Asif. 2022. "Crisis Ocean Modelling with a Relocatable Operational Forecasting System and Its Application to the Lakshadweep Sea (Indian Ocean)" Journal of Marine Science and Engineering 10, no. 11: 1579. https://doi.org/10.3390/jmse10111579
APA StyleShapiro, G. I., Gonzalez-Ondina, J. M., Salim, M., Tu, J., & Asif, M. (2022). Crisis Ocean Modelling with a Relocatable Operational Forecasting System and Its Application to the Lakshadweep Sea (Indian Ocean). Journal of Marine Science and Engineering, 10(11), 1579. https://doi.org/10.3390/jmse10111579







