Numerical Simulation on Dynamic Characteristics of Longitudinal Launching of Large Container Ships
Abstract
:1. Introductions
2. Numerical Modeling
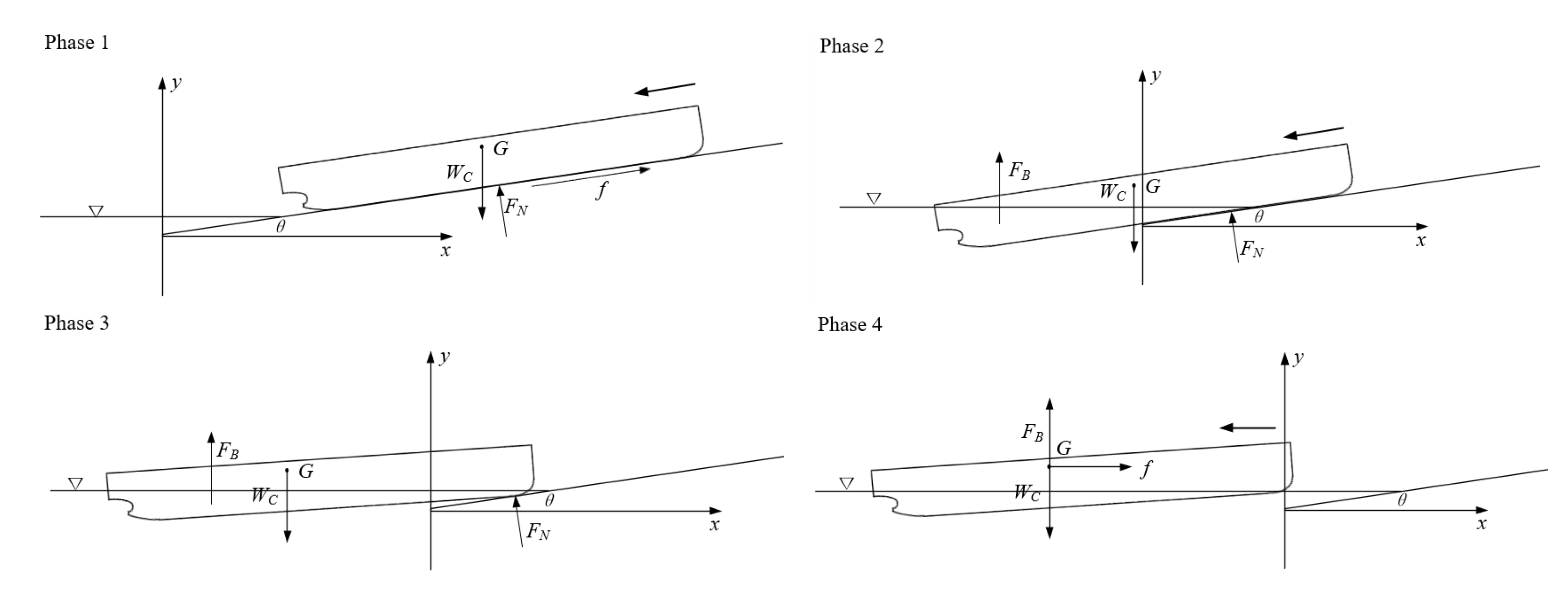
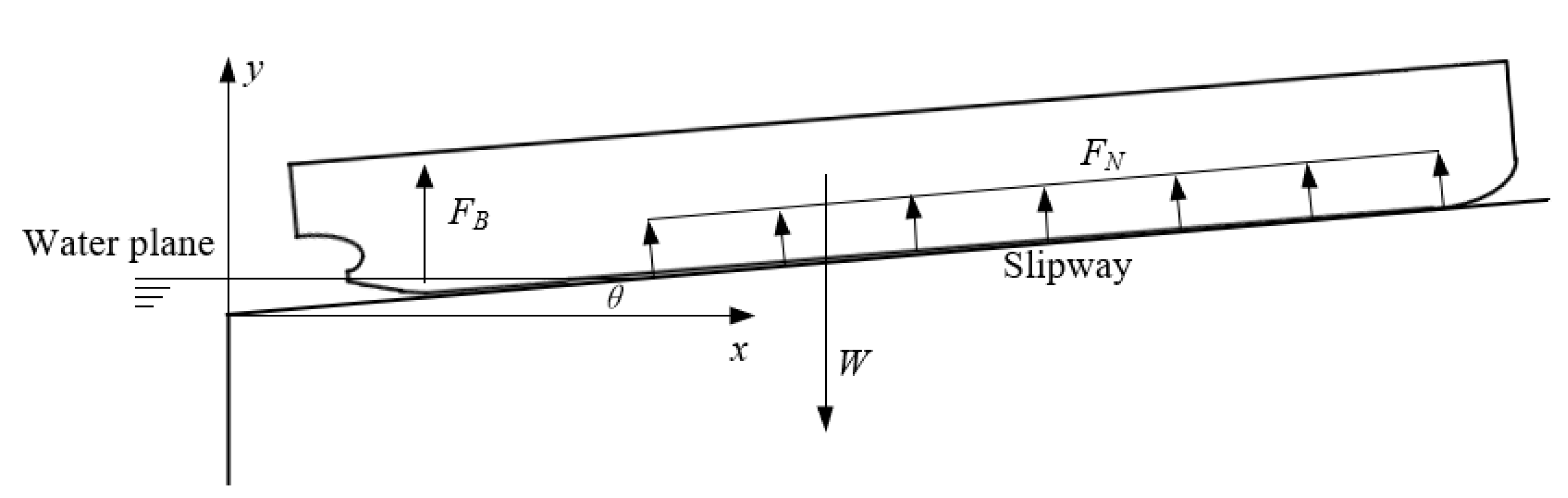
2.1. Theoretical Calculation of Ship Launching
2.2. Numerical Simulation of Flow Field
2.2.1. Governing Equations
2.2.2. Physics Modeling
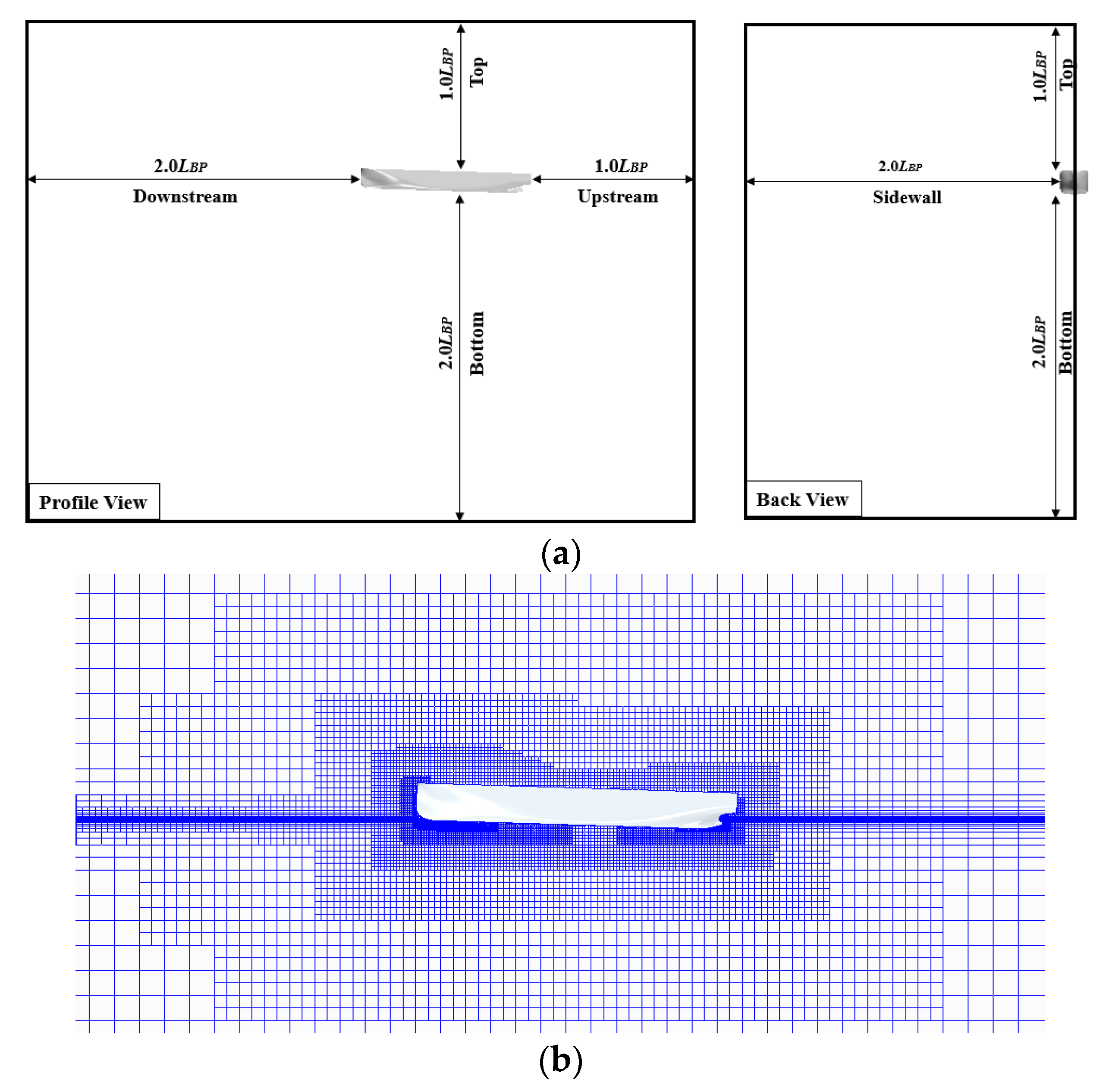
3. Ship Geometry and Mesh Generation
4. Results and Discussion
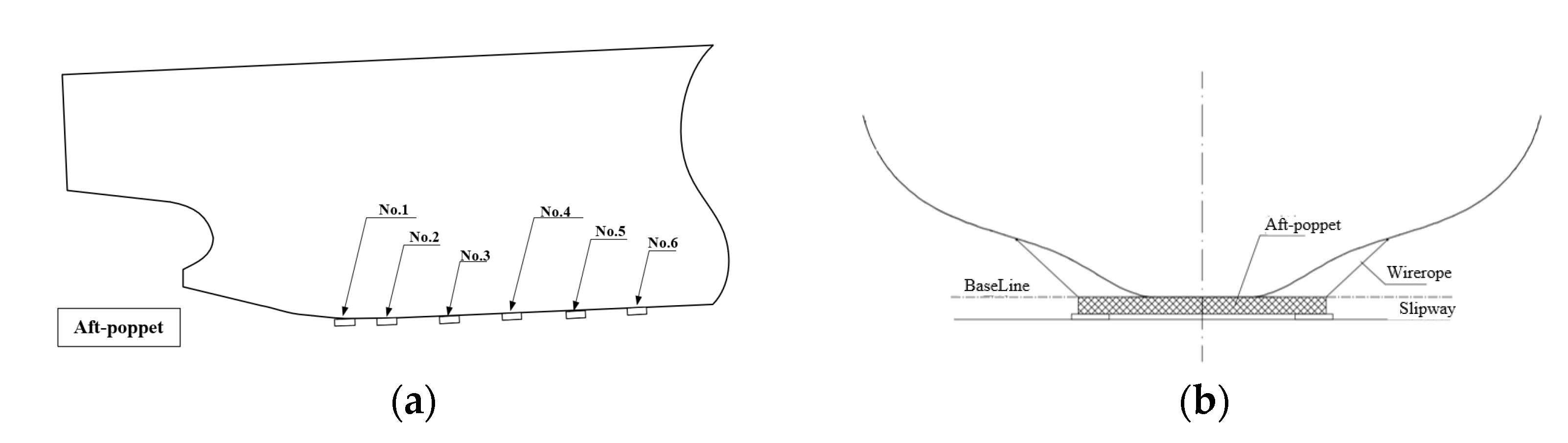
4.1. Validation Study
4.2. Influence of Ship Aft Poppet
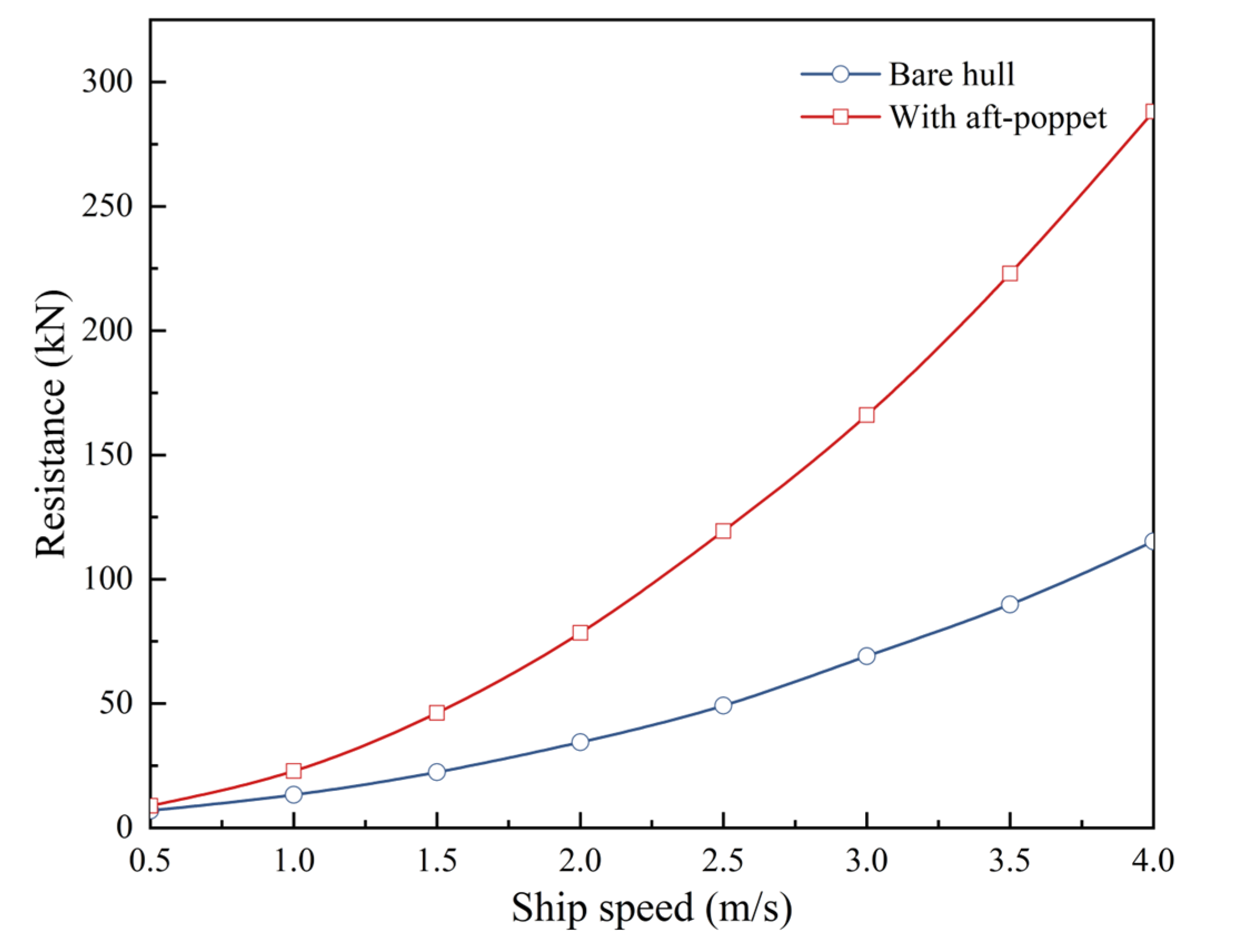
4.2.1. Ship Resistance Curve
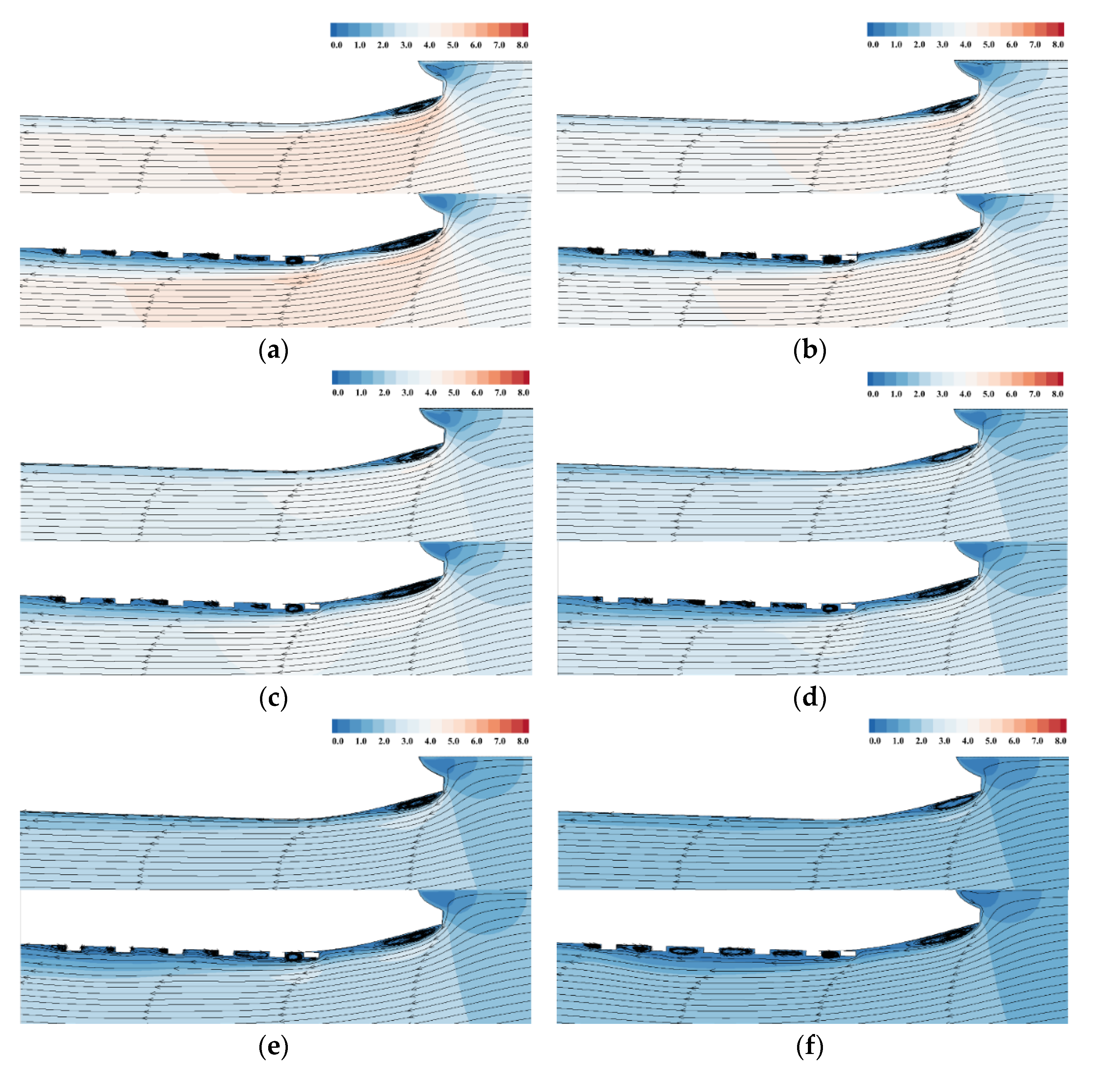
4.2.2. Flow Field Distribution
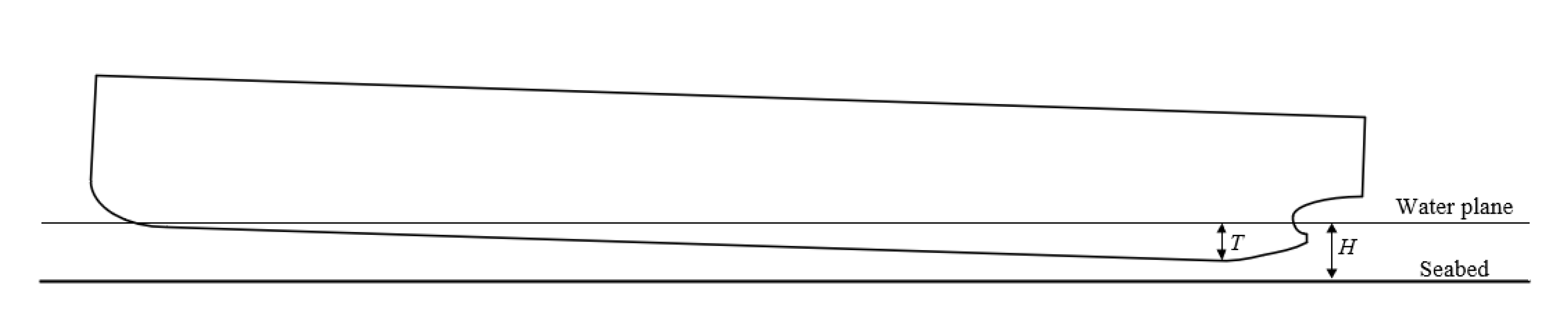
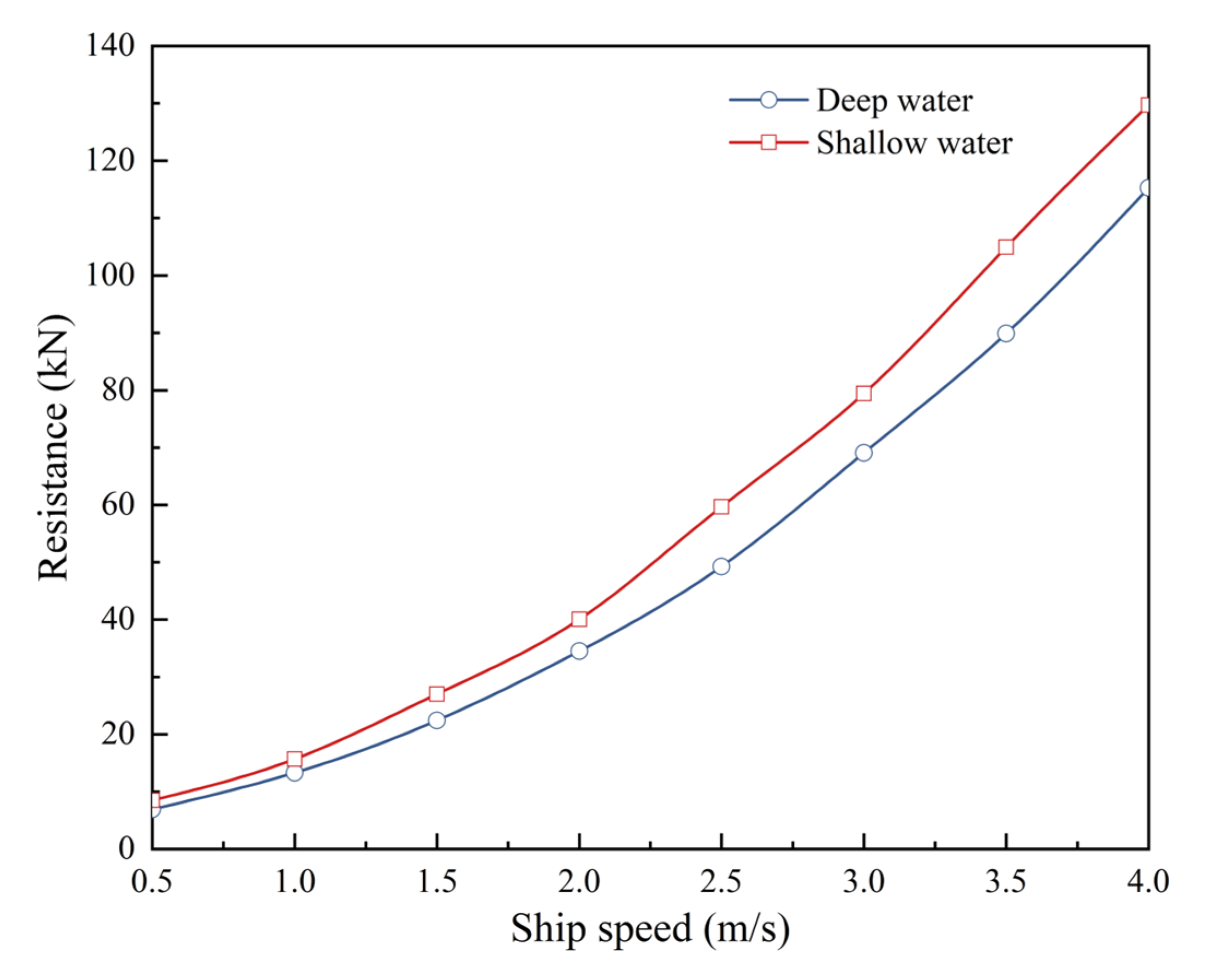
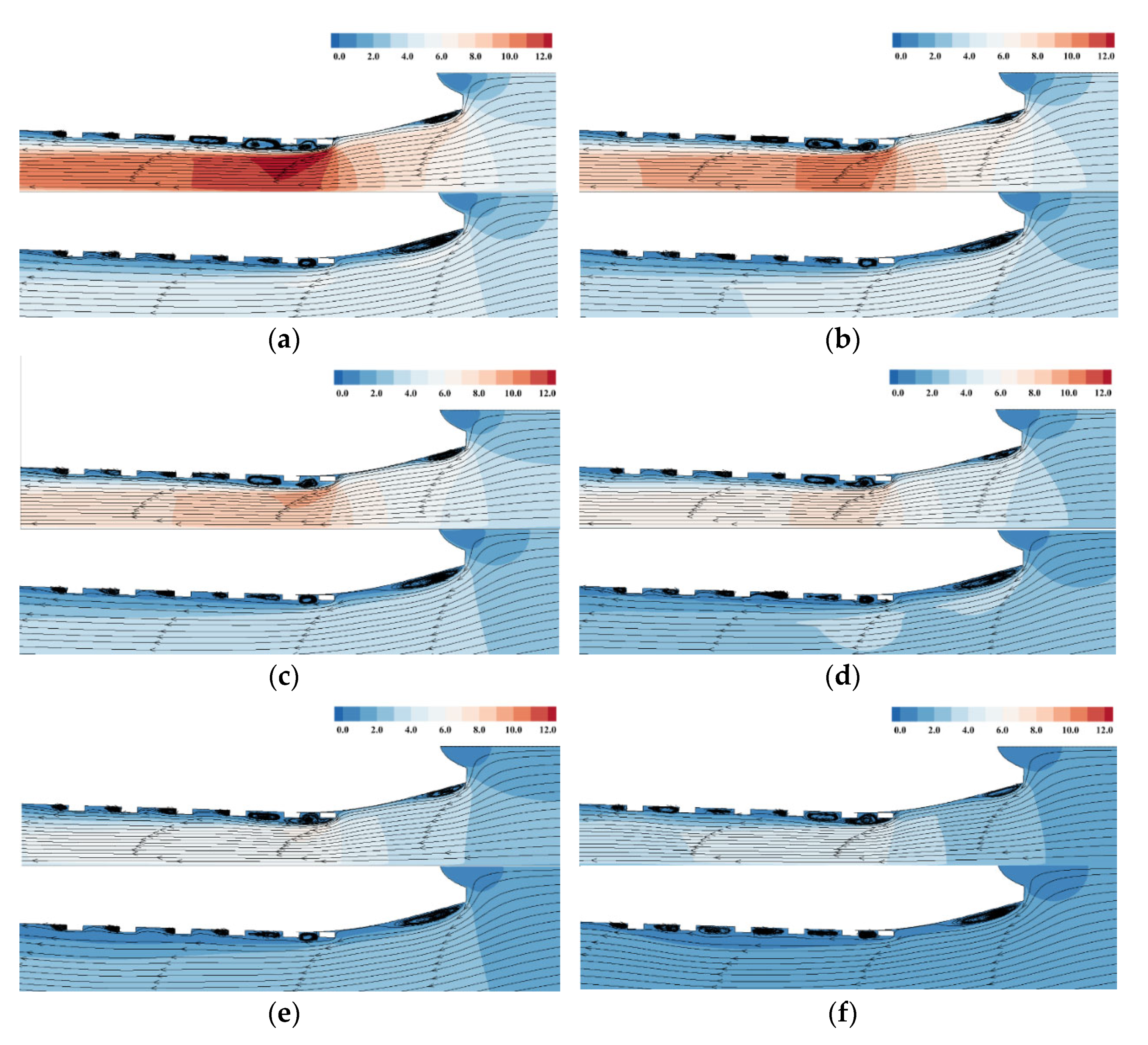
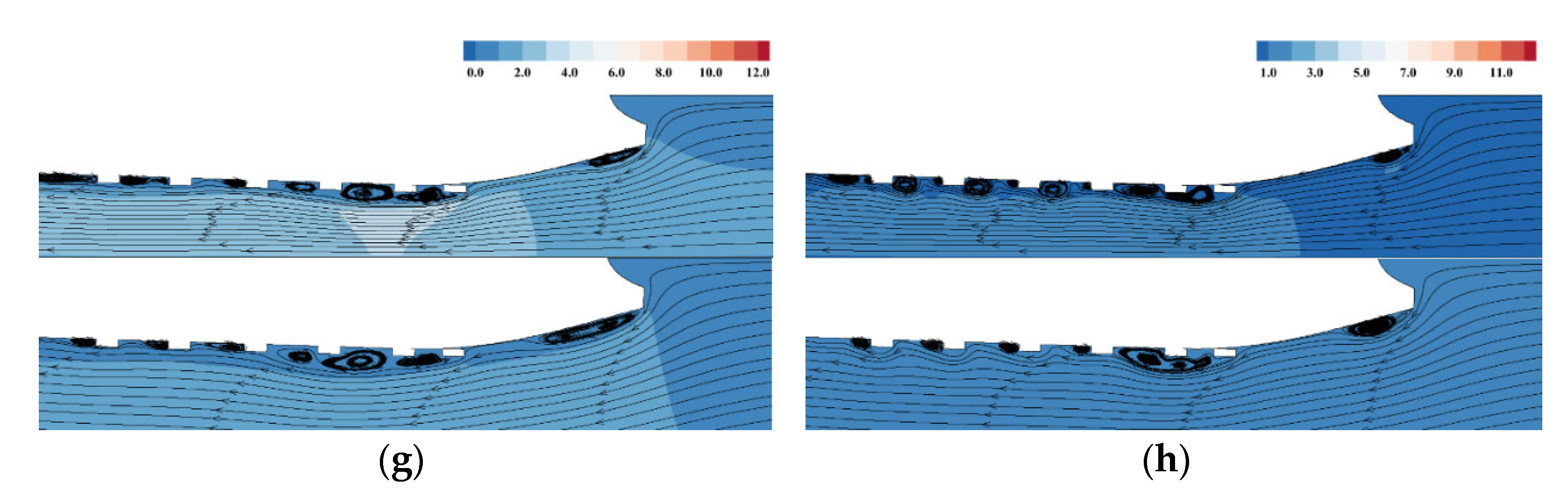
4.3. Influence of Water Depth
4.3.1. Ship Resistance Curve
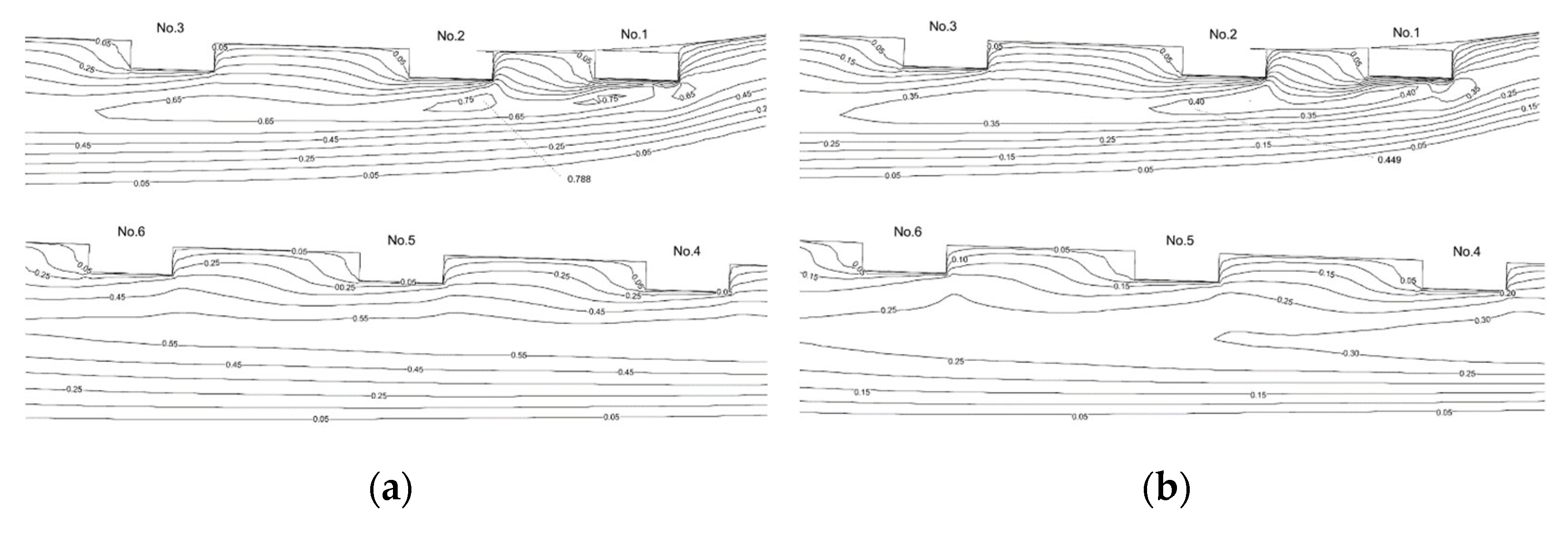
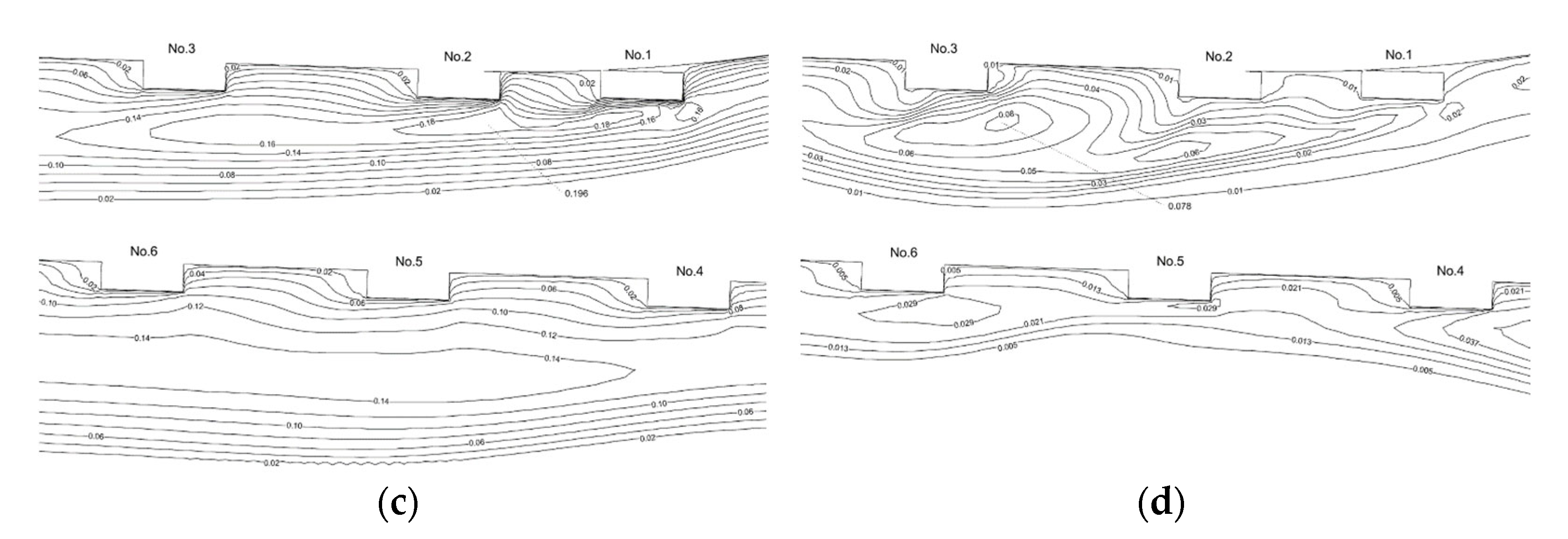
4.3.2. Flow Field Distribution
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sheng, Z.; Liu, Y. Principle of Naval Architecture, 1st ed.; Shanghai Jiao Tong University Press: Shanghai, China, 2003. [Google Scholar]
- Žgomba, D.; Turk, A.; Hadjina, M.; Hadjina, D.; Margić, I. Longitudinal Ship Launching. J. Mar. Trans. Sci. 2020, 3, 239–249. [Google Scholar] [CrossRef]
- Liu, J.; Yu, L. Numerical investigation on nonlinear contact coupling during ship launching process by an array of airbags. Ocean Eng. 2022, 255, 111481. [Google Scholar] [CrossRef]
- Li, H.; Fang, X.; Yu, L. Research on safety of ship launching with airbags under extreme condition of airbag explosion. Ship Eng. 2017, 39, 59–63+79. [Google Scholar]
- Zhong, J.; Cheng, Y.; Liu, J.; Zeng, G. Elastic calculation of ship end launching using ANSYS. J. Ship Mech. 2007, 05, 752–758. [Google Scholar]
- Lin, S.; Sun, J.; Zeng, J.; Xie, D. A direct calculation method for ship longitudinal launching curves. Chin. J. Ship Res. 2016, 11, 128–134. [Google Scholar]
- Farkas, A.; Degiuli, N.; Martić, I. Assessment of hydrodynamic characteristics of a full-scale ship at different draughts. Ocean Eng. 2018, 156, 135–152. [Google Scholar] [CrossRef]
- Degiuli, N.; Farkas, A.; Martić, I.; Zeman, I.; Ruggiero, V.; Vasiljević, V. Numerical and experimental assessment of the total resistance of a yacht. Brodogradnja 2021, 72, 61–80. [Google Scholar] [CrossRef]
- Zhao, C.; Wang, W.; Jia, P.; Xie, Y. Optimisation of hull form of ocean-going trawler. Brodogradnja 2021, 72, 33–46. [Google Scholar] [CrossRef]
- Farkas, A.; Degiuli, N.; Martić, I.; Dejhalla, R. Numerical and experimental assessment of nominal wake for a bulk carrier. J. Mar. Sci. Technol. 2019, 24, 1092–1104. [Google Scholar] [CrossRef]
- Bašić, J.; Degiuli, N.; Dejhalla, R. Total resistance prediction of an intact and damaged tanker with flooded tanks in calm water. Ocean Eng. 2017, 130, 83–91. [Google Scholar] [CrossRef]
- Senjanovic, I.; Katavić, J.; Vukcevic, V.; Vladimir, N.; Jasak, H. Launching of ships from horizontal berth by tipping tables—CFD simulation of wave generation. Eng. Struct. 2020, 210, 110343. [Google Scholar] [CrossRef]
- Fitriadhy, A.; Malek, A.M. Computational fluid dynamics analysis of a ship’s side launching in restricted waters. J. Mech. Eng. Sci. 2017, 11, 2993–3003. [Google Scholar] [CrossRef]
- Güzel, B.; Korkmaz, F.C. Reducing water entry impact loads on marine structures by surface modification. Brodogradnja 2020, 71, 1–18. [Google Scholar] [CrossRef]
- Li, H.; Yu, H.; Li, X.; Ren, H. Dynamic analysis of longitudinal ship launching in restricted water. Shipbuild. China 2009, 50, 61–66. [Google Scholar]
- Wang, W.; Wang, Y. Dynamic analysis for ship launching based on CFD method. J. Dalian Marit. Univ. 2009, 35, 1–4. [Google Scholar]
- Blagoveschensky, C.N. Manual of Ship Theory, 1st ed.; National Shipbuilding Literature Press: Leningrad, Russia, 1950. [Google Scholar]
- Ferziger, J.H.; Perić., M.; Street, R.L. Computational Methods for Fluid Dynamics, 4th ed.; Springer: Cham, Germany, 2020. [Google Scholar]
- Menter, F.R. Two-equation eddy-viscosity turbulence modeling for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef] [Green Version]
- Wilcox, D.C. Turbulence Modeling for CFD, 2nd ed.; DCW Industries Inc.: La Canada, CA, USA, 1998. [Google Scholar]
- Wilcox, D.C. Formulation of the k-ω turbulence model revisited. AIAA J. 2008, 46, 2823–2838. [Google Scholar] [CrossRef] [Green Version]
- Berberović, E.; Van Hinsberg, N.; Jakirlić, S.; Roisman, I.; Tropea, C. Drop impact onto a liquid layer of finite thickness: Dynamics of the cavity evolution. Phys. Rev. E 2009, 79, 036306. [Google Scholar] [CrossRef] [PubMed]
- Yang, K.; Duan, W.; Huang, L.; Zhang, P. A prediction method for ship added resistance based on symbiosis of data-driven and physics-based models. Ocean Eng. 2022, 260, 112012. [Google Scholar] [CrossRef]
- Park, S.; Park, S.; Rhee, S.; Lee, S.; Chol, J. Kang, S. Investigation on the wall function implementation for the prediction of ship resistance. Int. J. Nav. Archit. Ocean. Eng. 2013, 5, 33–46. [Google Scholar] [CrossRef] [Green Version]
- Islam, H.; Rahaman, M.; Akimoto, H.; Islam, M. Calm Water Resistance Prediction of a Container Ship Using Reynolds Averaged Navier-stokes Based Solver. Procedia Eng. 2017, 194, 25–30. [Google Scholar] [CrossRef]
- Zhang, W. Shallow water effect on ship and its empirical calculation method. Nav. Arch. Ocean Eng. 2019, 35, 6–12. [Google Scholar]




| Parameters | Symbols | Value |
|---|---|---|
| Draft fore | dF (m) | 0.1116 |
| Draft aft | dA (m) | 9.8832 |
| Initial velocity of drift stage | v (m/s) | 4.0589 |
| Main Particulars | Symbols | Value |
|---|---|---|
| Length between perpendiculars | LBP (m) | 300.5 |
| Length overall | LOA (m) | 306 |
| Breath molded | BWL (m) | 51.4 |
| Depth molded | D (m) | 29.5 |
| Launching weight | M (t) | 44,450 |
| Longitudinal center of gravity | LCG (m) | 123.87 |
| Vertical center of gravity | VCG (m) | 19.53 |
| Particulars | Symbols | Value |
|---|---|---|
| Temperature | Temp (°C) | 15.8 |
| Density | ρ (kg/m3) | 998.98 |
| Kinematic viscosity | v (m2/s) | 1.115 × 10−6 |
| Depth | DEXP (m) | 4.2 |
| Spatial Convergence | Temporal Convergence | |
|---|---|---|
| N1(Δt1) | 6,795,241 | 0.05 s |
| N2(Δt2) | 3,742,260 | 0.1 s |
| N3(Δt3) | 2,079,624 | 0.2 s |
| r21 | 1.35 | 2.0 |
| r23 | 1.34 | 2.0 |
| φ1 | 0.0020060 | 0.0020072 |
| φ2 | 0.0019892 | 0.0019927 |
| φ3 | 0.0019549 | 0.0019758 |
| ε32 | −3.43 × 10−5 | −1.69 × 10−5 |
| ε21 | −1.68 × 10−5 | −1.45 × 10−5 |
| s | 1.0 | 1.0 |
| 0.84% | 0.72% | |
| q | 2.90 × 10−2 | 0.0 |
| pa | 2.475 | 0.221 |
| 2.054 × 10−3 | 2.022 × 10−3 | |
| 2.64% | 0.72% | |
| 3.00% | 0.90% |
| Grid | Grid Quantity | Resistance Coefficient (Ct) | Error (%) |
|---|---|---|---|
| N3 | 2.079 | 0.0019549 | 3.17 |
| N2 | 3.742 | 0.0019892 | 1.47 |
| N1 | 6.795 | 0.0020060 | 0.64 |
| EFD | --- | 0.0020189 | --- |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, K.; Wang, Y.; Wu, Z.; Pi, J.; Gho, W.M.; Zhou, B. Numerical Simulation on Dynamic Characteristics of Longitudinal Launching of Large Container Ships. J. Mar. Sci. Eng. 2022, 10, 1583. https://doi.org/10.3390/jmse10111583
Liu K, Wang Y, Wu Z, Pi J, Gho WM, Zhou B. Numerical Simulation on Dynamic Characteristics of Longitudinal Launching of Large Container Ships. Journal of Marine Science and Engineering. 2022; 10(11):1583. https://doi.org/10.3390/jmse10111583
Chicago/Turabian StyleLiu, Kaihua, Yu Wang, Zhifei Wu, Juntao Pi, Wie Min Gho, and Bo Zhou. 2022. "Numerical Simulation on Dynamic Characteristics of Longitudinal Launching of Large Container Ships" Journal of Marine Science and Engineering 10, no. 11: 1583. https://doi.org/10.3390/jmse10111583
APA StyleLiu, K., Wang, Y., Wu, Z., Pi, J., Gho, W. M., & Zhou, B. (2022). Numerical Simulation on Dynamic Characteristics of Longitudinal Launching of Large Container Ships. Journal of Marine Science and Engineering, 10(11), 1583. https://doi.org/10.3390/jmse10111583








