Numerical Simulation of Wave Overtopping of an Ecologically Honeycomb-Type Revetment with Rigid Vegetation
Abstract
:1. Introduction
2. Numerical Model
2.1. Numerical Wave Tank
2.2. CFD-DPM Coupling Model
2.2.1. The Computation of Fluid Phase and Particle Phase
2.2.2. The Coupling of Fluid and Particle
2.3. DPM-VOF Coupling Model
3. Validations
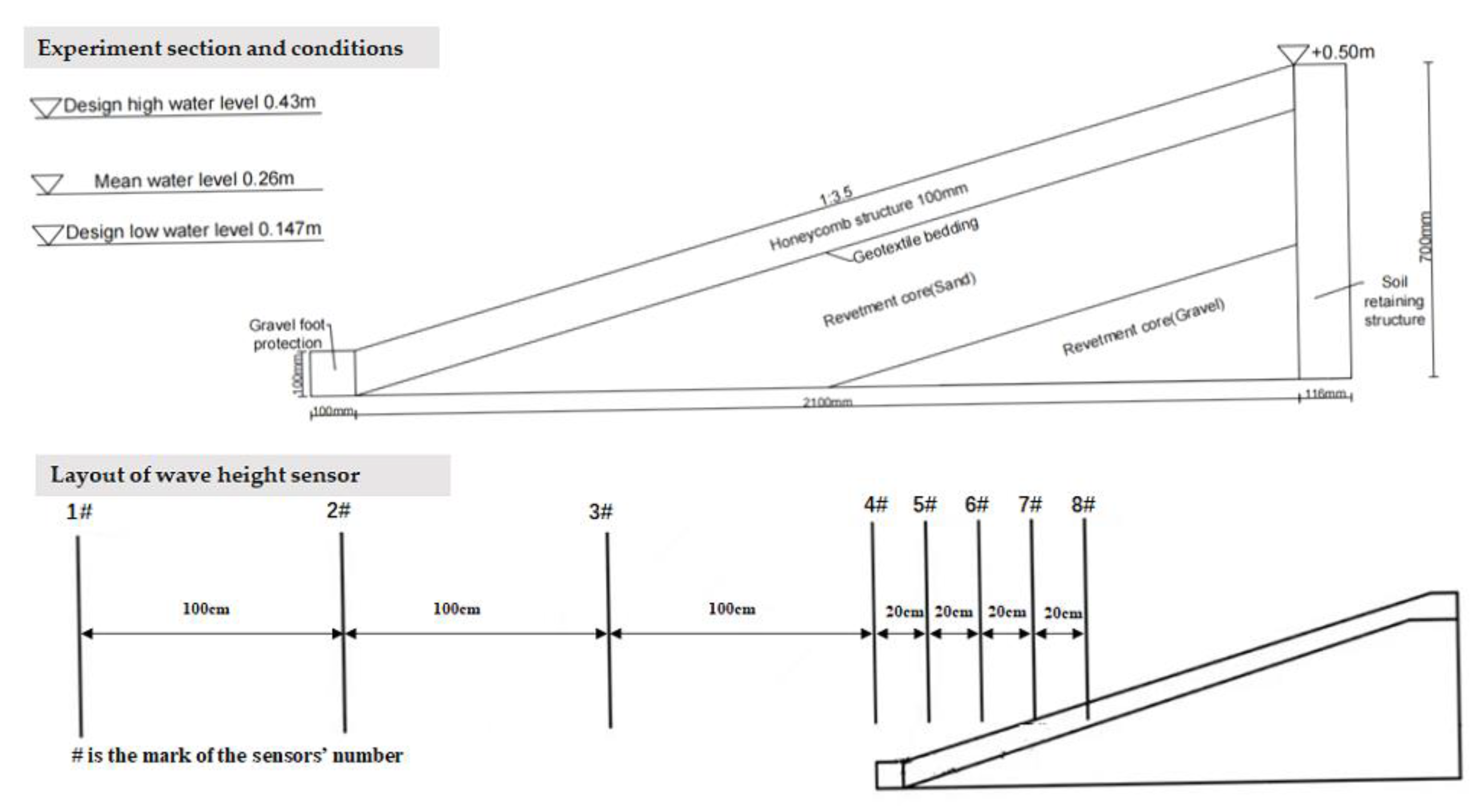
3.1. Brief Introduction of Physical Model Experiment
3.2. Establishment of Vegetated Honeycomb-Type Revetment Model
3.3. Model Verification
4. Effect of Honeycomb Revetment with a Rigid Plant on Wave Overtopping
4.1. Case Setting
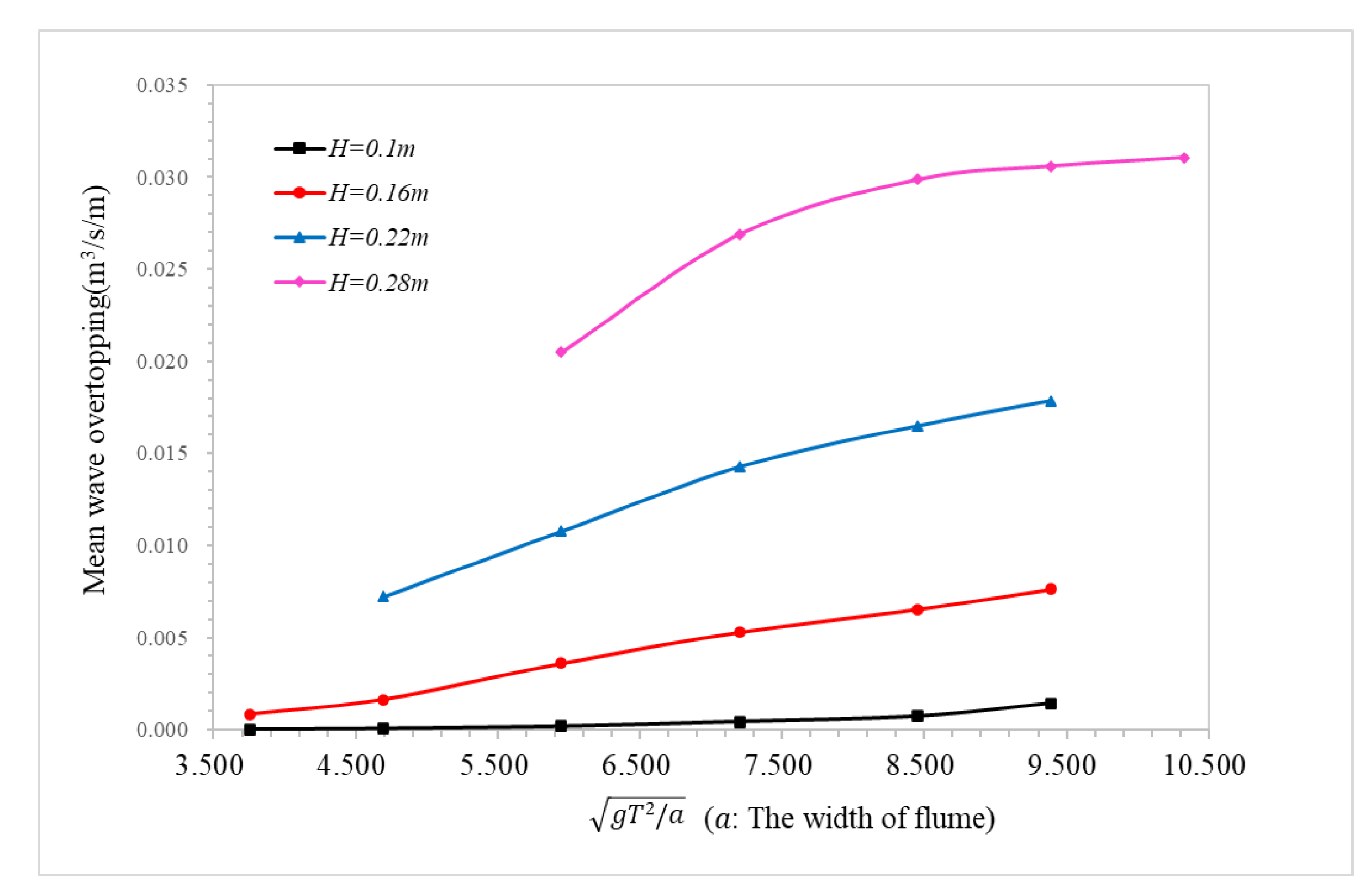
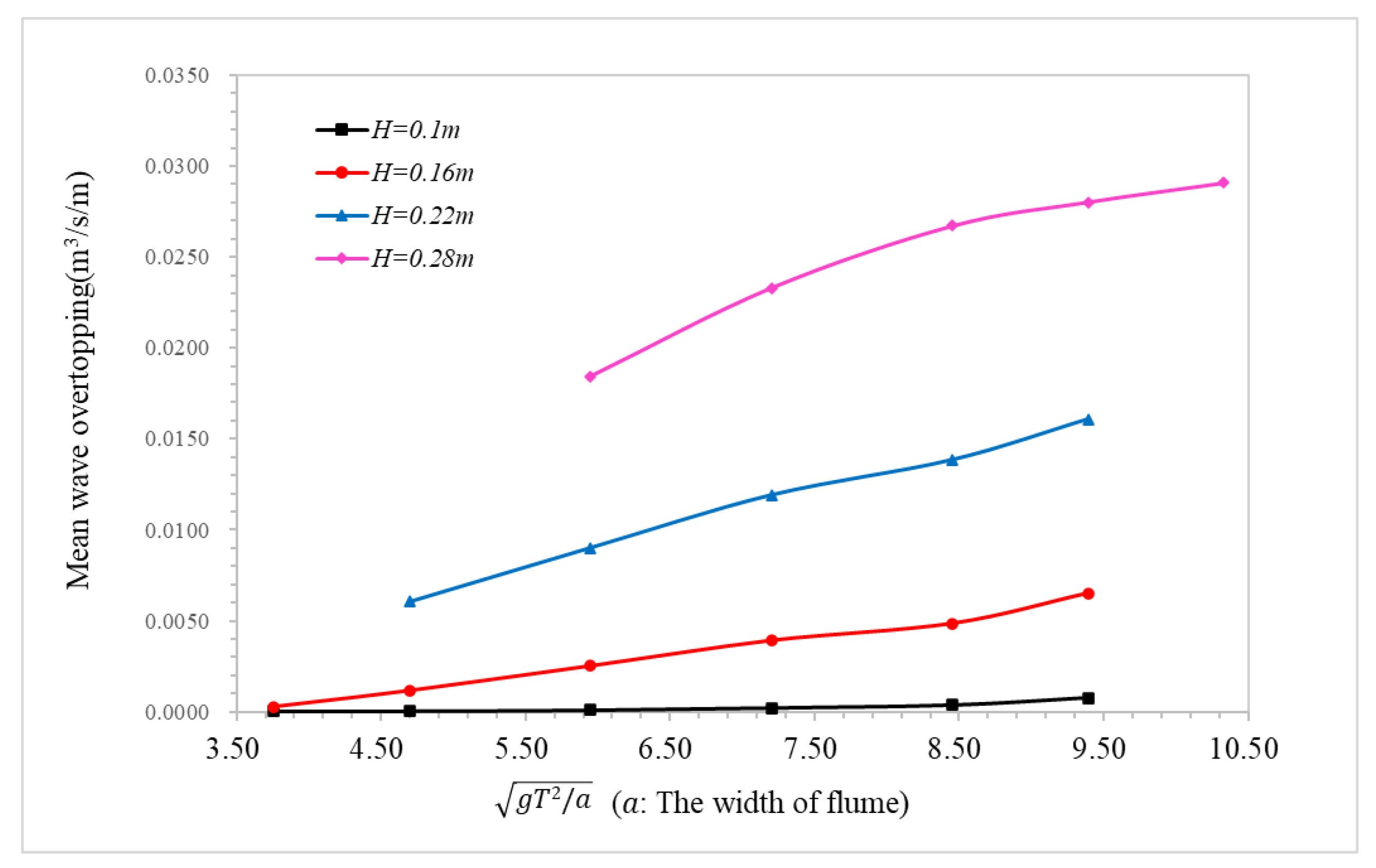
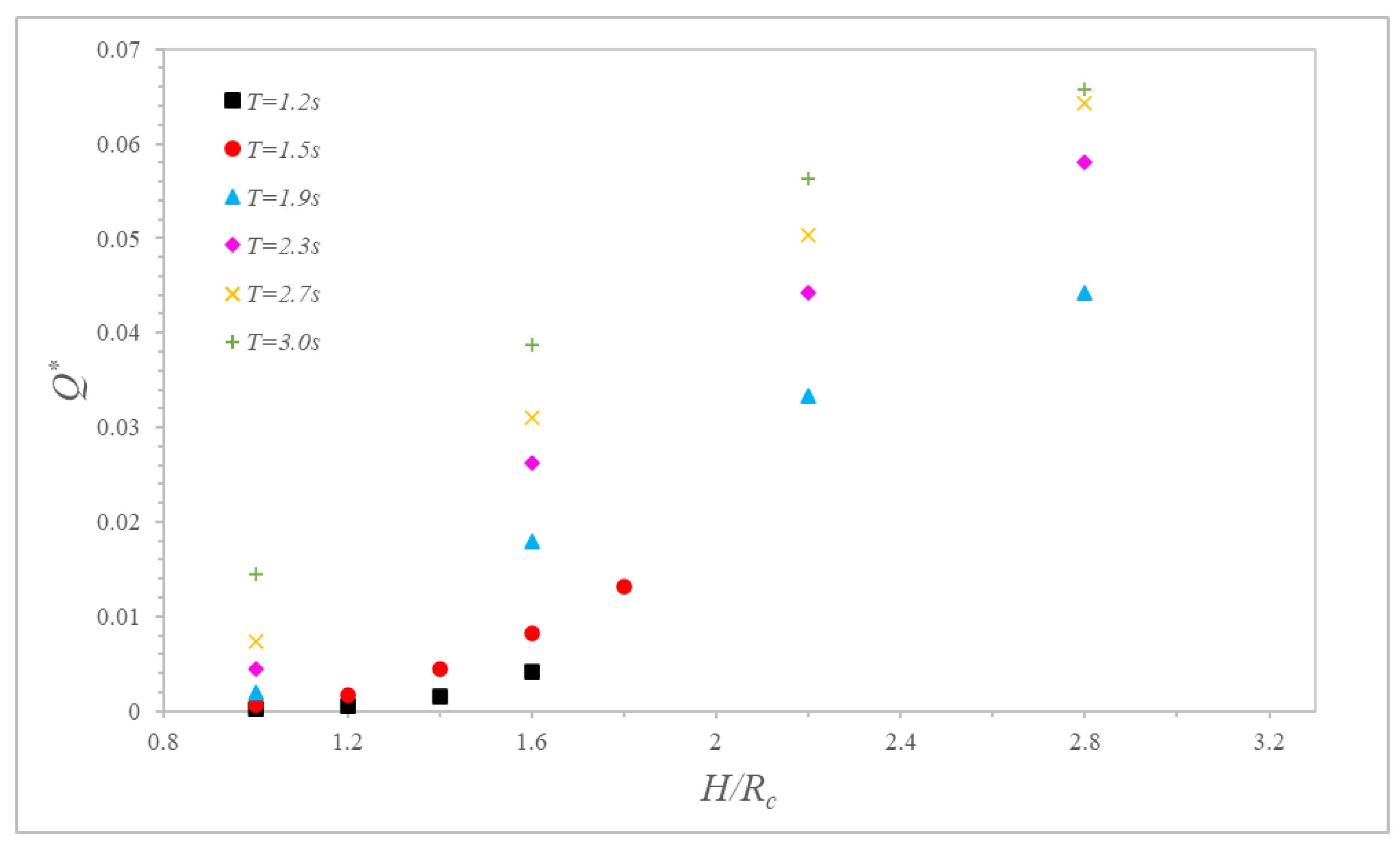
4.2. Effect of Wave Period on the Wave Overtopping
4.2.1. Low Vegetation Density
4.2.2. High Vegetation Density
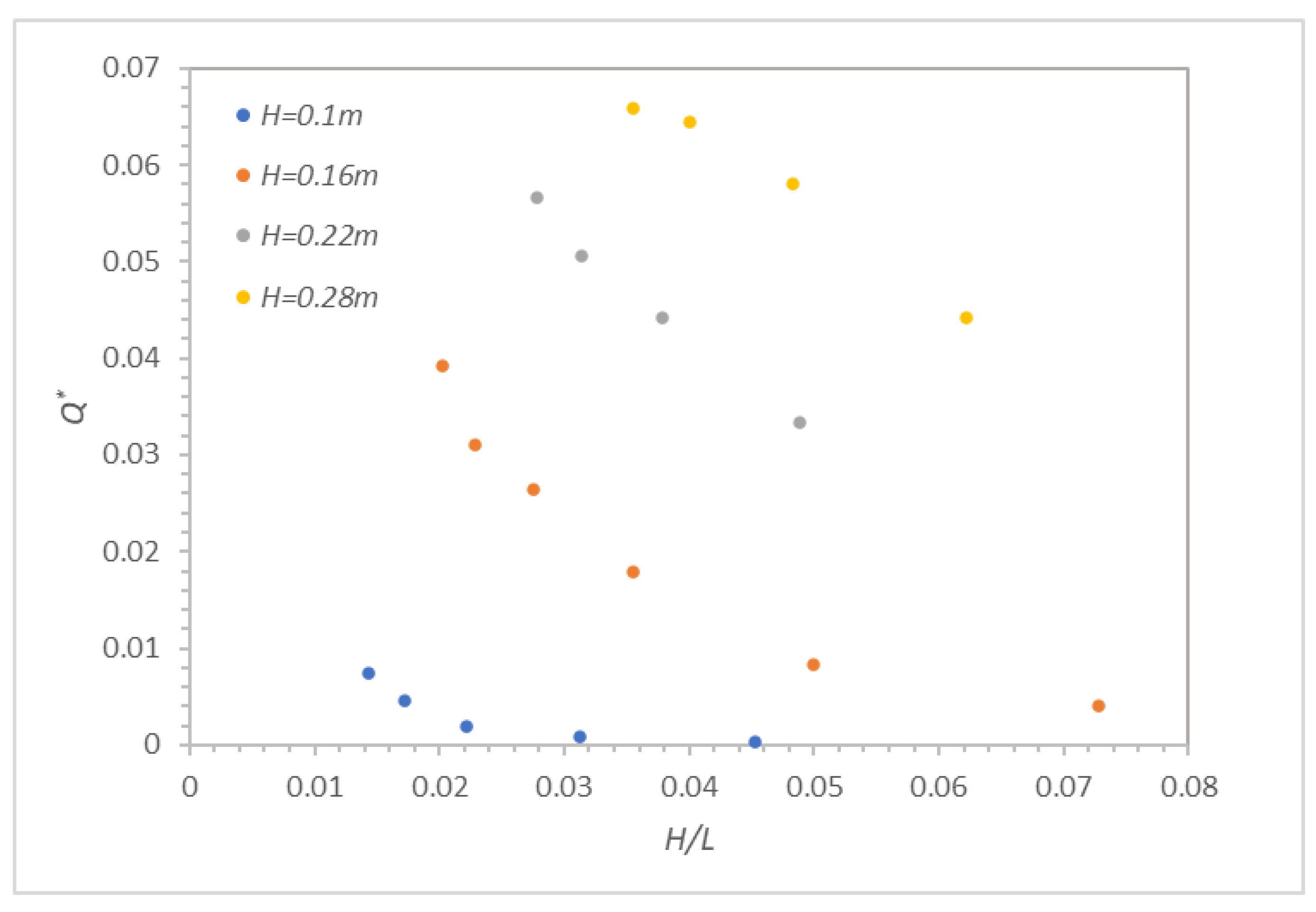
4.3. Effect of Wave Height on Wave Overtopping
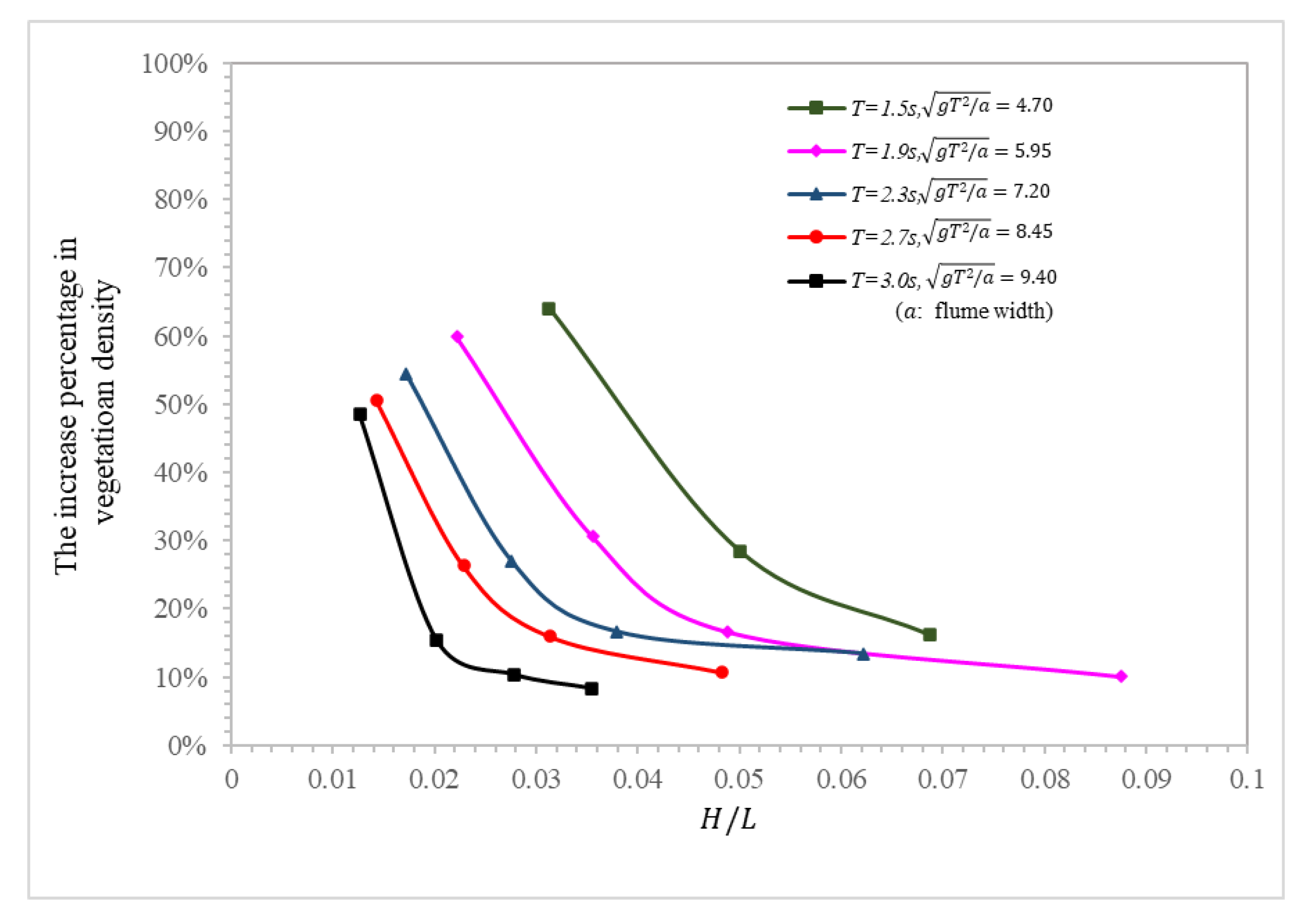
4.4. Effect of Vegetation Density on Wave Overtopping
4.5. Empirical Formula Fitting of the Wave Overtopping Considering the Effect of Rigid Plants
5. Conclusions
- (1)
- Based on OpenFOAM, the two-phase flow solver was combined with the Discrete Particle Model solver to establish the air-water-particle three-phase interaction model while considering the influence of plants. Several physical model experimental groups of honeycomb ecological revetment with vegetation were selected, and the correctness of the model was verified by comparing the wave run-up height, water level in sensors, and wave overtopping in the physical model test with the numerical simulation results.
- (2)
- The honeycomb-type ecological revetment model with the protection of plants was used to simulate the wave overtopping process of regular waves on honeycomb revetments, with plants under various wave conditions and different vegetation densities. Through analysis of the numerical simulation results, it was found that with increased wave height and wave period, the overtopping also gradually increased; but, with increased wave overtopping, the influence of the wave period on the overtopping gradually weakened. The increase in vegetation density could only effectively reduce wave overtopping, but does not change the trend of wave overtopping in terms of wave height and wave period.
- (3)
- Referring to the Eurotop formula, the relationship between Q* and the dimensionless coefficients H/Rc and H/L was established, and the empirical formula for overtopping the honeycomb-type ecological revetment model with plants was fitted according to the numerical modelling results. Parameter C in the formula was related to plant density.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Phillips, B.M. Design of Streambank Stabilization with Geogrid Reinforced Earth Systems. In Proceedings of the Joint Conference on Water Resource Engineering and Water Resources Planning and Management 2000, Minneapolis, MN, USA, July 30–2 August 2000; pp. 1–10. [Google Scholar]
- Yuan, S.; Tang, H.; Li, L.; Pan, Y.; Amini, F. Combined wave and surge overtopping erosion failure model of HPTRM levees: Accounting for grass-mat strength. Ocean Eng. 2015, 109, 256–269. [Google Scholar] [CrossRef] [Green Version]
- Kreyenschulte, M.; Schürenkamp, D.; Bratz, B.; Schüttrumpf, H.; Goseberg, N. Wave Run-Up on Mortar-Grouted Riprap Revetments. Water 2020, 12, 3396. [Google Scholar] [CrossRef]
- Vieira, F.; Taveira-Pinto, F.; Rosa-Santos, P. Novel time-efficient approach to calibrate VARANS-VOF models for simulation of wave interaction with porous structures using Artificial Neural Networks. Ocean Eng. 2021, 235, 109375. [Google Scholar] [CrossRef]
- Bakker, P.; Reedijk, B.; Manaois, J.R.; van de Koppel, M.; Muttray, M. Causes for Increased Wave Overtopping on Rubble Mound Breakwaters and Revetments. In Coasts, Marine Structures and Breakwaters 2017: Realising the Potential; Thomas Telford Limited: London, UK, 2018; pp. 1205–1215. [Google Scholar]
- Schoonees, T.; Kerpen, N.B.; Schlurmann, T. Full-scale experimental study on wave overtopping at stepped revetments. Coast. Eng. 2021, 167, 103887. [Google Scholar] [CrossRef]
- Capel, A. Wave run-up and overtopping reduction by block revetments with enhanced roughness. Coast. Eng. 2015, 104, 76–92. [Google Scholar] [CrossRef]
- Warmink, J.J.; van Bergeijk, V.M.; Chen, W.; Van Gent, M.R.; Hulscher, S.J.M. Modelling wave overtopping for grass covers and transitions in dike revetments. Coast. Eng. Proc. 2018, 36, 53. [Google Scholar] [CrossRef] [Green Version]
- Alcérreca-Huerta, J.C.; Oumeraci, H. Wave-induced pressures in porous bonded revetments. Part I: Pressures on the revetment. Coast. Eng. 2016, 110, 87–101. [Google Scholar] [CrossRef]
- Cao, D.; Yuan, J.; Chen, H. Towards modelling wave-induced forces on an armour layer unit of rubble mound coastal revetments. Ocean Eng. 2021, 239, 109811. [Google Scholar] [CrossRef]
- Chen, W.; Warmink, J.J.; Van Gent, M.R.A.; Hulscher, S.J.M.H. Numerical modelling of wave overtopping at dikes using OpenFOAM®. Coast. Eng. 2021, 166, 103890. [Google Scholar] [CrossRef]
- Yao, Y.; Chen, X.; Xu, C.; Jia, M.; Jiang, C. Numerical modelling of wave transformation and runup over rough fringing reefs using VARANS equations. Appl. Ocean Res. 2022, 118, 102952. [Google Scholar] [CrossRef]
- Tuan, T.Q.; Oumeraci, H. A numerical model of wave overtopping on seadikes. Coast. Eng. 2010, 57, 757–772. [Google Scholar] [CrossRef]
- Li, T.; Troch, P.; Rouck, J.D. Wave overtopping over a sea dike. J. Comput. Phys. 2004, 198, 686–726. [Google Scholar] [CrossRef]
- Mccabe, M.; Stansby, P.K.; Apsley, D.D. Random wave runup and overtopping a steep sea wall: Shallow-water and Boussinesq modelling with generalised breaking and wall impact algorithms validated against laboratory and field measurements. Coast. Eng. 2013, 74, 33–49. [Google Scholar] [CrossRef]
- Shao, S.; Ji, C.; Graham, D.I.; Reeve, D.E.; James, P.W.; Chadwick, A.J. Simulation of wave overtopping by an incompressible SPH model. Coast. Eng. 2006, 53, 723–725. [Google Scholar] [CrossRef]
- Zhang, N.; Zhang, Q.; Wang, K.H.; Zou, G.; Li, Y. Numerical Simulation of Wave Overtopping on Breakwater with an Armor Layer of Accropode Using SWASH Model. Water 2020, 12, 386. [Google Scholar] [CrossRef] [Green Version]
- Losada, I.J.; Lara, J.L.; Jesus, M.D. Modeling the Interaction of Water Waves with Porous Coastal Structures. J. Waterw. Port Coast. Ocean Eng. ASCE 2016, 6, 142. [Google Scholar] [CrossRef]
- Losada, I.J.; Lara, J.L.; Guanche, R.; Gonzalez-Ondina, J.M. Numerical analysis of wave overtopping of rubble mound breakwaters. Coast. Eng. 2008, 55, 47–62. [Google Scholar] [CrossRef]
- Lara, J.L.; Garcia, N.; Losada, I.J. RANS modelling applied to random wave interaction with submerged permeable structures. Coast. Eng. 2006, 53, 395–417. [Google Scholar] [CrossRef]
- Li, J.Y.; Zhang, Q.H.; Lu, Y.J. Numerical Simulation of Random Wave Overtopping of Rubble Mound Breakwater with Armor Units. China Ocean Eng. 2021, 35, 176–185. [Google Scholar] [CrossRef]
- Higuera, P.; Lara, J.L.; Losada, I.J. Realistic wave generation and active wave absorption for Navier–Stokes models: Application to OpenFOAM. Coast. Eng. 2013, 71, 102–118. [Google Scholar] [CrossRef]
- Higuera, P.; Lara, J.L.; Losada, I.J. Three-Dimensional Interaction of Waves and Porous Coastal Structures using OpenFOAM. Part II: Applications. Coast. Eng. 2014, 83, 259–270. [Google Scholar] [CrossRef]
- Augustin, L.N.; Irish, J.L.; Lynett, P. Laboratory and numerical studies of wave damping by emergent and near-emergent wetland vegetation. Coast. Eng. 2009, 56, 332–340. [Google Scholar] [CrossRef]
- Manca, E.; Cáceres, I.; Alsina, J.M.; Stratigaki, V.; Townend, I. Wave energy and wave-induced flow reduction by full-scale model Posidonia oceanica seagra. Cont. Shelf Res. 2012, 50–51, 100–116. [Google Scholar] [CrossRef]
- Maza, M.; Lara, J.L.; Losada, I.J. Tsunami wave interaction with mangrove forests: A 3-D numerical approach. Coast. Eng. 2015, 98, 33–54. [Google Scholar] [CrossRef]
- Maza, M.; Lara, J.L.; Losada, I.J. Solitary wave attenuation by vegetation patches. Adv. Water Resour. 2016, 98, 159–172. [Google Scholar] [CrossRef]
- Schmeeckle, M.W. The Mechanics of Bedload Sediment Transport; Bell & Howell Information Company: Arbor, MI, USA, 1998. [Google Scholar]
- Drake, T.G.; Calantoni, J. Discrete particle model for sheet flow sediment transport in the nearshore. J. Geophys. Res. 2001, 106, 859–868. [Google Scholar] [CrossRef]
- McEwan, I.K.; Heald, J. Discrete Particle Modeling of Entrainment from Flat Uniformly Sized Sediment Beds. J. Hydraul. Eng. 2001, 127, 588–597. [Google Scholar] [CrossRef] [Green Version]
- Xu, S.L.; Sun, R.; Cai, Y.Q.; Sun, H.l. Study of sedimentation of non-cohesive particles via CFD–DEM simulations. Granul. Matter 2017, 20, 4. [Google Scholar] [CrossRef] [Green Version]
- Sun, R.; Xiao, H. CFD–DEM simulations of current-induced dune formation and morphological evolution. Adv. Water Resour. 2016, 92, 228–239. [Google Scholar] [CrossRef] [Green Version]
- Finn, J.R.; Li, M.; Apte, S.V. Particle based modelling and simulation of natural sand dynamics in the wave bottom boundary layer. J. Fluid Mech. 2016, 796, 340–385. [Google Scholar] [CrossRef]
- Schmeeckle, M.W. Numerical simulation of turbulence and sediment transport of medium sand. J. Geophys. Res. Earth Surf. 2014, 119, 1240–1262. [Google Scholar] [CrossRef]
- Kafui, K.D.; Thornton, C.; Adams, M.J. Discrete particle-continuum fluid modelling of gas–solid fluidised beds. Chem. Eng. Sci. 2002, 57, 2395–2410. [Google Scholar] [CrossRef]
- Arolla, S.K.; Desjardins, O. Transport modeling of sedimenting particles in a turbulent pipe flow using Euler-Lagrange large eddy simulation. Int. J. Multiph. Flow 2015, 75, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Cundall, P.A.; Strack, O. A discrete numerical model for granular assemblies. Géotechnique 2008, 30, 331–336. [Google Scholar] [CrossRef]
- Crowe, C.T.; Schwarzkopf, J.D.; Sommerfeld, M.; Tsuji, Y. Multiphase Flows with Droplets and Particles; CRC Press: Boca Raton, FL, USA, 2011. [Google Scholar]
- Goda, Y. Random Seas and Design of Maritime Structures; World Scientific Publishing Co. Pte. Ltd.: Singapore, 1924. [Google Scholar]
- Code of Hydrology for Harbor and Waterway. 2015, JTS 145-2015. Available online: https://www.nssi.org.cn/nssi/english/88067670.html (accessed on 14 October 2022).
- Van der Meer, J.W.; Allsop, N.W.H.; Bruce, T.; Rouck, J.D.; Zanuttigh, B. EurOtop: Manual on Wave Overtopping of Sea Defences and Related Sturctures: An Overtopping Manual Largely Based on European Research, but for Worlwide Application. Available online: www.overtopping-manual.com (accessed on 1 June 2022).






| Wave Height | Wave Period | Depth | Wave Overtopping | |
|---|---|---|---|---|
| Case 1 | Model 0.1 m Prototype 1 m | Model 1.26 s Prototype 4.536 s | Model 0.46 m Protytope 4.6 m | No |
| Case 2 | Model 0.1 m Prototype 1 m | Model 1.58 s Prototype 5.688 s | Model 0.46 m Prototype 4.6 m | No |
| Case 3 | Model 0.1 m Prototype 1 m | Model1.9 s Prototype 6.840 s | Model 0.46 m Prototype 4.6 m | No |
| Case 4 | Model 0.1 m Prototype 1 m | Model 1.26 s Prototype 4.536 s | Model 0.63 m Prototype 6.3 m | Yes |
| Case 5 | Model 0.1 m Prototype 1 m | Model 1.58 s Prototype 5.688 s | Model 0.63 m Prototype 6.3 m | Yes |
| Case 6 | Model 0.1 m Prototype 1 m | Model1.9 s Prototype 6.840 s | Model 0.63 m Prototype 6.3 m | Yes |
| Honeycomb Revetment without Plants | Honeycomb Revetment with Plants | |||||
|---|---|---|---|---|---|---|
| Experiment | Numerical Simulation | Error | Experiment | Numerical Simulation | Error | |
| Case 1 | 0.081 | 0.070 | 13% | 0.079 | 0.065 | 18% |
| Case 2 | 0.100 | 0.098 | 2% | 0.087 | 0.082 | 5% |
| Case 3 | 0.116 | 0.116 | 0% | 0.093 | 0.099 | 6% |
| Honeycomb Revetment without Plants | Honeycomb Revetment with Plants | |||||
|---|---|---|---|---|---|---|
| Experiment | Numerical Simulation | Error | Experiment | Numerical Simulation | Error | |
| Case 4 | 3.37 × 10−4 | 2.37 × 10−4 | 29% | 2.6 × 10−6 | 9.3 × 10−6 | 257% |
| Case 5 | 7.88 × 10−4 | 8.53 × 10−4 | 8% | 1.39 × 10−5 | 2.18 × 10−5 | 57% |
| Case 6 | 1.45 × 10−3 | 1.448 × 10−3 | 0.1% | 3.07 × 10−5 | 4.3 × 10−5 | 40% |
| (m) | (s) | (m) | Plant Density/Height | Experimental Result | Calculation Result of Muttray | Ratio of Difference to Calculation Result |
|---|---|---|---|---|---|---|
| 0.06 | 1.58 | 0.46 | 750 plants/m2 | 5 | 8.1 | 38.27% |
| 0.08 | 1.58 | 0.46 | 1000 plants/m2 | 5.5 | 10.6 | 48.11% |
| 0.1 | 1.58 | 0.46 | 0.10 m | 7.7 | 13 | 40.77% |
| 0.1 | 1.58 | 0.46 | 0.20 m | 7.3 | 13 | 43.85% |
| (m) | (s) | (m) | Plant Density/Height | Experimental Result | Calculation Result of Eurotop | Ratio of Difference to Calculation Result |
|---|---|---|---|---|---|---|
| 0.1 | 1.9 | 0.63 | 750 plants/m2 | 2.59 × 10−4 | 4.42 × 10−4 | 41.40% |
| 0.1 | 1.9 | 0.63 | 1000 plants/m2 | 7.41 × 10−5 | 3.87 × 10−4 | 80.85% |
| 0.1 | 1.9 | 0.63 | 0.10 m | 3.07 × 10−5 | 3.87 × 10−4 | 92.07% |
| 0.1 | 1.9 | 0.63 | 0.20 m | 1.37 × 10−5 | 3.87 × 10−4 | 96.46% |
| T (s) | H (m) | T (s) | H (m) | T (s) | H (m) | |||
|---|---|---|---|---|---|---|---|---|
| Case 1 | 1.2 | 0.1 | Case 11 | 1.9 | 0.16 | Case 21 | 2.7 | 0.28 |
| Case 2 | 1.2 | 0.12 | Case 12 | 1.9 | 0.22 | Case 22 | 3.0 | 0.1 |
| Case 3 | 1.2 | 0.14 | Case 13 | 1.9 | 0.28 | Case 23 | 3.0 | 0.16 |
| Case 4 | 1.2 | 0.16 | Case 14 | 2.3 | 0.1 | Case 24 | 3.0 | 0.22 |
| Case 5 | 1.5 | 0.1 | Case 15 | 2.3 | 0.16 | Case 25 | 3.0 | 0.28 |
| Case 6 | 1.5 | 0.12 | Case 16 | 2.3 | 0.22 | Case 26 | 2.7 | 0.28 |
| Case 7 | 1.5 | 0.14 | Case 17 | 2.3 | 0.28 | Case 27 | 3.3 | 0.28 |
| Case 8 | 1.5 | 0.16 | Case 18 | 2.7 | 0.1 | Case 28 | 1.5 | 0.22 |
| Case 9 | 1.5 | 0.18 | Case 19 | 2.7 | 0.16 | |||
| Case 10 | 1.9 | 0.1 | Case 20 | 2.7 | 0.22 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.; Zhang, N.; Zhang, Q.; Jiao, F.; Xu, L.; Qi, J. Numerical Simulation of Wave Overtopping of an Ecologically Honeycomb-Type Revetment with Rigid Vegetation. J. Mar. Sci. Eng. 2022, 10, 1615. https://doi.org/10.3390/jmse10111615
Zhang J, Zhang N, Zhang Q, Jiao F, Xu L, Qi J. Numerical Simulation of Wave Overtopping of an Ecologically Honeycomb-Type Revetment with Rigid Vegetation. Journal of Marine Science and Engineering. 2022; 10(11):1615. https://doi.org/10.3390/jmse10111615
Chicago/Turabian StyleZhang, Jinfeng, Na Zhang, Qinghe Zhang, Fangqian Jiao, Lingling Xu, and Jiarui Qi. 2022. "Numerical Simulation of Wave Overtopping of an Ecologically Honeycomb-Type Revetment with Rigid Vegetation" Journal of Marine Science and Engineering 10, no. 11: 1615. https://doi.org/10.3390/jmse10111615
APA StyleZhang, J., Zhang, N., Zhang, Q., Jiao, F., Xu, L., & Qi, J. (2022). Numerical Simulation of Wave Overtopping of an Ecologically Honeycomb-Type Revetment with Rigid Vegetation. Journal of Marine Science and Engineering, 10(11), 1615. https://doi.org/10.3390/jmse10111615






