Numerical Investigation on Behavior of Compressive Piles in Coastal Tidal Flat with Fill
Abstract
1. Introduction
2. Project Description and Engineering Test
2.1. Geotechnical Characterization Methodology
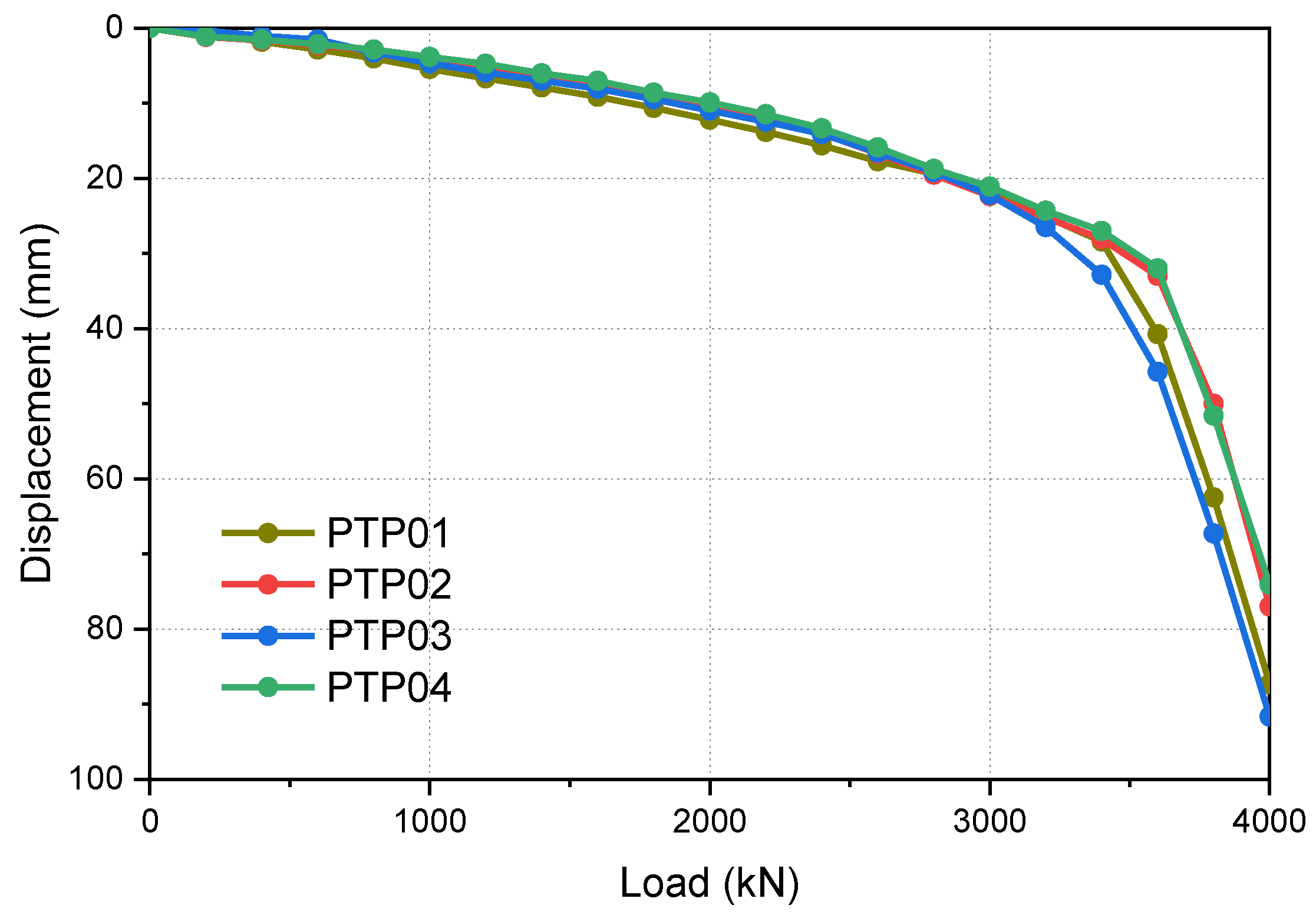
2.2. Pile Load Tests Interpretation
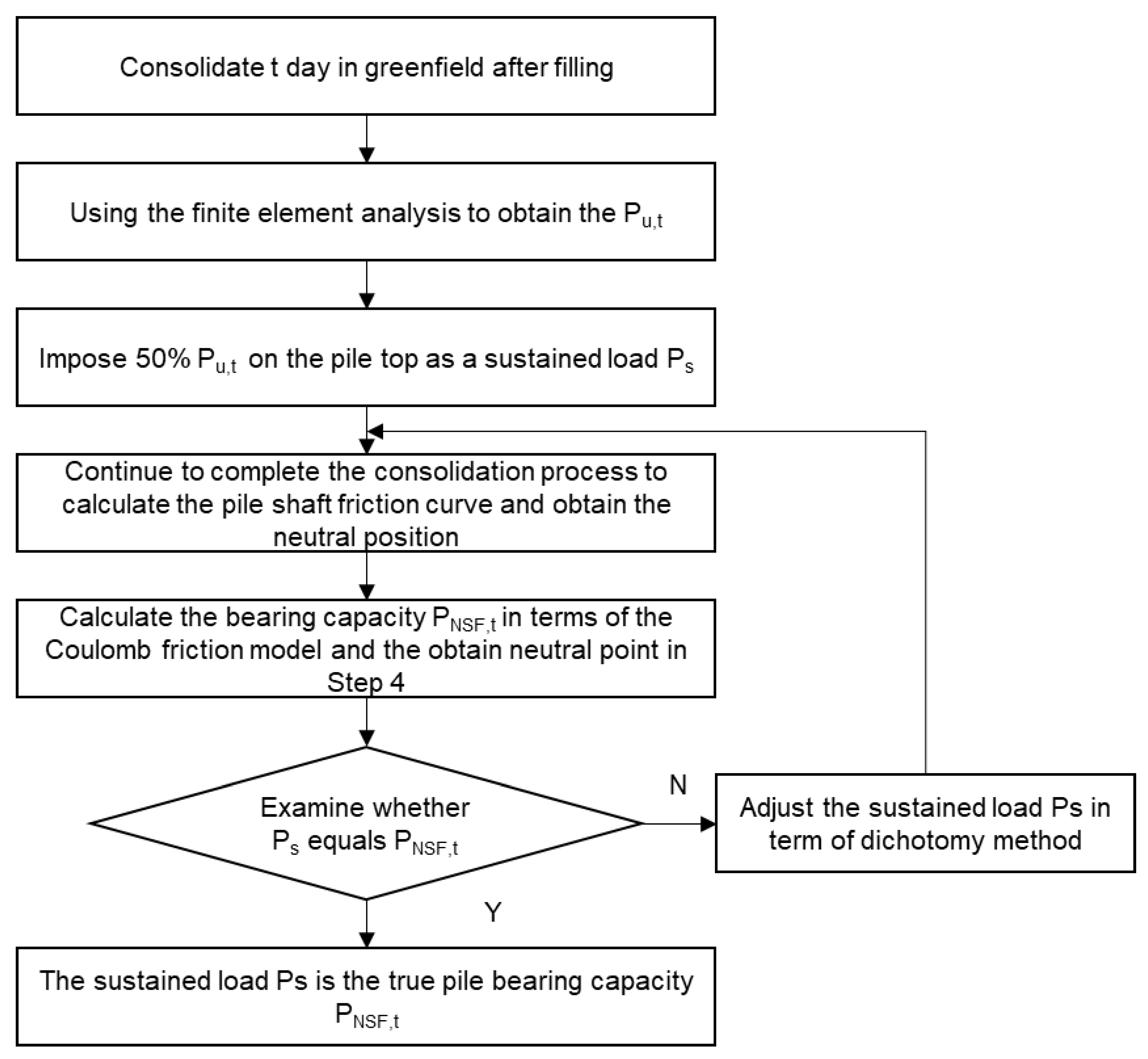
3. Numerical Analysis of Consolidation Influence on Pile Capacity
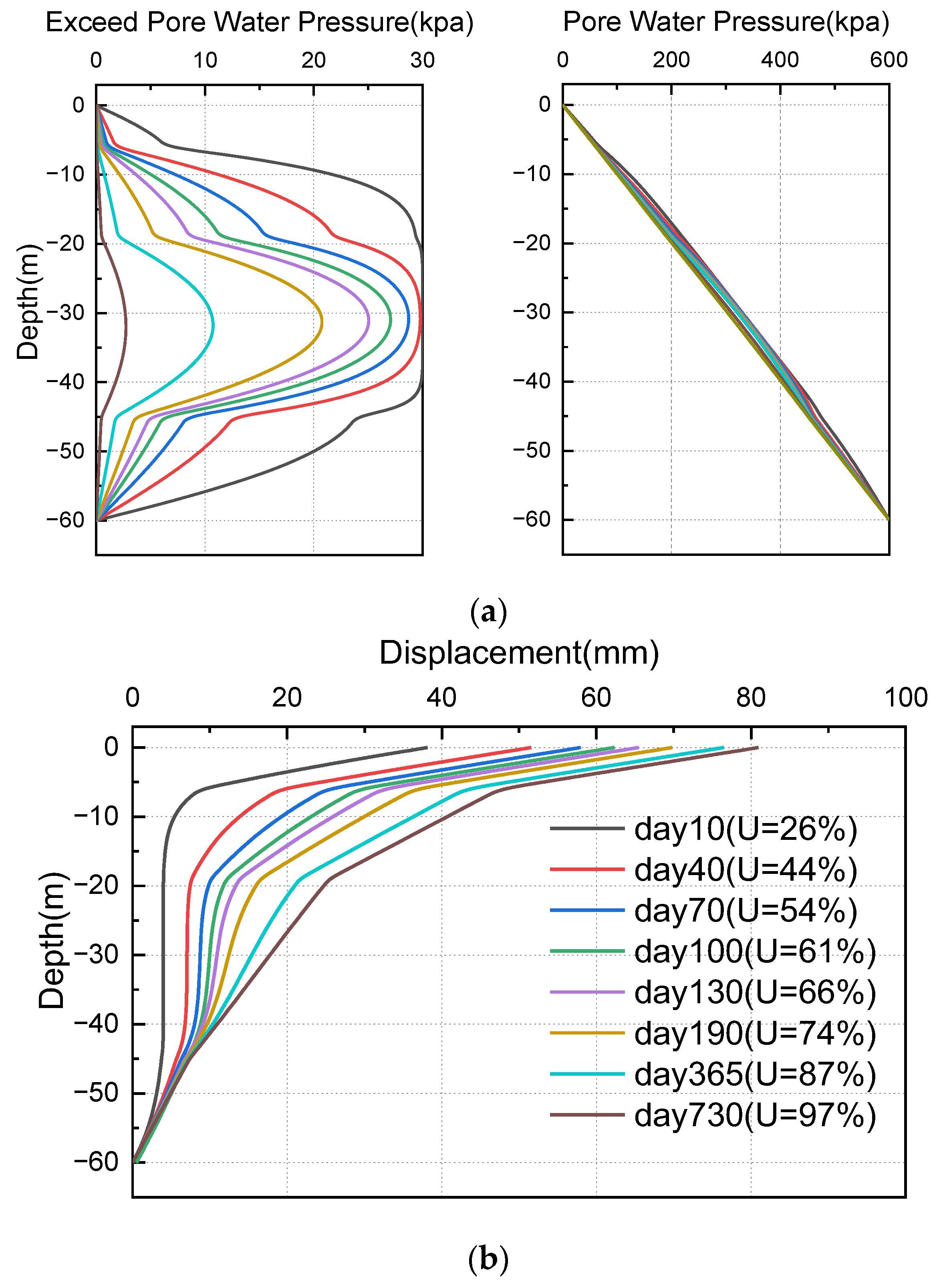
3.1. Finite Element Model
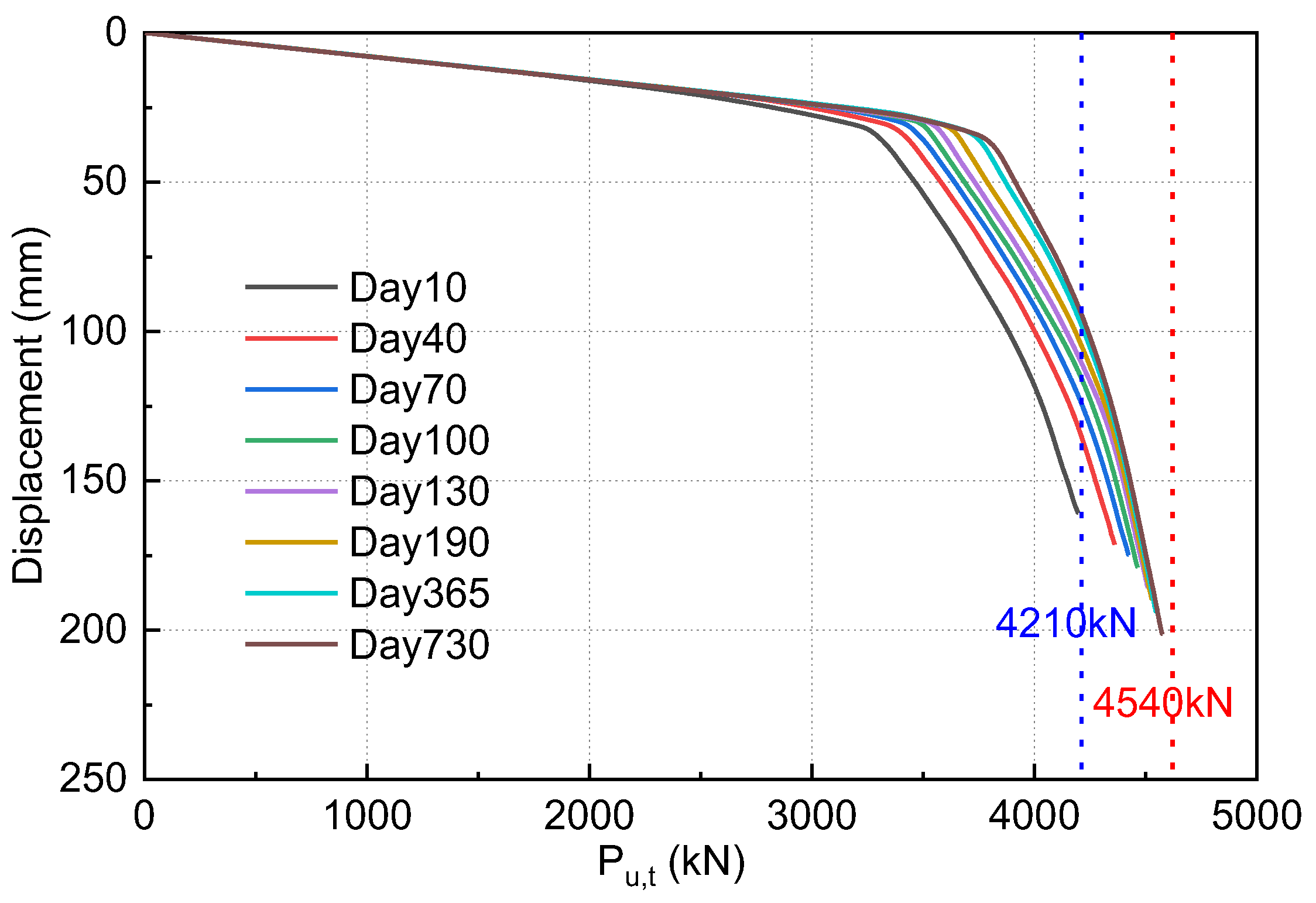
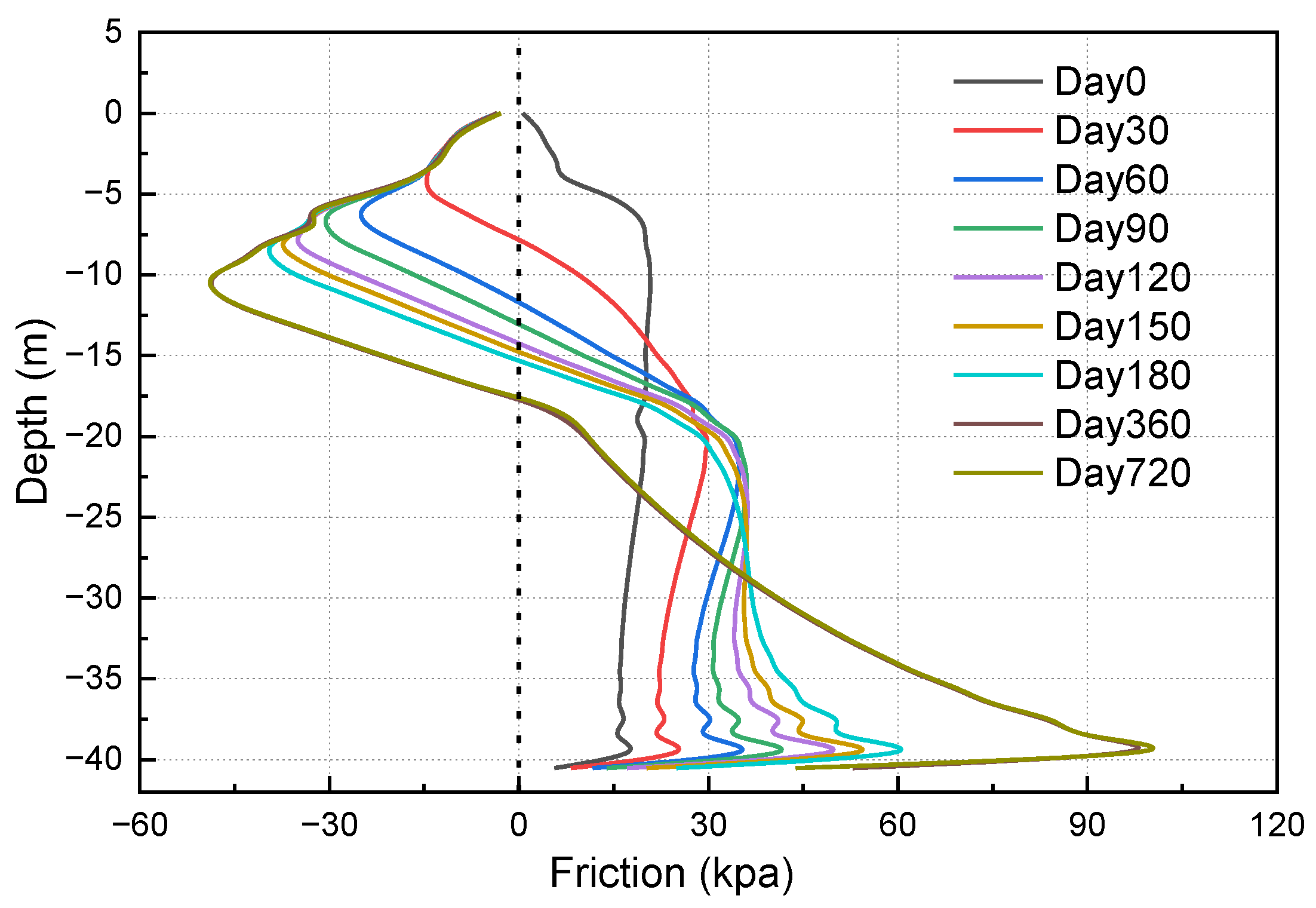
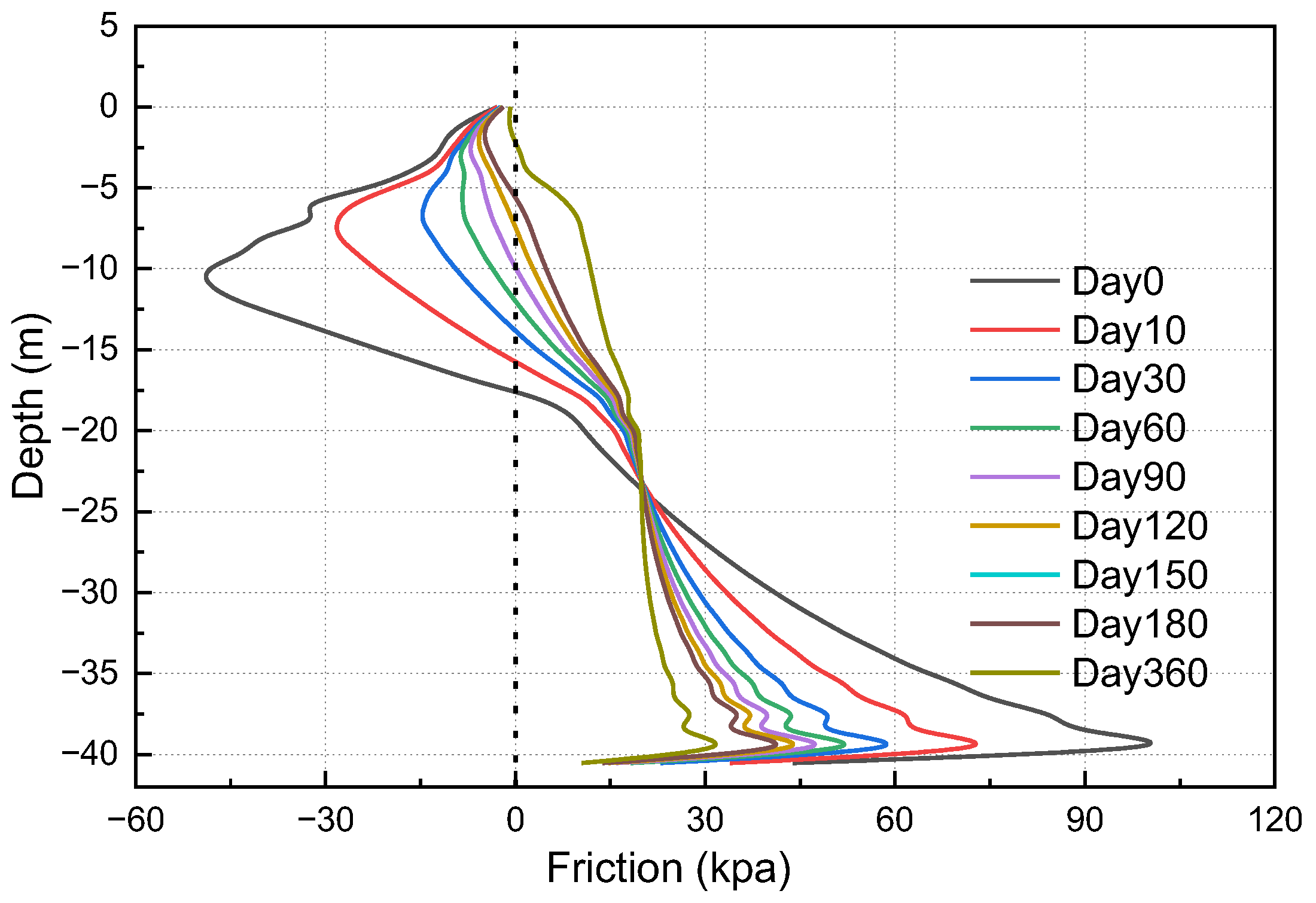
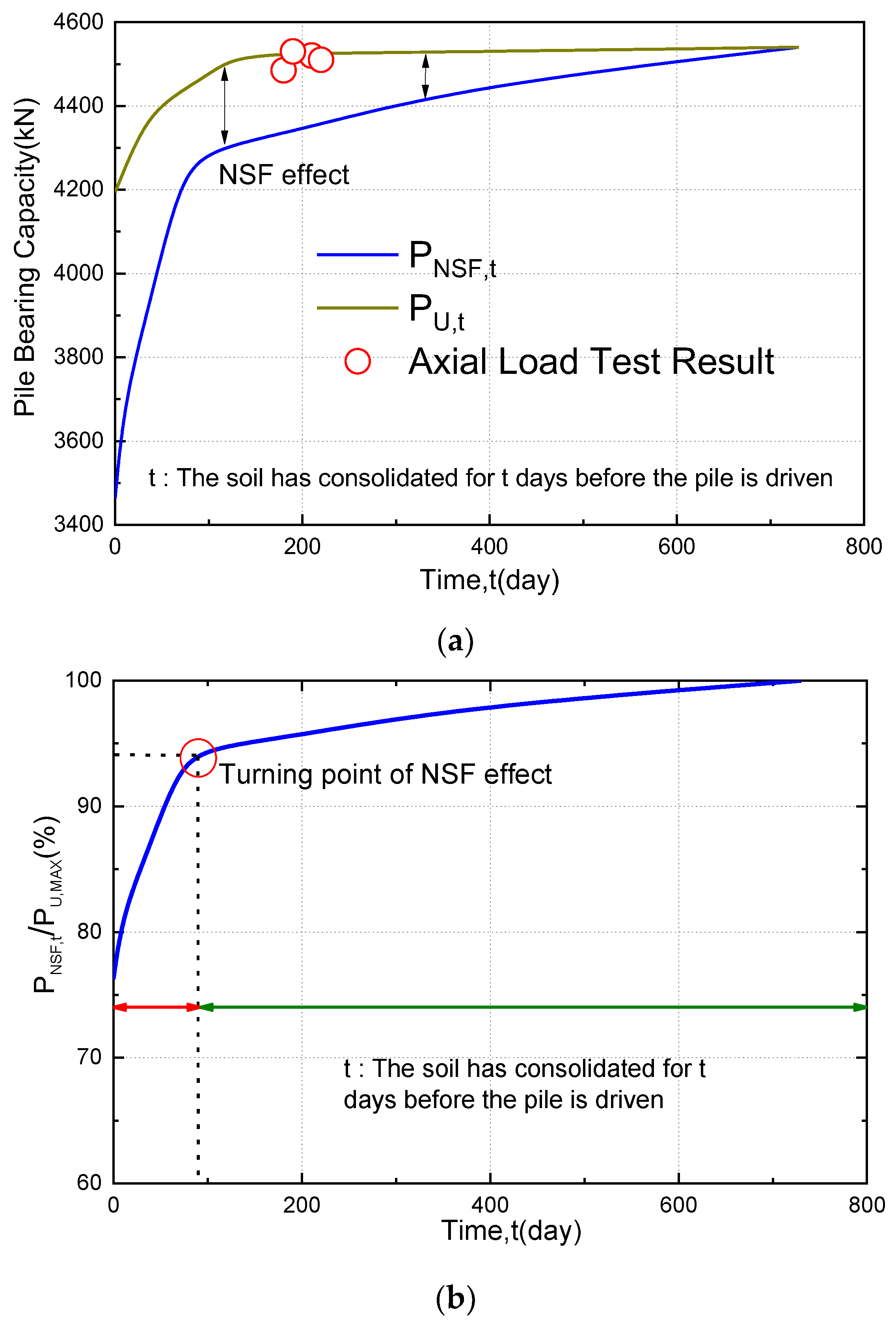
3.2. The Consolidation Effect on Pile-Bearing Capacity
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Henkel, D.J. The shear strength of saturated remolded clays. In Proceedings of the Research Conference on Shear Strength of Cohesive Soils, ASCE, Boulder, CO, USA, 13–17 June 1960; pp. 533–554. [Google Scholar]
- Terzaghi, K.; Peck, R.B. Soil Mechanics in Engineering Practice, 2nd ed.; Wiley: New York, NY, USA, 1967; p. 729. [Google Scholar]
- Shen, Z. Engineering properties of soft soils and design of soft ground. Chin. J. Geotech. Eng. 1998, 20, 12. [Google Scholar]
- Fellenius, B.H. Negative Skin Friction of Piles. Second International Seminar, Pile Foundations; Nanyang Technological Institution: Singapore, 1984; p. 12. [Google Scholar]
- Al-Tabbaa, A.; Lee, C.J.; Bolton, M.D. Numerical modelling of group effects on the distribution of dragloads in pile foundations. Géotechnique 2002, 52, 325–335. [Google Scholar]
- Liu, J.; Gao, H.; Liu., H. Finite element analyses of negative skin friction on a single pile. Acta Geotech. 2012, 7, 239–252. [Google Scholar] [CrossRef]
- Xu, D.S.; Xu, X.Y.; Li, W.; Fatahi, B. Field experiments on laterally loaded piles for an offshore wind farm. Mar. Struct. 2020, 69, 102684. [Google Scholar] [CrossRef]
- Skov, R.; Denver, H. Time-dependence of bearing capacity of piles. In Proceedings of the Third International Conference on the Application of Stress-Wave Theory to Piles, Ottawa, ON, Canada, 25–27 May 1988; pp. 25–27. [Google Scholar]
- Robertson, P.K. Soil classification using the cone penetration test. Can. Geotech. J. 1990, 27, 151–158. [Google Scholar] [CrossRef]
- Robertson, P.K. Interpretation of cone penetration tests—A unified approach. Can. Geotech. J. 2009, 46, 1337–1355. [Google Scholar] [CrossRef]
- Shuttle, D.A.; Cunning, J. Liquefaction potential of silts from CPTu. Can. Geotech. J. 2007, 44, 1–19. [Google Scholar] [CrossRef]
- Wride, C.E.; Robertson, P.K.; Biggar, K.W.; Campanella, R.G.; Hofmann, B.A.; Hughes, J.M.O.; Kupper, A.; Woeller, D.J. Interpretation of in situ test results from the CANLEX sites. Can. Geotech. J. 2000, 37, 505–529. [Google Scholar] [CrossRef]
- Bolton, M.D. The strength and dilatancy of sands. Géotechnique 1986, 36, 65–78. [Google Scholar] [CrossRef]
- Kulhawy, F.H.; Mayne, P.W. Manual on Estimating Soil Properties for Foundation Design (No. EPRI-EL-6800); Electric Power Research Inst.: Palo Alto, CA, USA; Cornell Univ.: Ithaca, NY, USA; Geotechnical Engineering Group: Exton, PA, USA, 1990. [Google Scholar]
- AASHTO LRFD (American Association of State Highway and Transportation Officials LRFD Bridge Design Specification). LRFDBDS-9; American Association of State Highway and Transportation Officials: Washington, DC, USA, 2020. [Google Scholar]
- Esrig, M.E.; Kirby, R.C. Advances in General Effective Stress Method for the Prediction of Axial Capacity for Driven Piles in Clay. In Proceedings of the 11th Annual Offshore Technology Conference, Houston, TX, USA, 30 April–3 May 1979; pp. 437–449. [Google Scholar]
- Kou, H.; Chu, J.; Guo, W.; Zhang, M. Pile load test of jacked open-ended prestressed high-strength concrete pipe pile in clay. Proc. Inst. Civ. Eng.-Geotech. Eng. 2018, 171, 243–251. [Google Scholar] [CrossRef]
- Chin, F.K. Estimation of the ultimate load of piles from tests not carried to failure. In Proceedings of the 2nd Southeast Asian Conference on Soil Engineering, Singapore, 11–15 June 1970; pp. 81–90. [Google Scholar]
- Chin, F.K. The inverse slope as a prediction of ultimate bearing capacity of piles. In Proceedings of the 3rd Southeast Asian Conference on Soil Engineering, Hong Kong, China, 6–10 November 1972; pp. 83–91. [Google Scholar]
- Borel, S.; Bustamante, M.; Gianeselli, L. An appraisal of the Chin method based on 50 instrumented pile tests. Ground Eng. 2004, 37, 22–26. [Google Scholar]
- Leung, C.F.; Radhakrishnan, R.; Tan, S.-A. Performance of precast driven piles in marine clay. J. Geotech. 1991, 117, 637–657. [Google Scholar] [CrossRef]
- Lee, C.J.; Ng, C.W.W. Development of downdrag on piles and pile groups in consolidating soil. J. Geotech Geoenviron. 2004, 130, 905–914. [Google Scholar] [CrossRef]
- Johannessen, I.J.; Bjerrum, L. Measurement of the compression of a steel pile to rock due to settlement of the surrounding clay. In Proceedings of the 6th International Conference on Soil Mechanics and Foundation Engineering, Montreal, QC, Canada, 8–15 September 1965; pp. 261–264. [Google Scholar]
- Comodromos, E.M.; Bareka, S.V. Evaluation of negative skin friction effects in pile foundations using 3D nonlinear analysis. Comput. Geotech 2005, 32, 210–221. [Google Scholar] [CrossRef]
- Feng, W.; Lalit, B.; Yin, Z.; Yin, J. Long-term Non-linear creep and swelling behavior of Hong Kong marine deposits in oedom-eter condition. Comput. Geotech. 2017, 84, 1–17. [Google Scholar] [CrossRef]
- Lee, C.J.; Ng, C.W.W.; Jeong, S.S. The effect of negative skin friction on piles and pile groups. In Linear and Nonlinear Numerical Analysis of Foundations; Bull, J.W., Ed.; Taylor & Francis: London, UK, 2009. [Google Scholar]
- MCC (Ministry of Construction of the People’s Republic of China). Technical Code for Building Pile Foundations, JGJ106 -2014; China Building Industry Press: Beijing, China, 2014.
- Alonso, E.E.; Josa, A.; Ledesma, A. Negative skin friction on piles: A simplified analysis and prediction procedure. Geotechnique 1984, 34, 341–357. [Google Scholar] [CrossRef]
- Wong, K.S.; The, C.I. Negative skin friction on piles in layered soil deposits. ASCE J. Geotech. Eng. 1995, 121, 457–465. [Google Scholar] [CrossRef]
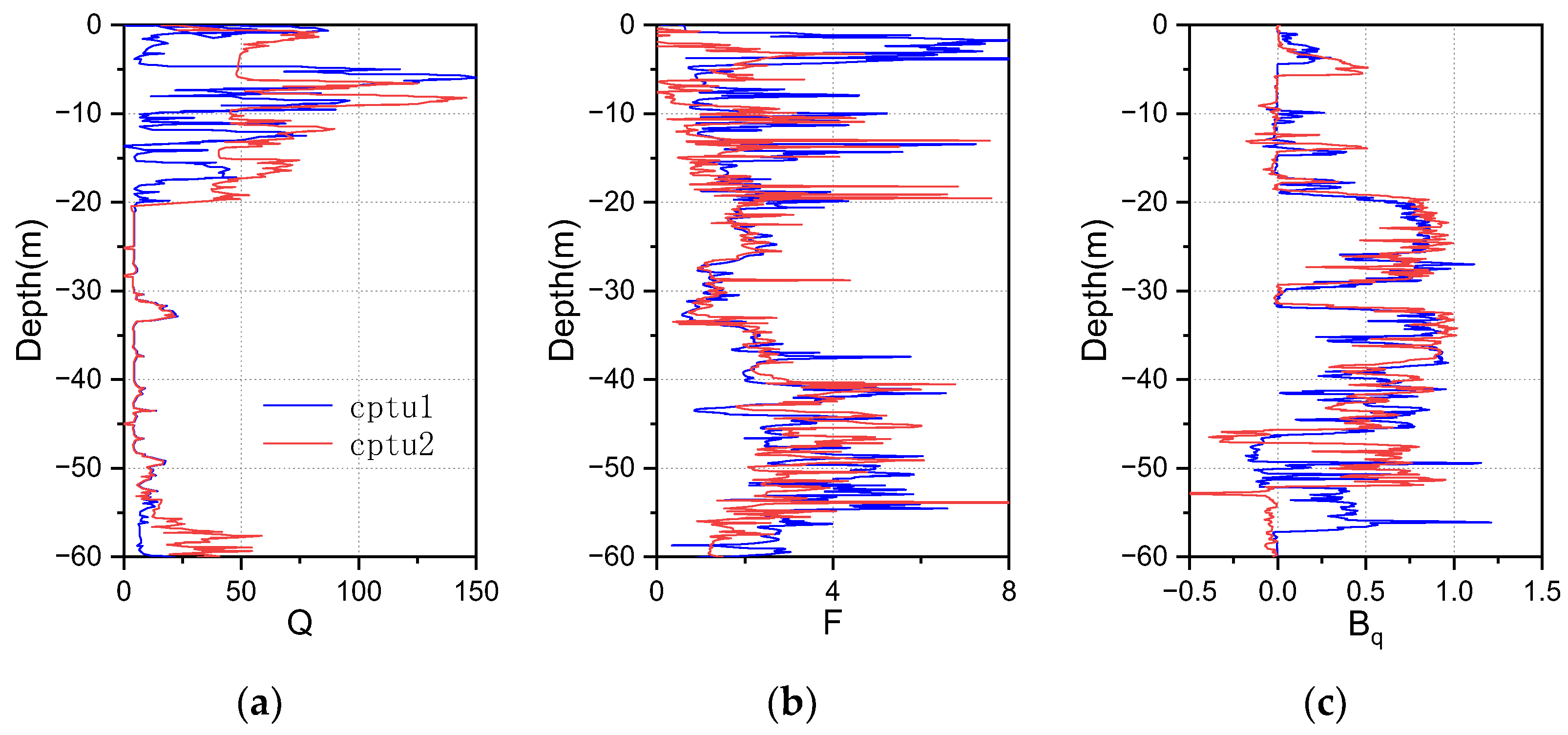
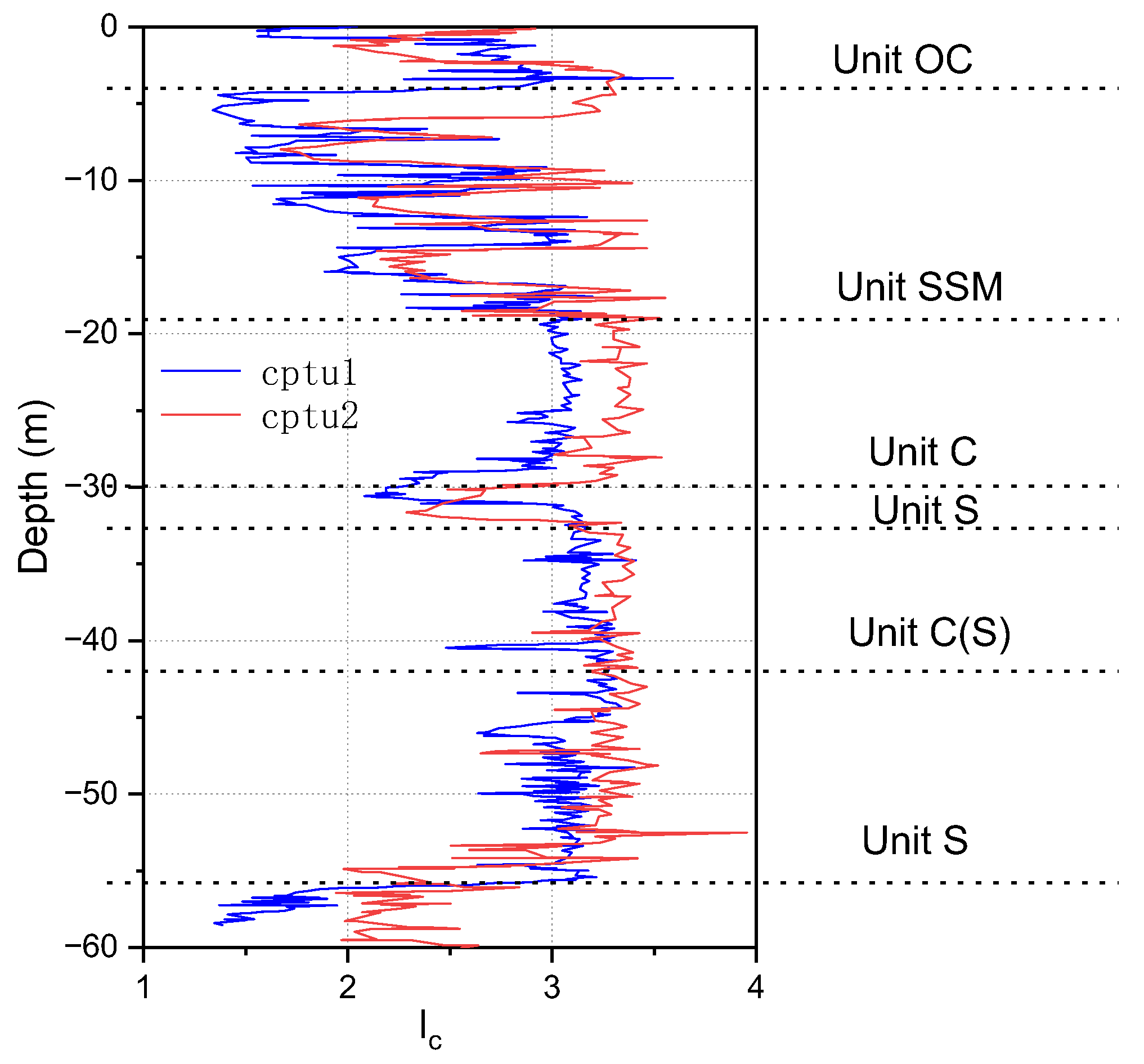
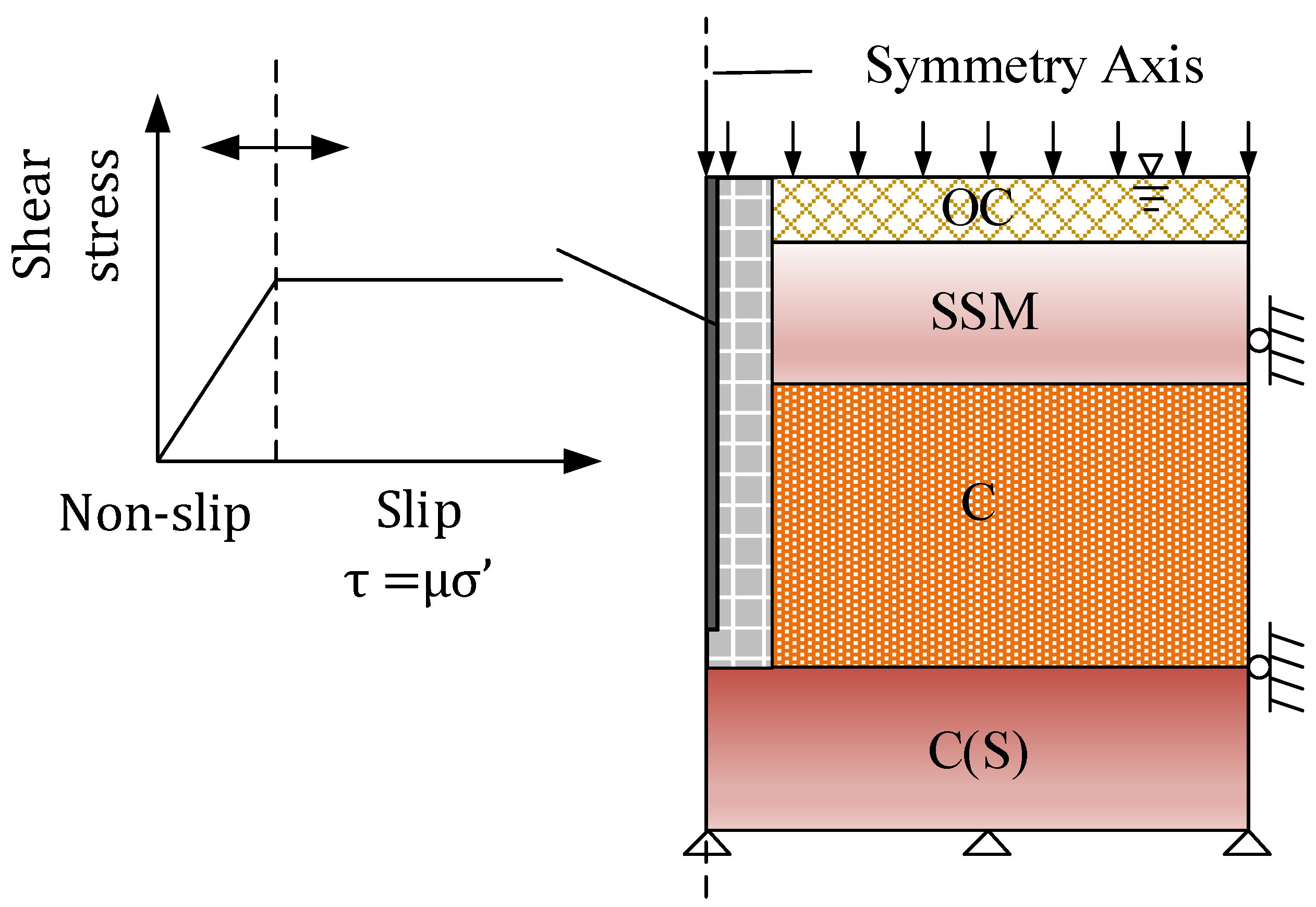
| Unit | h (m) | (kg/m3) | (°) | (kPa) | Cu (kPa) | k (m/s) | E (MPa) | e |
|---|---|---|---|---|---|---|---|---|
| OC | 0–6 | 16 | 20 | 10 | 20 | 10−8 | 4 | 1.5 |
| SSM | 6–19 | 19 | 33 | 0 | - | 10−9 | 13 | 1 |
| C | 19–45 | 18 | 25 | 10 | 25–60 | 10−10 | 30 | 1.2 |
| C(S) | 45–60 | 20 | 30 | 10 | 100 | 10−9 | 45 | 0.6 |
| S | >60 | - | - | - | - | 10−3 | - | - |
| H (m) | Cu (kPa) | Parameter for (kPa) | qp (kPa) | |
|---|---|---|---|---|
| OC | 0.0–6.0 | 20 | ||
| SSM | 6.0–19.0 | - | 2500 | |
| C | 19.0–45.0 | 25–60 | ||
| C(S) | 45.0–60.0 | 100 |
| Pile ID | Hyperbolic Extrapolation Result (kN) |
|---|---|
| PTP01 | 4485 |
| PTP02 | 4520 |
| PTP03 | 4510 |
| PTP04 | 4530 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shen, K.; Wang, K.; Yao, J.; Yu, J. Numerical Investigation on Behavior of Compressive Piles in Coastal Tidal Flat with Fill. J. Mar. Sci. Eng. 2022, 10, 1742. https://doi.org/10.3390/jmse10111742
Shen K, Wang K, Yao J, Yu J. Numerical Investigation on Behavior of Compressive Piles in Coastal Tidal Flat with Fill. Journal of Marine Science and Engineering. 2022; 10(11):1742. https://doi.org/10.3390/jmse10111742
Chicago/Turabian StyleShen, Kanmin, Kuanjun Wang, Juntian Yao, and Jian Yu. 2022. "Numerical Investigation on Behavior of Compressive Piles in Coastal Tidal Flat with Fill" Journal of Marine Science and Engineering 10, no. 11: 1742. https://doi.org/10.3390/jmse10111742
APA StyleShen, K., Wang, K., Yao, J., & Yu, J. (2022). Numerical Investigation on Behavior of Compressive Piles in Coastal Tidal Flat with Fill. Journal of Marine Science and Engineering, 10(11), 1742. https://doi.org/10.3390/jmse10111742







