Effect of Relative Stiffness of Pile and Soil on Pile Group Effect
Abstract
1. Introduction
2. Description of the Numerical Model
2.1. Brief Description of Field Test
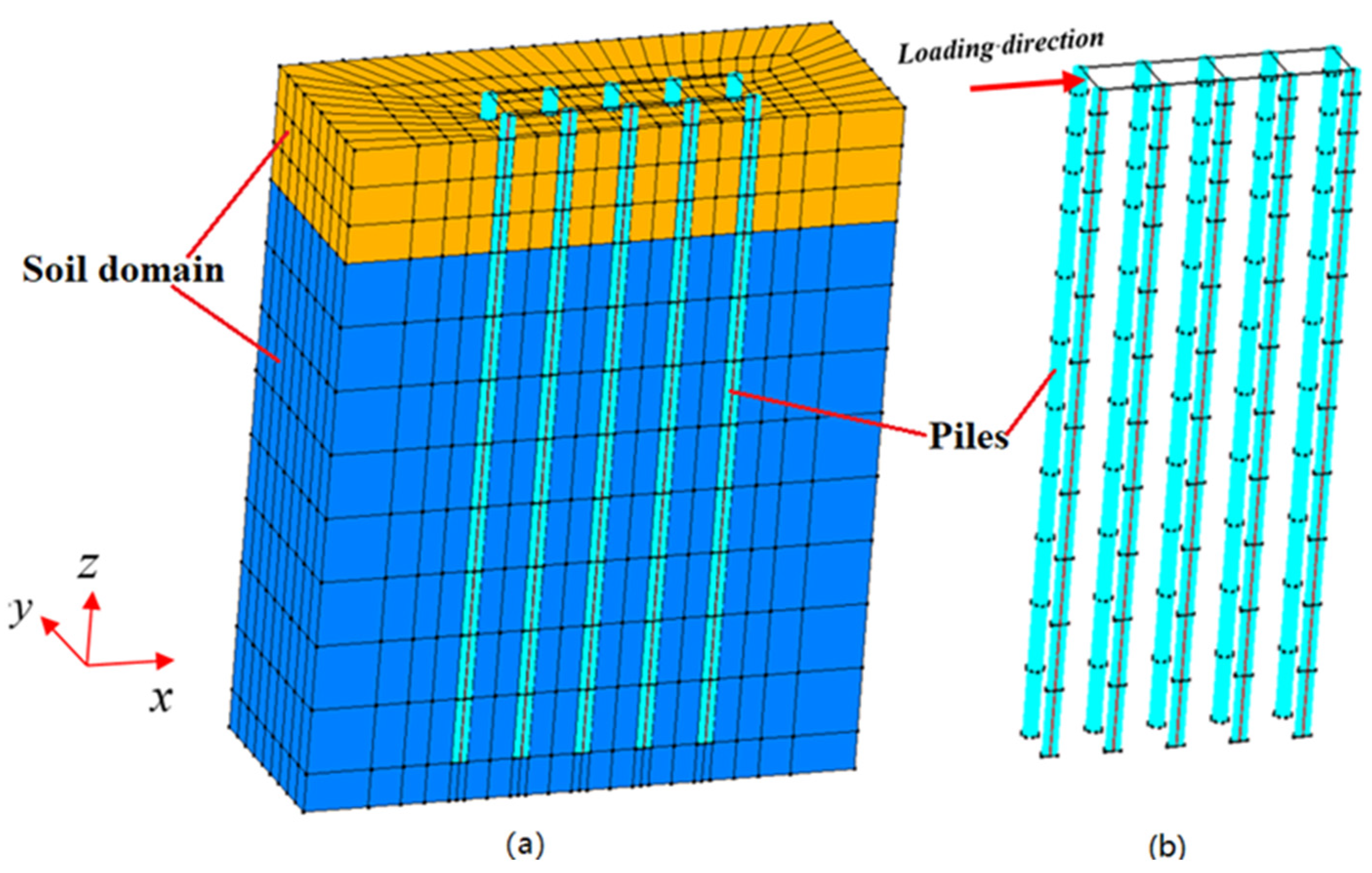
2.2. Introduction of FE Model
2.3. Constitutive Models and Soil Properties
2.4. Boundary Condition
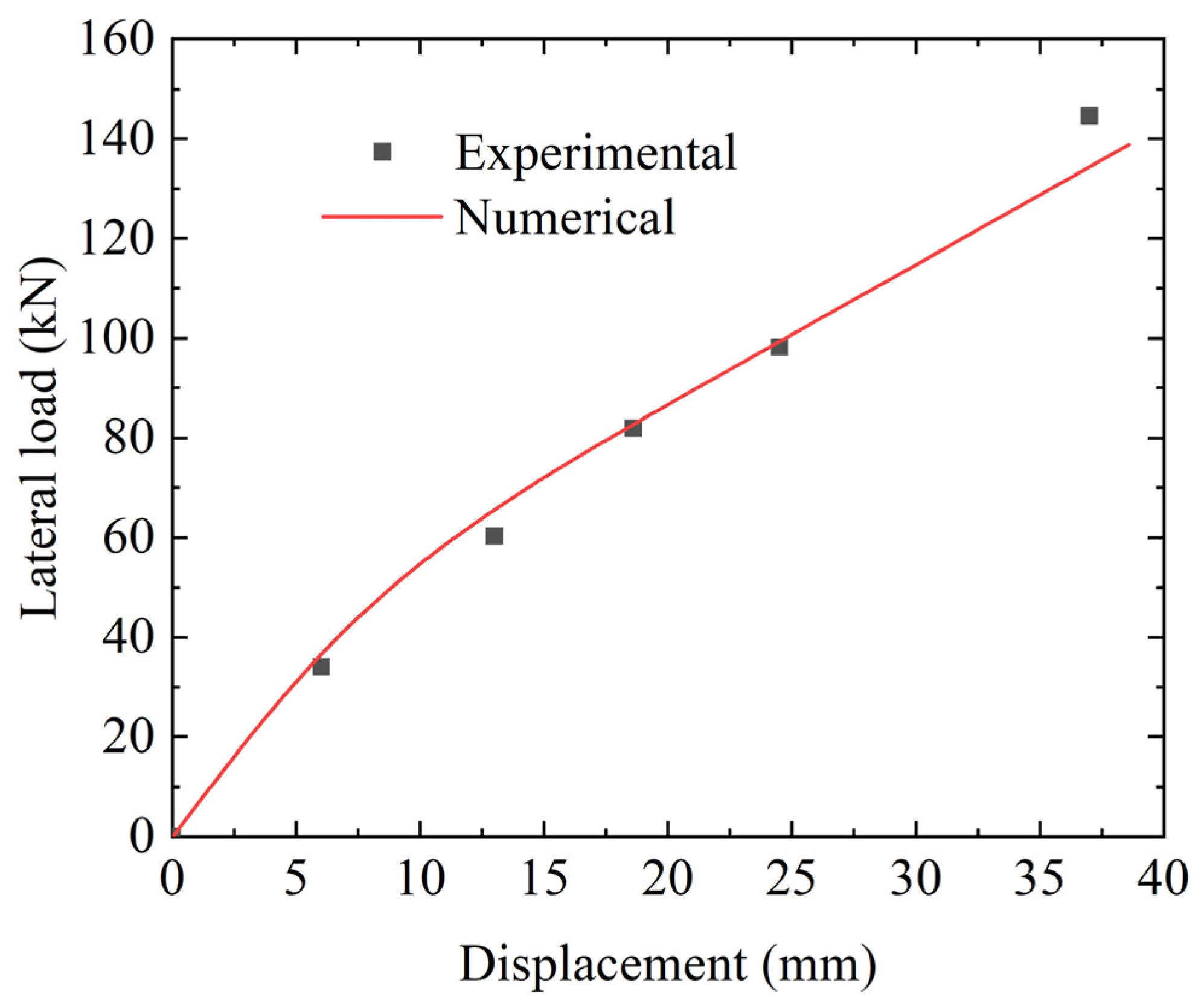
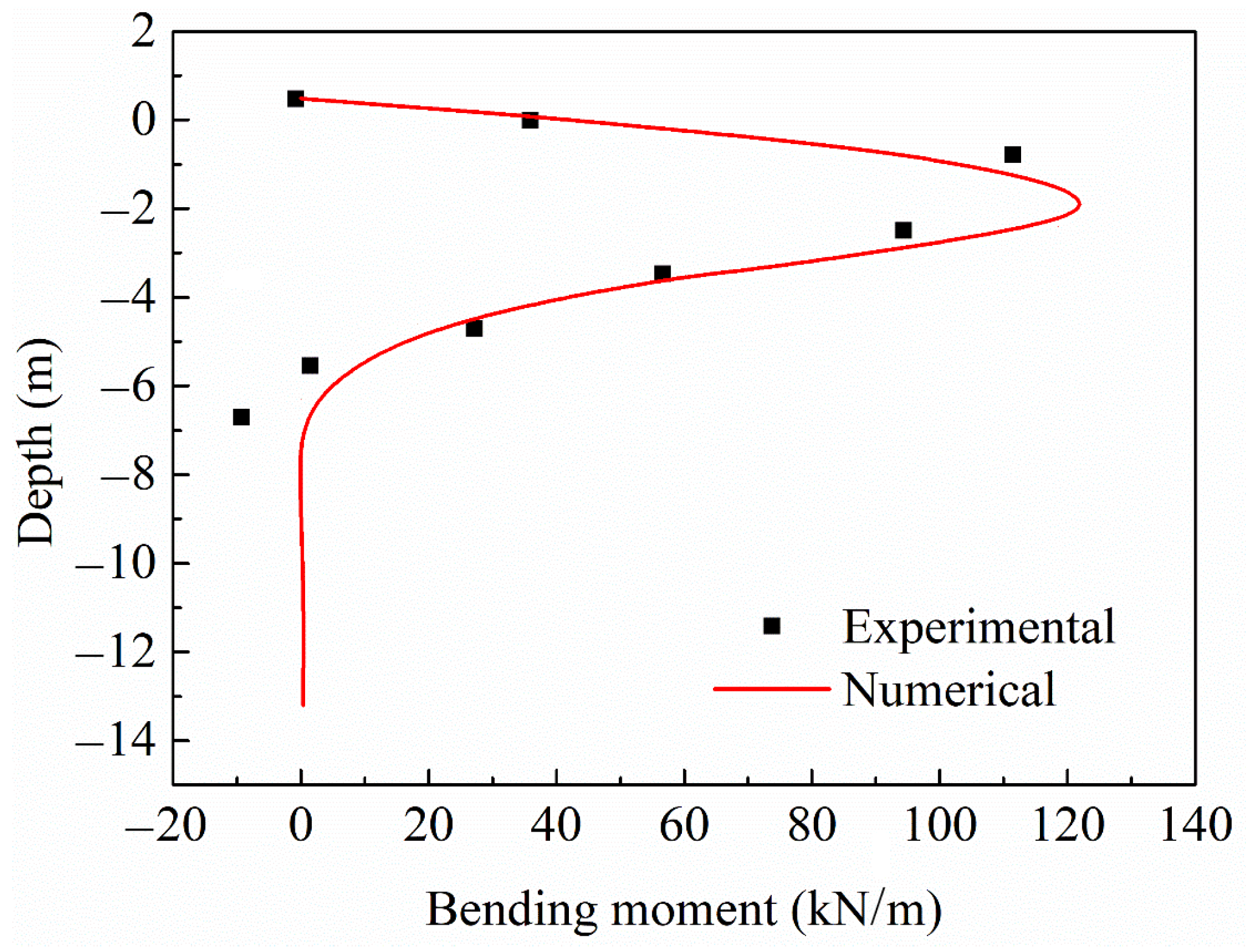
3. Validation of the Numerical Model
4. Results and Discussion
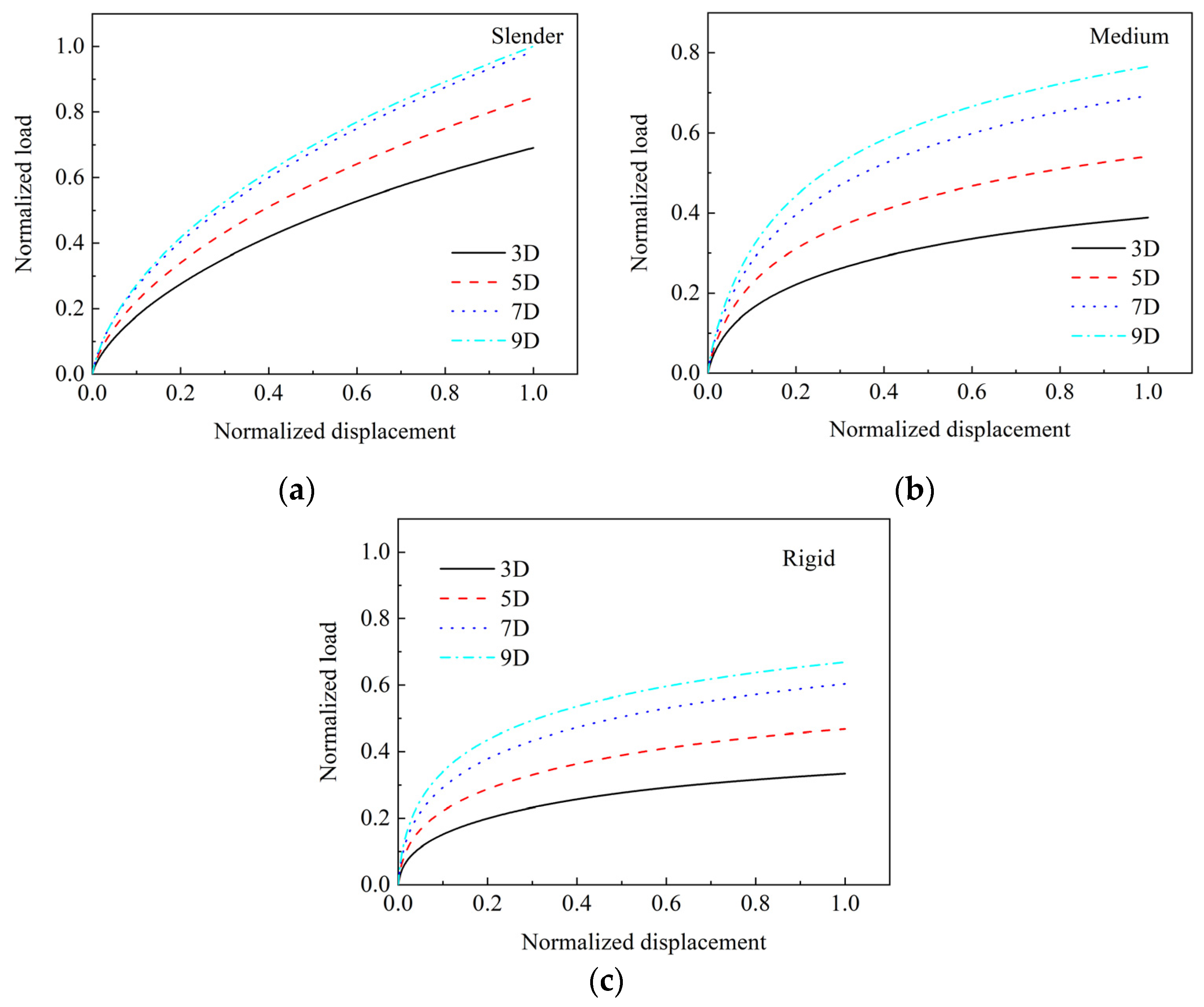
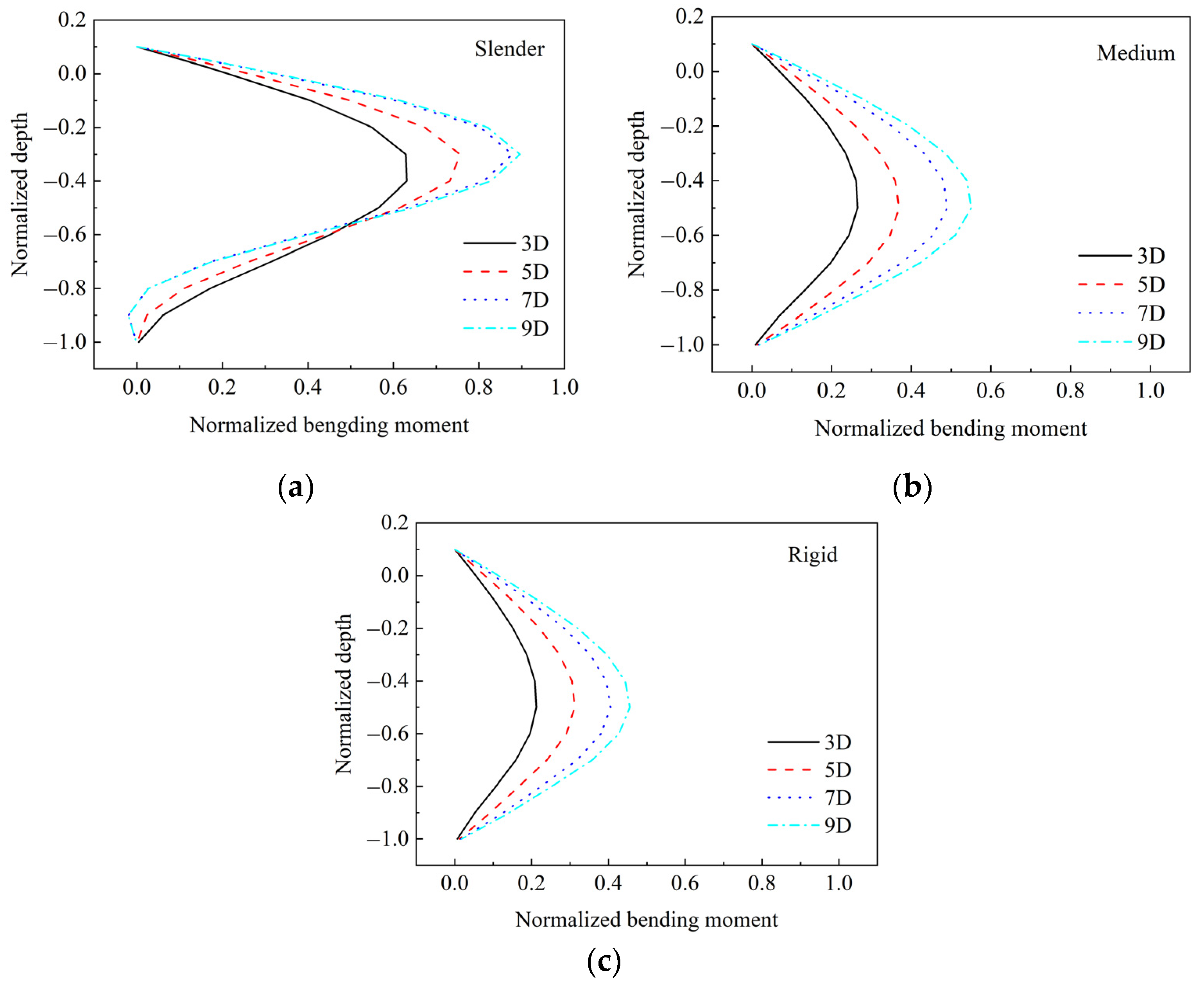
4.1. Pile Spacing
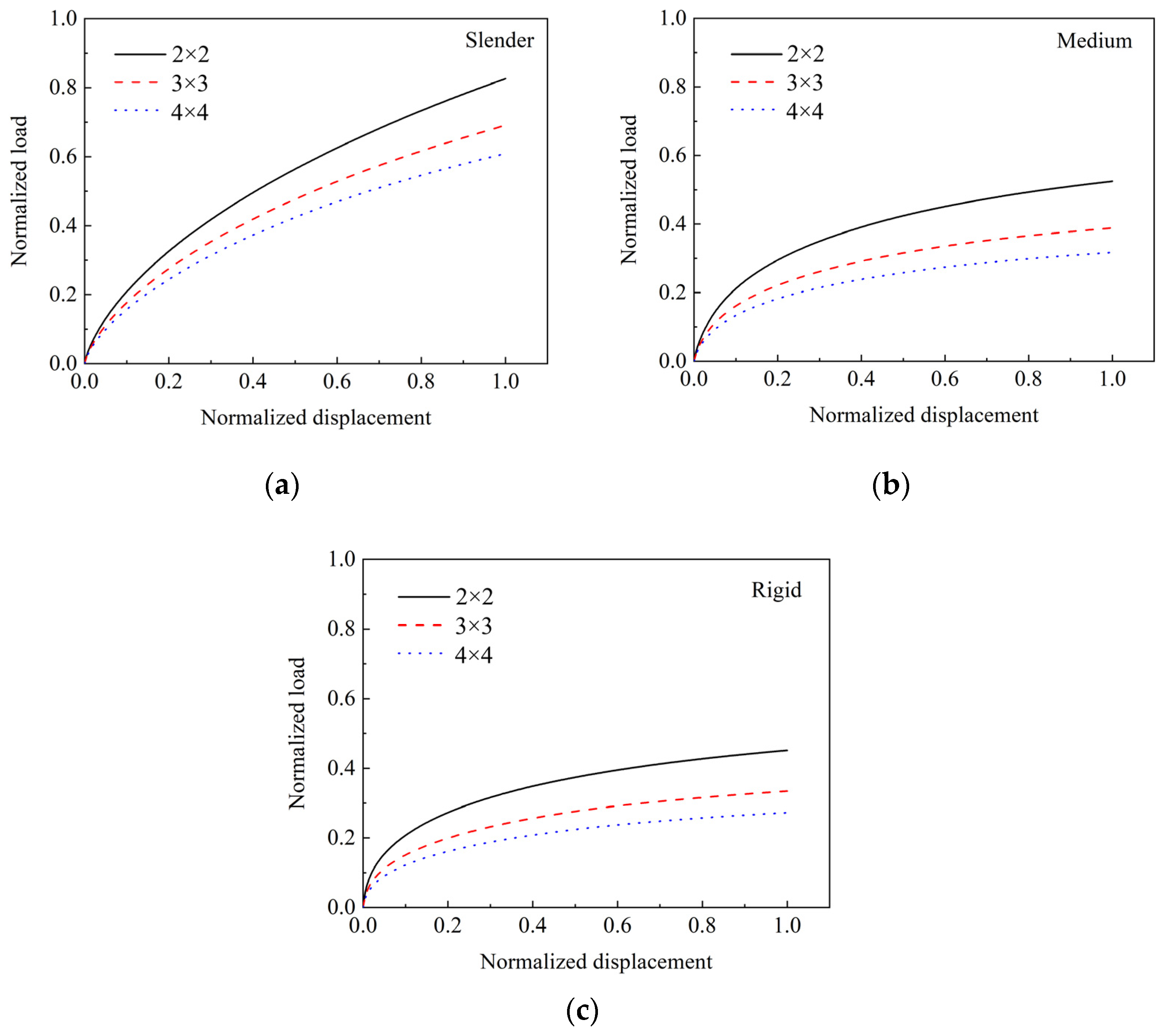
4.2. Number of Piles
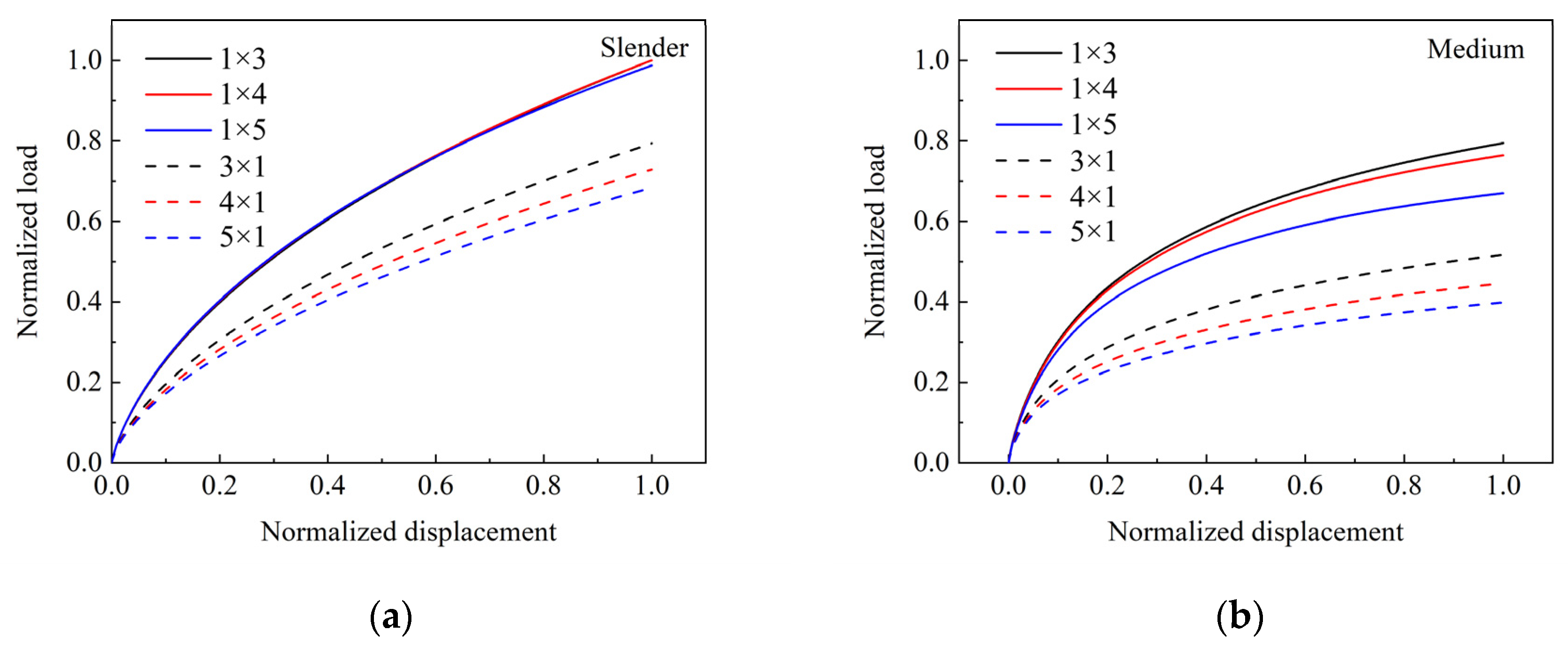
4.3. Pile Group Arrangement
5. Conclusions
- (1)
- The group reduction factors are closely related to pile relative stiffness, i.e., the group reduction factor decreases as the the pile relative stiffness increase.
- (2)
- The pile group effect of group with close spacing is more significant than that with the large spacing; the pile group effect decreases as the pile spacing increase. The pile group effect can be ignored for the pile group with pile spacing larger than 5 D.
- (3)
- For the pile group with 3 D pile spacing, the slender pile group’s group efficiencies are about two times that of the rigid pile group.
- (4)
- The pile group effect increases with the increase in the number of piles in the group; the pile group efficiency of the 2 × 2 pile group is about 1.5 times larger than that of the 4 × 4 pile group.
- (5)
- For the slender pile group (meaning the soil–pile relative stiffness is small), the “edge effect” can be neglected, while the “shadow effect” is significant for the medium rigid and rigid pile group, and the “shadow effect” is about 1.7 times larger than “edge effect”.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Liu, C.; Tang, L.; Ling, X.; Deng, L.; Su, L.; Zhang, X. Investigation of liquefaction-induced lateral load on pile group behind quay wall. Soil Dyn. Earthq. Eng. 2017, 102, 56–64. [Google Scholar] [CrossRef]
- Yu, Y.; Bao, X.; Liu, Z.; Chen, X. Dynamic Response of a Four-Pile Group Foundation in Liquefiable Soil Considering Nonlinear Soil-Pile Interaction. J. Mar. Sci. Eng. 2022, 10, 1026. [Google Scholar] [CrossRef]
- Nimbalkar, S.; Basack, S. Pile group in clay subjected to cyclic lateral load: Numerical modelling and design recommendation. Mar. Georesour. Geotechnol. 2022, 1–21. [Google Scholar] [CrossRef]
- Chen, L.; Chong, J.; Pang, L.; Zhang, C. Lateral capacity of a two-pile group foundation model located near slope in sand. Ocean Eng. 2022, 266, 112847. [Google Scholar] [CrossRef]
- Lemnitzer, A.; Khalili-Tehrani, P.; Ahlberg, E.R.; Rha, C.; Taciroglu, E.; Wallace, J.W.; Stewart, J.P. Nonlinear Efficiency of Bored Pile Group under Lateral Loading. J. Geotech. Geoenviron. Eng. 2010, 136, 1673–1685. [Google Scholar] [CrossRef]
- Liu, C.; Wang, C.; Fang, Q.; Ling, X. Soil-pile-quay wall interaction in liquefaction-induced lateral spreading ground. Ocean Eng. 2022, 264, 112592. [Google Scholar] [CrossRef]
- Huang, Y.; Wang, P.; Lai, Y.; Xu, Z. A small-strain soil constitutive model for initial stiffness evaluation of laterally loaded piles in drained marine sand. Ocean Eng. 2023, 268, 113417. [Google Scholar] [CrossRef]
- Wang, H.; Fu, D.; Yan, T.; Pan, D.; Liu, W.; Ma, L. Bearing Characteristics of Multi-Wing Pile Foundations under Lateral Loads in Dapeng Bay Silty Clay. J. Mar. Sci. Eng. 2022, 10, 1391. [Google Scholar] [CrossRef]
- Brown, D.A.; Morrison, C.; Reese, L.C. Lateral Load Behavior of Pile Group in Sand. J. Geotech. Eng. 1988, 114, 1261–1276. [Google Scholar] [CrossRef]
- Adeel, M.B.; Jan, M.A.; Aaqib, M.; Park, D. Development of Simulation Based p-Multipliers for Laterally Loaded Pile Groups in Granular Soil Using 3D Nonlinear Finite Element Model. Appl. Sci. 2021, 11, 26. [Google Scholar] [CrossRef]
- Ashour, M.; Ardalan, H. Employment of the P-Multiplier in Pile-Group Analysis. J. Bridg. Eng. 2011, 16, 612–623. [Google Scholar] [CrossRef]
- Su, D.; Yan, W.M. Relationship between p-multiplier and force ratio at pile head considering non-linear soil–pile interaction. Géotechnique 2019, 69, 1019–1025. [Google Scholar] [CrossRef]
- Fayyazi, M.S.; Taiebat, M.; Finn, W.D.L. Group reduction factors for analysis of laterally loaded pile groups. Can. Geotech. J. 2014, 51, 758–769. [Google Scholar] [CrossRef]
- Brown, D.A.; Reese, L.C.; O’Neill, M.W. Cyclic Lateral Loading of a Large-Scale Pile Group. J. Geotech. Eng. 1987, 113, 1326–1343. [Google Scholar] [CrossRef]
- Morrison, C.; Reese, L.C. Lateral-Load Test of a Full-Scale Pile Group in Sand; U.S. Army Engineer Waterway Experiment Station: Vicksburg, MS, USA, 1988. [Google Scholar]
- McVay, M.; Casper, R.; Shang, T.-I. Lateral Response of Three-Row Groups in Loose to Dense Sands at 3D and 5D Pile Spacing. J. Geotech. Eng. 1995, 121, 436–441. [Google Scholar] [CrossRef]
- Ruesta, P.F.; Townsend, F.C. Evaluation of Laterally Loaded Pile Group at Roosevelt Bridge. J. Geotech. Geoenviron. Eng. 1997, 123, 1153–1161. [Google Scholar] [CrossRef]
- McVay, M.; Zhang, L.; Molnit, T.; Lai, P. Centrifuge Testing of Large Laterally Loaded Pile Groups in Sands. J. Geotech. Geoenviron. Eng. 1998, 124, 1016–1026. [Google Scholar] [CrossRef]
- Huang, A.-B.; Hsueh, C.-K.; O’Neill, M.W.; Chern, S.; Chen, C. Effects of Construction on Laterally Loaded Pile Groups. J. Geotech. Geoenviron. Eng. 2001, 127, 385–397. [Google Scholar] [CrossRef]
- Rollins, K.M.; Sparks, A. Lateral Resistance of Full-Scale Pile Cap with Gravel Backfill. J. Geotech. Geoenviron. Eng. 2002, 128, 711–723. [Google Scholar] [CrossRef]
- Snyder, J.L. Full-Scale Lateral-Load Tests of a 3 × 5 Pile Group in Soft Clays and Silts. Master’s Thesis, Brigham Young University, Provo, UT, USA, 2004. [Google Scholar]
- Walsh, J.M. Full-Scale Lateral Load Tests of a 5 × 3 Pile Group in Sand. Master’s Thesis, Brigham Young University, Provo, UT, USA, 2005. [Google Scholar]
- Rollins, K.M.; Lane, J.D.; Gerber, T.M. Measured and Computed Lateral Response of a Pile Group in Sand. J. Geotech. Geoenviron. Eng. 2005, 131, 103–114. [Google Scholar] [CrossRef]
- Christensen, D.S. Full Scale Static Lateral Load Test of a 9 Pile Group in Sand. Master’s Thesis, Brigham Young University, Provo, UT, USA, 2006. [Google Scholar]
- Rollins, K.M.; Olsen, R.J.; Egbert, J.J.; Jensen, D.H.; Olsen, K.G.; Garrett, B.H. Pile Spacing Effects on Lateral Pile Group Behavior: Load Tests. J. Geotech. Geoenviron. Eng. 2006, 132, 1262–1271. [Google Scholar] [CrossRef]
- Mazzoni, S.; McKenna, F.; Scott, M.H.; Fenves, G.L. OpenSees Command Language Manual; Pacific Earthquake Engineering Research (PEER) Center: Berkeley, CA, USA, 2006; Volume 264. [Google Scholar]
- Zhang, W.; Esmaeilzadeh Seylabi, E.; Taciroglu, E. Validation of a three-dimensional constitutive model for nonlinear site response and soil-structure interaction analyses using centrifuge test data. Int. J. Numer. Anal. Methods Géoméch. 2017, 41, 1828–1847. [Google Scholar] [CrossRef]
- Ilankatharan, M.; Kutter, B. Modeling Input Motion Boundary Conditions for Simulations of Geotechnical Shaking Table Tests. Earthq. Spectra 2010, 26, 349–369. [Google Scholar] [CrossRef]
- Gorini, D.N.; Callisto, L. A macro-element approach to analyse bridge abutments accounting for the dynamic behaviour of the superstructure. Géotechnique 2020, 70, 711–719. [Google Scholar] [CrossRef]
- Su, L.; Zhou, L.; Zhang, X.; Ling, X. Experimental and numerical modeling on liquefaction resistance of geotextile reinforced sand. Soil Dyn. Earthq. Eng. 2022, 159, 107345. [Google Scholar] [CrossRef]
- Rollins, K.M.; Brown, D.A. Design Guidelines for Increasing the Lateral Resistance of Highway-Bridge Pile Foundations by Improving Weak Soils; Transportation Research Board: Washington, DC, USA, 2011; Volume 697. [Google Scholar]
- Elgamal, A.; Yan, L.; Yang, Z.; Conte, J.P. Three-Dimensional Seismic Response of Humboldt Bay Bridge-Foundation-Ground System. Eng. Struct. 2008, 134, 1165–1176. [Google Scholar] [CrossRef]
- Elgamal, A.; Yang, Z.; Parra, E.; Ragheb, A. Modeling of cyclic mobility in saturated cohesionless soils. Int. J. Plast. 2003, 19, 883–905. [Google Scholar] [CrossRef]
- Yang, Z.; Elgamal, A.; Parra, E. Computational Model for Cyclic Mobility and Associated Shear Deformation. J. Geotech. Geoenviron. Eng. 2003, 129, 1119–1127. [Google Scholar] [CrossRef]
- Poulos, H.G. Single Pile Response to Cyclic Lateral Load. J. Geotech. Eng. Div. 1982, 108, 355–375. [Google Scholar] [CrossRef]





| Researchers | Pile Group Arrangement | Test Type | Soil Type | Internal Friction Angle (°) | D (mm) | Pile Spacing | Group Reduction Factor |
|---|---|---|---|---|---|---|---|
| Brown et al. [14] | 3 × 3 | Full scale | Stiff clay | 273 | 3D | 0.6 | |
| 3 × 3 | Full scale | Stiff clay | 273 | 3D | 0.53 | ||
| Brown et al. [9] | 3 × 3 | Full scale | Medium dense sand | 38.5 | 273 | 3D | 0.5 |
| Morrison and Reese [15] | 3 × 3 | Full scale | Medium dense sand | 38.5 | 273 | 3D | 0.5 |
| McVay et al. [16] | 3 × 3 | Centrifuge | Medium loose sand | 30 | 430 | 5D | 0.85 |
| 3 × 3 | Centrifuge | Medium dense sand | 33 | 430 | 5D | 0.85 | |
| 3 × 3 | Centrifuge | Medium loose sand | 30 | 430 | 3D | 0.48 | |
| 3 × 3 | Centrifuge | Medium dense sand | 33 | 430 | 3D | 0.5 | |
| Ruesta and Townsend [17] | 4 × 4 | Full scale | Loose sand | 32 | 760 (square) | 3D | 0.52 |
| McVay et al. [18] | 3 × 3 | Centrifuge | Sand | 30, 33 | 429 (square) | 3D | 0.5 |
| 3 × 4 | Centrifuge | Sand | 30, 33 | 429 (square) | 3D | 0.45 | |
| 3 × 5 | Centrifuge | Sand | 30, 33 | 429 (square) | 3D | 0.4 | |
| 3 × 6 | Centrifuge | Sand | 30, 33 | 429 (square) | 3D | 0.37 | |
| 3 × 7 | Centrifuge | Sand | 30, 33 | 429 (square) | 3D | 0.34 | |
| Rollins et al. | 3 × 3 | Full scale | Clay and silt | 400 | 3D | 0.47 | |
| Huang et al. [19] | 2 × 3 | Full scale | Silty clay | 1500 | 3D | 0.79 | |
| 3 × 4 | Full scale | Silty clay | 800 | 3D | 0.69 | ||
| Rollins and Sparks [20] | 3 × 3 | Full scale | Silt and clay | 324 | 3D | 0.47 | |
| Snyder [21] | 3 × 5 | Full scale | Soft clay | 324 | 3.92D | 0.74 | |
| Walsh [22] | 3 × 5 | Full scale | Sand | 40 | 324 | 3.92D | 0.51 |
| Rollins et al. [23] | 3 × 3 | Full scale | Sand | 38 | 324 | 3.3D | 0.53 |
| Christensen [24] | 3 × 3 | Full scale | Sand | 38 | 324 | 5.65D | 0.78 |
| Rollins et al. [25] | 3 × 5 | Full scale | Stiff clay | 610 | 3D | 0.62 | |
| 3 × 3 | Full scale | Stiff clay | 324 | 5.65D | 0.87 | ||
| 3 × 4 | Full scale | Stiff clay | 324 | 4.4D | 0.78 | ||
| 3 × 5 | Full scale | Stiff clay | 324 | 3.3D | 0.57 |
| Parameters | Clay | Sand |
|---|---|---|
| Density of sand (ton/m3) | 1.91 | 1.67 |
| Cohesion (kPa) | 30 | 0 |
| Internal friction angle (°) | 0 | 40 |
| Shear modulus (kPa) | 87,000 | 50,000 |
| Bulk modulus (kPa) | 420,000 | 150,000 |
| Poisson’s ratio | 0.3 | 0.3 |
| Ge | Slender Pile | Medium Rigid Pile | Rigid Pile |
|---|---|---|---|
| 3 D | 0.691 | 0.389 | 0.334 |
| 5 D | 0.844 | 0.541 | 0.468 |
| 7 D | 0.985 | 0.693 | 0.603 |
| 9 D | 1.000 | 0.766 | 0.670 |
| Ge | Slender Pile | Medium Rigid Pile | Rigid Pile |
|---|---|---|---|
| 2 × 2 | 0.826 | 0.525 | 0.452 |
| 3 × 3 | 0.691 | 0.389 | 0.334 |
| 4 × 4 | 0.609 | 0.317 | 0.273 |
| Ge | Slender Pile | Medium Rigid Pile | Rigid Pile |
|---|---|---|---|
| 1 × 3 | 1 | 0.794 | 0.697 |
| 1 × 4 | 1 | 0.764 | 0.666 |
| 1 × 5 | 0.988 | 0.670 | 0.577 |
| 3 × 1 | 0.794 | 0.517 | 0.445 |
| 4 × 1 | 0.727 | 0.446 | 0.383 |
| 5 × 1 | 0.684 | 0.399 | 0.341 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, B.; Wang, X.; Liu, C.; Kong, J. Effect of Relative Stiffness of Pile and Soil on Pile Group Effect. J. Mar. Sci. Eng. 2023, 11, 192. https://doi.org/10.3390/jmse11010192
Liu B, Wang X, Liu C, Kong J. Effect of Relative Stiffness of Pile and Soil on Pile Group Effect. Journal of Marine Science and Engineering. 2023; 11(1):192. https://doi.org/10.3390/jmse11010192
Chicago/Turabian StyleLiu, Bo, Xiaomin Wang, Chunhui Liu, and Jingchang Kong. 2023. "Effect of Relative Stiffness of Pile and Soil on Pile Group Effect" Journal of Marine Science and Engineering 11, no. 1: 192. https://doi.org/10.3390/jmse11010192
APA StyleLiu, B., Wang, X., Liu, C., & Kong, J. (2023). Effect of Relative Stiffness of Pile and Soil on Pile Group Effect. Journal of Marine Science and Engineering, 11(1), 192. https://doi.org/10.3390/jmse11010192






