Experimental Investigation of Mooring Performance and Energy-Harvesting Performance of Eccentric Rotor Wave Energy Converter

Abstract

To obtain the optimal mooring mode and the best-matching wave condition of an eccentric rotor wave energy converter (ERWEC), a physical model of the ERWEC was developed. Ten mooring modes and eight wave conditions were set up. Several experiments were carried out to analyze the influence of mooring modes and wave conditions on the mooring and energy-harvesting performances of the ERWEC. The results showed that the mooring and energy-harvesting performances changed significantly for the same mooring mode under various regular wave conditions, but the opposite situation was found under irregular wave conditions. The wave-facing direction of the buoy was a critical factor affecting the mooring and energy-harvesting performances, while the number of anchor lines had little effect on them. In addition, a method to evaluate the motion response of the buoy based on the number of effective excitations and a method to evaluate the comprehensive performance based on the cloud chart are proposed. The mooring mode and wave condition combination that obtained the optimal mooring and energy-harvesting performances for the ERWEC was determined. This paper provides a novel perspective on how to balance the efficiency and reliability of wave energy converters.

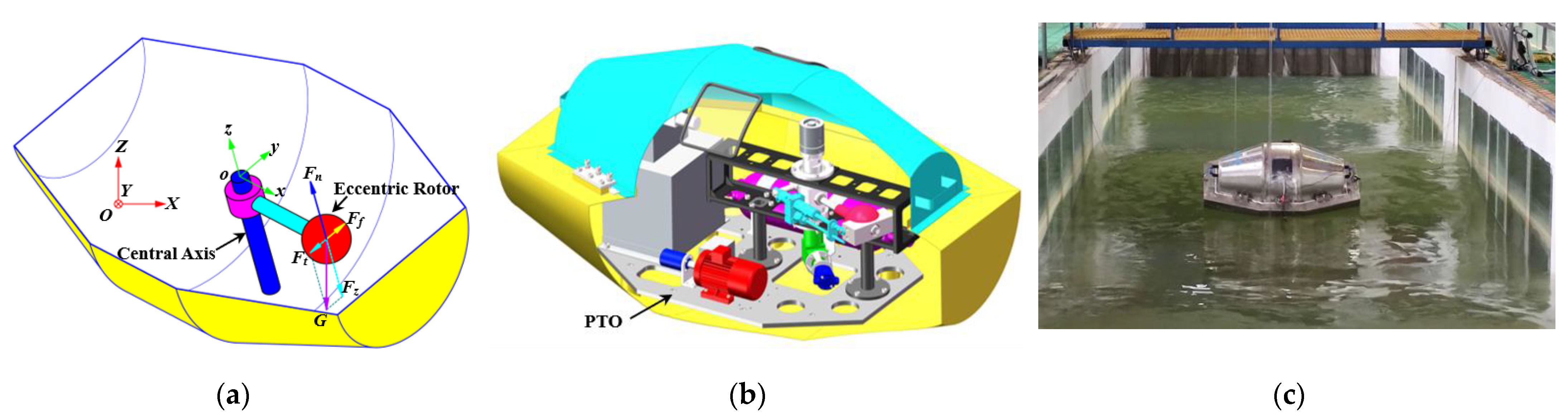
1. Introduction

Energy is an important foundation for social development, and the energy crisis has been receiving increasing attention in recent years. Traditional fossil energy, such as oil and coal, is mostly non-renewable and has limited reserves. The widespread utilization of fossil energy has caused serious problems, including environmental pollution and the greenhouse effect [1]. Therefore, the development of clean and renewable energy has become a promising solution to address the energy crisis [2].

A total of 71% of the Earth’s surface area is covered by oceans, which receive extensive solar radiation energy that is stored in their waters [3]. As a kind of marine resource, ocean wave energy is characterized by its cleanness and renewability, and its total reserves may be 8000~80,000 TWh. It is worth noting that the power density of wave energy can reach 2~3 kW/m², which is greater than that of solar energy and wind energy [4]. Hence, wave energy has great prospects for development.

To develop and utilize wave energy, various wave energy converters (WECs) have been designed, including oscillating water column devices [5], oscillating floating devices [6], overtopping wave devices [7], and hybrid devices [8]. The eccentric rotor wave energy converter (ERWEC) adopts a fully enclosed buoy structure [9], and its power take-off (PTO) system is installed inside the enclosed buoy, helping it contribute to resisting marine corrosion and organism attachment. Therefore, the ERWEC possesses the characteristics of higher reliability and longer service life. Inspired by this concept, the Wello Company in Finland developed the Penguin ERWEC in 2014 [10]. In addition, similar design concepts have been adopted for Searev [11], Pendulum Wave Energy Converter (PeWEC) [12], and Inertial Sea Wave Energy Converter (ISWEC) [13] WECs, and their reliable performances have been verified in stronger wave climates during storms.

The ERWEC is a kind of floating WEC, and its mooring and energy-harvesting performances are important indices [14]. Specifically, the mooring performance is highly dependent on the mooring pattern, and the energy-harvesting performance is closely connected to the motion response of the buoy under wave excitation.

In terms of mooring systems, the CFD method was employed in [15] for coupled mooring performance analysis considering wave conditions, the motion response of the buoy, and mooring constraints, and it accurately reflected the strong wave-height dependence of the response amplitude operator (RAO). Although the numerical simulation method has been widely exploited in the design of mooring systems for floating WECs, the scaled model experiment is still an irreplaceable investigation method for mooring performance [16]. Martinelli et al. [17] experimentally investigated the influence of the number of anchor lines and the arrangement of the mooring system on the power generation performance of a floating WEC raft. The results showed that increasing the number of anchor lines would disperse the load and improve reliability, and the optimal power generation performance could be obtained when the length direction of the floating raft was along the incident wave direction. Additionally, as demonstrated in [18], under wave conditions with a small period (Tp = 1.6 s), the anchor line tension showed stronger nonlinearities for a floating oscillating water column WEC, and the influence of the mooring system on the energy conversion performance was related to the wave height. With regard to floating horizontal rotor WECs, the influence of the mooring angle on the motion response was discussed in [19]. When the mooring angle was increased, the roll angle and the yaw angle decreased first and then increased, and the pitch angle barely changed. Gomes et al. [20] found that the number of anchor lines for compact floating WEC arrays could be reduced significantly through the application of arrays with inter-body connections, but high peak tensions were observed in the lines under extreme wave conditions.

In terms of the motion response of the buoy, time-varying fluid damping is an important factor causing a continuous and unpredictable difference between the water surface elevation and the buoy displacement [21]. Yu et al. [22] found that the pressure at the bottom of the buoy on the leeward side increased more obviously than the waveward side when the wave hit the buoy, which provides a theoretical foundation for the reliable design of a buoy. Furthermore, Homayoun et al. [23] analyzed the motion response of a monopile wind turbine combined with a floating buoy in a WEC, and the results showed that the WECs with an inward curvature at the bottom absorbed more energy from ocean waves. Li et al. [24] carried out numerical investigations on hinged double-body floating WECs and showed that the resonance state of the pitching motion of the buoys was highly dependent on their radius and draft rather than the length but that the length of the buoys had a significant effect on the pitching phase difference of the adjacent buoys. Zang et al. [25] investigated the motion response of buoys under regular waves and found that decreasing incident wave height or increasing PTO damping increased the nonlinearity between the heave motion and surrounding wave elevation. Liu et al. [26] analyzed the motion response of compact buoy array-type WECs, and the investigations revealed that a strong interaction between the waves and the buoys was generated under the waves of a small period (T = 1.5 s), and the phase difference between the buoys depended on the distance between them.

In terms of the mooring system and motion response of the ERWEC, the influence of parameters on the mean output power performance, including the number of anchor lines, the wave conditions, the eccentric rotor mass, and the eccentric rotor load torque, was researched in [27], and the eccentric rotor load torque was found to be the most critical factor that determined the net mean output power. That conclusion promoted development pathways for the ERWEC. Chen et al. [28] observed that the output power of the ERWEC also depended on the motion damping of the buoy. The authors suggested subjecting the eccentric rotor to short natural rocking periods to increase the output power. The underwater equivalent area was utilized as the variable to investigate the motion response of the ERWEC in low wave energy density seas, finding that the pitch RAOs of the cylindrical buoy were 0.6–52.59% larger than those of the hemispherical buoy because of the difference in force [29]. Duan et al. [30] adopted the time domain analysis method to study the effect of the buoy diameter on the instantaneous capture power and determined that the average wave energy conversion efficiency was 54.44% for an ERWEC in sea areas with low energy flow density, providing a reference value for performance evaluation of ERWECs.

However, ERWECs have not been widely promoted and applied. The research on ERWECs is not thorough enough, and the coupling relationships among the mooring system, buoy body, energy conversion system, and other modules are not clear. The mooring and energy-harvesting performances of ERWECs have not been investigated sufficiently; in particular, no comprehensive performance study covering the mooring and energy-harvesting performances of ERWECs has been conducted.

In this research, the anchor line tension and the motion response of an ERWEC under various mooring modes and wave conditions are analyzed experimentally, and their optimal combination is determined. Section 2 provides the mechanical structure of the physical model, mooring mode, and wave conditions for the ERWEC and describes the experimental procedure. Section 3 discusses the influence of various mooring modes and wave conditions on anchor line tension. Section 4 proposes a statistical method based on the number of effective excitations to evaluate the motion response of the buoy and discusses the influence of various mooring modes and wave conditions on motion response. Finally, Section 5 provides concluding statements.

2. Experimental Design

2.1. Mechanical Structure of ERWEC

The energy conversion principle of the ERWEC is shown in Figure 1a. OXYZ is a Eulerian coordinate system fixed to the Earth, and oxyz is a Lagrangian coordinate system fixed to the ERWEC buoy. The ox axis runs along the length of the buoy, and the oy axis runs along the width of the buoy. In a static state, there is a corresponding and coincident relationship of each coordinate axis between the OXYZ system and the oxyz system. The oxyz system generates a certain angle with respect to the OXYZ system because of the motion response of the buoy excited by the wave, which leads to a component force F_t from the gravity of the eccentric rotor G. F_t will actuate the eccentric rotor to rotate around the central axis, and if the driving torque exceeds the threshold of the drag torque, the eccentric rotor will rotate around the central axis. After the above process, wave energy is converted into the mechanical energy of the eccentric rotor, which can be further generated into usable electrical energy by a power take-off system (PTO).

Figure 1b is the 3D schematic diagram of a wave energy device designed according to the principle of the ERWEC. The hydraulic PTO was installed in a closed buoy composed of a cover shell and bottom case. The scale ratio of the device was 1:5. The buoy had a length of 1500 mm, a width of 1000 mm, and a height of 862 mm.

The physical model of the ERWEC and the experimental process are presented in Figure 1c. The total mass of the physical model was 210 kg, and the draught was 320 mm. To enhance the motion response of the buoy under wave excitation, a counterweight was used to position the center of buoyancy 110 mm below the waterline and the center of gravity 60 mm above the waterline. Because of the limited size of the wave flume, radiation and diffracted waves from the device may be reflected by the side walls, which would affect the motion response analysis. This specific impact is further analyzed in the Results and Discussion. An attitude sensor was installed inside the ERWEC to measure the motion response of the buoy under wave excitation. The angle measurement range of the attitude sensor was ±180°, the measurement accuracy was 0.01°, and the data output frequency was 10 Hz.

2.2. Mooring Modes

As schematically presented in Figure 2, the gravity anchor was selected for various mooring modes of the ERWEC. A force sensor was installed in the middle of each anchor line to record its tension. The range of the force sensor was 300 N, and the repetitive measurement error was 0.05% FS. A wave sensor was installed at the front of the ERWEC along the wave incidence direction to record the wave excitation parameters. The maximum sampling frequency of the wave sensor was 50 Hz.

To comprehensively analyze the influence of different mooring modes on mooring performance and energy-harvesting performance, 10 mooring modes were set up during the experiment, as illustrated in Figure 3. Here, Mooring Modes A and B adopted the single-anchor line mooring mode; Mooring Modes C, D, E, and F adopted the two-anchor line mooring mode; and Mooring Modes G, H, I, and J adopted the three-anchor line mooring mode. Moreover, for Mooring Modes A, C, E, G, and I, the length direction of the buoy was the same as the wave propagation direction. For Mooring Modes B, D, F, H, and J, the length direction of the buoy was vertical to the wave propagation direction. The mooring radius was 1.8 m, and the length of the anchor line was 2.6 m.

For mooring systems, it is generally assumed that the lower the maximum tension on the anchor line, the better the mooring performance. Therefore, the mooring performance was evaluated by the maximum tension on the anchor line during the experiment.

2.3. Wave Conditions and Motion Response

The experiments were conducted in the wave tank of the Qingdao National Marine Equipment Inspection & Testing Group Co., Ltd., Qingdao, China. A photograph of the wave tank is presented in Figure 4. The wave tank’s length was 30.0 m, its width was 4.0 m, and its maximum water depth was 2.0 m. The tank generated incident waves with a maximum height of 1.0 m.

During the experiment, the water depth was 1.8 m. The linear regular wave and irregular wave based on the Pierson–Moskowitz (PM) spectrum with different parameters were set as wave excitation conditions. The parameters of wave height H and period T of the linear regular waves are listed in

Table 1. The parameters of linear regular waves.

Wave Type	NO.	H	T
regular waves	Wave Condition a	0.2 m	1.9 s
	Wave Condition b	0.3 m	2.0 s
	Wave Condition c	0.4 m	2.1 s
	Wave Condition d	0.5 m	2.2 s

, and the parameters of significant wave height Hs and spectral peak period Tp of the irregular waves based on the PM spectrum are shown in

Table 2. The parameters of irregular waves.

Wave Type	NO.	Hs	Tp
irregular waves *	Wave Condition e	0.15 m	1.2 s
	Wave Condition f	0.25 m	1.3 s
	Wave Condition g	0.35 m	1.4 s
	Wave Condition h	0.45 m	1.5 s

* In this study, the PM spectrum is used to describe irregular waves.

.

Taking Wave Condition g as an example, the theoretical and measured wave spectra of the irregular waves based on the PM spectrum are presented in Figure 5. In this section, 80 sets of analysis experiments were carried out using the aforementioned mooring modes and wave excitation conditions. To facilitate the description of the experiment, the experiment serial number was marked by letter combinations. For example, Experiment Aa denoted the combination of Mooring Mode A and Wave Condition a. Limited by the experimental conditions, repeated experiments could not be carried out to evaluate the error of the experimental results, but meaningful general conclusions could still be drawn based on these experimental analyses.

Figure 6 shows the time-history curve of wave height corresponding to a significant height of 0.3 m and a peak period of 1.4 s (Wave Condition g). The time-history curves of mooring cable tension, roll, pitch, and yaw for Mooring Mode D under Wave Condition g are shown in Figure 7a–d. In the figure, the maximum tension of the mooring cable in Mooring Mode D is 151.8 N. The device was dominated by the roll and yaw motions, and the pitch response amplitude was relatively low.

3. Force Analysis of Anchor Line

3.1. Tension Analysis of the Single-Anchor Line Mooring Mode

Both Mooring Mode A and Mooring Mode B adopted the single-anchor line mooring mode, and the maximum tension on the anchor line was analyzed experimentally under different wave excitation conditions, as shown in Figure 8.

Figure 8a illustrates the variation in the maximum anchor line tension of the single-anchor line mooring mode with respect to the increase in the wave height and period under regular waves. The maximum anchor line tension of Mooring Mode A was on the rise. For Mooring Mode B, the maximum anchor line tension reached peak value when the wave height was 0.4 m and the period was 2.1 s, and then it dropped slightly.

As shown in Figure 8b, under irregular waves, with the increase in the significant wave height and spectral peak period, the maximum anchor line tension of the Mooring Mode A line first increased, then slightly decreased at a significant wave height of 0.35 m and a spectral peak period of 1.4 s, followed by a sharp increase. The maximum anchor line tension of the Mooring Mode B line reached a large value when the significant wave height was 0.25 m and the spectral peak period was 1.3 s and then remained unchanged.

As shown in Figure 3a,b, in Mooring Mode A, the incident wave was perpendicular to the bow of the device, and the effective action area between the wave and the device was relatively small, so the excitation force and mooring tension on the device were low. However, the incident wave acted vertically on the side of the mooring in Mooring Mode B, causing the effective action area to increase. The wave force on the device was stronger, and the corresponding mooring force was larger. Therefore, the maximum anchor line tension of Mooring Mode B was larger than that of Mooring Mode A for the same wave conditions.

The WECs using the single-point mooring mode can rotate 360° around the mooring point following the wind and wave currents. Because of the weathercock effect, the ERWEC will be moored in orientation with the fewest environmental forces. Still, the device’s heavy motion response was large, and the mooring cable provided less constraining force. Adopting this kind of mooring system will minimize environmental loads on systems [31]. This view coincided with the experimental phenomena in this paper.

3.2. Tension Analysis of the Two-Anchor Line Mooring Mode

Mooring Mode C, Mooring Mode D, Mooring Mode E, and Mooring Mode F all used two-anchor lines to moor the ERWEC, and the variation curves of the maximum tension on the anchor lines measured by the experiment with different wave excitation conditions are depicted in Figure 9.

In the case of regular waves, as the wave height and wave period increased, the maximum anchor line tension of Mooring Mode C increased to a peak value when the wave height was 0.3 m and the wave period was 2.0 s and then decreased. For Mooring Mode D, the maximum anchor line tension first increased, then began to decrease at the wave height of 0.4 m and the wave period of 2.1 s, and then increased slightly. The maximum anchor line tension of Mooring Mode E was on the rise. Moreover, the most obvious change was in the maximum anchor line tension of Mooring Mode F, where the tension increased slightly at first, decreased sharply at the wave height of 0.4 m and the wave period of 2.1 s, and then increased sharply.

Under irregular waves, with the increase in the significant wave height and spectral peak period, the maximum anchor line tension of Mooring Mode C increased to a peak value when the significant wave height was 0.25 m and the spectral peak period was 1.3 s, and then it showed a declining trend. For Mooring Mode D, the maximum anchor line tension reached a maximum value at the significant wave height of 0.35 m and the spectral peak period of 1.4 s and then had a slight decline. There was a peak value for the maximum anchor line tension of Mooring Mode E with a significant wave height of 0.25 m and the spectral peak period of 1.3 s, and then it remained the same. The maximum anchor line tension of Mooring Mode F experienced a small variation.

The maximum anchor line tension of Mooring Mode D was greater than that of other mooring modes under regular waves. For irregular waves, the maximum anchor line tension of Mooring Mode F was greater than that of other mooring modes. Predictably, the incident waves were perpendicular to the side of the device in Mooring Mode D and Mooring Mode F, producing mainly pitch motion (around the ox axis). The installation method of the anchor cables in Mooring Mode D hindered the pitch motion, requiring more tension to counteract the wave force, so its corresponding mooring forces were stronger. In irregular waves, the maximum anchor line tension of Mooring Mode F became more significant, primarily because irregular excitation forces caused the device to exhibit strong fluctuation characteristics. The device’s pitch and surge (around the oy axis) could not be adequately controlled by the mooring system, so the anchor cables exerted additional stress to prevent the device from making excessive movements.

3.3. Tension Analysis of the Three-Anchor Line Mooring Mode

There were three-anchor lines used in Mooring Mode G, Mooring Mode H, Mooring Mode I, and Mooring Mode J; Figure 10 shows the maximum tension of the anchor lines experimentally measured under different wave excitation conditions.

There was a continuous increase in the maximum anchor line tension of Mooring Mode G and Mooring Mode I with the increase in the wave height and wave period under regular waves. Moreover, the most obvious change occurred in the maximum anchor line tension of Mooring Mode H, where the tension first increased, and after reaching a local maximum value, there was a decrease until the wave height was 0.4 m and the wave period was 2.1 s, then it increased again, so the fluctuation of the curve was large. For Mooring Mode J, the maximum line tension increased to a peak value at the wave height of 0.3 m and the wave period of 2.0 s and then remained unchanged.

When the ERWEC was excited by irregular waves, as the significant wave height and spectral peak period increased, the maximum anchor line tension of Mooring Mode G showed an upward trend. The maximum anchor line tension for Mooring Mode H remained basically unchanged. Although there was a numerical discrepancy between Mooring Mode I and Mooring Mode J for the maximum anchor line tension, the two curves possessed similar trends, and first they gradually increased, reaching a maximum value when the significant wave height was 0.35 m and the spectral peak period was 1.4 s, and then decreased.

Compared to other mooring schemes, the maximum anchor line tension of Mooring Mode G was less than that of the other mooring modes under the same wave excitation conditions. This was caused by two main factors: The incident wave mainly interacted with the device’s bow; thus, the wave excitation force and mooring tension were relatively weak. Additionally, two anchor cables were installed on the wave-facing side of the device, which can contribute to alleviating sudden changes in tension.

4. Motion Response Analysis of the Buoy

4.1. The Statistical Method of the Number of Effective Excitations

The buoy of the ERWEC swung owing to the wave excitation, and the gravitational force on the eccentric rotor created a driving component force that drove the eccentric rotor to rotate around the central axis. If the swing amplitude of the buoy was small, the resistance torque caused by friction was difficult to overcome because of the small driving component force, and the eccentric rotor was unable to rotate around the central axis. Therefore, the necessary condition for an eccentric rotor to rotate around the central axis is that the swing amplitude of the buoy must be over a critical value, i.e., the angle threshold.

In addition, only the swing motion around the ox axis and the oy axis among the six degrees of freedom motion of the buoy could generate the driving force from the gravitational force. To evaluate the motion response of the buoy, the effective excitation number, which is defined as the number of swing amplitudes exceeding the critical value of the angular threshold, should be counted. The larger the number of effective excitations, the more satisfactory the motion response and the better the energy-harvesting performance of the ERWEC. The statistical method of counting the effective excitation number in a given time is shown in Figure 11.

The critical value of the swing motion was influenced by the mass of the eccentric rotor, the coefficient of friction at the central axis, the damping of the energy conversion system, etc. There were differences in critical values for various ERWEC devices. The critical value of swing amplitude of the ERWEC physical model developed in this paper was 15° according to several experimental measurements.

Taking Experiment Dg as an example, the motion response of the buoy around the ox axis is shown in Figure 12. The red line represents the forward effective excitation of the buoy rotating clockwise around the ox axis, and the blue line represents the backward effective excitation of the buoy rotating counterclockwise around the ox axis, and the sum of the forward and backward effective excitations is the number of effective excitations around the ox axis. For example, the number of effective excitations around the ox axis in Experiment Dg was 51. The number of effective excitations is used to evaluate the effect of the motion response of the buoy under different mooring systems and different wave conditions.

4.2. The Number of Effective Excitations in the Single-Anchor Line Mooring Mode

The number of effective excitations obtained for the buoy in the single-anchor line mooring mode is shown in Figure 13. The horizontal coordinates indicate the number of effective excitations, and the vertical coordinates indicate the corresponding experiment number. The blue color indicates the number of effective rotations of the ERWEC around the ox axis, and the orange color indicates the number of effective rotations of the device around the oy axis. When the length direction of the buoy is parallel to the wave incidence direction, the dominant wave excitation is around the oy axis. When the length direction of the buoy is perpendicular to the wave incidence direction, the dominant wave excitation is around the ox axis. That means the dominant wave excitation is around the axis perpendicular to the wave incidence direction.

The total number of effective excitations for the buoy under different wave conditions was obtained by adding the numbers of effective excitations around the ox axis and oy axis, as shown in Figure 14. The numbers of effective excitations for Mooring Modes A and B both reached the peak under a regular wave with a height of 0.3 m and a period of 2.0 s. Under irregular waves, the number of effective excitations was not significantly influenced by the wave parameters. Overall, the number of effective excitations acting on the buoy in Mooring Mode B was obviously larger than in Mooring Mode A.

4.3. The Number of Effective Excitations in the Two-Anchor Line Mooring Mode

The number of effective excitations acting on the buoy in the two-anchor line mooring mode obtained from experiments is shown in Figure 15.

It is worth noting that some tests (such as Experiment Cb, Experiment Fd, and so on) indicated that the device had effective excitations in both the ox and oy axes, and the possible reasons were radiation waves and diffracted waves reflected from the side walls of the wave flume. Figure 16 shows the total number of effective excitations of the buoy in the two-anchor line mooring mode under different wave conditions.

As can be seen in Figure 16, the number of effective excitations in Mooring Mode E was not significantly influenced by wave parameters under regular waves, while the maximum number of effective excitations was obtained for all other mooring modes at a wave height of 0.3 m and a period of 2.0 s. In the case of irregular waves, the numbers of effective excitations of all mooring modes were not significantly influenced by the wave parameters. Overall, Mooring Mode F had the largest number of effective excitations, and Mooring Mode E had the smallest number of effective float excitations.

In the experiment, the effective excitation times of Mooring Mode F with two anchor lines were significantly higher than those of other mooring modes, which may have been caused by the extension of the degrees of freedom of the WEC system owing to the reasonable configuration of the mooring cables [32]. The additional degrees of freedom increased the motion response of the WEC, which is potentially advantageous for wave energy conversion efficiency.

4.4. The Number of Effective Excitations in the Three-Anchor Line Mooring Mode

Figure 17 shows the number of effective excitations acting on the buoy in the three-anchor line mooring mode.

The total number of effective excitations in the three-anchor line mooring mode under different wave conditions is shown in Figure 18. Mooring Mode G obtained a larger number of effective excitations under a regular wave with a wave height of 0.4 m and a period of 2.1 s. The number of effective excitations in Mooring Mode I was obtained only when the wave height was 0.5 m and the wave period was 2.2 s. The numbers of effective excitations for Mooring Mode H and Mooring Mode J fluctuated between 35 and 106, which indicated that these two modes were significantly affected by wave parameters, whereas the numbers of effective excitations of all mooring modes were not significantly influenced by the wave parameters under irregular wave conditions. In general, Mooring Mode H and Mooring Mode J had larger numbers of effective excitations, while Mooring Mode G and Mooring Mode I had smaller numbers of effective excitations.

As for the mooring system with three anchor lines, the interaction between each mooring chain constrained the ERWEC owing to their different directions of action. The movement of the device was limited, and the number of effective excitations was significantly reduced. Therefore, the energy collection effect was poor.

4.5. Comprehensive Performance of the ERWEC

To facilitate the visual analysis of the effects of mooring mode and wave condition on mooring performance, the maximum tension values of the anchor lines under various mooring modes and various wave conditions were normalized, and a cloud chart of the maximum tension of the anchor lines was drawn, as shown in Figure 19. The blue blocks represent the large maximum tension of the anchor line and poor mooring performance, while the red blocks represent the small maximum tension of the anchor line and excellent mooring performance.

It can be seen in Figure 19 that the mooring performances of different mooring modes were satisfactory in Wave Condition a, while in Wave Condition h, the mooring performances of different mooring modes were poor. Mooring Mode G achieved good mooring performance under different wave conditions, while Mooring Mode F suffered poor mooring performance in all wave conditions except Wave Condition a and Wave Condition c.

Similarly, the effects of mooring mode and wave condition on the motion response were analyzed, and a cloud chart of the number of effective excitations was drawn and is shown in Figure 20. The darker green blocks represent the smaller number of effective excitations and the poorer motion response and energy-harvesting performance, as opposed to yellow blocks representing a larger number of effective excitations and better motion response and energy-harvesting performance.

In Figure 20, there is no mooring mode that is good for each wave condition. Only under Wave Conditions b and c were the motion responses acceptable for most of the mooring modes. Mooring Mode F achieved good motion response under each wave condition. However, Mooring Mode E and Mooring Mode I both had poor responses for each wave condition.

Furthermore, the maximum anchor line tension and the number of effective excitations were considered to filter the mooring modes and wave conditions for optimal ERWEC mooring and energy-harvesting performances. A combined performance index $\mathrm{r}=·{\mathrm{a}}_{\mathrm{t}}+\mathrm{n}·{\mathrm{a}}_{\mathrm{n}}$ was set, where t is the normalized maximum anchor line tension, n is the normalized number of effective excitations, ${\mathrm{a}}_{\mathrm{t}}$ and ${\mathrm{a}}_{\mathrm{n}}$ represent the weights of mooring performance and energy-harvesting performance, respectively.

Figure 21 illustrates the cloud chart of the comprehensive performance index with different weighting combinations. The cyan blocks represent a small comprehensive performance index and poor comprehensive performance. The red blocks represent the opposite.

When the mooring performance weights were relatively small (${\mathrm{a}}_{\mathrm{t}}=0.1~0.5$), the comprehensive performance of the ERWEC was more sensitive to the mooring mode. It is not difficult to see that Mooring Mode F had the most significant effect on the comprehensive performance, showing excellent properties under all wave conditions, followed by Mooring Modes B and D. As ${\mathrm{a}}_{\mathrm{t}}$ increased, the remarkable features in Mooring Mode F gradually diminished. This indicated that the mooring and energy-harvesting performances were mutually constrained. If researchers pursue the high reliability of mooring systems, they may reduce the energy conversion capability of the ERWEC to some extent. It is important to note that the pursuit of increased efficiency in energy conversion may bring high benefits in a short period. However, mooring performance is closely related to the device’s reliability and cost over an extended period. As reported in [31], mooring systems account for 18% of the total cost of WECs, which is a very high percentage compared to other marine equipment. Therefore, we had to make sacrifices regarding the overall long-term benefits.

When the ${\mathrm{a}}_{\mathrm{t}}$ was relatively large (${\mathrm{a}}_{\mathrm{t}}=0.6~0.8$), the comprehensive performance was dominated by the mooring performance and was more sensitive to the change in wave conditions. The ERWEC was subjected to reduced wave loading because of the smaller wave heights in Wave Conditions a and e, and all mooring modes operated well. Meanwhile, when ${\mathrm{a}}_{\mathrm{t}}=0.9$, Mooring Modes A and G showed good comprehensive performance in almost all wave conditions. In this case, Mooring Modes A and G were the preferred solutions.

Based on the above analysis, we concluded that the selection of weighting factors requires integrated consideration of wave load, power generation, operations and maintenance cost, customer demand, etc. Designers can select different weighting factors according to their different needs. When the wave energy is low, the energy output performance of the ERWEC should be considered the primary reference indicator to satisfy the energy supply needs of customers. In this case, Mooring Mode F was selected as the best solution for the ERWEC. When the wave resources in the deployment area are rich, the device is subjected to larger wave loads. Designers should focus on the mooring performance of the ERWEC to guarantee the reliability and the operation and maintenance costs of the system. In this case, Mooring Modes A and G were selected as the best solution for the ERWEC.

5. Conclusions

This paper introduced the mechanical structure and wave energy harvesting principle of the ERWEC, and the maximum tension of the anchor line and the number of effective excitations of the buoy were analyzed using experimental methods under 10 mooring modes and 8 wave conditions. The mooring performance and energy harvesting performance were considered comprehensively, and a comprehensive performance index cloud chart of the ERWEC was drawn.

Limited by the experimental conditions, repeated experiments could not be carried out to evaluate the error of the experimental results, but meaningful general conclusions could still be drawn based on the experimental results. The major findings of this work are summarized as follows.

For the same mooring mode, the mooring performance and energy-harvesting performance changed significantly with variations in the regular wave parameters, but there was a contrary situation under irregular waves. For instance, the maximum tension on the anchor line for Mooring Mode F varied significantly under regular waves, which denoted a significant variation in the mooring performance. However, it is worth noting that there was a contrary situation under irregular waves. In another example, there was an obvious change in the number of effective excitations and the energy-harvesting performance for Mooring Mode J under regular waves, but the change was not significant under irregular waves.

For the same wave excitation conditions, the mooring mode in which the length direction of the buoy was parallel to the wave propagation direction achieved better mooring performance, but the energy-harvesting performance was poor. This indicated that the relationship between the mooring direction of the buoy and the wave propagation direction was a key factor affecting mooring performance and energy-harvesting performance. The mooring mode also affected the comprehensive performance under the same wave condition. For example, the maximum tension on the anchor line was low and the mooring performance was good for Mooring Mode A under regular waves, but the mooring performance was poor for Mooring Mode B under the same wave condition. In another example, there was a small number of effective excitations, and energy-harvesting performance was poor for Mooring Mode I under irregular waves, but the energy-harvesting performance was conversely good for Mooring Mode J under the same condition.

There was little influence on the maximum anchor line tension and the number of effective excitations from the number of anchor lines in the different mooring modes. In other words, the number of anchor lines was not a critical factor in the mooring performance and energy harvesting performance.

In addition, this paper proposed a buoy motion response evaluation method based on the number of effective excitations and a comprehensive ERWEC performance evaluation method based on the cloud chart. The mooring mode and the wave condition that enabled the ERWEC to obtain the optimal mooring and energy-harvesting performances were determined. This paper has important reference significance for the development and optimization of wave energy converters.

In the future, an physical ERWEC prototype will be developed, and sea experiments will be carried out to test mooring and energy-harvesting performances under actual sea conditions.