Efficiency and Wave Run-Up of Porous Breakwater with Sloping Deck
Abstract
:1. Introduction
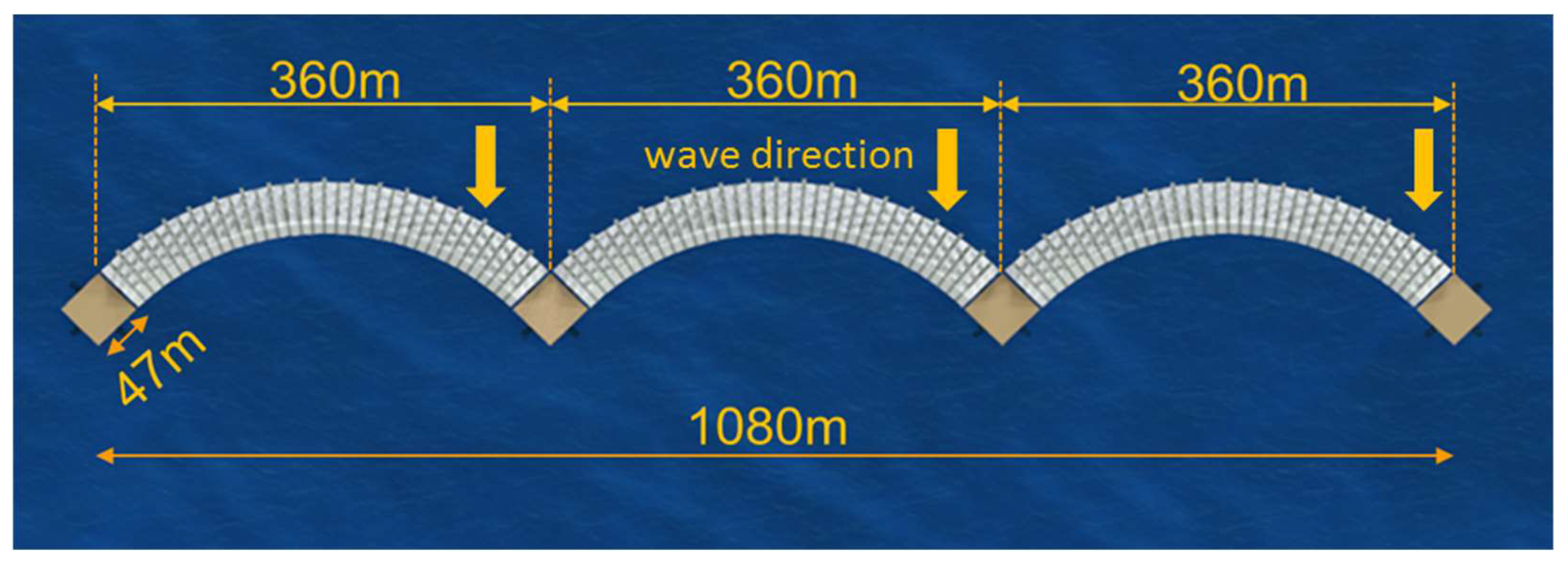
2. Concept of Floating Breakwater-Windbreak
3. Experimental Setup and Test Matrix
4. Test Data Processing
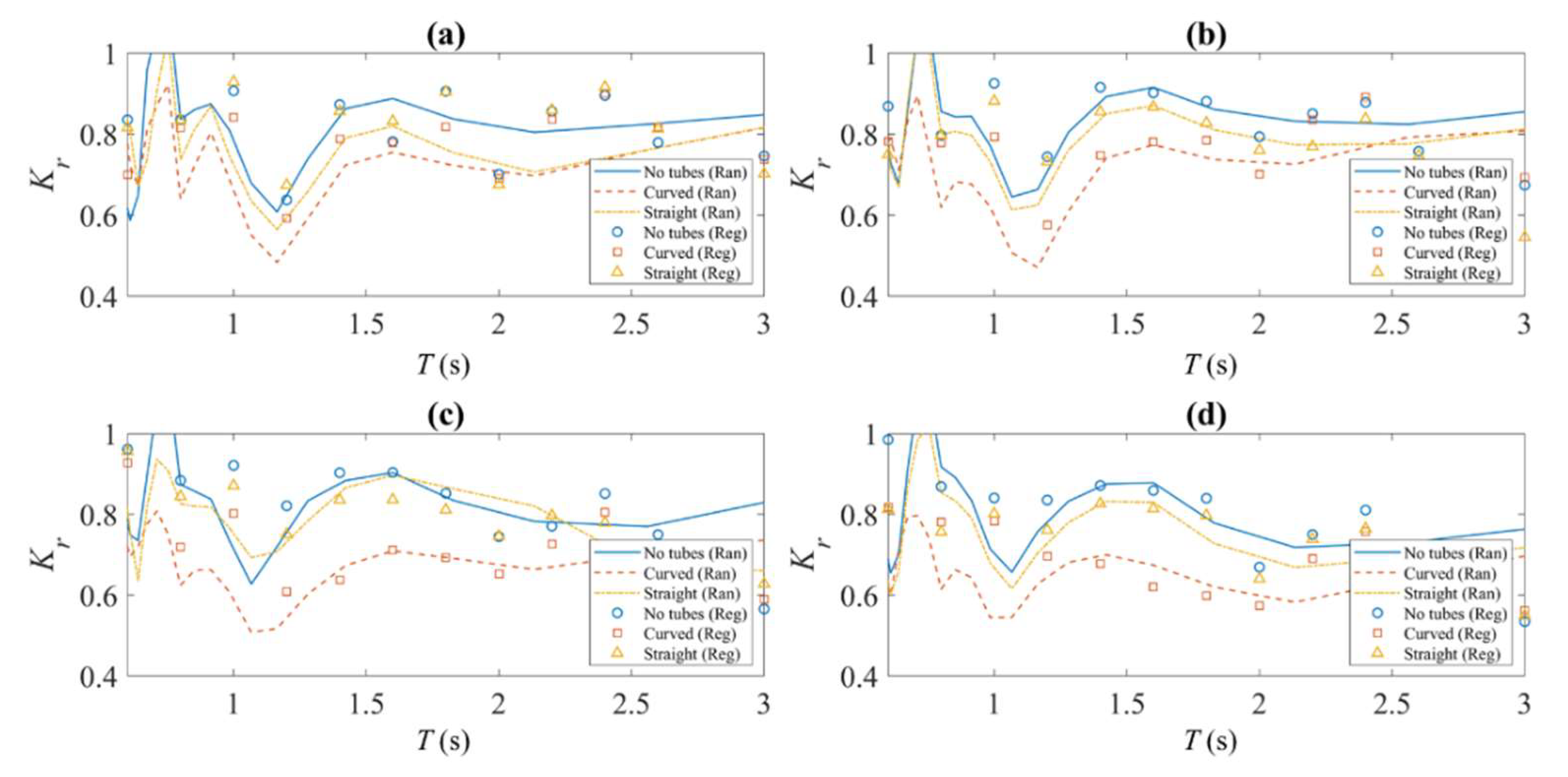
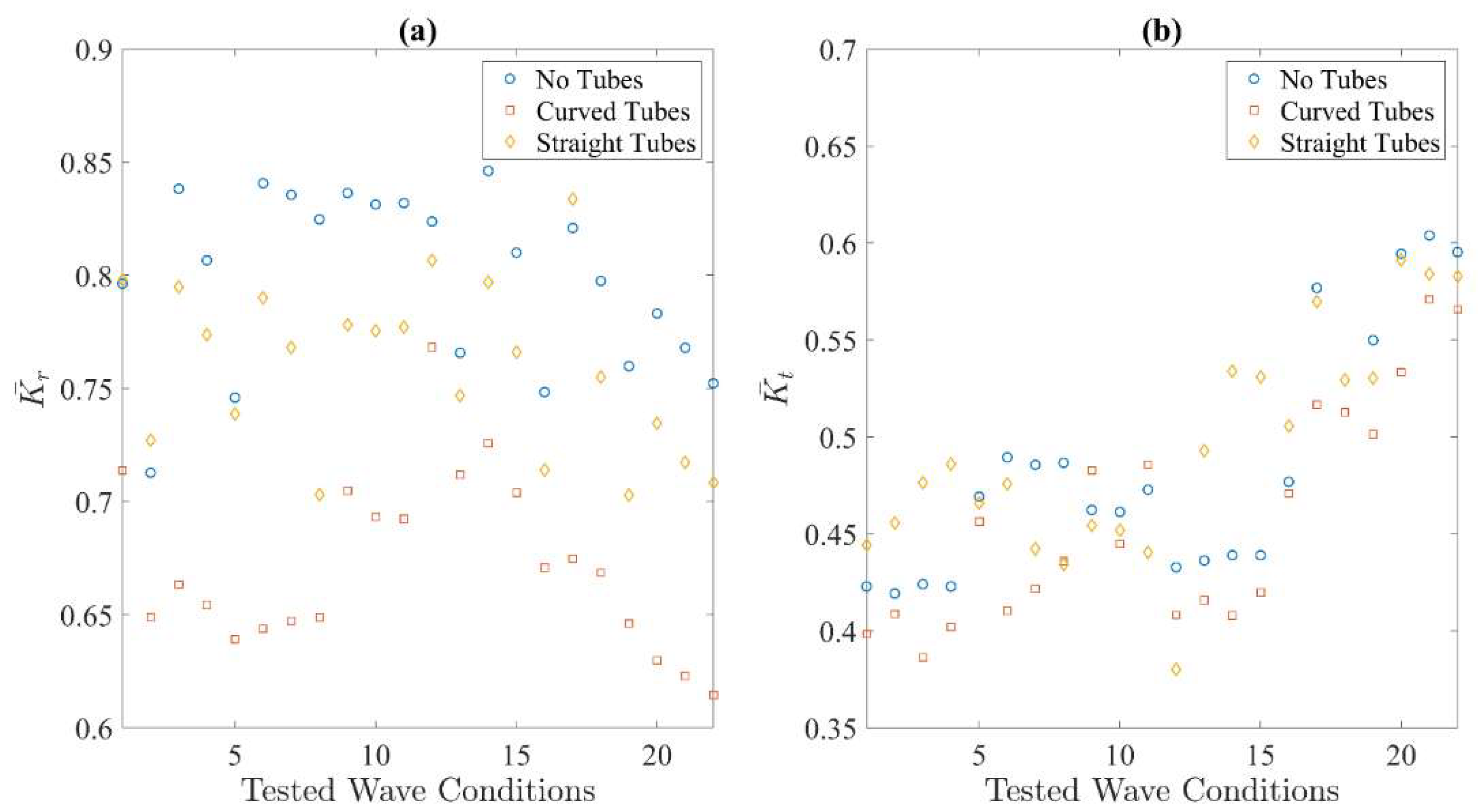
5. Experimental Results of Breakwater Efficiency
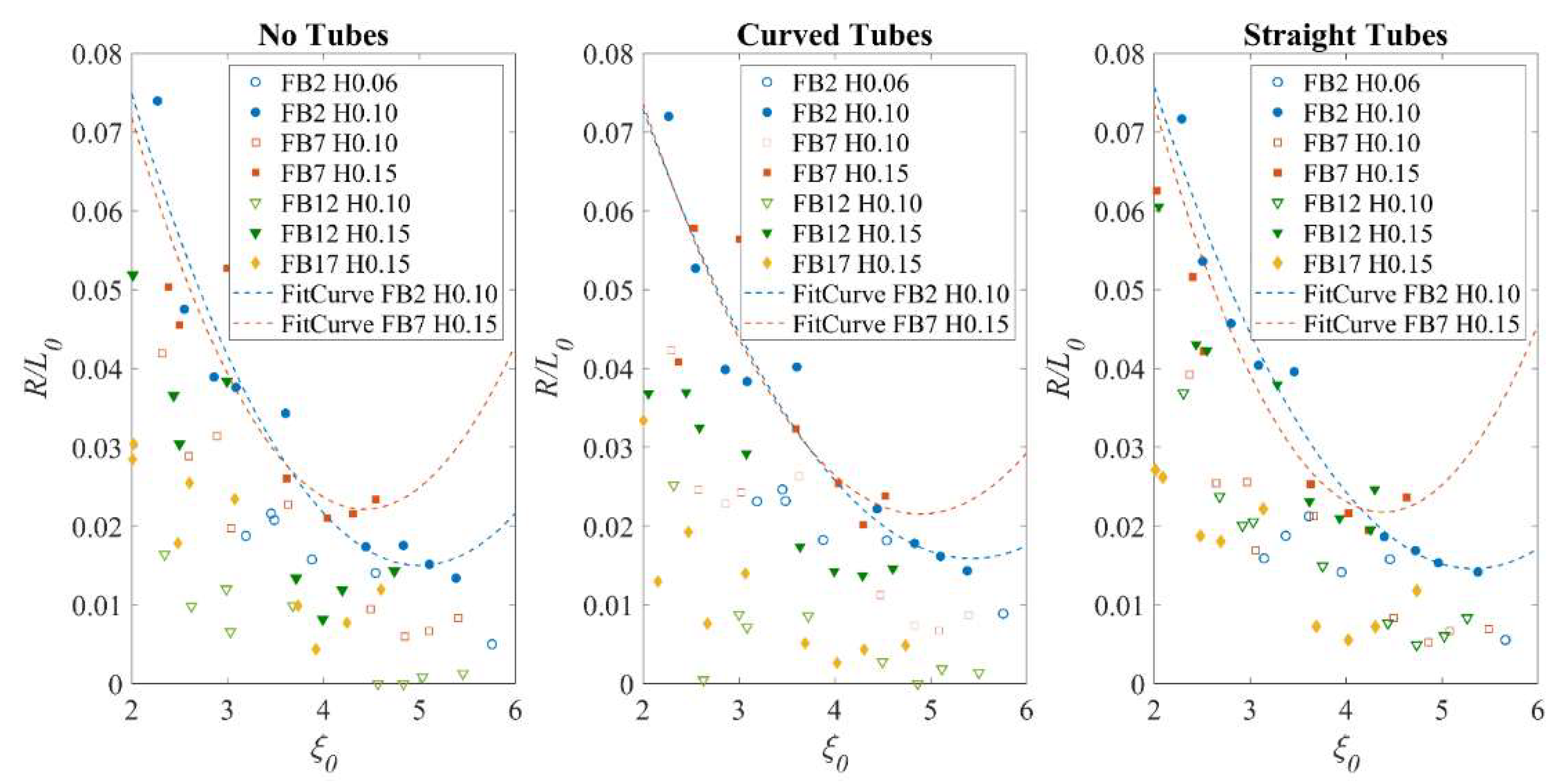
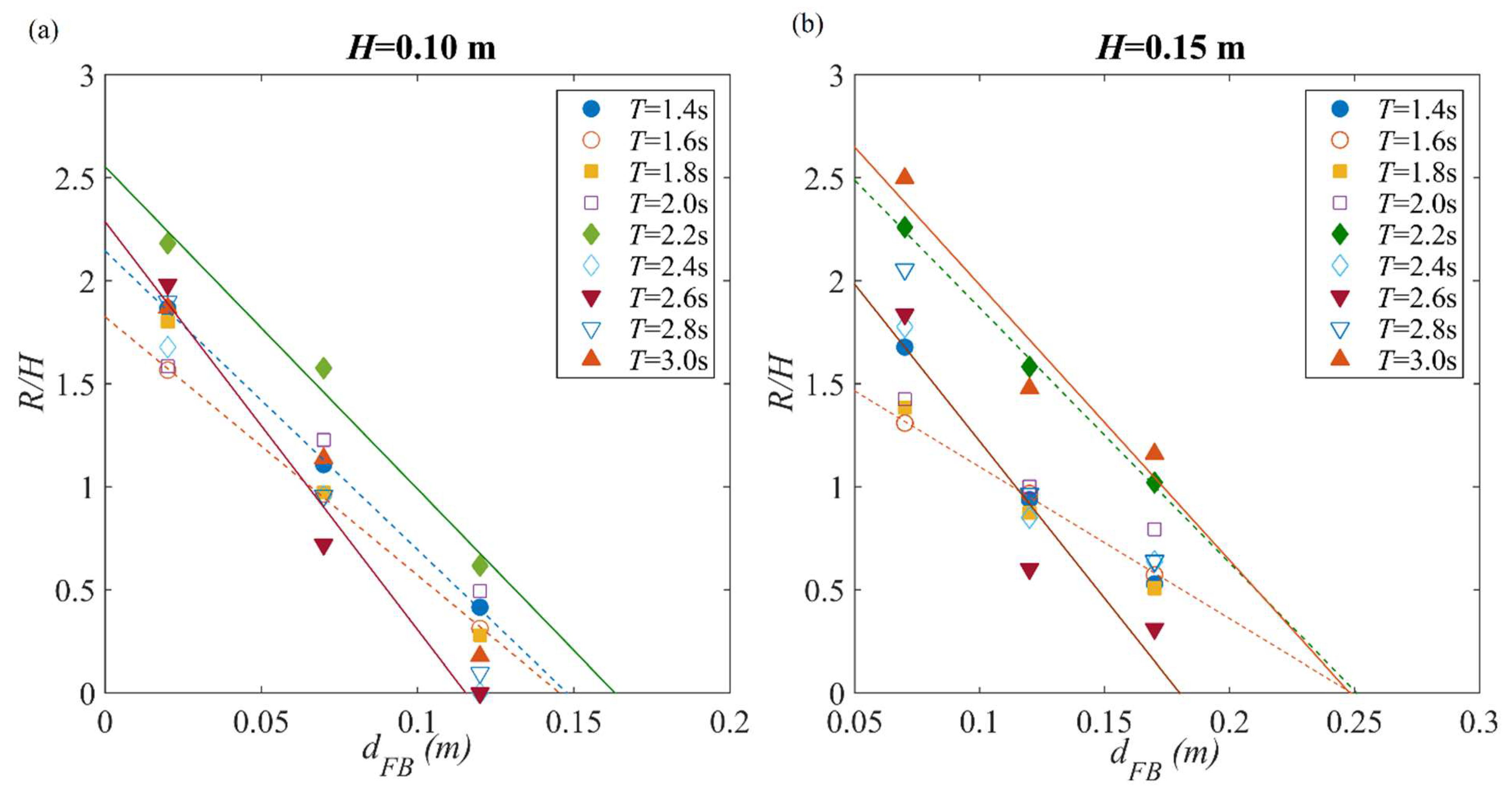
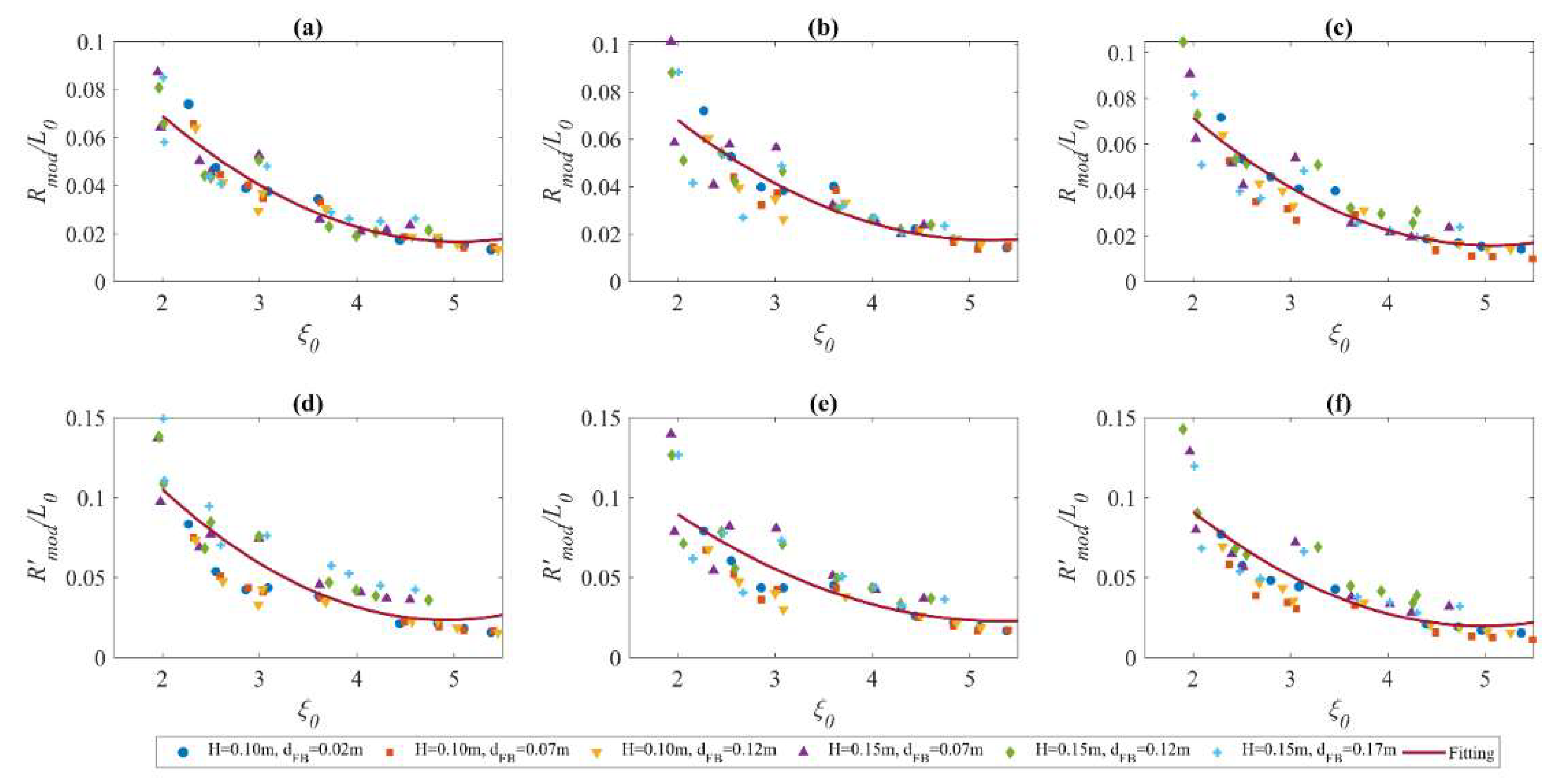
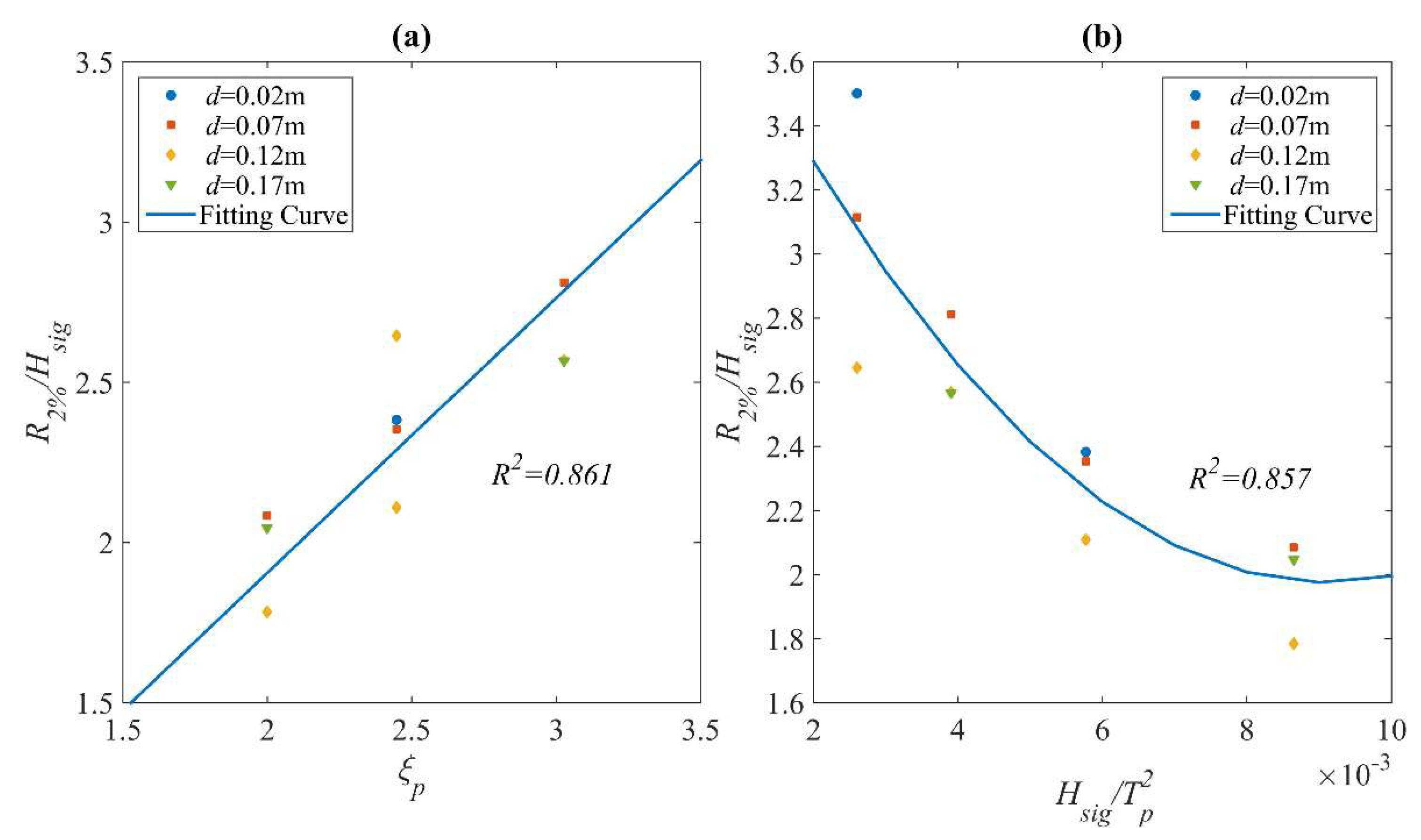
6. Analysis of Wave Run-Up on Sloping Deck
6.1. Analysis of Regular Wave Test Results
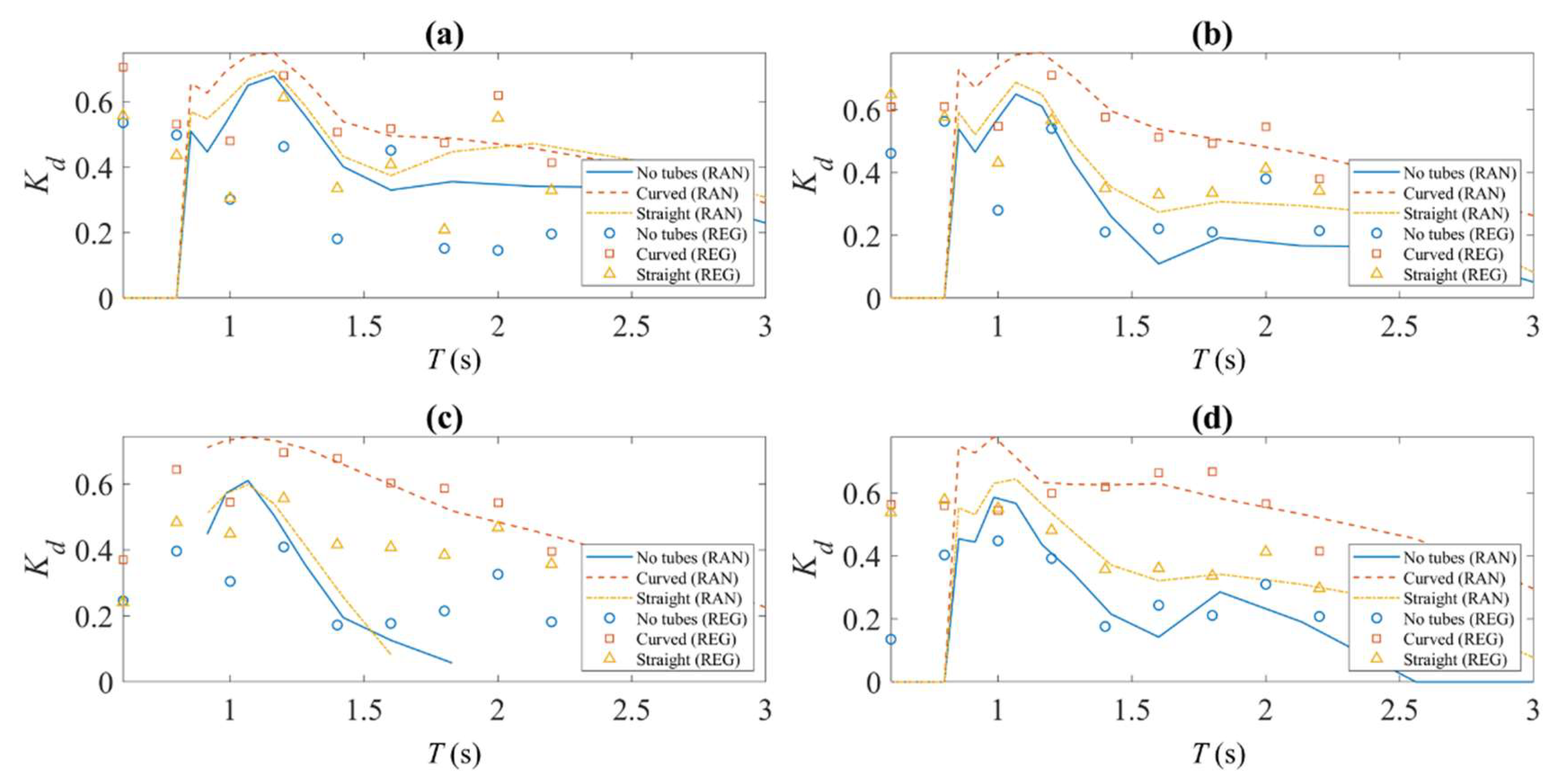
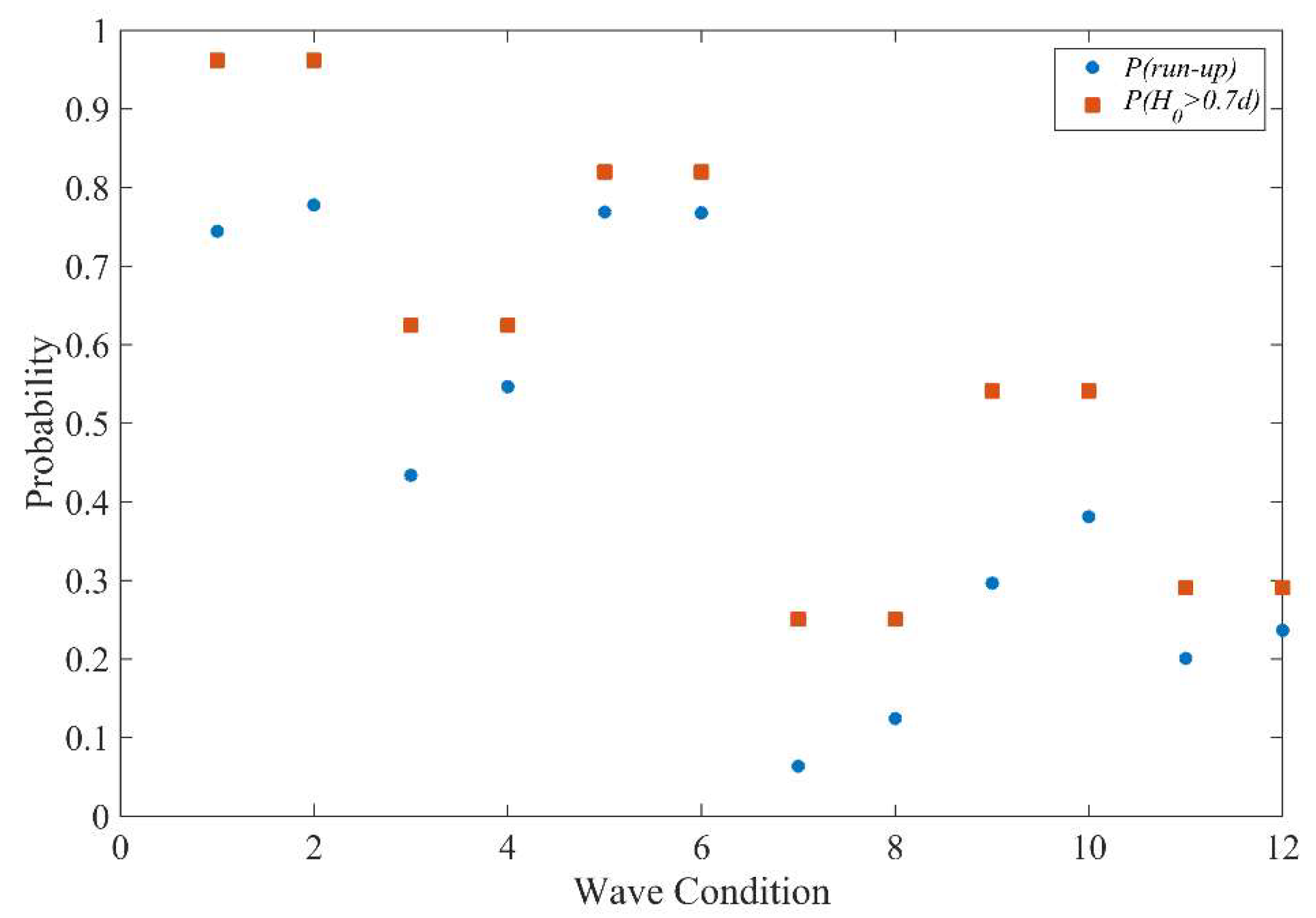
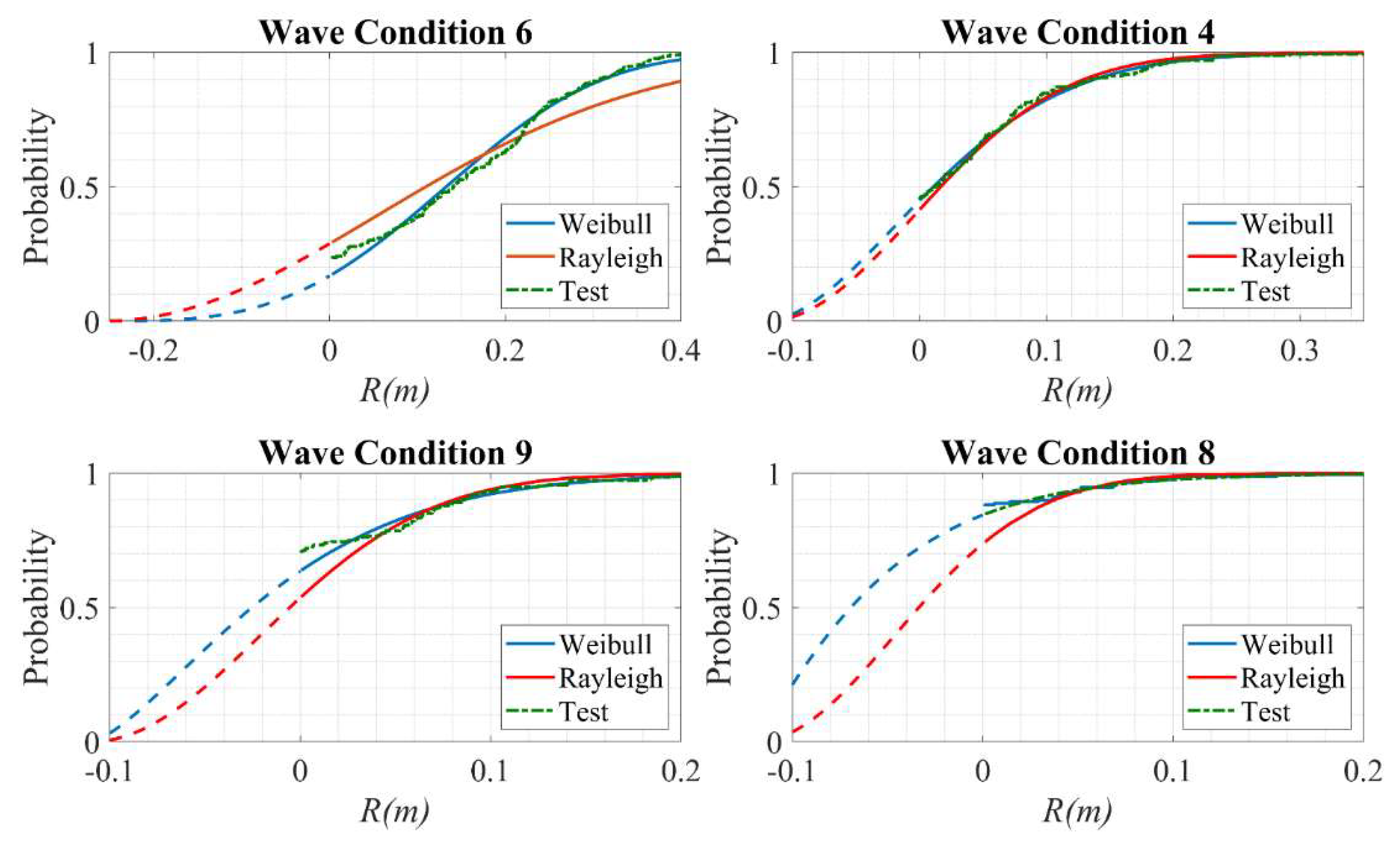
6.2. Analysis of Random Wave Test Results
7. Conclusions
- (1)
- The breakwater is proved to provide a calm sea state for the operations of protected coastal and offshore structures in the sheltered area. The random wave test results show an average wave transmission coefficient of about 0.5, which means only one fourth of the wave energy is transferred to the downstream side. In addition, the tubes installed inside the breakwater hull can reduce the wave reflection at the upstream side; thereby creating a less rough sea at the front of the breakwater. From higher wave dissipation coefficients obtained, it can be concluded that the mechanism of internal water tubes is mainly that of a viscous effect, and no obvious side effects (e.g., increasing wave height in the downstream) have been observed. In addition, the L-shaped tubes are more efficient in reducing wave reflection.
- (2)
- It is found that both the regular and random wave run-up data can be treated in traditional empirical methods, on the condition that the reduced wave run-up on the deck due to positive freeboard heights is considered. After adding the correction term, several empirical equations in existing literature estimating the wave run-up on smooth slopes or beaches have been found applicable. The corrected terms are found to be sensitive to wave heights and periods, and the relationship among these parameters can be established by using either experimental data or numerical simulation.
- (3)
- Under random wave condition, it is found that the possibility of a non-zero wave run-up on the deck is related to the incoming wave exceeding a certain freeboard limit. This is consistent with the behaviour of wave run-up under regular wave condition, which suggests that the wave run-up could be forecasted by accurately predicting the wave elevation near the breakwater. After taking the imaginary negative wave run-ups into consideration, the peak value distribution of the wave run-up data follows the Weibull distribution. Its extreme value follows the empirical equations proposed by Van der Meer [8] and Ahrens [19] and can be estimated accordingly. Once the possibility of occurrence, probability distribution and extreme value are all known, stochastic analysis with any target function can be performed and an optimized freeboard can be decided.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Dai, J.; Wang, C.M.; Utsunomiya, T.; Duan, W. Review of recent research and developments on floating breakwaters. Ocean Eng. 2018, 158, 132–151. [Google Scholar] [CrossRef]
- Gao, J.; Ma, X.; Dong, G.; Chen, H.; Liu, Q.; Zang, J. Investigation on the effects of Bragg reflection on harbor oscillations. Coast. Eng. 2021, 170, 103977. [Google Scholar] [CrossRef]
- Guo, Y.C.; Mohapatra, S.C.; Soares, C.G. Review of developments in porous membranes and net-type structures for breakwaters and fish cages. Ocean Eng. 2020, 200, 107027. [Google Scholar] [CrossRef]
- Wang, C.M.; Han, M.; Lyu, J.; Duan, W.; Jung, K. Floating forest: A novel breakwater-windbreak structure against wind and wave hazards. Front. Struct. Civ. Eng. 2021, 15, 1111–1127. [Google Scholar] [CrossRef]
- Hunt, I.A. Design of seawalls and breakwaters. J. Waterw. Harb. Div. 1959, 85, 123–152. [Google Scholar] [CrossRef]
- Battjes, J.A. Surf similarity. In Proceedings of the 14th International Coastal Engineering Conference, Copenhagen, Denmark, 24–28 June 1974; Volume 1, pp. 466–480. [Google Scholar]
- Wassing, F. Model investigation on wave run-up carried out in the Netherlands during the past twenty years. In Proceedings of the 6th International Coastal Engineering Conference, Gainesville, FL, USA, 29 January 1957; American Society of Civil Engineers: Reston, VI, USA, 1957; pp. 700–714. [Google Scholar]
- De Waal, J.P.; van der Meer, J.W. Wave runup and overtopping on coastal structures. In Proceedings of the 23rd International Coastal Engineering Conference, Venice, Italy, 29 January 1990; American Society of Civil Engineers: Reston, VI, USA, 1992; Volume 2, pp. 1758–1771. [Google Scholar]
- van der Meer, J.W.; Stam, C.-J.M. Wave runup on smooth and rock slopes of coastal structures. J. Waterw. Port Coast. Ocean Eng. 1992, 118, 534–550. [Google Scholar] [CrossRef]
- Holman, R.A. Extreme value statistics for wave run-up on a natural beach. Coast. Eng. 1986, 9, 527–544. [Google Scholar] [CrossRef]
- van Gent, M.R. Wave runup on dikes with shallow foreshores. J. Waterw. Port Coast. Ocean Eng. 2001, 127, 254–262. [Google Scholar] [CrossRef]
- Atkinson, A.L.; Power, H.E.; Moura, T.; Hammond, T.; Callaghan, D.P.; Baldock, T.E. Assessment of runup predictions by empirical models on non-truncated beaches on the south-east Australian coast. Coast. Eng. 2017, 119, 15–31. [Google Scholar] [CrossRef] [Green Version]
- van der Meer, J.W.; Janssen, J. Wave run-up and wave overtopping at dikes and Revetments, Delft Hydraulics, publication no. 485. In VdM VML EB MT2; Delft Hydraulics: Delft, The Netherlands, 1994. [Google Scholar]
- Lander, V.; van der Meer, J.W.; Troch, P. Probability distribution of individual wave overtopping volumes for smooth impermeable steep slopes with low crest freeboards. Coast. Eng. 2012, 64, 87–101. [Google Scholar]
- van der Meer, J.W. Wave run-up and wave overtopping at dikes. In Wave Forces on Inclined and Vertical Structures; Kobayashi, N., Demirbilek, Z., Eds.; ASCE: New York, NY, USA, 1995. [Google Scholar]
- Franco, L.; De Gerloni, M.; van der Meer, J.W. Wave overtopping on vertical and composite breakwaters. In Proceedings Coastal Engineering; ASCE: New York, NY, USA, 1994; pp. 1030–1045. [Google Scholar]
- Mase, H.; Iwagaki, Y. Run-up of random waves on gentle slopes. In Proceedings of the 19th Conference on Coastal Engineering, Houston, TX, USA, 29 January 1984; American Society of Civil Engineers: Reston, VI, USA, 1984; pp. 593–609. [Google Scholar]
- Naess, A.; Stansberg, C.T.; Gaidai, O.; Baarholm, R.J. Statistics of extreme events in airgap measurements. J. Offshore Mech. Arct. Eng. 2009, 131, 041107. [Google Scholar] [CrossRef]
- Sweetman, B. Practical airgap prediction for offshore structures. J. Offshore Mech. Arct. Eng. 2004, 126, 147–155. [Google Scholar] [CrossRef] [Green Version]
- Ahrens, J.P. Irregular Wave Runup on Smooth Slopes; Q CETA No. 81-17; U.S. Army Corps of Engineers, Coastal Engineering Research Centre: Ft. Belvoir, VA, USA, 1981. [Google Scholar]
- Hughes, S.A.; Nadal, N.C. Laboratory study of combined wave overtopping and storm surge overflow of a levee. Coast. Eng. 2009, 56, 244–259. [Google Scholar] [CrossRef]
- Lander, V.; Troch, P. Wave overtopping at smooth impermeable steep slopes with low crest freeboards. J. Waterw. Port Coast. Ocean Eng. 2012, 138, 372–385. [Google Scholar]
- Kofoed, J.P.; Burcharth, H.F. Estimation of overtopping rates on slopes in wave power devices and other low crested structures. In Coastal Engineering 2002: Solving Coastal Conundrums; World Scientific: Singapore, 2003; pp. 2191–2202. [Google Scholar]
- Park, H.; Cox, D.T. Empirical wave run-up formula for wave, storm surge and berm width. Coast. Eng. 2016, 115, 67–78. [Google Scholar] [CrossRef] [Green Version]
- Han, M.M.; Wang, C.M. Modelling wide perforated breakwater with horizontal slits using Hybrid-BEM method. Ocean Eng. 2021, 222, 108630. [Google Scholar] [CrossRef]
- Han, M.M.; Wang, C.M. Coupled analytical-numerical approach for determining hydrodynamic responses of breakwater with multiple OWCs. Mar. Struct. 2021, 80, 103097. [Google Scholar] [CrossRef]
- Lyu, J.; Mason, M.S.; Wang, C.M. Predicting far-lee wind flow characteristics behind a 2D wedge-shaped obstacle: Experiments, numerical simulations and empirical equations. Build. Environ. 2021, 194, 107673. [Google Scholar] [CrossRef]
- Goda, Y.; Suzuki, Y. Estimation of incident and reflected waves in random wave experiments. Coast. Eng. 1976, 15, 828–845. [Google Scholar] [CrossRef] [Green Version]
- Mansard, E.P.D.; Funke, E.R. The measurement of incident and reflected spectra using a least squares method. In Proceedings of the 17th Conference on Coastal Engineering, Sydney, Australia, 29 January 1980; ASCE: New York, NY, USA, 1980; Volume 1, pp. 154–172. [Google Scholar]
- Gu, Z.; Wang, H. Gravity waves over porous bottoms. Coast. Eng. 1991, 15, 497–524. [Google Scholar] [CrossRef]
- Han, M.M.; Wang, C.M. Hydrodynamics study on rectangular porous breakwater with horizontal internal water channels. J. Ocean Eng. Mar. Energy 2020, 6, 377–398. [Google Scholar] [CrossRef]
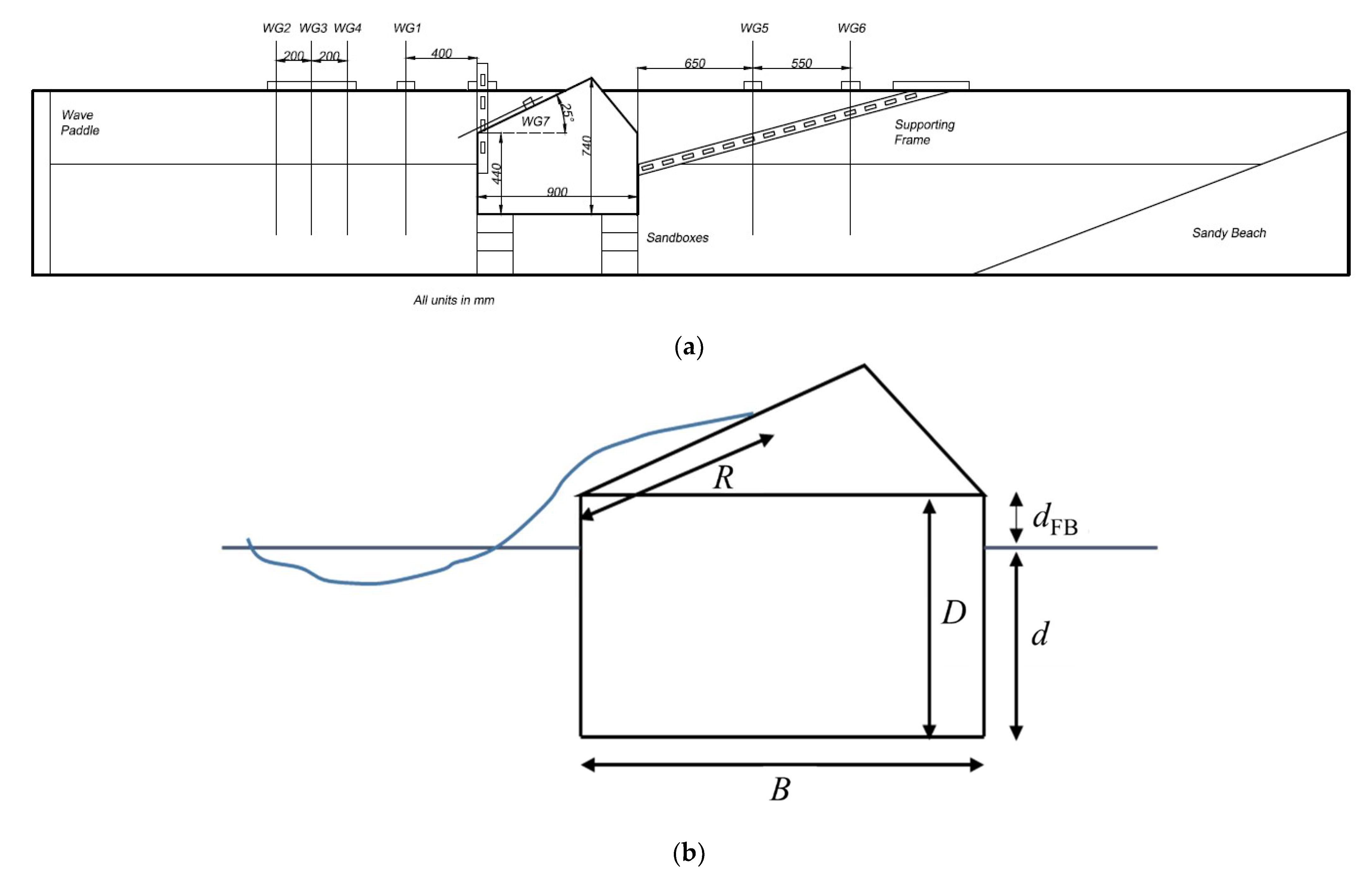



| Parameter | Quantity |
|---|---|
| Length (Lb) | 0.9 m |
| Width (B) | 0.9 m |
| Model Depth (D) | 0.44 m |
| Draft (d) | 0.27–0.42 m |
| Freeboard height (dFB) | 0.17–0.02 m |
| Mass (without Tubes) | 67.91 kg |
| Deck tilting angle α | 25 deg |
| Deck height | 0.3 m |
| Tube diameter | 0.05 m |
| Model Test Parameters | |
|---|---|
| Regular Wave Tests | Wave height H = 0.06 m, 0.10 m, 0.15 m |
| Wave period T = 0.6 s to 3.0 s | |
| Draft d = 0.42 m, 0.37 m, 0.32 m, 0.27 m | |
| Random Wave Tests | Significant wave height Hs = 0.06 m, 0.10 m, 0.15 m |
| Peak wave period Tp = 1.33 s, 1.98 s | |
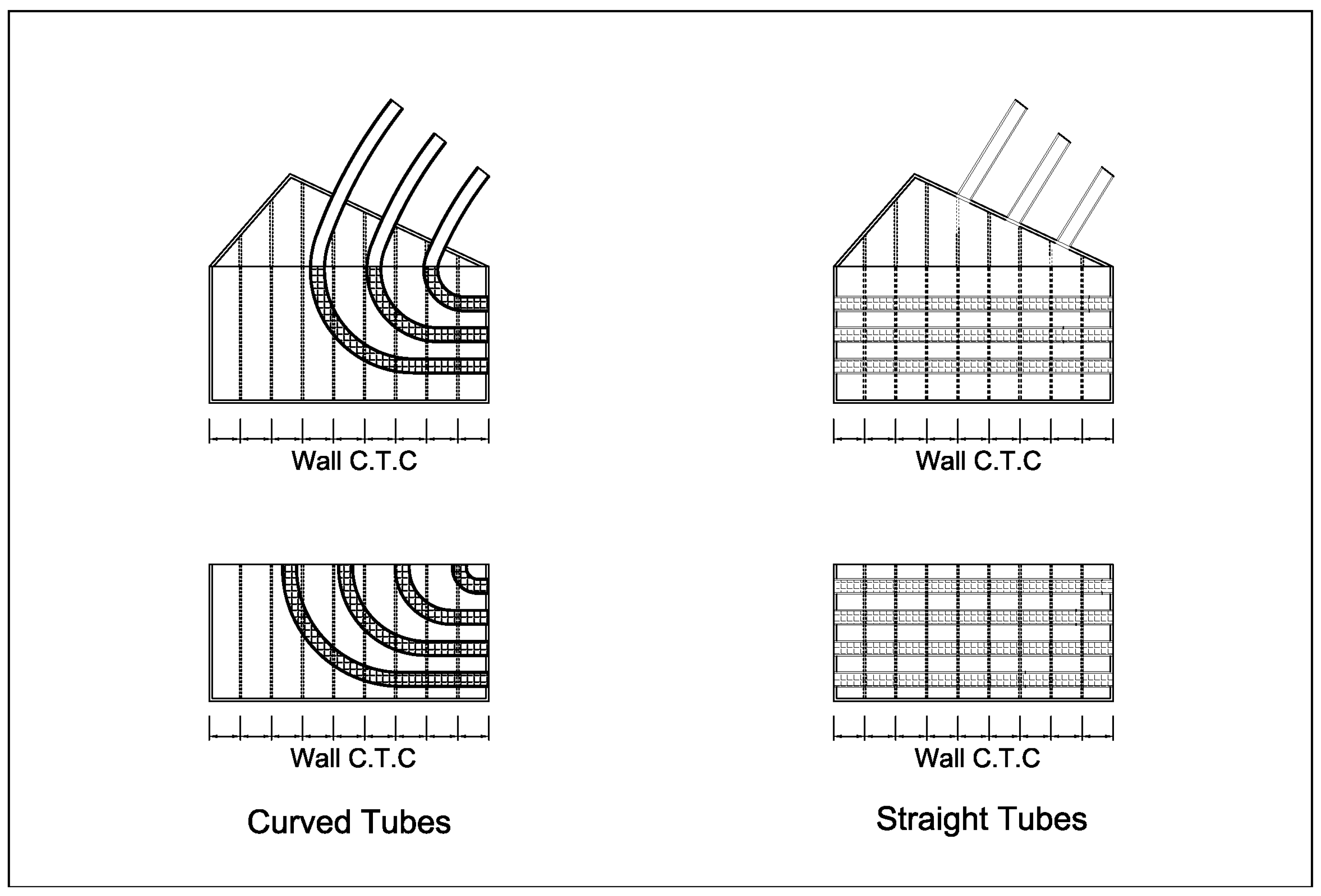
| Internal Tube Setup | No tubes, straight tubes and curved tubes |
| Wave Condition No. | Tp (s) | dFB (m) | Hs(m) |
|---|---|---|---|
| 1 | 1.33 | 0.02 | 0.06 |
| 2 | 0.10 | ||
| 3 | 0.07 | 0.06 | |
| 4 | 0.10 | ||
| 5 | 0.15 | ||
| 6 | 0.12 | 0.06 | |
| 7 | 0.10 | ||
| 8 | 0.15 | ||
| 9 | 0.17 | 0.06 | |
| 10 | 0.10 | ||
| 11 | 0.15 | ||
| 12 | 1.98 | 0.02 | 0.06 |
| 13 | 0.10 | ||
| 14 | 0.07 | 0.06 | |
| 15 | 0.10 | ||
| 16 | 0.15 | ||
| 17 | 0.12 | 0.06 | |
| 18 | 0.10 | ||
| 19 | 0.15 | ||
| 20 | 0.17 | 0.06 | |
| 21 | 0.10 | ||
| 22 | 0.15 |
| Fitted Curve No. | C0 | C1 | C2 | R-Square |
|---|---|---|---|---|
| a | 0.0056 | −0.0570 | 0.1606 | 0.88 |
| b | 0.0049 | −0.0510 | 0.1505 | 0.77 |
| c | 0.0059 | −0.0599 | 0.1677 | 0.82 |
| d | 0.0095 | −0.0940 | 0.2551 | 0.77 |
| e | 0.0061 | −0.0646 | 0.1945 | 0.69 |
| f | 0.0080 | −0.0801 | 0.2192 | 0.75 |
| Wave Condition No. | D (m) | Hs (m) | Tp (s) | Rmax (m) |
|---|---|---|---|---|
| 1 | 0.02 | 0.10 | 1.33 | 0.320 |
| 2 | 0.02 | 0.10 | 1.98 | 0.447 |
| 3 | 0.07 | 0.10 | 1.33 | 0.209 |
| 4 | 0.07 | 0.10 | 1.98 | 0.369 |
| 5 | 0.07 | 0.15 | 1.33 | 0.413 |
| 6 | 0.07 | 0.15 | 1.98 | 0.445 |
| 7 | 0.12 | 0.10 | 1.33 | 0.118 |
| 8 | 0.12 | 0.10 | 1.98 | 0.222 |
| 9 | 0.12 | 0.15 | 1.33 | 0.217 |
| 10 | 0.12 | 0.15 | 1.98 | 0.421 |
| 11 | 0.17 | 0.15 | 1.33 | 0.177 |
| 12 | 0.17 | 0.15 | 1.98 | 0.405 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, M.; Wang, C.M. Efficiency and Wave Run-Up of Porous Breakwater with Sloping Deck. J. Mar. Sci. Eng. 2022, 10, 1896. https://doi.org/10.3390/jmse10121896
Han M, Wang CM. Efficiency and Wave Run-Up of Porous Breakwater with Sloping Deck. Journal of Marine Science and Engineering. 2022; 10(12):1896. https://doi.org/10.3390/jmse10121896
Chicago/Turabian StyleHan, Mengmeng, and Chien Ming Wang. 2022. "Efficiency and Wave Run-Up of Porous Breakwater with Sloping Deck" Journal of Marine Science and Engineering 10, no. 12: 1896. https://doi.org/10.3390/jmse10121896
APA StyleHan, M., & Wang, C. M. (2022). Efficiency and Wave Run-Up of Porous Breakwater with Sloping Deck. Journal of Marine Science and Engineering, 10(12), 1896. https://doi.org/10.3390/jmse10121896







