Offshore, Unmanned Auto-Leveling Sea-Surface Drifting Platform with Compact Size

Abstract

This paper proposes an offshore, unmanned auto-leveling sea-surface drifting platform, with a compact size of 0.7 m in diameter, used for obtaining air-sea interface environmental parameters. The platform was designed based on the parallel mechanism with limited degrees of freedom. The mechanical structure, control system hardware, and software of the principal prototype are introduced. A ground-based device was developed to simulate wave disturbance, based on which the static and dynamic simulation experiments were carried out. Experimental results show that the auto-leveling system can achieve real-time leveling against the angle deviation induced by waves, with a leveling accuracy of 0.2° in a simulated wave with an angle of 12°, which meets the requirements of observation equipment.

1. Introduction

In recent years, the world has been confronted with great challenges such as an energy shortage, environmental pollution, excessive greenhouse gas emission, and instability of energy supply in many areas, which pose a huge risk to sustainable development [1,2]. To address these problems, renewable energy has been extensively discussed worldwide, among which ocean energy is considered to be promising due to its rich economic, political, scientific, and military values.

Floating structures based on marine engineering can be good options to realize surface information acquisition, early warning, and reconnaissance, and are applicable to both civil and military needs. Actually, the conception of floating structures is not something novel. Countless floating villages have been found in different geographical conditions and throughout history, while modern floating houses entered into use in the 1980s [3]. Around 2500 years ago, Persian king Xerxes built a pontoon bridge across Greece for an invasion; 3000 years ago, King Wen of the Zhou Dynasty created a pontoon bridge to go across rivers; during World War II, floating docks entered into use, among which Mulberry Harbour built by the British in 1945 [3] is the most typical example. Additionally, various kinds of offshore platforms were designed for oil drilling, such as Stalin’s Atlantis platform constructed by the Soviet Union. Besides, numerous entertainment venues are established upon floating structures, such as the Jumbo restaurant in Hong Kong, and the floating crab restaurant at the National University of Singapore. Mobile floating structures have been widely used since the late 20th Century, including floating power plants such as Akademik Lomonosov in Russia, and Kagoshima Nanatsujima Mega Solar, as well as offshore floating wind power platforms that have emerged in the last two decades. These structures can be moored or towed to locations where the need arises. Floating power plants are the most common representations of floating structures, such as Akademik Lomonosov in Russia, and Kagoshima Nanatsujima Mega Solar. In addition, numerous offshore floating wind power platforms were built in the last decades.

Many kinds of floating platforms or special marine-used materials/structures have been developed for different marine applications [4,5,6]. However, most of these designs are aimed at large/very large/mega-sized platforms [7,8], and very few designs are aimed towards small, self-leveling drifting platforms or drifters that can be used for special observations or in areas where anchoring equipment is more difficult to install, such as in an abyssal area. Large and small floating platforms react very differently to waves. Normal waves have almost no effect on large floating structures. However, for small floating platforms such as a platform with only 2 m in diameter, sea waves have a big effect. In the process of wave transmission, the small platform will move in all directions along with the rise and fall of the wave, and the platform will produce periodic angle tilt and flutter in all directions.

Small floating structures are subjected to harsh environments on the sea surface such as wind and waves, which generate platform motions such as surging, swaying, heaving, pitching, rolling, yawing, etc. The motions then lead to other problems on the equipment on top of the floating platform, such as tracking errors of the observation system, and energy capture loss of the wind turbine system [9]. Therefore, small floating structures tend to have control strategies for better performance. Typical control strategies can be found in wind energy systems, where blade pitch is relevant to the efficiency of energy harvest. Some researchers applied different control algorithms [10,11,12,13,14,15,16] to realize the precise control effect of blade pitch, such as PID, H_∞ loop shaping, fuzzy integral sliding mode, fuzzy logic control, etc.

However, as for the floating platform itself, there are few designs with self-leveling capabilities. When the equipment above the platform needs a stable pitch angle and the equipment itself does not have pitching control ability, the floating platform itself needs to be able to level itself to provide a stable platform for the integrated equipment. An unmanned platform drifting freely on the surface of the sea tends to have attitude deviations due to the strong interference of continuous waves and currents, especially for those with a large height radius ratio [17,18]. While a stable base with automatic leveling abilities is needed by some integrated devices with the requirements of searching and tracking functions. Thus, to provide a stable platform, these deviations need to be reduced to the greatest extent to avoid a large tilt angle of the equipment. Therefore, it is of great significance to develop an automatic attitude stabilization system for such applications.

Platform leveling is commonly used to describe systems or methods of aligning platforms with a horizontal plane, particularly important in building, machine alignment, weapon firing, and accurate target positioning. Leveling technology has been developed rapidly and applied widely in various fields. As one of the most important components in geodetic engineering, leveling technology has made great progress in data collection and processing. Leveling technology has a long history. In the 17th century, astronomers began to use instruments such as the theodolite to measure the angle between different points on the earth’s surface, thus laying the foundation for the development of leveling technology. In the 19th century, leveling technology was further developed. Spirit leveling is a remarkably simple, yet inherently precise measurement system that has remained virtually unchanged for over a century. It was introduced in the first place for the vertical control needs of the geodetic, cartographic, and engineering communities, which have been well served by this system [19]. In the 20th century, digital leveling technology emerged, which greatly improved the accuracy of leveling measurements. Digital leveling has also been used in combination with total stations, GPS, lasers, and other instruments [20].

At present, the development of leveling technology has become digital and automatic. With the help of computer technology and other technologies, the data acquisition speed and accuracy of the leveling have been greatly improved. For example, Farooq used artificial neural networks for determining the leveling action point at the auto-leveling draw frame [21]. Compared with traditional manual leveling, this method is more efficient and stable and can obtain more reliable and accurate results.

The data collected by the leveling system needs to be analyzed and processed before it can be used. Therefore, the selection of algorithms is very important. At present, there are many algorithms commonly used in leveling technology, including PID (Proportional-Integral-Derivative) control, least squares adjustment, artificial neural networks, Kalman filtering algorithm, etc. [22,23,24,25]. PID control its improved algorithms such as fuzzy-PID are the most common methods used to achieve fast and real-time leveling, due to their simple structure, good performance, and clear physical interpretation. For example, Mat Ali used PID control to develop a self-balancing platform mobile robot [26]. The design of the platform was verified based on the position accuracy of the platform, the results of which show that the PID control can make the performance of the platform reach the expected design objectives. In order to optimize the leveling algorithm, Sun proposed a special PID control strategy with the leveling matrix and applied it to the leveling system [27]. The experiment shows that the new leveling system can improve the efficiency and stability of the leveling performance. In addition, Fan et al. designed a fuzzy-PID controller with a Kalman filter for an orchards lifting platform [28]. The results of the simulation show that the performance of fuzzy PID control systems is better than that of traditional PID.

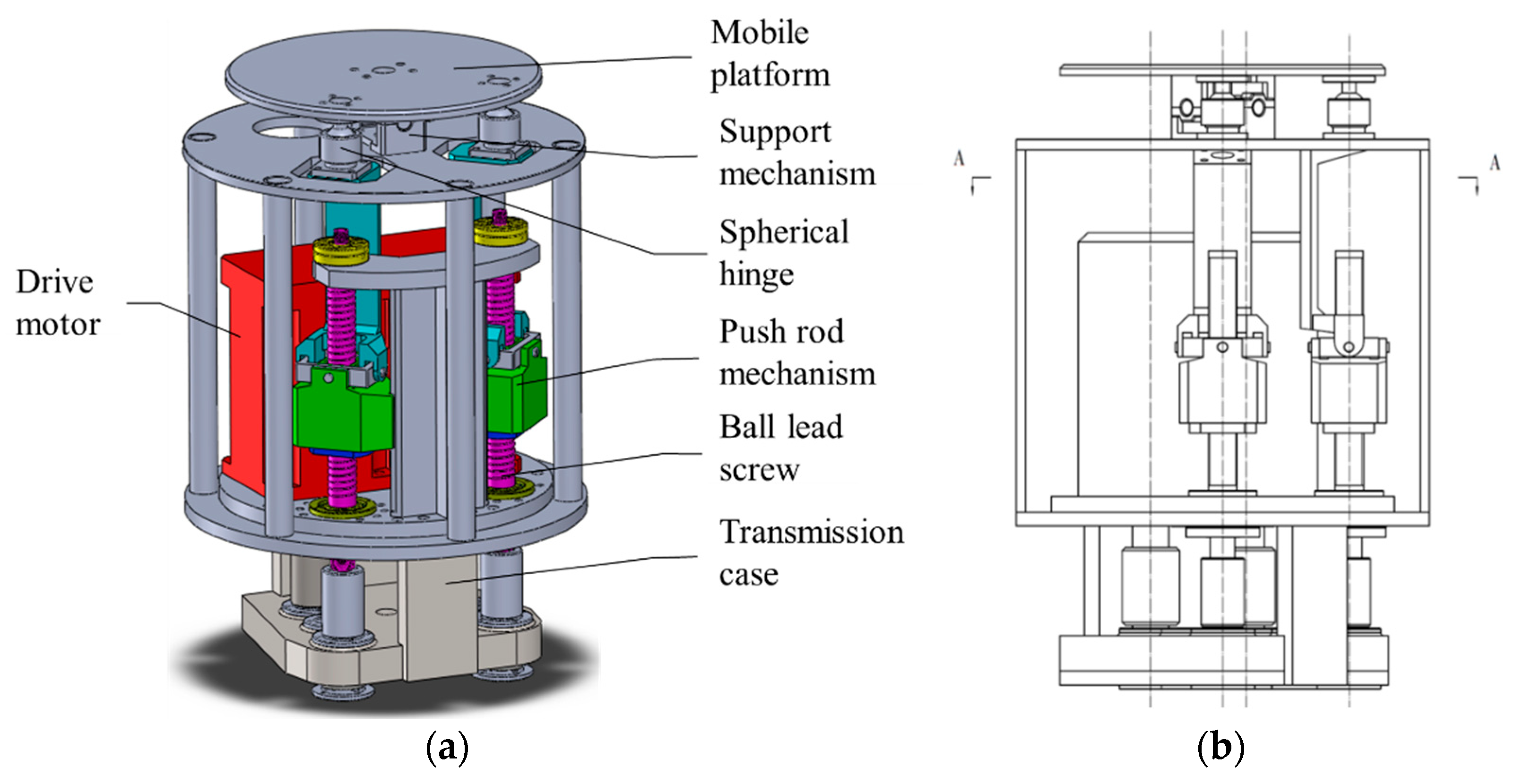
This paper proposes an unmanned auto-leveling sea-surface drifting platform, which is characterized by a small size, compact structure, and convenient transportation and assembly. It is designed to be independently controlled or remotely controlled, repeatedly used or disposable. The platform can be dropped into a predetermined sea area by the ship and has the capability of continuous duty reconnaissance of the surrounding sea area and air space. The platform was designed based on the parallel mechanism with minimum degrees of freedom (DOF). The mechanical structure and hardware and software of the principal prototype are designed and manufactured, and a ground simulation device was designed to simulate wave disturbance, based on which the simulation experiment was carried out. Further verification experiments were designed and executed in a water pool.

2. System Design

The unmanned auto-leveling drifting platforms are mainly used to provide a stable platform for their integrated equipment, which need a stable base for function on the ocean surface. In this study, the attitude stabilization system needs to keep the tilt angle of the stabilized equipment less than 0.4° under the disturbance condition that the disturbance frequency of the base is about 1 Hz and the amplitude is 12.5°.

2.1. System Configuration and Overall Structure Scheme

System Configuration

Attitude stability systems of unmanned platforms mainly consist of three parts: the leveling platform, the load equipment, and a drifting body unit. The specific composition of the system is shown in Figure 1.

Figure 2a shows the prototype of attitude stabilization system of the platform. The main part of the leveling platform is a parallel stabilized platform. It is mainly composed of the top mobile platform, transmission case, drive motor, spherical hinge, push rod mechanism, ball lead screw, and support mechanism. The mobile platform is a 2-DOF parallel stabilized platform. Each transmission support chain within the platform contains a ball screw, a hook hinge, a support rod, and a ball hinge. The ball lead screw is fixed to the base and it rotates about its axis with only one DOF. The screw rod has only one translational freedom. The support mechanism has a hook hinge that connects with the mobile platform. The hook hinge is actually a double-ring structure, and the angle of rotation between the inner ring and the outer ring is 90°. The geometric centers of the spherical hinge and hook hinge coincide with the rotation axis of the ball lead screw. When the mobile platform is parallel to the two planes of the base, the connection of the three components is perpendicular to the mobile platform plane. When the two ball screws rotate independently, the mobile platform has a unique position and attitude at all times. The structural parameters of the drifting platform are shown in

Table 1. Structural parameters of platform.

Parameters	Reference Value
Platform element profile	Height 1 m, Diameter 1 m
Size of platform carrier	Height 5 m, Diameter 0.7 m
Circle radius of drifting element	5 m
Drifting unit mass	3 kg
Moment of inertia of platform element	0.5 kg·m2
Platform carrier mass	900 kg
Moment of inertia of the platform carrier	30 kg·m2
Underwater depth of platform carrier	3.5 m
Underwater depth of drifting unit	0.8 m

.

In order to improve the stability of the platform on the water surface, equipment other than the load on the mobile platform should be installed in the floating platform below the water surface as far as possible. This leaves the center of gravity of the whole system as low as possible (lower than the center of flotation of the system), so as to ensure that the unmanned platform will not capsize under the designed limit sea condition. In this case, the dynamic coupling effect of load equipment on the floating platform is reduced. This counterweight method can lower the center of gravity and maximize the relative inertia parameters of the floating platform.

Figure 3 is the schematic diagram of the principal structure of the serial-parallel stable platform designed in this research, which is mainly composed of a load device, mobile platform, three-degree-of-freedom ball hinge, support rod, two-degree-of-freedom Hooke hinge, screw nut and ball screw, base, and other components. The mobile platform is connected to the base of the platform and the transmission branch chain by three fulcrums: A₁, A_2, and O, respectively, and forms a right triangle A₁A₂O with O as the right angle. A rotary motor is installed between the mobile platform and the load equipment to provide a DOF of horizontal azimuth rotation. In the principal prototype of the parallel stable platform shown in Figure 3, the two transmission branches are parallel to each other, and the symmetry axis is 90° from the section view.

The mobile platform is connected to the base of the platform and the transmission branch chain respectively by three fulcrum points A₁, A_2, and O, and forms an isosceles right triangle A₁A₂O with point O as a right angle. Restricted by the hook hinge at point O, the mobile platform can only move with two degrees of freedom around the X and Y axes. The platform base coordinate system {C_b} is fixed on the base of the lower platform of the attitude tracking platform, and the rotation angles around axis X_b and Y_b are θ and φ respectively. Mobile platform coordinate system {C_m} is fixed on the mobile platform of the electric observation platform, and the origin O_m outside the origin coincides with the origin O of the {C_b} coordinate system.

The platform is a space mechanism, which contains many moving parts and has redundant constraints. It is difficult to calculate the DOF by conventional methods. With the modified Grubler-Kutzbach Equation (1), the spatial freedom of the spatial actuator can be calculated:

$$M=d(n-g-1)-{\displaystyle \sum _{i=1}^g{f}_i}+v$$

(1)

where n is the number of components in the spatial motion mechanism, g is the number of motion pairs, f_i is the DOF of the ith motion pair, d is the order of the mechanism, and v is the number of redundant parallel constraints.

Thus, it can be calculated that the DOF of the series-parallel stable platform is M = 3, and the DOF of the parallel stable platform is 2.

3. Principal Prototype Experiment

3.1. Experimental System Composition and Prototype Test

Experimental System Setup

• Mechanical structure composition

Figure 4 shows the ground simulation system of attitude stabilization system of the platform. The white bracket is the ground-simulated swing test platform as shown in Figure 4a, including the suspended bracket of the support system, crank rocker mechanism, and rocker drive motor. The platform is connected to the platform by a connecting shaft so that the platform can input a single DOF swing angle around the connecting shaft to the drifting platform. The end of the rocker is connected to the bottom of the platform prototype. The crank rocker can be swung by hand or a three-phase AC asynchronous motor to make the platform gain an inclination angle and realize the simulation of external disturbance force. The platform prototype can adjust the angle relative to the circumferential rotation of the bracket on the swing test platform to simulate the disturbance caused by sea waves of different incident angles.

The installation of two gyroscope sensors is shown in Figure 4. One is mounted on the mobile platform and the other is mounted on the base platform, which is located above and below the ball hinge, respectively. Since such installation can make the X and Y axis directions of the sensor correspond to the connection between the two ball hinges and the center of the platform, the change of the platform plane inclination caused by the movement of the two ball hinges can be detected. In Figure 4a, one of the axes of the sensor coincides with the axis of the bracket. Therefore, this experimental setup can measure the real-time inclination change of the platform around the Y axis of the sensor, while there is no change around the X axis. As the platform in Figure 4b rotated 45° in the circumferential direction, the direction of oscillation, i.e., the incident angle of the simulated wave, would cause the platform to produce an inclination angle along the X and Y axes of the sensor.

• Control system setup

The control system of the platform is composed of a power supply, servo motor and driver, control system, and three-axis gyroscope, as shown in Figure 5. The servo motor adopts the precision AC servo motor (model blt-192, driver CD1a-400) from Infranor, Switzerland, with a rated power of 13.84 kw, a maximum speed of 2800 rpm, a peak torque of 328 N·m, and a resolution of 65,536 ppr. The three-axis gyroscope adopts the attitude azimuth reference system (3dm-s10b) of Beijing 7d Aerial Survey Technology Co., LTD., (Beijing, China) with 100 Hz measuring bandwidth, error 0.05°, and resolution 0.01°. The attitude stability control box mainly adopts the TMS320F2812 system for the sensor signal acquisition, tracking algorithm, and motor instruction transmission. A working flow diagram of the attitude stabilization system is shown in Figure 6.

• Auto-leveling control strategy

After initialization of the control system, the real-time attitude information of the load system is continuously received from the gyroscope module. After receiving the real-time attitude of the system, the attitude error is obtained by comparing this data with the horizontal attitude. The attitude error should be limited and judged firstly, and then the signal should be filtered to eliminate the influence of noise in the process of signal acquisition and transmission, and the attitude change trend is also predicted at the same time. Then, combined with the position solution of the structural parameters, the target angles of the two axes need to be adjusted and are finally obtained. PID control is applied to calculate the target angle, as shown in Figure 7. The PID control algorithm includes angle PID control and velocity PID control. The combination of the two aspects can quickly and accurately complete the angle adjustment.

In Figure 7, r_α(t) is the real-time angle calculated by the control system, and error e_α(k) is generated when compared with the measurement feedback angle. r_v(t) is the real-time angular velocity calculated by the control system, and error e_v(k) is obtained when compared with the measurement feedback angular velocity. u_αpid(k) is the control parameter of the angle error obtained by the PID algorithm, u_vpid(k) is the angular velocity error obtained by the PID control parameter, and the two parameters are combined in the final control parameter by the PID algorithm, and the actuator is controlled by PWM wave control. The principal equation of speed tracking and position compensation algorithm is as follows:

$$u_{pid}=A·u_{\alpha pid}+B·u_{vpid}$$

(2)

where A and B are proportionality constants of angle PID control quantity and velocity PID control quantity, respectively. The method of adjusting the proportional constant is the same as that of the PID proportional and integral proportional constant (the speed PID result can be regarded as a proportional term and the Angle PID result as a differential term to adjust).

3.2. Ground System Static Test

According to the prototype experiment, the practical range of its reach is tested. The results are shown in

Table 2. Design and measured values of the workspace of the platform prototype.

Freedom of Motion	Design Value	Measured Value
Roll Angle range	−31.3°~31.7°	−29.9°~31.5°
Pitch Angle range	−30.1°~29.8°	−29.5°~29.3°

. The parameters of the crank and rocker mechanism of the swing table are designed to meet the maximum swing angle of ±18°. In the actual experiment, the swing table can simulate the swing motion of any amplitude (≤30°) with the given cycle reciprocating instruction of the driving motor of the swing table.

The measured value in Table 2 is close to the design value, and the design value has a sufficient margin relative to the system requirements. Therefore, it can be considered that the actual working space of the platform prototype meets the requirements.

Static tests can verify whether the freedom degree, motion range, and motor drive of the system meet the requirements and whether the system has structural defects such as large transmission clearance or structure interference. The experimental data show that the mechanical structure and the motor drive device meet the requirements of the system. Experimental setup of the static test is shown in Figure 8. The maximum inclination angle produced by the swing system is about 12.5°. Two tests were carried out, one a holds test at equilibrium position and the other a fixed angle tracking test. Figure 9 and Figure 10 shows the results of the two tests, which show the designed structure has the ability to achieve the required function without any interference. Figure 9 shows that the leveling mechanism can make the mobile platform maintain a relatively high precision horizontal state with an error of about 0.2° in the equilibrium position without wave disturbance. While given a target angle command, as shown in Figure 10, the leveling system can quickly level the inclination of the mobile platform, and the 10° target angle takes a time of less than 0.5 s.

3.3. Ground Dynamic Experiment

The experimental process is as follows: the periodic motion of the swing system drives the drifting platform, and dynamic motion interference is thus applied to the platform to verify the effects of the attitude stability control of the mobile platform. Considering that the ground-simulated swing table has only one DOF, the mounting frame of the swing table can rotate the prototype around its own rotating axis at a certain angle when the control performance of the two degrees of freedom of the platform needs to be verified at the same time, so as to simulate the swing motion caused by the incident wave at any angle and verify the attitude stability effect of the joint action of the two axes.

In order to verify the attitude stability ability of the platform control system, the tested axis of the platform prototype is first aligned with the rotation axis of the simulated swing table. To verify the coupling effect of the parallel mechanism, deflect a small angle (15° ≤ a ≤ 20°) on the basis of alignment. According to the simulation in the early stage of the project, the maximum swing frequency of the platform when it encounters the ultimate four-grade wave is about 0.8 Hz, and the swing amplitude is slightly more than ±10°. Figure 11 shows the effect of attitude stabilization during a complete motion period. It shows that the control system has the ability to stabilize the attitude of the moving platform in the process of the periodic swinging motion.

Figure 12 shows the rolling (about X-axis) attitude stability test results of the platform which is adjusted via the stability algorithm. It shows that the average swing amplitude of the drifting platform is about ±12°. At this time, the maximum angular displacement of the platform after dynamic leveling, i.e., the maximum angular displacement of the load equipment, is 0.14° and the isolation degree is 38.7 db.

The platform rotates until its X-axis is about 35° counterclockwise from the axis of the swinging platform. Figure 13 is the experimental result curve for dynamic leveling. The rolling and pitching attitude stability errors of the load equipment are 0.18° and 0.2° respectively.

From the experimental results, it can be seen that the platform proposed in this paper can automatically level itself under the interference of level-3 sea waves with around 12° angle of sea surface slope, and the leveling accuracy is about 0.2°, which meets the system design requirements.

3.4. Simulated Sea-Wave Experiments in a Water Pool

• Experiment setup

In order to verify the attitude stability of the drifting platform on the free water surface, the drifting platform was tested in an experimental water pool. The experiment was conducted in the Water Equipment Laboratory of Nanjing University of Science and Technology, with the experimental pool size of 6 × 6 × 3 m. Before the surface experiment, the sealing and waterproofing of the drifting platform were carried out. The test setup is shown in Figure 14.

The experimental procedures are as follows:

• Experiment one: Static experiment

(1) After the pool is filled with water, the drifting platform floats 30 cm away from the bottom of the pool, without interference with the bottom of the pool during the movement.

(2) The system is started, and the system levels itself at an equilibrium position for 10 min.

• Experiment two: Quick leveling experiment under a large-angle target

Drifting platforms are launched from the air or underwater. Due to the disturbance of wave fluctuation, the load system angle on the mobile platform is in a random state, so the leveling system of the mobile platform needs to adjust itself via the control system to the horizontal equilibrium position.

(1) The load system is adjusted to the maximum angle allowed by the platform, which is around 12°, as shown in Figure 15a. A protective device is installed on the top of the platform to prevent the drifting platform from overturning.

(2) The system is started to enable the system to level the mobile platform to the horizontal equilibrium position, as shown in Figure 15b.

(3) The procedure is repeated three times.

• Experiment three: Continuous leveling experiment under continuous disturbance

(1) The system is started in a floating state, and the leveling system adjusts the moving platform to the horizontal equilibrium position by itself through the control system.

(2) The water wave disturbance is exerted by the disturbance rope on both sides. After the system reaches an equilibrium position, a periodical angle of about 0.4 Hz and ±10° is artificially created respectively to obtain the attitude stability curve.

(3) The procedure is repeated three times.

Figure 16 shows the results of the static experiment. The stability curve represents the motion state of the load system, while the disturbance curve represents the motion state of the platform body. As can be seen from Figure 16, the attitude stability error of the drifting platform is around ±0.13°. The leveling accuracy of the two axes is similar, with higher precision. It also shows that the leveling system plays a stabilizing role in the small swing of the balance position and reduces the amplitude of the swing. Under the working state of the motor, the drifting platform can float on the water stably and provide a stable base for the system load.

Figure 17 shows the experimental results of large angle (at around 6°) leveling. It can be seen that after the servo motor is enabled, the drifting platform completes the load starting within 1 s, and the system achieves the horizontal equilibrium position after a dynamic adjustment of about 2 s. The attitude stability error is within the range of ±0.12°, which meets the requirements of the system design. The experimental results show that the attitude stabilization system can quickly adjust the load system into the equilibrium position.

The result of this continuous leveling experiment under continuous disturbance is shown in Figure 18. Periodic tension load is applied via the disturbance rope connected to both sides of the platform to form a wave simulation with a similar period. After the platform control system is started, the disturbance rope is pulled to create a slosh angle of about 0.4 Hz with a maximum value of ±10°, respectively. The obtained disturbance curve and real-time leveling attitude stability curve are shown in Figure 18.

As can be seen from Figure 18, under the simulated wave disturbance of ±10° and 0.5 Hz, the stabilized platform can stabilize the load system within the range of ±0.36°. After the floating tank system and attitude stabilization system, the base of the load system is stabilized within a certain swing angle, meeting the design requirements and restraining the input wave angle to a greater extent. However, the leveling error of the floating platform is slightly larger than that of the ground experiment.

4. Conclusions

In this paper, an offshore, unmanned, auto-leveling drifting platform is proposed and tested. The platform can provide a stable horizontal state for the equipment mounted on its top.

(1)

The mechanical structure design of the auto-leveling drifting platform is introduced, including system configuration and force analysis of the hinges.

(2)

The experimental system composition of the auto-leveling mechanism and control system including control strategy are detailed described.

(3)

A ground-based device was developed to simulate wave disturbance, based on which the static and dynamic simulation experiments were carried out. This experiment shows that the average swing amplitude of the drifting platform is about ±12°, while the maximum angular displacement of the mobile platform after dynamic leveling is within 0.2° and the isolation degree is 38.7 db.

(4)

Simulated sea-wave experiments in a water pool were conducted. Experimental results show that the auto-leveling system plays a stabilizing role in the small swing of the balance position and reduces the amplitude of the swing, and can quickly adjust the load system into the equilibrium position when started from a larger angle of the platform. The experiment also shows that under the simulated wave disturbance of ±10° and 0.5 Hz, the stabilized platform can stabilize the load system within the range of ±0.36°.

The results above show that the designed platform meets the design requirements.