Stability Characteristics of Horizontal Wells in the Exploitation of Hydrate-Bearing Clayey-Silt Sediments
Abstract
:1. Introduction
2. Mechanical Parameters of HBS-CS
3. Model Description
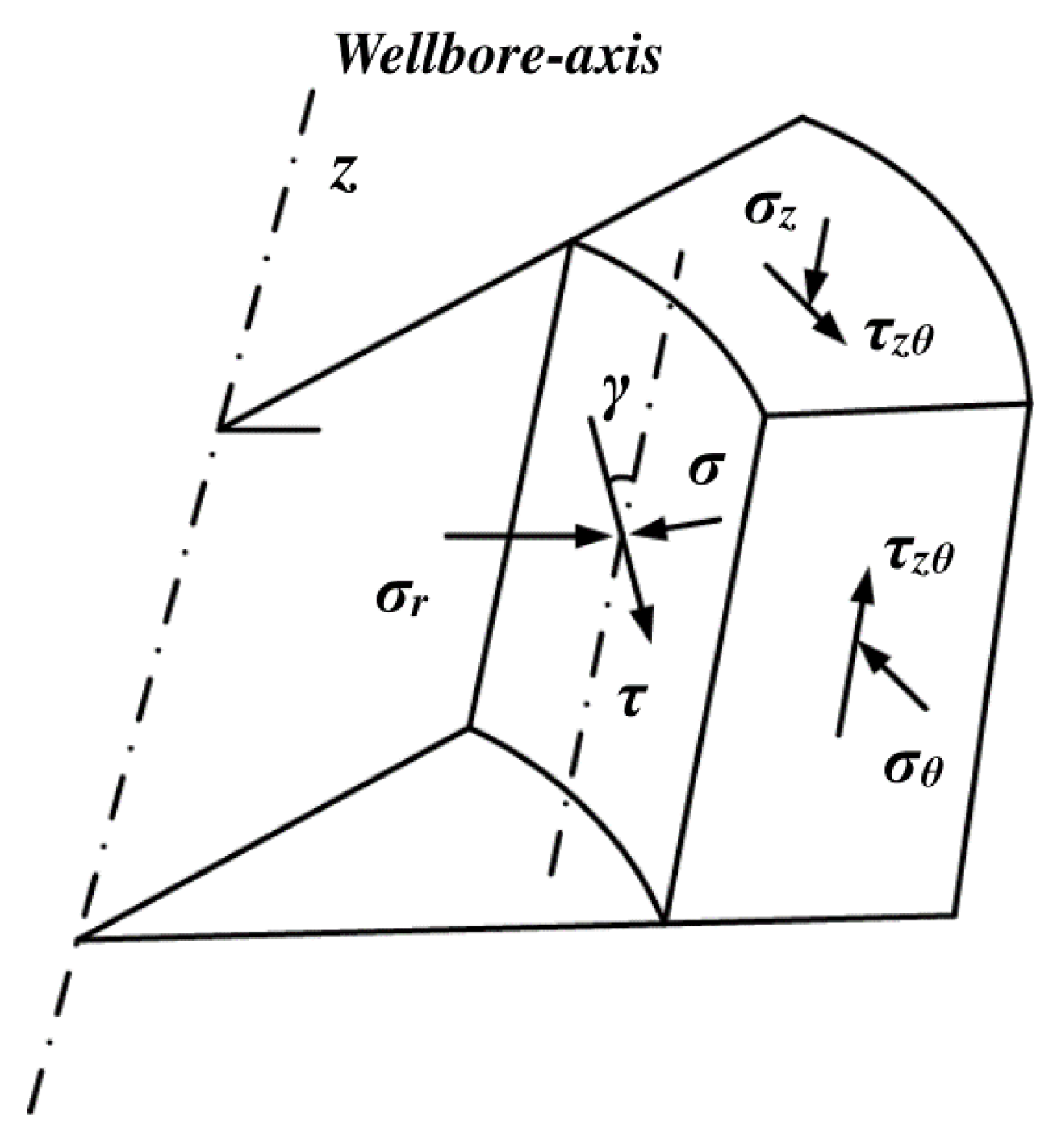
3.1. Stress Distribution around the Wellbore
3.1.1. Conversion of Axis Coordinates of Wellbore
3.1.2. The Elastic Solution of the Stress around the Wellbore
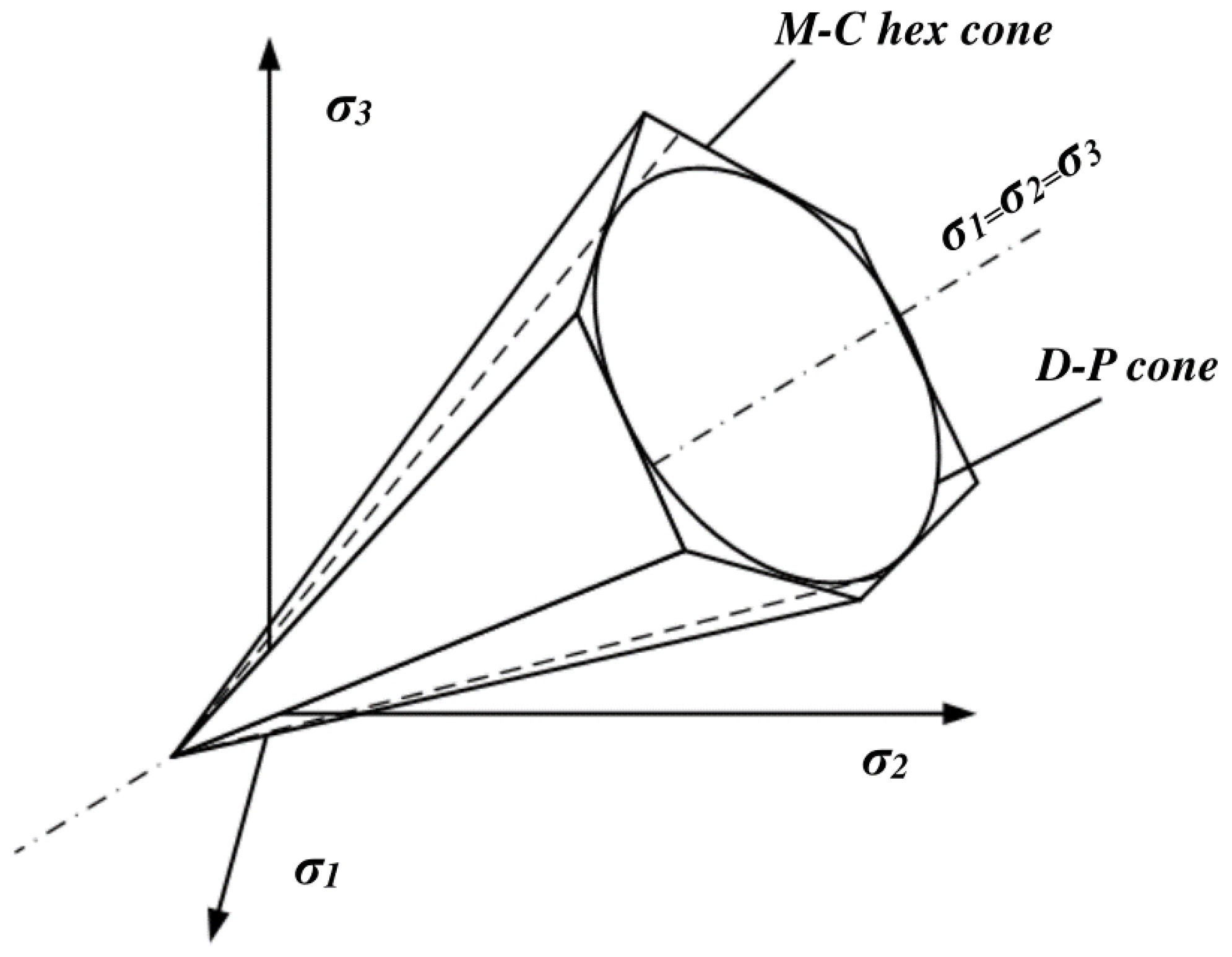
3.2. Failure Criteria
3.2.1. The M-C Failure Criterion
3.2.2. The D-P Failure Criterion
3.3. Collapse Pressure and Fracture Pressure
4. Wellbore Stability Analyses
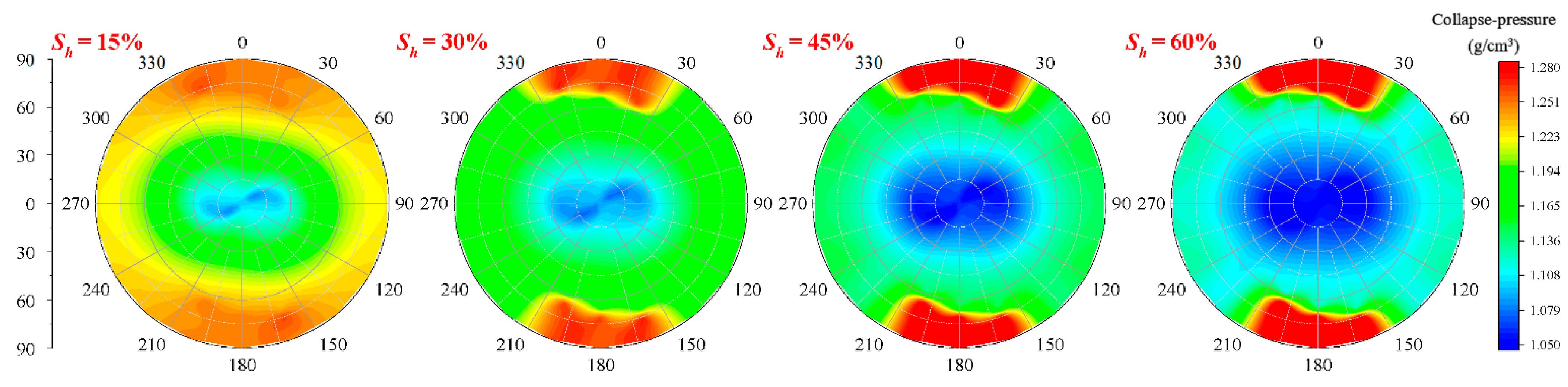
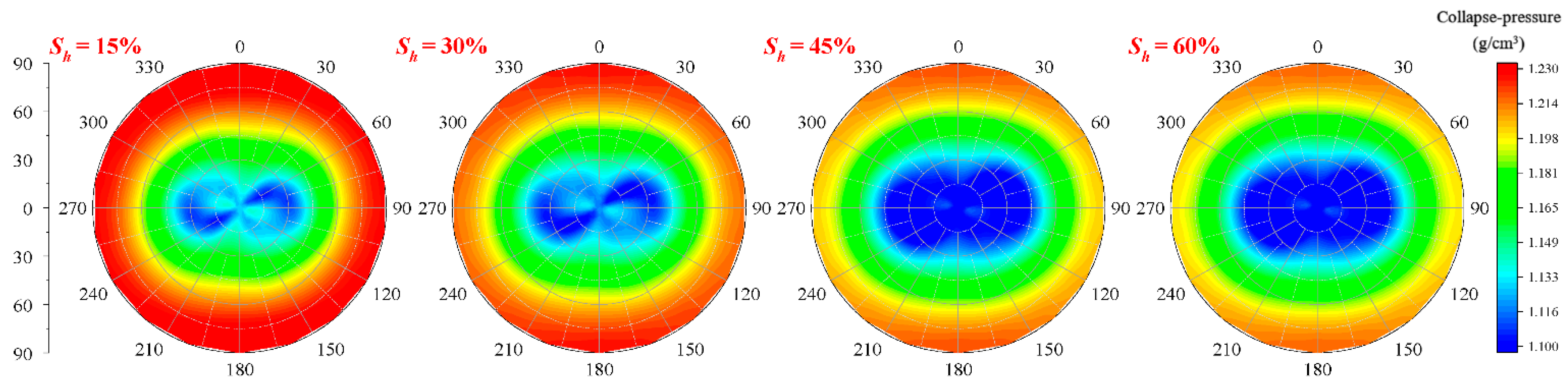
4.1. Effect of Sh on Collapse Pressure of Wellbore
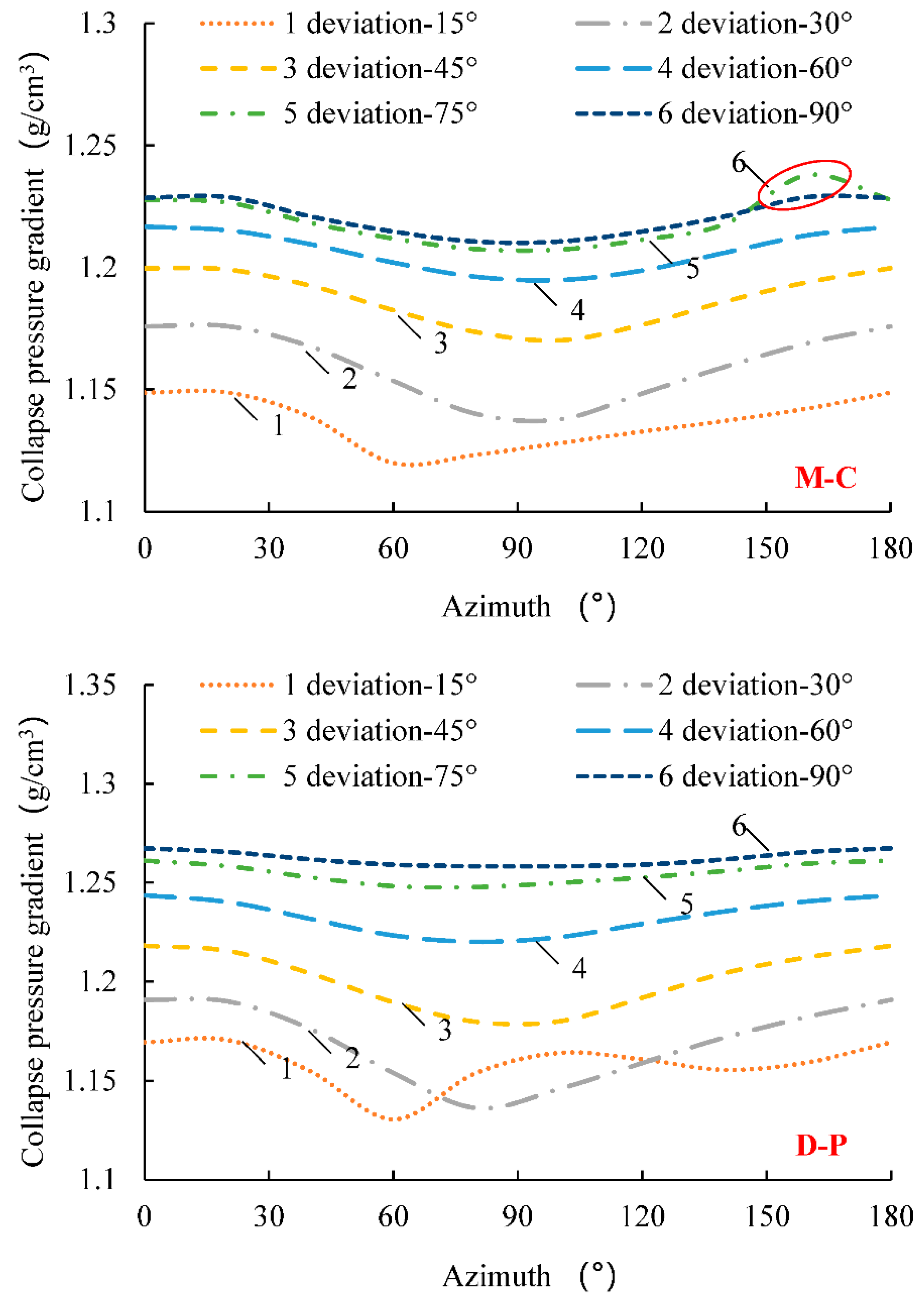
4.2. Influence of the Deviation Angle on the Collapse Pressure Gradient of the Wellbore
4.3. Effect of the Azimuth on the Collapse Pressure Gradient of the Wellbore
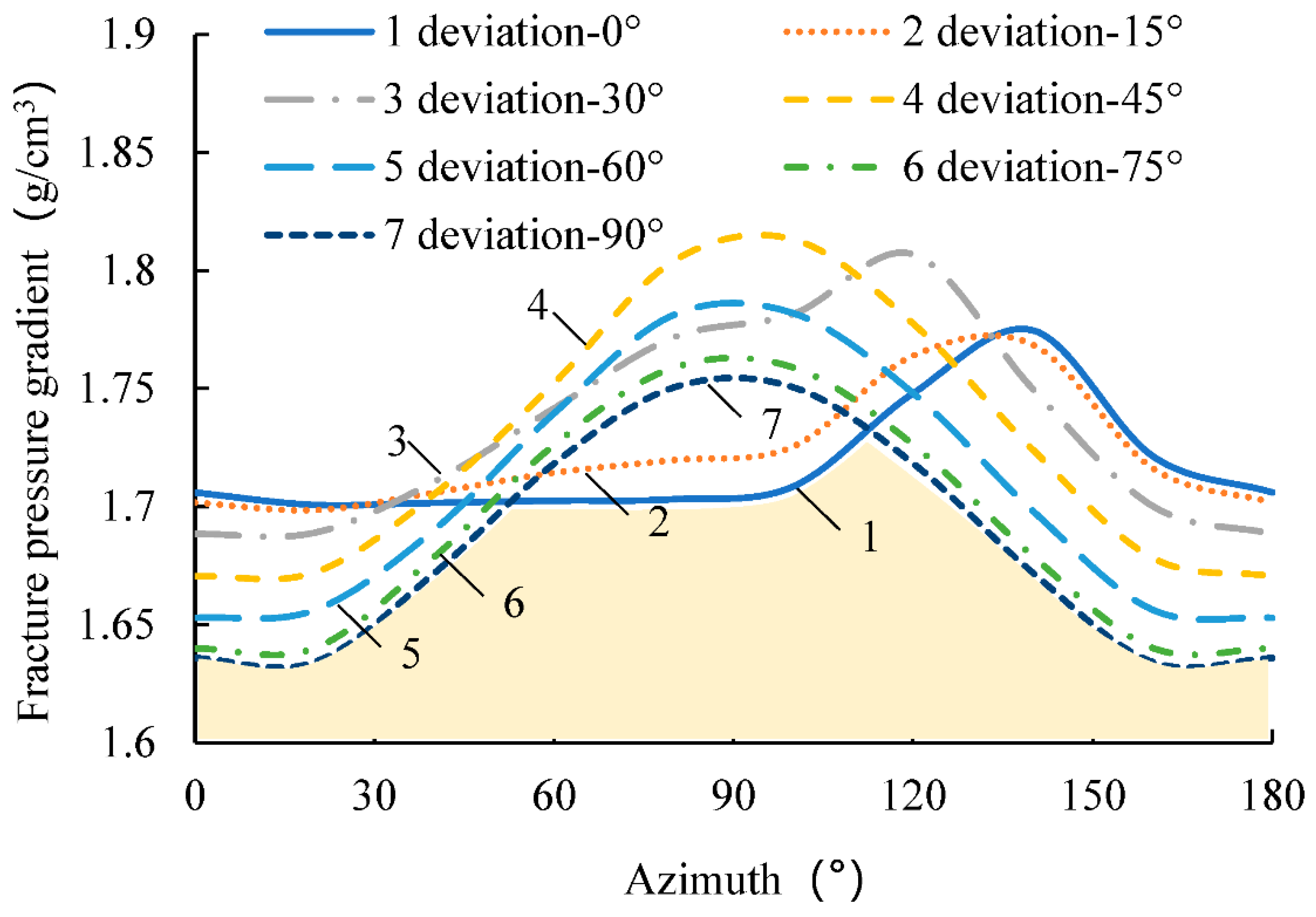
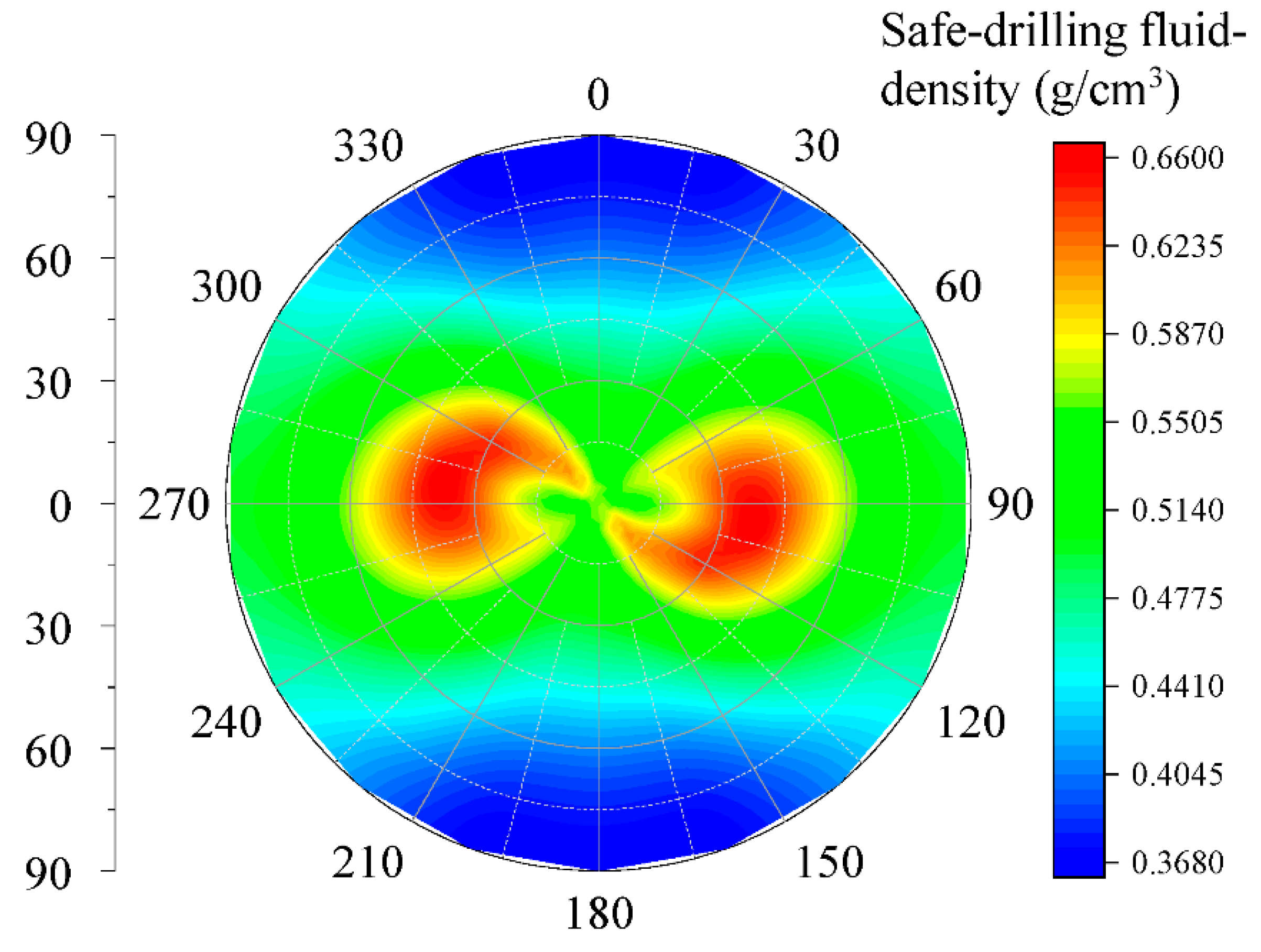
4.4. Fracture Pressure Gradient and the Safe Drilling Fluid Density Window
5. Conclusions and Suggestions
- The window distribution cloud chart of the collapse pressure gradient and the safe drilling fluid density of HBS-CS has a centrosymmetric distribution with a deviation angle and azimuth.
- Hydrate decomposition will lead to a higher collapse pressure and poorer stability of the formation. Therefore, the drilling fluid density should be appropriately increased by 7~10% during drilling to ensure the stability of formation after hydrate decomposition.
- The collapse pressure gradient increases by 7.2–9.2% from the vertical wellbore to the horizontal wellbore. From the perspective of preventing wellbore collapse, the safe density that satisfies the horizontal section can also ensure the wellbore stability of other sections. To prevent the wellbore fracture, a safe density that satisfies both the horizontal and vertical sections is necessary to ensure wellbore stability in all sections.
- Considering the combined effects of collapse, fracture pressure gradient, and safety density window, it is suggested that the borehole be arranged along the azimuth of 60–120°, which could greatly reduce the risk of the drilling operation.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wan, Z.; Luo, J.; Yang, X.; Zhang, W.; Liang, J.; Zuo, L.; Sun, Y. The Thermal Effect of Submarine Mud Volcano Fluid and Its Influence on the Occurrence of Gas Hydrates. J. Mar. Sci. Eng. 2022, 10, 832. [Google Scholar] [CrossRef]
- Hu, G.; Bu, Q.; Lyu, W.; Wang, J.; Chen, J.; Li, Q.; Gong, J.; Sun, J.; Wu, N. A comparative study on natural gas hydrate accumulation models at active and passive continental margins. Nat. Gas Ind. B 2021, 8, 115–127. [Google Scholar] [CrossRef]
- Qin, X.-W.; Lu, J.-A.; Lu, H.-L.; Qiu, H.-J.; Liang, J.-Q.; Kang, D.-J.; Zhan, L.-S.; Lu, H.-F.; Kuang, Z.-G. Coexistence of natural gas hydrate, free gas and water in the gas hydrate system in the Shenhu Area, South China Sea. China Geol. 2020, 3, 210–220. [Google Scholar] [CrossRef]
- Makogon, Y.F. Natural gas hydrates—A promising source of energy. J. Nat. Gas Sci. Eng. 2010, 2, 49–59. [Google Scholar] [CrossRef]
- Makogon, Y.; Omelchenko, R. Commercial gas production from Messoyakha deposit in hydrate conditions. J. Nat. Gas Sci. Eng. 2013, 11, 1–6. [Google Scholar] [CrossRef]
- Kurihara, M.; Sato, A.; Funatsu, K.; Ouchi, H.; Yamamoto, K.; Numasawa, M.; Ebinuma, T.; Narita, H.; Masuda, Y.; Dallimore, S.R.; et al. Analysis of Production Data for 2007/2008 Mallik Gas Hydrate Production Tests in Canada. In Proceedings of the International Oil and Gas Conference and Exhibition in China, Beijing, China, 8–10 June 2010; p. SPE-132155-MS. [Google Scholar] [CrossRef]
- Dubreuil-Boisclair, C.; Gloaguen, E.; Bellefleur, G.; Marcotte, D. Non-Gaussian gas hydrate grade simulation at the Mallik site, Mackenzie Delta, Canada. Mar. Pet. Geol. 2012, 35, 20–27. [Google Scholar] [CrossRef]
- Boswell, R.; Yamamoto, K.; Collett, T.S.; Okinaka, N. Virtual Special Issue of Recent Advances on Gas Hydrates Scientific Drilling in Alaska. Energy Fuels 2022, 36, 7921–7924. [Google Scholar] [CrossRef]
- Li, X.-S.; Xu, C.-G.; Zhang, Y.; Ruan, X.-K.; Li, G.; Wang, Y. Investigation into gas production from natural gas hydrate: A review. Appl. Energy 2016, 172, 286–322. [Google Scholar] [CrossRef] [Green Version]
- Yu, T.; Guan, G.; Abudula, A.; Yoshida, A.; Wang, D.; Song, Y. Gas recovery enhancement from methane hydrate reservoir in the Nankai Trough using vertical wells. Energy 2018, 166, 834–844. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, Z.; Sun, J.; Chen, L.; Wang, J.; Sun, B. Risk and preventive strategies of hydrate reformation in offshore gas hydrate production trials: A case study in the Eastern Nankai Trough. J. Nat. Gas Sci. Eng. 2022, 103, 104602. [Google Scholar] [CrossRef]
- Li, J.-F.; Ye, J.-L.; Qin, X.-W.; Qiu, H.-J.; Wu, N.-Y.; Lu, H.-L.; Xie, W.-W.; Lu, J.-A.; Peng, F.; Xu, Z.-Q.; et al. The first offshore natural gas hydrate production test in South China Sea. China Geol. 2018, 1, 5–16. [Google Scholar] [CrossRef]
- Ye, J.; Qin, X.; Xie, W.; Lu, H.; Ma, B.; Qin, H.; Liang, J.; Lu, J.; Kuang, Z.; Lu, C.; et al. Main progress of the second gas hydrate trial production in the South China Sea. Geol. China 2020, 47, 557–568. [Google Scholar] [CrossRef]
- Wei, N.; Zhao, J.; Liu, A.; Zhou, S.; Zhang, L.; Jiang, L. Evaluation of Physical Parameters and Construction of the Classification System of Natural Gas Hydrate in the Northern South China Sea. Energy Fuels 2021, 35, 7637–7645. [Google Scholar] [CrossRef]
- Rodger, P.M. Stability of gas hydrates. J. Phys. Chem. 1990, 94, 6080–6089. [Google Scholar] [CrossRef]
- Liu, C.; Li, Y.; Liu, L.; Hu, G.; Chen, Q.; Wu, N.; Meng, Q. An integrated experimental system for gas hydrate drilling and production and a preliminary experiment of the depressurization method. Nat. Gas Ind. B 2020, 7, 56–63. [Google Scholar] [CrossRef]
- Li, Y.; Cheng, Y.; Yan, C.; Song, L.; Liu, H.; Tian, W.; Ren, X. Mechanical study on the wellbore stability of horizontal wells in natural gas hydrate reservoirs. J. Nat. Gas Sci. Eng. 2020, 79, 103359. [Google Scholar] [CrossRef]
- Freij-Ayoub, R.; Tan, C.; Clennell, B.; Tohidi, B.; Yang, J. A wellbore stability model for hydrate bearing sediments. J. Pet. Sci. Eng. 2006, 57, 209–220. [Google Scholar] [CrossRef]
- Zhang, H.; Cheng, Y.; Li, Q.; Yan, C.; Han, X. Numerical analysis of wellbore instability in gas hydrate formation during deep-water drilling. J. Ocean Univ. China 2018, 17, 8–16. [Google Scholar] [CrossRef]
- Sun, J.; Ning, F.; Lei, H.; Gai, X.; Sánchez, M.; Lu, J.; Li, Y.; Liu, L.; Liu, C.; Wu, N.; et al. Wellbore stability analysis during drilling through marine gas hydrate-bearing sediments in Shenhu area: A case study. J. Pet. Sci. Eng. 2018, 170, 345–367. [Google Scholar] [CrossRef]
- Yuan, Y.; Xu, T.; Xin, X.; Xia, Y.; Li, B. Mechanical stability analysis of strata and wellbore associated with gas production from oceanic hydrate-bearing sediments by depressurization. Chin. J. Theor. Appl. Mech. 2020, 52, 544–555. [Google Scholar] [CrossRef]
- Dong, L.; Li, Y.; Liu, C.; Liao, H.; Chen, G.; Chen, Q.; Liu, L.; Hu, G. Mechanical Properties of Methane Hydrate-Bearing Interlayered Sediments. J. Ocean Univ. China 2019, 18, 1344–1350. [Google Scholar] [CrossRef]
- Jin, Y.; Wu, N.; Li, Y.; Yang, D. Characterization of Sand Production for Clayey-Silt Sediments Conditioned to Hydraulic Slotting and Gravel Packing: Experimental Observations, Theoretical Formulations, and Modeling. SPE J. 2022, 1–20. [Google Scholar] [CrossRef]
- Lu, J.; Lin, D.; Li, D.; Liang, D.; Wen, L.; Wu, S.; Zhang, Y.; He, Y.; Shi, L.; Xiong, Y. Microcosmic Characteristics of Hydrate Formation and Decomposition in the Different Particle Size Sediments Captured by Cryo-SEM. J. Mar. Sci. Eng. 2022, 10, 769. [Google Scholar] [CrossRef]
- Li, Y.; Liu, C.; Liao, H.; Lin, D.; Bu, Q.; Liu, Z. Mechanical properties of the clayey-silty sediment-natural gas hydrate mixed system. Nat. Gas Ind. B 2021, 8, 154–162. [Google Scholar] [CrossRef]
- Dong, L.; Liao, H.; Li, Y.; Meng, Q.; Hu, G.; Wang, J.; Wu, N. Analysis of the Mechanical Properties of the Reconstituted Hydrate-Bearing Clayey-Silt Samples from the South China Sea. J. Mar. Sci. Eng. 2022, 10, 831. [Google Scholar] [CrossRef]
- Tan, C.P.; Clennell, M.B.; Freij-Ayoub, R.; Tohidi, B.; Yang, J. Mechanical and Petrophysical Characterisation and Wellbore Stability Management in Gas Hydrate-Bearing Sediments. In Proceedings of the Alaska Rocks 2005, the 40th US Symposium on Rock Mechanics (USRMS), Anchorage, Alaska, 25–29 June 2005; OnePetro: Richardson, TX, USA, 2005. [Google Scholar]
- Birchwood, R.; Noeth, S.; Hooyman, P.; Winters, W.; Jones, E. Wellbore Stability Model for Marine Sediments Containing Gas Hydrates. In Proceedings of the American Association of Drilling Engineers National Conference and Exhibition, Houston, TX, USA, 5–7 April 2005. [Google Scholar]
- Risnes, R.; Bratli, R.K.; Horsrud, P. Sand Stresses Around a Wellbore. Soc. Pet. Eng. J. 1982, 22, 883–898. [Google Scholar] [CrossRef]
- Yan, C.; Ren, X.; Cheng, Y.; Song, B.; Li, Y.; Tian, W. Geomechanical issues in the exploitation of natural gas hydrate. Gondwana Res. 2020, 81, 403–422. [Google Scholar] [CrossRef]
- Liu, X.; Sun, Y.; Guo, T.; Rabiei, M.; Qu, Z.; Hou, J. Numerical simulations of hydraulic fracturing in methane hydrate reservoirs based on the coupled thermo-hydrologic-mechanical-damage (THMD) model. Energy 2021, 238, 122054. [Google Scholar] [CrossRef]
- Sujatono, S. Determination of cohesion and friction angle on sedimentary rock based on geophysical log. Géoméch. Geophys. Geo-Energy Geo-Resour. 2022, 8, 1–10. [Google Scholar] [CrossRef]
- Jiang, H.; Xie, Y. A note on the Mohr–Coulomb and Drucker–Prager strength criteria. Mech. Res. Commun. 2011, 38, 309–314. [Google Scholar] [CrossRef]
- Labuz, J.F.; Zang, A. Mohr–Coulomb Failure Criterion. Rock Mech. Rock Eng. 2012, 45, 975–979. [Google Scholar] [CrossRef] [Green Version]
- Kesarev, A.G.; Vlasova, A.M. Generalized von Mises Criterion as a Tool for Determining the Strength Properties of Hexagonal Materials. Phys. Met. Met. 2022, 123, 186–192. [Google Scholar] [CrossRef]
- Zhao, Y.; Wang, Y.; Tang, L. The compressive-shear fracture strength of rock containing water based on Druker-Prager failure criterion. Arab. J. Geosci. 2019, 12, 542. [Google Scholar] [CrossRef]
- Chen, L.; Feng, Y.; Okajima, J.; Komiya, A.; Maruyama, S. Production behavior and numerical analysis for 2017 methane hydrate extraction test of Shenhu, South China Sea. J. Nat. Gas Sci. Eng. 2018, 53, 55–66. [Google Scholar] [CrossRef]
- Li, G.; Moridis, G.J.; Zhang, K.; Li, X.-S. Evaluation of the Gas Production Potential of Marine Hydrate Deposits in the Shenhu Area of the South China Sea. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 3–6 May 2010; p. OTC-20548-MS. [Google Scholar] [CrossRef]
- Zoback, M.D. Reservoir Geomechanics; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Li, W.; Gao, D.; Yang, J. Study of mud weight window of horizontal wells drilled into offshore natural gas hydrate sediments. J. Nat. Gas Sci. Eng. 2020, 83, 103575. [Google Scholar] [CrossRef]
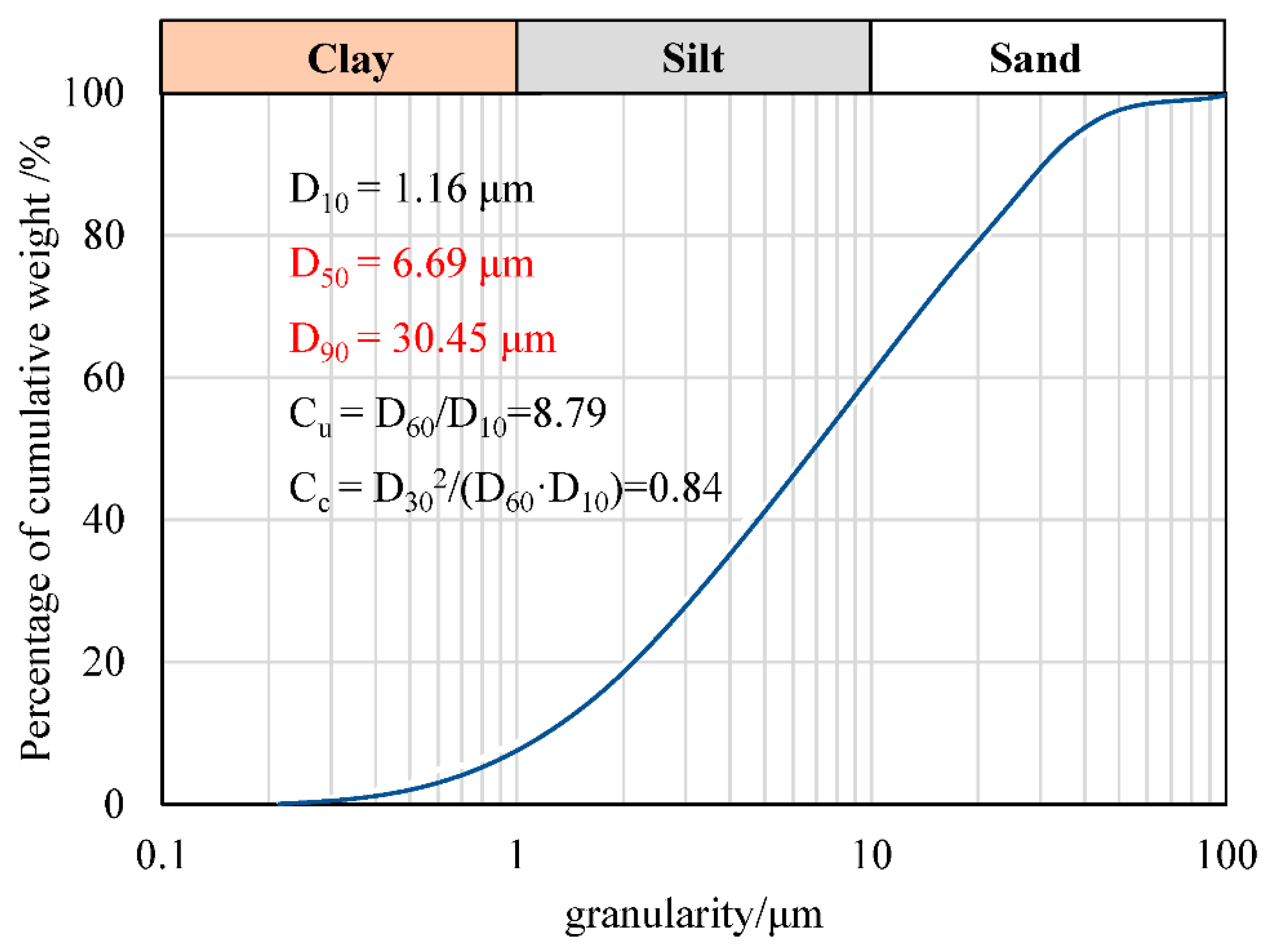



| Sh | σ3/MPa | σ1/MPa | Cohesion C/MPa | Friction Angle ϕ/° |
|---|---|---|---|---|
| 15% | 1 | 1.62 | 0.0953 | 10.340 |
| 2 | 3.17 | |||
| 4 | 5.95 | |||
| 30% | 1 | 2.48 | 0.426 | 11.612 |
| 2 | 4.16 | |||
| 4 | 7.03 | |||
| 45% | 1 | 3.54 | 0.811 | 12.275 |
| 2 | 5.12 | |||
| 4 | 8.17 | |||
| 60% | 1 | 4.29 | 1.071 | 13.568 |
| 2 | 6.00 | |||
| 4 | 9.15 |
| σr | σθ | τθr |
|---|---|---|
| / | ||
| τrz | τθz |
|---|---|
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, X.; Hu, Q.; Li, Y.; Chen, M.; Zhang, Y. Stability Characteristics of Horizontal Wells in the Exploitation of Hydrate-Bearing Clayey-Silt Sediments. J. Mar. Sci. Eng. 2022, 10, 1935. https://doi.org/10.3390/jmse10121935
Sun X, Hu Q, Li Y, Chen M, Zhang Y. Stability Characteristics of Horizontal Wells in the Exploitation of Hydrate-Bearing Clayey-Silt Sediments. Journal of Marine Science and Engineering. 2022; 10(12):1935. https://doi.org/10.3390/jmse10121935
Chicago/Turabian StyleSun, Xiaofeng, Qiaobo Hu, Yanlong Li, Mingtao Chen, and Yajuan Zhang. 2022. "Stability Characteristics of Horizontal Wells in the Exploitation of Hydrate-Bearing Clayey-Silt Sediments" Journal of Marine Science and Engineering 10, no. 12: 1935. https://doi.org/10.3390/jmse10121935
APA StyleSun, X., Hu, Q., Li, Y., Chen, M., & Zhang, Y. (2022). Stability Characteristics of Horizontal Wells in the Exploitation of Hydrate-Bearing Clayey-Silt Sediments. Journal of Marine Science and Engineering, 10(12), 1935. https://doi.org/10.3390/jmse10121935








