A Nonlinear Phase Transition Dynamic Model for Shape Memory Alloys Based Deep Sea Actuators
Abstract
:1. Introduction
2. Hydrostatic Pressure Dependence of SMA Phase Transition Process
3. Constitutive Model of Nonlinear Phase Transition
3.1. Thermodynamic Constitutive Equations of SMAs in the Deep Sea Environment
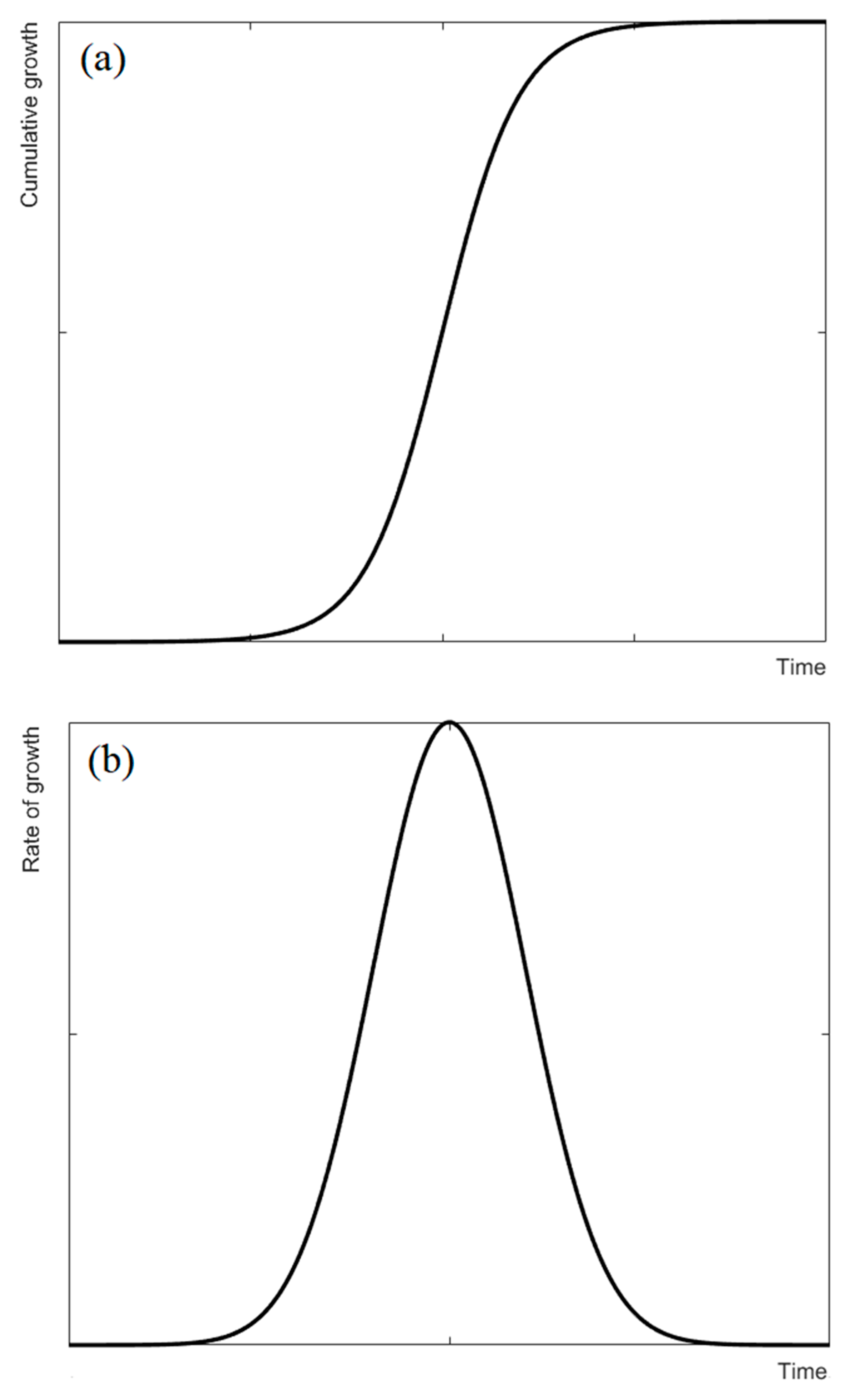
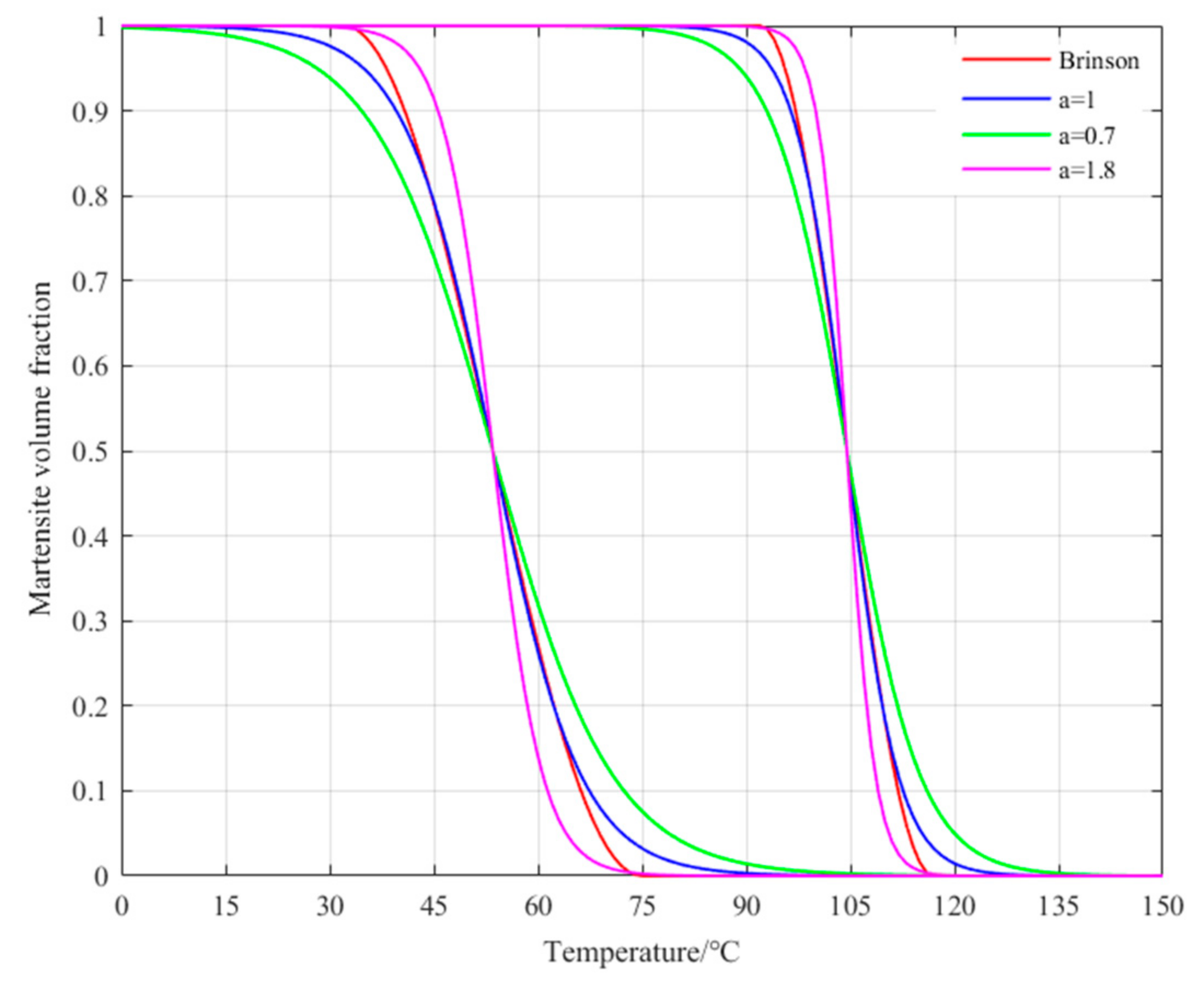
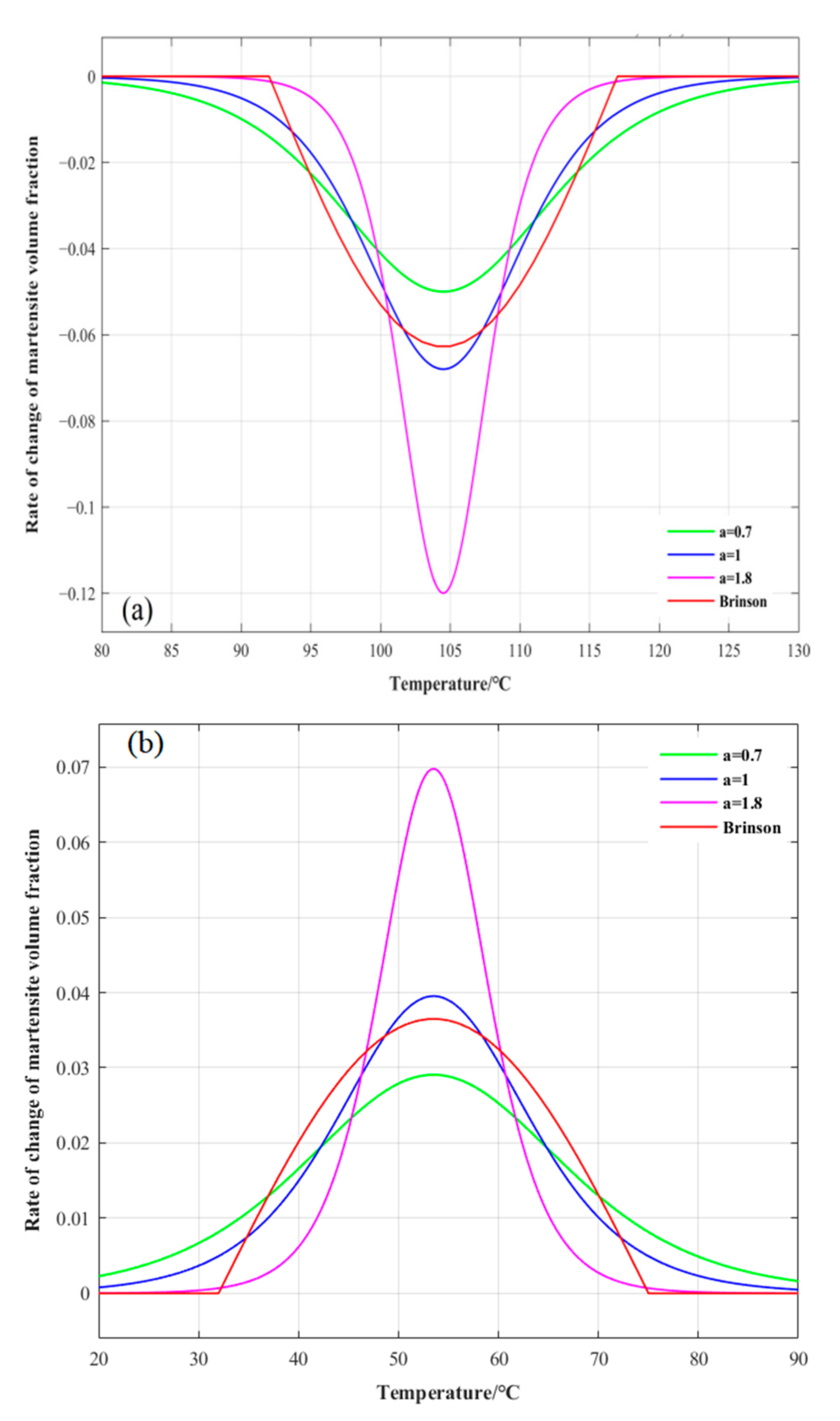
3.2. Dynamic Equation of Phase Transition Based on Logistic Function
4. Results and Discussion
4.1. Logistic Variable Speed Phase Transition Kinetics Fitting and Analysis
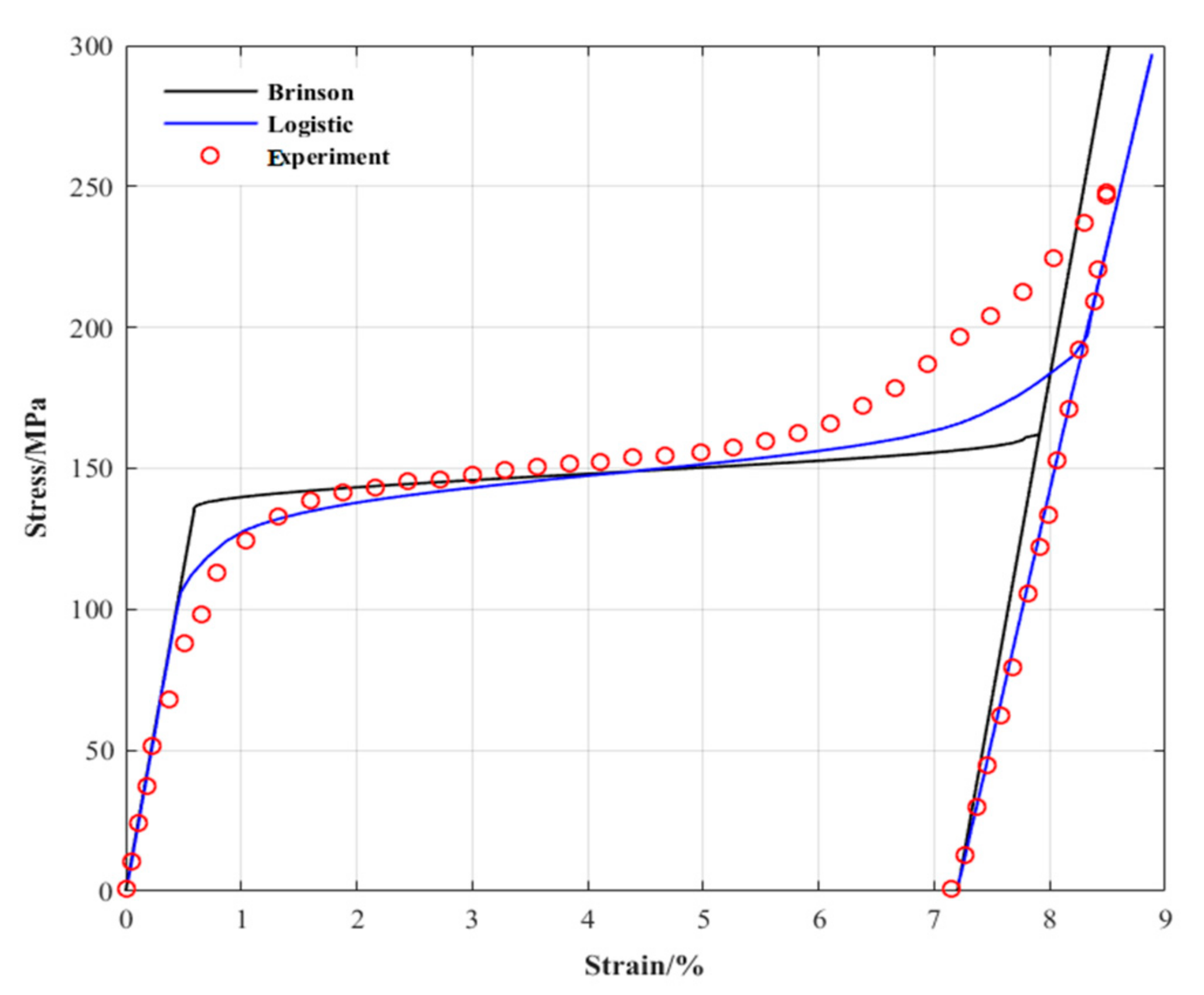
4.2. Numerical Fitting and Analysis of Phenomenological Constitutive Model
4.2.1. Different Load Cycles at Constant Temperature
4.2.2. Different Temperature Cycles under a Constant Load
4.3. Consideration of Marine Engineering Application
4.3.1. Conductivity of Seawater
4.3.2. Strong Corrosive
4.3.3. High Hydrostatic Pressure
4.3.4. Low-Temperature Environment
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, C. The potential and challenges of China’s marine science and technology development. People’s Forum Acad. Front. 2017, 18, 37–43. [Google Scholar]
- Li, J.; Liu, F.; Ma, W. Development status of intelligent equipment industry for marine unmanned systems at home and abroad. Ship Eng. 2020, 42, 25–31. [Google Scholar]
- Guo, J.; Pan, B.; Cui, W.; Hu, S.; Han, Z. Review of deep-sea actuators and marine bionic robots based on intelligent materials. Ship Mech. 2022, 26, 13. [Google Scholar]
- Bai, Z. Summary of research progress and application of smart materials. Mil. Civ. Dual-Use Technol. Prod. 2020, 3, 15–20. [Google Scholar]
- Guo, K.; Xia, P. Research progress of smart composite materials. Funct. Mater. 2019, 50, 4017–4022, 4029. [Google Scholar]
- Hao, L. Research on Mechanical Properties of Shape Memory Alloy Bulge. Ph.D. Thesis, Nanjing University of Aeronautics and Astronautics, Nanjing, China, 2018. [Google Scholar]
- Moumni, Z.; Zaki, W.; Nguyen, Q.S. Theoretical and Numerical Modeling of Solid–Solid Phase Change: Application to the Description of the Thermomechanical Behavior of Shape Memory Alloys. Int. J. Plast. 2008, 24, 614–645. [Google Scholar] [CrossRef]
- Yang, J.; Huang, B.; Gu, X.; Wang, J.; Zhang, Y.; Zhu, J.; Zhang, W. Review of Mechanical Behavior and Application of Shape Memory Alloys. J. Solid Mech. 2021, 42, 345–375. [Google Scholar]
- Liu, K. Design and Control Technology of Underwater Vector Deflection Actuator Based on Ni-Ti Shape Memory Alloy. Master’s Thesis, South China University of Technology, Guangzhou, China, 2020. [Google Scholar]
- Cisse, C.; Zaki, W.; Zineb, T.B. A review of constitutive models and modeling techniques for shape memory alloys. Int. J. Plast. 2016, 76, 244–284. [Google Scholar] [CrossRef]
- Lagoudas, D.; Hartl, D.; Chemisky, Y.; Machado, L.; Popov, P. Constitutive model for the numerical analysis of phase transformation in polycrystalline shape memory alloys. Int. J. Plast. 2012, 32–33, 155–183. [Google Scholar] [CrossRef]
- He, J.; Toi, Y. Improved constitutive modeling for phase transformation of shape memory alloys. J. Solid Mech. Mater. Eng. 2013, 7, 11–26. [Google Scholar] [CrossRef] [Green Version]
- Lagoudas, D.C.; Entchev, P.B.; Popov, P.; Patoor, E.; Catherine Brinson, L.; Gao, X. Shape memory alloys, Part II: Modeling of polycrystals. Mech. Mater. 2006, 38, 430–462. [Google Scholar] [CrossRef]
- Kucharavy, D.; Guio, R.D. Application of S-shaped curves. Procedia Eng. 2011, 9, 559–572. [Google Scholar] [CrossRef] [Green Version]
- Guan, J.H.; Pei, Y.C.; Wu, J.T. A driving strategy of shape memory alloy wires with electric resistance modeled by logistic function for power consumption reduction. Mech. Syst. Signal Process. 2021, 160, 107839. [Google Scholar] [CrossRef]
- Ding, Y. Research on the Multidimensional Constitutive Relation of Shape Memory Alloys. Master’s Thesis, Xi’an University of Architecture and Technology, Xi’an, China, 2005. [Google Scholar]
- Johari, G.P.; McAnanama, J.G.; Sartor, G. Effect of hydrostatic pressure on the thermoelastic transformation of Ni-Ti alloy and the entropy of transformation. Philos. Mag. B 1996, 74, 243–257. [Google Scholar] [CrossRef]
- Wan, J.L.; Chen, Z.B.; Qin, S.J.; Shang, J. Effect of hydrostatic pressure on thermally induced phase transformation in NiTi alloy: A molecular dynamics study. Comput. Mater. Sci. 2018, 153, 119–125. [Google Scholar] [CrossRef]
- Ikuta, K.; Tsukamoto, M.; Hirose, S. Mathematical model and experimental verification of shape memory alloy for designing micro actuator. In Proceedings of the IEEE Micro Electro Mechanical Systems, Nara, Japan, 30–2 January 1991; pp. 103–108. [Google Scholar]
- Liu, B. Study on the Phase Transformation Mechanism and Mechanical Properties of Porous Shape Memory Alloys. Ph.D. Thesis, Beijing Jiaotong University, Beijing, China, 2013. [Google Scholar]
- Zhu, X.; Dui, G. Modeling of superelastic–plastic behavior of porous shape memory alloys incorporating void shape effects. Acta Mech. Solida Sin. 2021, 34, 632–644. [Google Scholar] [CrossRef]
- Sumoto, H.; Yamaguchi, S. A study on a control meth- od of artificial muscle using segmented binary control for an up-scaled fish type robot. In Proceedings of the 21st International Offshore and Polar Engineering Conference, Maui, HI, USA, 19–24 June 2011; pp. 223–229. [Google Scholar]
- Angilella, A.J.; Gandhi, F.S.; Miller, T.F. Design and testing of a shape memory alloy buoyancy engine for unmanned underwater vehicles. Smart Mater. Struct. 2015, 24, 115018. [Google Scholar] [CrossRef]
- Hartl, D.J.; Lagoudas, D.C. Thermomechanical Characterization of Shape Memory Alloy Materials. In Shape Memory Alloys: Modeling and Engineering Applications; Springer: Boston, MA, USA, 2008. [Google Scholar]
- Li, J.; Yang, Z. Numerical analysis and modification of thermodynamic empirical constitutive model for shape memory alloys. Mater. Rev. 2021, 35, 18116–18123. [Google Scholar]
- Kudryashov, N.A. Logistic function as solution of many nonlinear differential equations. Appl. Math. Model. 2015, 39, 5733–5742. [Google Scholar] [CrossRef]

| Phase Transition Temperature | Thermal Coefficient | Elastic Modulus | Phase Transition Parameters | Maximum Residual Strain |
|---|---|---|---|---|
| Mf = 22 °C | = 1 × 10−5 °C−1 | DTM = 22,800 MPa | CM = 5 MPa/°C | = 0.072 |
| Ms = 65 °C | b = 6.8 | DDM = 17,600 MPa | CA = 5 MPa/°C | |
| As = 82 °C | DA = 42,800 MPa | = 136 MPa | ||
| Af = 107 °C | = 161 MPa |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, J.; Pan, B.; Cui, W.; Hu, S. A Nonlinear Phase Transition Dynamic Model for Shape Memory Alloys Based Deep Sea Actuators. J. Mar. Sci. Eng. 2022, 10, 1951. https://doi.org/10.3390/jmse10121951
Guo J, Pan B, Cui W, Hu S. A Nonlinear Phase Transition Dynamic Model for Shape Memory Alloys Based Deep Sea Actuators. Journal of Marine Science and Engineering. 2022; 10(12):1951. https://doi.org/10.3390/jmse10121951
Chicago/Turabian StyleGuo, Jian, Binbin Pan, Weicheng Cui, and Shengbing Hu. 2022. "A Nonlinear Phase Transition Dynamic Model for Shape Memory Alloys Based Deep Sea Actuators" Journal of Marine Science and Engineering 10, no. 12: 1951. https://doi.org/10.3390/jmse10121951





