Efficient Structural Dynamic Analysis Using Condensed Finite Element Matrices and Its Application to a Stiffened Plate
Abstract
:1. Introduction
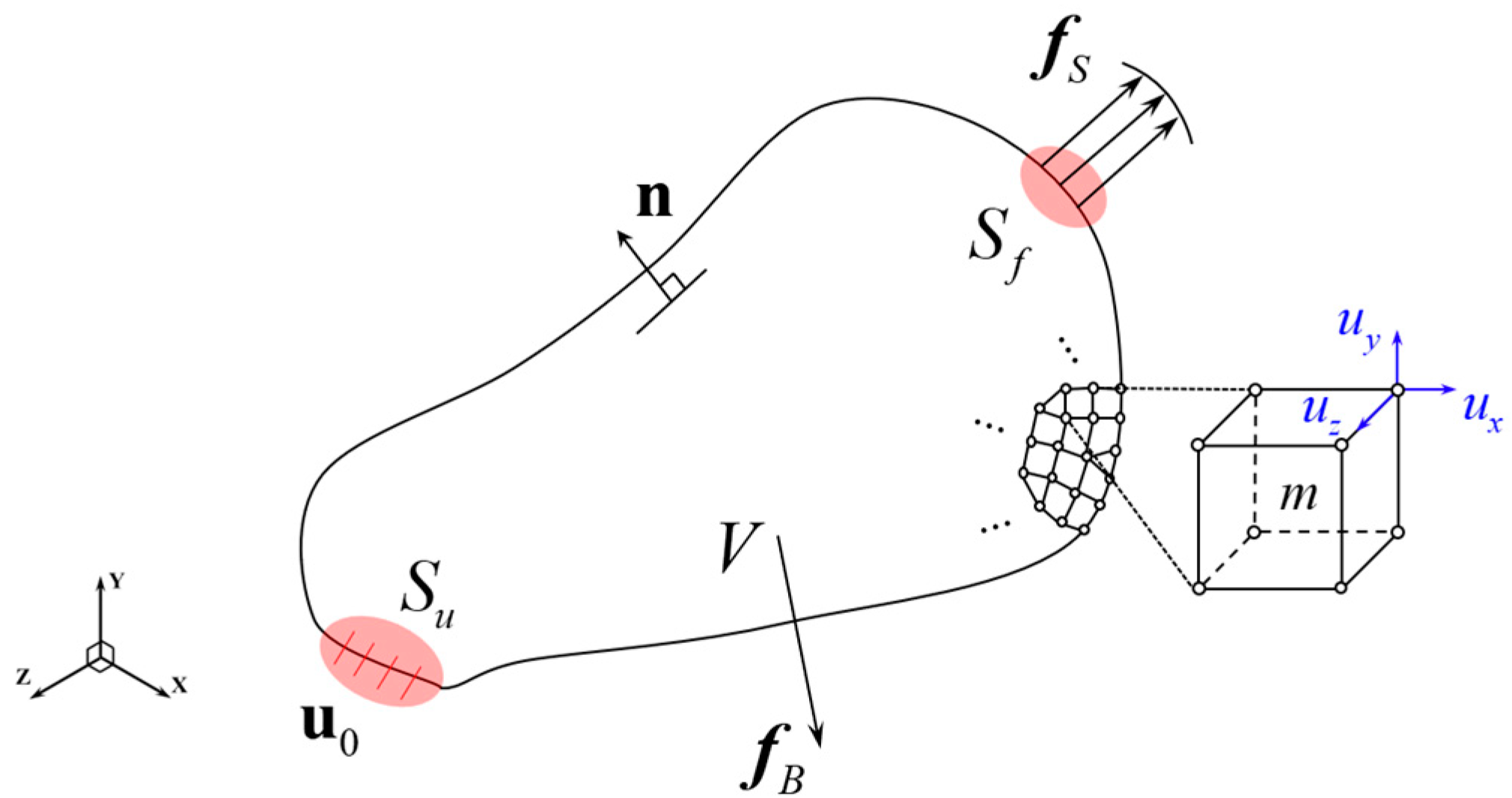
2. FE Formulation for Dynamic Analysis
3. Construction of Condensed Matrices
4. Structural Dynamic Formulations Using Condensed Matrices
4.1. Modal Analysis
4.2. Frequency Response Analysis
4.3. Transient Analysis
5. Structural Dynamic Analysis for a Stiffened Plate
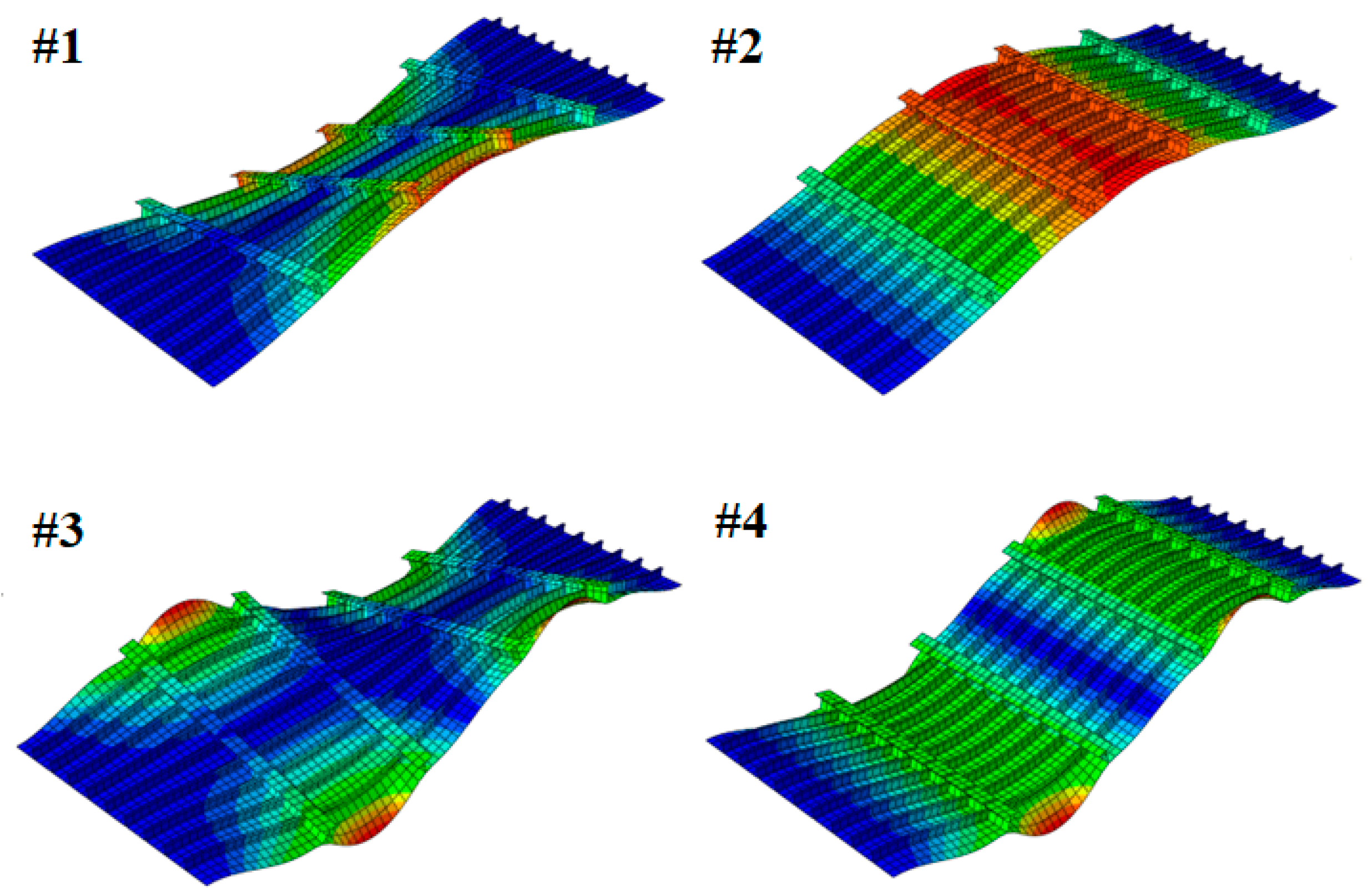
5.1. Modal Analysis Results
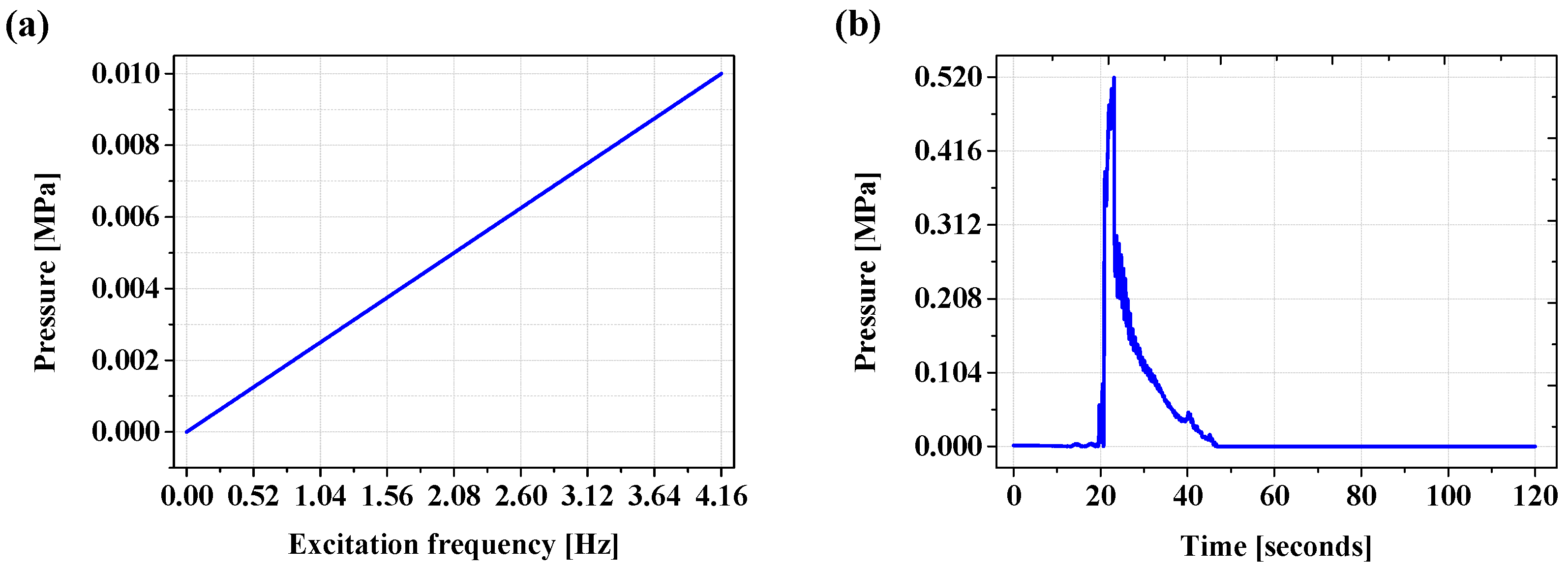
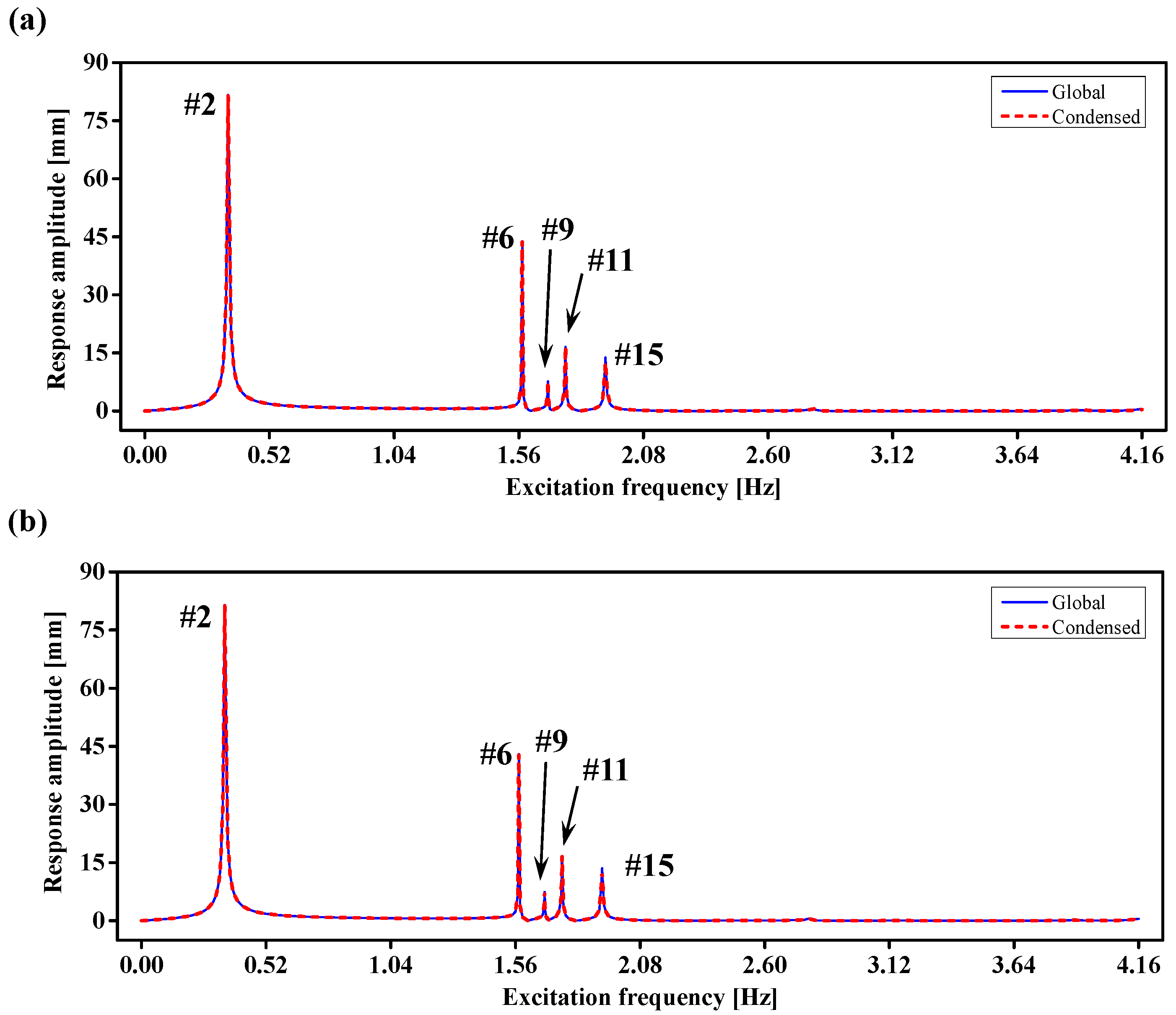
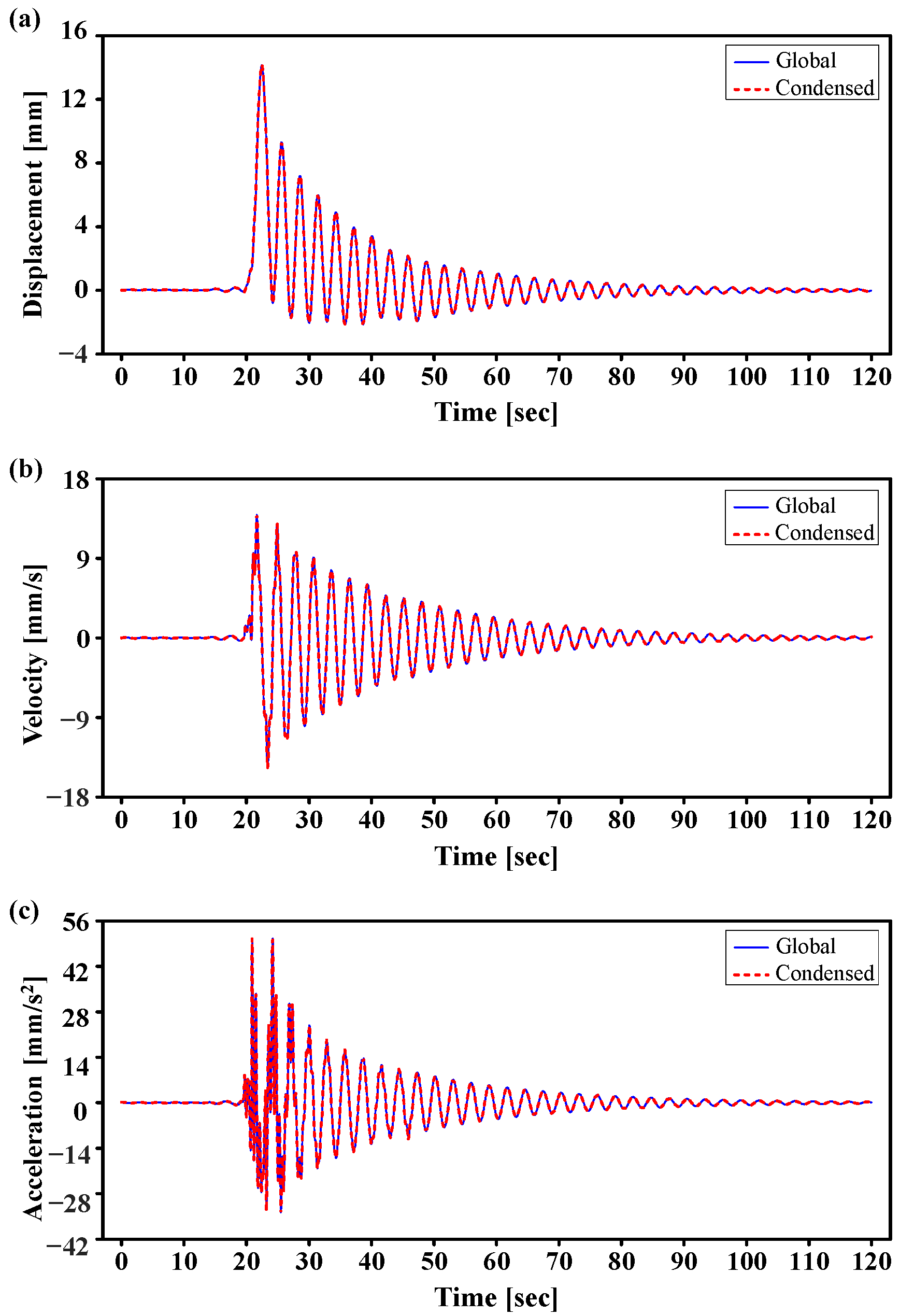
5.2. Frequency Response and Transient Analysis Results
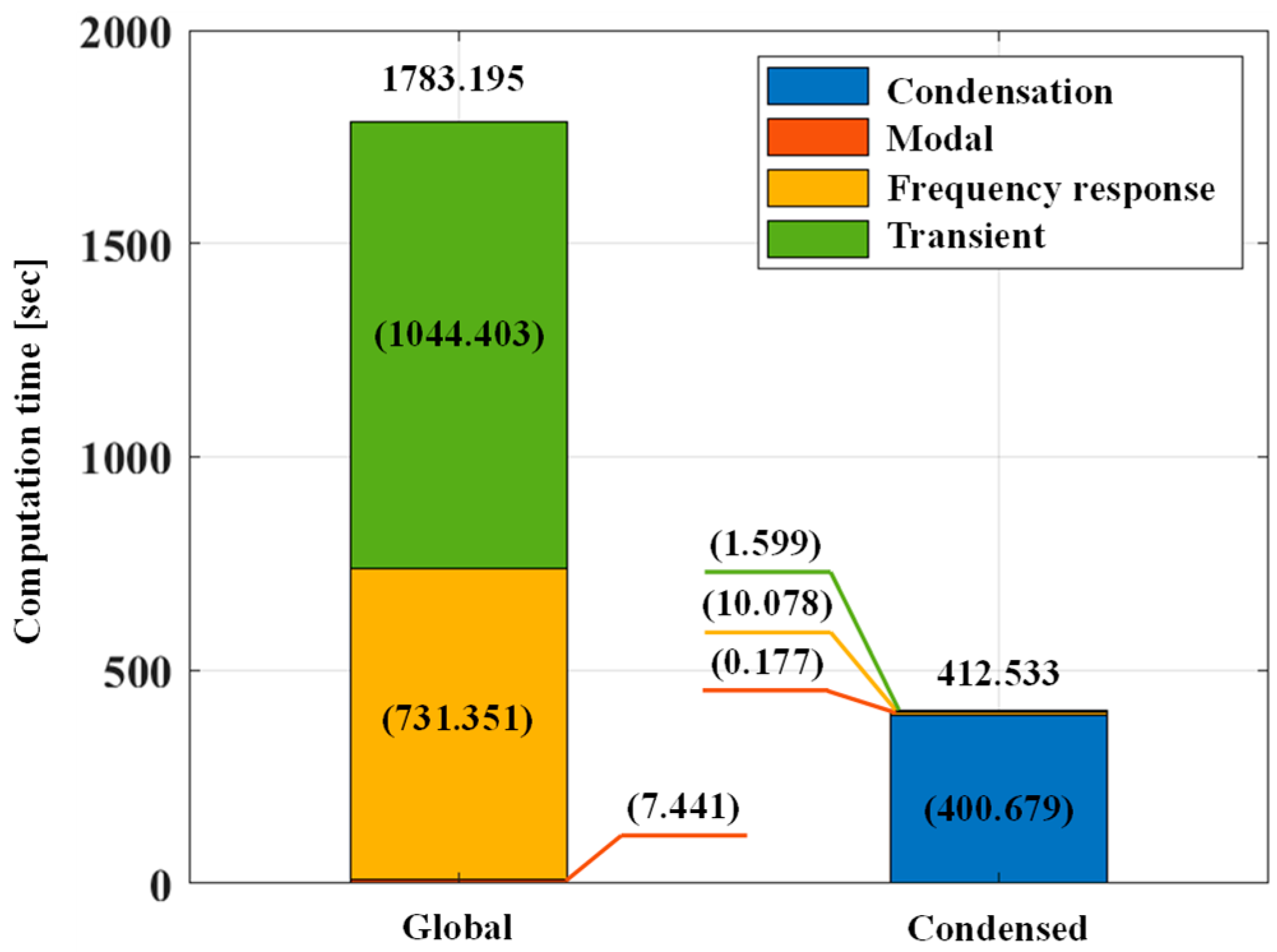
5.3. Computational Efficiency Analysis
6. Conclusions
- Using the proposed formulation for modal analysis, the natural frequencies and mode shapes were calculated for 40 modes, and the maximum errors for these were 0.361%, confirming that solutions with very high accuracy were derived.
- In the frequency response analysis, all errors resulting from the proposed formulation were less than 0.3% in all frequency ranges except for the resonance frequencies, showing excellent accuracy. For the resonance frequencies, the maximum error was 3.817%.
- In the transient analysis, all errors were less than 0.070% for the displacement, velocity, and acceleration results obtained from the condensed model, also showing excellent accuracy.
- The proposed formulations provided highly accurate solutions for the structural dynamic analysis, with excellent computational efficiency. Once the condensed matrices were calculated, the computation time for the structural dynamics analysis was only 0.665% of the total computation time, a very attractive aspect of the proposed method.
- In future work, it will be valuable to apply the condensed matrices to other practical engineering and design problems, such as fatigue, quasi-static, local impact, and transient conduction-radiation analyses [30].
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kirk, C.L. Natural frequencies of stiffened rectangular plates. J. Sound Vib. 1970, 13, 375–388. [Google Scholar] [CrossRef]
- Gong, S.W.; Lam, K.Y. Transient response of stiffened composite plates subjected to low velocity impact. Compos. Pt. B-Eng. 1998, 30, 473–484. Available online: https://www.sciencedirect.com/science/article/abs/pii/S1359836899000025?via%3Dihub (accessed on 1 October 2022). [CrossRef]
- Bathe, K.J. Finite Element Procedure; Prentice Hall: Hoboken, NJ, USA, 2006. [Google Scholar]
- Feriani, A.; Perotti, F.; Simoncini, V. Iterative system solvers for the frequency analysis of linear mechanical systems. Comput. Meth. Appl. Mech. Eng. 2000, 190, 1719–1739. [Google Scholar] [CrossRef]
- Kim, H.; Melhem, H. Damage detection of structures by wavelet analysis. Eng. Struct. 2004, 26, 347–362. [Google Scholar] [CrossRef]
- Ramos, L.F.; Aguilar, R.; Lourenco, P.B.; Moreira, S. Dynamic structural health monitoring of Saint Torcato church. Mech. Syst. Signal Proc. 2013, 35, 1–15. [Google Scholar] [CrossRef]
- Yue, N.; Khodael, Z.S.; Aliabadi, M.H. Damage detection in large composite stiffened panels based on a novel SHM building block philosophy. Smart Mater. Struct. 2021, 30, 045004. [Google Scholar] [CrossRef]
- Guyan, R.J. Reduction of stiffness and mass matrices. AIAA 1965, 3, 380. [Google Scholar] [CrossRef]
- O’Callahan, J. A procedure for an improved reduced system (IRS) model. In Proceedings of the 7th International Modal Analysis Conference, Las Vegas, NV, USA, 30 January–1 February 1989; pp. 17–21. [Google Scholar]
- Friswell, M.I.; Garvey, S.D.; Penny, J.E.T. Model reduction using dynamic and iterated IRS techniques. J. Sound Vib. 1995, 186, 311–323. [Google Scholar] [CrossRef]
- Friswell, M.I.; Garvey, S.D.; Penny, J.E.T. The convergence of the iterated IRS method. J. Sound Vib. 1998, 211, 123–132. [Google Scholar] [CrossRef]
- Qu, Z.Q.; Fu, Z.F. An iterative method for dynamic condensation of structural matrices. Mech. Syst. Signal Proc. 2000, 14, 667–678. [Google Scholar] [CrossRef]
- Li, W.M.; Hong, J.Z. New iterative method for model updating based on model reduction. Mech. Syst. Signal Proc. 2011, 25, 180–192. [Google Scholar] [CrossRef]
- Luo, K.; Liu, C.; Tian, Q.; Hu, H. An efficient model reduction method for buckling analyses of thin shells based on IGA. Comput. Meth. Appl. Mech. Eng. 2016, 309, 243–268. [Google Scholar] [CrossRef]
- Yue, Y.; Feng, L.; Benner, P. Reduced-order modeling of parametric system via interpolation of heterogeneous surrogates. Adv. Model. Simul. Eng. Sci. 2019, 6, 10. [Google Scholar] [CrossRef] [Green Version]
- Shin, H.S.; Boo, S.H. Welding simulation using a reduced order model for efficient residual stress evaluation. J. Comput. Des. Eng. 2022, 9, 1196–1213. [Google Scholar] [CrossRef]
- Rao, S.S. Mechanical Vibrations; Pearson Education, Inc.: London, UK, 2006. [Google Scholar]
- Craig, R.R.; Kurdila, A.J. Fundamentals of Structural Dynamics; Wiley: Hoboken, NJ, USA, 2006. [Google Scholar]
- Udwadia, F.E.; Kalaba, R.E. On the foundations of analytical dynamics. Int. J. Non-Linear Mech. 2002, 37, 1079–1090. [Google Scholar] [CrossRef]
- Caughey, T.K.; O’Kelly, M.E. Classical normal modes in damped linear dynamics systems. J. Appl. Mech. 1960, 32, 269–271. [Google Scholar] [CrossRef]
- Liang, Z.; Lee, G.C. Representation of damping matrix. J. Eng. Mech. 1991, 117, 1005–1020. [Google Scholar] [CrossRef]
- Xia, Y.; Lin, R. Improvement on the iterated IRS method for structural eigensolutions. J. Sound Vibr. 2004, 270, 713–727. [Google Scholar] [CrossRef]
- Boo, S.H.; Lee, P.S. An iterative algebraic dynamic condensation method and its performance. Comput. Struct. 2017, 182, 419–429. [Google Scholar] [CrossRef]
- Newmark, N.M. A method of computation for structural dynamics. J. Eng. Mech. 1959, 85, 67–94. [Google Scholar] [CrossRef]
- Rao, S.S. The Finite Element Method in Engineering, 5th ed.; Butterworth-Heinemann: Oxford, UK, 2011. [Google Scholar]
- Hughes, T.J.R. A note on the stability of Newmark’s algorithm in nonlinear structural dynamics. Int. J. Numer. Methods Eng. 1977, 11, 383–386. [Google Scholar] [CrossRef]
- Laulusa, A.; Bauchau, O.A.; Choi, J.Y.; Tan, V.B.C.; Li, L. Evaluation of some shear deformable shell elements. Int. J. Solids Struct. 2006, 43, 5033–5054. [Google Scholar] [CrossRef] [Green Version]
- Henshell, R.D.; Ong, J.H. Automatic masters for eigenvalue economization. Earthq. Eng. Struct. Dyn. 1974, 3, 375–383. [Google Scholar] [CrossRef]
- Pastor, M.; Binda, M. Modal assurance criterion. Procedia Eng. 2012, 48, 543–548. [Google Scholar] [CrossRef]
- Das, R.; Subhash, C.; Mishra, M.; Ajith, R.; Uppaluri, R. An inverse analysis of a transient 2-D conduction-radiation problem using the lattice Boltzmann method and the finite volume method coupled with the genetic algorithm. J. Quant. Spectrosc. Radiat. Transf. 2008, 109, 2060–2077. [Google Scholar] [CrossRef]




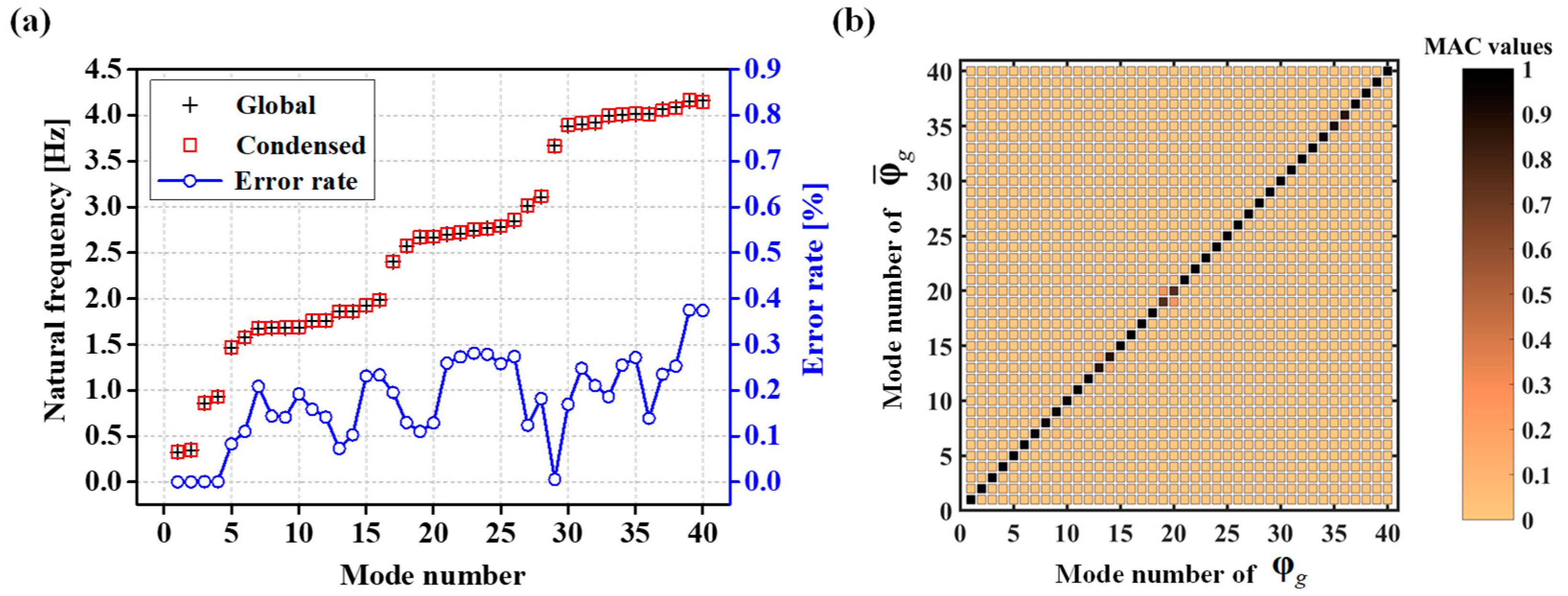


| Mode Number | Natural Frequency ω [Hz] | Error Rate ej [%] | MAC Values | |
|---|---|---|---|---|
| Global | Condensed | |||
| 39 | 4.151 | 4.166 | 0.361 | 0.998 |
| 40 | 4.162 | 4.147 | 0.360 | 0.995 |
| 23 | 2.744 | 2.752 | 0.292 | 0.999 |
| 26 | 2.848 | 2.856 | 0.281 | 1.000 |
| 35 | 4.010 | 4.021 | 0.274 | 0.989 |
| 21 | 2.700 | 2.707 | 0.259 | 0.990 |
| 22 | 2.713 | 2.720 | 0.258 | 0.989 |
| 24 | 2.768 | 2.761 | 0.253 | 0.994 |
| 25 | 2.785 | 2.792 | 0.251 | 0.994 |
| 34 | 4.001 | 4.011 | 0.250 | 0.957 |
| Analysis | Conditions | |
|---|---|---|
| Frequency response | Analysis range | 0~4.16 Hz |
| 0.01 Hz | ||
| Transient | Analysis range | 0~120 s |
| 0.05 s | ||
| Node Number | Mode Number | Resonance Response Amplitude [mm] | Error [%] | |
|---|---|---|---|---|
| Global | Condensed | |||
| #1 | 2 | 81.570 | 81.244 | 0.400 |
| 6 | 43.848 | 43.575 | 0.623 | |
| 9 | 7.646 | 7.494 | 1.988 | |
| 11 | 16.572 | 16.241 | 1.997 | |
| 15 | 13.779 | 13.333 | 3.237 | |
| #2 | 2 | 81.499 | 81.265 | 0.287 |
| 6 | 43.012 | 42.718 | 0.684 | |
| 9 | 7.432 | 7.311 | 1.628 | |
| 11 | 16.639 | 16.267 | 2.236 | |
| 15 | 13.546 | 13.029 | 3.817 | |
| Node Number | Maximum Result | Global | Condensed | Error [%] |
|---|---|---|---|---|
| #1 | Displacement [mm] | 10.652 | 10.656 | 0.038 |
| Velocity [mm/s] | 10.351 | 10.354 | 0.029 | |
| Acceleration [mm/s2] | 40.284 | 40.272 | 0.030 | |
| #2 | Displacement [mm] | 14.139 | 14.134 | 0.035 |
| Velocity [mm/s] | 13.921 | 13.914 | 0.050 | |
| Acceleration [mm/s2] | 48.849 | 48.829 | 0.041 |
| Methods | Items | Computation Time | |
|---|---|---|---|
| [Seconds] | [%] | ||
| Global | Modal analysis | 7.441 | 0.417 |
| Frequency response analysis | 731.351 | 41.014 | |
| Transient analysis | 1044.403 | 58.569 | |
| Total | 1783.195 | 100.000 | |
| Condensed | Calculating of the condensed matrices | 400.679 | 22.470 |
| Modal analysis | 0.177 | 0.010 | |
| Frequency response analysis | 10.078 | 0.565 | |
| Transient analysis | 1.599 | 0.090 | |
| Total | 412.533 | 23.134 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ko, D.-H.; Boo, S.-H. Efficient Structural Dynamic Analysis Using Condensed Finite Element Matrices and Its Application to a Stiffened Plate. J. Mar. Sci. Eng. 2022, 10, 1958. https://doi.org/10.3390/jmse10121958
Ko D-H, Boo S-H. Efficient Structural Dynamic Analysis Using Condensed Finite Element Matrices and Its Application to a Stiffened Plate. Journal of Marine Science and Engineering. 2022; 10(12):1958. https://doi.org/10.3390/jmse10121958
Chicago/Turabian StyleKo, Do-Hyun, and Seung-Hwan Boo. 2022. "Efficient Structural Dynamic Analysis Using Condensed Finite Element Matrices and Its Application to a Stiffened Plate" Journal of Marine Science and Engineering 10, no. 12: 1958. https://doi.org/10.3390/jmse10121958





