Development of Three-Dimensional Scour below Pipelines in Regular Waves
Abstract
:1. Introduction
- Revealing the elementary scour development mechanism by observing sediment movement under the pipeline;
- Measuring the scour propagation rate based on direct observation;
- Analyzing the effects of the pipeline embedment ratio and the KC number on the scour propagation rate.
2. Experimental Setup
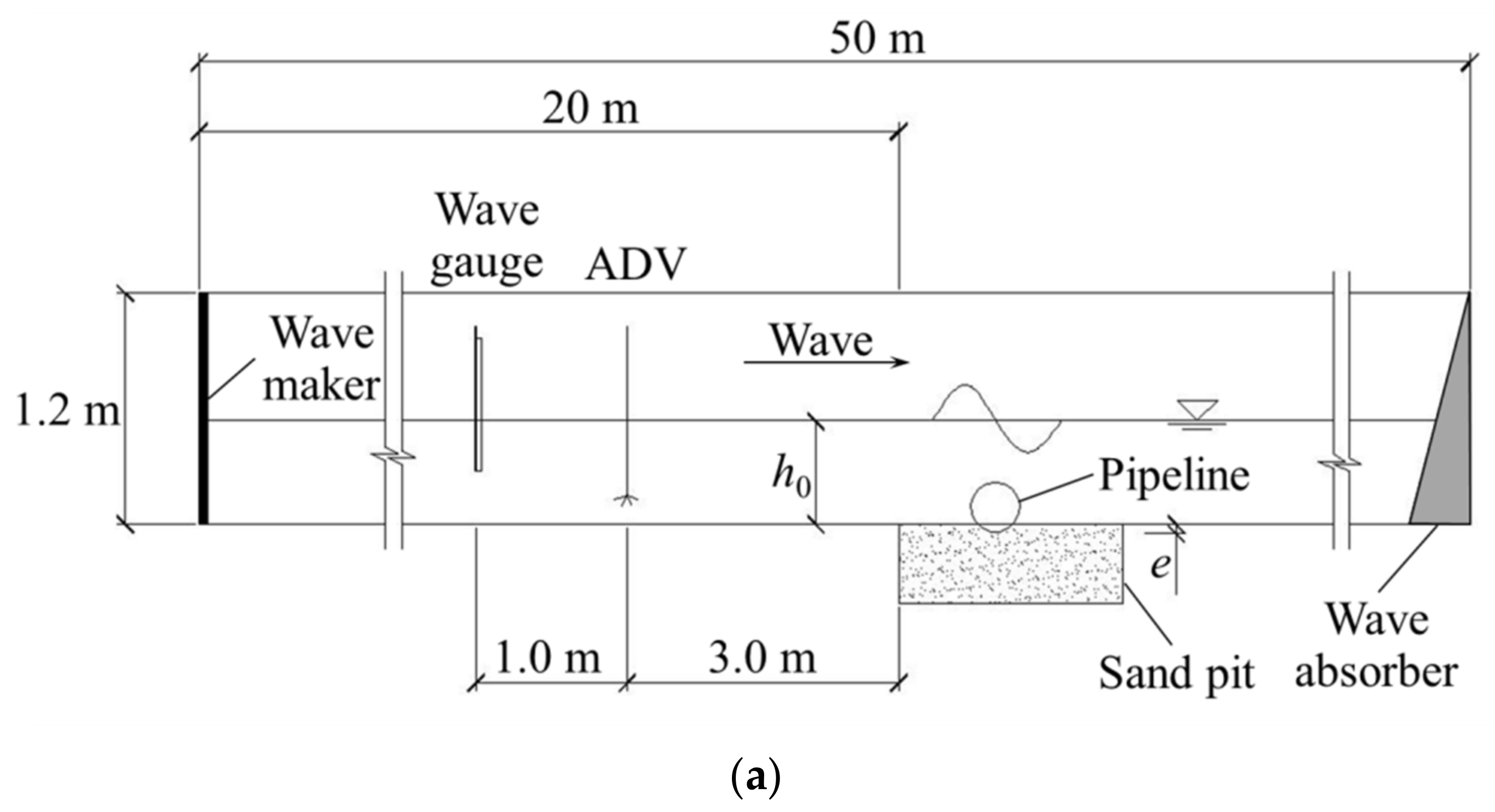
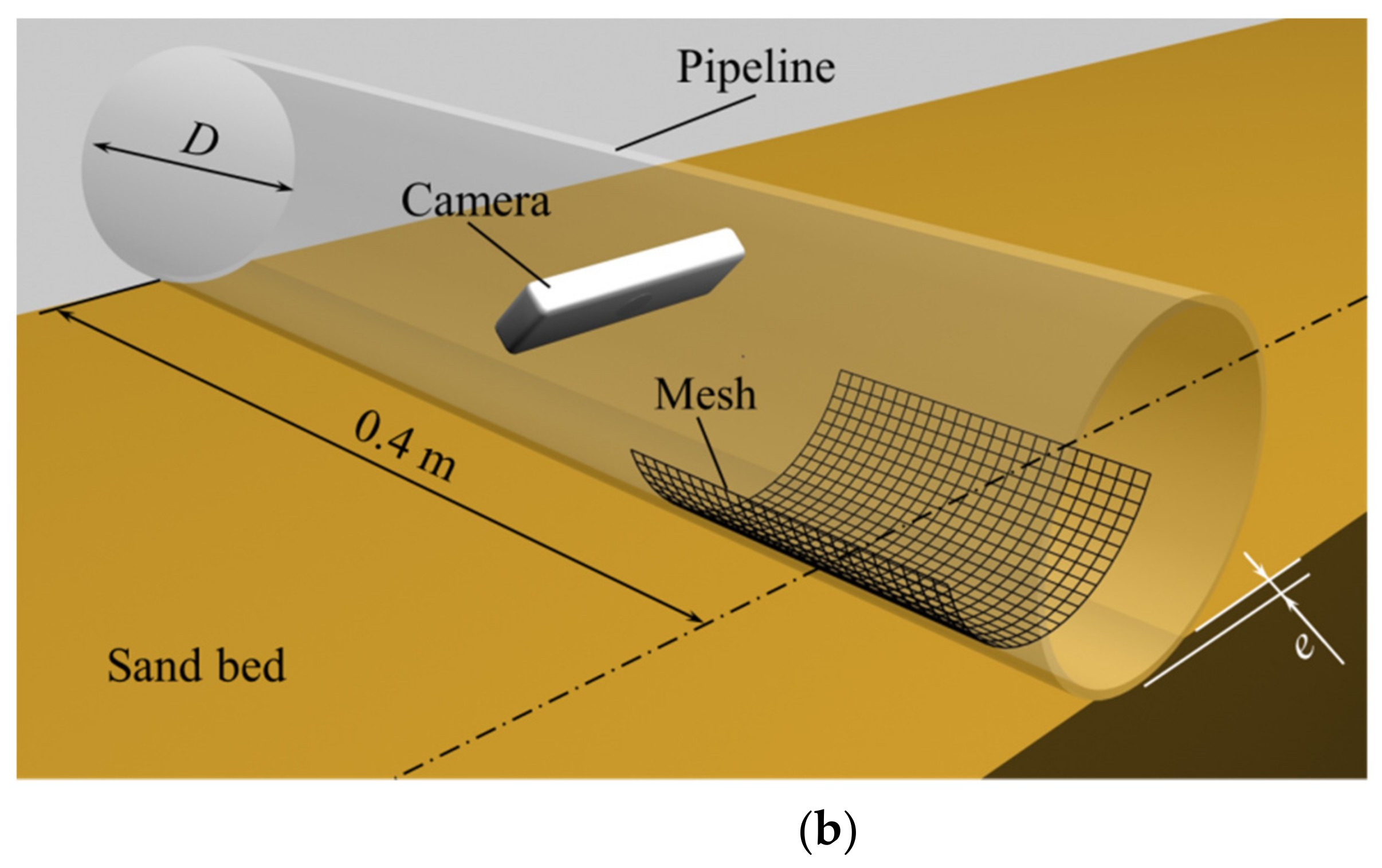
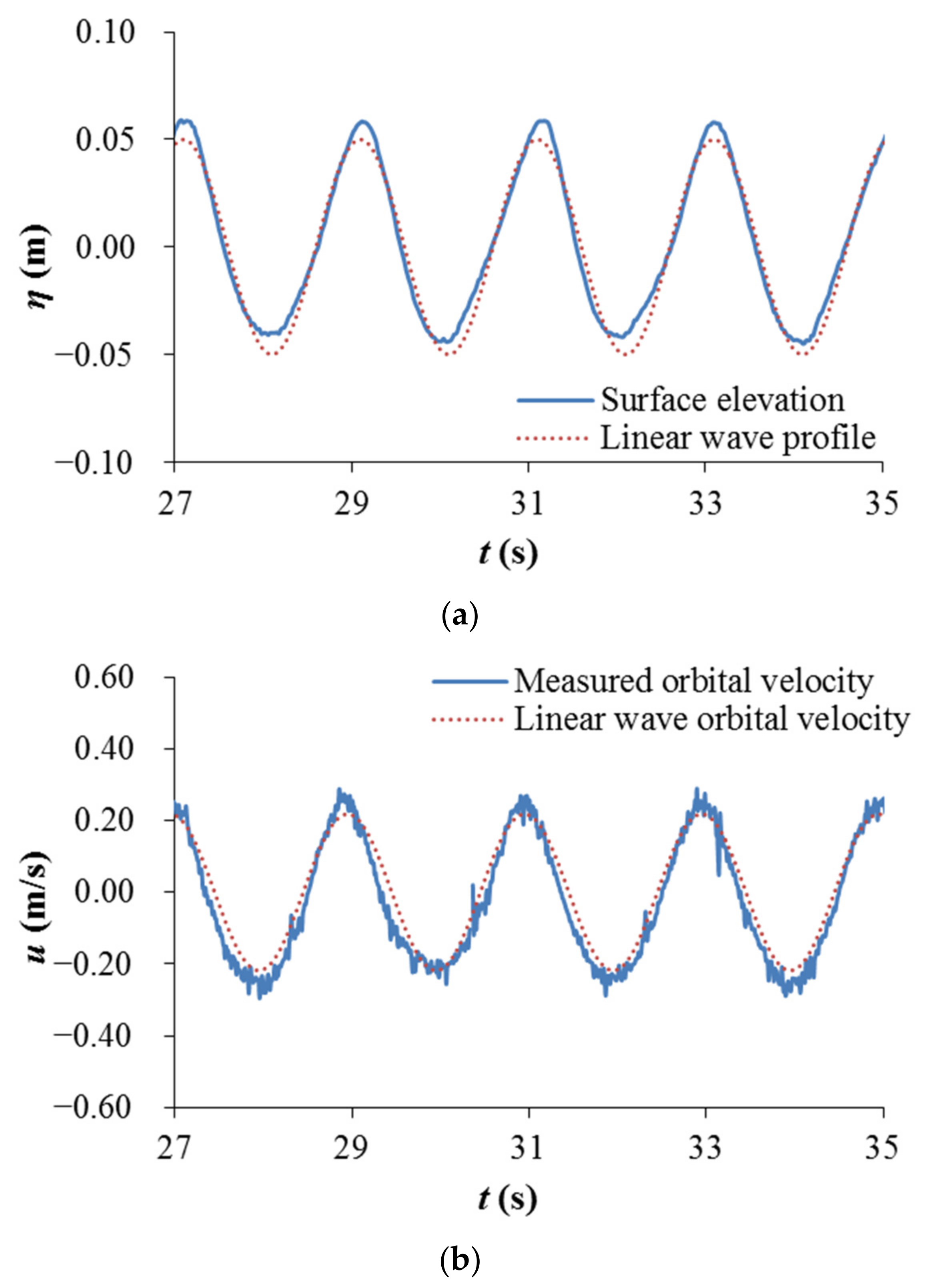
2.1. Experimental Apparatus
2.2. Dimensional Analysis of Effects on Scour Hole Propagation Rate
2.3. Experimental Cases
3. Scour Hole Extension Process in a Wave Period
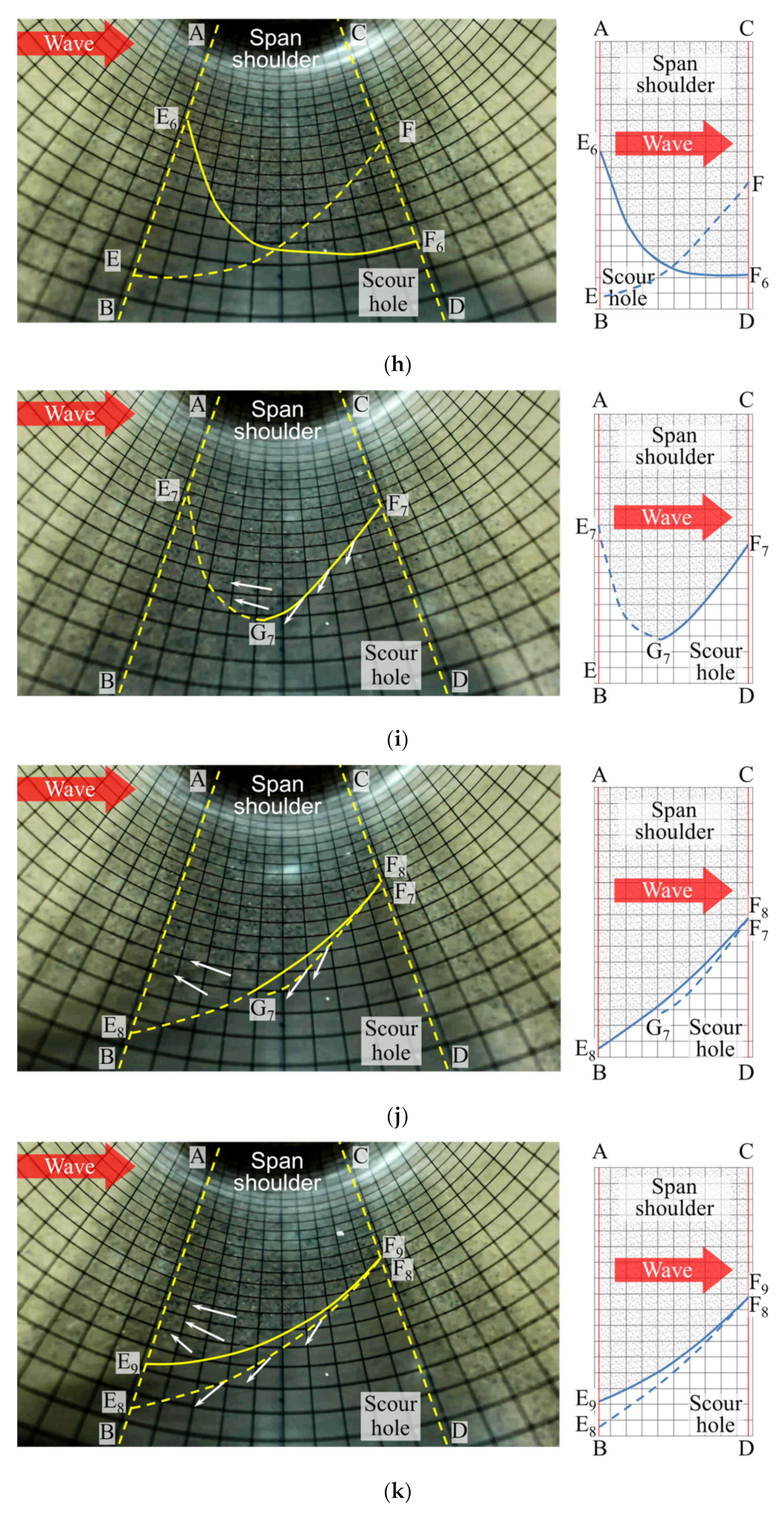
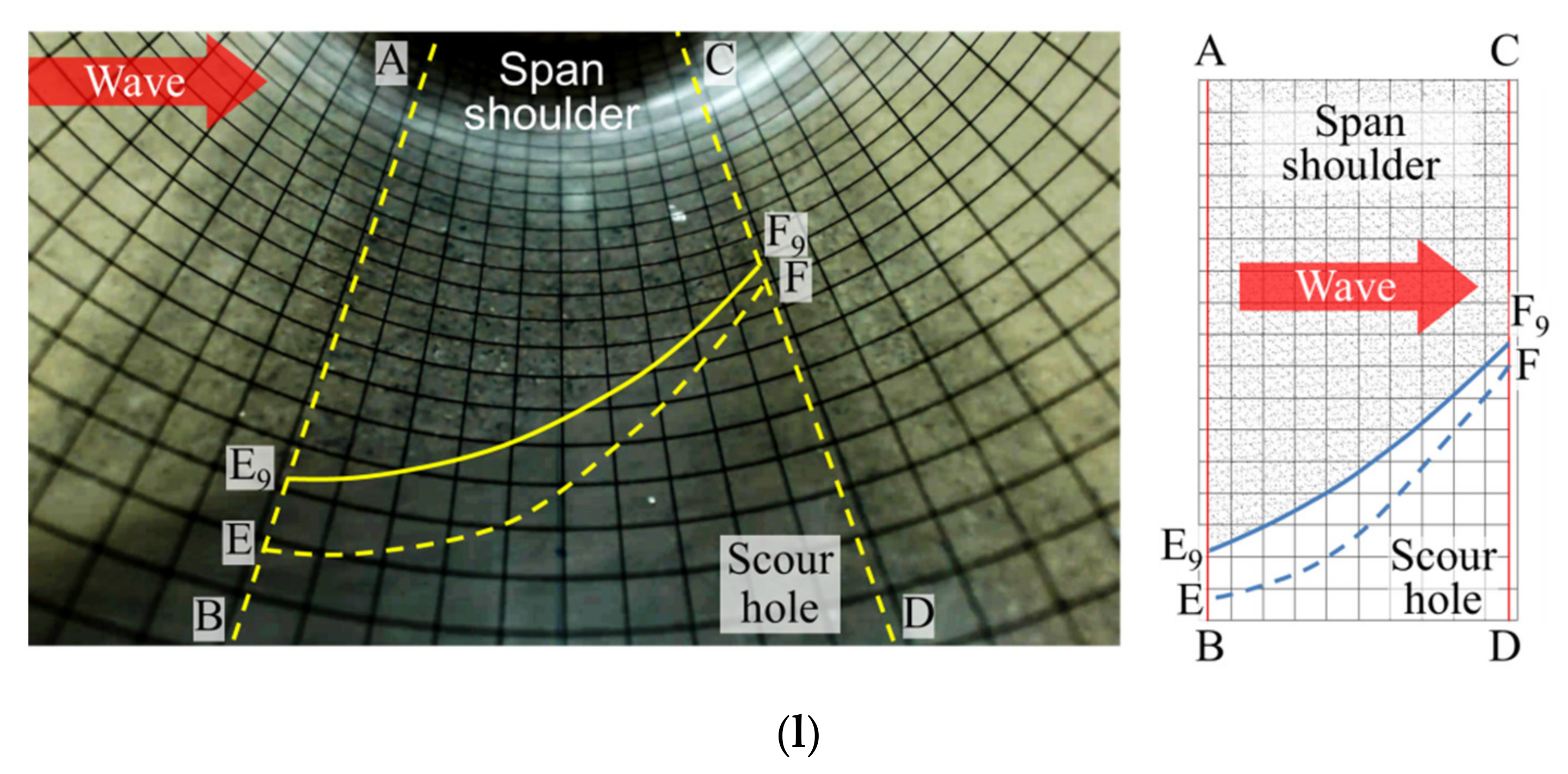
3.1. Visualization Results
3.2. Discussion on the Scour Hole Evolution Process
4. Parametric Effects on Scour Propagation Rate
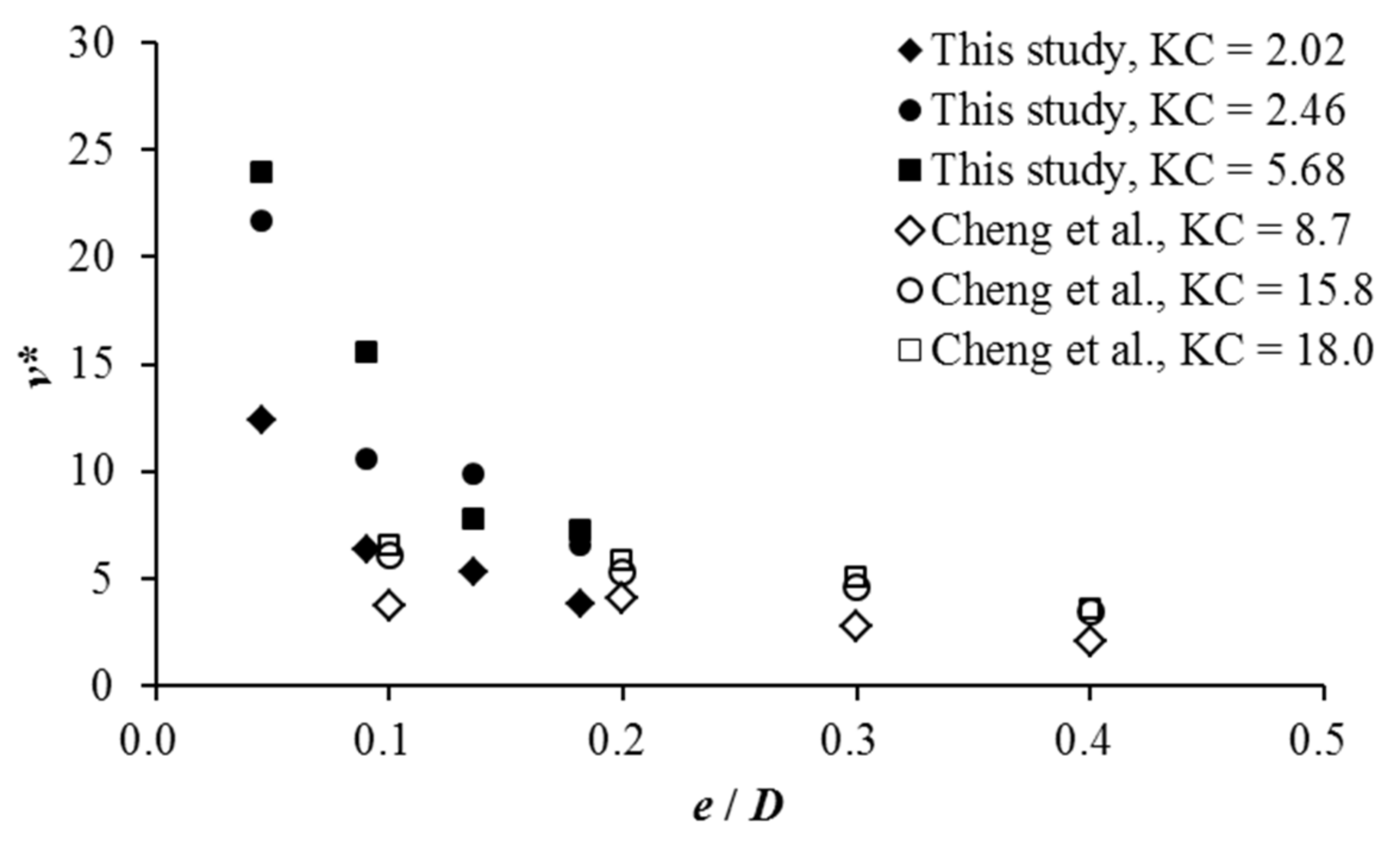
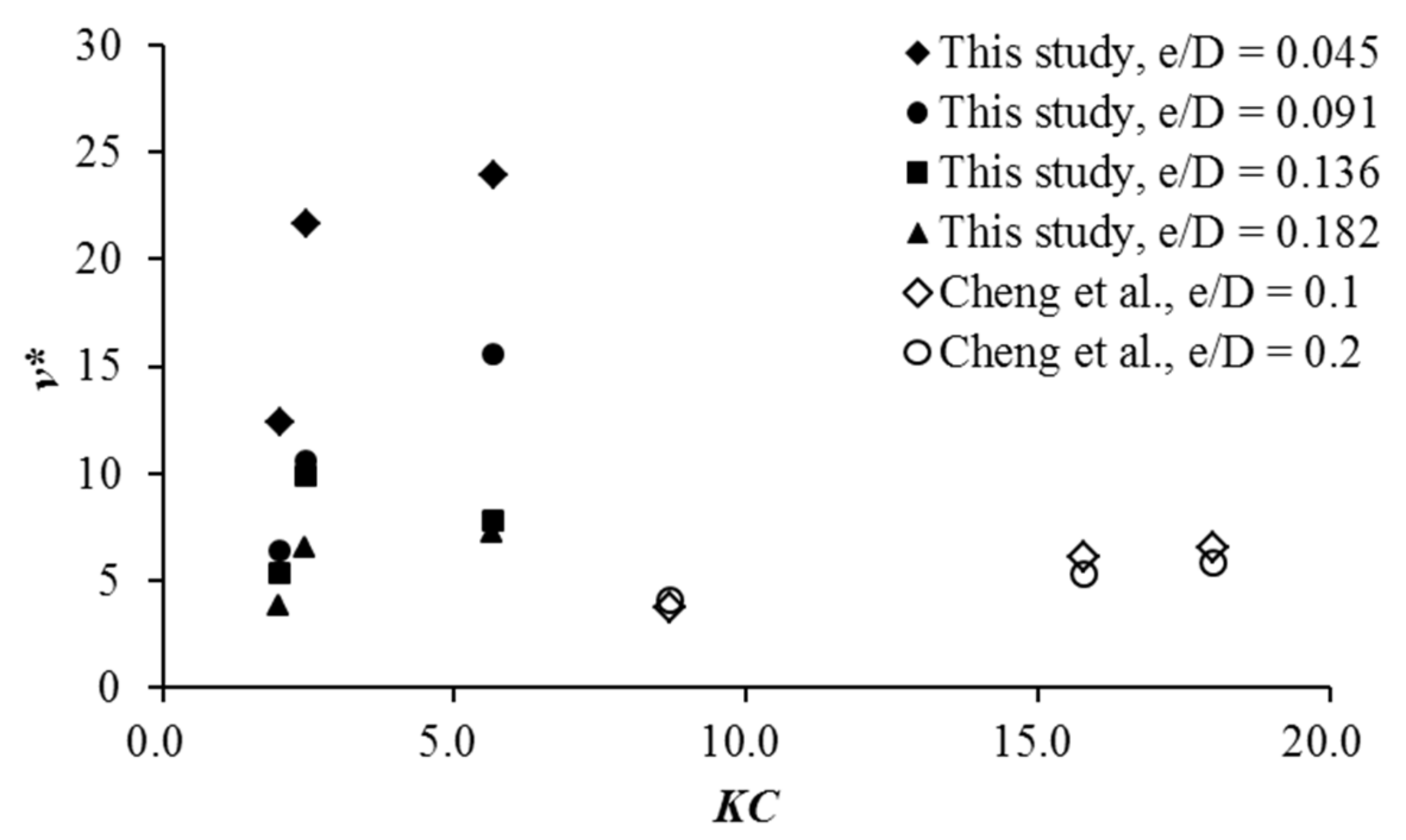
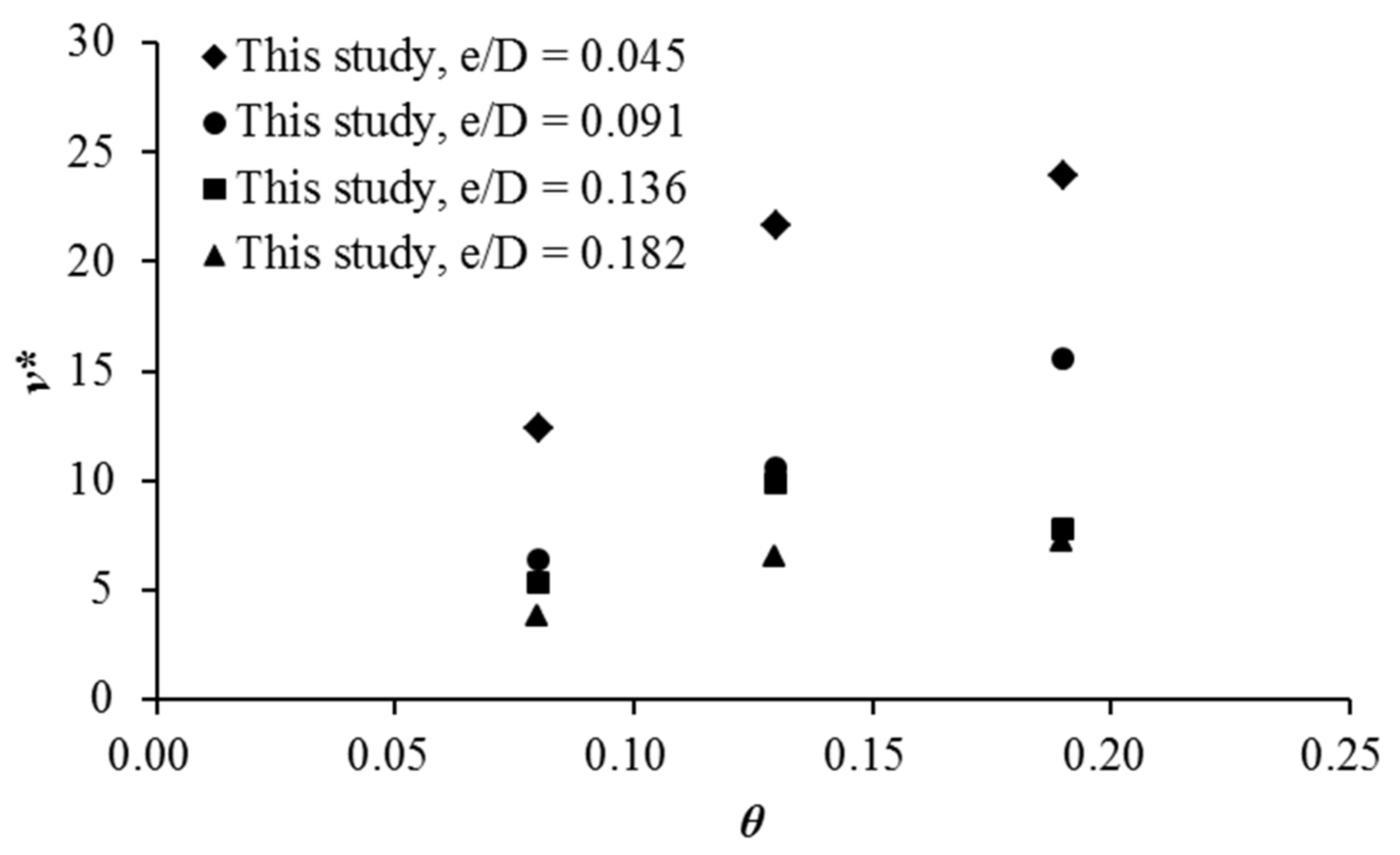
4.1. Effect of Pipeline Embedment
4.2. Effects of KC Number and Shields Number
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chiew, Y.M. Mechanics of local scour around submarine pipelines. J. Hydraul. Eng. 1990, 116, 515–529. [Google Scholar] [CrossRef]
- Sumer, B.M.; Truelsen, C.; Sichmann, T.; Fredsøe, J. Onset of scour below pipelines and self-burial. Coast. Eng. 2001, 42, 313–335. [Google Scholar] [CrossRef]
- Chiew, Y.M. Prediction of maximum scour depth at submarine pipelines. J. Hydraul. Eng. 1991, 117, 452–466. [Google Scholar] [CrossRef]
- Dogan, M.; Aksoy, A.O.; Arisoy, Y.; Guney, M.S.; Abdi, V. Experimental investigation of the equilibrium scour depth below submerged pipes both in live-bed and clear-water regimes under the wave effect. Appl. Ocean Res. 2018, 80, 49–56. [Google Scholar] [CrossRef]
- Zhang, Z.; Guo, Y.; Yang, Y.; Shi, B.; Wu, X. Scale model experiment on local scour around submarine pipelines under bidirectional tidal currents. J. Mar. Sci. Eng. 2021, 9, 1421. [Google Scholar] [CrossRef]
- Zhang, Q.; Draper, S.; Cheng, L. Scour below a subsea pipeline in time varying flow conditions. Appl. Ocean Res. 2016, 55, 151–162. [Google Scholar] [CrossRef] [Green Version]
- Zang, Z.; Tang, G.; Cheng, L. Time scale of scour below submarine pipeline under combined waves and currents with oblique incident angle. In ASME 2017, Proceedings of the 36th International Conference on Ocean, Offshore and Arctic Engineering, Trondheim, Norway, 25–30 June 2017; ASME: New York, NY, USA, 2017; p. V009T10A019. [Google Scholar]
- Myrhaug, D.; Ong, M.C. Time scale for scour beneath pipelines due to long-crested and short-crested nonlinear random waves plus current. J. Mar. Sci. Eng. 2021, 9, 114. [Google Scholar] [CrossRef]
- Liang, D.; Cheng, L.; Li, F. Numerical modeling of flow and scour below a pipeline in currents: Part II. Scour simulation. Coast. Eng. 2005, 52, 43–62. [Google Scholar] [CrossRef]
- Zang, Z.; Cheng, L.; Zhao, M.; Liang, D.; Teng, B. A numerical model for onset of scour below offshore pipelines. Coast. Eng. 2009, 56, 458–466. [Google Scholar] [CrossRef]
- Huang, P.; Meng, X.; Dong, H.; Chong, L. Numerical modeling of submarine pipeline scouring under tropical storms. Water 2021, 13, 1425. [Google Scholar] [CrossRef]
- Huang, J.; Yin, G.; Ong, M.C.; Myrhaug, D.; Jia, X. Numerical investigation of scour beneath pipelines subjected to an oscillatory flow condition. J. Mar. Sci. Eng. 2021, 9, 1102. [Google Scholar] [CrossRef]
- Cheng, L.; Yeow, K.; Zhang, Z.; Teng, B. Three-dimensional scour below offshore pipelines in steady currents. Coast. Eng. 2009, 56, 577–590. [Google Scholar] [CrossRef]
- Wu, Y.; Chiew, Y.M. Mechanics of pipeline scour propagation in the spanwise direction. J. Waterw. Port Coast. Ocean Eng. 2014, 141, 04014045. [Google Scholar] [CrossRef]
- Wu, Y.; Chiew, Y.M. Three-dimensional scour at submarine pipelines. J. Hydraul. Eng. 2012, 138, 788–795. [Google Scholar] [CrossRef]
- Draper, S.; Yao, W.; Cheng, L.; Tom, J.; An, H. Estimating the rate of scour propagation along a submarine pipeline in time-varying currents and in fine grained sediment. In ASME 2018, Proceedings of the 37th International Conference on Ocean, Offshore and Arctic Engineering, Madrid, Spain, 17–22 June 2018; ASME: New York, NY, USA, 2018; p. V005T04A019. [Google Scholar]
- Wu, Y.; Chiew, Y.M. Mechanics of three-dimensional pipeline scour in unidirectional steady current. J. Pipeline Syst. Eng. Pract. 2013, 4, 3–10. [Google Scholar] [CrossRef]
- Zhu, Y.; Xie, L.; Su, T.C. Visualization tests on scour rates below pipelines in steady currents. J. Hydraul. Eng. 2019, 145, 04019005. [Google Scholar] [CrossRef]
- Cheng, L.; Yeow, K.; Zang, Z.; Li, F. 3D scour below pipelines under waves and combined waves and currents. Coast. Eng. 2014, 83, 137–149. [Google Scholar] [CrossRef] [Green Version]
- Leckie, S.H.; Draper, S.; White, D.J.; Cheng, L.; Fogliani, A. Lifelong embedment and spanning of a pipeline on a mobile seabed. Coast. Eng. 2015, 95, 130–146. [Google Scholar] [CrossRef]
- Leckie, S.H.; Mohr, H.; Draper, S.; McLean, D.L.; White, D.J.; Cheng, L. Sedimentation-induced burial of subsea pipelines: Observations from field data and laboratory experiments. Coast. Eng. 2016, 114, 137–158. [Google Scholar] [CrossRef]
- Fredsøe, J. Pipeline-seabed interaction. J. Waterw. Port Coast. Ocean Eng. 2016, 142, 03116002. [Google Scholar] [CrossRef] [Green Version]
- Xie, L.; Zhu, Y.; Su, T.C. Visualization tests on variation of scour front under a pipeline in steady currents. J. Mar. Sci. Eng. 2019, 7, 345. [Google Scholar] [CrossRef] [Green Version]
- Saha, R.; Lee, S.O.; Hong, S.H. A Comprehensive Method of Calculating Maximum Bridge Scour Depth. Water 2018, 10, 1572. [Google Scholar] [CrossRef] [Green Version]
- Cui, Y.; Lam, W.H.; Zhang, T.; Sun, C.; Robinson, D.; Hamill, G. Temporal model for ship twin-propeller jet induced sandbed scour. J. Mar. Sci. Eng. 2019, 7, 339. [Google Scholar] [CrossRef] [Green Version]
- Arboleda Chavez, C.E.; Stratigaki, V.; Wu, M.; Troch, P.; Schendel, A.; Welzel, M.; Villanueva, R.; Schlurmann, T.; De Vos, L.; Kisacik, D.; et al. Large-scale experiments to improve monopile scour protection design adapted to climate change—the PROTEUS Project. Energies 2019, 12, 1709. [Google Scholar] [CrossRef] [Green Version]
- Qi, W.; Gao, F. Equilibrium scour depth at offshore monopile foundation in combined waves and current. Sci. China Tech. Sci. 2014, 57, 1030–1039. [Google Scholar] [CrossRef] [Green Version]
- An, H.; Cheng, L.; Zhao, M.; Tang, G.; Draper, S. Detecting scour and liquefaction using OBS sensors. In Scour and Erosion, Proceedings of the 8th International Conference on Scour and Erosion, Oxford, UK, 12–15 September 2016; Harris, J., Whitehouse, R., Moxon, S., Eds.; CRC Press: Boca Raton, FL, USA, 2016; pp. 535–542. [Google Scholar]
- Sumer, B.M.; Hatipoglu, F.; Fredsøe, J. Wave scour around a pile in sand, medium dense, and dense silt. J. Waterw. Port Coast. Ocean Eng. 2007, 133, 14–27. [Google Scholar] [CrossRef]
- Zhu, Y.; Xie, L.; Liang, X. Scour patterns below pipelines and scour hole expansion rate. In Scour and Erosion, Proceedings of the 8th International Conference on Scour and Erosion, Oxford, UK, 12–15 September 2016; Harris, J., Whitehouse, R., Moxon, S., Eds.; CRC Press: Boca Raton, FL, USA, 2016; pp. 387–394. [Google Scholar]
- Raaijmakers, Q.; Rudolph, D. Time-dependent scour development under combined current and waves conditions—Laboratory experiments with only monitoring technique. In Proceedings of the 4th International Conference on Scour and Erosion, Tokyo, Japan, 5–7 November 2008. [Google Scholar]
- Schendel, A.; Welzel, M.; Schlurmann, T.; Hsu, T.W. Scour around a monopile induced by directionally spread irregular waves in combination with oblique currents. Coast. Eng. 2020, 161, 103751. [Google Scholar] [CrossRef]
- Soulsby, R. Dynamics of Marine Sands: A Manual for Practical Applications; Thomas Telford: London, UK, 1997. [Google Scholar]
- Zhu, Y.; Xie, L.; Wong, T.-M.; Su, T.-C. Visualization of the onset of scour under a pipeline in waves. Appl. Sci. 2020, 10, 2994. [Google Scholar] [CrossRef]
- Shen, W.; Griffiths, T.; Zan, Z.; Leggoe, J. Shear stress amplification around subsea pipelines: Part 3, 3D study of spanning pipelines. In Scour and Erosion: Proceedings of the 7th International Conference on Scour and Erosion, Perth, Australia, 2–4 December 2014; Cheng, L., Draper, S., An, H., Eds.; CRC Press: Boca Raton, FL, USA, 2014; pp. 325–335. [Google Scholar]
| Case | e/D | H (m) | T (s) | Um (m/s) | KC | θ |
|---|---|---|---|---|---|---|
| 1 | 0.045 | 0.05 | 1.5 | 0.148 | 2.02 | 0.08 |
| 2 | 0.091 | 0.05 | 1.5 | 0.148 | 2.02 | 0.08 |
| 3 | 0.136 | 0.05 | 1.5 | 0.148 | 2.02 | 0.08 |
| 4 | 0.182 | 0.05 | 1.5 | 0.148 | 2.02 | 0.08 |
| 5 | 0.045 | 0.08 | 1.3 | 0.208 | 2.46 | 0.13 |
| 6 | 0.091 | 0.08 | 1.3 | 0.208 | 2.46 | 0.13 |
| 7 | 0.136 | 0.08 | 1.3 | 0.208 | 2.46 | 0.13 |
| 8 | 0.182 | 0.08 | 1.3 | 0.208 | 2.46 | 0.13 |
| 9 | 0.045 | 0.10 | 2.0 | 0.312 | 5.68 | 0.19 |
| 10 | 0.091 | 0.10 | 2.0 | 0.312 | 5.68 | 0.19 |
| 11 | 0.136 | 0.10 | 2.0 | 0.312 | 5.68 | 0.19 |
| 12 | 0.182 | 0.10 | 2.0 | 0.312 | 5.68 | 0.19 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, Y.; Xie, L.; Wong, T.; Su, T.-C. Development of Three-Dimensional Scour below Pipelines in Regular Waves. J. Mar. Sci. Eng. 2022, 10, 124. https://doi.org/10.3390/jmse10020124
Zhu Y, Xie L, Wong T, Su T-C. Development of Three-Dimensional Scour below Pipelines in Regular Waves. Journal of Marine Science and Engineering. 2022; 10(2):124. https://doi.org/10.3390/jmse10020124
Chicago/Turabian StyleZhu, Yehui, Liquan Xie, Tsunming Wong, and Tsung-Chow Su. 2022. "Development of Three-Dimensional Scour below Pipelines in Regular Waves" Journal of Marine Science and Engineering 10, no. 2: 124. https://doi.org/10.3390/jmse10020124
APA StyleZhu, Y., Xie, L., Wong, T., & Su, T.-C. (2022). Development of Three-Dimensional Scour below Pipelines in Regular Waves. Journal of Marine Science and Engineering, 10(2), 124. https://doi.org/10.3390/jmse10020124







