The Impact of Typhoon Intensity on Wave Height and Storm Surge in the Northern East China Sea: A Comparative Case Study of Typhoon Muifa and Typhoon Lekima
Abstract
:1. Introduction
2. Data and Methodology
2.1. Model Description
2.1.1. SWAN
2.1.2. ADCIRC
2.1.3. The Coupled Model
2.2. Model Setup
2.3. Experimental Design
2.3.1. Maximum Wind Speed of Typhoons
2.3.2. The Radius of Maximum Wind
2.3.3. The Typhoon Translation Speed
3. Results
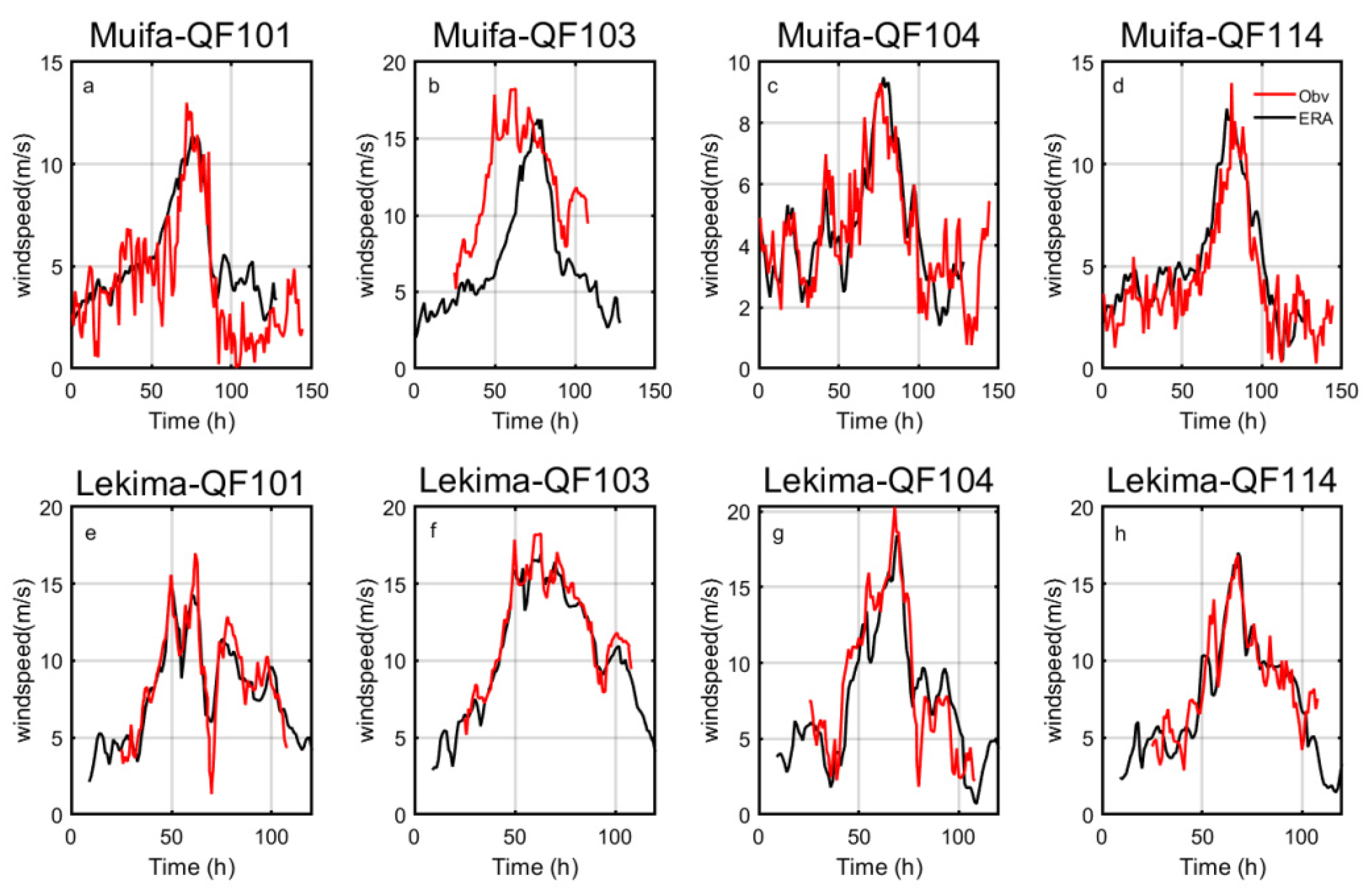
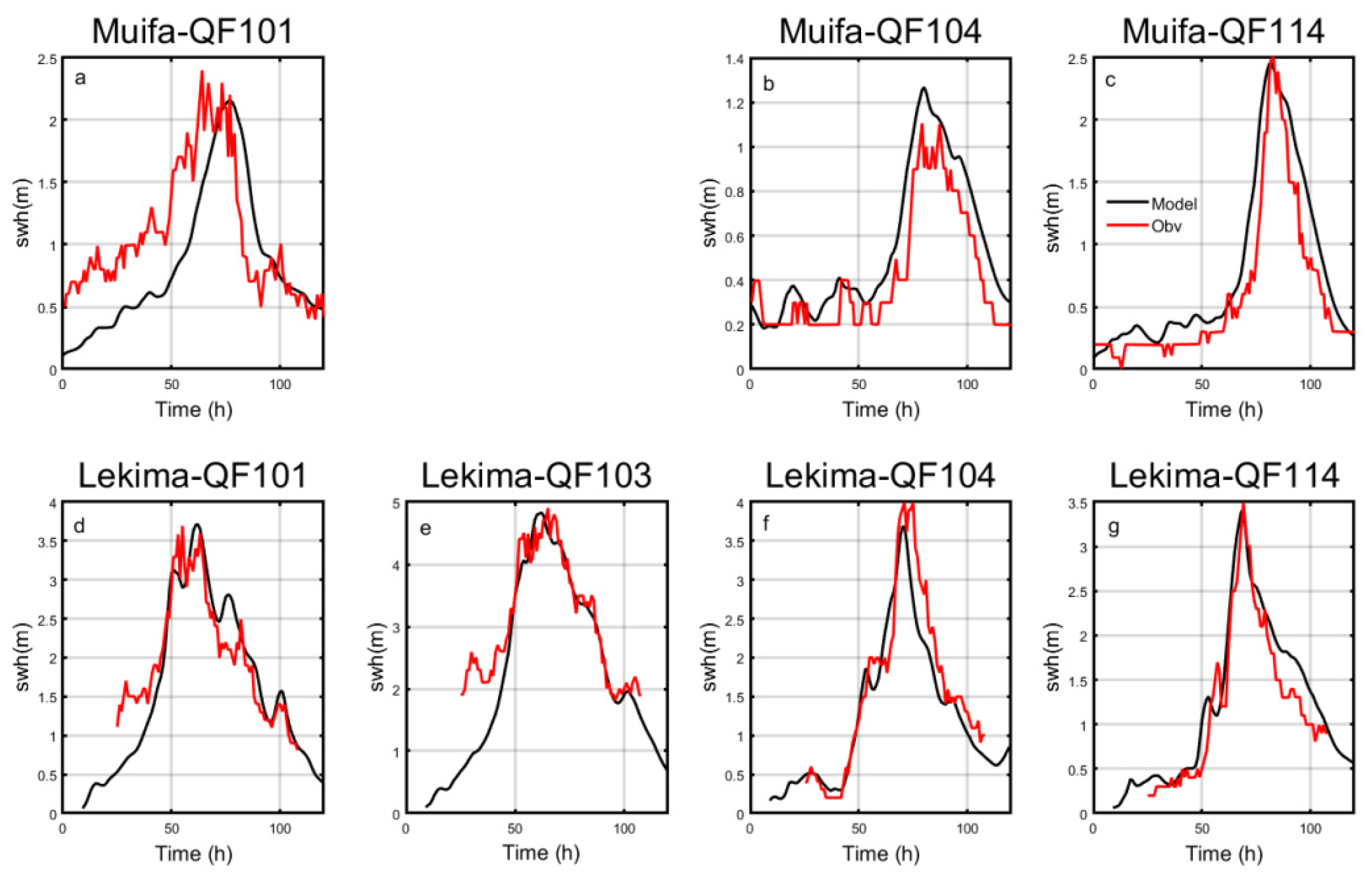
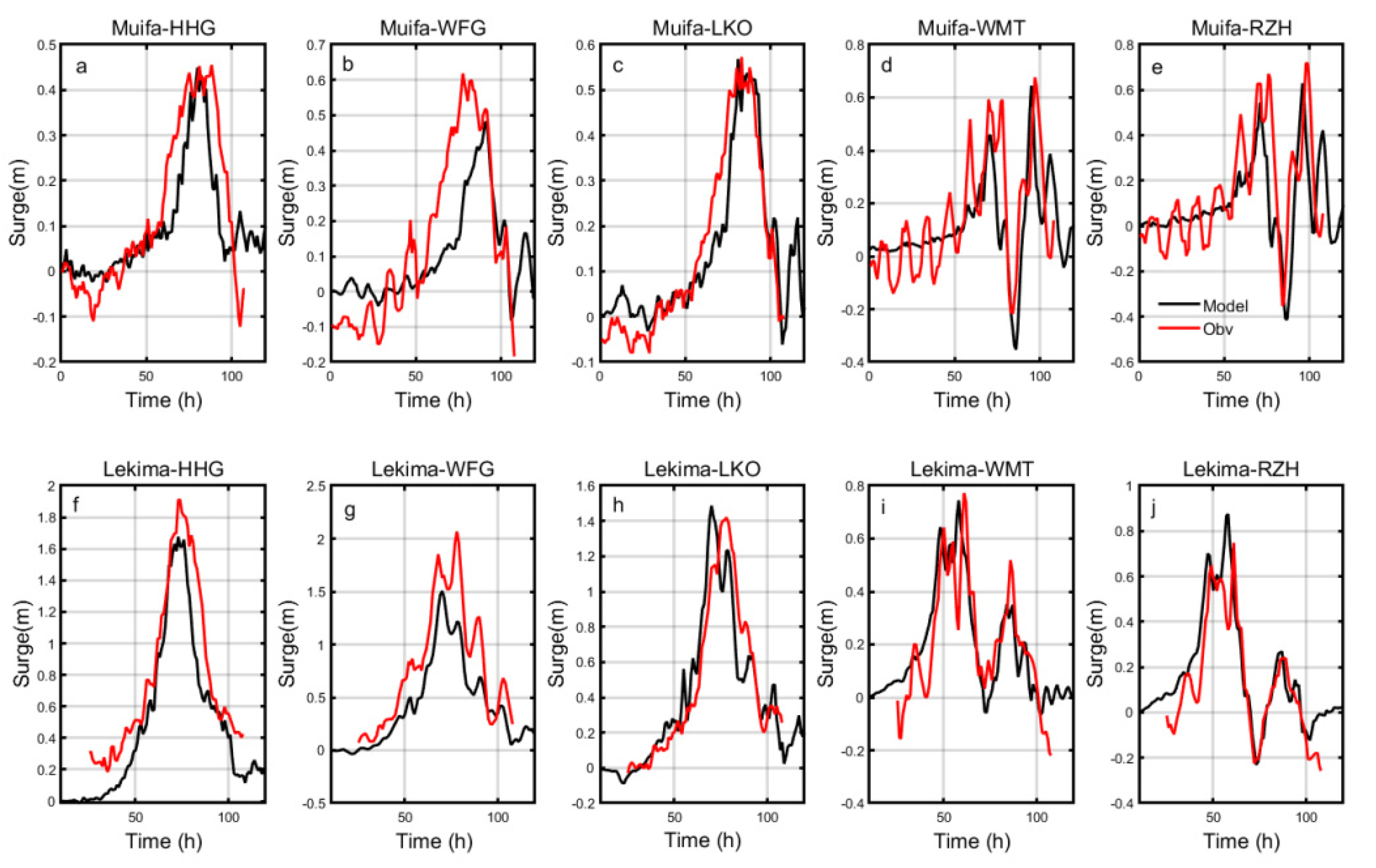
3.1. Model Validation
3.2. Maximum Wind Speed
3.3. Radius of Maximum Wind
3.4. Translation Speed
4. Discussion
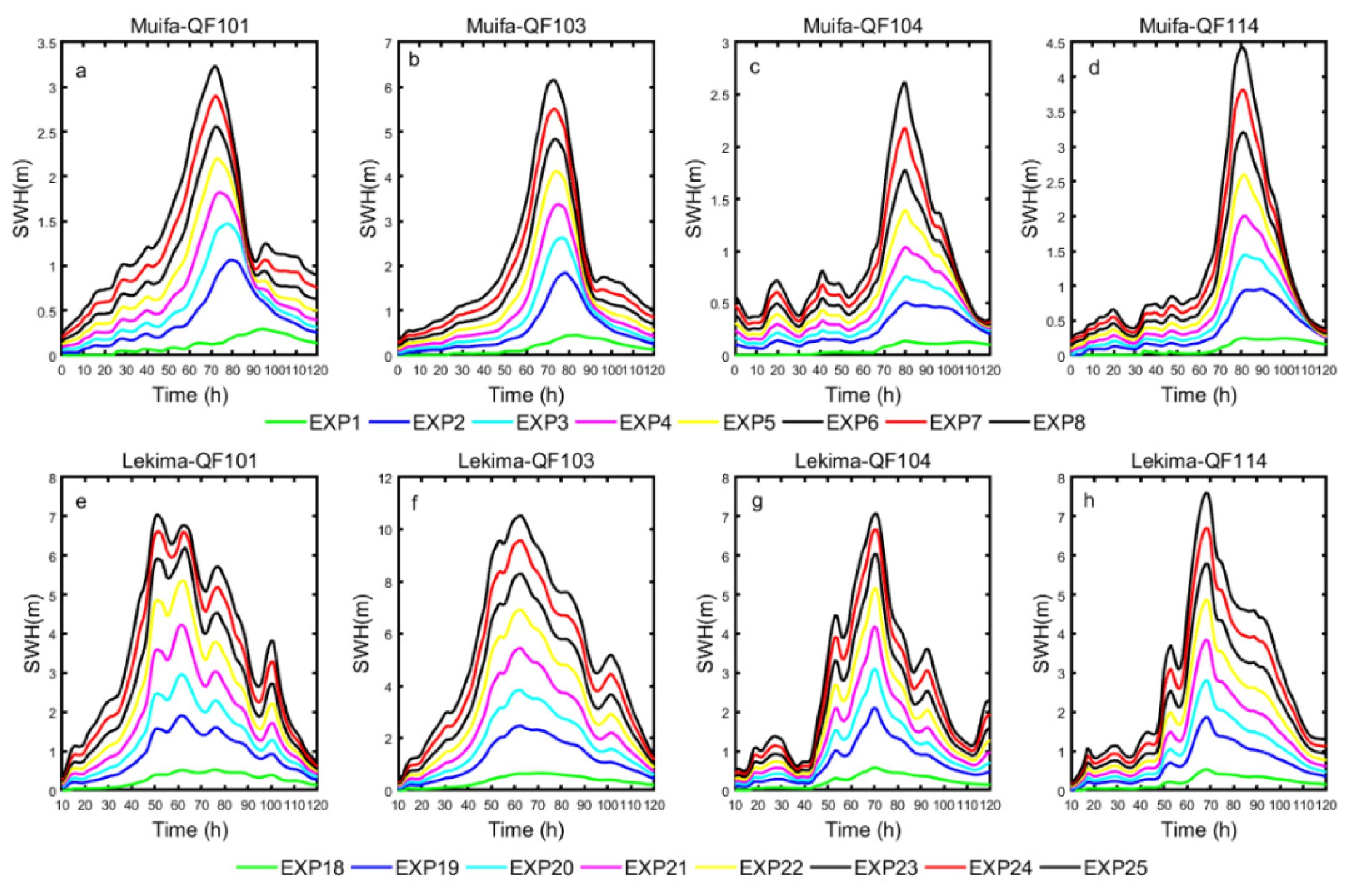
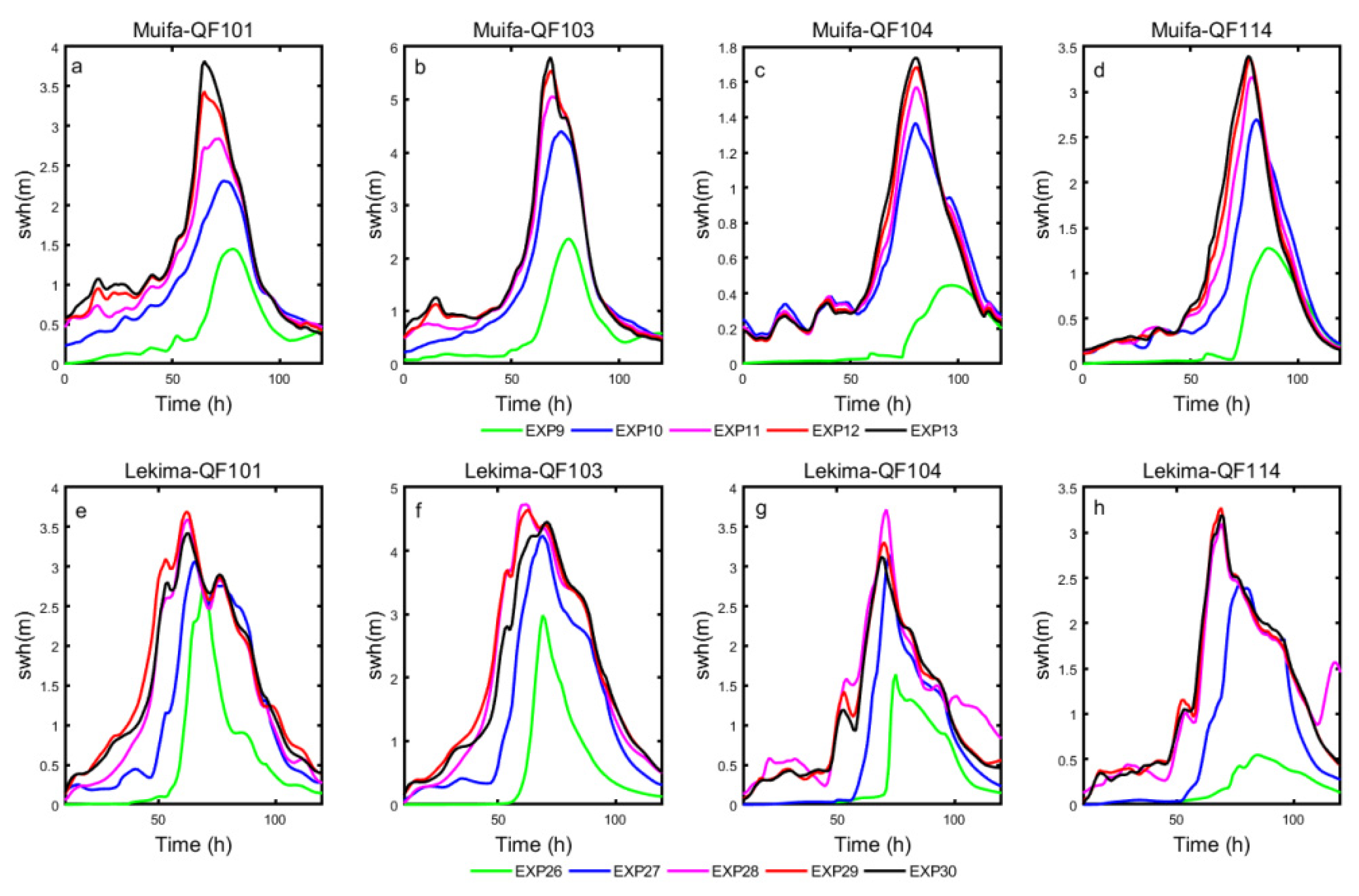
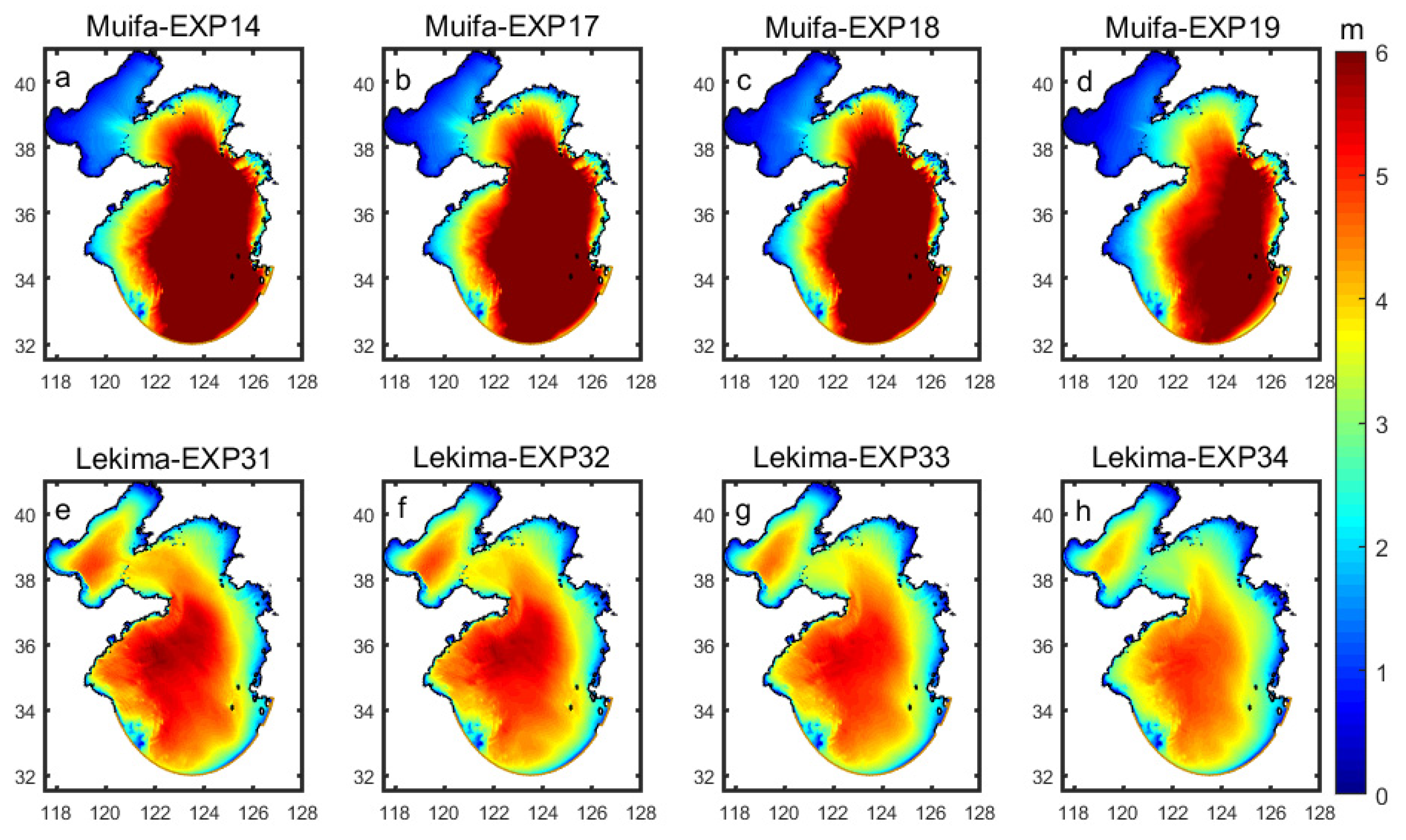
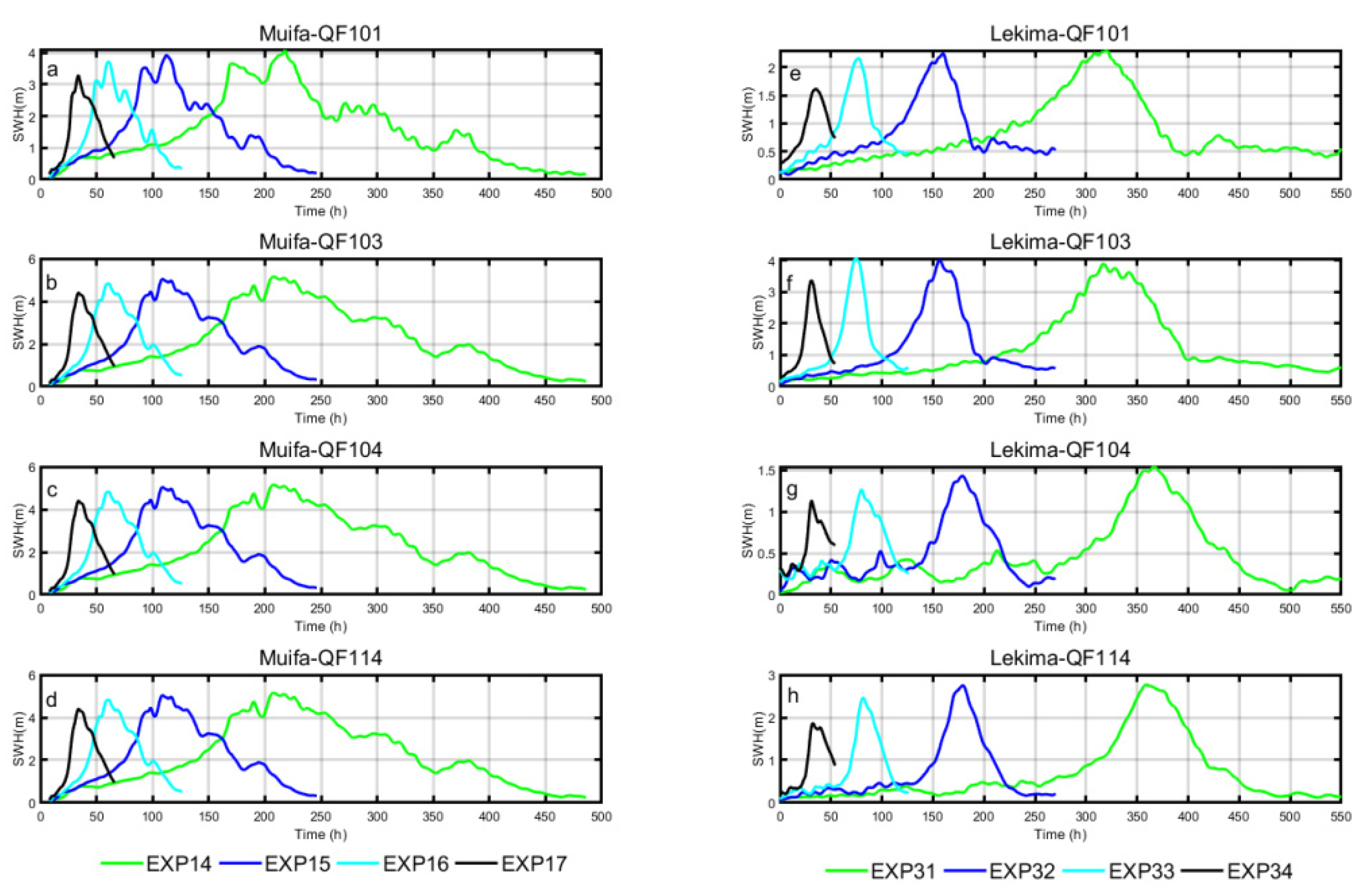
4.1. The Impacts of Typhoon Parameters on Significant Wave Height
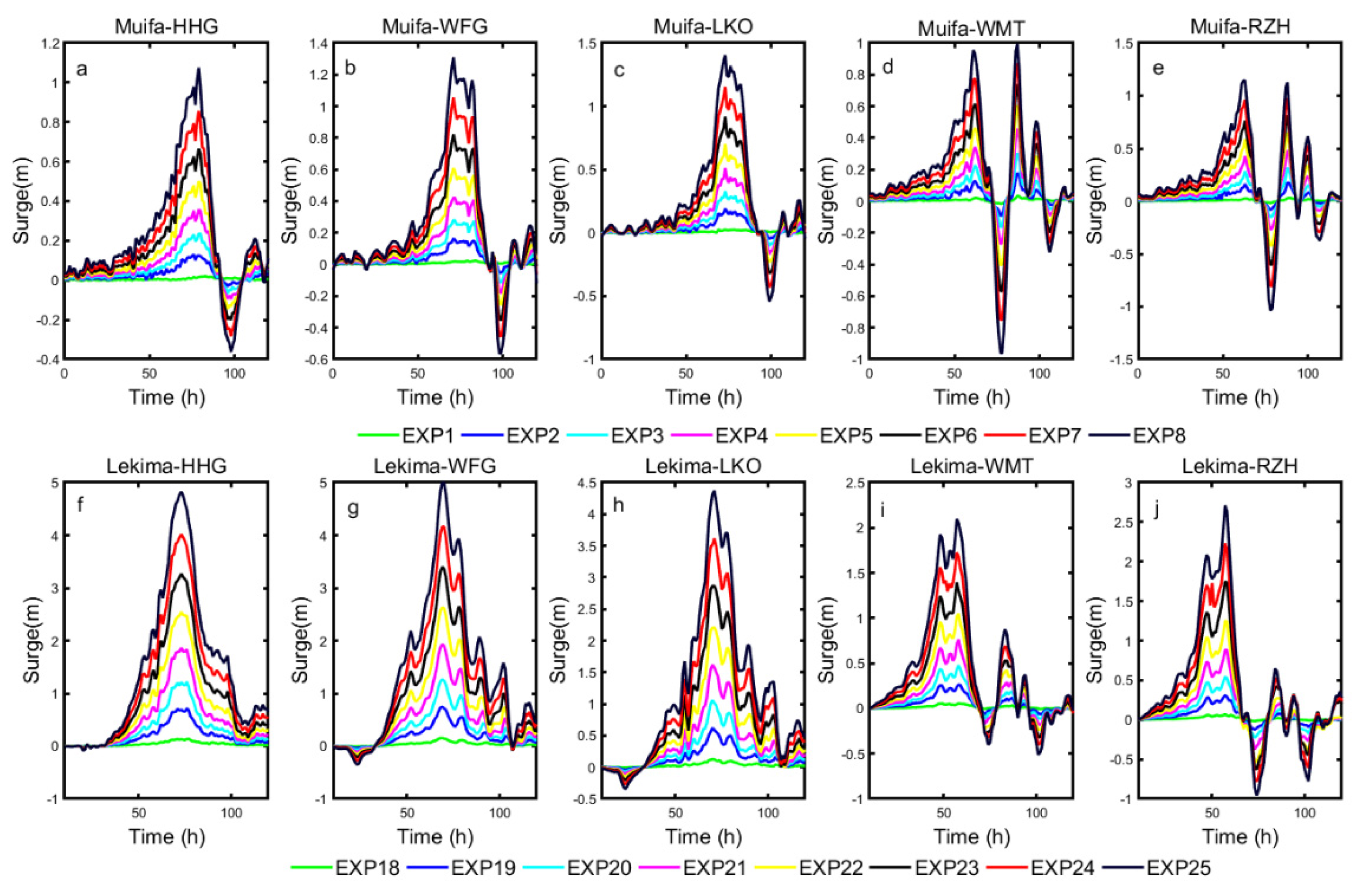
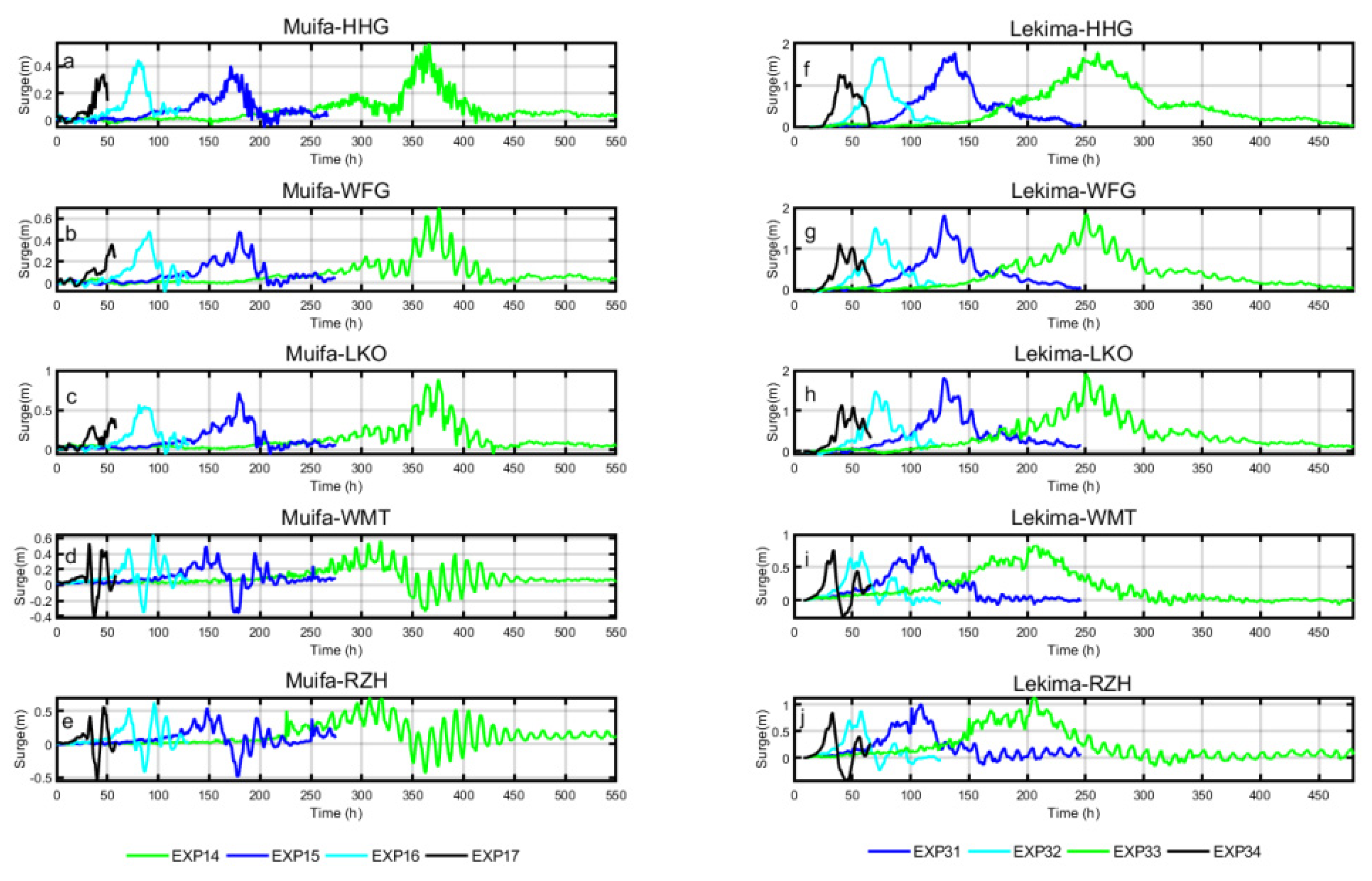
4.2. The Impact of Typhoon Parameters on Storm Surge
4.3. A Comparative Study of Typhoons Muifa and Typhoon Lekima
4.4. Resonance of the Storm Surge
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chan, J.C.L.; Shi, J.-E. Long-term trends and interannual variability in tropical cyclone activity over the western North Pacific. Geophys. Res. Lett. 1996, 23, 2765–2767. [Google Scholar] [CrossRef]
- You, S.H.; Seo, J.-W. Storm surge prediction using an artificial neural network model and cluster analysis. Nat. Hazards 2009, 51, 97–114. [Google Scholar] [CrossRef]
- Yang, Z.; Wang, T.; Leung, R.; Hibbard, K.; Janetos, T.; Kraucunas, I.; Rice, J.; Preston, B.; Wilbanks, T. A modeling study of coastal inundation induced by storm surge, sea-level rise, and subsidence in the Gulf of Mexico. Nat. Hazards 2013, 71, 1771–1794. [Google Scholar] [CrossRef]
- Xu, J.; Zhang, Y.; Cao, A.; Liu, Q.; Lv, X. Effects of tide-surge interactions on storm surges along the coast of the Bohai Sea, Yellow Sea, and East China Sea. Sci. China Earth Sci. 2016, 59, 1308–1316. [Google Scholar] [CrossRef]
- Andrade, C.A.; Thomas, Y.F.; Lerma, A.N.; Durand, P.; Anselme, B. Coastal Flooding Hazard Related to Swell Events in Cartagena de Indias, Colombia. J. Coast. Res. 2013, 290, 1126–1136. [Google Scholar] [CrossRef]
- Wang, H.; Loftis, J.; Liu, Z.; Forrest, D.; Zhang, J. The Storm Surge and Sub-Grid Inundation Modeling in New York City during Hurricane Sandy. J. Mar. Sci. Eng. 2014, 2, 226–246. [Google Scholar] [CrossRef] [Green Version]
- Yin, J.; Lin, N.; Yu, D. Coupled modeling of storm surge and coastal inundation: A case study in New York City during Hurricane Sandy. Water Resour. Res. 2016, 52, 8685–8699. [Google Scholar] [CrossRef]
- Sheng, Y.P.; Zhang, Y.; Paramygin, V.A. Simulation of storm surge, wave, and coastal inundation in the Northeastern Gulf of Mexico region during Hurricane Ivan in 2004. Ocean. Model. 2010, 35, 314–331. [Google Scholar] [CrossRef]
- Bilskie, M.V.; Hagen, S.C.; Medeiros, S.C.; Cox, A.T.; Salisbury, M.; Coggin, D. Data and numerical analysis of astronomic tides, wind-waves, and hurricane storm surge along the northern Gulf of Mexico. J. Geophys. Res. Ocean. 2016, 121, 3625–3658. [Google Scholar] [CrossRef]
- Bhaskaran, P.K.; Gayathri, R.; Murty, P.L.N.; Bonthu, S.; Sen, D. A numerical study of coastal inundation and its validation for Thane cyclone in the Bay of Bengal. Coast. Eng. 2014, 83, 108–118. [Google Scholar] [CrossRef]
- Bhaskaran, P.K.; Nayak, S.; Bonthu, S.R.; Murty, P.L.N.; Sen, D. Performance and validation of a coupled parallel ADCIRC–SWAN model for THANE cyclone in the Bay of Bengal. Environ. Fluid Mech. 2013, 13, 601–623. [Google Scholar] [CrossRef]
- Gayathri, R.; Bhaskaran, P.K.; Sen, D. Numerical Study on Storm Surge and Associated Coastal Inundation for 2009 AILA Cyclone in the Head Bay of Bengal. Aquat. Procedia 2015, 4, 404–411. [Google Scholar] [CrossRef]
- Du, M.; Hou, Y.; Hu, P.; Wang, K. Effects of Typhoon Paths on Storm Surge and Coastal Inundation in the Pearl River Estuary, China. Remote Sens. 2020, 12, 1851. [Google Scholar] [CrossRef]
- Yin, K.; Xu, S.; Huang, W.; Xie, Y. Effects of sea level rise and typhoon intensity on storm surge and waves in Pearl River Estuary. Ocean. Eng. 2017, 136, 80–93. [Google Scholar] [CrossRef]
- Li, A.; Guan, S.; Mo, D.; Hou, Y.; Hong, X.; Liu, Z. Modeling wave effects on storm surge from different typhoon intensities and sizes in the South China Sea. Estuar. Coast. Shelf Sci. 2020, 235, 106551. [Google Scholar] [CrossRef]
- Wang, K.; Hou, Y.; Li, S.; Du, M.; Li, R. Numerical Study of Storm Surge Inundation in the Southwestern Hangzhou Bay Region During Typhoon Chan-Hom in 2015. J. Ocean Univ. China 2020, 19, 263–271. [Google Scholar] [CrossRef]
- Du, M.; Hou, Y.; Qi, P.; Wang, K. The impact of different historical typhoon tracks on storm surge: A case study of Zhejiang, China. J. Mar. Syst. 2020, 206, 103318. [Google Scholar] [CrossRef]
- Yin, J.; Yin, Z.-E.; Hu, X.-M.; Xu, S.-Y.; Wang, J.; Li, Z.-H.; Zhong, H.-D.; Gan, F.-B. Multiple scenario analyses forecasting the confounding impacts of sea level rise and tides from storm induced coastal flooding in the city of Shanghai, China. Environ. Earth Sci. 2010, 63, 407–414. [Google Scholar] [CrossRef]
- Pan, Z.-h.; Liu, H. Extreme storm surge induced coastal inundation in Yangtze Estuary regions. J. Hydrodyn. 2019, 31, 1127–1138. [Google Scholar] [CrossRef]
- Chang, T.Y.; Chen, H.E.; Hsiao, S.C.; Wu, H.L.; Chen, W.B. Numerical Analysis of the Effect of Binary Typhoons on Ocean Surface Waves in Waters Surrounding Taiwan. Front. Mar. Sci. 2021, 8, 749185. [Google Scholar] [CrossRef]
- Chen, W.B.; Chen, H.; Hsiao, S.C.; Chang, C.H.; Lin, L.Y. Wind forcing effect on hindcasting of typhoon-driven extreme waves. Ocean. Eng. 2019, 188, 106260. [Google Scholar] [CrossRef]
- Hsiao, S.C.; Chen, H.; Chen, W.B.; Chang, C.H.; Lin, L.Y. Quantifying the contribution of nonlinear interactions to storm tide simulations during a super typhoon event. Ocean. Eng. 2019, 194, 106661. [Google Scholar] [CrossRef]
- Hsiao, S.C.; Chen, H.E.; Wu, H.L.; Chen, W.B.; Chang, C.H.; Guo, W.D.; Chen, Y.M.; Lin, L.Y. Numerical Simulation of Large Wave Heights from Super Typhoon Nepartak (2016) in the Eastern Waters of Taiwan. J. Mar. Sci. Eng. 2020, 8, 217. [Google Scholar] [CrossRef] [Green Version]
- Shih, H.J.; Chen, H.; Liang, T.Y.; Fu, H.S.; Chang, C.H.; Chen, W.B.; Su, W.R.; Lin, L.Y. Generating potential risk maps for typhoon-induced waves along the coast of it Taiwan. Ocean. Eng. 2018, 163, 1–14. [Google Scholar] [CrossRef]
- Hsiao, S.-C.; Wu, H.-L.; Chen, W.-B.; Guo, W.-D.; Chang, C.-H.; Su, W.-R. Effect of Depth-Induced Breaking on Wind Wave Simulations in Shallow Nearshore Waters off Northern Taiwan during the Passage of Two Super Typhoons. J. Mar. Sci. Eng. 2021, 9, 706. [Google Scholar] [CrossRef]
- Feng, X.; Yin, B.; Yang, D. Effect of hurricane paths on storm surge response at Tianjin, China. Estuar. Coast. Shelf Sci. 2012, 106, 58–68. [Google Scholar] [CrossRef]
- Pelling, H.E.; Uehara, K.; Green, J.A.M. The impact of rapid coastline changes and sea level rise on the tides in the Bohai Sea, China. J. Geophys. Res. Ocean. 2013, 118, 3462–3472. [Google Scholar] [CrossRef] [Green Version]
- Yang, G. Historical change and future trends of storm surge disaster in China’s coastal area. J. Nat. Disasters 2000, 3, 23–30. [Google Scholar]
- Wang, X.; Qian, C.; Wang, W.; Yan, T. An elliptical wind field model of typhoons. J. Ocean Univ. China 2004, 3, 33–39. [Google Scholar] [CrossRef]
- Feng, J.; Lu, X.; Yu, H.; Zhang, W.; Ying, M.; Fan, Y.; Zhu, Y.; Chen, D. An Overview of the China Meteorological Administration Tropical Cyclone Database. JAtOT 2014, 31, 287–301. [Google Scholar]
- Lu, X.; Yu, H.; Ying, M.; Zhao, B.; Zhang, S.; Lin, L.; Bai, L.; Wan, R. Western North Pacific Tropical Cyclone Database Created by the China Meteorological Administration. AdAtS 2021, 38, 690–699. [Google Scholar] [CrossRef]
- CMA Tropical Cyclone Data Center. Available online: https://tcdata.typhoon.org.cn/ (accessed on 10 November 2021).
- Li, J.; Hou, Y.; Mo, D.; Liu, Q.; Zhang, Y. Influence of Tropical Cyclone Intensity and Size on Storm Surge in the Northern East China Sea. Remote Sens. 2019, 11, 3033. [Google Scholar] [CrossRef] [Green Version]
- Weisberg, R.H.; Zheng, L.Y. Hurricane storm surge simulations for Tampa Bay. Estuar. Coasts 2006, 29, 899–913. [Google Scholar] [CrossRef]
- Zhong, L.; Li, M.; Zhang, D.-L. How do uncertainties in hurricane model forecasts affect storm surge predictions in a semi-enclosed bay? Estuar. Coast. Shelf Sci. 2010, 90, 61–72. [Google Scholar] [CrossRef]
- Booij, N.; Ris, R.C.; Holthuijsen, L.H. A third-generation wave model for coastal regions: 1. Model description and validation. J. Geophys. Res. Ocean. 1999, 104, 7649–7666. [Google Scholar] [CrossRef] [Green Version]
- Wood, D.J.; Muttray, M.; Oumeraci, H. The SWAN model used to study wave evolution in a flume. Ocean. Eng. 2001, 28, 805–823. [Google Scholar] [CrossRef]
- Feng, X.; Yin, B.; Yang, D. Development of an unstructured-grid wave-current coupled model and its application. Ocean. Model. 2016, 104, 213–225. [Google Scholar] [CrossRef]
- De-zhou, Y.; Jin, W.; Bao-shu, Y.; Yan-qing, X.; Ri-na, S. Application of the SWAN wave model to Bohai Sea: Improvement of Phillips linear growth term. Adv. Water Sci. 2005, 16, 710–714. [Google Scholar]
- Ris, R.C.; Holthuijsen, L.H.; Booij, N. A third-generation wave model for coastal regions: 2. Verification. J. Geophys. Res. Ocean. 1999, 104, 7667–7681. [Google Scholar] [CrossRef]
- Jin, K.R.; Ji, Z.G. Calibration and verification of a spectral wind-wave model for Lake Okeechobee. Ocean. Eng. 2001, 28, 571–584. [Google Scholar] [CrossRef]
- Padilla-Hernandez, R.; Monbaliu, J. Energy balance of wind waves as a function of the bottom friction formulation. Coast. Eng. 2001, 43, 131–148. [Google Scholar] [CrossRef]
- Rogers, W.E.; Hwang, P.A.; Wang, D.W. Investigation of wave growth and decay in the SWAN model: Three regional-scale applications. J. Phys. Oceanogr. 2003, 33, 366–389. [Google Scholar] [CrossRef]
- Alari, V.; Raudsepp, U.; Kõuts, T. Wind wave measurements and modelling in Küdema Bay, Estonian Archipelago Sea. J. Mar. Syst. 2008, 74, S30–S40. [Google Scholar] [CrossRef]
- Westerink, J.; Luettich, J.R.; Baptista, A.; Scheffner, N.; Farrar, P. Tide and Storm Surge Predictions Using Finite Element Model. J. Hydraul. Eng. 1992, 118, 1373–1390. [Google Scholar] [CrossRef]
- Luettich, J.R.; Westerink, J.; Scheffner, N. ADCIRC: An Advanced Three-Dimensional Circulation Model for Shelves, Coasts, and Estuaries. Report 1. Theory and Methodology of ADCIRC-2DDI and ADCIRC-3DL; DRP-92-6; US Army Corps of Engineers: Washington, DC, USA, 1992; p. 143. [Google Scholar]
- Westerink, J.; Luettich, J.R.; Blain, C.; Scheffner, N. ADCIRC: An Advanced Three-Dimensional Circulation Model for Shelves, Coasts, and Estuaries. Report 2. User’s Manual for ADCIRC-2DDI; DRP-92-6; US Army Corps of Engineers: Washington, DC, USA, 1994; p. 168. [Google Scholar]
- Ebersole, B.A.; Westerink, J.J.; Bunya, S.; Dietrich, J.C.; Cialone, M.A. Development of storm surge which led to flooding in St. Bernard Polder during Hurricane Katrina. Ocean. Eng. 2010, 37, 91–103. [Google Scholar] [CrossRef]
- Blain, C.A.; Westerink, J.J.; Luettich Jr, R.A. Grid convergence studies for the prediction of hurricane storm surge. Int. J. Numer. Methods Fluids 1998, 26, 369–401. [Google Scholar] [CrossRef]
- Yong-hua, C.; Qing-he, Z.; Shu-wang, Y.; Ze-zhou, J.; Hua, Y. Two Dimensional Current Field Analysis of Huanghua Port. China Harb. Eng. 2005, 136, 1–4. [Google Scholar]
- Xin-gru, F.; Bao-shu, Y.; De-zhou, Y. Refined simulation and establishment of a tide and tidal current forecasting system in the Bohai Sea and the Yellow Sea. Mar. Forecast. 2011, 28, 65–69. [Google Scholar]
- Murty, P.L.N.; Rao, A.D.; Srinivas, K.S.; Rao, E.P.R.; Bhaskaran, P.K. Effect of Wave Radiation Stress in Storm Surge-Induced Inundation: A Case Study for the East Coast of India. PApGe 2019, 177, 2993–3012. [Google Scholar] [CrossRef]
- Dietrich, J.C.; Zijlema, M.; Westerink, J.J.; Holthuijsen, L.H.; Dawson, C.; Luettich, R.A.; Jensen, R.E.; Smith, J.M.; Stelling, G.S.; Stone, G.W. Modeling hurricane waves and storm surge using integrally-coupled, scalable computations. Coast. Eng. 2011, 58, 45–65. [Google Scholar] [CrossRef]
- Dietrich, J.C.; Tanaka, S.; Westerink, J.J.; Dawson, C.N.; Luettich, R.A.; Zijlema, M.; Holthuijsen, L.H.; Smith, J.M.; Westerink, L.G.; Westerink, H.J. Performance of the Unstructured-Mesh, SWAN+ADCIRC Model in Computing Hurricane Waves and Surge. JSCom 2011, 52, 468–497. [Google Scholar] [CrossRef]
- Deb, M.; Ferreira, C.M. Simulation of cyclone-induced storm surges in the low-lying delta of Bangladesh using coupled hydrodynamic and wave model ( SWAN+ADCIRC). J. Flood Risk Manag. 2016, 11, S750–S765. [Google Scholar] [CrossRef]
- Yin, C.; Huang, H.; Wang, D.; Liu, Y.; Guo, Z. The Characteristics of Storm Wave Behavior and Its Effect on Cage Culture Using the ADCIRC+SWAN Model in Houshui Bay, China. J. Ocean Univ. China 2020, 19, 307–319. [Google Scholar] [CrossRef]
- Cavaleri, L.; Bertotti, L. The improvement of modelled wind and wave fields with increasing resolution. Ocean. Eng. 2006, 33, 553–565. [Google Scholar] [CrossRef]
- Moeini, M.H.; Etemad-Shahidi, A.; Chegini, V. Wave modeling and extreme value analysis off the northern coast of the Persian Gulf. Appl. Ocean. Res. 2010, 32, 209–218. [Google Scholar] [CrossRef] [Green Version]
- Signell, R.P.; Carniel, S.; Cavaleri, L.; Chiggiato, J.; Doyle, J.D.; Pullen, J.; Sclavo, M. Assessment of wind quality for oceanographic modelling in semi-enclosed basins. J. Mar. Syst. 2005, 53, 217–233. [Google Scholar] [CrossRef]
- Xiangui, M. Preliminarily assessment of ERA5 reanalysis data. J. Mar. Meteorol. 2018, 38, 91–99. [Google Scholar]
- Ai-lian, L. Applicability of the ERA5 reanalysis data to China adjacent Sea under typhoon condition. Mar. Sci. 2021, 45, 71–80. [Google Scholar]
- Du, M.; Hou, Y.; Guo, Y.; Wang, K. Numerical Simulation and Risk Analysis of Coastal Inundation in Land Reclamation Areas: A Case Study of the Pearl River Estuary. J. Ocean Univ. China 2020, 19, 1221–1234. [Google Scholar] [CrossRef]
- Wu, G.; Shi, F.; Kirby, J.T.; Liang, B.; Shi, J. Modeling wave effects on storm surge and coastal inundation. Coast. Eng. 2018, 140, 371–382. [Google Scholar] [CrossRef]
- Holland, G. A revised hurricane pressure-wind model. MWRv 2008, 136, 3432–3445. [Google Scholar] [CrossRef] [Green Version]
- Landsea, C. A Climatology of Intense (or Major) Atlantic Hurricanes. MWRv 1993, 121, 1703–1713. [Google Scholar] [CrossRef] [Green Version]
- Harper, B. Tropical Cyclone Parameter Estimation in the Australian Region: Wind-Pressure Relationships and Related Issues for Engineering Planning and Design—A Discussion Paper; J0106-PR003E; Systems Engineering Australia Pty Ltd.: Newstead, QLD, Australia, 2002; p. 93. [Google Scholar]
- Knaff, J.A.; Zehr, R.M. Reexamination of tropical cyclone wind-pressure relationships. Weather Forecast. 2007, 22, 71–88. [Google Scholar] [CrossRef]
- Carrasco, C.A.; Landsea, C.W.; Lin, Y.-L. The Influence of Tropical Cyclone Size on Its Intensification. Weather Forecast. 2014, 29, 582–590. [Google Scholar] [CrossRef] [Green Version]
- Irish, J.L.; Resio, D.T.; Ratcliff, J.J. The Influence of Storm Size on Hurricane Surge. J. Phys. Oceanogr. 2008, 38, 2003–2013. [Google Scholar] [CrossRef]
- Condon, A.J.; Sheng, Y.P. Optimal storm generation for evaluation of the storm surge inundation threat. Ocean. Eng. 2012, 43, 13–22. [Google Scholar] [CrossRef]
- Rego, J.L.; Li, C. On the importance of the forward speed of hurricanes in storm surge forecasting: A numerical study. Geophys. Res. Lett. 2009, 36, L07609. [Google Scholar] [CrossRef] [Green Version]
- Clarke, A.J.; Battisti, D.S. The effect of continental shelves on tides. Deep. Sea Res. Part A Oceanogr. Res. Pap. 1981, 28, 665–682. [Google Scholar] [CrossRef]
- Wenxin, S.; Wensheng, J.; Lei, L. Numerical Model of Offshore Environment Fluid Dynamics; Science Press: Beijing, China, 2004; pp. 11–13. [Google Scholar]












| Typhoon Number | Typhoon Name | Maximum Wind (m/s) | Duration of Wind above 40 m/s (h) | Duration of Winds above 60 m/s (h) | Landfall on Shandong Peninsula |
|---|---|---|---|---|---|
| 200004 | Kai_Tai | 35 | 0 | 0 | N |
| 200209 | Fengshen | 55 | 186 | 0 | Y |
| 200509 | Matsa | 45 | 66 | 0 | Y |
| 200515 | Khanun | 50 | 54 | 0 | N |
| 200713 | Wipha | 55 | 30 | 0 | Y |
| 201105 | Meari | 30 | 0 | 0 | Y |
| 201109 | Muifa | 65 | 144 | 6 | N |
| 201210 | Damrey | 40 | 6 | 0 | Y |
| 201410 | Matmo | 42 | 18 | 0 | Y |
| 201810 | Ampil | 28 | 0 | 0 | Y |
| 201818 | Rumbia | 25 | 0 | 0 | Y |
| 201909 | Lekima | 62 | 63 | 3 | Y |
| Typhoon | MUIFA | LEKIMA | ||
|---|---|---|---|---|
| Variate | Number | Value | Number | Value |
| Max Wind Speed (m/s) | 1 | 10 | 18 | 10 |
| 2 | 20 | 19 | 20 | |
| 3 | 25 | 20 | 25 | |
| 4 | 30 | 21 | 30 | |
| 5 | 35 | 22 | 35 | |
| 6 | 40 | 23 | 40 | |
| 7 | 45 | 24 | 45 | |
| 8 | 50 | 25 | 50 | |
| Radius (km) | 9 | 10 | 26 | 10 |
| 10 | 20 | 27 | 20 | |
| 11 | 30 | 28 | 30 | |
| 12 | 40 | 29 | 40 | |
| 13 | 50 | 30 | 50 | |
| Translation Speed (km/s) | 14 | 7.5 | 31 | 7.5 |
| 15 | 15 | 32 | 15 | |
| 16 | 30 | 33 | 30 | |
| 17 | 60 | 34 | 60 | |
| Maximum Wind Speed (m/s) | 10 | 20 | 25 | 30 | 35 | 40 | 45 | 50 |
| Minimum Pressure (hPa) | 1003 | 993 | 987 | 981 | 974 | 967 | 960 | 953 |
| Typhoon | Typhoon Muifa | Typhoon Lekima | ||
|---|---|---|---|---|
| Station | Absolute Error (m) | Relative Error | Absolute Error (m) | Relative Error |
| QF101 | 1.014 | 0.221 | −0.085 | −0.003 |
| QF103 | −3.686 | −0.565 | −0.381 | −0.035 |
| QF104 | −0.109 | −0.108 | −0.207 | −0.123 |
| QF114 | 0.681 | 0.094 | −0.285 | −0.076 |
| Typhoon | Typhoon Muifa | Typhoon Lekima | ||
|---|---|---|---|---|
| Station | Absolute Error (m) | Relative Error | Absolute Error (m) | Relative Error |
| QF101 | −0.218 | −0.693 | −0.012 | −0.113 |
| QF103 | −0.348 | −0.318 | ||
| QF104 | 0.136 | 0.214 | −0.178 | −0.090 |
| QF114 | 0.255 | 0.276 | 0.184 | 0.139 |
| Typhoon | Typhoon Muifa | Typhoon Lekima | ||
|---|---|---|---|---|
| Station | Absolute Error (m) | Relative Error | Absolute Error (m) | Relative Error |
| HHG | −0.008 | −7.845 | −0.208 | −3.31 |
| WFG | −0.034 | 3.048 | −0.207 | 0.010 |
| LKO | 0.014 | 0.515 | −0.010 | 0.218 |
| WMT | −0.032 | 0.261 | 0.028 | 6.524 |
| RZH | −0.017 | −4.639 | 0.078 | −0.923 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Mo, D.; Hou, Y.; Li, S.; Li, J.; Du, M.; Yin, B. The Impact of Typhoon Intensity on Wave Height and Storm Surge in the Northern East China Sea: A Comparative Case Study of Typhoon Muifa and Typhoon Lekima. J. Mar. Sci. Eng. 2022, 10, 192. https://doi.org/10.3390/jmse10020192
Wang J, Mo D, Hou Y, Li S, Li J, Du M, Yin B. The Impact of Typhoon Intensity on Wave Height and Storm Surge in the Northern East China Sea: A Comparative Case Study of Typhoon Muifa and Typhoon Lekima. Journal of Marine Science and Engineering. 2022; 10(2):192. https://doi.org/10.3390/jmse10020192
Chicago/Turabian StyleWang, Junyan, Dongxue Mo, Yijun Hou, Shuiqing Li, Jian Li, Mei Du, and Baoshu Yin. 2022. "The Impact of Typhoon Intensity on Wave Height and Storm Surge in the Northern East China Sea: A Comparative Case Study of Typhoon Muifa and Typhoon Lekima" Journal of Marine Science and Engineering 10, no. 2: 192. https://doi.org/10.3390/jmse10020192
APA StyleWang, J., Mo, D., Hou, Y., Li, S., Li, J., Du, M., & Yin, B. (2022). The Impact of Typhoon Intensity on Wave Height and Storm Surge in the Northern East China Sea: A Comparative Case Study of Typhoon Muifa and Typhoon Lekima. Journal of Marine Science and Engineering, 10(2), 192. https://doi.org/10.3390/jmse10020192






