A Mathematical Modeling Method for an Analytical Solution of Ship Hydrodynamic Pressure Fields in Complex Restricted Waters
Abstract
:1. Introduction
2. Mathematical Modeling
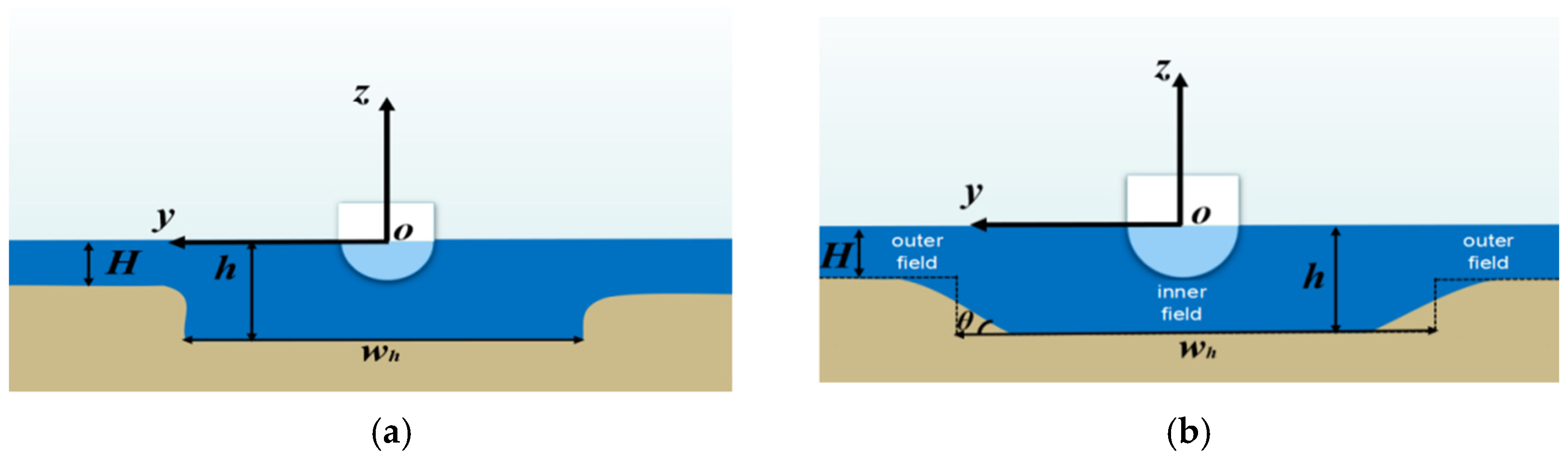
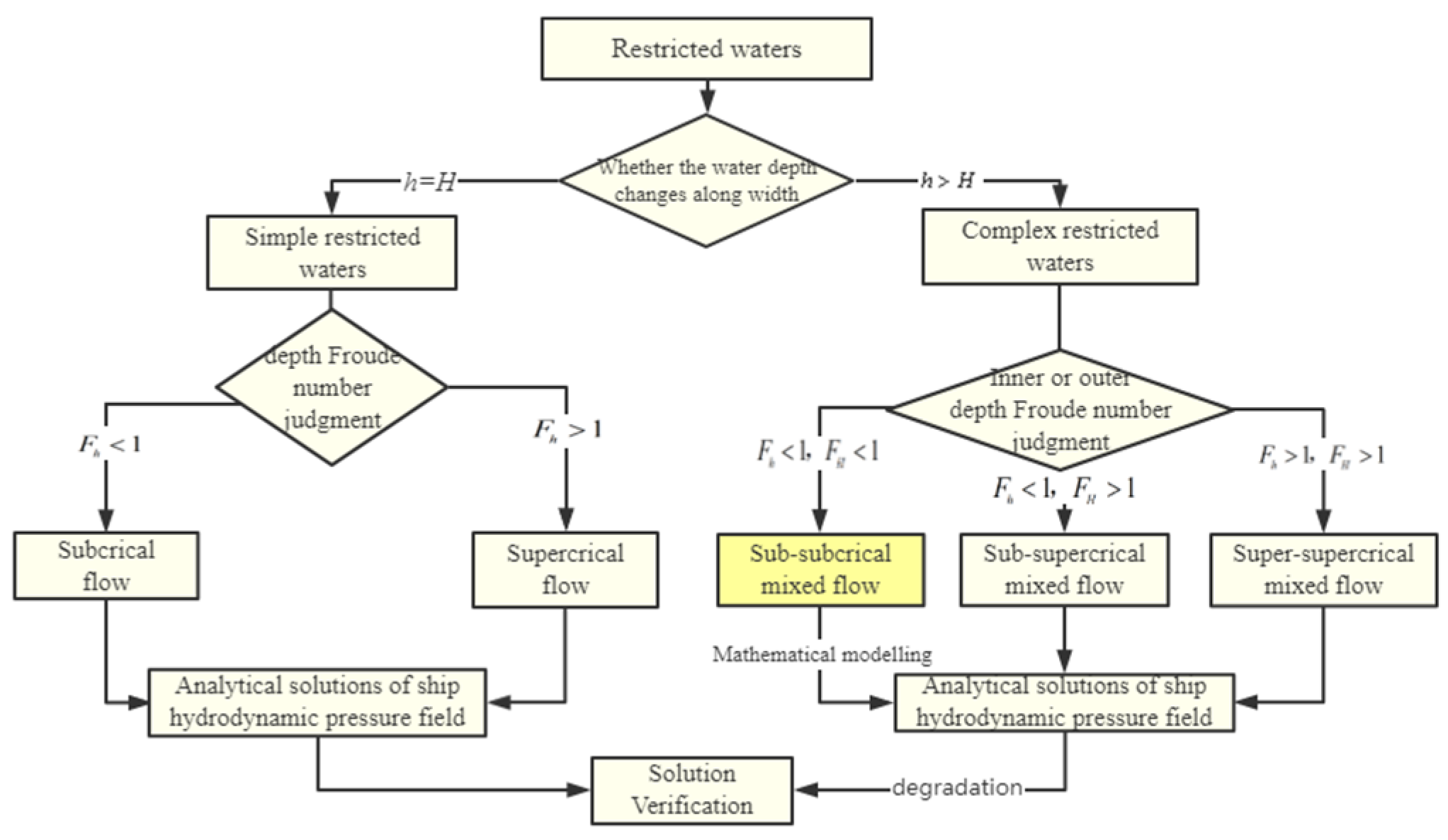
2.1. Simplification of Complex Restricted Waters
2.2. Construction of Governing Equations and Boundary Conditions
2.3. Fourier Transform of Governing Equations and Boundary Conditions
2.3.1. Inner Domain
2.3.2. Outer Domain
3. Derivation of Analytical Solution
3.1. Analytical Solution of the Velocity Field for a Sub-Subcritical Mixed Flow
3.1.1. Inner Domain
3.1.2. Outer Domain
- where if , ,
- ; if , ,
- ; if , ,
- .
3.2. Analytical Solution of the Pressure Field for a Sub-Subcritical Mixed Flow
- where if , ,
- ;
- if , ,
- ;
- if ,,
- .
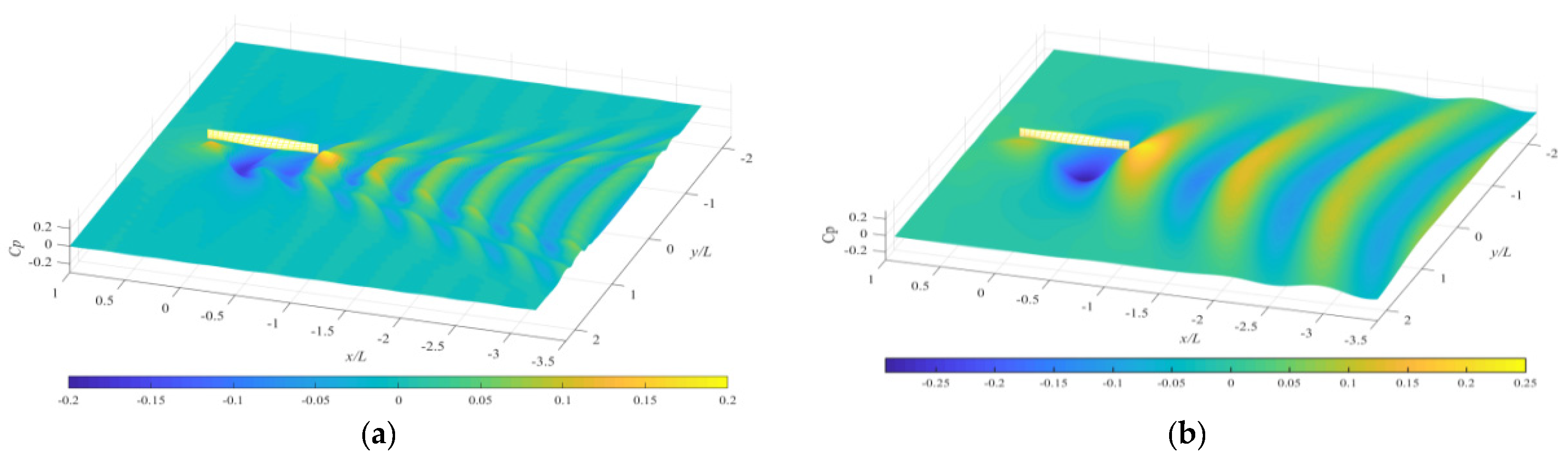
4. Validation and Results
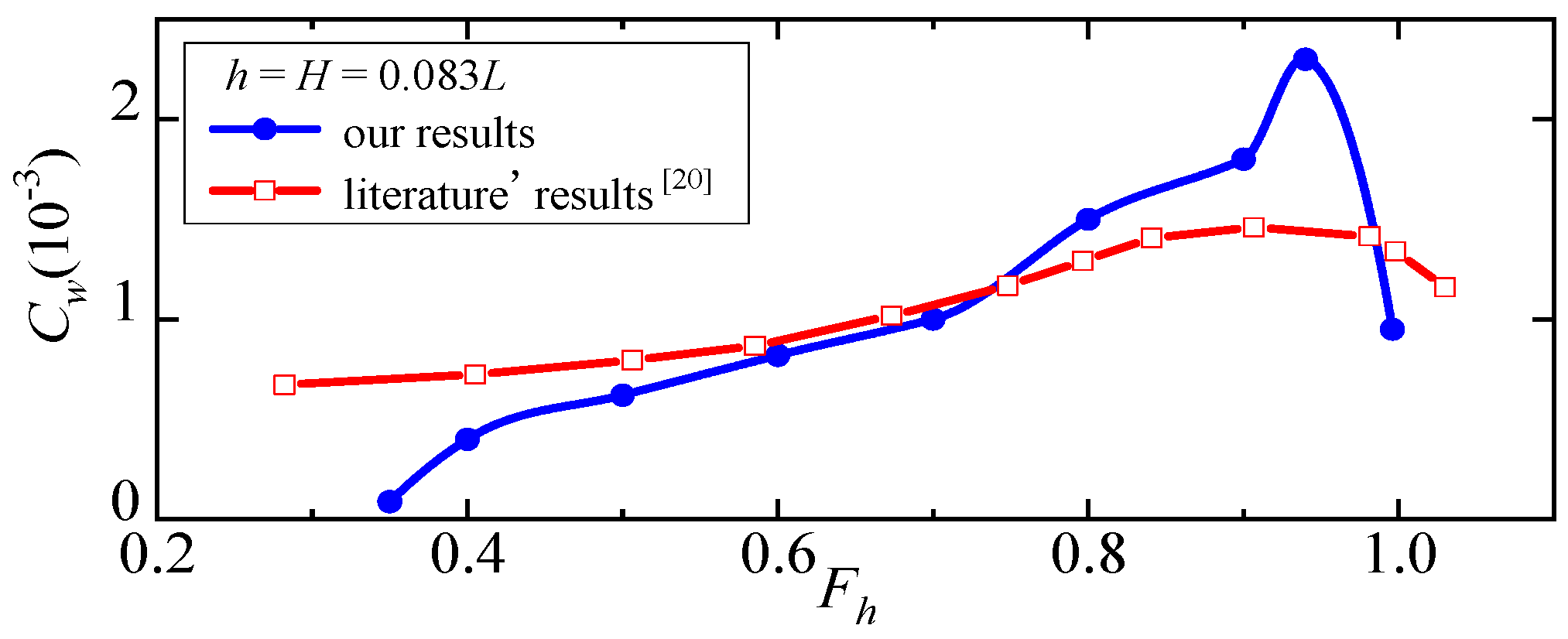
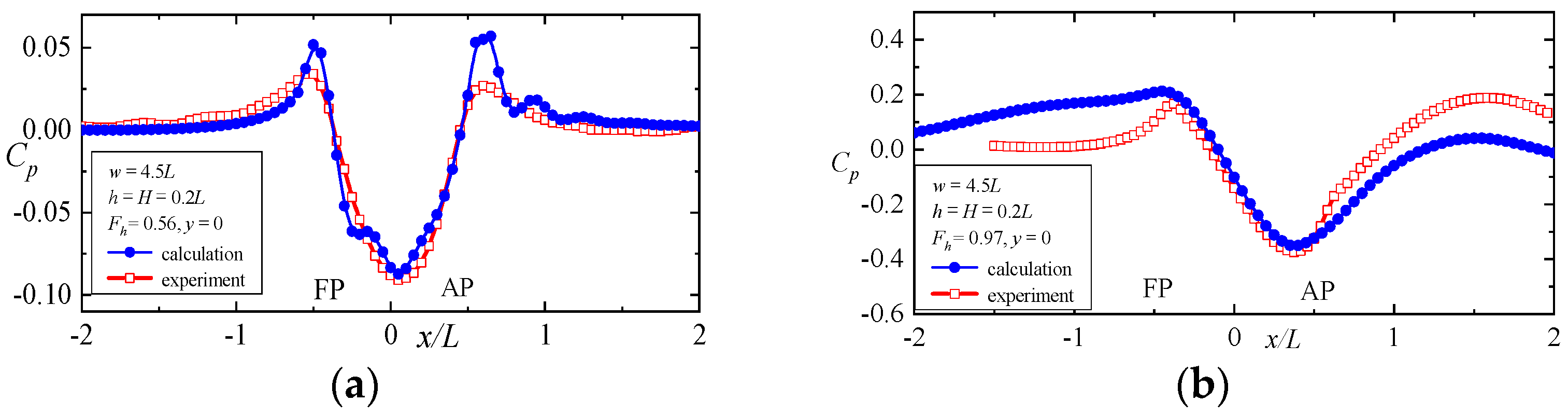
4.1. Continuity Validation
4.2. Simplify to Open Sea
4.3. Simplify to Rectangular Channel
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Jiang, M. Waterway Engineering; China Water Conservancy and Hydropower Press: Beijing, China, 2009; pp. 11–18. [Google Scholar]
- Zhang, W. Effects of shallow waters effects on ships and empirical estimation methods. Ship Mar. Eng. 2019, 35, 6–12. [Google Scholar]
- Ni, H.; She, H.Q. Status and development trend of foreign submarine mines. Mine Warfare Ship Protect. 2013, 21, 1–8. [Google Scholar]
- Tuck, E.O. Shallow-water flows past slender bodies. J. Fluid Mech. 1966, 26, 81–95. [Google Scholar] [CrossRef]
- Tuck, E.O. Hydrodynamic Problems of Ships in Restricted Waters. Annu. Rev. Fluid Mech. 1978, 10, 33–46. [Google Scholar] [CrossRef]
- Tuck, E.O. Bottom Pressure Signatures; Department of Applied Mathematics, The University of Adelaide: Adelaide, Australia, 1998. [Google Scholar]
- Terziev, M.; Tezdogan, T.; Oguz, E.; Gourlay, T.; Demirel, Y.K.; Incecik, A. Numerical investigation of the behaviour and performance of ships advancing through restricted shallow waters. J. Fluids Struct. 2018, 76, 185–215. [Google Scholar] [CrossRef] [Green Version]
- Tafuni, A.; Sahin, I. Seafloor Pressure Signatures of a High-Speed Boat in Shallow Water With SPH. In Proceedings of the ASME 2014 33rd International Conference on Ocean, Offshore and Arctic Engineering, San Francisco, CA, USA, 8–13 June 2014; American Society of Mechanical Engineers: New York, NY, USA, 2014. OMAE2014-24080. [Google Scholar] [CrossRef]
- Tafuni, A.; Sahin, I.; Hyman, M. Numerical investigation of wave elevation and bottom pressure generated by a planing hull in finite-depth water. Appl. Ocean Res. 2016, 58, 281–291. [Google Scholar] [CrossRef]
- Veen, D.; Gourlay, T. A combined strip theory and Smoothed Particle Hydrodynamics approach for estimating slamming loads on a ship in head seas. Ocean Eng. 2012, 43, 64–71. [Google Scholar] [CrossRef] [Green Version]
- Gourlay, T.P. A brief history of mathematical ship-squat prediction, focussing on the contributions of EO Tuck. J. Eng. Math. 2011, 70, 5–16. [Google Scholar] [CrossRef]
- Gourlay, T.P. Shallow Flow: A Program to Model Ship Hydrodynamics in Shallow Water. In Proceedings of the ASME 2014 33rd International Conference on Ocean, Offshore and Arctic Engineering, San Francisco, CA, USA, 8–13 June 2014. [Google Scholar]
- Gourlay, T.P.; Jeong, H.H.; Philipp, M. Sinkage and trim of modern container ships in shallow water. In Proceedings of the Australasian Coasts & Ports Conference, Auckland, New Zealand, 15–18 September 2015. [Google Scholar]
- Hui, D.; Zhi-Hong, Z.; Ju-Bin, L.; Jian-Nong, G. Research on the calculation method of pressure field for shallow water subcritical speed ships. J. Appl. Math. Mech. 2013, 34, 846–854. [Google Scholar]
- Hui, D.; Zhi-Hong, Z.; Jian-Nong, G.; Ju-Bin, L. Hydrodynamic pressure field caused by a ship sailing near the coast. J. Coast. Res. 2016, 32, 890–897. [Google Scholar]
- Sun, B.B.; Zhi-Hong, Z.; Ju-Bin, L.; Hui, D. The theoretical solution and calculation of the hydrodynamic pressure field of ship in the shallow channel. Ship Sci. Technol. 2014, 36, 11–16. [Google Scholar]
- Zhi-Hong, Z.; Hui, D.; Chong, W. Analytical models of sub-supercritical ship hydrodynamic pressure field with the dispersive effect. Ocean Eng. 2017, 133, 66–72. [Google Scholar] [CrossRef]
- Qing-Chang, M.; Hui, D.; Zhi-Hong, Z. Analytical models of ship hydrodynamic pressure field with dispersive effect in super-supercritical mixed flow. Ocean Eng. 2018, 167, 95–101. [Google Scholar]
- Xue-Nong, C.; Sharma, S.D. A slender ship moving at a near-critical speed in a shallow channel. J. Fluid Mech. 1995, 291, 263–285. [Google Scholar]
- Bo, C. Numerical Studying of Ship Waves in Shallow Water based on Green-Naghdi Equations; Huazhong University of Science and Technology: Wuhan, China, 2004. [Google Scholar]

| Dimensionless Parameters | Ship A | Ship B |
|---|---|---|
| Ship length between perpendiculars | 1 | 1 |
| Ship breadth | 0.133 | 0.20 |
| Ship draft | 0.021 | 0.052 |
| Block coefficient | 0.60 | 0.46 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Deng, H.; Zhang, Z.; Yi, W.; Xia, W. A Mathematical Modeling Method for an Analytical Solution of Ship Hydrodynamic Pressure Fields in Complex Restricted Waters. J. Mar. Sci. Eng. 2022, 10, 232. https://doi.org/10.3390/jmse10020232
Deng H, Zhang Z, Yi W, Xia W. A Mathematical Modeling Method for an Analytical Solution of Ship Hydrodynamic Pressure Fields in Complex Restricted Waters. Journal of Marine Science and Engineering. 2022; 10(2):232. https://doi.org/10.3390/jmse10020232
Chicago/Turabian StyleDeng, Hui, Zhihong Zhang, Wenbin Yi, and Weixue Xia. 2022. "A Mathematical Modeling Method for an Analytical Solution of Ship Hydrodynamic Pressure Fields in Complex Restricted Waters" Journal of Marine Science and Engineering 10, no. 2: 232. https://doi.org/10.3390/jmse10020232
APA StyleDeng, H., Zhang, Z., Yi, W., & Xia, W. (2022). A Mathematical Modeling Method for an Analytical Solution of Ship Hydrodynamic Pressure Fields in Complex Restricted Waters. Journal of Marine Science and Engineering, 10(2), 232. https://doi.org/10.3390/jmse10020232






