Stabilization of Neural Network Models for VIV Force Data Using Decoupled, Linear Feedback
Abstract
:1. Introduction
2. Methods and Applications
2.1. Experimental Details
2.2. Feedback Stabilization
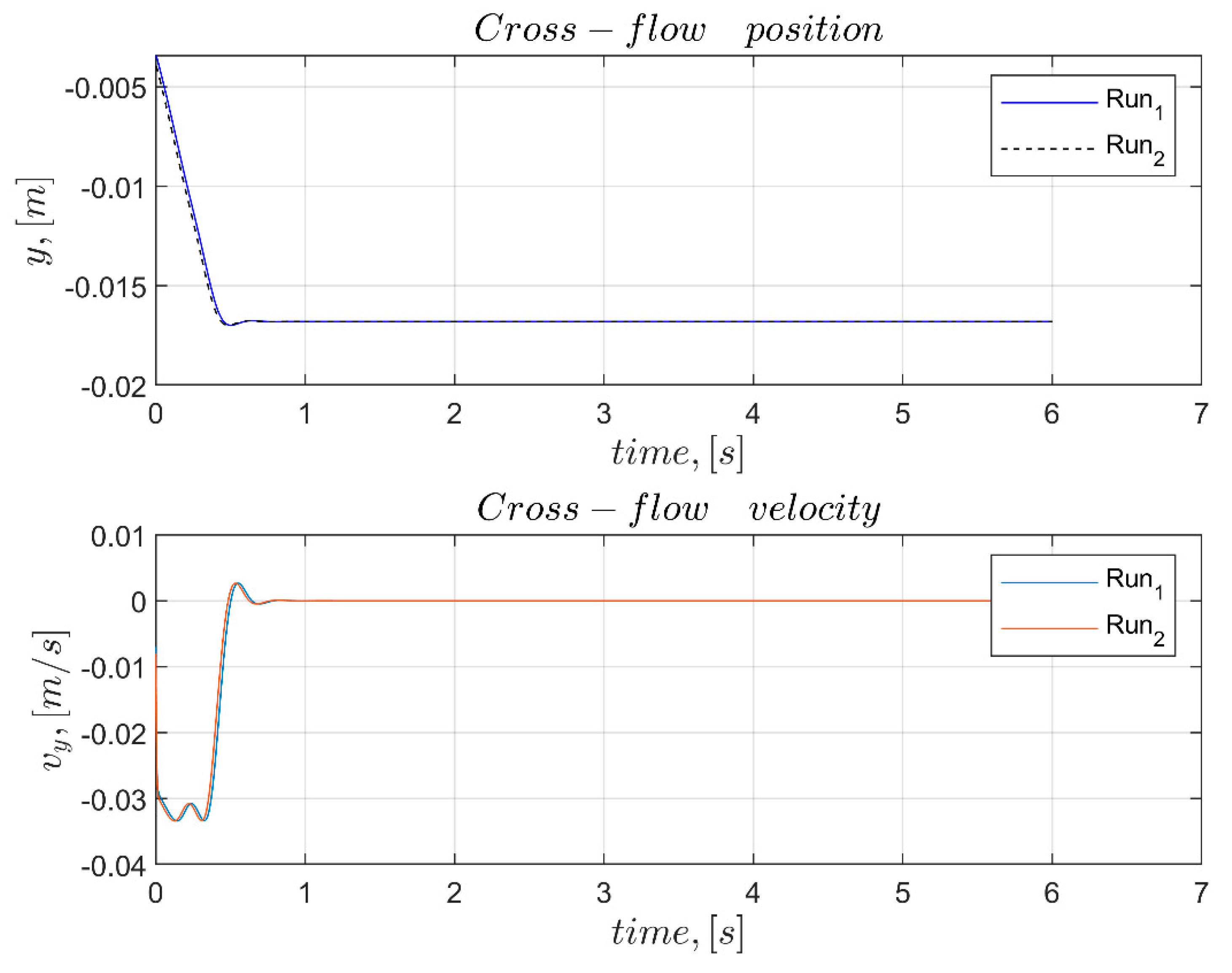
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
Appendix A
| = | −408.35 | −20.00 | −14.58 | 11.85 | |||
| 263.15 | 174.77 | −121.83 | 58.67 | ||||
| −415.43 | −11.93 | −14.41 | 15.41 | ||||
| 59.09 | 225.15 | −52.05 | 151.70 | ||||
| 601.33 | −29.76 | −4.20 | −28.36 | ||||
| −206.66 | −355.86 | −10.24 | 73.79 | ||||
| −483.88 | −327.53 | −17.44 | 15.33 | ||||
| = | −2.63 | 0.65 | 2.93 | 0.57 | −0.54 | −0.70 | −0.61 |
| T = | 1.31 | −6.63 | 1.73 | 0.14 | 0.84 | 0.59 | −3.44 |
| = | −0.51 |
| = | −689.54 | −27.06 | −10.79 | −4.42 | |||||||
| 1084.52 | −349.18 | 111.62 | 103.74 | ||||||||
| −998.47 | −312.31 | −21.76 | 149.14 | ||||||||
| −414.45 | 105.55 | 141.44 | 11.39 | ||||||||
| 907.02 | 131.82 | 20.28 | −144.25 | ||||||||
| 2331.12 | −1081.89 | −12.68 | −241.50 | ||||||||
| 1134.92 | −539.28 | 121.41 | 51.80 | ||||||||
| 397.76 | −1282.72 | −61.90 | −106.97 | ||||||||
| 609.99 | 891.26 | −161.93 | −15.21 | ||||||||
| 3020.09 | 584.58 | 126.47 | −48.11 | ||||||||
| −590.76 | 221.95 | −29.37 | 105.45 | ||||||||
| = | −0.71 | −0.40 | −4.68 | −0.34 | −4.72 | −0.22 | 0.31 | 0.29 | −0.33 | 0.33 | 0.24 |
| T = | 1.17 | −1.81 | 5.64 | −3.22 | −5.56 | −3.32 | −3.66 | −4.50 | 5.46 | 9.16 | −3.11 |
| = | 1.04 |
References
- Sarpkaya, T. Vortex-Induced Oscillations: A Selective Review. J. Appl. Mech. 1979, 46, 241–258. [Google Scholar] [CrossRef]
- Williamson, C.H.K.; Govardhan, R. Vortex-Induced Vibrations. Annu. Rev. Fluid Mech. 2004, 36, 413–455. [Google Scholar] [CrossRef] [Green Version]
- Bearman, P.W. Circular cylinder wakes and vortex-induced vibrations. J. Fluids Struct. 2011, 27, 648–658. [Google Scholar] [CrossRef]
- Parkinson, G. Phenomena and modelling of flow-induced vibrations of bluff bodies. Prog. Aerosp. Sci. 1989, 26, 169–224. [Google Scholar] [CrossRef]
- Bearman, P.W. Vortex Shedding from Oscillating Bluff Bodies. Annu. Rev. Fluid Mech. 1984, 16, 195–222. [Google Scholar] [CrossRef]
- Sarpkaya, T. A critical review of the intrinsic nature of vortex-induced vibrations. J. Fluids Struct. 2004, 19, 389–447. [Google Scholar] [CrossRef]
- Lee, J.H.; Xiros, N.; Bernitsas, M.M. Virtual damper–spring system for VIV experiments and hydrokinetic energy conversion. Ocean Eng. 2011, 38, 732–747. [Google Scholar] [CrossRef]
- Dahl, J.M.; Hover, F.S.; Triantafyllou, M.S.; Dong, S.; Karniadakis, G.E. Resonant Vibrations of Bluff Bodies Cause Multivortex Shedding and High Frequency Forces. Phys. Rev. Lett. 2007, 99, 144503. [Google Scholar] [CrossRef] [Green Version]
- Dahl, J.M.; Hover, F.S.; Triantafyllou, M.S.; Oakley, O.H. Dual resonance in vortex-induced vibrations at subcritical and supercritical Reynolds numbers. J. Fluid Mech. 2010, 643, 395–424. [Google Scholar] [CrossRef] [Green Version]
- Jauvtis, N.; Williamson, C.H.K. The effect of two degrees of freedom on vortex-induced vibration at low mass and damping. J. Fluid Mech. 2004, 509, 23–62. [Google Scholar] [CrossRef]
- Staubli, T. Calculation of the Vibration of an Elastically Mounted Cylinder Using Experimental Data From Forced Oscillation. J. Fluids Eng. 1983, 105, 225–229. [Google Scholar] [CrossRef]
- Gopalkrishnan, R. Vortex-Induced Forces on Oscillating Bluff Cylinders. Ph.D. Thesis, Massachusetts Institute of Technology, Dept. of Ocean Engineering, Cambridge, MA, USA, 1993. Available online: https://dspace.mit.edu/handle/1721.1/12539 (accessed on 30 December 2021).
- Morse, T.L.; Williamson, C.H.K. Prediction of vortex-induced vibration response by employing controlled motion. J. Fluid Mech. 2009, 634, 5–39. [Google Scholar] [CrossRef]
- Chaplin, J.R.; Bearman, P.W.; Cheng, Y.; Fontaine, E.; Graham, J.M.R.; Herfjord, K.; Huera Huarte, F.J.; Isherwood, M.; Lambrakos, K.; Larsen, C.M.; et al. Blind predictions of laboratory measurements of vortex-induced vibrations of a tension riser. J. Fluids Struct. 2005, 21, 25–40. [Google Scholar] [CrossRef]
- Bernitsas, M.M.; Ofuegbe, J.; Chen, J.-U.; Sun, H. Eigen-Solution for Flow Induced Oscillations (VIV and Galloping) Revealed at the Fluid-Structure Interface. In Proceedings of the Volume 2: CFD and FSI; American Society of Mechanical Engineers: New York, NY, USA, 2019. [Google Scholar]
- Liu, C.; Fu, S.; Zhang, M.; Ren, H. Time-varying hydrodynamics of a flexible riser under multi-frequency vortex-induced vibrations. J. Fluids Struct. 2018, 80, 217–244. [Google Scholar] [CrossRef]
- Liu, C.; Fu, S.; Zhang, M.; Ren, H.; Xu, Y. Hydrodynamics of a flexible cylinder under modulated vortex-induced vibrations. J. Fluids Struct. 2020, 94, 102913. [Google Scholar] [CrossRef]
- Dahl, J.M. Vortex-Induced Vibration of a Circular Cylinder with Combined In-Line and Cross-Flow Motion; Massachusetts Institute of Technology: Cambridge, MA, USA, 2008. [Google Scholar]
- Zheng, H.; Dahl, J.M.; Modarres-Sadeghi, Y.; Triantafyllou, M.S. Coupled Inline-Cross Flow VIV Hydrodynamic Coefficients Database. In Proceedings of the Volume 2: CFD and VIV; American Society of Mechanical Engineers: New York, NY, USA, 2014. [Google Scholar]
- Aktosun, E.; Dahl, J.M. Experimental Force Database From Controlled In-Line and Cross Flow Cylinder Motion. In Proceedings of the 28th International Ocean and Polar Engineering Conference, Sapporo, Japan, 10–15 June 2018. [Google Scholar]
- Dahl, J.; Aktosun, E. Force and wake observations for a circular cylinder undergoing forced 2-DOF motion in a free stream. APS 2019, 2019, C48-004. [Google Scholar]
- Aktosun, E.; Gedikli, E.D.; Dahl, J.M. Wake observations for a circular cylinder undergoing forced two-degrees-of-freedom motions. In Proceedings of the APS Division of Fluid Dynamics Meeting Abstracts, Virtual, Chicago, IL, USA, 22–24 November 2020; p. Y11-006. [Google Scholar]
- Aktosun, E.; Xiros, N.I.; Dahl, J.M. A Neural Network Time Dependent Hydrodynamic Force Model for Forced Two-Degree-of-Freedom Sinusoidal Motion of a Circular Cylinder in a Free Stream. In Proceedings of the Volume 9: Ocean Renewable Energy; American Society of Mechanical Engineers: New York, NY, USA, 2021. [Google Scholar]
- Aktosun, E.; Xiros, N.I.; Dahl, J.M. A Data Model for In-stream Forces on a Cylinder Using Neural Networks and Linear Prediction Filters. Acta Sci. Comput. Sci. 2021, 3, 50–64. [Google Scholar]
- Dahl, J.M.; Hover, F.S.; Triantafyllou, M.S. Two-degree-of-freedom vortex-induced vibrations using a force assisted apparatus. J. Fluids Struct. 2006, 22, 807–818. [Google Scholar] [CrossRef]
- Xiros, N.I.; Bernitsas, M.M.; Sun, H.; Saxton, R.; Ioup, J.W. Dynamic Modeling of Flow Induced Vibration Power-Plants. In Proceedings of the Volume 10: Ocean Renewable Energy; American Society of Mechanical Engineers: New York, NY, USA, 2018. [Google Scholar]
- Xiros, N.I.; An, P.-C.E. Control Theory and Applications. In Springer Handbook of Ocean Engineering; Springer International Publishing: Cham, Switzerland, 2016; pp. 227–276. [Google Scholar]
- Strogatz, S.H. Nonlinear Dynamics and Chaos; CRC Press: New York, NY, USA, 2015; ISBN 13: 978-0-8133-4910-7. [Google Scholar]
- Abarbanel, H.D.I. Analysis of Observed Chaotic Data; Institute for Nonlinear Science: San Diego, CA, USA; Springer: New York, NY, USA, 1996; ISBN 978-0-387-98372-1. [Google Scholar]



















| k (N/m) | b (kg/s) | Offset Force, f (N) | |
|---|---|---|---|
| y | 186.01 | 9.25 | 0.007 |
| x | 188.84 | −0.35 | 0.72 |
| Initial Values | Experiment 1D-1 | Experiment 1D-2 | Experiment 1D-3 | Experiment 1D-4 | ||||
|---|---|---|---|---|---|---|---|---|
| Run1 | Run2 | Run1 | Run2 | Run1 | Run2 | Run1 | Run2 | |
| x (m) | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| y (m) | 0.0019 | 0.0015 | 0.0039 | 0.0041 | −0.0030 | −0.0032 | −0.0034 | −0.0039 |
| vx (m/s) | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| vy (m/s) | −0.0205 | −0.0211 | −0.0032 | −0.0041 | 0.0140 | 0.0150 | −0.0070 | −0.0080 |
| Initial Values | Experiment D-1 | Experiment 2D-2 | Experiment D-3 | Experiment 2D-4 | ||||
|---|---|---|---|---|---|---|---|---|
| Run1 | Run2 | Run1 | Run2 | Run1 | Run2 | Run1 | Run2 | |
| x (m) | −0.0031 | −0.0029 | −0.0033 | −0.0034 | −0.0031 | −0.0029 | 0.0035 | 0.0035 |
| y (m) | −0.0030 | −0.0031 | −0.0030 | −0.0030 | 0.0030 | 0.0029 | −0.0031 | −0.0032 |
| vx (m/s) | −0.0254 | −0.0275 | −0.0126 | −0.0128 | −0.0233 | −0.0224 | −0.0209 | −0.0213 |
| vy (m/s) | 0.0132 | 0.0136 | 0.0141 | 0.0135 | −0.0044 | −0.0038 | −0.0124 | −0.0118 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiros, N.I.; Aktosun, E. Stabilization of Neural Network Models for VIV Force Data Using Decoupled, Linear Feedback. J. Mar. Sci. Eng. 2022, 10, 272. https://doi.org/10.3390/jmse10020272
Xiros NI, Aktosun E. Stabilization of Neural Network Models for VIV Force Data Using Decoupled, Linear Feedback. Journal of Marine Science and Engineering. 2022; 10(2):272. https://doi.org/10.3390/jmse10020272
Chicago/Turabian StyleXiros, Nikolaos I., and Erdem Aktosun. 2022. "Stabilization of Neural Network Models for VIV Force Data Using Decoupled, Linear Feedback" Journal of Marine Science and Engineering 10, no. 2: 272. https://doi.org/10.3390/jmse10020272





