A Model for Translation and Rotation Resistance Tensors for Superellipsoidal Particles in Stokes Flow
Abstract
1. Introduction
2. Governing Equations
Boundary Element Solution of Stokes Flow over a Particle
3. A Particle in Stokes Flow
4. Numerical Setup
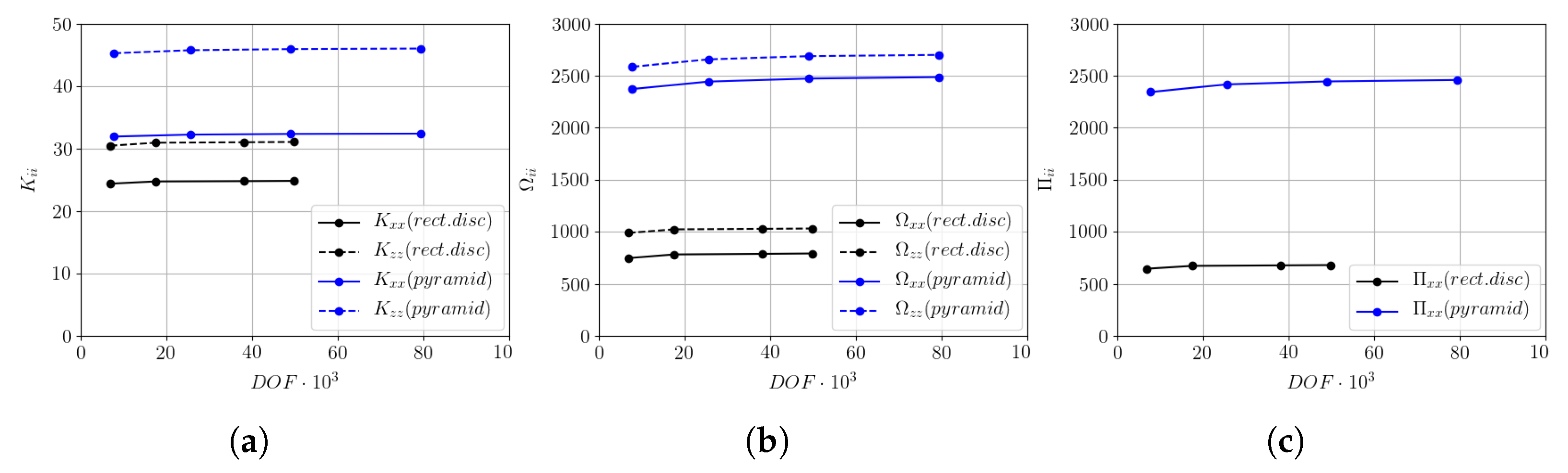
5. Mesh Study and Validation
6. Results
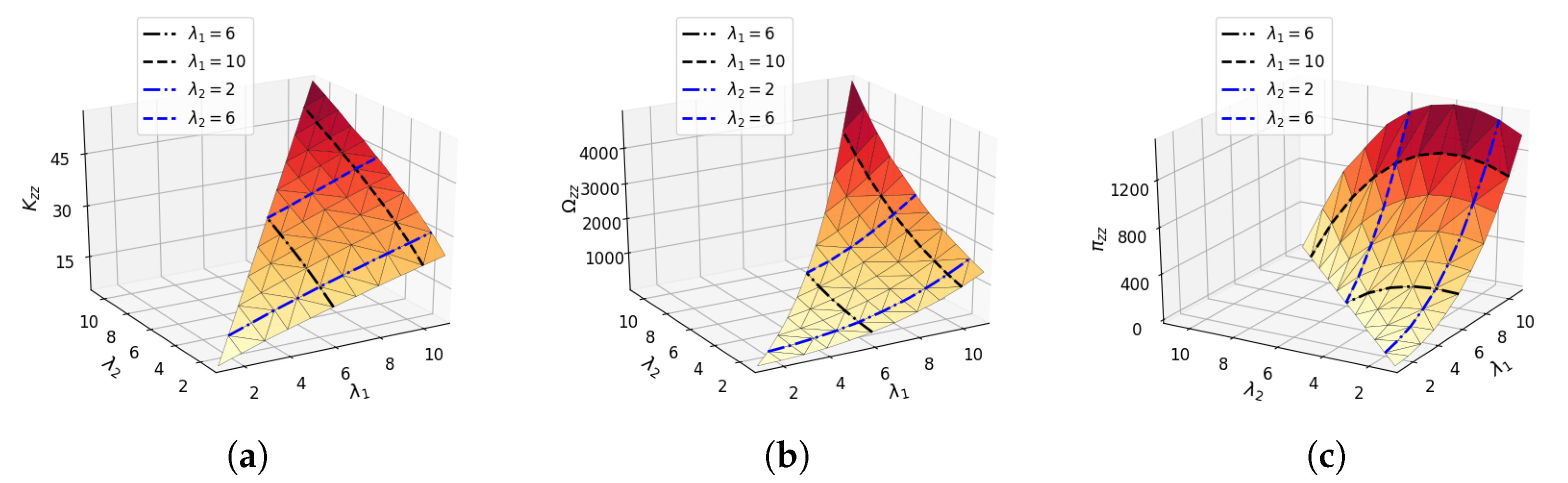
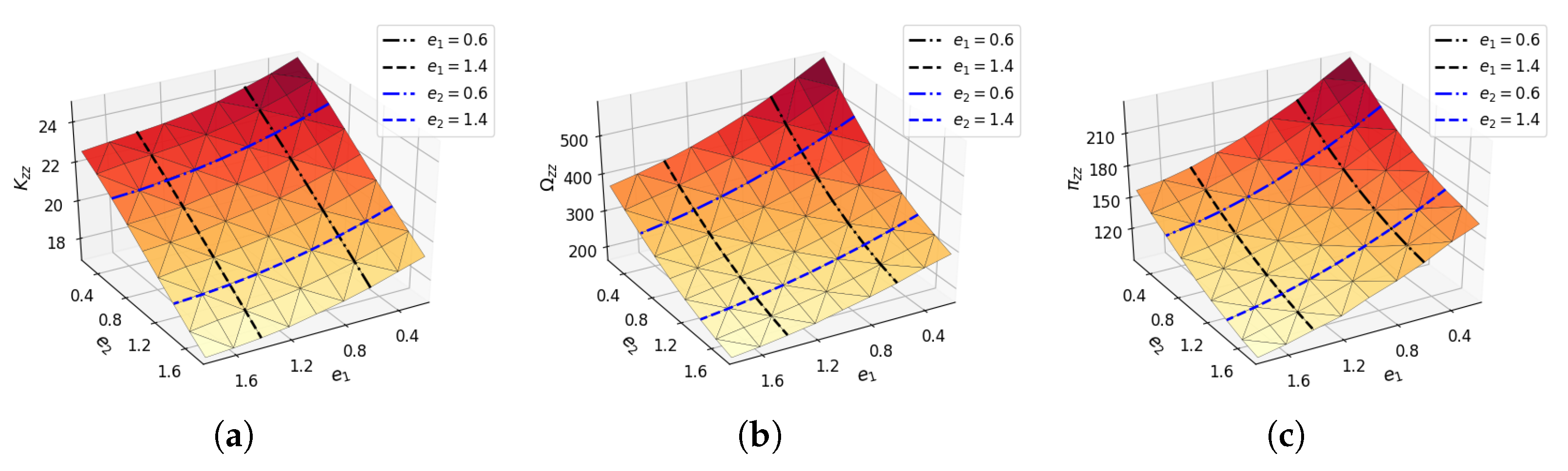
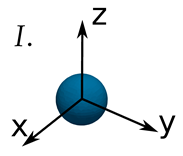
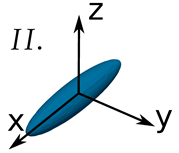
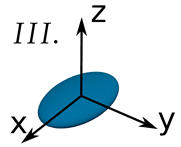
6.1. Data Inspection
6.2. Approximation Scheme Derivation
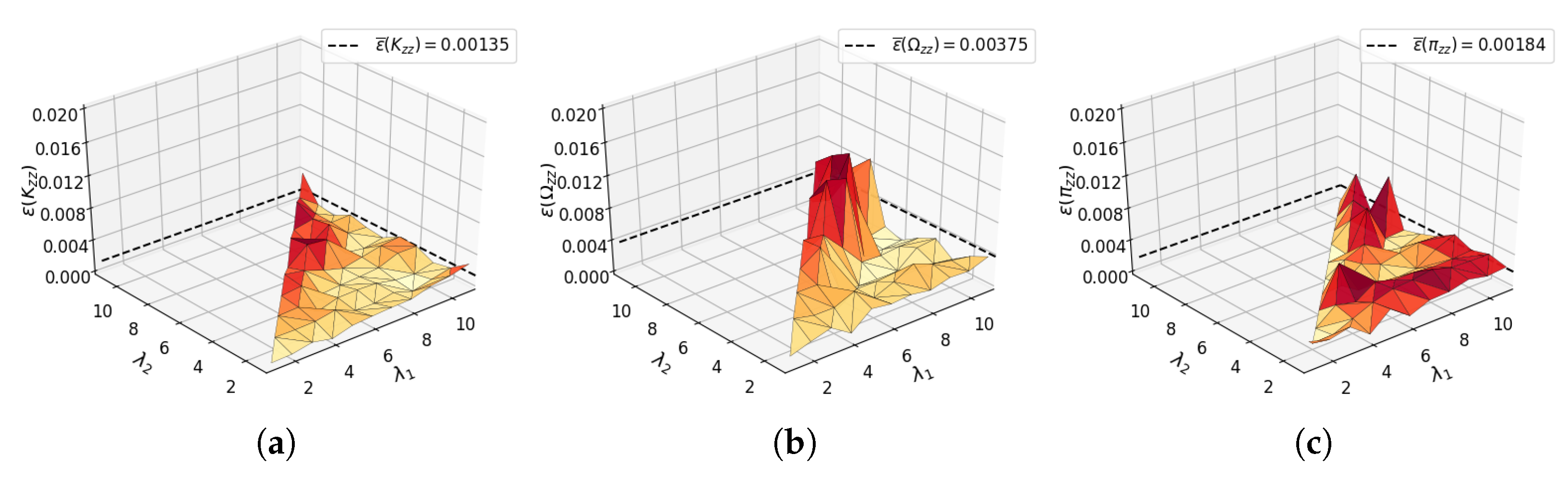
6.3. Validation of the Approximation Scheme
6.4. Demonstration of the Force and Torque Model Using Parametrically Defined Particles
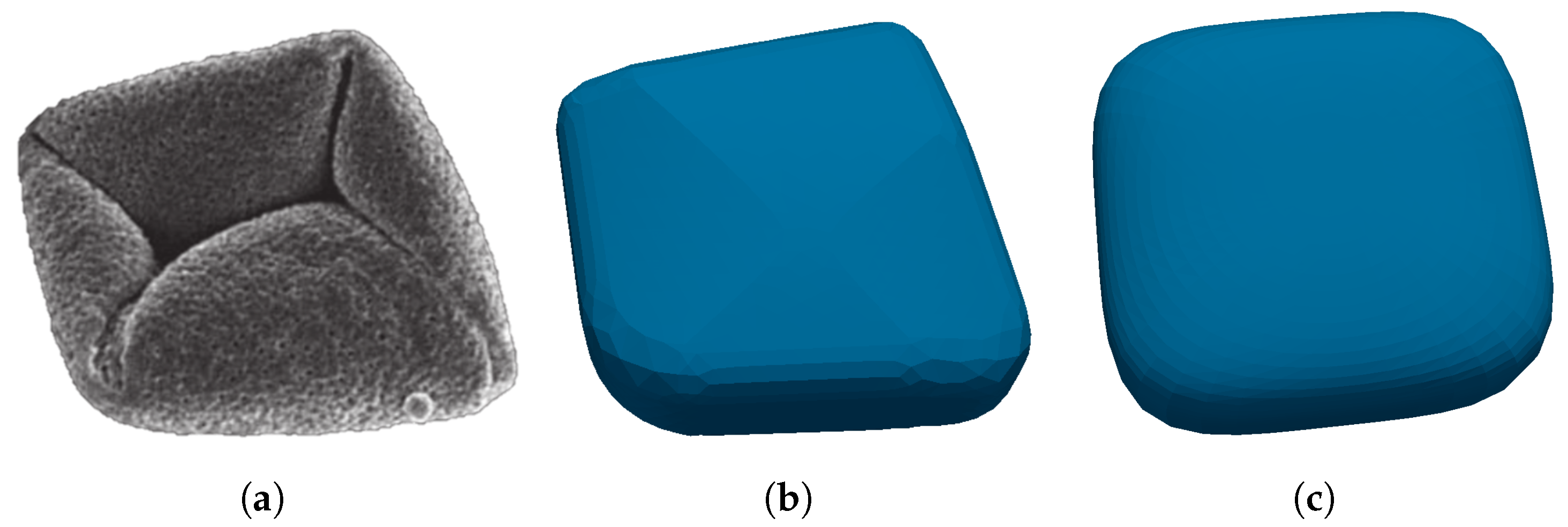
6.5. Demonstration of the Force and Torque Model Using a Realistic Particle
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Coefficient Matrices A for Closing the Approximation Scheme (22)
Appendix A.1. Coefficient Matrices for Range
Appendix A.2. Coefficient Matrices for Range
References
- Crowe, C.T.; Sommerfeld, M.; Tsuji, Y. Multiphase Flows with Droplets and Particles; CRC Press: Boca Raton, FL, USA, 1998. [Google Scholar]
- Maxey, M.R.; Riley, J.J. Equation of motion for a small rigid sphere in a nonuniform flow. Phys. Fluids 1983, 26, 883. [Google Scholar] [CrossRef]
- Kuerten, J.G.M. Point-Particle DNS and LES of Particle-Laden Turbulent flow—A state-of-the-art review. Flow Turbul. Combust. 2016, 97, 689–713. [Google Scholar] [CrossRef] [PubMed]
- Balachandar, S.; Eaton, J.K. Turbulent Dispersed Multiphase Flow. Annu. Rev. Fluid Mech. 2010, 42, 111–133. [Google Scholar] [CrossRef]
- Armenio, V.; Fiorotto, V. The importance of the forces acting on particles in turbulent flows. Phys. Fluids 2001, 13, 2437–2440. [Google Scholar] [CrossRef]
- Oseen, C. Neuere Methoden und Ergebnisse in der Hydrodynamik; Akademische Verlagsgesellschaft: Leipzig, Germany, 1927. [Google Scholar]
- Schiller, L.; Naumann, A. Über die grundlegenden Berechnungen bei der Schwerkraftaufbereitung. Verein Deutscher Ingenieure 1933, 77, 318–320. [Google Scholar]
- Happel, J.; Brenner, H. Low Reynolds Number Hydrodynamics; Martinus Nijhoff Publishers, Kluwer: The Hague, The Netherlands, 1983. [Google Scholar] [CrossRef]
- Koullapis, P.; Kassinos, S.C.; Muela, J.; Perez-segarra, C.; Rigola, J.; Lehmkuhl, O.; Cui, Y.; Sommerfeld, M.; Elcner, J.; Jicha, M.; et al. Regional aerosol deposition in the human airways: The SimInhale benchmark case and a critical assessment of in silico methods. Eur. J. Pharm. Sci. 2017, 113, 77–94. [Google Scholar] [CrossRef]
- Wedel, J.; Steinmann, P.; Štrakl, M.; Hriberšek, M.; Ravnik, J. Can CFD establish a connection to a milder COVID-19 disease in younger people? Aerosol deposition in lungs of different age groups based on Lagrangian particle tracking in turbulent flow. Comput. Mech. 2021, 67, 1497–1513. [Google Scholar] [CrossRef]
- Wedel, J.; Steinmann, P.; Štrakl, M.; Hriberšek, M.; Ravnik, J. Risk Assessment of Infection by Airborne Droplets and Aerosols at Different Levels of Cardiovascular Activity. Arch. Comput. Methods Eng. 2021, 28, 4297–4316. [Google Scholar] [CrossRef]
- Radhika, T.; Raja Rani, T.; Dwivedi, D. Creeping flow of a viscous fluid past a pair of porous separated spheres. Bull. Pure Appl. Sci. Sec. E Math. Stat. 2020, 39e, 58. [Google Scholar] [CrossRef]
- Vogel, A.; Durant, A.J.; Cassiani, M.; Clarkson, R.J.; Slaby, M.; Diplas, S.; Krüger, K.; Stohl, A. Simulation of volcanic ash ingestion into a Large Aero Engine: Particle-Fan interactions. J. Turbomach. 2019, 141, 011010. [Google Scholar] [CrossRef]
- Oberbeck, A. Ueber stationäre flüssigkeitsbewegungen mit berücksichtigung der inneren reibung. J. Fur Die Reine Und Angew. Math. 1876, 1876, 62–80. [Google Scholar] [CrossRef]
- Dassios, G.; Hadjinicolaou, M.; Protopapas, E. Blood plasma flow past a red blood cell: Mathematical modelling and analytical treatment. Math. Methods Appl. Sci. 2012, 35, 1547–1563. [Google Scholar] [CrossRef]
- Dassios, G.; Hadjinicolaou, M.; Payatakes, A.C. Generalized eigenfunctions and complete semiseparable solutions for Stokes flow in spheroidal coordinates. Q. Appl. Math. 1994, 52, 157–191. [Google Scholar] [CrossRef]
- Hadjinicolaou, M.; Protopapas, E. Eigenfunction Expansions for the Stokes Flow Operators in the Inverted Oblate Coordinate System. Math. Probl. Eng. 2016, 2016, 9049131. [Google Scholar] [CrossRef]
- Marchioli, C.; Soldati, A. Rotation statistics of fibers in wall shear turbulence. Acta Mech. 2013, 224, 2311–2329. [Google Scholar] [CrossRef]
- Ravnik, J.; Marchioli, C.; Soldati, A. Application limits of Jeffery’s theory for elongated particle torques in turbulence: A DNS assessment. Acta Mech. 2018, 229, 827–839. [Google Scholar] [CrossRef]
- Zhang, H.; Ahmadi, G.; Fan, F.G.; McLaughlin, J.B. Ellipsoidal particles transport and deposition in turbulent channel flows. Int. J. Multiph. Flow 2001, 27, 971–1009. [Google Scholar] [CrossRef]
- Jeffery, G.B. The motion of ellipsoidal particles immersed in a viscous fluid. Proc. R. Soc. A 1922, 102, 161–179. [Google Scholar]
- Koch, D.L.; Subramanian, G. Collective Hydrodynamics of Swimming Microorganisms: Living Fluids. Annu. Rev. Fluid Mech 2011, 43, 637–659. [Google Scholar] [CrossRef]
- Meyer, C.R.; Byron, M.L.; Variano, E.A. Rotational diffusion of particles in turbulence. Limnol. Oceanogr. Fluids Environ. 2013, 3, 89–102. [Google Scholar] [CrossRef]
- Sturm, R. A computer model for the simulation of nonspherical particle dynamics in the human respiratory tract. Phys. Res. Int. 2012, 2012, 142756. [Google Scholar] [CrossRef][Green Version]
- Lundell, F.; Söderberg, L.D.; Alfredsson, P.H. Fluid mechanics of papermaking. Annu. Rev. Fluid Mech. 2011, 43, 195–217. [Google Scholar] [CrossRef]
- Hazelton, R. Characteristics of Fuel Crud and Its Impact on Storage, Handling, and Shipment of Spent Fuel; Technical Report; Pacific Northwest National Laboratory (PNNL): Richland, WA, USA, 1987. [Google Scholar] [CrossRef]
- Haider, A.; Levenspiel, O. Drag coefficient and terminal velocity of spherical and nonspherical particles. Powder Technol. 1989, 58, 63–70. [Google Scholar] [CrossRef]
- Leith, D. Drag on nonspherical objects. Aerosol Sci. Technol. 1987, 6, 153–161. [Google Scholar] [CrossRef]
- Hölzer, A.; Sommerfeld, M. New simple correlation formula for the drag coefficient of non-spherical particles. Powder Technol. 2008, 184, 361–365. [Google Scholar] [CrossRef]
- Witham, C.; Hort, M.; Thomson, D.; Leadbetter, S.; Devenish, B.; Webster, H.; Beckett, F.; Kristiansen, N. The current volcanic ash modelling set-up at the London VAAC. In Met Office Technical Summary; Met Office: London, UK, 2021; p. 12. [Google Scholar]
- Saxby, J.; Rust, A.; Beckett, F.; Cashman, K.; Rodger, H. Estimating the 3D shape of volcanic ash to better understand sedimentation processes and improve atmospheric dispersion modelling. Earth Planet. Sci. Lett. 2020, 534, 116075. [Google Scholar] [CrossRef]
- Norde, E.; Senoner, J.m.; Der, E.T.A.V.; Trontin, P.; Willem, H.; Hoeijmakers, M.; Villedieu, P.; Norde, E.; Senoner, J.m.; Theodorus, E.; et al. Eulerian and Lagrangian Ice Crystal Trajectory Simulations in a Generic Turbofan Compressor. J. Propuls. Power 2019, 35, 26–40. [Google Scholar] [CrossRef]
- Gomez Bonilla, J.S.; Dechet, M.A.; Schmidt, J.; Peukert, W.; Bück, A. Thermal rounding of micron-sized polymer particles in a downer reactor: Direct vs indirect heating. Rapid Prototyp. J. 2020, 26, 1637–1646. [Google Scholar] [CrossRef]
- Bagheri, G.; Bonadonna, C. On the drag of freely falling non-spherical particles. Powder Technol. 2016, 301, 526–544. [Google Scholar] [CrossRef]
- Williams, J.R.; Pentland, A.P. Superquadrics and modal dynamics for discrete elements in interactive design. Eng. Comput. 1992, 9, 115–127. [Google Scholar] [CrossRef]
- Tropea, C.; Yarin, L.A.; Foss, F.J. Springer Handbook of Experimental Fluid Mechanics; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar] [CrossRef]
- Pozrikidis, C. A Practical Guide to Boundary Element Methods with the Software Library BEMLIB; CRC Press: Boca Raton, FL, USA, 2002. [Google Scholar]
- Šušnjara, A.; Verhnjak, O.; Poljak, D.; Cvetković, M.; Ravnik, J. Stochastic-deterministic boundary element modelling of transcranial electric stimulation using a three layer head model. Eng. Anal. Bound. Elem. 2021, 123, 70–83. [Google Scholar] [CrossRef]
- Šušnjara, A.; Verhnjak, O.; Poljak, D.; Cvetković, M.; Ravnik, J. Uncertainty quantification and sensitivity analysis of transcranial electric stimulation for 9-subdomain human head model. Eng. Anal. Bound. Elem. 2022, 135, 1–11. [Google Scholar] [CrossRef]
- Jaklič, A.; Leonardis, A.; Solina, F. Segmentation and Recovery of Superquadrics; Computational Imaging and Vision Book Series; Springer Netherlands: Dordrecht, The Netherlands, 2000; Volume 20. [Google Scholar] [CrossRef]
- Jaklič, A.; Solina, F. Moments of superellipsoids and their application to range image registration. IE Trans. Syst. Man Cybern. Part B Cybern. 2003, 33, 648–657. [Google Scholar] [CrossRef] [PubMed]
- You, Y.; Zhao, Y. Discrete element modelling of ellipsoidal particles using super-ellipsoids and multi-spheres: A comparative study. Powder Technol. 2018, 331, 179–191. [Google Scholar] [CrossRef]
- Lorentz, H.A. A general theorem concerning the motion of a viscous fluid and a few consequneces derived from it. In Collected Papers; Martinus Nijhoff Publishers, Kluwer: The Haque, The Netherlands, 1937. [Google Scholar]
- Chadil, M.A.; Vincent, S.; Estivalezes, J.L. Accurate estimate of drag forces using particle-resolved direct numerical simulations. Acta Mech. 2019, 230, 569–595. [Google Scholar] [CrossRef]
- Zastawny, M.; Mallouppas, G.; Zhao, F.; van Wachem, B. Derivation of drag and lift force and torque coefficients for non-spherical particles in flows. Int. J. Multiph. Flow 2012, 39, 227–239. [Google Scholar] [CrossRef]
- Andersson, H.I.; Jiang, F. Forces and torques on a prolate spheroid: Low-Reynolds-number and attack angle effects. Acta Mech. 2019, 230, 431–447. [Google Scholar] [CrossRef]
- Štrakl, M.; Wedel, J.; Steinmann, P.; Hriberšek, M.; Ravnik, J. Numerical drag and lift prediction framework for superellipsoidal particles in multiphase flows. Int. J. Comput. Methods Exp. Meas. 2022, 10, 38–49. [Google Scholar] [CrossRef]
- Gallily, I.; Cohen, A.H. On the orderly nature of the motion of nonspherical aerosol particles II. Inertial collision between a spherical large droplet and axially symmetrical elongated particle. J. Colloid Interface Sci. 1979, 68, 338–356. [Google Scholar] [CrossRef]
- Macedo, H.D.; Oliveira, J.N. Typing linear algebra: A biproduct-oriented approach. Sci. Comput. Program. 2013, 78, 2160–2191. [Google Scholar] [CrossRef]
- Beal, L.; Hill, D.; Martin, R.; Hedengren, J. GEKKO Optimization Suite. Processes 2018, 6, 106. [Google Scholar] [CrossRef]
- Matamoro-Vidal, A.; Prieu, C.; Furness, C.A.; Albert, B.; Gouyon, P.H. Evolutionary stasis in pollen morphogenesis due to natural selection. New Phytol. 2016, 209, 376–394. [Google Scholar] [CrossRef] [PubMed]
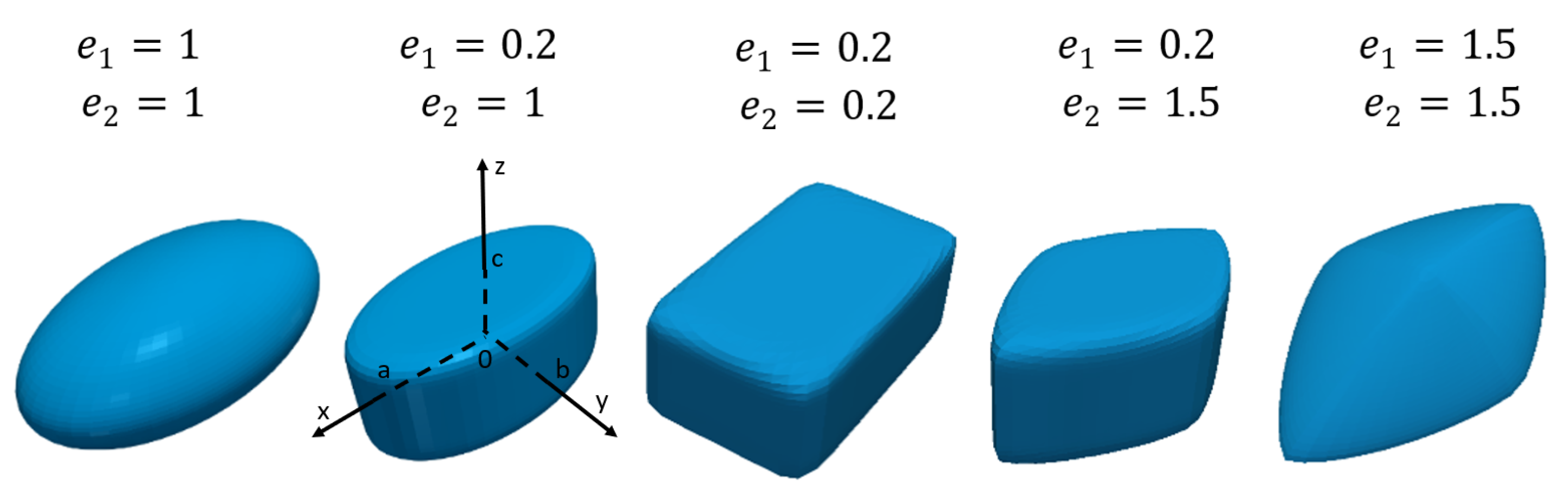
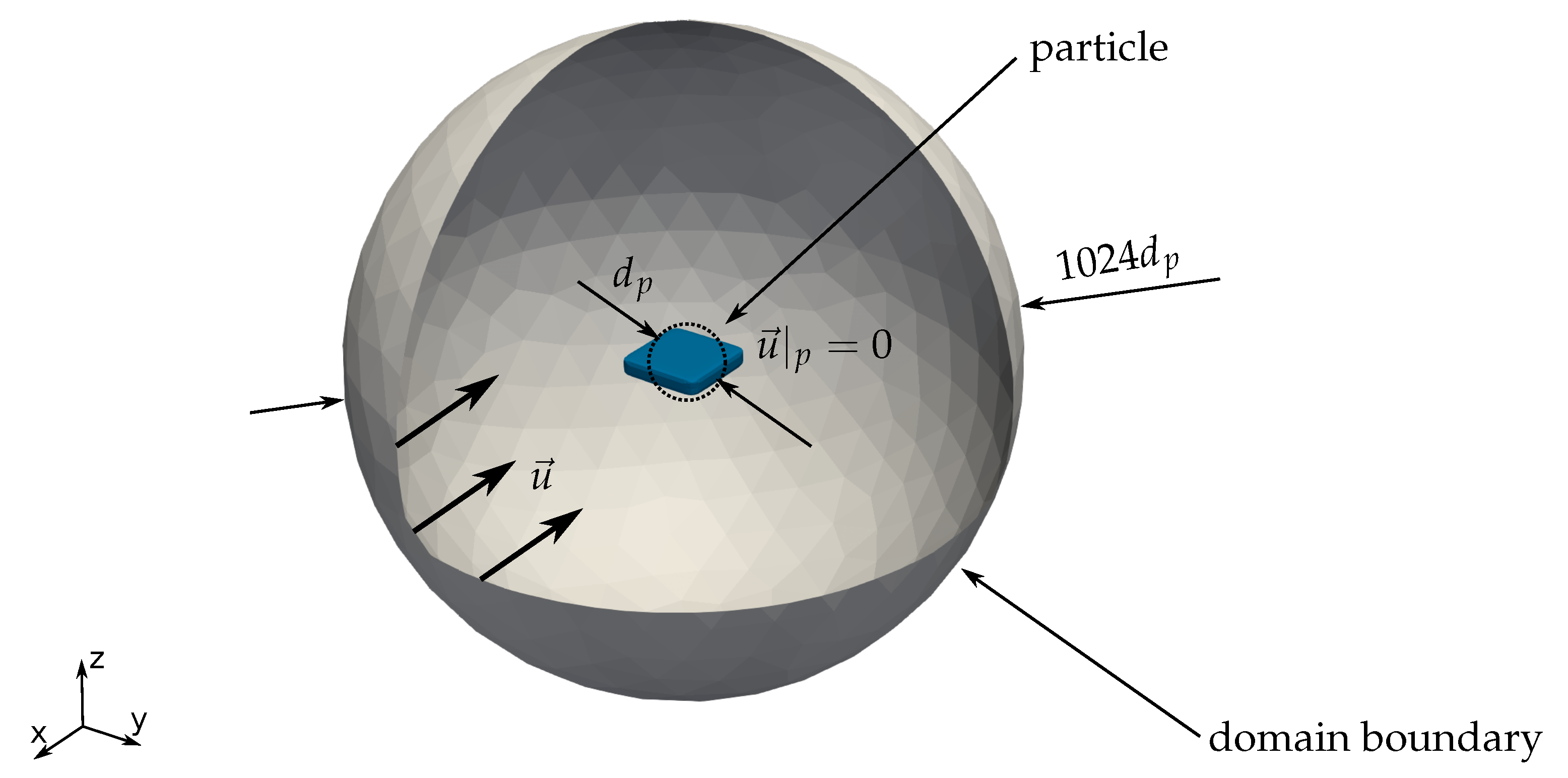
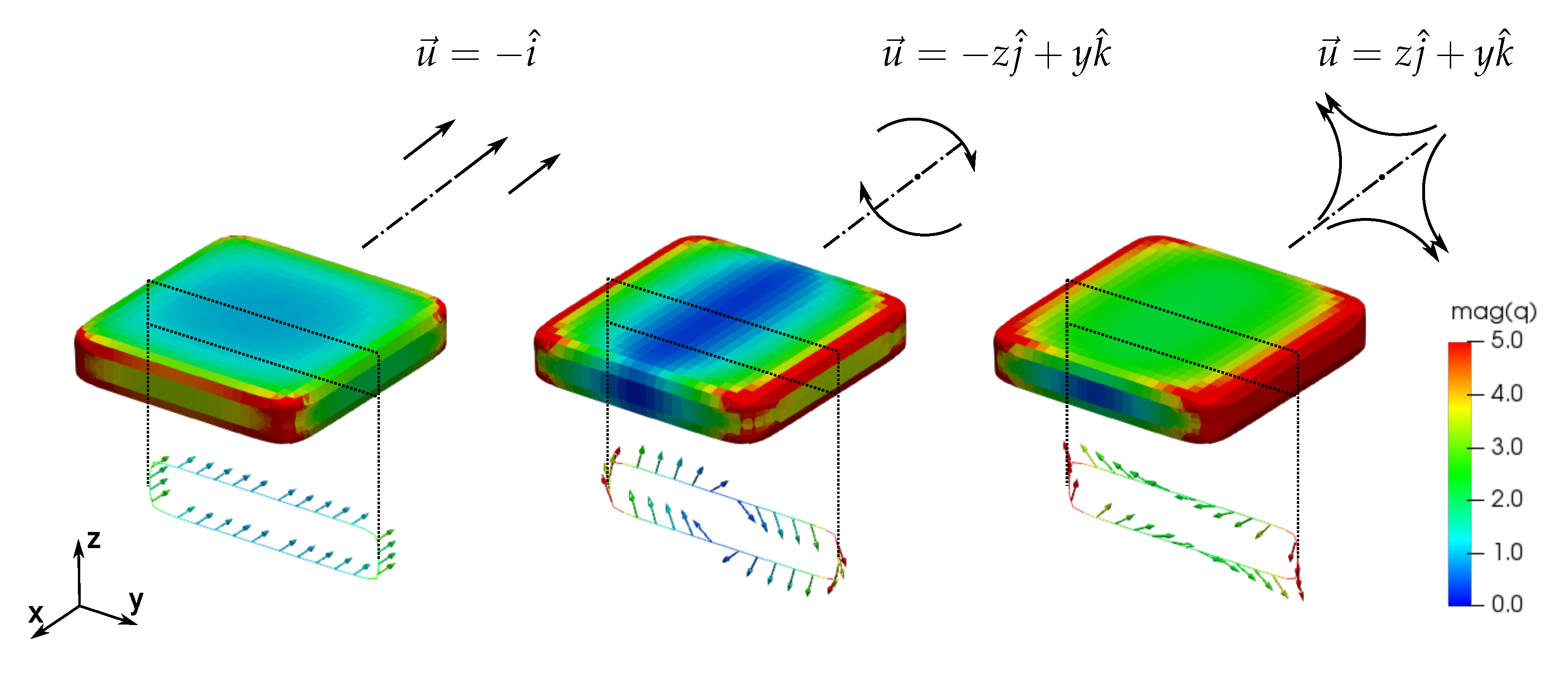
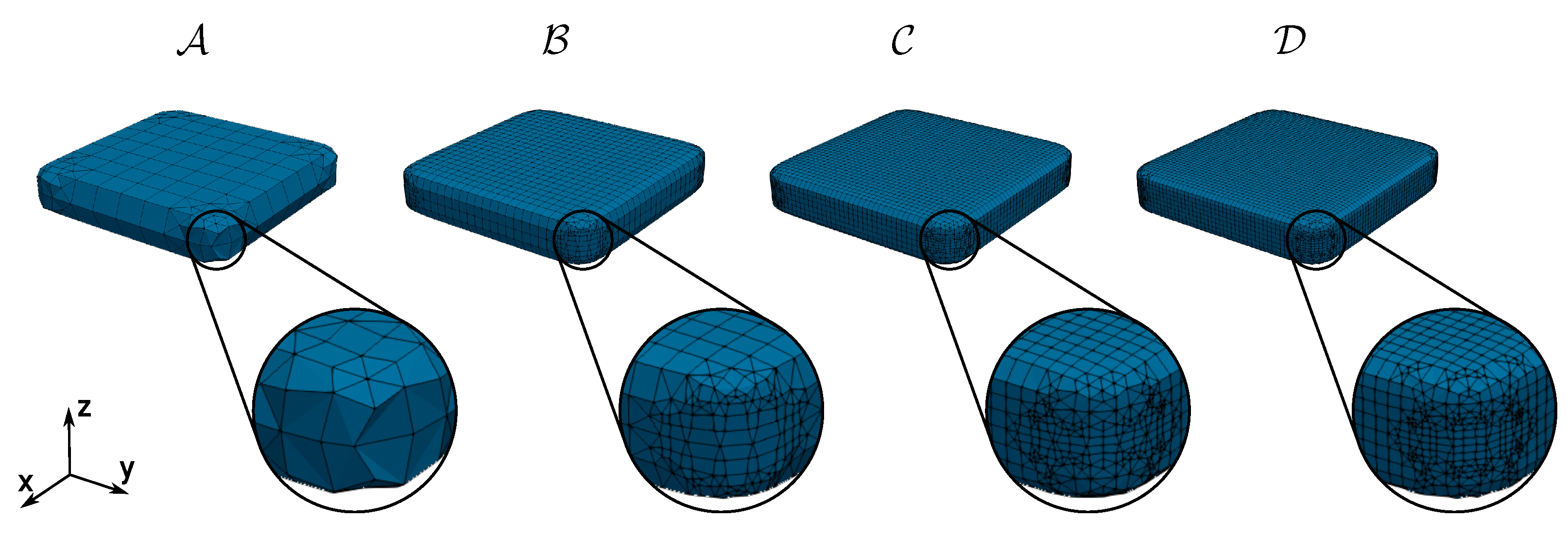

| Value | Analytical | Mesh | Mesh | Mesh | Mesh | |
|---|---|---|---|---|---|---|
| 1 | 6 | 5.953 | 6.002 | 6.009 | 6.012 | |
| 1 | 8 | 7.759 | 7.954 | 7.983 | 7.993 | |
| 1 | 0 | 0.006 | 0.002 | 0.004 | 0.000 | |
| 2 | 7.224 | 7.150 | 7.219 | 7.230 | 7.234 | |
| 2 | 8.273 | 8.217 | 8.274 | 8.285 | 8.289 | |
| 2 | 12.91 | 12.35 | 12.79 | 12.86 | 12.88 | |
| 2 | 24.08 | 23.58 | 23.93 | 24.01 | 24.04 | |
| 2 | 0 | 0.016 | 0.004 | −0.008 | 0.000 | |
| 2 | 14.45 | 14.42 | 14.40 | 14.43 | 14.46 | |
| 5 | 10.71 | 10.50 | 10.69 | 10.72 | 10.72 | |
| 5 | 14.23 | 14.00 | 14.22 | 14.25 | 14.26 | |
| 5 | 28.24 | 25.44 | 27.76 | 28.05 | 28.14 | |
| 5 | 185.6 | 179.2 | 184.3 | 185.0 | 185.3 | |
| 5 | 0 | −0.320 | 0.021 | −0.005 | 0.069 | |
| 5 | 171.3 | 166.4 | 170.3 | 170.8 | 171.1 |
| Particle a | Coeff. K | An. Res. | Pres. BEM | Sphere | Prolate ell. b | [27] | [28] | [29] | Approx. Scheme |
|---|---|---|---|---|---|---|---|---|---|
 | 6.0 | 6.002 | 6.0 | 6.0 | 6.046 | 5.845 | 5.871 | 6.003 | |
| 6.0 | 6.002 | 6.0 | 6.0 | 6.046 | 5.894 | 5.876 | 6.003 | ||
| 6.0 | 6.002 | 6.0 | 6.0 | 6.046 | 5.845 | 5.854 | 6.004 | ||
| Average error: | 0.0% | 0.0% | 0.44% | 1.34% | 1.28% | 0.03% | |||
 | 10.71 | 10.69 | 6.0 | 10.71 | 10.54 | 9.728 | 11.16 | 10.70 | |
| 14.23 | 14.22 | 6.0 | 14.23 | 10.54 | 12.23 | 12.03 | 14.23 | ||
| 14.23 | 14.22 | 6.0 | 14.23 | 10.54 | 12.12 | 11.97 | 14.24 | ||
| Average error: | 30.95% | 0.00% | 11.04% | 7.44% | 7.17% | 0.05% | |||
 | − | 15.50 | 6.0 | 10.71 | 15.24 | 14.73 | 16.39 | 15.50 | |
| − | 17.07 | 6.0 | 14.23 | 15.24 | 15.82 | 16.62 | 17.06 | ||
| − | 20.56 | 6.0 | 14.23 | 15.24 | 18.87 | 18.40 | 20.57 | ||
| Average error: | 37.91% | 15.08% | 8.00% | 4.00% | 3.78% | 0.02% | |||
 | − | 24.73 | 6.0 | 10.71 | 22.37 | 22.18 | 25.27 | 24.83 | |
| − | 24.73 | 6.0 | 14.23 | 22.37 | 22.22 | 25.29 | 24.82 | ||
| − | 30.92 | 6.0 | 14.23 | 22.37 | 27.97 | 28.25 | 30.98 | ||
| Average error: | 44.54% | 29.44% | 9.48% | 5.72% | 2.69% | 0.17% | |||
 | − | 32.33 | 6.0 | 15.88 | 29.76 | 30.00 | 35.39 | 32.40 | |
| − | 32.31 | 6.0 | 22.87 | 29.76 | 30.41 | 35.43 | 32.35 | ||
| − | 45.87 | 6.0 | 22.87 | 29.76 | 42.16 | 41.44 | 45.98 | ||
| Average error: | 47.62% | 25.16% | 10.93% | 4.08% | 5.47% | 0.11% | |||
| Particle a | Coeff. | An. Res. | Pres. BEM | Sphere | Prolate ell. b | Approx. Scheme |
|---|---|---|---|---|---|---|
 | 8.0 | 7.954 | 8.0 | 8.0 | 7.978 | |
| 8.0 | 7.954 | 8.0 | 8.0 | 7.978 | ||
| 8.0 | 7.954 | 8.0 | 8.0 | 7.968 | ||
| Average error: | 0.0% | 0.0% | 0.18% | |||
 | 28.24 | 27.76 | 8.0 | 28.24 | 27.91 | |
| 185.6 | 184.4 | 8.0 | 185.6 | 185.2 | ||
| 185.6 | 184.2 | 8.0 | 185.6 | 185.0 | ||
| Average error: | 47.41% | 0.0% | 0.19% | |||
 | − | 155.1 | 8.0 | 28.24 | 154.9 | |
| − | 316.3 | 8.0 | 185.6 | 316.8 | ||
| − | 303.0 | 8.0 | 185.6 | 303.3 | ||
| Average error: | 53.83% | 26.89% | 0.06% | |||
 | − | 782.0 | 8.0 | 28.24 | 784.5 | |
| − | 782.0 | 8.0 | 185.6 | 784.0 | ||
| − | 1023 | 8.0 | 185.6 | 1025 | ||
| Average error: | 56.71% | 48.40% | 0.14% | |||
 | − | 2443 | 8.0 | 54.44 | 2465 | |
| − | 2443 | 8.0 | 1069.4 | 2466 | ||
| − | 2656 | 8.0 | 1069.4 | 2677 | ||
| Average error: | 57.51% | 40.91% | 0.50% | |||
| Particle a | Coeff. | An. Res. | Pres. BEM | Sphere | Prolate ell. b | Approx. Scheme |
|---|---|---|---|---|---|---|
 | 0.0 | 0.001 | 0.0 | 0.0 | 0.001 | |
| 0.0 | 0.004 | 0.0 | 0.0 | 0.002 | ||
| 0.0 | 0.001 | 0.0 | 0.0 | 0.000 | ||
| Average error: | ||||||
 | 0.0 | 0.021 | 0.0 | 0.0 | 0.021 | |
| −171.3 | −170.4 | 0.0 | −171.3 | −171.1 | ||
| 171.3 | 170.2 | 0.0 | 171.3 | 170.8 | ||
| Average error: | 47.14% | 0.0% | 0.11% | |||
 | − | 124.1 | 0.0 | 0.0 | 123.7 | |
| − | −292.0 | 0.0 | −171.3 | −292.3 | ||
| − | 142.7 | 0.0 | 171.3 | 143.2 | ||
| Average error: | 53.54% | 26.20% | 0.11% | |||
 | − | 672.9 | 0.0 | 0.0 | 676.1 | |
| − | −671.9 | 0.0 | −171.3 | −675.2 | ||
| − | −0.083 | 0.0 | 171.3 | −0.006 | ||
| Average error: | 47.14% | 47.14% | 0.23% | |||
 | − | 2416 | 0.0 | 0.0 | 2440 | |
| − | −2414 | 0.0 | −1048.3 | −2440 | ||
| − | 0.744 | 0.0 | 1048.3 | −0.011 | ||
| Average error: | 47.15% | 47.13% | 0.49% | |||
| Coeff. , , | Pres. BEM | Sphere | Prolate ell. b | [27] | [28] | [29] | Approx. Scheme |
|---|---|---|---|---|---|---|---|
| 10.77 | 6.0 | 7.174 | 9.505 | 9.324 | 9.922 | 10.58 | |
| 10.80 | 6.0 | 8.184 | 9.505 | 9.431 | 9.968 | 10.71 | |
| 12.01 | 6.0 | 8.184 | 9.505 | 10.36 | 10.46 | 11.86 | |
| Average error: | 26.76% | 17.24% | 8.70% | 7.68% | 5.56% | 0.74% | |
| 50.07 | 8.0 | 12.70 | − | − | − | 47.23 | |
| 50.88 | 8.0 | 23.14 | − | − | − | 50.71 | |
| 63.20 | 8.0 | 23.14 | − | − | − | 61.65 | |
| Average error: | 49.00% | 36.77% | − | − | − | 1.60% | |
| 25.31 | 0.0 | 0.0 | − | − | − | 23.51 | |
| −26.22 | 0.0 | −13.57 | − | − | − | −27.56 | |
| 0.86 | 0.0 | 13.57 | − | − | − | 3.791 | |
| Average error: | 47.90% | 46.34% | − | − | − | 2.36% | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Štrakl, M.; Hriberšek, M.; Wedel, J.; Steinmann, P.; Ravnik, J. A Model for Translation and Rotation Resistance Tensors for Superellipsoidal Particles in Stokes Flow. J. Mar. Sci. Eng. 2022, 10, 369. https://doi.org/10.3390/jmse10030369
Štrakl M, Hriberšek M, Wedel J, Steinmann P, Ravnik J. A Model for Translation and Rotation Resistance Tensors for Superellipsoidal Particles in Stokes Flow. Journal of Marine Science and Engineering. 2022; 10(3):369. https://doi.org/10.3390/jmse10030369
Chicago/Turabian StyleŠtrakl, Mitja, Matjaž Hriberšek, Jana Wedel, Paul Steinmann, and Jure Ravnik. 2022. "A Model for Translation and Rotation Resistance Tensors for Superellipsoidal Particles in Stokes Flow" Journal of Marine Science and Engineering 10, no. 3: 369. https://doi.org/10.3390/jmse10030369
APA StyleŠtrakl, M., Hriberšek, M., Wedel, J., Steinmann, P., & Ravnik, J. (2022). A Model for Translation and Rotation Resistance Tensors for Superellipsoidal Particles in Stokes Flow. Journal of Marine Science and Engineering, 10(3), 369. https://doi.org/10.3390/jmse10030369







