Adaptive Formation Control of Unmanned Underwater Vehicles with Collision Avoidance under Unknown Disturbances
Abstract
:1. Introduction
- An adaptive formation control law of UUVs with collision avoidance under unknown bounded disturbance is proposed. The stability of the proposed method is proved, and simulation results are presented to verify its effectiveness;
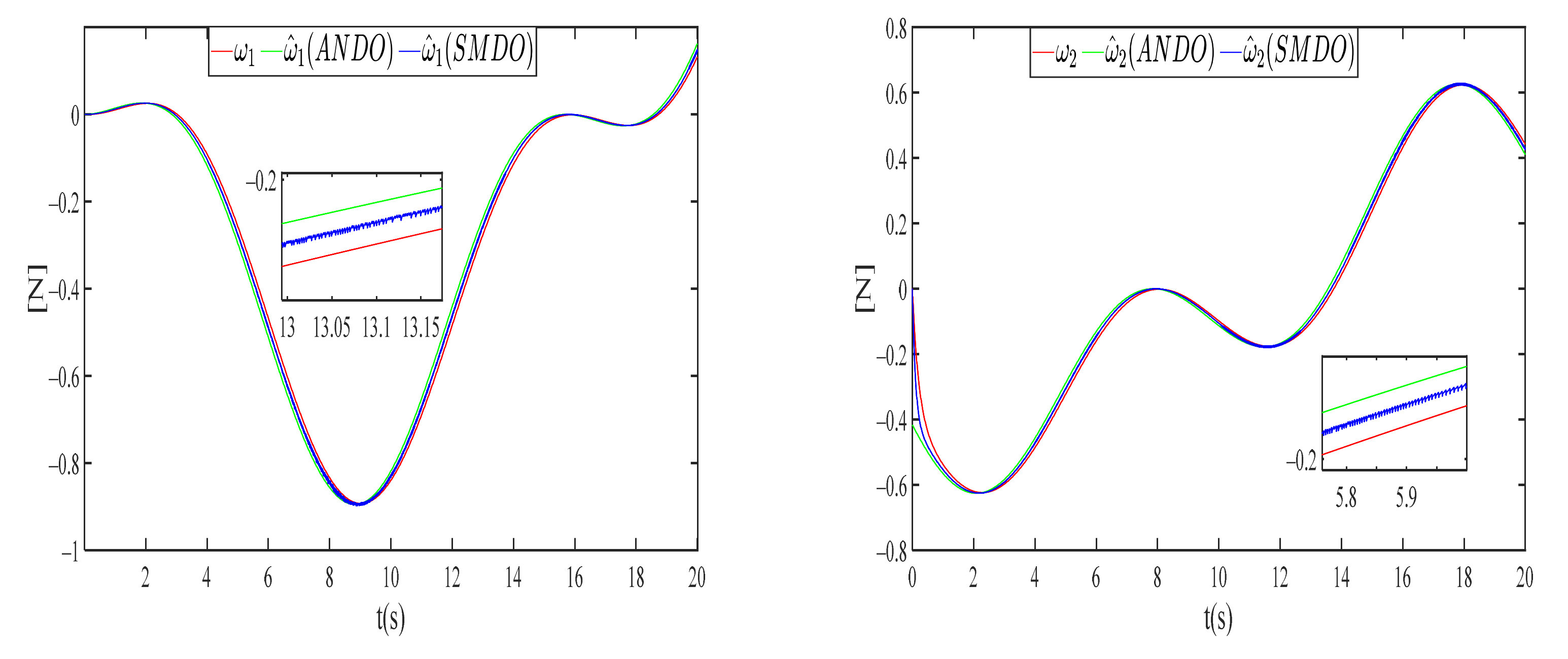
- Based on sliding mode control theory, a novel sliding mode disturbance observer was designed to approximate the unknown, nonlinear, and bounded disturbance. The simulation results show the observer achieves a good performance;
- The studies on collision avoidance for multi-UUV formation are mostly on the three degree of freedom (DOF)F model in the horizontal plane. The state feedback linearization method is used to transfer the nonlinear and coupling mathematical model of UUVs into a second-order system model in 5-DOF. The artificial potential field theory is applied to cope with the collision avoidance among the UUVs. The form of the potential function is much simpler;
- Based on the Lyapunov theory, the stability of the formation system is proven, and the proposed controller is valid and performs well, which can be seen in the 3-D simulation figures.
2. Preliminaries and Problem Formulation
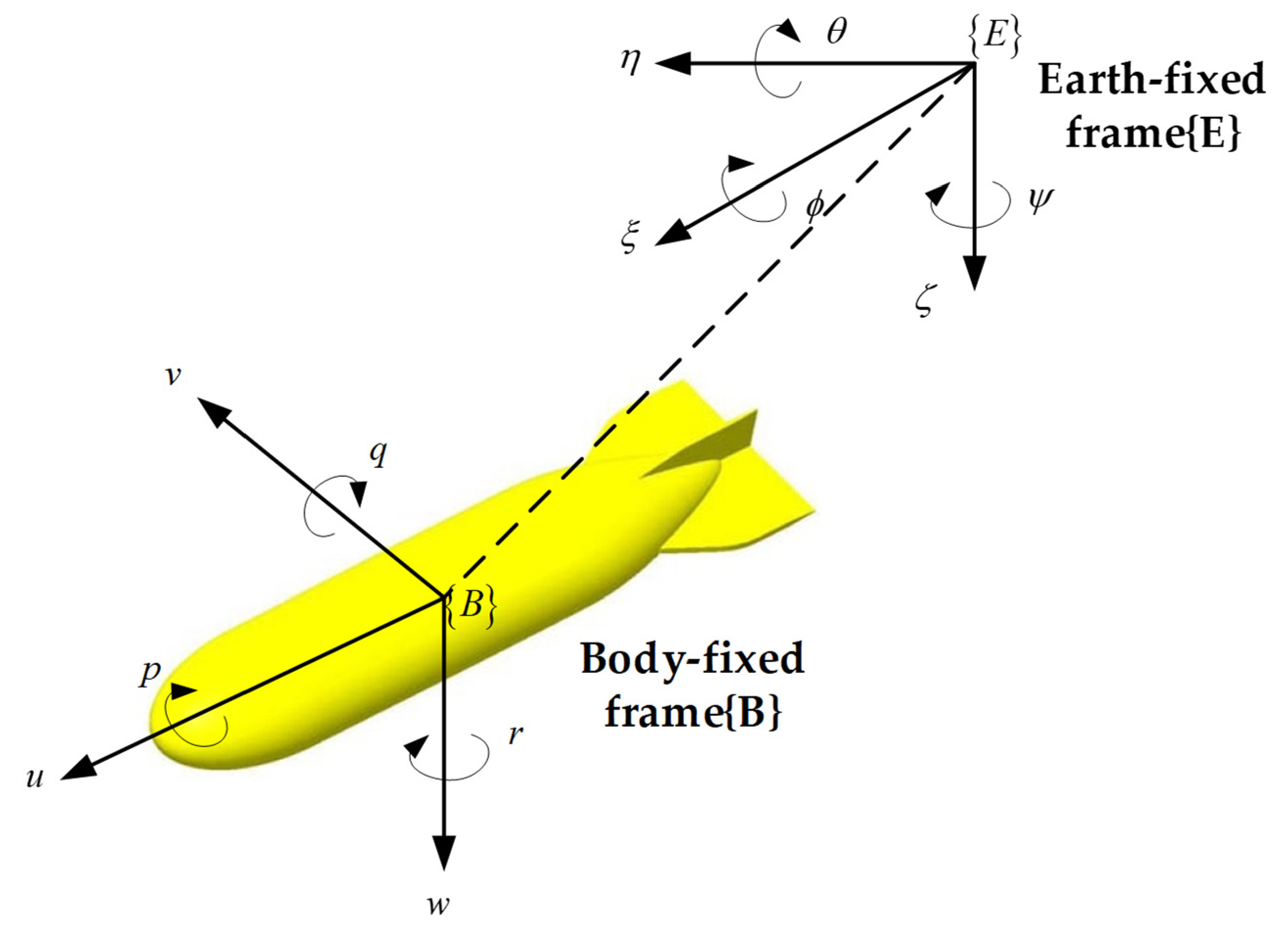
2.1. Feedback Linearization of UUV Model
2.2. Graph Theory
2.3. Artificial Potential Field
3. Adaptive Formation Control Scheme Design
3.1. Adaptive Sliding Mode Disturbance Observer Design
3.2. Adaptive Formation Control with Collision Avoidance under Unknown Disturbances
4. Experimental Results and Simulation
4.1. Disturbance Observer Simulation Result
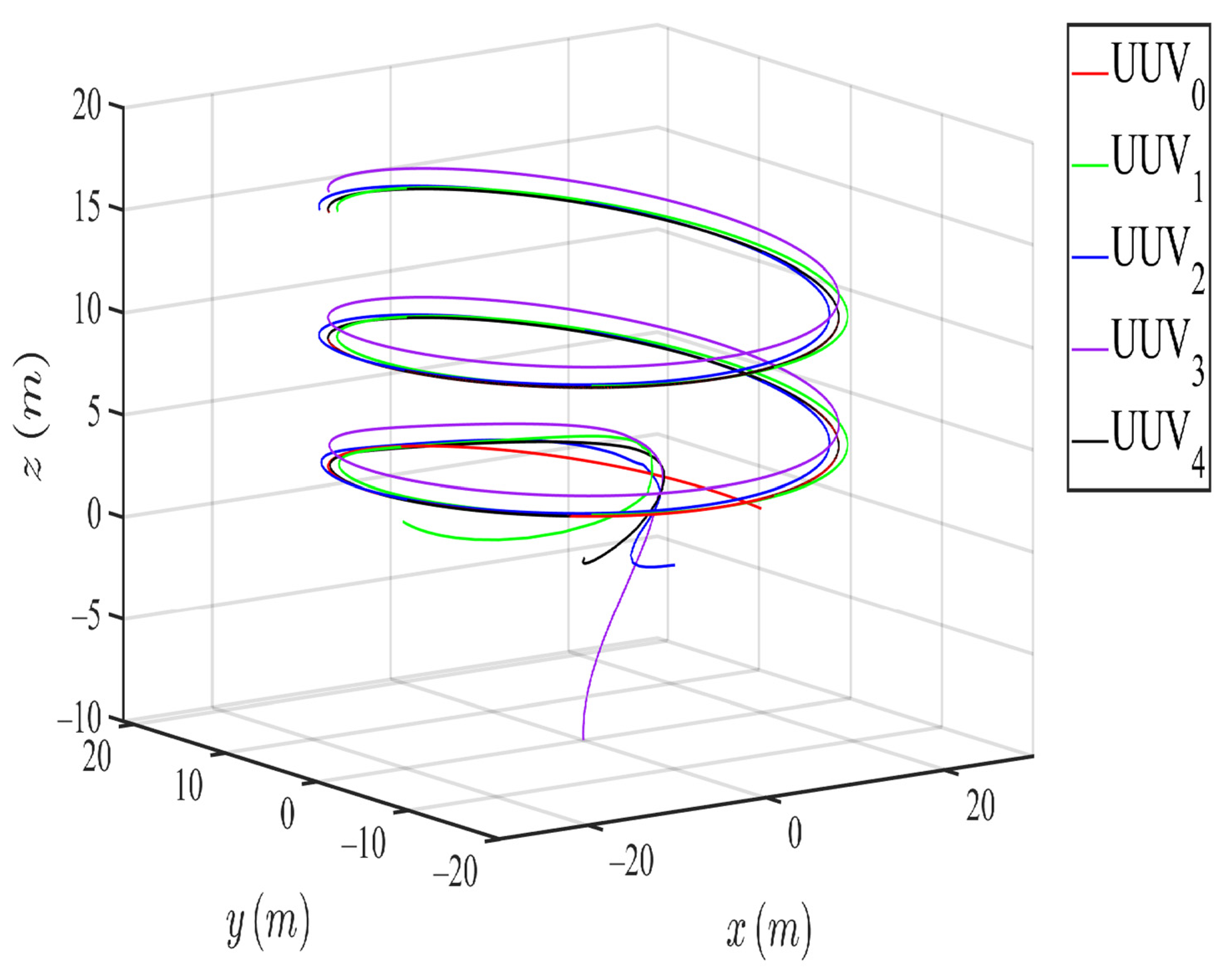
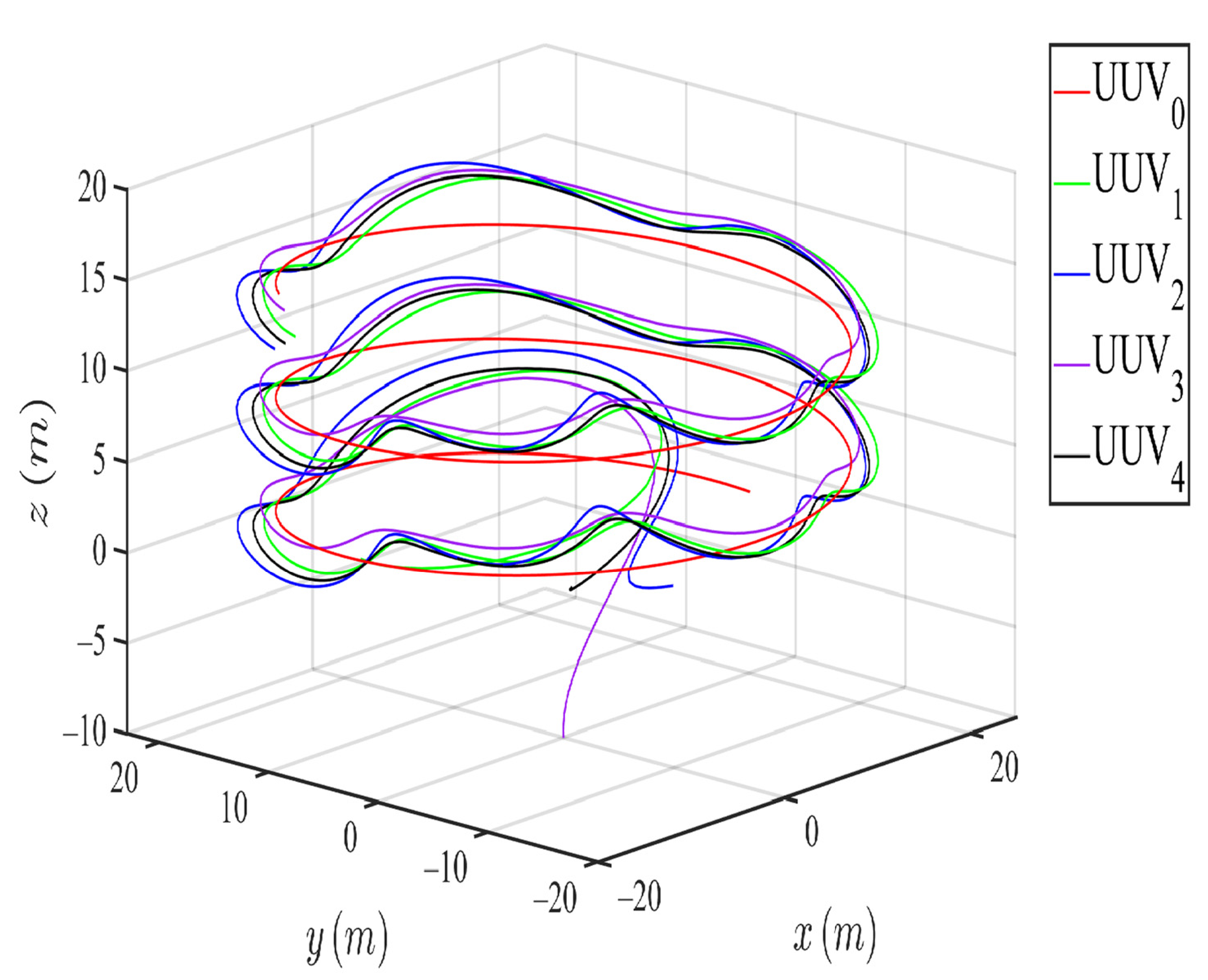
4.2. Collision Avoidance Simulation Result
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Liang, H.; Zhang, L.; Sun, Y.; Huang, T. Containment Control of Semi-Markovian Multiagent Systems with Switching Topologies. IEEE Trans. Syst. Man Cybern. Syst. 2019, 51, 3889–3899. [Google Scholar] [CrossRef]
- Liu, Y.; Shi, P.; Lim, C.-C. Collision-Free Formation Control for Multi-Agent Systems with Dynamic Mapping. IEEE Trans. Circuits Syst. II Express Briefs 2020, 67, 1984–1988. [Google Scholar] [CrossRef]
- Li, X.; Wen, C.; Chen, C. Adaptive Formation Control of Networked Robotic Systems with Bearing-Only Measurements. IEEE Trans. Cybern. 2021, 51, 199–209. [Google Scholar] [CrossRef] [PubMed]
- Zhou, K.-B.; Wu, X.-K.; Ge, M.-F.; Liang, C.-D.; Hu, B.-L. Neural-Adaptive Finite-Time Formation Tracking Control of Multiple Nonholonomic Agents with a Time-Varying Target. IEEE Access 2020, 8, 62943–62953. [Google Scholar] [CrossRef]
- Damasceno, B.C.; Xie, X. Deadlock-free scheduling of manufacturing systems using petri nets and dynamic programming. IFAC Proc. Vol. 1999, 32, 4870–4875. [Google Scholar] [CrossRef]
- Foumani, M.; Gunawan, I.; Smith-Miles, K. Resolution of deadlocks in a robotic cell scheduling problem with post-process inspection system: Avoidance and recovery scenarios. In Proceedings of the 2015 IEEE International Conference on Industrial Engineering and Engineering Management (IEEM), Singapore, 6–9 December 2015; pp. 1107–1111. [Google Scholar]
- Chen, W.; Wu, X.; Lu, Y. An Improved Path Planning Method Based on Artificial Potential Field for a Mobile Robot. Cybern. Inf. Technol. 2015, 15, 181–191. [Google Scholar] [CrossRef] [Green Version]
- Ghommam, J.; Saad, M. Backstepping-based cooperative and adaptive tracking control design for a group of underactuated AUVs in horizontal plan. Int. J. Control 2014, 87, 1076–1093. [Google Scholar] [CrossRef]
- Park, B.S. Adaptive formation control of underactuated autonomous underwater vehicles. Ocean Eng. 2015, 96, 1–7. [Google Scholar] [CrossRef]
- Huang, H.; Zhang, G.-C.; Li, Y.-M.; Li, J.-Y. Fuzzy sliding-mode formation control for multiple underactuated autonomous underwater vehicles. In Proceedings of the International Conference on Swarm Intelligence, Bali, Indonesia, 25–30 June 2016; pp. 503–510. [Google Scholar]
- Gao, Z.; Guo, G. Fixed-time sliding mode formation control of AUVs based on a disturbance observer. IEEE/CAA J. Autom. Sin. 2020, 7, 539–545. [Google Scholar] [CrossRef]
- Lu, Y.; Zhang, G.; Sun, Z.; Zhang, W. Robust adaptive formation control of underactuated autonomous surface vessels based on MLP and DOB. Nonlinear Dyn. 2018, 94, 503–519. [Google Scholar] [CrossRef]
- Park, B.S.; Kwon, J.-W.; Kim, H. Neural network-based output feedback control for reference tracking of underactuated surface vessels. Automatica 2017, 77, 353–359. [Google Scholar] [CrossRef]
- Franze, G.; Casavola, A.; Famularo, D.; Lucia, W. Distributed Receding Horizon Control of Constrained Networked Leader–Follower Formations Subject to Packet Dropouts. IEEE Trans. Control Syst. Technol. 2018, 26, 1798–1809. [Google Scholar] [CrossRef]
- Ajorlou, A.; Aghdam, A.G. A bounded distributed connectivity preserving aggregation strategy with collision avoidance property. Syst. Control Lett. 2013, 62, 1098–1104. [Google Scholar] [CrossRef]
- Sakai, D.; Fukushima, H.; Matsuno, F. Leader-Follower Navigation in Obstacle Environments While Preserving Connectivity without Data Transmission. IEEE Trans. Control Syst. Technol. 2018, 26, 1233–1248. [Google Scholar] [CrossRef] [Green Version]
- Dong, Y.; Su, Y.; Liu, Y.; Xu, S. An internal model approach for multi-agent rendezvous and connectivity preservation with nonlinear dynamics. Automatica 2018, 89, 300–307. [Google Scholar] [CrossRef]
- Wen, G.; Chen, C.L.P.; Liu, Y.-J. Formation Control with Obstacle Avoidance for a Class of Stochastic Multiagent Systems. IEEE Trans. Ind. Electron. 2018, 65, 5847–5855. [Google Scholar] [CrossRef]
- Park, B.S.; Yoo, S.J. An Error Transformation Approach for Connectivity-Preserving and Collision-Avoiding Formation Tracking of Networked Uncertain Underactuated Surface Vessels. IEEE Trans. Cybern. 2019, 49, 2955–2966. [Google Scholar] [CrossRef]
- Zhong, H.; Wang, Y.; Miao, Z.; Tan, J.; Li, L.; Zhang, H.; Fierro, R. Circumnavigation of a Moving Target in 3D by Multi-agent Systems with Collision Avoidance: An Orthogonal Vector Fields-based Approach. Int. J. Control Autom. Syst. 2019, 17, 212–224. [Google Scholar] [CrossRef]
- He, S.; Wang, M.; Dai, S.-L.; Luo, F. Leader–Follower Formation Control of USVs With Prescribed Performance and Collision Avoidance. IEEE Trans. Ind. Inform. 2019, 15, 572–581. [Google Scholar] [CrossRef]
- Huang, Y.; Liu, W.; Li, B.; Yang, Y.; Xiao, B. Finite-time formation tracking control with collision avoidance for quadrotor UAVs. J. Frankl. Inst. 2020, 357, 4034–4058. [Google Scholar] [CrossRef]
- Pan, L.; Bao, G.; Xu, F.; Zhang, L. Adaptive robust sliding mode trajectory tracking control for 6 degree-of-freedom industrial assembly robot with disturbances. Assem. Autom. 2018, 38, 259–267. [Google Scholar] [CrossRef]
- Chen, Z.; Yang, C.; Liu, X.; Wang, M. Learning control of flexible manipulator with unknown dynamics. Assem. Autom. 2017, 37, 304–313. [Google Scholar] [CrossRef]
- Yang, C.; Jiang, Y.; He, W.; Na, J.; Li, Z.; Xu, B. Adaptive Parameter Estimation and Control Design for Robot Manipulators with Finite-Time Convergence. IEEE Trans. Ind. Electron. 2018, 65, 8112–8123. [Google Scholar] [CrossRef]
- Nair, R.R.; Behera, L. Robust adaptive gain higher order sliding mode observer based control-constrained nonlinear model predictive control for spacecraft formation flying. IEEE/CAA J. Autom. Sin. 2016, 5, 367–381. [Google Scholar] [CrossRef]
- Hua, Y.; Dong, X.; Han, L.; Li, Q.; Ren, Z. Finite-Time Time-Varying Formation Tracking for High-Order Multiagent Systems with Mismatched Disturbances. IEEE Trans. Syst. Man Cybern. Syst. 2019, 50, 1–9. [Google Scholar] [CrossRef]
- Yan, Z.-P.; Liu, Y.-B.; Yu, C.-B.; Zhou, J.-J. Leader-following coordination of multiple UUVs formation under two independent topologies and time-varying delays. J. Cent. South Univ. 2017, 24, 382–393. [Google Scholar] [CrossRef]
- Shi, Q.; Li, T.; Li, J.; Chen, C.P.; Xiao, Y.; Shan, Q. Adaptive leader-following formation control with collision avoidance for a class of second-order nonlinear multi-agent systems. Neurocomputing 2019, 350, 282–290. [Google Scholar] [CrossRef]
- Yu, S.; Yu, X.; Shirinzadeh, B.; Man, Z. Continuous finite-time control for robotic manipulators with terminal sliding mode. Automatica 2005, 41, 1957–1964. [Google Scholar] [CrossRef]
- Wen, G.; Chen, C.L.P.; Dou, H.; Yang, H.; Liu, C. Formation control with obstacle avoidance of second-order multi-agent systems under directed communication topology. Sci. China Inf. Sci. 2019, 62, 1–14. [Google Scholar] [CrossRef] [Green Version]
- Pang, Z.-H.; Zheng, C.-B.; Sun, J.; Han, Q.-L.; Liu, G.-P. Distance- and Velocity-Based Collision Avoidance for Time-Varying Formation Control of Second-Order Multi-Agent Systems. IEEE Trans. Circuits Syst. II Express Briefs 2021, 68, 1253–1257. [Google Scholar] [CrossRef]
- Mondal, A.; Bhowmick, C.; Behera, L.; Jamshidi, M. Trajectory Tracking by Multiple Agents in Formation with Collision Avoidance and Connectivity Assurance. IEEE Syst. J. 2018, 12, 2449–2460. [Google Scholar] [CrossRef]
- Li, J.; Du, J.; Hu, X. Robust adaptive prescribed performance control for dynamic positioning of ships under unknown disturbances and input constraints. Ocean Eng. 2020, 206, 107254. [Google Scholar] [CrossRef]



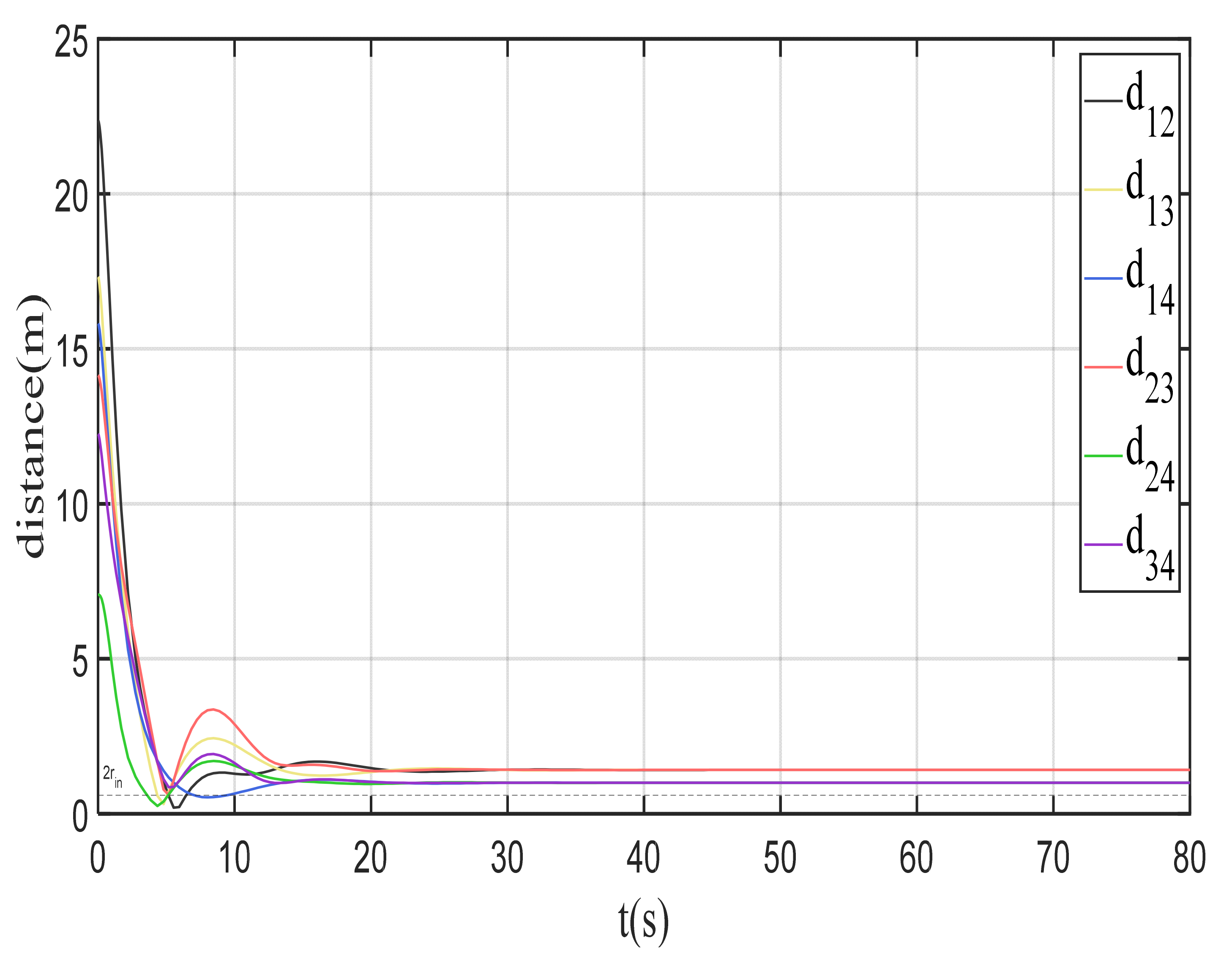
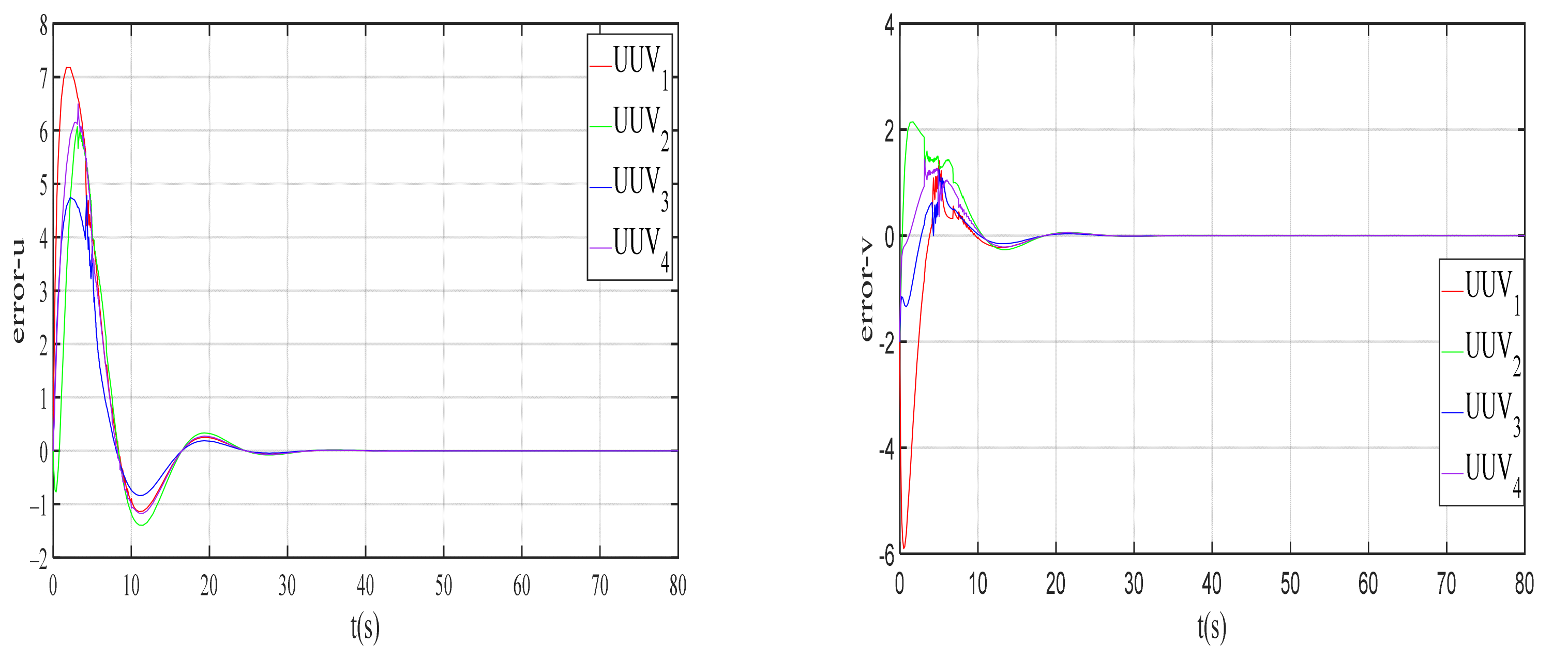
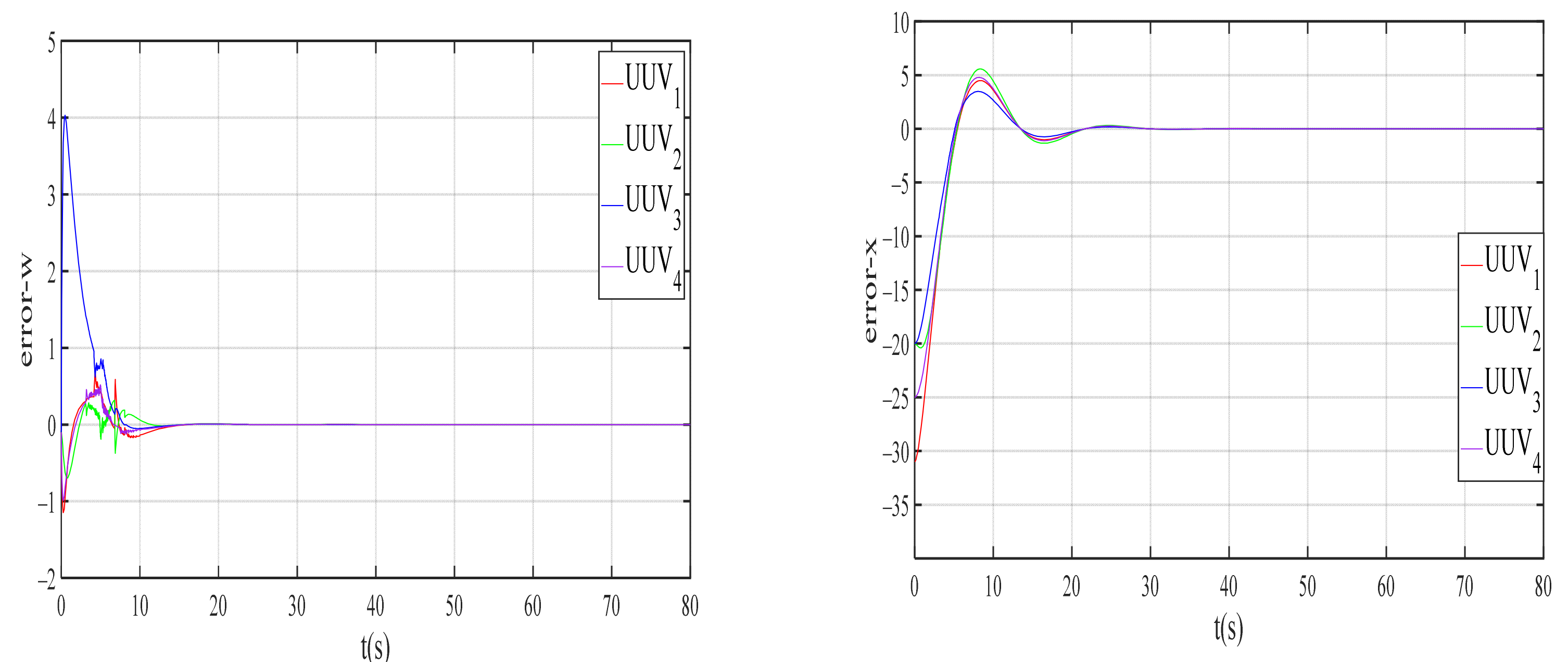
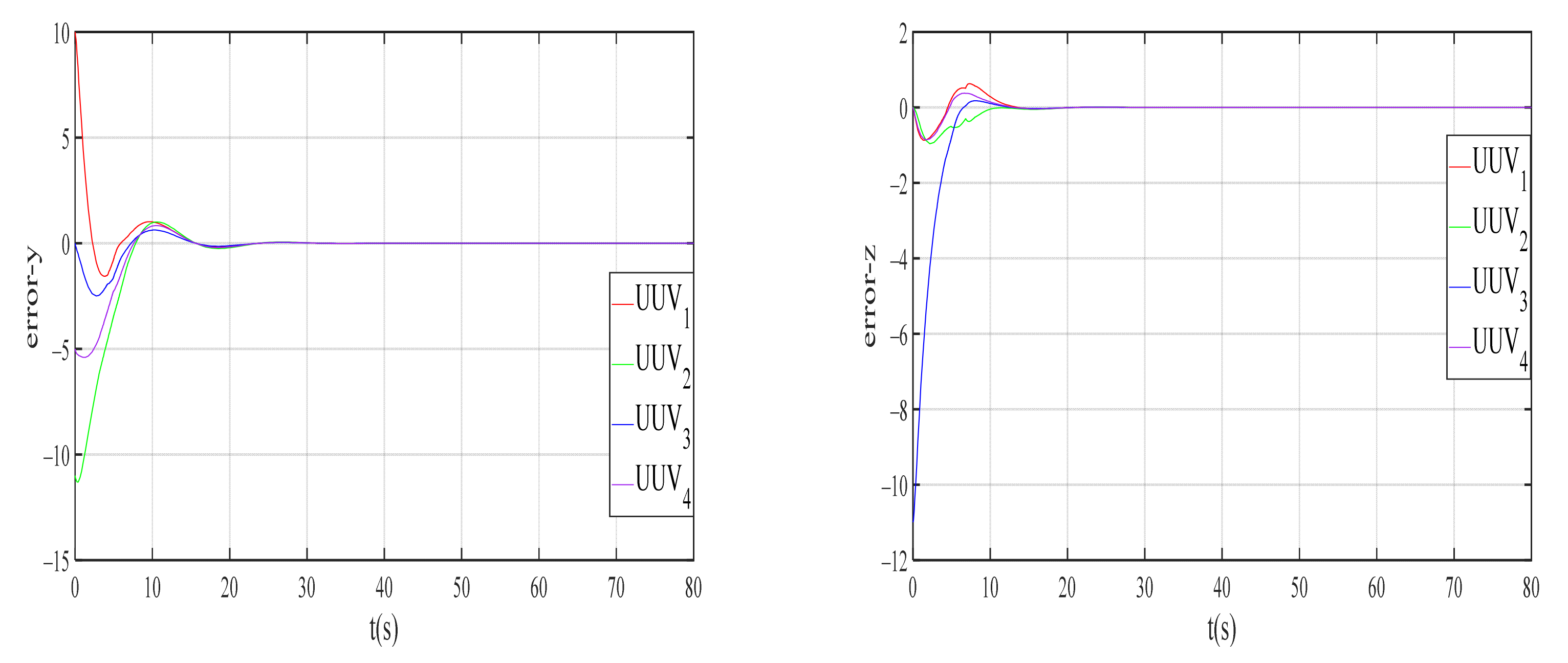
| Entry | Value | Entry | Value | Entry | Value |
|---|---|---|---|---|---|
| 0 | 0 | 1 | |||
| 1 | 1 | 2 | |||
| 0.3 | 1 | 5 | |||
| 0.8 | 2 | 2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, Z.; Jiang, A.; Lai, C. Adaptive Formation Control of Unmanned Underwater Vehicles with Collision Avoidance under Unknown Disturbances. J. Mar. Sci. Eng. 2022, 10, 516. https://doi.org/10.3390/jmse10040516
Yan Z, Jiang A, Lai C. Adaptive Formation Control of Unmanned Underwater Vehicles with Collision Avoidance under Unknown Disturbances. Journal of Marine Science and Engineering. 2022; 10(4):516. https://doi.org/10.3390/jmse10040516
Chicago/Turabian StyleYan, Zheping, Anzuo Jiang, and Chonglang Lai. 2022. "Adaptive Formation Control of Unmanned Underwater Vehicles with Collision Avoidance under Unknown Disturbances" Journal of Marine Science and Engineering 10, no. 4: 516. https://doi.org/10.3390/jmse10040516






