Numerical Investigation of the Sediment Hyperpycnal Flow in the Yellow River Estuary
Abstract
:1. Introduction
2. Methodology
2.1. Hydrodynamic Model
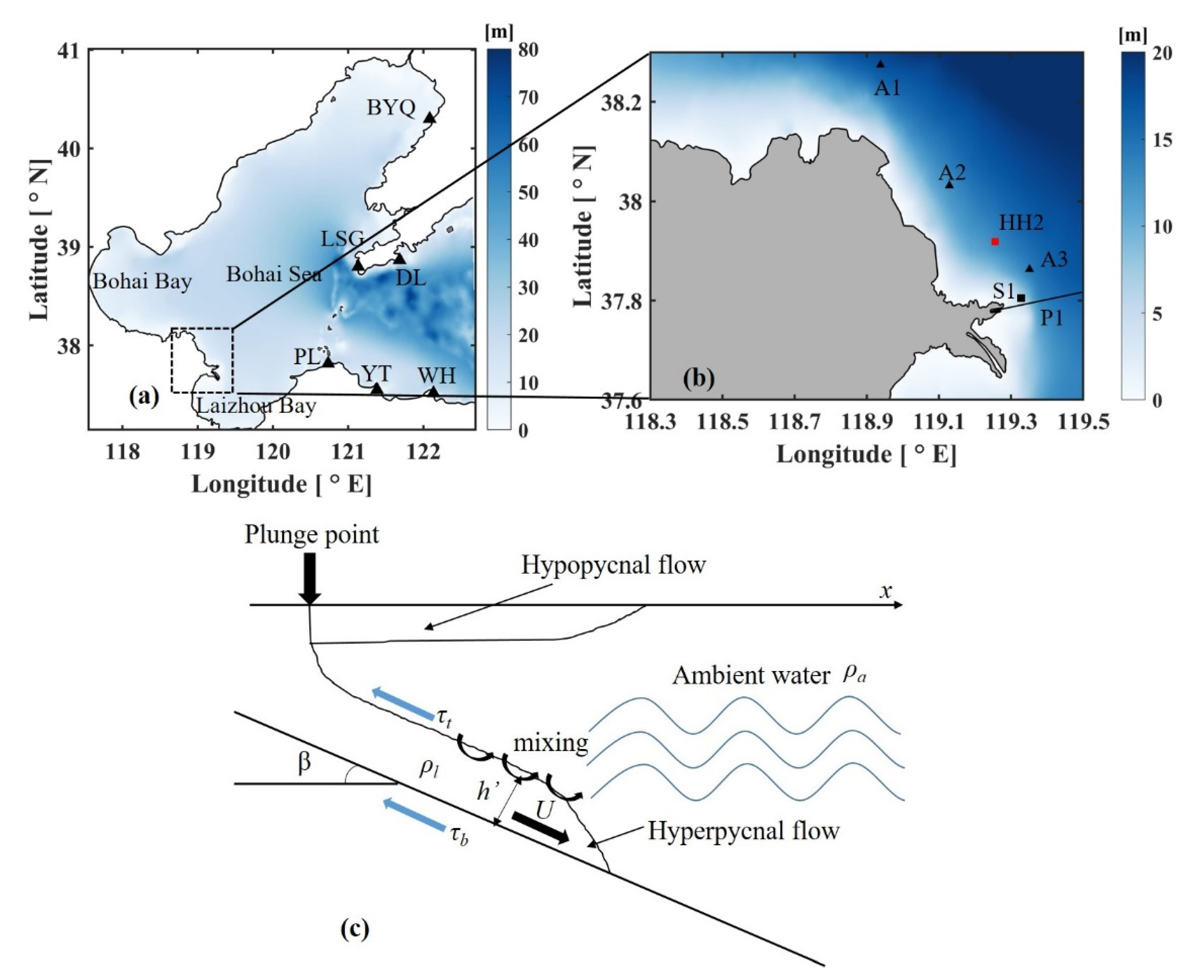
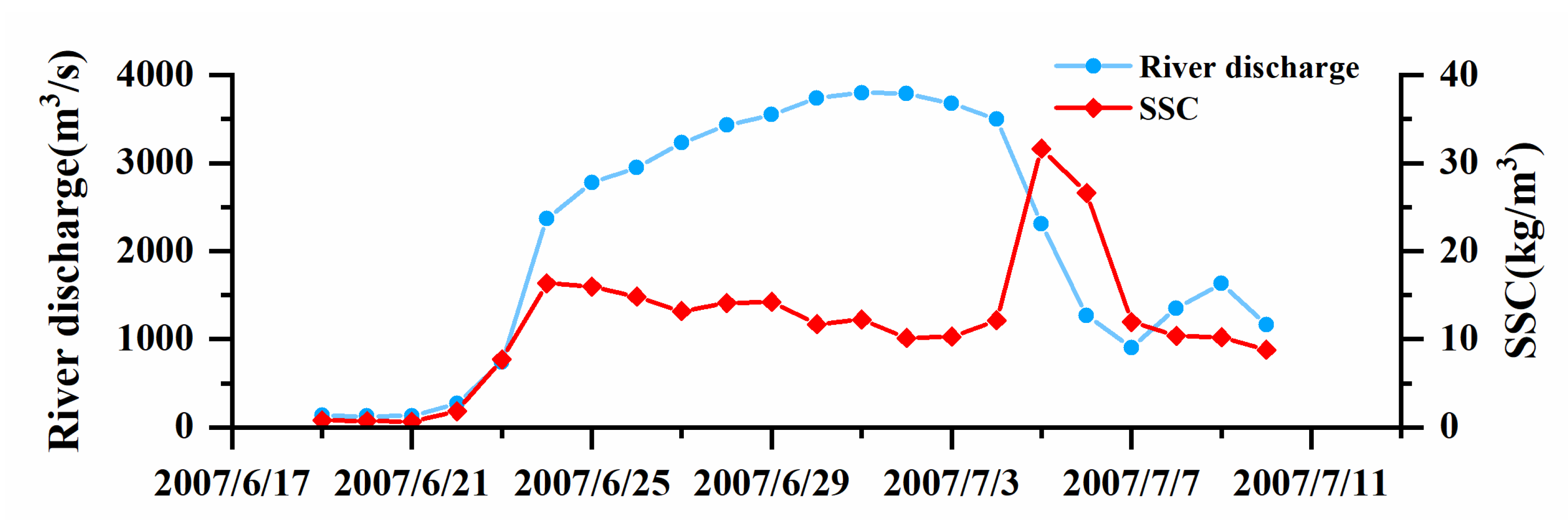
2.2. Model Configuration
2.3. Numerical Tests
2.4. Definition of Important Parameters of Hyperpycnal Flow
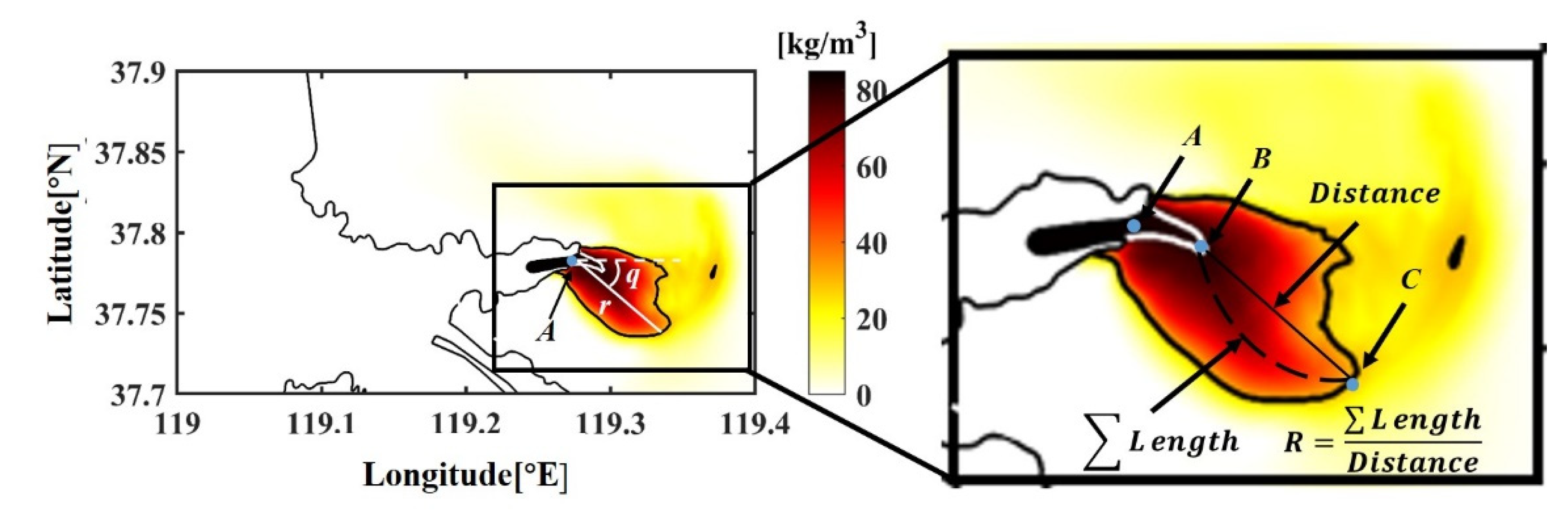
2.4.1. Path Index
2.4.2. Density
2.4.3. Potential Energy
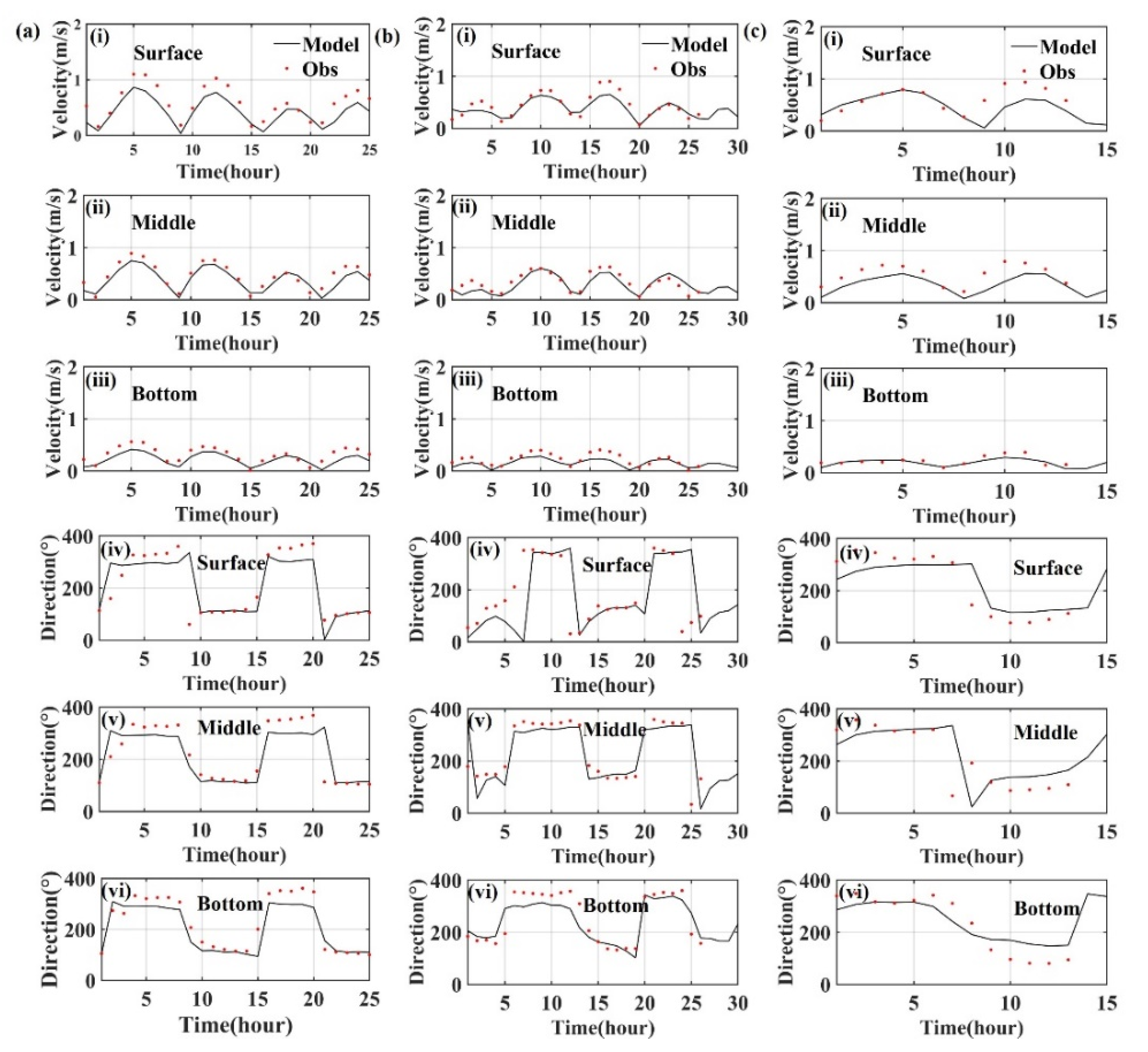
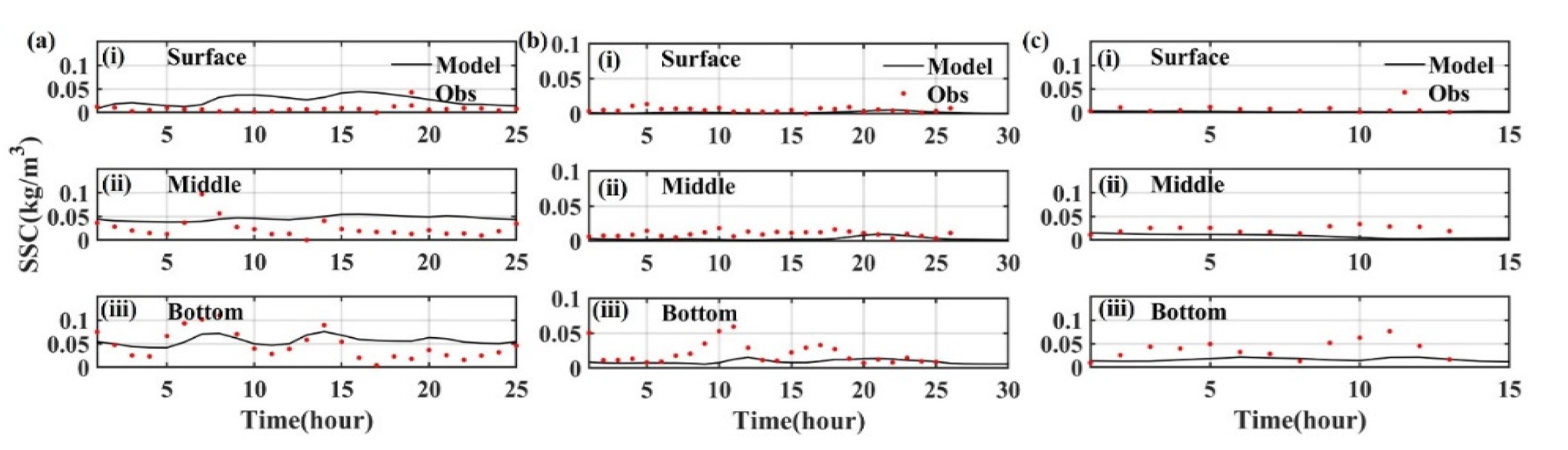
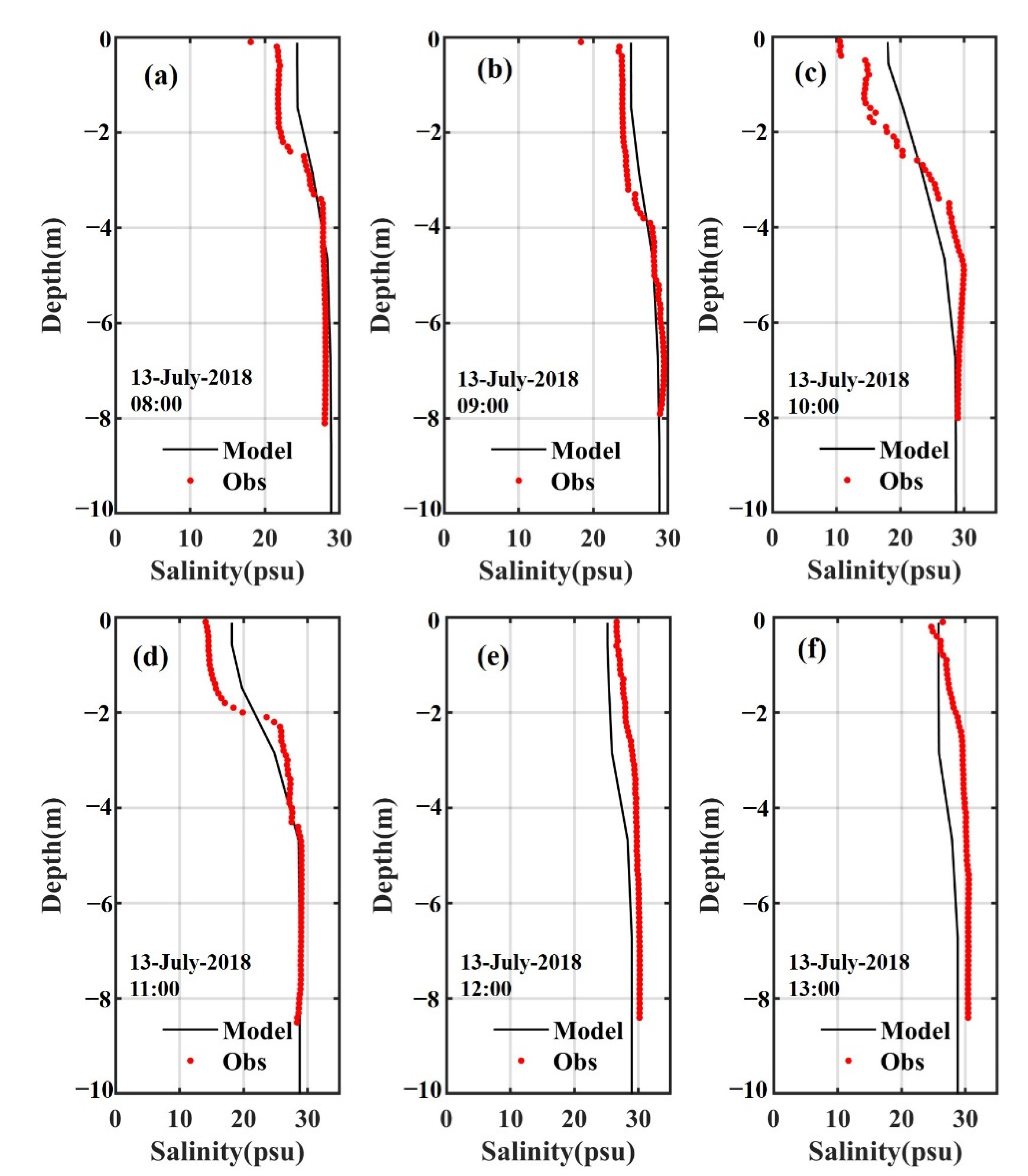
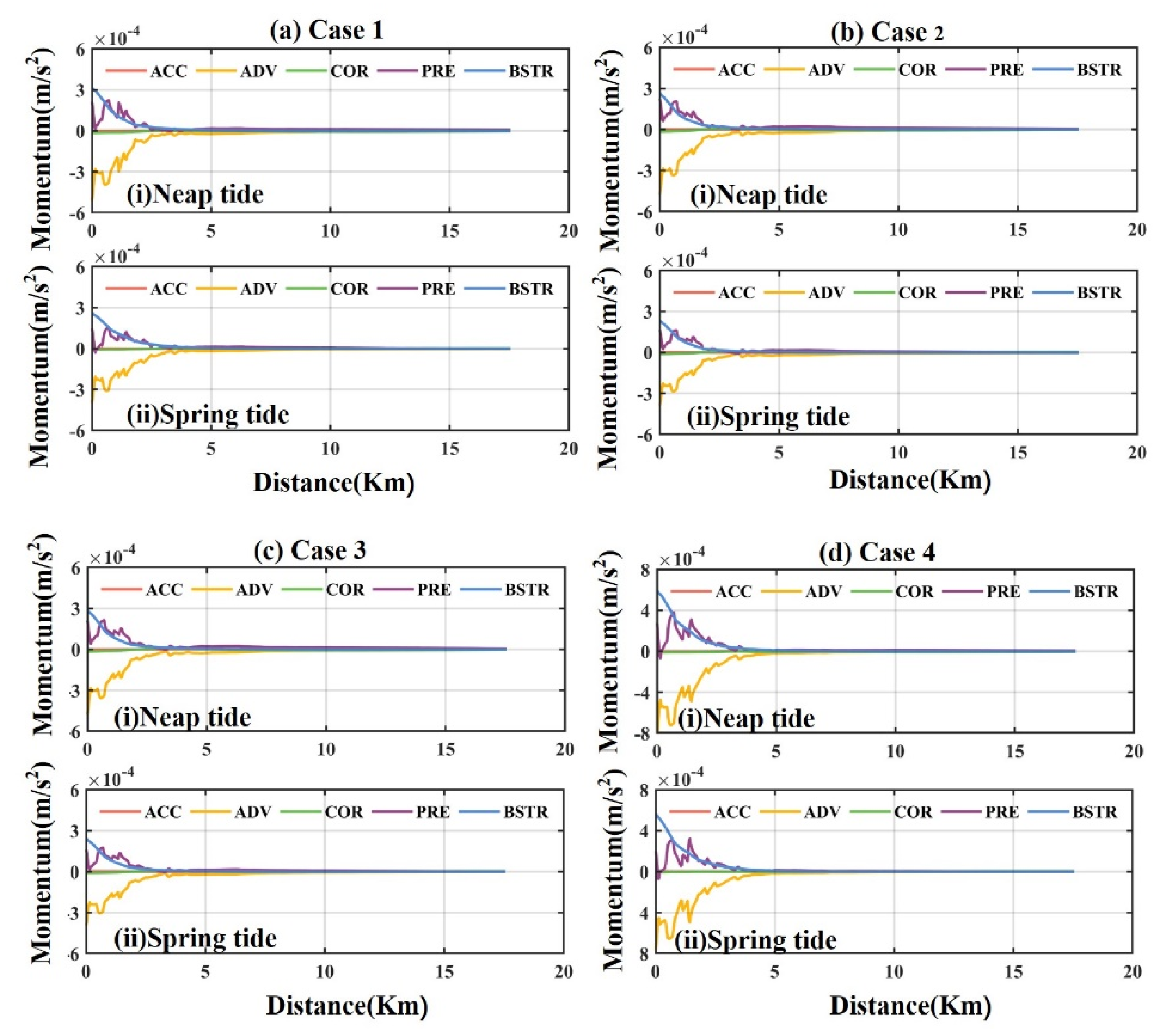
3. Model Validation
4. Results
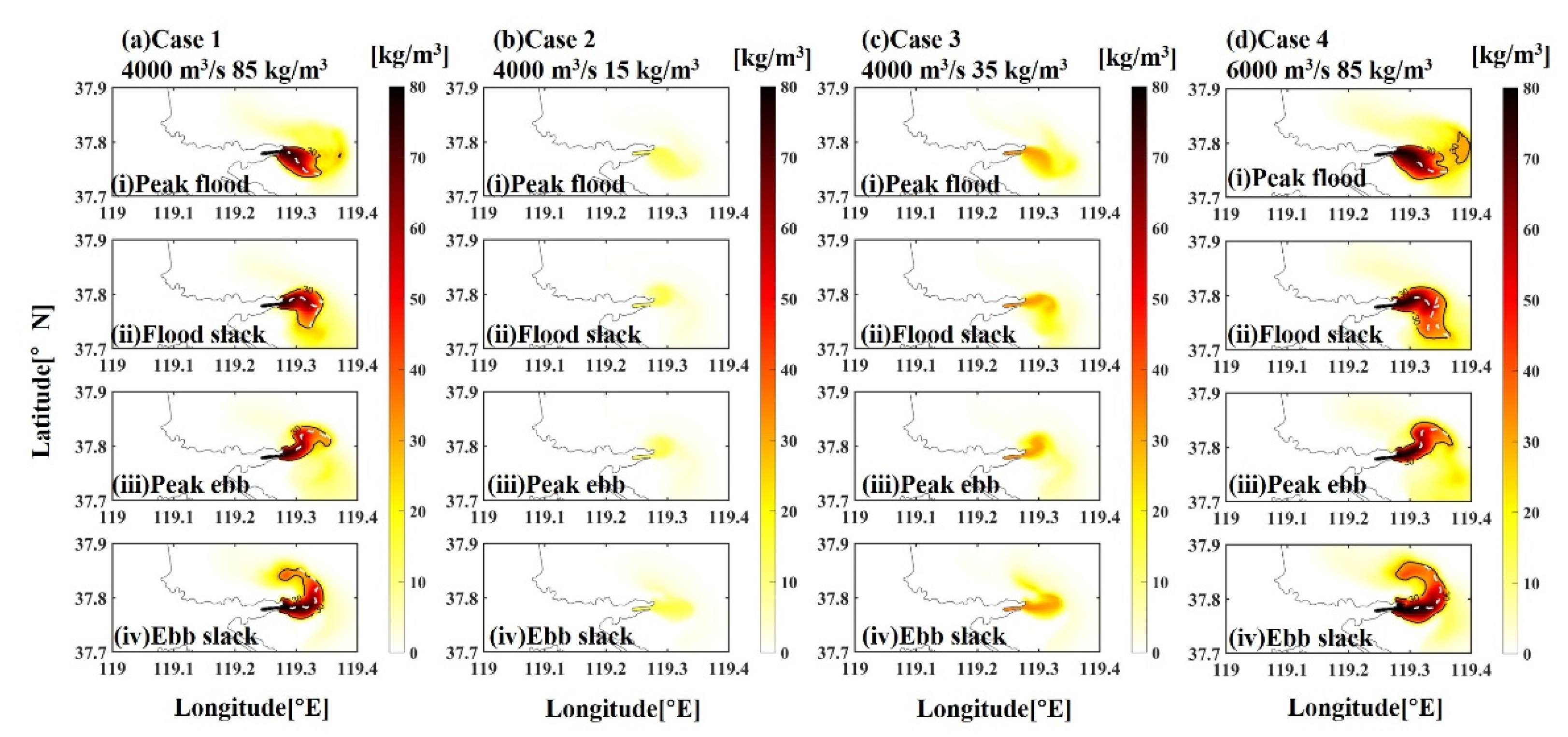
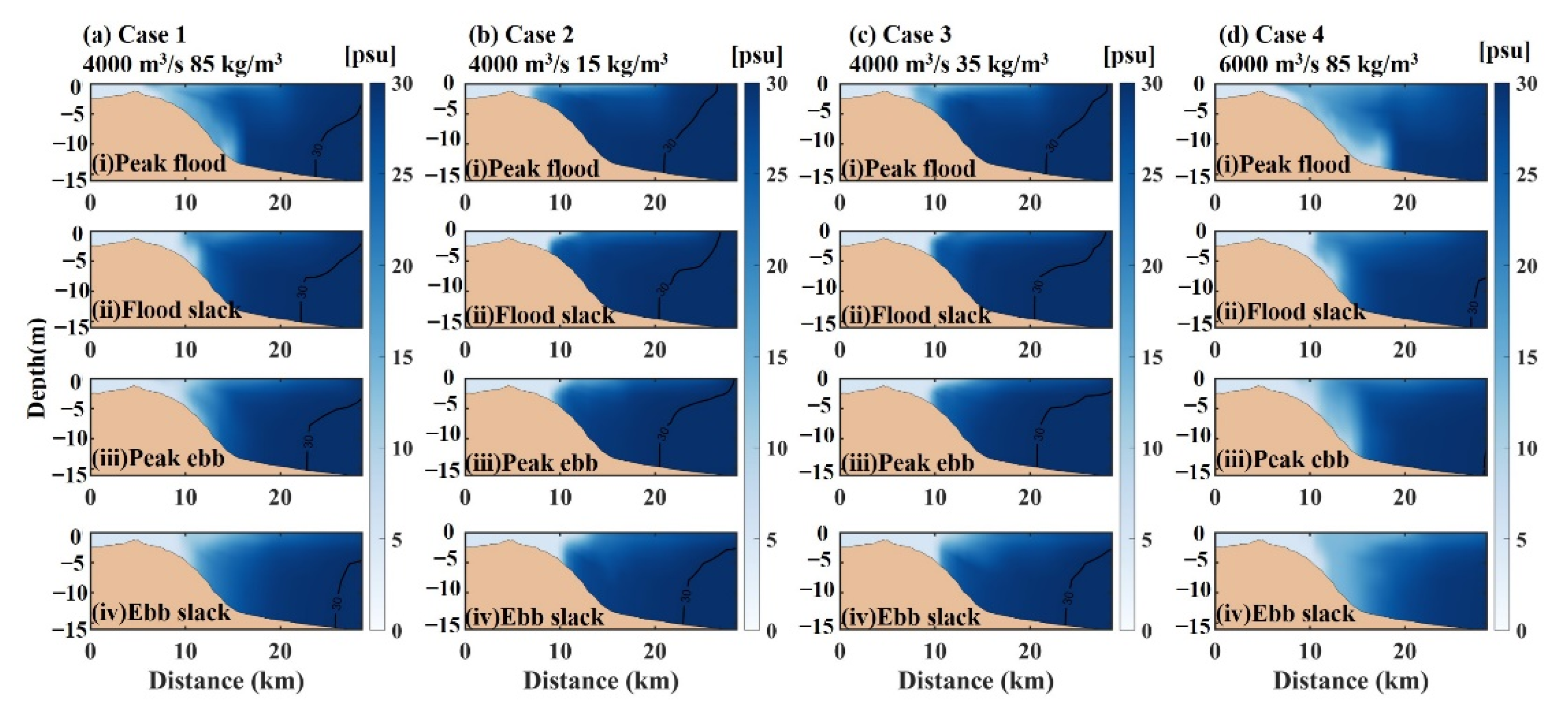
4.1. Variations of the Hyperpycnal Flow with Tides
4.2. Effects of River Sediment Load on Hyperpycnal Flows
4.3. Effects of River Discharge on Hyperpycnal Flows
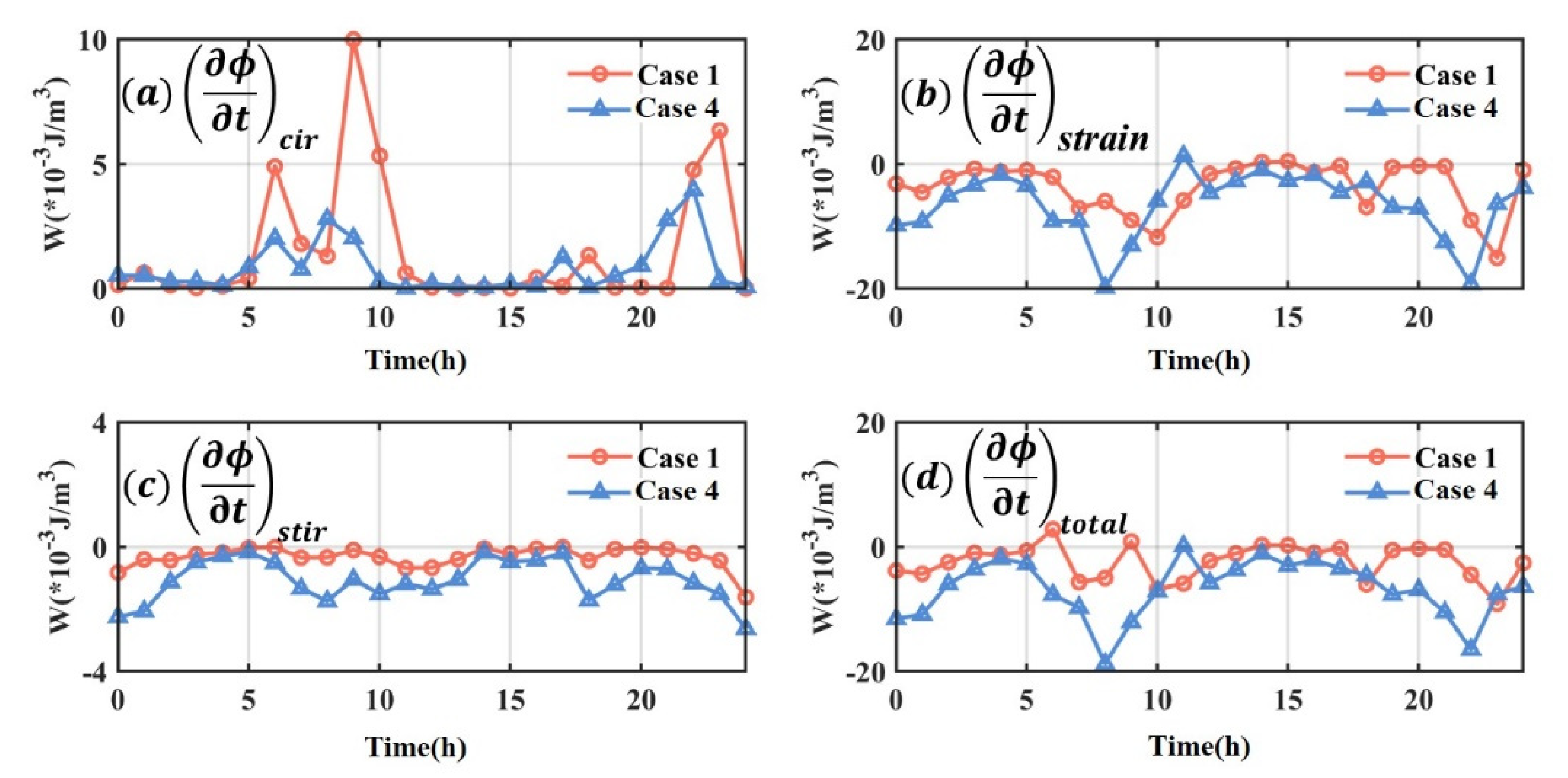
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Shanmugam, G. Global significance of wind forcing on deflecting sediment plumes at river mouths: Implications for hyperpycnal flows, sediment transport, and provenance. J. Indian Assoc. Sedimentol. 2019, 36, 1–37. [Google Scholar]
- Wright, L.D.; Friedrichs, C.T. Gravity-driven sediment transport on continental shelves: A status report. Cont. Shelf Res. 2006, 26, 2092–2107. [Google Scholar] [CrossRef]
- Shi, F.; Chickadel, C.C.; Hsu, T.J.; Kirby, J.T.; Farquharson, G.; Ma, G. High-resolution non-hydrostatic modeling of frontal features in the mouth of the Columbia River. Estuar Coast. 2017, 40, 296–309. [Google Scholar] [CrossRef]
- Wang, H.; Bi, N.; Wang, Y.; Saito, Y.; Yang, Z. Tide-modulated hyperpycnal flows off the Huanghe (Yellow River) mouth, China. Earth Surf. Process. Landf. 2010, 35, 1315–1329. [Google Scholar] [CrossRef]
- Bates, C.C. Rational theory of delta formation. Aapg Bull. 1953, 37, 2119–2162. [Google Scholar]
- Khan, S.M.; Imran, J.; Bradford, S.; Syvitski, J. Numerical modeling of hyperpycnal plume. Mar. Geol. 2005, 222, 193–211. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, H.; Bi, N.; Yang, Z. Numerical modeling of hyperpycnal flows in an idealized river mouth. Estuar. Coast. Shelf Sci. 2011, 93, 228–238. [Google Scholar] [CrossRef]
- Zhao, L.; Ouillon, R.; Vowinckel, B.; Meiburg, E.; Kneller, B.; He, Z. Transition of a Hyperpycnal Flow Into a Saline Turbidity Current Due to Differential Diffusivities. Geophys. Res. Lett. 2018, 45, 11875–11884. [Google Scholar] [CrossRef] [Green Version]
- Shanmugam, G. Mass Transport, Gravity Flows, and Bottom Currents: Downslope and Alongslope Processes and Deposits; Elsevier: Amsterdam, The Netherlands, 2020. [Google Scholar]
- Mulder, T.; Syvitski, J.P.M. Turbidity currents generated at river mouths during exceptional discharges to the world oceans. J. Geol. 1995, 103, 285–299. [Google Scholar] [CrossRef]
- Forel, F.A. Le Léman: Monographie Limnologique; F. Rouge: Dearborn, MI, USA, 1892. [Google Scholar]
- Bhattacharya, J.P.; MacEachern, J.A. Hyperpycnal rivers and prodeltaic shelves in the Cretaceous seaway of North America. J. Sediment. Res. 2009, 79, 184–209. [Google Scholar] [CrossRef]
- Gihm, Y.S.; Hwang, I.G. Lacustrine hyperpycnal flow deposits after explosive volcanic eruptions, Cretaceous Beolkeum Member, Wido Island, Korea. Geosci. J. 2016, 20, 157–166. [Google Scholar] [CrossRef]
- Collins, D.S.; Johnson, H.D.; Allison, P.A.; Guilpain, P.; Damit, A.R. Coupled ‘storm-flood’depositional model: Application to the Miocene–Modern Baram Delta Province, north-west Borneo. Sedimentology 2017, 64, 1203–1235. [Google Scholar] [CrossRef] [Green Version]
- Pan, S.; Liu, H.; Zavala, C.; Liu, C.; Liang, S.; Zhang, Q.; Bai, Z. Sublacustrine hyperpycnal channel-fan system in a large depression basin: A case study of Nen 1 Member, Cretaceous Nenjiang Formation in the Songliao Basin, NE China. Pet. Explor. Dev. 2017, 44, 911–922. [Google Scholar] [CrossRef]
- Ford, D.E.; Johnson, M.C. An Assessment of Reservoir Density Currents and Inflow Processes; Technical Report E-83-7; United States Army Engineer Waterways Experiment Station: Vicksburg, MS, USA, 1983. [Google Scholar]
- Mulder, T.; Syvitski, J.P.M.; Migeon, S.; Faugères, J.-C.; Savoye, B. Marine hyperpycnal flows: Initiation, behavior and related deposits. A review. Mar. Pet. Geol. 2003, 20, 861–882. [Google Scholar] [CrossRef]
- Mountjoy, J.J.; Howarth, J.D.; Orpin, A.R.; Barnes, P.M.; Bowden, D.A.; Rowden, A.A.; Schimel, A.C.; Holden, C.; Horgan, H.J.; Nodder, S.D.; et al. Earthquakes drive large-scale submarine canyon development and sediment supply to deep-ocean basins. Sci. Adv. 2018, 4, eaar3748. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wright, L.D.; Wiseman, W.J.; Bornhold, B.D.; Prior, D.B.; Suhayda, J.N.; Keller, G.H.; Yang, Z.-S.; Fan, Y.B. Marine dispersal and deposition of Yellow River silts by gravity-driven underflows. Nature 1988, 332, 629–632. [Google Scholar] [CrossRef]
- Wang, H.; Bi, N.; Saito, Y.; Wang, Y.; Sun, X.; Zhang, J.; Yang, Z. Recent changes in sediment delivery by the Huanghe (Yellow River) to the sea: Causes and environmental implications in its estuary. J. Hydrol. 2010, 391, 302–313. [Google Scholar] [CrossRef]
- Lamb, M.P.; Mohrig, D. Do hyperpycnal-flow deposits record river-flood dynamics? Geology 2009, 37, 1067–1070. [Google Scholar] [CrossRef]
- Snow, K.; Sutherland, B.R. Particle-laden flow down a slope in uniform stratification. J. Fluid Mech. 2014, 755, 251–273. [Google Scholar] [CrossRef] [Green Version]
- He, Z.; Zhao, L.; Lin, T.; Hu, P.; Lv, Y.; Ho, H.-C.; Lin, Y.-T. Hydrodynamics of Gravity Currents down a Ramp in Linearly Stratified Environments. J. Hydraul. Eng. 2017, 143, 04016085. [Google Scholar] [CrossRef]
- Wilson, R.I.; Friedrich, H.; Stevens, C. Turbulent entrainment in sediment-laden flows interacting with an obstacle. Phys. Fluids 2017, 29, 036603. [Google Scholar] [CrossRef]
- Zordan, J.; Juez, C.; Schleiss, A.J.; Franca, M.J. Entrainment, transport and deposition of sediment by saline gravity currents. Adv. Water Resour. 2018, 115, 17–32. [Google Scholar] [CrossRef]
- He, Z.; Zhu, R.; Zhao, L.; Chen, J.; Lin, Y.-T.; Yuan, Y. Hydrodynamics of weakly and strongly stratified two-layer lock-release gravity currents. J. Hydraul. Res. 2021, 59, 989–1003. [Google Scholar] [CrossRef]
- Wang, X.H.; Wang, H. Tidal straining effect on the suspended sediment transport in the Huanghe (Yellow River) Estuary, China. Ocean Dyn. 2010, 60, 1273–1283. [Google Scholar] [CrossRef]
- Wright, L.D.; Wiseman, W.J., Jr.; Yang, Z.S.; Bornhold, B.D.; Keller, G.H.; Prior, D.B.; Suhayda, J.N. Processes of marine dispersal and deposition of suspended silts off the modern mouth of the Huanghe (Yellow River). Cont. Shelf Res. 1990, 10, 1–40. [Google Scholar] [CrossRef]
- Peakall, J.; Kane, I.A.; Masson, D.G.; Keevil, G.; McCaffrey, W.; Corney, R. Global (latitudinal) variation in submarine channel sinuosity. Geology 2012, 40, 11–14. [Google Scholar] [CrossRef]
- Davarpanah Jazi, S.; Wells, M.G.; Peakall, J.; Dorrell, R.M.; Thomas, R.E.; Keevil, G.M.; Darby, S.E.; Sommeria, J.; Viboud, S.; Valran, T. Influence of Coriolis force upon bottom boundary layers in a large-scale gravity current experiment: Implications for evolution of sinuous deep-water channel systems. J. Geophys. Res. Ocean. 2020, 125, e2019JC015284. [Google Scholar] [CrossRef]
- Tseng, C.-Y.; Chou, Y.-J. Nonhydrostatic simulation of hyperpycnal river plumes on sloping continental shelves: Flow structures and nonhydrostatic effect. Ocean Model. 2018, 124, 33–47. [Google Scholar] [CrossRef]
- Yu, J.; Fu, Y.; Li, Y.; Han, G.; Wang, Y.; Zhou, D.; Sun, W.; Gao, Y.; Meixner, F.X. Effects of water discharge and sediment load on evolution of modern Yellow River Delta, China, over the period from 1976 to 2009. Biogeosciences 2011, 8, 2427–2435. [Google Scholar] [CrossRef] [Green Version]
- Milliman, J.D. River inputs. In Encyclopedia of Ocean Sciences; Steele, J.H., Turekian, K.K., Thorpe, S.A., Eds.; Academic Press: Cambridge, UK; London, UK, 2001; Volume 4, pp. 2419–2427. [Google Scholar]
- Milliman, J.D.; Meade, R.H. World-wide delivery of river sediment to the oceans. J. Geol. 1983, 91, 1–21. [Google Scholar] [CrossRef]
- Chen, S.-N.; Geyer, W.R.; Hsu, T.-J. A numerical investigation of the dynamics and structure of hyperpycnal river plumes on sloping continental shelves. J. Geophys. Res. Oceans 2013, 118, 2702–2718. [Google Scholar] [CrossRef]
- Bi, N.; Wang, H.; Yang, Z. Recent changes in the erosion–accretion patterns of the active Huanghe (Yellow River) delta lobe caused by human activities. Cont. Shelf Res. 2014, 90, 70–78. [Google Scholar] [CrossRef]
- Wu, X.; Bi, N.; Yuan, P.; Li, S.; Wang, H. Sediment dispersal and accumulation off the present Huanghe (Yellow River) delta as impacted by the Water-Sediment Regulation Scheme. Cont. Shelf Res. 2015, 111, 126–138. [Google Scholar] [CrossRef]
- Fan, Y.; Chen, S.; Pan, S.; Dou, S. Storm-induced hydrodynamic changes and seabed erosion in the littoral area of Yellow River Delta: A model-guided mechanism study. Cont. Shelf Res. 2020, 205, 104171. [Google Scholar] [CrossRef]
- Ji, H.; Pan, S.; Chen, S. Impact of river discharge on hydrodynamics and sedimentary processes at Yellow River Delta. Mar. Geol. 2020, 425, 106210. [Google Scholar] [CrossRef]
- Chen, C.; Liu, H.; Beardsley, R.C. An unstructured grid, finite-volume, three-dimensional, primitive equations ocean model: Application to coastal ocean and estuaries. J. Atmos. Ocean. Technol. 2003, 20, 159–186. [Google Scholar] [CrossRef]
- Wu, L.; Chen, C.; Guo, P.; Shi, M.; Qi, J.; Ge, J. A FVCOM-based unstructured grid wave, current, sediment transport model, I. Model description and validation. J. Ocean Univ. China 2011, 10, 1–8. [Google Scholar] [CrossRef]
- Warner, J.C.; Sherwood, C.R.; Signell, R.P.; Harris, C.K.; Arango, H.G. Development of a three-dimensional, regional, coupled wave, current, and sediment-transport model. Comput. Geosci. 2008, 34, 1284–1306. [Google Scholar] [CrossRef]
- Smagorinsky, J. General circulation experiments with the primitive equations: I. The basic experiment. Mon. Weather Rev. 1963, 91, 99–164. [Google Scholar] [CrossRef]
- Mellor, G.L.; Yamada, T. Development of a turbulence closure model for geophysical fluid problems. Rev. Geophys. 1982, 20, 851–875. [Google Scholar] [CrossRef] [Green Version]
- Winterwerp, J.C. Stratification effects by cohesive and noncohesive sediment. J. Geophys. Res. Ocean. 2001, 106, 22559–22574. [Google Scholar] [CrossRef] [Green Version]
- Wang, X.H. Tide-induced sediment resuspension and the bottom boundary layer in an idealized estuary with a muddy bed. J. Phys. Oceanogr. 2002, 32, 3113–3131. [Google Scholar] [CrossRef]
- Wang, X.H.; Byun, D.S.; Wang, X.L.; Cho, Y.K. Modelling tidal currents in a sediment stratified idealized estuary. Cont. Shelf Res. 2005, 25, 655–665. [Google Scholar] [CrossRef]
- Adams, C.E., Jr.; Weatherly, G.L. Some effects of suspended sediment stratification on an oceanic bottom boundary layer. J. Geophys. Res. Ocean. 1981, 86, 4161–4172. [Google Scholar] [CrossRef]
- Wang, Q.; Guo, X.; Takeoka, H. Seasonal variations of the Yellow River plume in the Bohai Sea: A model study. J. Geophys. Res. Earth Surf. 2008, 113, C08046. [Google Scholar] [CrossRef]
- Simpson, J.H.; Allen, C.M.; Morris, N.C.G. Fronts on the continental shelf. J. Geophys. Res. Ocean. 1978, 83, 4607. [Google Scholar] [CrossRef]
- Simpson, J.H.; Bowers, D. Models of stratification and frontal movement in shelf seas. Deep.-Sea Res. Part I-Oceanogr. Res. Pap. 1981, 28, 727–738. [Google Scholar] [CrossRef]
- Simpson, J.H.; Brown, J.; Matthews, J.; Allen, G. Tidal straining, density currents, and stirring in the control of estuarine stratification. Estuaries 1990, 13, 125–132. [Google Scholar] [CrossRef]
- Li, L.; He, Z.; Xia, Y.; Dou, X. Dynamics of sediment transport and stratification in Changjiang River Estuary, China. Estuar. Coast. Shelf Sci. 2018, 213, 1–17. [Google Scholar] [CrossRef]
- Zu, T.; Gan, J. A numerical study of coupled estuary–shelf circulation around the Pearl River Estuary during summer: Responses to variable winds, tides and river discharge. Deep-Sea Res. Part II 2015, 117, 53–64. [Google Scholar] [CrossRef]
- Chen, Z.; Jiang, Y.; Liu, J.T.; Gong, W. Development of upwelling on pathway and freshwater transport of Pearl River plume in northeastern South China Sea. J. Geophys. Res. Ocean. 2017, 122, 6090–6109. [Google Scholar] [CrossRef]
- Yu, X.; Guo, X.; Gao, H.; Zou, T. Upstream extension of a bottom-advected plume and its mechanism: The case of the Yellow River. J. Phys. Oceanogr. 2021, 51, 2351–2371. [Google Scholar] [CrossRef]
- Zheng, S.; Guan, W.; Cai, S.; Wei, X.; Huang, D. A model study of the effects of river discharges and interannual variation of winds on the plume front in winter in Pearl River Estuary. Cont. Shelf Res. 2014, 73, 31–40. [Google Scholar] [CrossRef]
- Pan, J.; Gu, Y.; Wang, D. Observations and numerical modeling of the Pearl River plume in summer season. J. Geophys. Res. Ocean. 2014, 119, 2480–2500. [Google Scholar] [CrossRef]





| Parameters | Values |
|---|---|
| Sediment diameter | 0.02 mm |
| Setting velocity | 0.1 mm/s |
| Model time steps | 3 s for the outer mode, 0.3 s for the internal mode |
| Bottom friction coefficient | Sediment-laden BBL |
| Horizontal diffusion | Smagorinsky scheme |
| Vertical eddy viscosity | M–Y 2.5 turbulent closure |
| Node, element, vertical layers | 99,385 elements and 51,540 nodes (reference experiment 1), 11 vertical layers |
| Open boundary condition | Sea surface elevation time series from TPXO 7.2 |
| Experiments | Q (m3/s) | SSC (kg/m3) | Descriptions |
|---|---|---|---|
| Case 1 | 4000 | 85 | Reference experiment |
| Case 2 | 4000 | 15 | Analyze the influence of sediment concentration |
| Case 3 | 4000 | 35 | Analyze the influence of sediment concentration |
| Case 4 | 6000 | 85 | Analyze the influence of river discharge |
| Stations | Velocity | Direction | ||
|---|---|---|---|---|
| CC | Skill | CC | Skill | |
| A1-sur | 0.913 | 0.825 | 0.748 | 0.874 |
| A1-mid | 0.890 | 0.906 | 0.821 | 0.915 |
| A1-bed | 0.842 | 0.757 | 0.915 | 0.959 |
| Ave | 0.881 | 0.829 | 0.828 | 0.916 |
| A2-sur | 0.861 | 0.785 | 0.487 | 0.653 |
| A2-mid | 0.886 | 0.885 | 0.686 | 0.725 |
| A2-bed | 0.839 | 0.750 | 0.802 | 0.817 |
| Ave | 0.862 | 0.807 | 0.658 | 0.731 |
| A3-sur | 0.591 | 0.569 | 0.864 | 0.931 |
| A3-mid | 0.879 | 0.877 | 0.799 | 0.906 |
| A3-bed | 0.734 | 0.814 | 0.814 | 0.922 |
| Ave | 0.735 | 0.753 | 0.825 | 0.920 |
| Tidal Cycles | Parameters | Case 1 | Case 3 | Case 4 |
|---|---|---|---|---|
| Peak Flood | Maximum Runoff Distance (r) | 8.2 km | 4.2 km | 12.4 km |
| Runoff Direction (q) | −18.5° | −31.6° | −3.4° | |
| Curvature (R) | 1.17 | - | 1.19 | |
| Flood Slack | Maximum Runoff Distance (r) | 8.1 km | 3.7 km | 11.1 km |
| Runoff Direction (q) | 4.6° | 21.3° | 7.0° | |
| Curvature (R) | 2.23 | - | 2.03 | |
| Peak Ebb | Maximum Runoff Distance (r) | 9.3 km | 4.2 km | 11.8 km |
| Runoff Direction (q) | 28.6° | 59.8° | 11.5° | |
| Curvature (R) | 1.82 | - | 1.62 | |
| Ebb Slack | Maximum Runoff Distance (r) | 9.3 km | 4.7 km | 11.8 km |
| Runoff Direction (q) | 55.5° | 30.6° | 46.8° | |
| Curvature (R) | 1.35 | - | 1.37 |
| Time | Tidal Cycles | Development Process |
|---|---|---|
| 0:00 | low slack water | fully developed |
| 1:00 | flood tide | thickness decreases |
| 2:00 | flood tide | thickness decreases |
| 4:00 | high slack water | thickness becomes thinnest |
| 5:00 | ebb tide | start to develop, thickness increases |
| 6:00 | ebb tide | thickness increases |
| 9:00 | peak ebb | thickness increases |
| 10:00 | ebb tide | thickness increases |
| 11:00 | low slack water | fully developed |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, Z.; Xu, B.; Okon, S.U.; Li, L. Numerical Investigation of the Sediment Hyperpycnal Flow in the Yellow River Estuary. J. Mar. Sci. Eng. 2022, 10, 943. https://doi.org/10.3390/jmse10070943
He Z, Xu B, Okon SU, Li L. Numerical Investigation of the Sediment Hyperpycnal Flow in the Yellow River Estuary. Journal of Marine Science and Engineering. 2022; 10(7):943. https://doi.org/10.3390/jmse10070943
Chicago/Turabian StyleHe, Zhiguo, Baoxin Xu, Samuel Ukpong Okon, and Li Li. 2022. "Numerical Investigation of the Sediment Hyperpycnal Flow in the Yellow River Estuary" Journal of Marine Science and Engineering 10, no. 7: 943. https://doi.org/10.3390/jmse10070943
APA StyleHe, Z., Xu, B., Okon, S. U., & Li, L. (2022). Numerical Investigation of the Sediment Hyperpycnal Flow in the Yellow River Estuary. Journal of Marine Science and Engineering, 10(7), 943. https://doi.org/10.3390/jmse10070943







