On the Adaptation of an AUV into a Dedicated Platform for Close Range Imaging Survey Missions
Abstract
:1. Introduction
2. The SPARUS II AUV
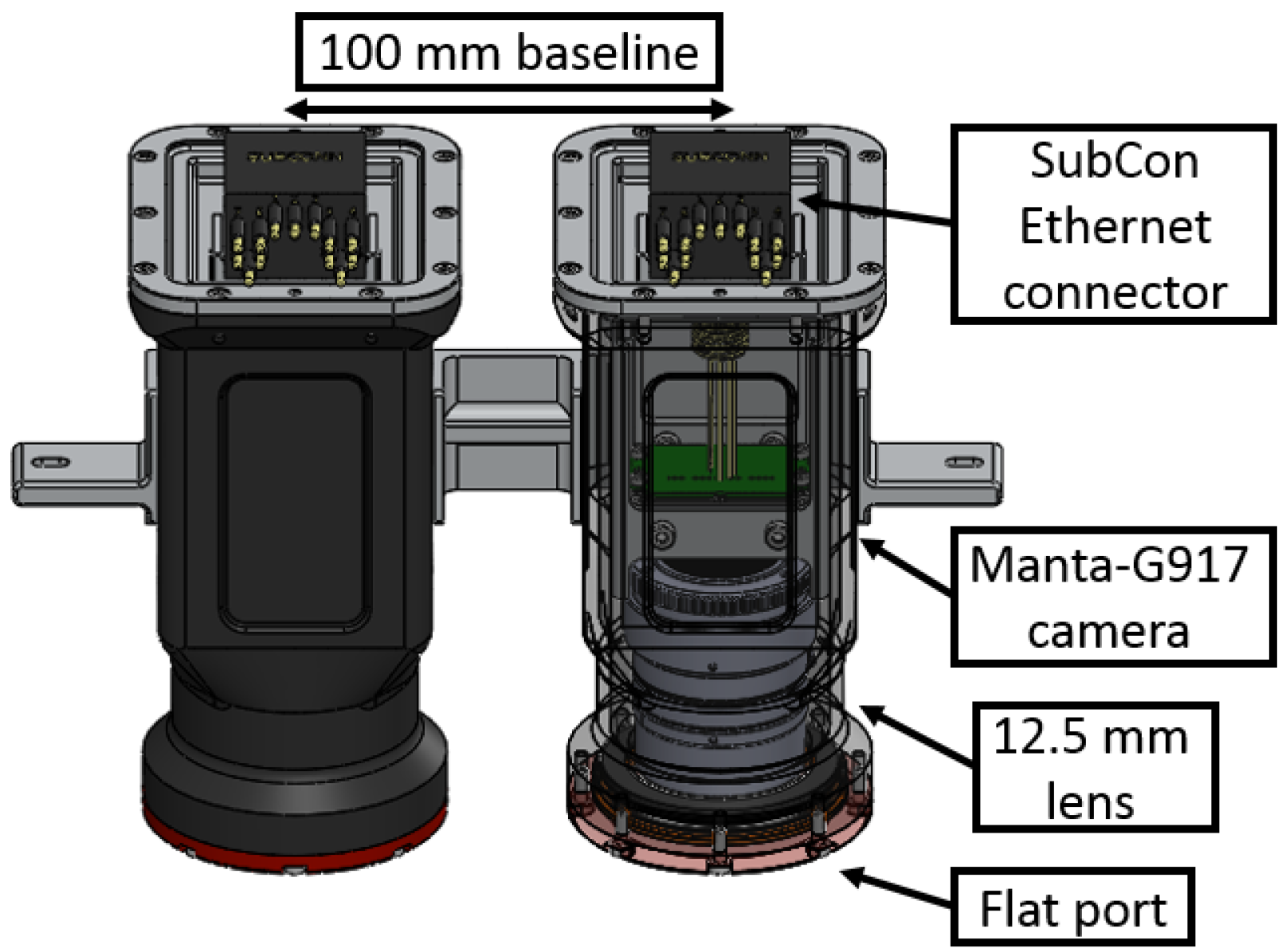
3. Development of a Dedicated Imaging Payload
4. Mission Planning for High-Resolution Imaging
5. Modified SPARUS II AUV—ALICE
6. Dynamic Modeling for Performance Evaluation of ALICE
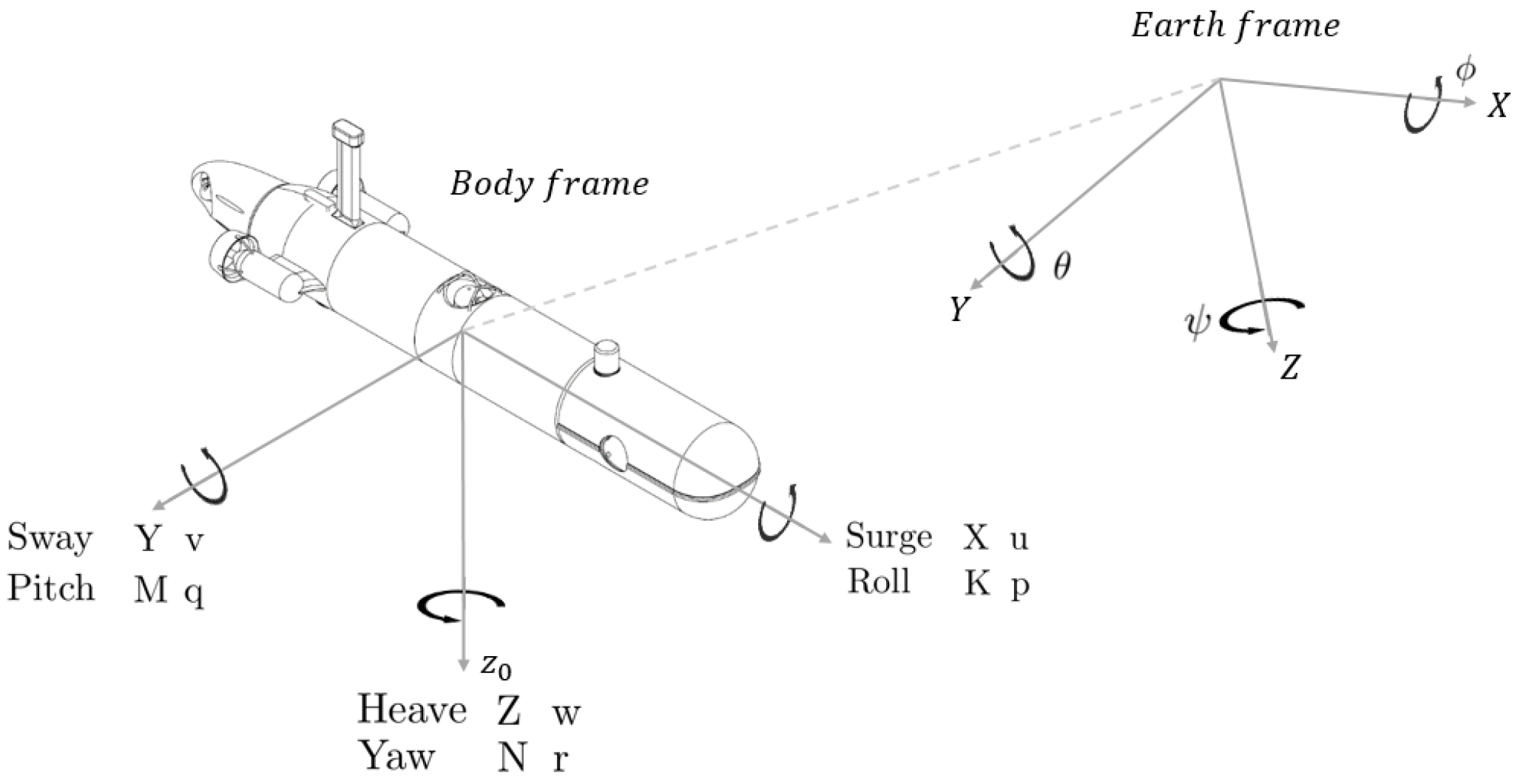
6.1. Equations of Motion
6.2. Modeling of ALICE’s Propulsion System
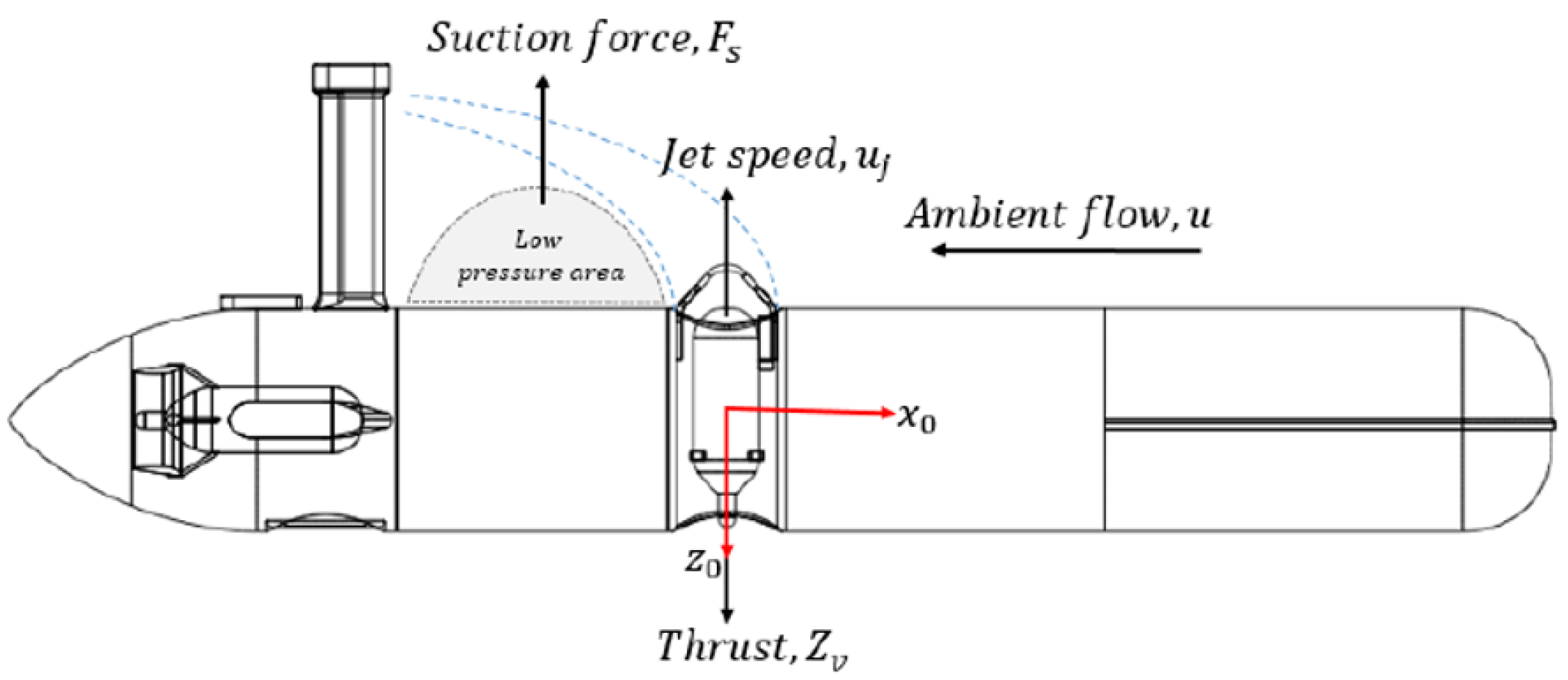
6.2.1. Interactions between the Tunnel Thrusters and the Hull
6.2.2. Thruster Configuration Matrix
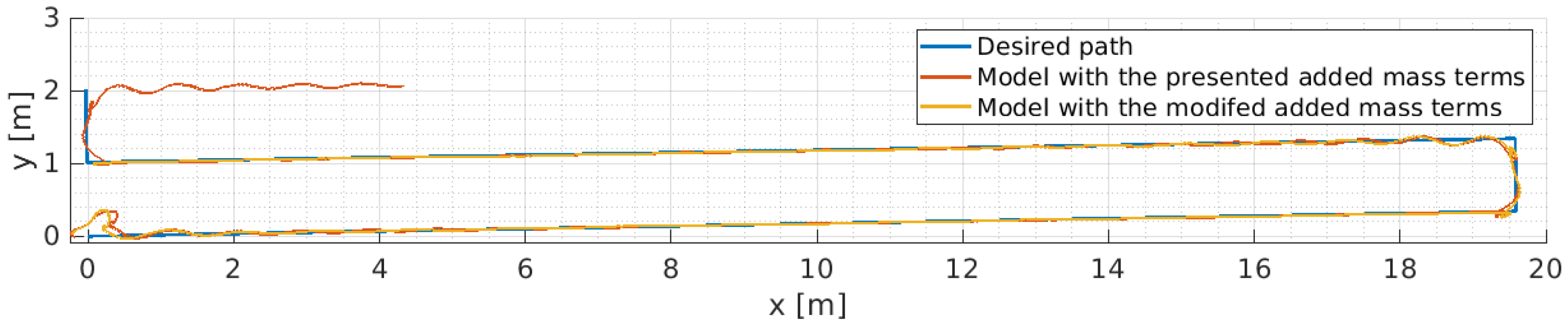
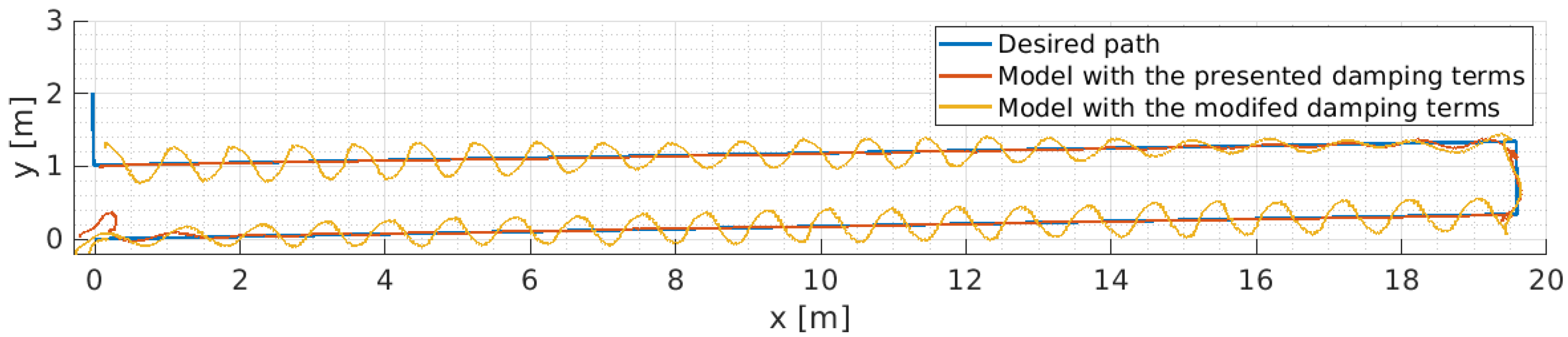
6.3. Identification of the Hydrodynamic Coefficients
- Forward motion at various surge speeds to determine and ;
- Vertical ascent/descent at a constant heave speed to determine and ;
- Horizontal turns, performed by the horizontal thrusters, to determine and .
6.4. Numerical Implementation of the Dynamic Model
7. AUV Motion Control System
7.1. Upgraded Thruster Allocation Algorithm
| Algorithm 1: RPI method with dynamic weighting matrix. |
 |
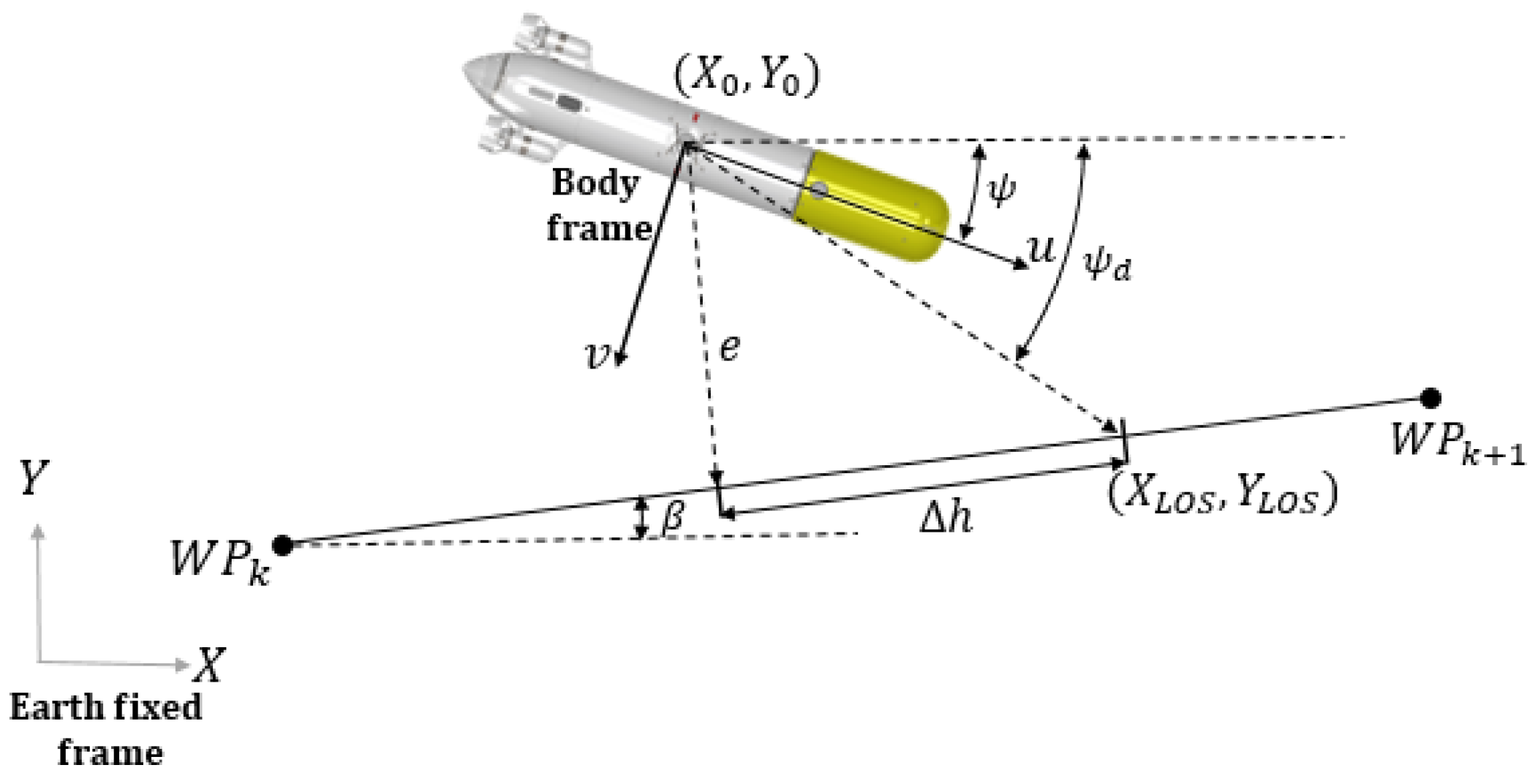
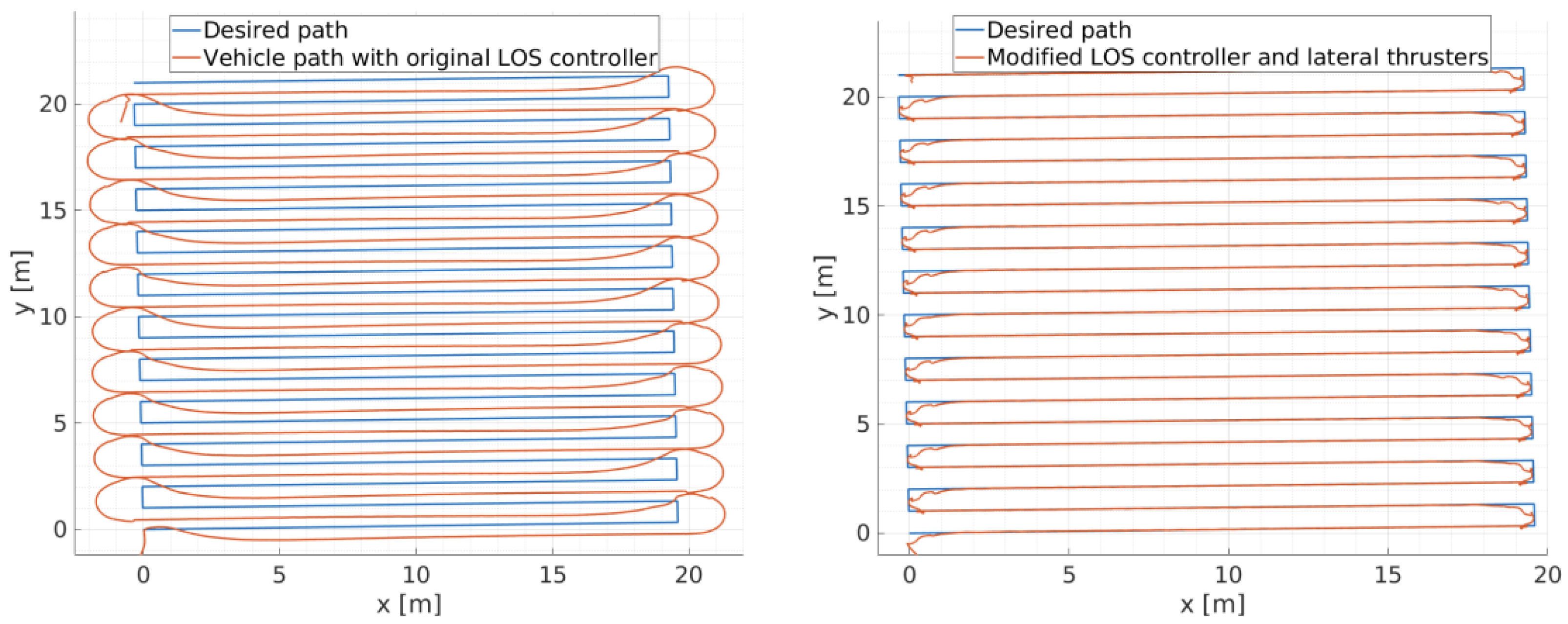
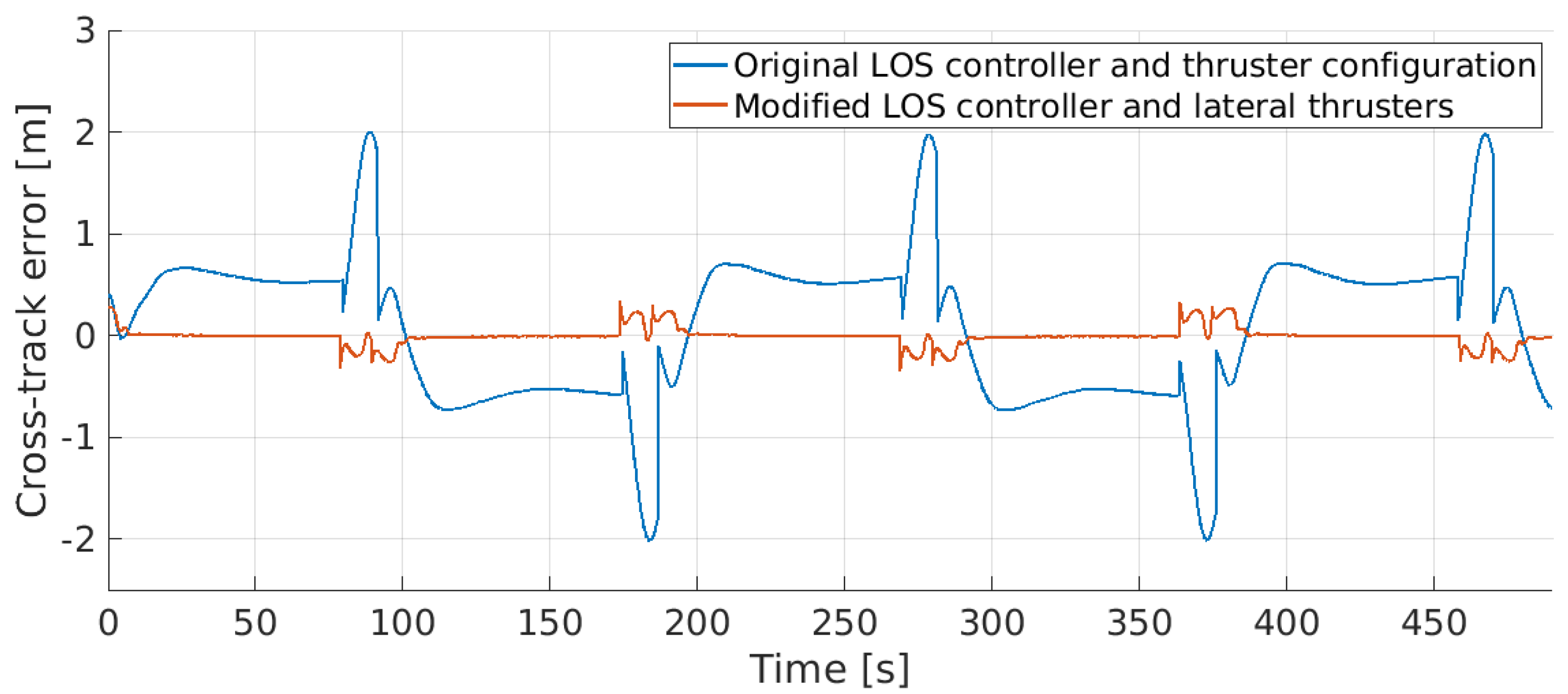
7.2. Improved Path-Following Controller
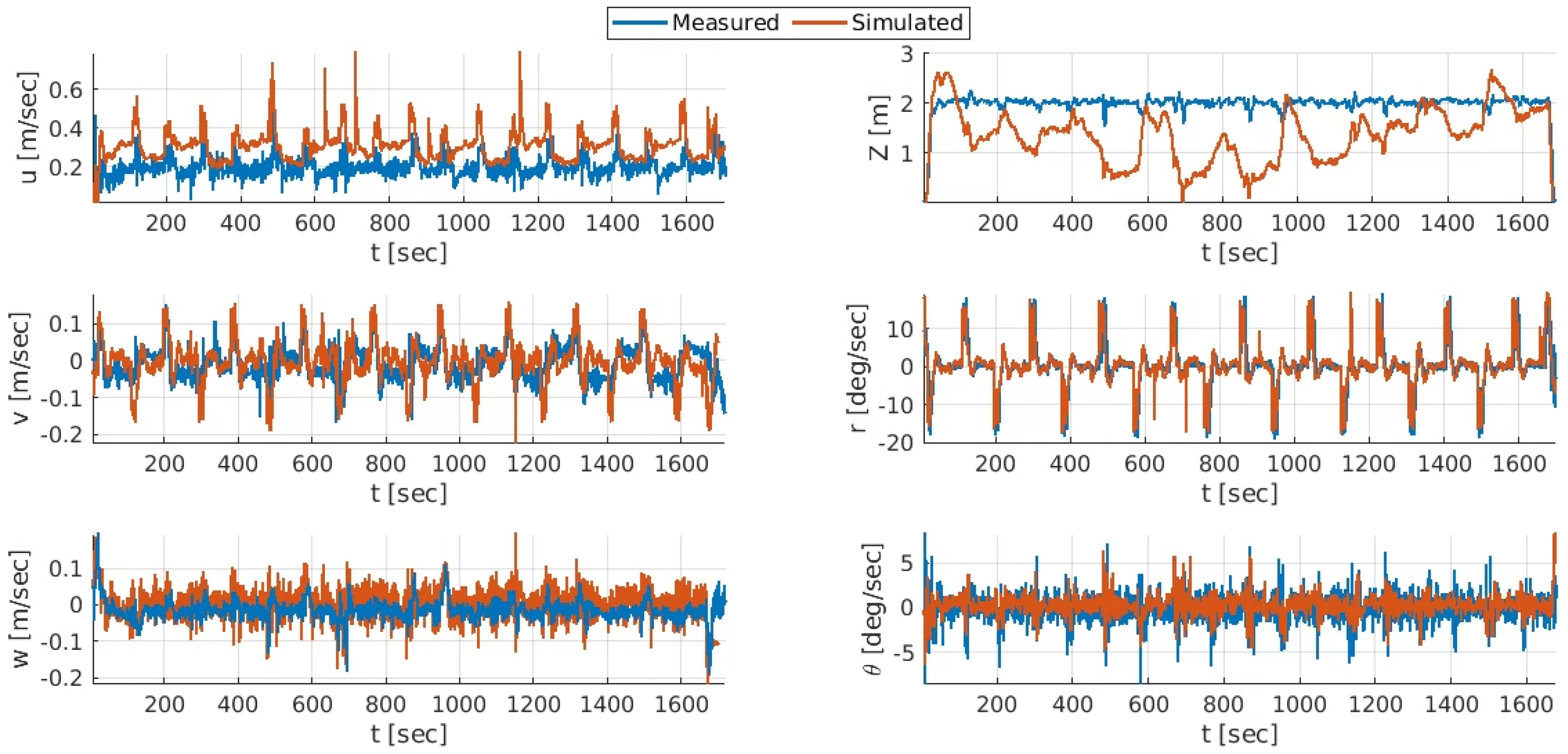
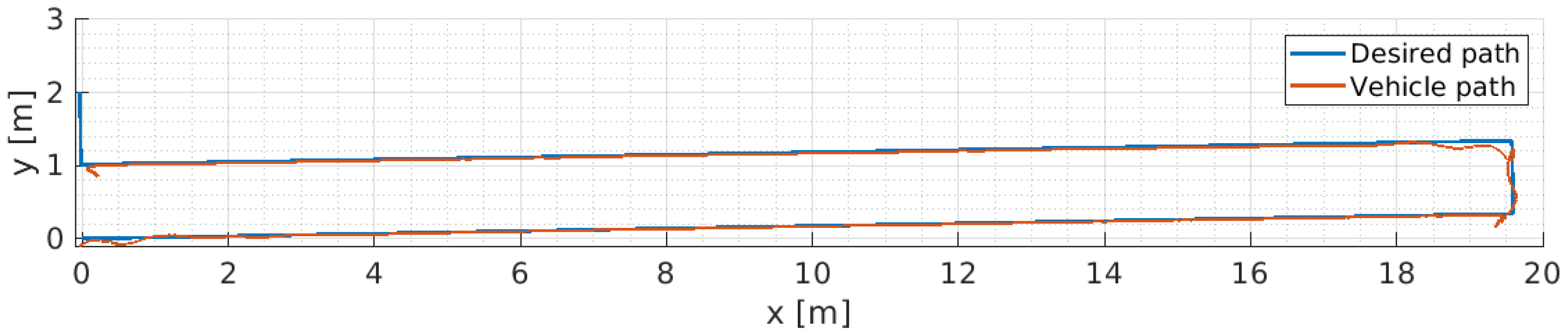
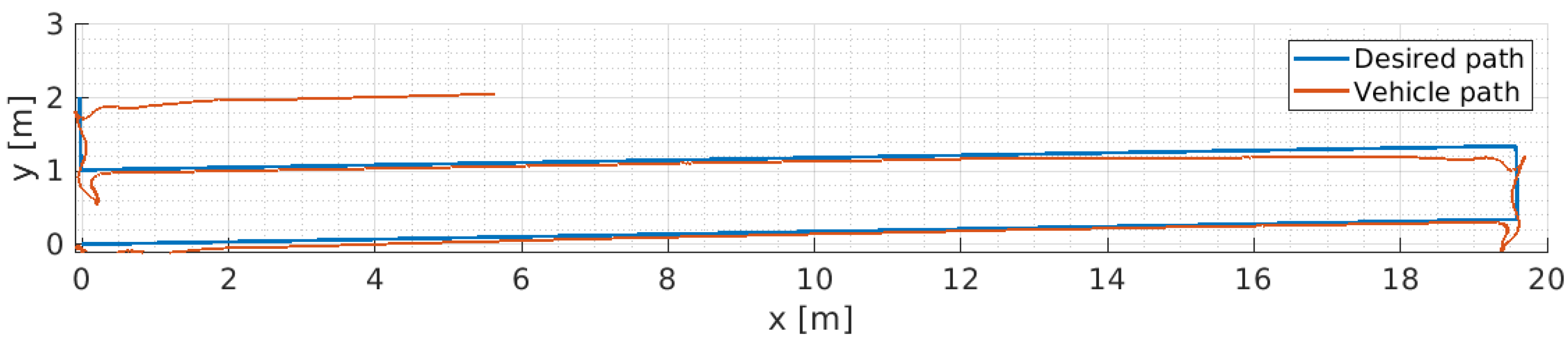
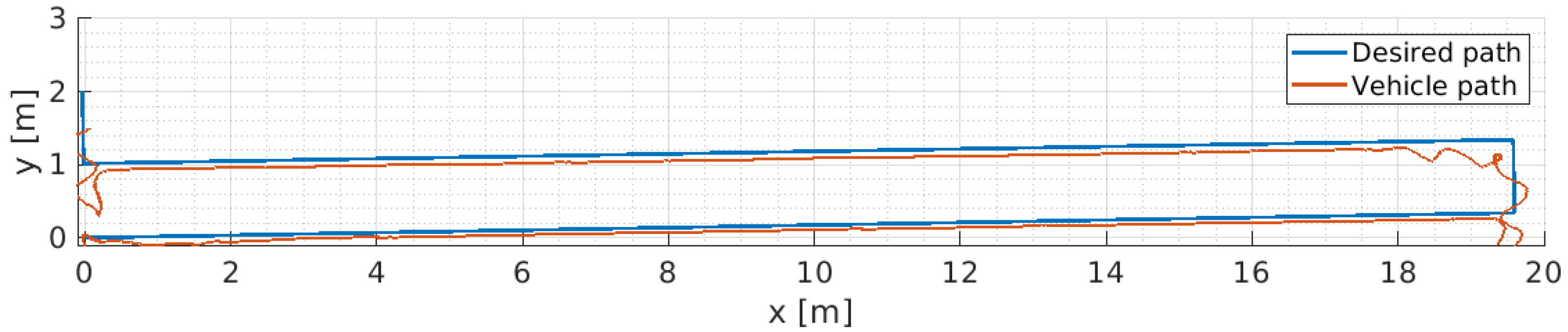
8. Software-in-the-Loop Simulation for ALICE’s Performance Evaluation
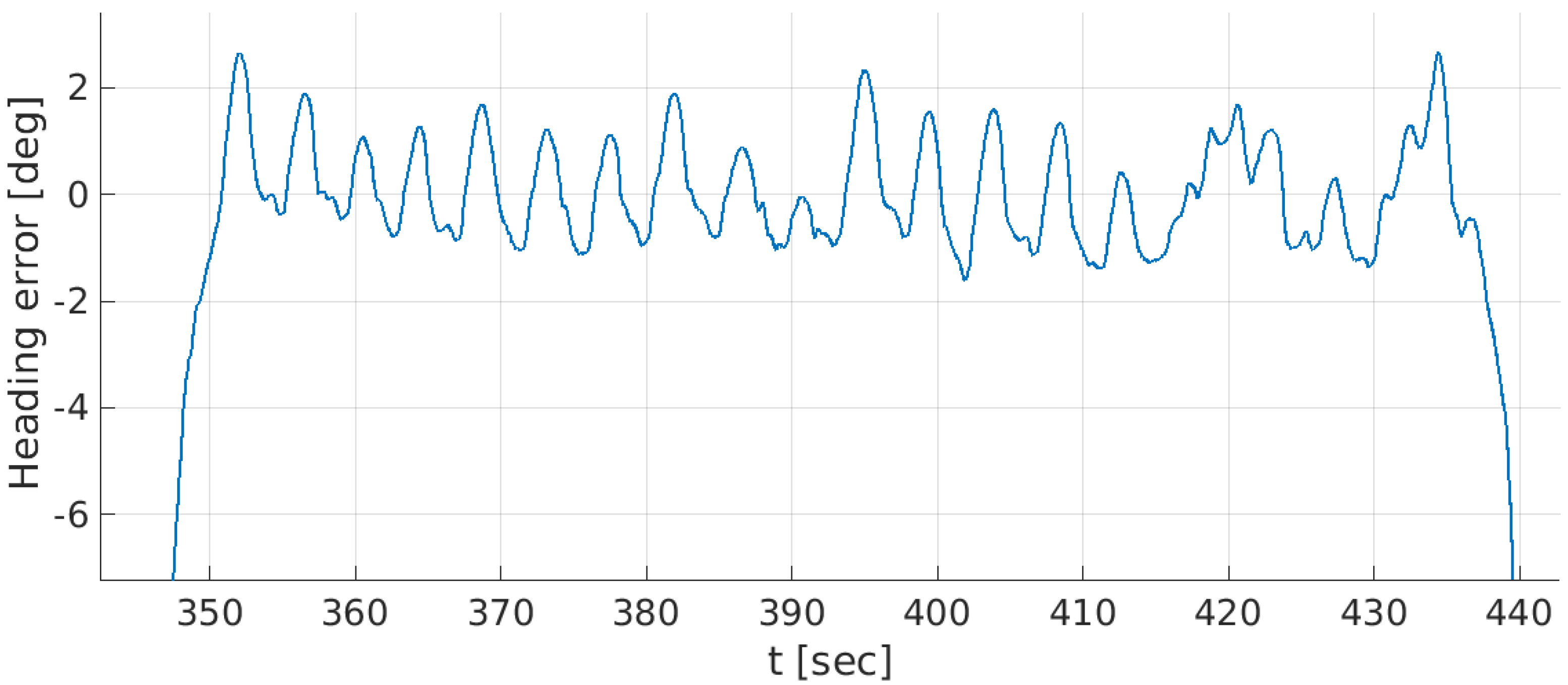
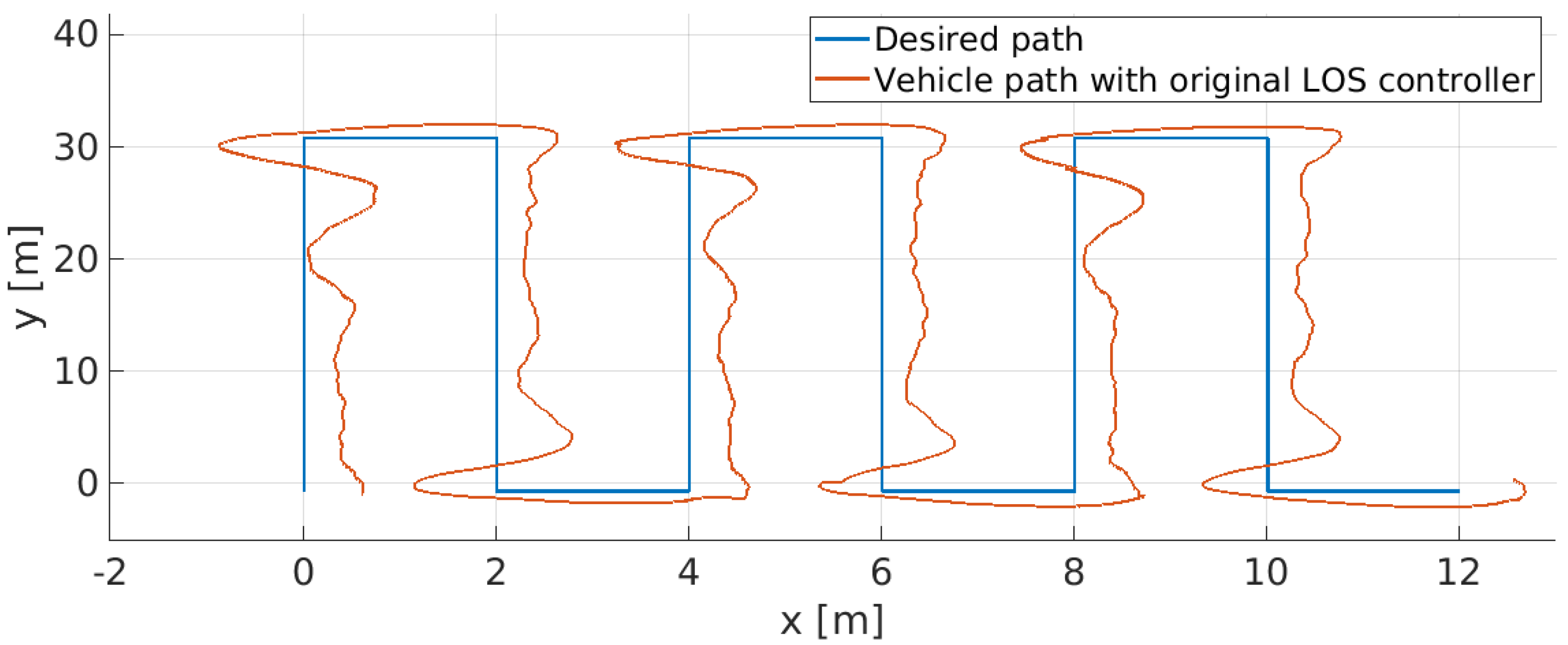
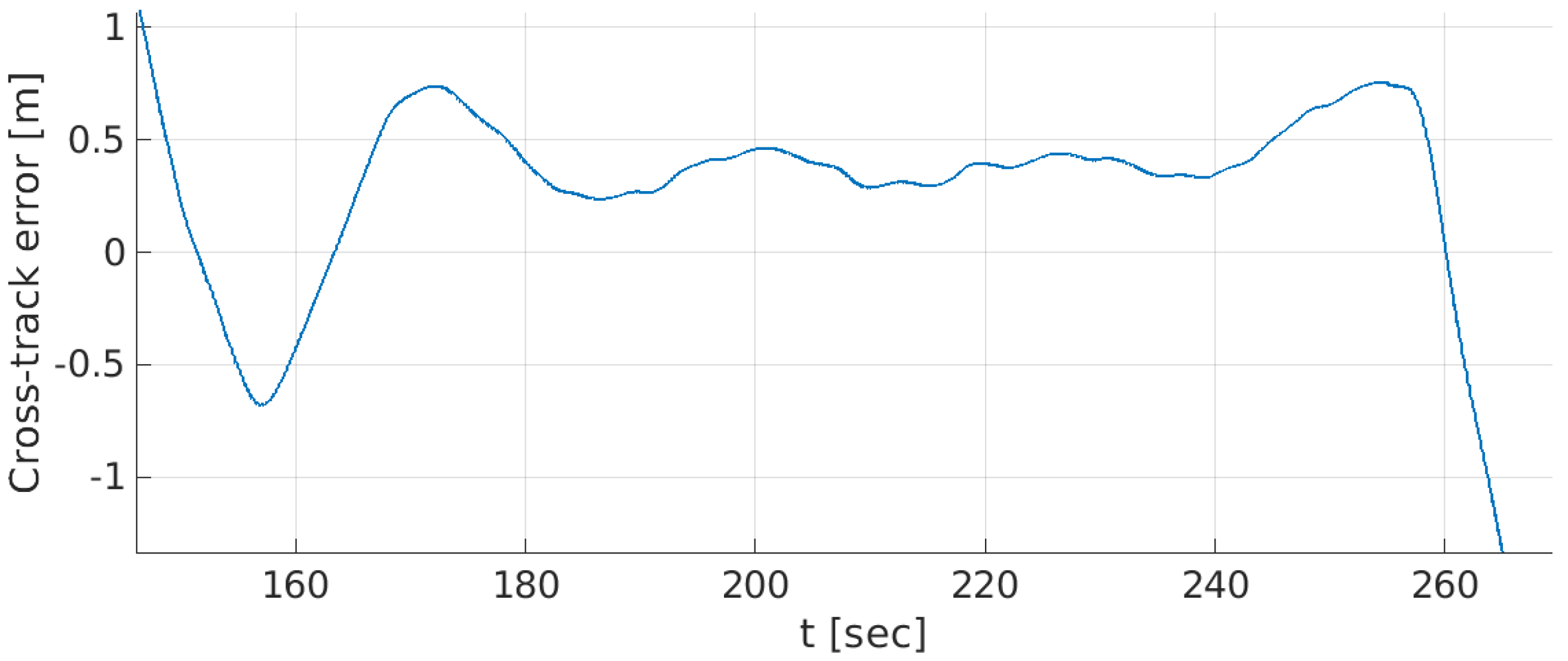
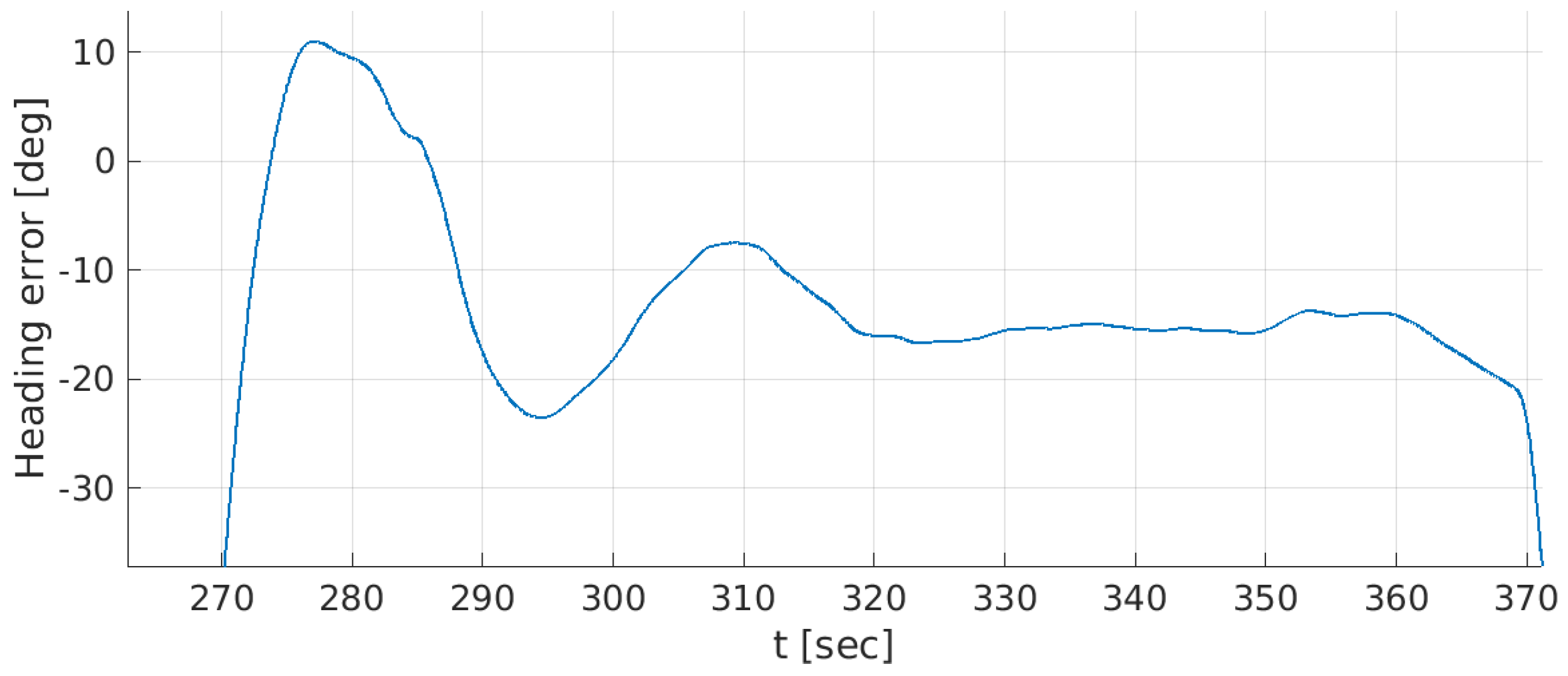
9. Real Sea Experiments and Discussion
10. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pizarro, O.; Friedman, A.; Bryson, M.; Williams, S.B.; Madin, J. A simple, fast, and repeatable survey method for underwater visual 3D benthic mapping and monitoring. Ecol. Evol. 2017, 7, 1770–1782. [Google Scholar] [CrossRef] [PubMed]
- Tolimieri, N.; Clarke, M.E.; Singh, H.; Goldfinger, C. Evaluating the SeaBED AUV for monitoring groundfish in untrawlable habitat. In Marine Habitat Mapping Technology for Alaska; Alaska Sea Grant: Fairbanks, AK, USA, 2008; pp. 129–141. [Google Scholar]
- Gracias, N.; Ridao, P.; Garcia, R.; Escartín, J.; l’Hour, M.; Cibecchini, F.; Campos, R.; Carreras, M.; Ribas, D.; Palomeras, N.; et al. Mapping the Moon: Using a lightweight AUV to survey the site of the 17th century ship ‘La Lune’. In Proceedings of the 2013 MTS/IEEE OCEANS, Bergen, Norway, 10–14 June 2013. [Google Scholar]
- Albiez, J.; Joyeux, S.; Gaudig, C.; Hilljegerdes, J.; Kroffke, S.; Schoo, C.; Arnold, S.; Mimoso, G.; Alcantara, P.; Saback, R.; et al. Flatfish-a compact subsea-resident inspection AUV. In Proceedings of the OCEANS 2015 MTS/IEEE, Washington, DC, USA, 19–22 October 2015. [Google Scholar]
- Vidal, E.; Palomeras, N.; Carreras, M. Online 3D underwater exploration and coverage. In Proceedings of the 2018 IEEE/OES Autonomous Underwater Vehicle Workshop (AUV), Porto, Portugal, 6–9 November 2018. [Google Scholar]
- Ludvigsen, M.; Sortland, B.; Johnsen, G.; Singh, H. Applications of geo-referenced underwater photo mosaics in marine biology and archaeology. Oceanogr 2007, 20, 140–149. [Google Scholar] [CrossRef] [Green Version]
- Pizarro, O.; Singh, H. Toward large-area mosaicing for underwater scientific applications. IEEE J. Ocean. Eng. 2003, 28, 651–672. [Google Scholar] [CrossRef]
- Prados, R.; Garcia, R.; Gracias, N.; Escartin, J.; Neumann, L. A novel blending technique for underwater gigamosaicing. IEEE J. Ocean. Eng. 2012, 37, 626–644. [Google Scholar] [CrossRef] [Green Version]
- Pyo, J.; Cho, H.; Joe, H.; Ura, T.; Yu, S.C. Development of hovering type AUV “Cyclops” and its performance evaluation using image mosaicing. Ocean Eng. 2015, 109, 517–530. [Google Scholar] [CrossRef] [Green Version]
- Houts, S.E.; Rock, S.M.; McEwen, R. Aggressive terrain following for motion-constrained AUVs. In Proceedings of the IEEE/OES Autonomous Underwater Vehicles AUV, Southampton, UK, 24–27 September 2012. [Google Scholar]
- Song, Y.; Nakath, D.; She, M.; Köser, K. Optical Imaging and Image Restoration Techniques for Deep Ocean Mapping: A Comprehensive Survey. PFG–J. Photogramm. Remote Sens. Geoinf. Sci. 2022, 1–25. [Google Scholar] [CrossRef]
- Pinto, A.M.; Matos, A.C. MARESye: A hybrid imaging system for underwater robotic applications. Inf. Fusion 2020, 55, 16–29. [Google Scholar] [CrossRef]
- Kwasnitschka, T.; Köser, K.; Sticklus, J.; Rothenbeck, M.; Weiß, T.; Wenzlaff, E.; Schoening, T.; Triebe, L.; Steinführer, A.; Devey, C.; et al. DeepSurveyCam—A deep ocean optical mapping system. Sensors 2016, 16, 164. [Google Scholar] [CrossRef] [Green Version]
- Viswanathan, V.K.; Lobo, Z.; Lupanow, J.; von Fock, S.S.; Wood, Z.; Gambin, T.; Clark, C. AUV motion-planning for photogrammetric reconstruction of marine archaeological sites. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 5096–5103. [Google Scholar]
- Preston, V.; Salumäe, T.; Kruusmaa, M. Underwater confined space mapping by resource-constrained autonomous vehicle. J. Field Robot. 2018, 35, 1122–1148. [Google Scholar] [CrossRef]
- Noguchi, Y.; Sakamaki, T.; Ito, S.; Humblet, M.; Furushima, Y.; Maki, T. Wide area seafloor imaging by a low-cost AUV. In Proceedings of the Global Oceans 2020: Singapore–US Gulf Coast, Biloxi, MS, USA, 5–30 October 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1–7. [Google Scholar]
- Iscar, E.; Barbalata, C.; Goumas, N.; Johnson-Roberson, M. Towards low cost, deep water AUV optical mapping. In Proceedings of the OCEANS 2018 MTS/IEEE Charleston, Charleston, SC, USA, 22–25 October 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1–6. [Google Scholar]
- Wu, J.; Bingham, R.C.; Ting, S.; Yager, K.; Wood, Z.J.; Gambin, T.; Clark, C.M. Multi-AUV motion planning for archeological site mapping and photogrammetric reconstruction. J. Field Robot. 2019, 36, 1250–1269. [Google Scholar] [CrossRef]
- Okamoto, A.; Seta, T.; Sasano, M.; Inoue, S.; Ura, T. Visual and Autonomous Survey of Hydrothermal Vents Using a Hovering-Type AUV: Launching Hobalin into the Western Offshore of Kumejima Island. Geochem. Geophys. Geosyst. 2019, 20, 6234–6243. [Google Scholar] [CrossRef]
- Modasshir, M.; Rahman, S.; Youngquist, O.; Rekleitis, I. Coral identification and counting with an autonomous underwater vehicle. In Proceedings of the 2018 IEEE International Conference on Robotics and Biomimetics (ROBIO), Kuala Lumpur, Malaysia, 12–15 December 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 524–529. [Google Scholar]
- Turner, J.A.; Babcock, R.C.; Hovey, R.; Kendrick, G.A. AUV-based classification of benthic communities of the Ningaloo shelf and mesophotic areas. Coral Reefs 2018, 37, 763–778. [Google Scholar] [CrossRef]
- Ribas, D.; Palomeras, N.; Ridao, P.; Carreras, M.; Mallios, A. Girona 500 AUV: From survey to intervention. IEEE/ASME Trans. Mechatron. 2011, 17, 46–53. [Google Scholar] [CrossRef]
- Williams, S.B.; Pizarro, O.; How, M.; Mercer, D.; Powell, G.; Marshall, J.; Hanlon, R. Surveying noctural cuttlefish camouflage behaviour using an AUV. In Proceedings of the 2009 IEEE International Conference on Robotics and Automation, Kobe, Japan, 12–17 May 2009; IEEE: Piscataway, NJ, USA, 2009; pp. 214–219. [Google Scholar]
- Cruz, N.A.; Matos, A.C.; Almeida, R.M.; Ferreira, B.M.; Abreu, N. TriMARES-a hybrid AUV/ROV for dam inspection. In Proceedings of the OCEANS’11 MTS/IEEE KONA, Waikoloa, HI, USA, 19–22 September 2011; IEEE: Piscataway, NJ, USA, 2011; pp. 1–7. [Google Scholar]
- Singh, W.; Örnólfsdóttir, E.B.; Stefansson, G. A small-scale comparison of Iceland scallop size distributions obtained from a camera based autonomous underwater vehicle and dredge survey. PLoS ONE 2014, 9, e109369. [Google Scholar] [CrossRef] [PubMed]
- Jaffre, F.; Littlefield, R.; Grund, M.; Purcell, M. Development of a new version of the remus 6000 autonomous underwater vehicle. In Proceedings of the OCEANS 2019-Marseille, Marseille, France, 17–20 June 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1–7. [Google Scholar]
- Bakken, E.M.; Midtgaard, Ø. Underwater Image Mosaics for AUV-Mounted Cameras. In Proceedings of the Global Oceans: Singapore–US Gulf Coast, Biloxi, MS, USA, 5–30 October 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1–6. [Google Scholar]
- Madureira, L.; Sousa, A.; Braga, J.; Calado, P.; Dias, P.; Martins, R.; Pinto, J.; Sousa, J. The light autonomous underwater vehicle: Evolutions and networking. In Proceedings of the 2013 MTS/IEEE OCEANS-Bergen, Bergen, Norway, 10–14 June 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 1–6. [Google Scholar]
- Packard, G.E.; Stokey, R.; Christenson, R.; Jaffre, F.; Purcell, M.; Littlefield, R. Hull inspection and confined area search capabilities of REMUS autonomous underwater vehicle. In Proceedings of the OCEANS 2010 MTS/IEEE, Seattle, WA, USA, 20–23 September 2010. [Google Scholar]
- Carreras, M.; Hernández, J.D.; Vidal, E.; Palomeras, N.; Ribas, D.; Ridao, P. SPARUS II AUV—A hovering vehicle for seabed inspection. IEEE J. Ocean. Eng. 2018, 43, 344–355. [Google Scholar] [CrossRef]
- Quigley, M.; Conley, K.; Gerkey, B.; Faust, J.; Foote, T.; Leibs, J.; Wheeler, R.; Ng, A.Y. Ros: An open-source robot operating system. ICRA Workshop Open Source Softw. 2009, 3, 5. [Google Scholar]
- Xia, Y.; Xu, K.; Li, Y.; Xu, G.; Xiang, X. Improved line-of-sight trajectory tracking control of under-actuated AUV subjects to ocean currents and input saturation. Ocean Eng. 2019, 174, 14–30. [Google Scholar] [CrossRef]
- Treibitz, T.; Schechner, Y.; Kunz, C.; Singh, H. Flat refractive geometry. IEEE Trans. Pattern Anal. Mach. Intell. 2011, 34, 51–65. [Google Scholar] [CrossRef] [Green Version]
- Fossen, T.I. Handbook of Marine Craft Hydrodynamics and Motion Control; Wiley: Hoboken, NJ, USA, 2011. [Google Scholar]
- Carlton, J. Marine Propellers and Propulsion; Butterworth-Heinemann: Oxford, UK, 2018. [Google Scholar]
- Van Manen, J.D. Recent research on propellers in nozzles. Int. Shipbuild. Prog. 1957, 4, 395–424. [Google Scholar] [CrossRef]
- Palmer, A.R. Analysis of the Propulsion and Manoeuvring Characteristics of Survey-Style AUVs and the Development of a Multi-Purpose AUV. Ph.D. Thesis, University of Southampton, Southampton, UK, 2009. [Google Scholar]
- Horner, S. Fluid Dynamic Drag, Practical Information on Aerodynamic Drag and Hydrodynamic Resistance; Hoerner Fluid Dynamics: Midland Park, NJ, USA, 1965. [Google Scholar]
- Hoerner, S.F.; Borst, H.V. Fluid-dynamic lift: Practical information on aerodynamic and hydrodynamic lift. STIA 1975, 76, 32167. [Google Scholar]
- Cardenas, P.; de Barros, E.A. Estimation of AUV hydrodynamic coefficients using analytical and system identification approaches. IEEE J. Ocean. Eng. 2019, 45, 1157–1176. [Google Scholar] [CrossRef]
- Prestero, T.T.J. Verification of a Six-Degree of Freedom Simulation Model for the REMUS Autonomous Underwater Vehicle. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2001. [Google Scholar]
- de Kruif, B.J.; Ypma, E. Self-Propulsion Parameter Identification for Control of Marin’s AUV. In Proceedings of the IEEE/OES Autonomous Underwater Vehicles Symposium (AUV), St. Johns, NL, Canada, 30 September–2 October 2020; pp. 1–6. [Google Scholar]
- Allotta, B.; Costanzi, R.; Pugi, L.; Ridolfi, A. Identification of the main hydrodynamic parameters of Typhoon AUV from a reduced experimental dataset. Ocean Eng. 2018, 147, 77–88. [Google Scholar] [CrossRef]
- Johansen, T.A.; Fossen, T.I. Control allocation—A survey. Automatica 2013, 49, 1087–1103. [Google Scholar] [CrossRef] [Green Version]
- Khan, H.Z.I.; Rajput, J.; Ahmed, S.; Sarmad, M.; Sharjil, M. Robust control of overactuated autonomous underwater vehicle. In Proceedings of the 2018 15th International Bhurban Conference on Applied Sciences and Technology (IBCAST), Islamabad, Pakistan, 9–13 January 2018; pp. 269–275. [Google Scholar]
- Palomeras, N.; Vallicrosa, G.; Mallios, A.; Bosch, J.; Vidal, E.; Hurtos, N.; Carreras, M.; Ridao, P. AUV homing and docking for remote operations. Ocean Eng. 2018, 154, 106–120. [Google Scholar] [CrossRef]











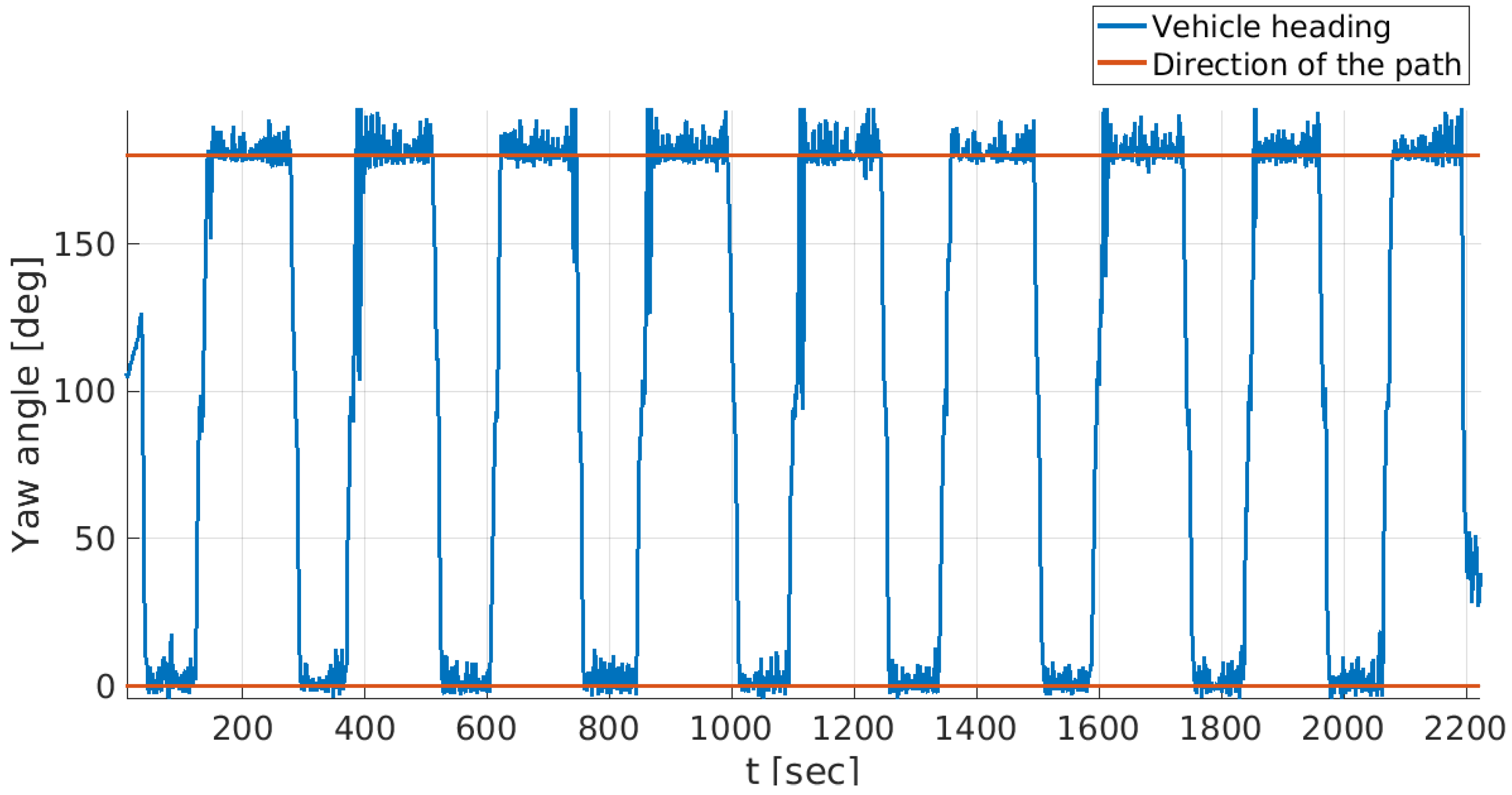
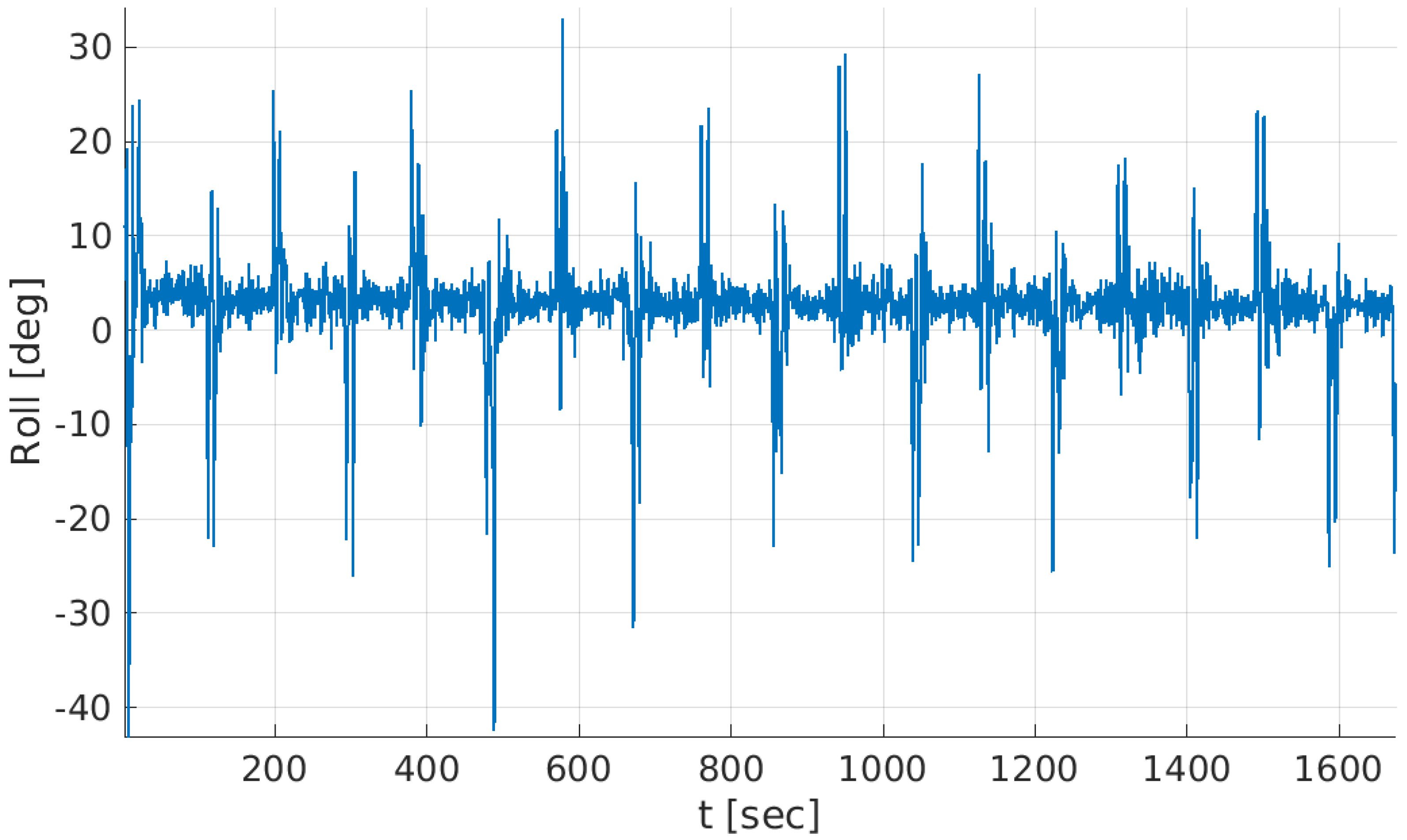
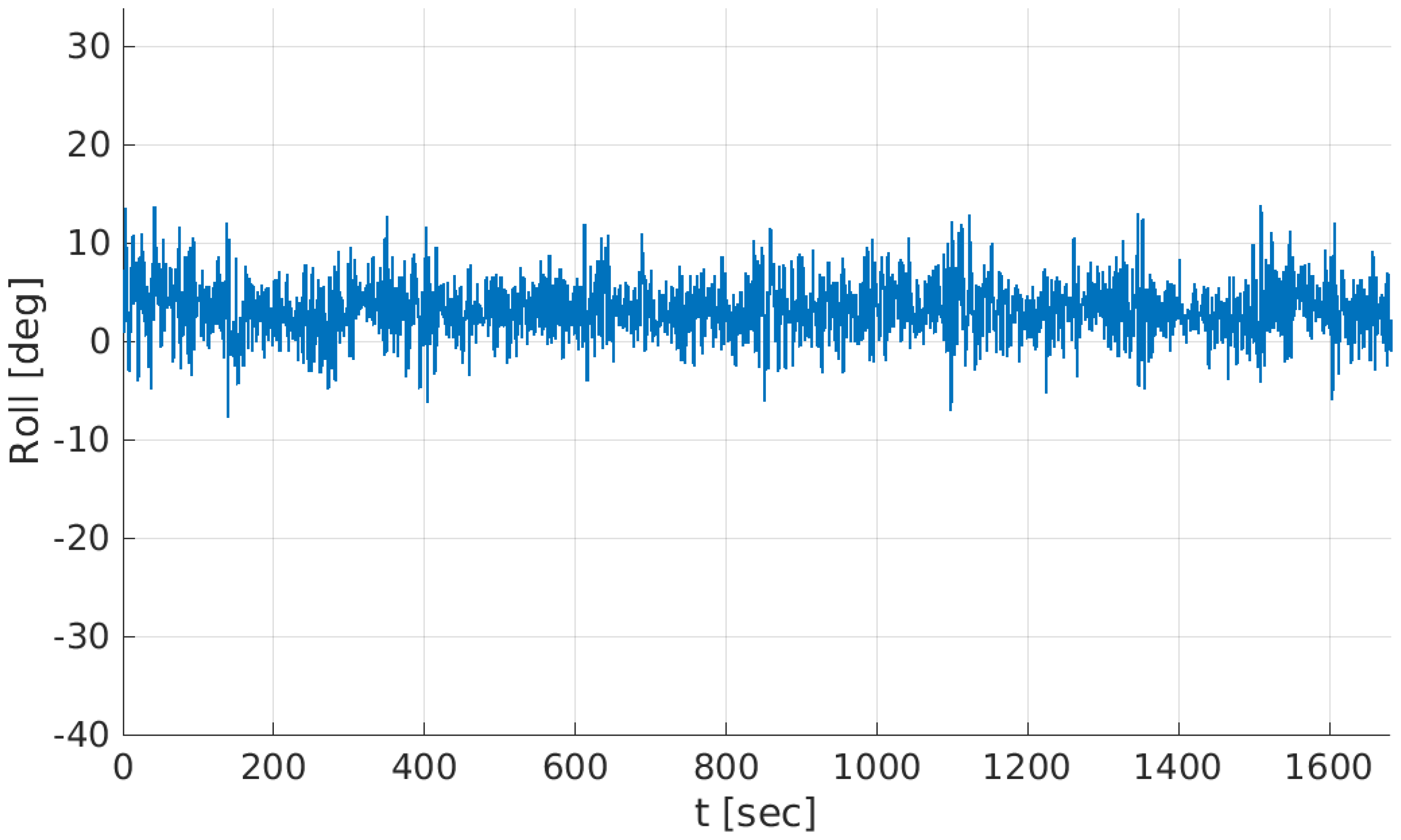


| Coefficient | Value | Coefficient | Value |
|---|---|---|---|
| −28.06 | −15.23 | ||
| −23.53 | −321.59 | ||
| −27.81 | −326.16 | ||
| −0.04 | −3.4 | ||
| −10.48 | −0.19 | ||
| −5.6 | −180 | ||
| −11.26 | 26.63 | ||
| −8.53 | 0.14 | ||
| −39.7 | −54.1 | ||
| −8.49 | −1.95 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gutnik, Y.; Avni, A.; Treibitz, T.; Groper, M. On the Adaptation of an AUV into a Dedicated Platform for Close Range Imaging Survey Missions. J. Mar. Sci. Eng. 2022, 10, 974. https://doi.org/10.3390/jmse10070974
Gutnik Y, Avni A, Treibitz T, Groper M. On the Adaptation of an AUV into a Dedicated Platform for Close Range Imaging Survey Missions. Journal of Marine Science and Engineering. 2022; 10(7):974. https://doi.org/10.3390/jmse10070974
Chicago/Turabian StyleGutnik, Yevgeni, Aviad Avni, Tali Treibitz, and Morel Groper. 2022. "On the Adaptation of an AUV into a Dedicated Platform for Close Range Imaging Survey Missions" Journal of Marine Science and Engineering 10, no. 7: 974. https://doi.org/10.3390/jmse10070974
APA StyleGutnik, Y., Avni, A., Treibitz, T., & Groper, M. (2022). On the Adaptation of an AUV into a Dedicated Platform for Close Range Imaging Survey Missions. Journal of Marine Science and Engineering, 10(7), 974. https://doi.org/10.3390/jmse10070974







