Simulation Study on the Performance and Emission Parameters of a Marine Diesel Engine
Abstract
:1. Introduction
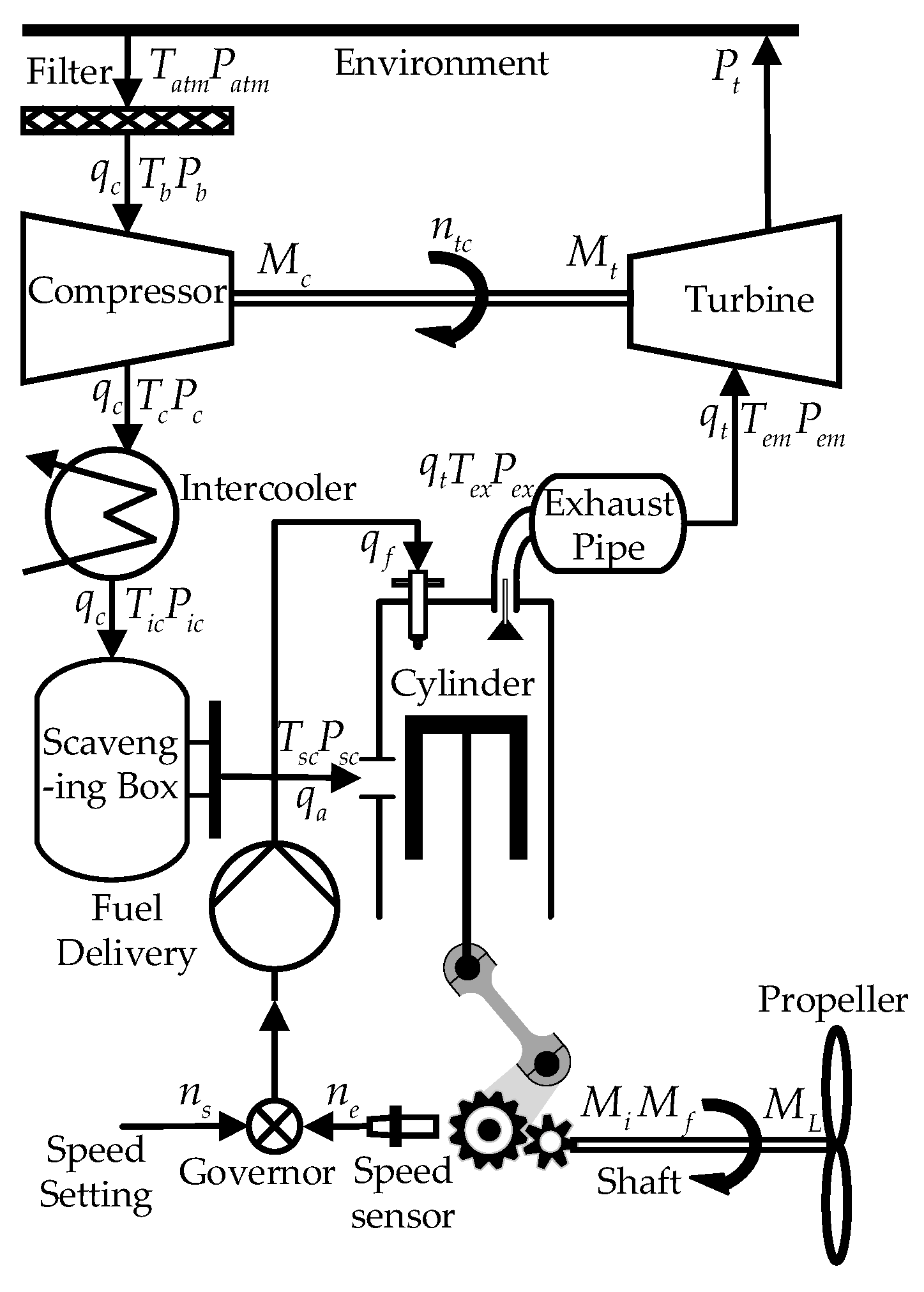
2. Model of Marine Diesel Engine
2.1. Overview of the Mean Value Engine Model (MVEM)
2.2. Engine Simulated
2.3. Mean Value Engine Model
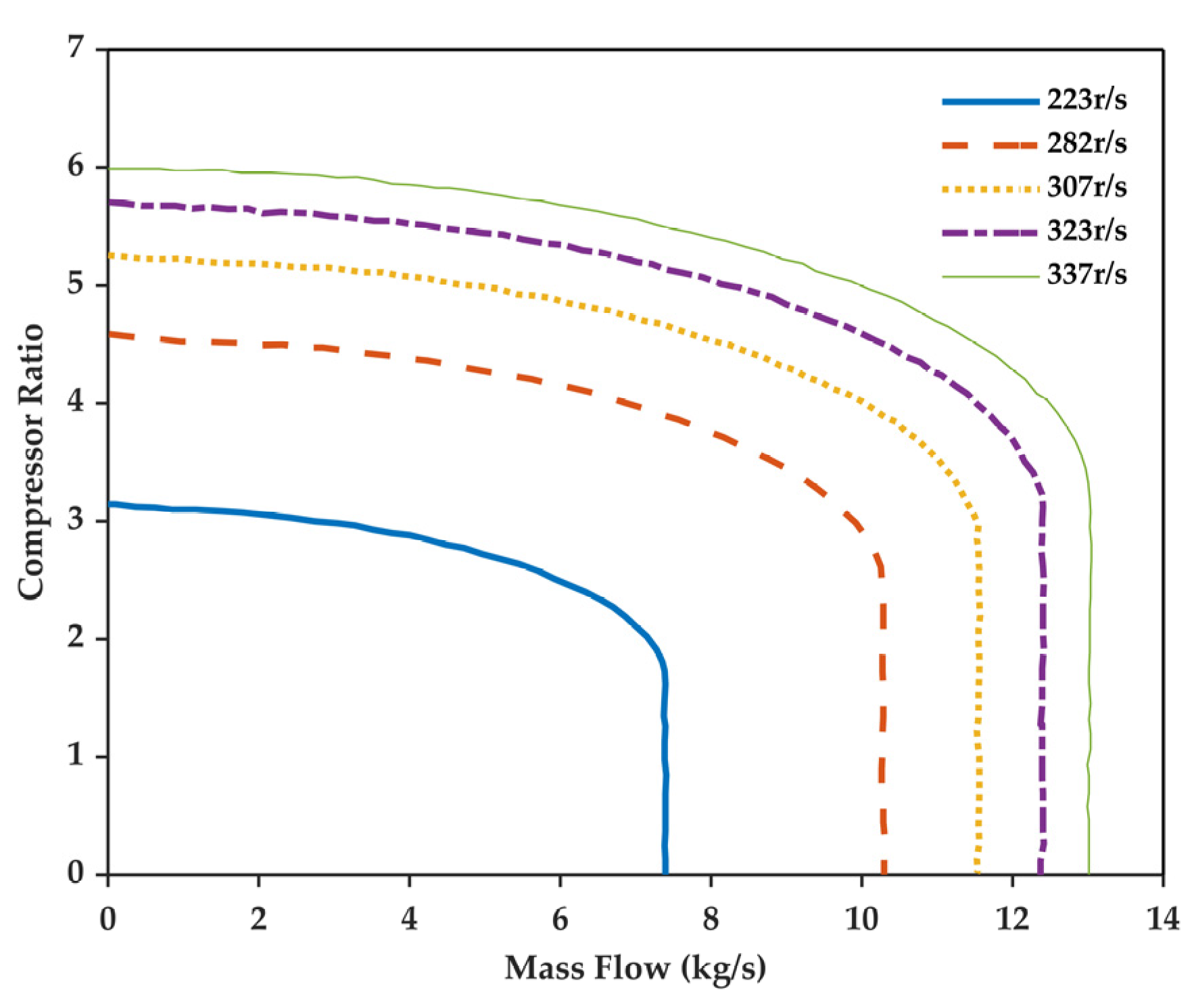
2.3.1. Turbocharger
2.3.2. Intercooler
2.3.3. Scavenging Box
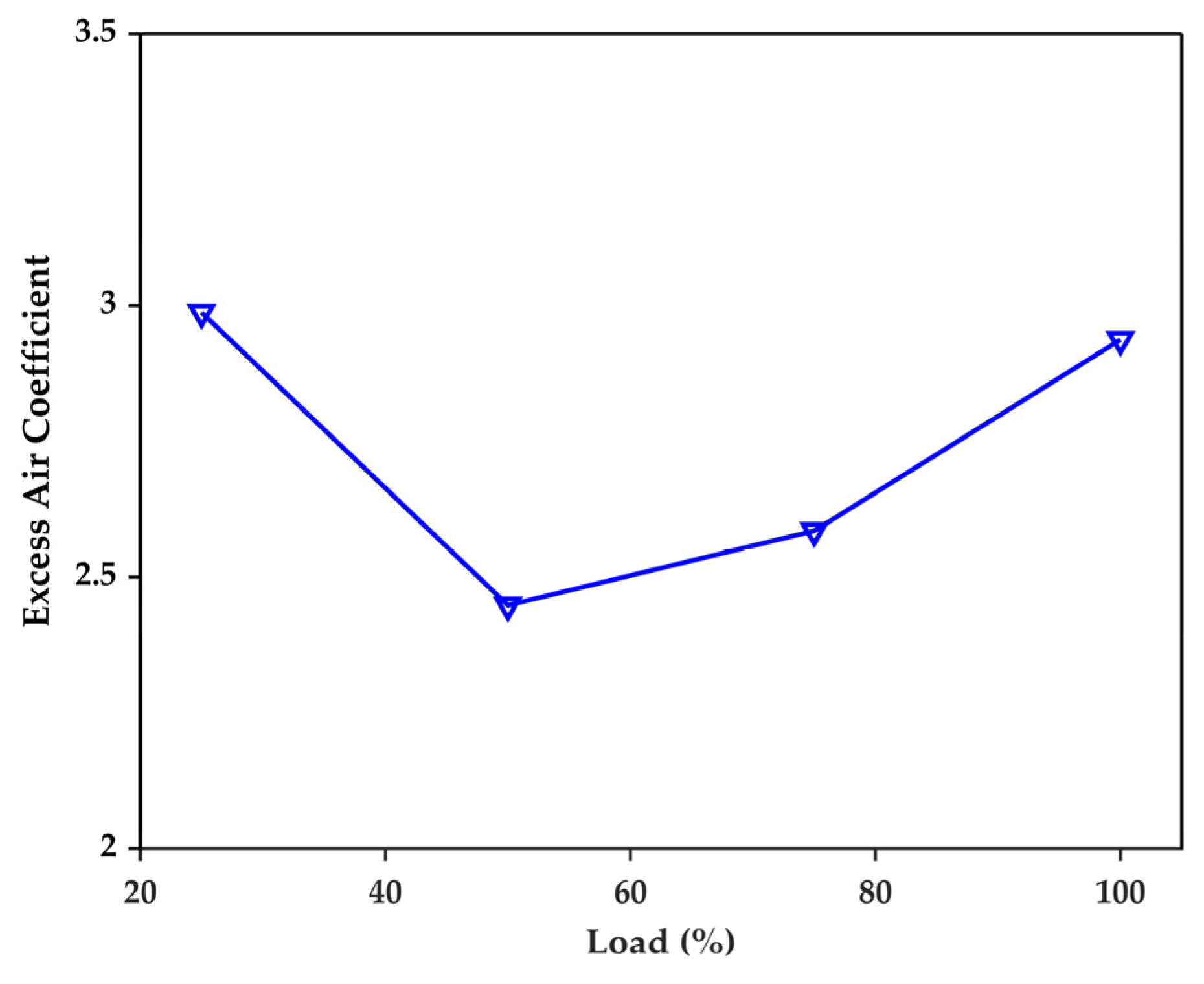
2.3.4. Excess Air Coefficient
2.3.5. Indicated Torque and Exhaust Temperature
2.3.6. Friction Torque and Load Torque
2.3.7. Governor
2.4. Pollutant Emission Calculation Model
2.4.1. Calculation Model of CO2
2.4.2. Calculation Model of NOX
2.4.3. Calculation Model of CO
2.4.4. Calculation Model of HC
3. Result and Discussion
3.1. Propulsion Performance Simulation
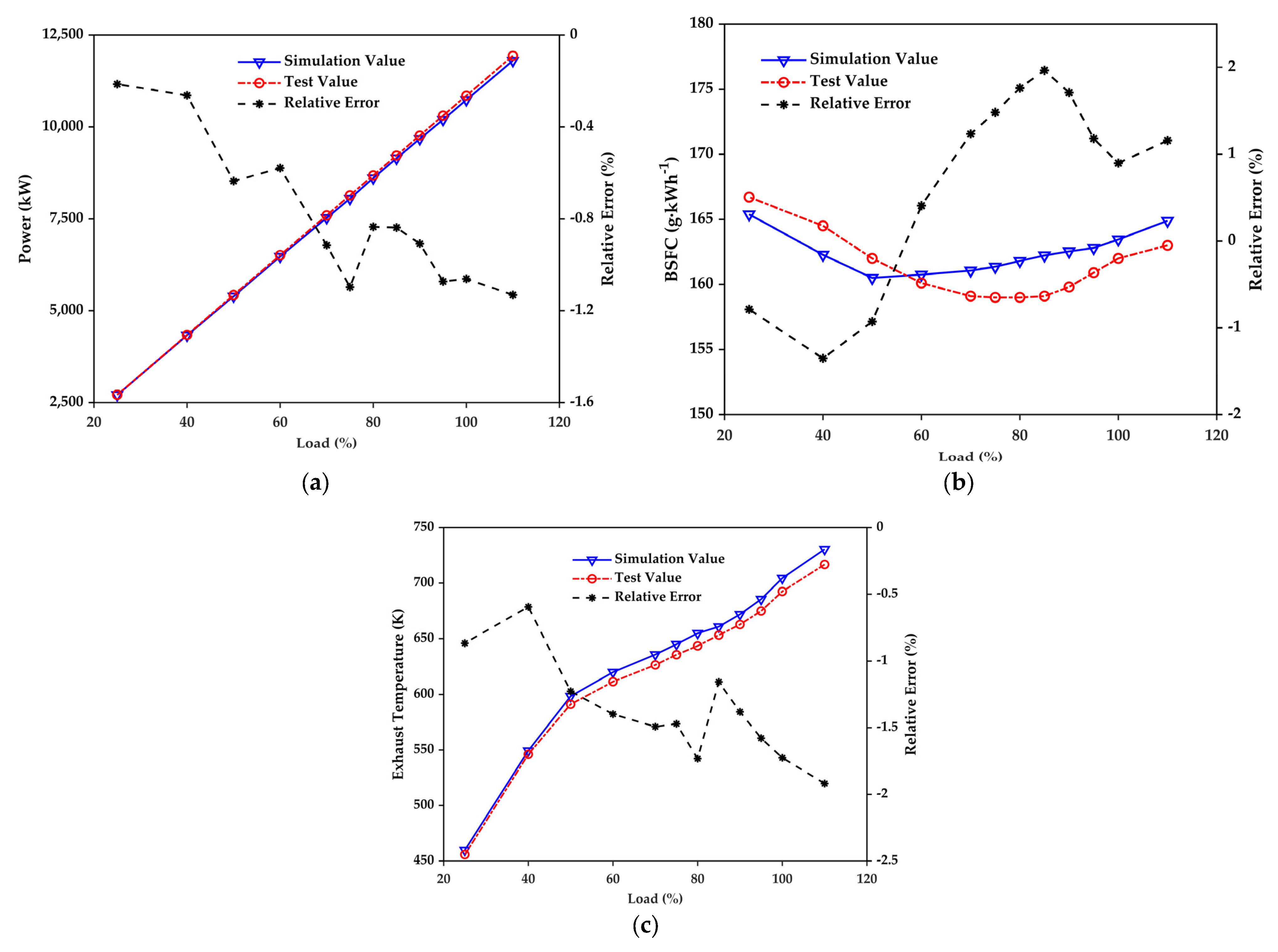
3.1.1. Steady-State Simulation
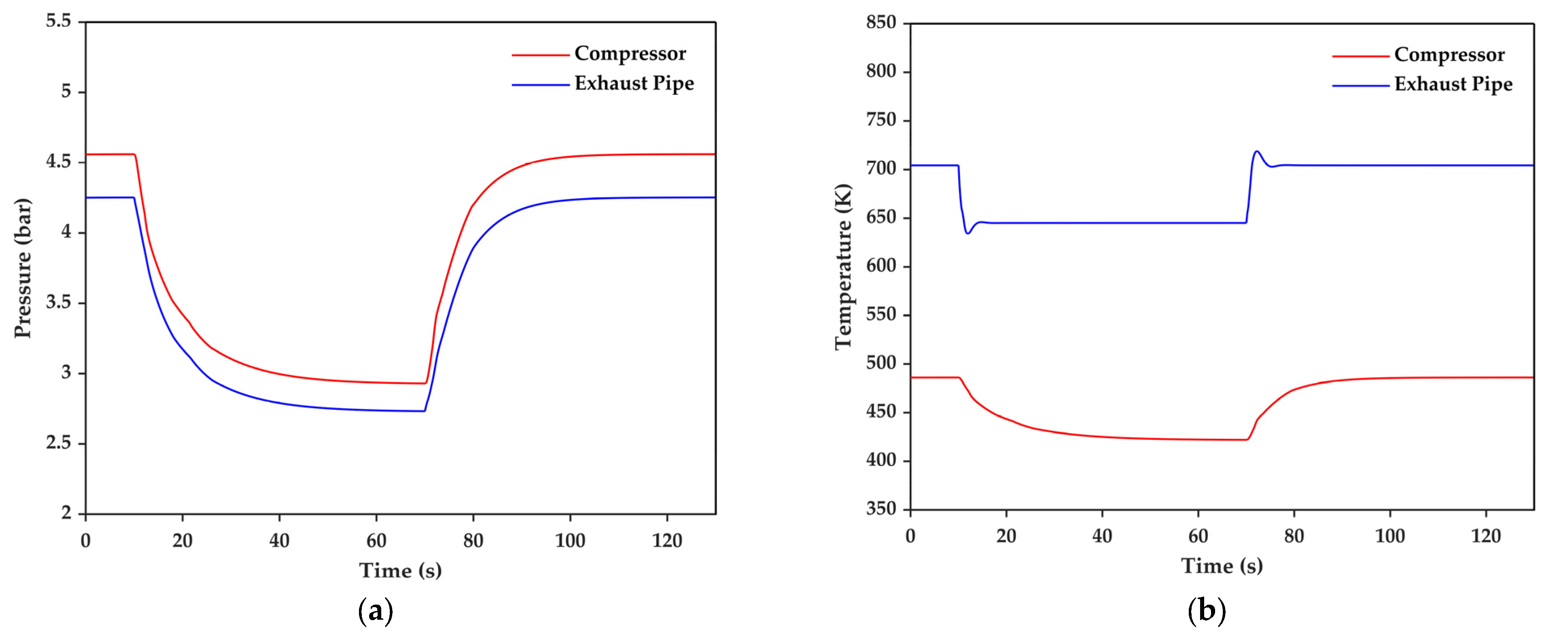
3.1.2. Dynamic Simulation
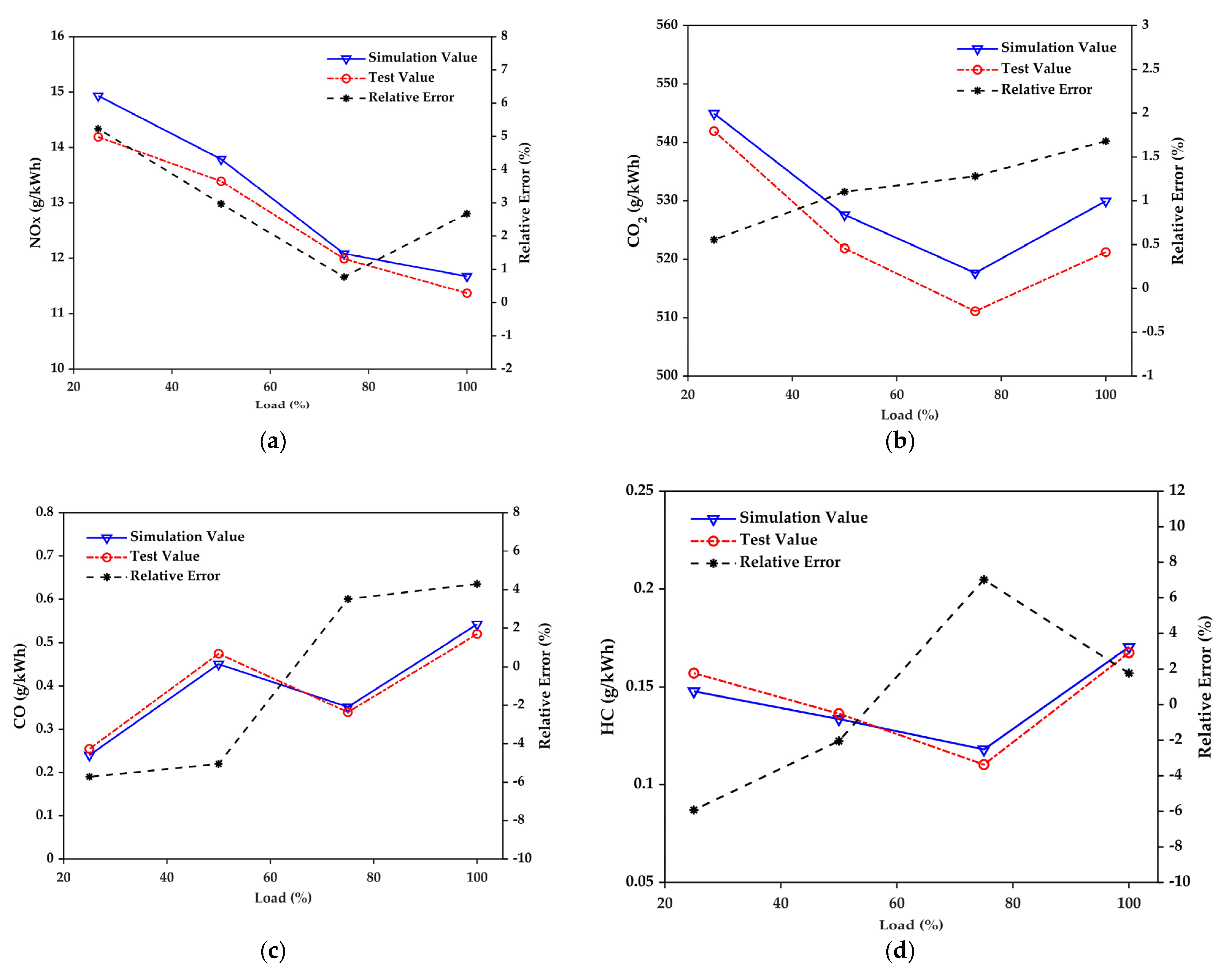
3.2. Emission Simulation
4. Conclusions
- When compared against the engine’s actual performance data, the relative error of major parameters from this model in steady-state simulation is within 2.2%, indicating a decent high accuracy.
- The exhaust emissions models of CO2, CO, HC and NOX are established as a function of the load, and the relative error is found to be within 7%.
- Three particular dynamic processes with sudden increase and decrease of the engine load at corresponding engine’s speed are simulated. The pressure of the compressor varies more greatly than that at the exhaust pipe under load variations and the exhaust pipe temperature fluctuation is more significant when the load varies from 50% to 25% MCR.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yuan, Y.; Wang, J.; Yan, X.; Shen, B.; Long, T. A review of multi-energy hybrid power system for ships. Renew. Sust. Energ. Rev. 2020, 132, 110081. [Google Scholar] [CrossRef]
- Inal, O.B.; Charpentier, J.; Deniz, C. Hybrid power and propulsion systems for ships: Current status and future challenges. Renew. Sust. Energ. Rev. 2022, 156, 111965. [Google Scholar] [CrossRef]
- Third IMO Greenhouse Gas Study 2014. Available online: https://www.imo.org/en/OurWork/Environment/Pages/Greenhouse-Gas-Studies-2014.aspx (accessed on 1 July 2014).
- IMO MEPC.328 Full MARPOL Annex VI. Available online: https://imorules.com/MEPCRES_328.75.html (accessed on 17 June 2021).
- Resolution MEPC.304 Initial IMO Strategy on Reduction of GHG Emissions from Ships. Available online: https://wwwcdn.imo.org/localresources/en/KnowledgeCentre/IndexofIMOResolutions/MEPCDocuments/MEPC.304(72).pdf (accessed on 13 April 2018).
- Hendricks, E. Mean Value Modeling of Large Turbo-charged Two-Stroke Diesel Engines. SAE 1989, 890564. Available online: https://www.sae.org/publications/technical-papers/content/890564/ (accessed on 13 July 2022).
- Theotokatos, G. On the cycle mean value modelling of a large two-stroke marine diesel engine. Proc. Inst. Mech. Eng. Part M J. Eng. Marit. Environ. 2010, 224, 193–205. [Google Scholar] [CrossRef]
- Haiyan, W.; Ren, G.; Zhang, J. Dynamic Modeling of Large Two-Stroke Marine Diesel Engine. Trans. CSICE 2006, 24, 452–458. [Google Scholar]
- Hui, C.; Peili, W.; Jundong, Z. Modeling and Simulation of Working Process of Marine Diesel Engine with a Comprehensive Method. Int. J. Comput. Inform. Syst. and Ind. Manage. Appl. 2013, 5, 480–487. [Google Scholar]
- Han, Z.; Zou, T.; Wang, J.; Dong, J.; Deng, Y.; Pan, X. A Novel Method for Simultaneous Removal of NO and SO2 from Marine Exhaust Gas via In-Site Combination of Ozone Oxidation and Wet Scrubbing Absorption. J. Mar. Sci. Eng. 2020, 8, 943. [Google Scholar] [CrossRef]
- Yusuf, A.A.; Inambao, F.L.; Ampah, J.D. Evaluation of biodiesel on speciated PM2.5, organic compound, ultrafine particle and gaseous emissions from a low-speed EPA Tier II marine diesel engine coupled with DPF, DEP and SCR filter at various loads. Energy 2022, 239, 121837. [Google Scholar] [CrossRef]
- Charles, K.W.; Frederick, L.D. Chemical kinetic modeling of hydrocarbon combustion. Prog. Energy Combust. Sci. 1984, 10, 1–57. [Google Scholar]
- Westenberg, A.A. Kinetics of NO and CO in Lean, Premixed Hydrocarbon-Air Flames. Combust. Sci. Technol. 1971, 4, 59–64. [Google Scholar] [CrossRef]
- Muqeem, M.; Sherwani, A.F.; Ahmad, M.; Khan, Z.A. Optimization of diesel engine input parameters for reducing hydrocarbon emission and smoke opacity using Taguchi method and analysis of variance. Energ. Environ. 2018, 29, 410–431. [Google Scholar] [CrossRef]
- Altosole, M.; Campora, U.; Figari, M.; Laviola, M.; Martelli, M. A Diesel Engine Modelling Approach for Ship Propulsion Real-Time Simulators. J. Mar. Sci. Eng. 2019, 7, 138. [Google Scholar] [CrossRef] [Green Version]
- Taburri, M.; Chiara, F.; Canova, M.; Wang, Y. A model-based methodology to predict the compressor behavior for the simulation of turbocharged engines. Proc. Inst. Mech. Eng. Part D J. Auto. Eng. 2012, 226, 560–574. [Google Scholar] [CrossRef]
- Guan, C.; Theotokatos, G.; Zhou, P.; Chen, H. Computational investigation of a large containership propulsion engine operation at slow steaming conditions. Appl. Energy 2014, 130, 370–383. [Google Scholar] [CrossRef] [Green Version]
- Hountalas, D.T.; Kouremenos, D.A.; Sideris, M. A Diagnostic Method for Heavy-Duty Diesel Engines Used in Stationary Applications. Trans. ASME 2004, 126, 886–898. [Google Scholar] [CrossRef]
- Ernst, E.S.; Gary, L.B. Mathematical Simulation of a Large Turbocharged Two-Stroke Diesel Engine. SAE 1971, 710176, 733–768. [Google Scholar]
- Zhu, J. Modeling and Simulating of Container Ship’s Main Diesel Engine. Proc. IMECS 2008, 2, 19–21. [Google Scholar]
- Piero, A.; Giorgio, M.; Davide, M. Air-Fuel Ratio Control for a High Performance Engine using Throttle Angle Information. SAE 1999, 1999-01-1169. Available online: https://www.sae.org/publications/technical-papers/content/1999-01-1169/?PC=DL2BUY (accessed on 13 July 2022).
- John, R.; Wagner, D.M.; Dawson, L. Nonlinear Air-to-Fuel Ratio and Engine Speed Control for Hybrid Vehicles. IEEE Trans. Veh. Technol. 2003, 52, 184–195. [Google Scholar]
- Jensen, J.P.; Kristensen, A.F.; Sorenson, S.C.; Houbak, N.; Hendricks, E. Mean Value Modeling of a Small Turbocharged Diesel Engine. SAE 1991, 910070. Available online: https://saemobilus.sae.org/content/910070 (accessed on 13 July 2022).
- Damir, R.; Asgeir, J.S.; Tor, A.J. Inertial Control of Marine Engines and Propellers. IFAC Proc. Vol. 2007, 40, 323–328. [Google Scholar]
- Theotokatos, G.; Tzelepis, V.A. computational study on the performance and emission parameters mapping of a ship propulsion system. Proc. Inst. Mech. Eng. Part M J. Eng. Marit. Environ. 2015, 229, 58–76. [Google Scholar] [CrossRef] [Green Version]
- Roberto, F.; Ezio, S. A real time zero-dimensional diagnostic model for the calculation of in-cylinder temperatures, HRR and nitrogen oxides in diesel engines. Energ. Convers. Manag. 2014, 79, 498–510. [Google Scholar]
- Psota, M.A.; Mellor, A.M. Dynamic Application of a Skeletal Mechanism for DI Diesel NOx Emissions. SAE 2001, 2001-01-1984. [Google Scholar]
- Mellor, A.M.; Mello, J.P.; Duffy, K.P.; Easley, W.L.; Faulkner, J.C. Skeletal Mechanism for NOx Chemistry in Diesel Engines. SAE 1998, 981450. Available online: https://www.jstor.org/stable/44746494 (accessed on 13 July 2022).
- Meng, Z.; Yang, D.; Yan, Y. Study of carbon black oxidation behavior under different heating rates. J. Therm. Anal. Calorim. 2014, 118, 551–559. [Google Scholar] [CrossRef]
- Hiroyasu, H.; Kadota, T. Models for Combustion and Formation of Nitric Oxide and Soot in Direct Injection Diesel Engines. SAE 1976, 760129, 513–526. [Google Scholar]


| Name | Parameter |
|---|---|
| Engine type | 6RT-flex58T-D |
| Number of cylinders | 6 |
| MCR power [kW] | 10,850 |
| MCR BSFC [g/kWh] | 162 |
| MCR speed [r/min] | 105 |
| Bore [mm] | 580 |
| Stroke [mm] | 2416 |
| Compression ratio | 15 |
| Maximum cylinder pressure [bar] | 155.2 |
| Mean effective pressure [bar] | 16.2 |
| Turbocharger | 2 × A165-L34 |
| Air cooler | 2 × SAC245F |
| Name | Value |
|---|---|
| Fuel oil specification | 0# DMA (GB 19147-2013) |
| LHV [MJ/kg] | 42.7625 |
| Density [kg/m3] at 15 °C | 841.7 |
| Viscosity [cSt] at 40 °C | 3.02 |
| Component | Content |
|---|---|
| C | 85.89 wt% |
| H | 12.97 wt% |
| N | 0.41 wt% |
| O | 0.28 wt% |
| S | 0.008 wt% |
| Parameters | Lower Bound | Upper Bound | Calibrated Value (Load) | |||
|---|---|---|---|---|---|---|
| 25% | 50% | 75% | 1005 | |||
| 2.05 | 2.47 | 2.47 | 2.37 | 2.29 | 2.05 | |
| 0.50 | 0.62 | 0.62 | 0.55 | 0.50 | 0.50 | |
| 0.039 | 0.044 | 0.040 | 0.039 | 0.042 | 0.044 | |
| 1.80 | 2.28 | 2.28 | 2.1 | 2.01 | 1.80 | |
| 4.35 × 10−26 | 3.65 × 10−26 | 4.35 × 10−26 | 3.65 × 10−26 | 4.18 × 10−26 | 3.89 × 10−26 | |
| Name | Point A | Point B | Point C | Point D |
|---|---|---|---|---|
| Load percentage | 100% | 75% | 50% | 25% |
| Load [kW] | 10850.0 | 8137.5 | 5425.0 | 2712.5 |
| Speed percentage | 100% | 91% | 80% | 63% |
| Speed [r/min] | 105 | 95.4 | 83.3 | 66.1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xin, R.; Zhai, J.; Liao, C.; Wang, Z.; Zhang, J.; Bazari, Z.; Ji, Y. Simulation Study on the Performance and Emission Parameters of a Marine Diesel Engine. J. Mar. Sci. Eng. 2022, 10, 985. https://doi.org/10.3390/jmse10070985
Xin R, Zhai J, Liao C, Wang Z, Zhang J, Bazari Z, Ji Y. Simulation Study on the Performance and Emission Parameters of a Marine Diesel Engine. Journal of Marine Science and Engineering. 2022; 10(7):985. https://doi.org/10.3390/jmse10070985
Chicago/Turabian StyleXin, Rongbin, Jinguo Zhai, Chang Liao, Zongyu Wang, Jifeng Zhang, Zabihollah Bazari, and Yulong Ji. 2022. "Simulation Study on the Performance and Emission Parameters of a Marine Diesel Engine" Journal of Marine Science and Engineering 10, no. 7: 985. https://doi.org/10.3390/jmse10070985
APA StyleXin, R., Zhai, J., Liao, C., Wang, Z., Zhang, J., Bazari, Z., & Ji, Y. (2022). Simulation Study on the Performance and Emission Parameters of a Marine Diesel Engine. Journal of Marine Science and Engineering, 10(7), 985. https://doi.org/10.3390/jmse10070985






