Fast Multigrid Algorithm for Non-Linear Simulation of Intact and Damaged Ship Motions in Waves

Abstract

This paper proposes a fast multigrid algorithm to simulate the non-linear motion of ships in both intact and damaged conditions. The simulations of ship motions in waves are known to require much time to calculate due to the strong non-linear interactions between ship and waves. To improve the calculation efficiency while retaining the accuracy, a prediction-correction strategy was designed to accelerate the simulation through three sets of locally refined meshes. The flow field was first estimated in a coarse mesh and then mapped to a locally refine mesh for further higher-fidelity corrections. A partitioned radial basis function (PRBF) method is proposed to interpolate and reconstruct the flow field for the refined mesh. A new two-phase flow solver was developed with a fast multigrid algorithm based on the Reynolds-averaged Navier–Stokes equations (RANSE). The new solver was applied to study the non-linear behavior of a damaged ship in beam waves and the effect of damaged compartments on ship rolling motion. Validation against the solution with the original method of single set meshes and experimental data indicates that the proposed algorithm yields satisfactory results while saving 30–40% of the computational time.

1. Introduction

The stability of damaged ships is known as one of the most important issues for vessel designers and safety authorities. Unlike an intact ship, the behavior of a damaged ship is not only affected by the significant hydrodynamic loading exerted by sea waves, but is also aggravated by the water that floods into the damaged compartments [1]. The connection and interaction of water inside and outside of the compartments through an opening makes the numerical study of damaged ships much more complicated than in intact situations. Therefore, it is crucial to be able to accurately and quickly describe and predict the very non-linear motion of ships with damaged surfaces amid waves.

For problems concerning ship seakeeping, flow simulations for damaged ships rely largely on the potential flow theory [2,3,4,5,6,7,8,9] with semi-empirical approaches. In these studies, the amount of flooded water was estimated by modified Bernoulli equations and the free surface of the flooded water was treated as a flat plane. Potential flow theory is useful for practical problems and has high efficiency, but fails to accurately describe the physical phenomena due to the neglection of the viscosity effect. For the highly non-linear interactions between large ship motion and large free surface deformation, the potential flow theory fails to provide adequate results for ship hydrodynamic loads [1]. The simple treatment for the floodwater’s motion neglects the transient characteristics of water flow through an opening. The momentum flux of the in-flooding water is considered in simplified flooding simulation models alongside flat inclined water levels. However, the sloshing and the resulting non-linear effects generated by the highly turbulent vortices, separate flow, and breaking waves cannot to be modelled in potential flow theory simulations [10]. To understand the complexity of damaged ship motion together with interactions between the hydrodynamic loads that are induced by both sea waves and water flooding and sloshing, computational fluid dynamics (CFD) techniques based on the Navier–Stokes equations have been used in a growing number of applications over the past two decades.

There are still few studies that relate to the behavior of damaged ships in waves based on CFD techniques. Some researchers [11,12,13,14,15] have investigated the free motions of a damaged ship in still water or head sea. The numerical tests were carried out using Navier–Stokes-based solvers along with standard turbulent models and the volume of fluid (VOF) method for free surface description. The interaction of ship motions in waves were investigated. However, CFD tools are known to be highly time-consuming compared to the potential flow theory methods. The high-fidelity and solution efficiency of complex viscous flow problems have always been among the most important factors that limit the development of the CFD applications.

A concept that combined both potential flow theory and viscous flow simulations was one of the solutions presented to improve the computational efficiency. The ship motions induced by the sea waves were predicted by potential flow theory, while the behavior of the sloshing flooding water inside was calculated by using RANS solvers with the VOF method or smoothed particle hydrodynamics (SPH) method to capture the free surface [16,17,18]. A dynamic mesh approach was applied to handle the mesh, which was updated alongside the ship’s motion. These studies showed the ability for numerical ship motion simulations to be accomplished using a single set of mesh. However, to capture the complex flow field around the ship, the number of cells required was still large. Additionally, the sliding between dynamic mesh layers could reduce the original accuracy [19].

An alternative choice is the multigrid (MG) approach. As one of the most efficient techniques for solving partial differential equations [20], it is used to speed up the solutions for Poisson equations in CFD tools. According to the mesh type, the MG approach can be divided into two groups, the classical multigrid methods and cascadic multigrid (CMG) methods. In the classical multigrid methods (GMG, geometry multigrid; and AMG, algebraic multigrid), the solutions are interpolated and transferred between the multigrids, and the oscillatory errors dampen and converge through correction processes. Several researchers have tested the applicability of the classical multigrid method in hydrodynamic computations [21] and landslide tsunami simulations [22]. Better parallel efficiency was obtained in these situations.

The cascadic multigrid (CMG) method was first proposed by F.A. Bornemann and P. Deuflhard [23]. The solution was computed based on the coarse grid and directly interpolated to fine grids without any coarse grid correction steps [24]. This strategy avoids the calculation processes of correction steps and further improves the computational efficiency. The CMG method has been widely used in elliptic problems [25] and parabolic problems [26] due to its advantages of high efficiency and simplicity. He and Liu [27] applied the CMG method in the solution of Navier–Stokes problems. Based on the concept of the CMG method, Hu et al. [20] and Pan et al. [24] proposed an extrapolation cascadic multigrid method (EXCMG) method and verified its convergence and accuracy through a set of numerical test cases.

The multigrid method is still in the developmental stage, and many more problems need to be further studied. Existing studies are limited to mathematical models or simplified test cases. For CFD simulations, they are only used to implicitly solve pressure Poisson equations. Very few investigations have covered the prediction of the strong, non-linear motion of intact and damaged ships in wave scenarios. In this paper, a multigrid prediction-correction acceleration strategy is proposed to quickly predict the high-fidelity flow field in the rolling of damaged ships. Based on the concept of the CMG method, a multigrid system was designed to build an efficient prediction process for the ship motions. Three sets of locally refined mesh were generated and were defined as coarse, medium, and fine meshes according to the grid sizes. The flow field information, such as velocity, pressure, and volume fraction, was first solved on a coarse mesh. Then, the information was updated and mapped onto a locally refined mesh for further iterative corrections. A partitioned radial basis function (PRBF) is proposed to interpolate and reconstruct the flow field for the refined mesh.

We developed a two-phase flow solver that was coupled with a multigrid algorithm, and was based on a computational model with Reynolds-averaged Navier–Stokes equations (RANSE) for turbulent flow simulation. We also included the volume of fluid (VOF) method for free surface capturing. The new solver was applied to study the non-linear behavior of a damaged ship in beam waves. The results of an intact ship were added as a reference to investigate the damage’s effect on the ship’s motion in waves. Two sets of test cases, a roll decay test in clam water and quasi-steady state of flooding in a damaged ship, were carried out. A validation of the solution based on an original single set mesh and experimental data showed that the proposed algorithm yielded satisfactory results while reducing the time of computation by 30–40%. This study proves and provides a new method for quickly predicting, with high-fidelity, the flow field and motion response of damaged ships.

2. Materials and Methods

2.1. Navier–Stokes Equations for Fluid Motion

The governing equations for incompressible viscous flows are the Navier–Stokes equations:

$$\nabla ·\mathit{U}=0,$$

(1)

$$\frac{\partial \left(\rho \mathit{U}\right)}{\partial t}+\nabla ·\left(\rho \mathit{U}\mathit{U}\right)=-\nabla p+\nabla ·\mathit{T}+\rho {\mathit{f}}_b$$

(2)

where $\mathit{U}$ is the velocity field throughout the domain, $\rho$ is the density of fluid,$p$ is the pressure, $\mathit{T}$ is the viscous stress tensor, and ${\mathit{f}}_b$ represents the body forces per unit mass, which are the acceleration due to gravity and surface tension effects at the interface.

The air and water are considered as two incompressible, isothermal, and immiscible fluids. A VOF method is used to track the free surface:

$$\frac{\partial \alpha }{\partial t}+\nabla ·\left(\mathit{U}\alpha \right)=0,$$

(3)

where $\alpha$ is the volume fraction, which is defined as the relative proportion of water in each cell. If $\alpha =1$, the cell is full of water, and if $\alpha =0$, the cell is full of air. In any other case, the cell contains an interface between the two phases.

A standard RANS k-$\mathsf{\epsilon }$ turbulence model is used to describe the turbulence flow, which mainly exists in the area around the ship and free surface zone. This model has performed well in the fully turbulent region and in free shear layers [28]. It is a semi-empirical model based on two transport equations for the turbulent kinetic energy $k$ and its rate of dissipation $\epsilon$. The two equations are:

$$\frac{\partial \left(\rho k\right)}{\partial t}+\frac{\partial \left(\rho k{u}_i\right)}{\partial x_i}=\frac{\partial }{\partial x_j}\left[\frac{{\mu }_t}{{\sigma }_k}\frac{\partial k}{\partial x_j}\right]+2{\mu }_t{E}_{ij}{E}_{ij}-\rho \epsilon$$

(4)

$$\frac{\partial \left(\rho \epsilon \right)}{\partial t}+\frac{\partial \left(\rho \epsilon u_i\right)}{\partial x_i}=\frac{\partial }{\partial x_j}\left[\frac{{\mu }_t}{{\sigma }_{\epsilon }}\frac{\partial \epsilon }{\partial x_j}\right]+C_{1\epsilon }\frac{\epsilon }{k}2{\mu }_t{E}_{ij}{E}_{ij}-C_{2\epsilon }\rho \frac{{\epsilon }^2}{k}$$

(5)

Here, $E_{ij}$ is the component of the rate of deformation; ${\sigma }_k$, ${\sigma }_{\epsilon }$, $C_{1\epsilon }$, and $C_{2\epsilon }$ are constants; and ${\mu }_t$ is the turbulent viscosity and calculated by combining $k$ and $\epsilon$ as follows:

$${\mu }_t=\rho C_{\mu }\frac{k^2}{\epsilon }$$

(6)

where $C_{\mu }$ is a constant.

2.2. Multi-Degree-of-Freedom Equations for Ship Motion

The ship is assumed to be a rigid body and freely floats in the waves. The equation for the translation of the center of mass of the ship body is given as [29]:

$$m\frac{dv}{dt}=\mathit{f}$$

(7)

where $m$ represents the mass of the body, $\mathit{f}$ is the resultant force acting on the body, and $v$ is the velocity of the center of mass. An angular momentum equation of the body is formulated in the body’s local coordinate system, with the origin in the center of the body:

$$M·\frac{d\omega }{dt}+\omega \times M·\omega =n$$

(8)

where $M$ is the tensor of moments of inertia, $\omega$ is the angular velocity of the rigid body, and $n$ is the resultant moment acting on the body. The resulting force and moment acting on the ship are obtained from the fluid pressure and shear force acting on each boundary face of the body. The translations of the ship are estimated according to the computed velocity and pressure fields in the flow domain.

2.3. A Fast Algorithm of CMG Method with Radial Basis Function (RBF)

In the typical rolling motion of damaged ships, the viscosity is locally dominant with strong non-linear phenomena, such as highly turbulent vortices, separation flows, free liquid surface curling, and crushing around the damaged compartment. A high spatial resolution is needed to accurately describe the complex ship flow. A relatively fine mesh is required around the ship’s hull, the damaged compartment, and the free surface. However, as discussed in the Introduction, the finer the mesh is, the larger the number of cells, and the longer it takes to finish the simulations.

Therefore, a fast multigrid algorithm was developed in the present study to efficiently predict the ship’s motion while accurately describing the viscous flow around the ship. The basic idea of this method was to solve the flow field on a coarse mesh, interpolate the flow information to a refined mesh, and correct the solution on the fine mesh. A partitioned radial basis function (PRBF) interpolation technique was used to interpolate and map the information from the coarse mesh to the refined mesh.

In Section 2.3.1, convergent reconstruction judgment criteria were applied based on the concept of CMG method. The region of local refined mesh was identified and re-constructed when the flow field reached the convergent state. In Section 2.3.2, a detailed description of the RBF method is given to explain how the physical information trans-formed between the meshes.

2.3.1. Convergent Reconstruction Judgment Criteria

The convergence and reconstruction criteria aimed to accurately capture the influence of ship motion on the flow field in the prediction and correction stage. In the prediction stage, the flow field variables, pressure, velocity, fluid volume fraction, etc., on the coarse grid nodes in the convergent state were obtained based on judgments such as the pre-convergence of the flow field. In the correction stage, the PRBF interpolation technology, combined with an unstructured grid index to switch the recursion mode, transmitted the convergent flow field variable values on the coarse grid nodes to the fine grid nodes (see Figure 1). The fine mesh was obtained by locally refining the coarse mesh according to the position of the ship and free surface. The position of the nodes from the coarse mesh stayed the same, while new nodes were added when the fine mesh was generated.

Since the initial state of the fine grid flow field is based on the iterative convergent and smoothed results of the coarse grid, it theoretically has the same approximate convergence order as the fine grid. This reduces the number of iterations in the fine grid. The computational efficiency is significantly improved compared with the traditional simulations processing the whole calculation with a single set of mesh.

2.3.2. Radial Basis Function (RBF) Interpolation Technique

The number of cells required in a viscous flow simulation is extremely large (around 1 × 10⁵–1 × 10⁸), and the dimensions of the coefficient matrix of equations are also very large. Though a CMG multigrid approach is being applied, the number of cells included in the prediction-correction iterative acceleration process is still too large. This results in a significant reduction in the efficiency of solving equations during the interpolation process between the meshes. The radial basis interpolation function (RBF) is suitable for the fitting and interpolation of multivariate scattered data, with the advantages of simplicity and applicability for structured and unstructured grids. However, a large full-rank matrix is constructed by defining points at distances for the interpolation. The key problem when solving the inter-grid interpolation is the method that we use to efficiently and accurately solve large full-rank matrices. A partitioned radial basis function (PRBF) interpolation technique was developed to solve the problem of a low solution efficiency of the full-rank matrix caused by the millions of grids. The premise of the PRBF technique is to decompose the global interpolation domain into a series of small and independent subdomains. Physical parameters, such as pressure and velocity, are first calculated based on a series of independent subdomains and then interpolated to the whole global domain through weighting functions. The decomposition of the global interpolation domain provides an accurate solution of the flow fields and significantly improves the efficiency of the global domain interpolation.

According to the mesh sizes and mesh arrangement, a uniform sampling method was used to balance the calculation stability and efficiency. For a domain with a coarse background mesh, assuming that there are $n_c$ points in the grid area $M$, the coordinates and the corresponding function value are given as ${\mathit{X}}_i$ and $S_c\left({\mathit{X}}_i\right)$, respectively, where $i=1,2,\dots ,n_c$. We take every kth point from the $n_c$ points and form a new array for $M_i$, where $i=1,2,\dots ,k$. The number of nodes in the subdomain $M_1$ is $m$ ($\approx n/k$), and corresponds to the following relationship:

$$m_i\left(x,y,z\right)=n_{i+\left(i-1\right)k}\left(x,y,z\right)$$

(9)

$$S_1\left({\mathit{X}}_{m_i}\right)=S_c\left({\mathit{X}}_{n_{i+\left(i-1\right)k}}\right)$$

(10)

The original domain M is therefore decomposed into the $k$ subdomains $M_i$, and the dimension of the coefficient matrix with $n_c$ nodes is reduced into the m-dimension accordingly. A lower dimensional interpolation structure is built, and the function values on the selected grid node are determined by the current dimension m. The coordinates ${\mathit{X}}_i$ and the value $S_1\left({\mathit{X}}_i\right)$ on the selected nodes in the corresponding subdomains are interpolated into the global domain along the refined mesh through the RBF interpolation method.

The equations for the RBF function are given as:

$$s\left(x\right)={{\displaystyle \sum }}_{i=1}^m{\alpha }_i\phi \left(\Vert x-{\alpha }_i\Vert \right)$$

(11)

where $\phi \left(x\right)$ is the radial basis function and$r=\Vert x-{\alpha }_i\Vert$ is the distance from grid point to interpolation point.

The radial basis function weighting coefficient ${\alpha }_i$ is calculated by:

$${\alpha }_{\phi }=\left(\begin{array}{ccc}\phi \left(r_{11}\right)& \cdots & \phi \left(r_{1n}\right)\\ ⋮& \ddots & ⋮\\ \phi \left(r_{n1}\right)& \cdots & \phi \left(r_{nn}\right)\end{array}\right)$$

(12)

The resulting values calculated based on the subdomain $M_1$ are defined as an interpolation solution $S_1^{*}\left({\mathit{X}}_i\right)$, where $i=1,2,\dots ,n_f$, with $n_f$ being the total number of refined meshes. Repeatedly applying the uniform sampling method for $k$ times and a series of interpolated solutions, $S_1^{*}\left({\mathit{X}}_i\right)$, $S_2^{*}\left({\mathit{X}}_i\right)$, …, $S_k^{*}\left({\mathit{X}}_i\right)$ are obtained. The final solution of the global domain is obtained by averaging.

A simple case with $k=2$ is shown in Figure 2 to better demonstrate the whole process of the PRBF method. The domain $M$ with $n_c=25$ nodes is divided into two subdomains, $M_1$ with nodes $m_1=13$ and $M_2$ with nodes $m_2=12$. The calculation amount using partition radial basis function interpolation is only in a $k\times m^2$ ($k\times m^3$ for a three-dimensional case) order of magnitude, while the calculation amount when directly adopting global radial basis function interpolation is in a ${\left(km\right)}^2$ order of magnitude (${\left(km\right)}^3$ for a three-dimensional case). Compared with global radial basis function interpolation, the proposed partition interpolation technique significantly improves the computational efficiency.

$$S_f\left({\mathit{X}}_i\right)=\frac{1}{L}{{\displaystyle \sum }}_{i=1}^k{S}_k^{*}\left({\mathit{X}}_i\right),wherei=1,2,\dots ,n_f.$$

(13)

2.3.3. Solution Procedure

The fast multigrid algorithm of the CMG method combined with the PRBF approach is being published here for the first time. It has been coded using Fortran 90 and was only applied for CFD tools based on the Eulerian mesh. The algorithm was coupled with a typical two-phase flow solver in the commercial code STAR-CCM+ to deal with the problems of long calculation times and low calculation efficiency in ship simulations. A flow chart of the fast algorithm of the CMG method combined with the RBF approach is shown in Figure 3. The basic computational process is given. The whole simulation process mainly consists of three stages: estimation, interpolation, and correction.

The simulation started from a numerical wave tank with a coarse background mesh. The numerical discretization schemes and solver settings were chosen according to the coarse mesh. The flow field was initialized with given flow field properties, such as the physics for velocity, pressure, volume fraction, etc.; the flow field was iteratively solved until it reached a state of convergence.

The next step was to design a set of refined meshes based on the coarse background mesh according to convergent reconstruction judgment criteria. In the case of ship motion in waves, the mesh is locally refined according to the geometry of the ship and the position of the free surface. The PRBF interpolation technique was used to interpolate the flow field from the background mesh to the refined mesh. The resulting flow field was then used as an initial condition for the correction stage.

The last step was to continue the simulation with the updated flow field based on the refined mesh. The solution setting could be reselected accordingly.

The interpolation and correction process can be repeated many times according to the actual situation to improve the calculation efficiency. In the cases of intact/damaged ship motions in waves relevant to the present work, we designed three sets of meshes, namely the coarse, medium, and fine mesh. The interpolation and correction process were repeated twice to obtain a balance of numerical efficiency and accuracy.

3. Results

3.1. Test Ship and Numerical Setup

The fast multigrid algorithm was applied for the time-domain simulation of ship motions in beam waves, in both intact and damaged conditions. The benchmark case has been studied in several papers [30,31,32] via experiments and numerical simulations. Begovic et al. [30] reported a series of model tests of the motion of the DTMB 5415 ship in calm water and in waves. The intact ship model used in the present work utilized the same parameters as the DTMB 5415 experiment, whose parameters are listed in

Table 1. Parameters for the DTMB 5415 in the intact condition.

Properties	Full Scale	Model Scale
Length of waterline (L)	142.00 m	2.79 m
Breadth of waterline (B)	19.08 m	0.37 m
Draft (T)	6.15 m	0.12 m
Displacement (∇)	8635.00 m3	63.50 m3
Centre of gravity above base (KG)	7.56 m	0.15 m
$\mathrm{Roll}\mathrm{radius}\mathrm{of}\mathrm{gyration}(K_{xx}$)	6.93 m	0.12 m

. The damaged DTMB 5415 ship shared the same main properties as the intact ship, with two damaged compartments. The main properties of the intact ship are listed in Table 1, and the geometries of the intact and damaged ship model are shown in Figure 4.

The DTMB 5415 ship, with two damaged compartments, was used in the present work to investigate the motions of a damaged ship in calm water and in beam waves. The main parameters of the damaged compartment are shown in Figure 5 and

Table 2. Parameters for the damaged compartments.

Properties	Full Scale	Model Scale
$\mathrm{Length}(L_c$)	24.36 m	0.478 m
$\mathrm{Breadth}(B_c$)	19.458 m	0.382 m
$\mathrm{Draft}(T_c$)	7.41 m	0.145 m
$\mathrm{Centre}\mathrm{of}\mathrm{gravity}\mathrm{above}\mathrm{base}(K{G}_c$)	6.654 m	0.13 m
$\mathrm{Volume}\mathrm{of}\mathrm{flooded}\mathrm{water}({\nabla }_c$)	2638.90 m3	0.02 m3

. The damaged compartments change the hull mass, buoyancy, and center of gravity. Therefore, it is necessary to consider the changes in the hull series parameters, such as the increase in draft, the height of the ship’s metacentric height, the change in the center of gravity, etc. The water inside of the damaged compartments is connected to the outboard sea water, forcing the sloshing inside of the tank to be stimulated by outboard waves. The strong, non-linear free surface flow near the open cabin, generated from things such as highly turbulent flow and breaking waves, adds more complexity to the simulation of a damaged ship in waves.

The simulations were conducted on a 3D computational domain of x = 2 L, y = 6 L, and z = 1.7 L, where L is the length of the ship. The incident regular waves entered in from the inlet boundary and exited out from the outlet boundary. As shown in Figure 6, the damaged ship was initially placed at the center of the numerical tank. The inlet and outlet were arranged at a distance of 2 L from each other, the sides were arranged at a distance of 1 L from the bow and stern, the top surface was arranged at a distance of 0.7 L from the calm water level, and the bottom surface was arranged at a distance of 1 L from the free surface. The velocity and pressure of the incident waves were imposed on the inlet boundary, the open channel type pressure outlet condition was used on the outlet boundary, and the non-slip boundary condition was imposed on the ship’s hull. The regions that measured twice as large as the incident wavelength from the inlet and outlet boundaries were set as the wave generation and dissipation zones. Slip boundary conditions were used at all the other boundaries.

3.2. Mesh Generation and Mesh Independence Study

An all-hexahedral, unstructured grid was generated throughout the whole computational domain. According to the fast algorithm of the CMG method combined with the PRBF method, three sets of grids, namely the coarse mesh A, medium mesh B, and fine mesh C, were designed as described in Figure 7. They were designed to properly resolve the flow field around the ship’s hull, damaged compartments, and at the wave surface within an acceptable computational time in the whole simulation process. The finer mesh was obtained by locally refining the coarse mesh according to the position of the ship and the free surface. The size of the refined mesh was half the original background mesh for all three directions. A sketch of the mesh arrangement around the ship’s hull for the coarse mesh is shown in Figure 7a. The fundamental size was set to 1 m, the number of prism layers was 8, and the elongation of the prism layer was 1.2. A more refined mesh was employed around the ship hull and the regular waves, compared with the rest of the domain, to better capture the near-wall turbulent flow and the free surface behaviors. The three sets of mesh shown in Figure 7 were used for the prediction, transition, and correction stages, respectively. The total number of cells was 1,532,798 for mesh A, 1,948,924 for mesh B, and 3,547,924 for mesh C.

For all of the simulations, the non-equilibrium wall function was employed with respect to the near-wall. The distance to the wall was defined by the non-dimensional parameter y+. For the finest mesh, the minimum value of y+ around the damaged compartment reached 20. The size of the element near the free surface in the z-axis is 0.004 m, which is around 0.125 times the incident wave height. The element size was chosen to preserve the accuracy of wave propagation.

In order to compare the behavior of the ship in intact and damaged conditions, a similar mesh generation process was performed for the intact ship hull. Apart from the mesh inside the damaged compartments, the mesh refinement area for the intact ship remained the same for the damaged ship.

The three sets of single set mesh were first applied to simulate the roll decay of the DTMB 5415 ship in calm water to check the mesh independence of the simulations. This allowed for the direct comparison of the ship in a damaged condition without the excitation of incident waves. The ship initially heeled at the port side at an angle of 18.3°. The free surface inside and outside of the ship were set as zero level.

Figure 8 shows a roll decay test of the damaged ship in calm water obtained by the experiment and numerical simulations with the three sets of meshes. Good agreement was obtained with the three mesh sizes. The natural roll periods remained similar to the experiment, where almost no visible phase shift was observed, and the roll amplitudes were in good agreement with the experiments. The numerical result obtained with the medium mesh B almost overlapped with that obtained by the fine mesh C.

Table 3. Roll nature periods and roll peak obtained by the different meshes at the ninth cycle of the roll decay for the damaged ship.

Mesh	${\mathit{T}}_{\mathit{i}}={\mathit{t}}_{\mathit{i}+1}-{\mathit{t}}_{\mathit{i}}$			${\mathit{\alpha }}_{\mathit{i}}$
	Exp. (s)	Num. (s)	Error (%)	Exp. (°)	Num. (°)	Error (%)
Mesh A	1.515	1.555	2.623	1.556	1.713	10.12
Mesh B	1.515	1.546	2.04	1.556	1.637	5.24
Mesh C	1.515	1.538	1.51	1.556	1.579	1.47

gives the comparison of the roll natural periods ($T_i$) [30] and the maximum roll degree (${\alpha }_i$) observed at the ninth cycle of roll decay and obtained with different meshes. The $t_i$ and ${\alpha }_i$ are the initial time instant and heel angle at each cycle of roll motion. The numerical errors accumulated with time and the relative errors in the ninth cycle represent the accuracy of the numerical simulations.

The computed natural roll periods obtained with the three mesh sets were similar and close to the experimental data. For the coarse mesh A, the average error of the first nine natural roll periods was about 1%, with the largest relative error being 2.6%. For the roll peak, the computed result slightly overestimated in comparison with the experimental data, and the relative error grew with the mesh size. The differences between the numerical results and the experiment data were less than 0.5°. The numerical errors of the simulation using the finest mesh C for the roll decay were similar to the results published by other researchers [30,32,33]. This indicates that the fine mesh size C can ensure acceptable numerical accuracy for the ship motion predictions and was used in the simulation of motion of a damaged ship in waves found in Section 3.3 and Section 3.4.

To investigate the damage’s effect on ship motion, the roll decay motions of the damaged ship were compared with the results in the intact condition. As shown in Figure 9, the numerical solution agreed well with the experimental data. Large differences were observed between the results in the intact and damaged conditions. The damage at midship had a significant influence on the ship’s roll motion. The natural roll period for the damaged ship was 1.57 s, which was significantly larger than 1.4 s in the case of an intact ship. Affected by the flooding water in the damaged compartments, the damaged ship had a larger draft, the vertical position of the center of gravity was lower, and the restoring moment increased. This caused the damaged ship to recover to a stable state more quickly than the intact ship with a same initial heel angle. In addition, the interactions of water inside and outside of the compartments and the sloshing of the liquid tank in the compartments cause changes in the natural roll period of the ship, resulting in the roll damping of the damaged ship being greater than that of the intact ship.

3.3. Time-Domain Simulation Process

The two-phase flow solver with the fast algorithm was applied to simulate the pitching and heaving of the damaged DTMB 5415 ship in regular beam waves. The incident wave height was set as 0.061 m, velocity inlet condition was set as 2.12 m/s, and frequency of encounter was 0.714 Hz. The ship needed to experience several periodic waves before the heaving and pitching motions and the flow field around the hull would reach a convergent state. 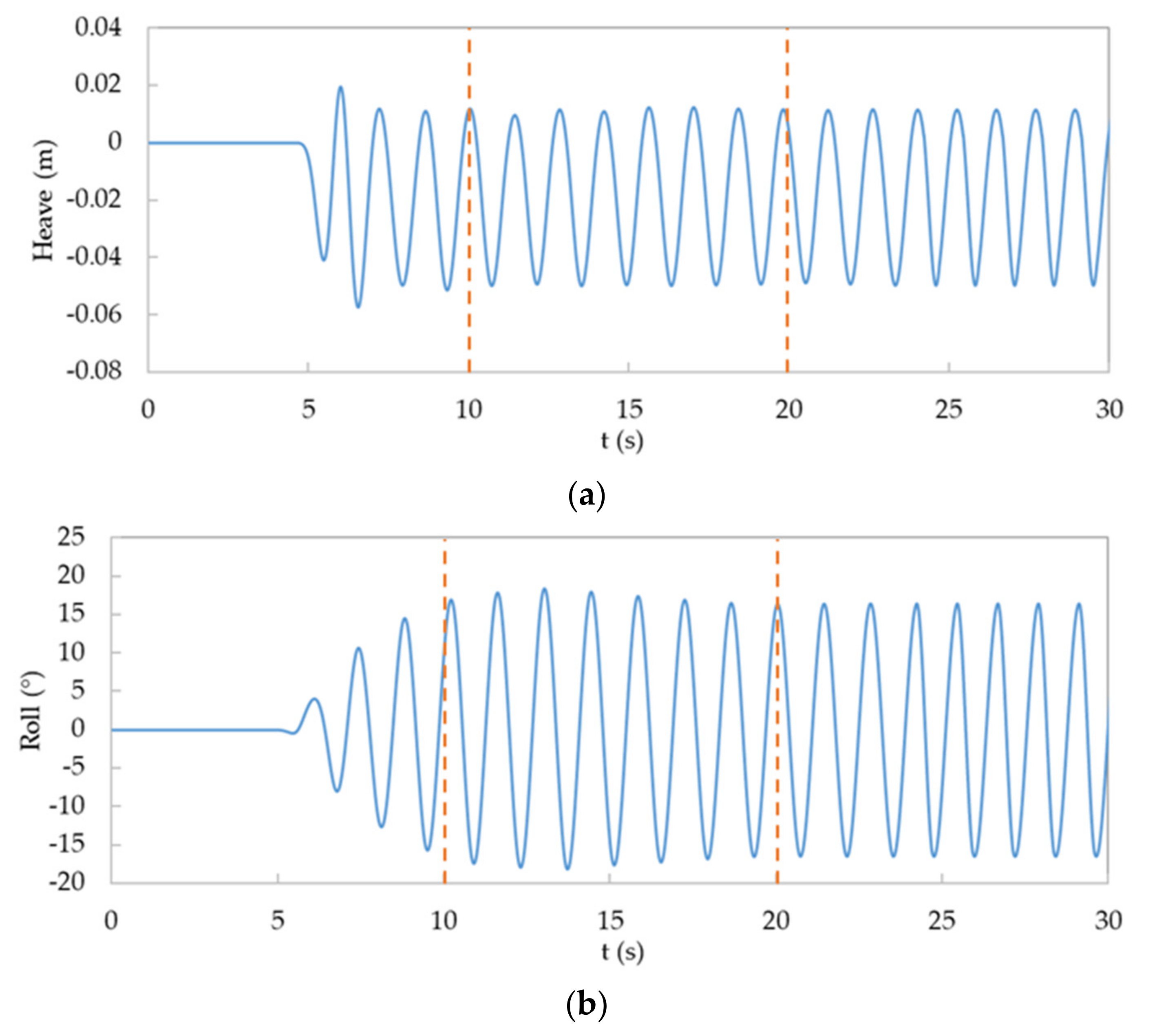Figure 10 shows the time histories of the heave and pitch motions of the intact ship. The whole simulation process consisted of three stages, namely the prediction stage using the coarse mesh A (t = 0–10 s), transition stage using the medium mesh B (t = 10–20 s) and correction stage using fine mesh C (t = 20–30 s). A snapshot of the free surface contour at different stages is shown in Figure 11.

The coarse mesh A was first used to predict the flow field around the damaged ship and its ship motions. At the beginning of the simulation, the damaged ship was set as fixed in the numerical wave tanks, and only the flow around the ship was solved. As shown in Figure 10, for the first 5 s, no ship motions were captured. The flow field around and behind the ship was generally generated by the waves. The free surface elevation changed periodically according to the incident regular waves.

When the flow field reached a convergence state (at around t = 5 s), two degrees of freedom of rotation were released around the y-axis for the pitching and displacement along the z-axis for heaving. The coarse background mesh A was continually used to predict the interactions of ship motions with the incident waves to save computational resources. Figure 11b showed the free surface elevations at the end of the estimation stage. The difference induced by the ship motions was clear when compared with Figure 11a. This stage stopped at around t = 10 s, when the simulation reached a convergence state.

The next stage was the interpolation process. A set of locally refined meshes was generated around the ship hull and the free surface and interpolated the flow field information from the coarse mesh A into the medium mesh B (shown in Figure 7b). We set the mesh refinement area for free surface waves to be three times the wave height. In the parts of the ship surface that had a large curvature, a larger area of the local refinement was set to avoid the distortion of the hull shape. The size of the refined mesh was half of the original background mesh for all three directions. A total of 416,126 grids were added, and the total number of meshes during the interpolation stage was 1,948,924.

The RBF interpolation technique mentioned in Section 2.3.2 was used to interpolate the information from the background mesh into the first set of refined mesh. The number of interpolation partitions was set as k = 120 to speed up the interpolation process. The resulting flow field was used as the initial condition for the medium mesh B, and the simulation continued with the updated solution as the initial flow field. The simulation ran for another 10 s until the solution reached the convergence state. Figure 11c shows the free surface contour at the end of the transition stage. It took a much shorter time compared with the simulations, with the same number of meshes starting with a uniform velocity, pressure field, and still free surface.

The last stage was the correction process. A second set of refined meshes (shown in Figure 7c) were generated based on the medium mesh B. We set the mesh refinement area for the free surface waves to be twice the wave height and in the parts of the ship surface that had a large curvature, we set the local refinement. We repeated the process of the interpolation stage, and the RBF interpolation approach was used again for the information transition between the medium mesh B and fine mesh C. The simulation results of the ship motions in the regular head waves were obtained in the correction stage (20~30 s). The heave and pitch motions varied periodically with the incident waves (see Figure 10). The final free surface evolution is shown in Figure 8d.

To properly assess the computational accuracy, the computed heave and roll amplitudes were compared to the mean values of the experimental results and the relative errors were listed in

Table 4. Errors of motion amplitude using the different meshes.

Mesh	Roll
	Exp. (°)	Num. (°)	Error (%)
Mesh A	17.4	14.2	18.4
Mesh B	17.4	15.4	11.5
Mesh C	17.4	16.0	6.3
Multigrid	17.4	16.0	6.3

. It was quicker for the simulation using coarse mesh C to reach a stable statement, but the relative error was also the largest. The numerical results obtained by the medium mesh B were better, with a relative error of 11.5% for the roll motion. The roll motion amplitudes obtained by the numerical simulation with the multigrid and fine mesh C were in excellent agreement.

A ship generally needs to go through several wave periods before the flow field around it and the heave and pitch motions become stable in beam waves. The time needed to complete these types of simulations increases dramatically with the number of cells. Figure 12 summarizes the total solution time to complete a 30 s simulation with single set meshes, namely mesh A, mesh B, and mesh C. The solution time of the multigrid solver was added as a reference. It took approximately 22, 70, and 166 CPU hours to complete the simulations, respectively. The time needed for calculations increases exponentially with the number of mesh elements.

As for the simulation with the multigrid process, it took a total of about 109 CPU hours to complete the whole process, which saved 34% of the time taken using the fine mesh C. The roll motion test case indicated that the proposed multigrid approach was able to provide the same accuracy as the fine mesh in less time. The three stages of prediction (0–10 s), transition (10–20 s), and correction (20–30 s) took about 10, 28, and 62 CPU hours, respectively. It is important to note that the interpolation process also took a considerable amount of time, even though a PRBF technique was applied. The required time mainly depended on the number of grid elements in the coarse mesh.

3.4. Roll Motions in Beam Waves

The above analysis of the computation process validates the effectiveness of the proposed multigrid approach. To check the accuracy of the multigrid approach, the response amplitude operators (RAOs) of the damaged ship were calculated under different wave conditions; the RAOs were compared with the results using mesh C and the published experimental data, and are shown in Figure 13a, where $\eta$, k, and A are the roll amplitude, wave number, and wave amplitude, respectively. The motion responses were evaluated at the ship’s center of gravity. The numerical results using the two solvers overlapped and show a great agreement with the experimental data. It is therefore proven that the proposed multigrid approach improves the efficiency while maintaining the accuracy of the hydrodynamic simulations.

The behavior of the intact ship in regular beam waves was also investigated as a reference to the study of the damaged ship. Figure 13b shows the computed roll RAOs of the intact ship. The period of peak response of both intact and damaged ship occurred at t = 1.4 s, which was close to the natural period calculated from the roll decay test in Section 3.2. However, the peak response of the damaged ship was significantly weakened compared to the case of the intact ship. The large differences between the two conditions were, in part, attributed to the change in the main properties of the ship that was caused by the two damaged compartments, such as the center of gravity above the base, the draft, and the displacements. The sloshing moments inside of the damaged compartments also caused the dramatic reduction in the roll motion.

The maximum roll motion of the ship in both intact and damaged conditions occurred at the wave period of 1.4 s. To further understand the rolling of a damaged ship in beam waves, a comparison of the time history of the ship’s roll motion, in intact and damaged conditions, using the fast multigrid technique is shown in Figure 14. When the ship motion became stable, the average value of roll amplitude was 24.77° for the intact ship and 16.39° for the damaged ship. The water inside of the damaged compartment acted as an anti-rolling device and played an important role in damaged ship roll motion.

Figure 15 shows several representative snapshots within a rolling cycle of the internal wave motion at the position x = −1.64 m in the damaged compartment. In the resonance frequency range of the roll motion, a small amplitude wave was generated inside of the damaged compartment. Compared to the sea waves, a large formation of the water surface and strong non-linear behavior were observed within the compartment. The phase of the internal wave slightly shifted from the outside sea waves. Although the amplitude of the internal wave was mild, the difference between the sloshing and wave excitation moments reduced the ship roll amplitude.

4. Conclusions

A fast multigrid algorithm is proposed to simulate non-linear ship motion in intact and damaged conditions. This work was based on a typical two-phase flow solver to deal with the problems of long calculation times and low calculation efficiency in ship simulations by using CFD tools and providing a new approach for the fast prediction of the high-fidelity flow field and motion response of damaged ships.

A PRBF interpolation technique was developed to solve the problem of the low solution efficiency of the large full-rank matrix caused by the millions of grids needed. The global interpolation domain was decomposed into a series of small and independent subdomains, as well as the large global full-rank matrix. The decomposition of the global interpolation domain provides an accurate solution and significantly improves the efficiency of the global domain interpolation. A prediction-correction strategy, coupled with a PRBF interpolation approach, was designed to accelerate the simulation through three sets of locally refined meshes. The computational efficiency highly depended on the mesh size, and the time of the computations increased exponentially with the number of mesh elements. The prediction of flow field based on the coarse mesh provides a convergent solution for the fine mesh as the initial condition, while reducing the computational time. For a typical case of a damaged ship’s motions in beam waves for a 30 s simulation, it was shown to reduce the calculation time by 34% with the fast multigrid approach, compared with just using a single set of fine mesh.

The fast multigrid algorithm was applied to understand the roll motions of a damaged ship in beam waves. The damage’s effect on ship motion was investigated through the comparison of the ship in intact and damaged conditions. The peculiar phenomena of the damaged ship in beam waves, such as the increase in the ship’s natural roll period, the decrease in the peak response, and the sloshing motion inside the damaged compartment, were accurately predicted by the proposed fast multigrid algorithm in comparison with the experimental data.

The interactions of the internal and external liquid motion together with the ship hull motion are worth investigating in a coupled analysis of a damaged ship with internal sloshing in beam seas; however, this is beyond the scope of the present work. Further applications of this solver in handling the non-linear phenomena in the flooding process of a damaged ship should be investigated in future studies.