Impacts of High-Density Suspended Aquaculture on Water Currents: Observation and Modeling
Abstract
:1. Introduction
2. Materials and Methods
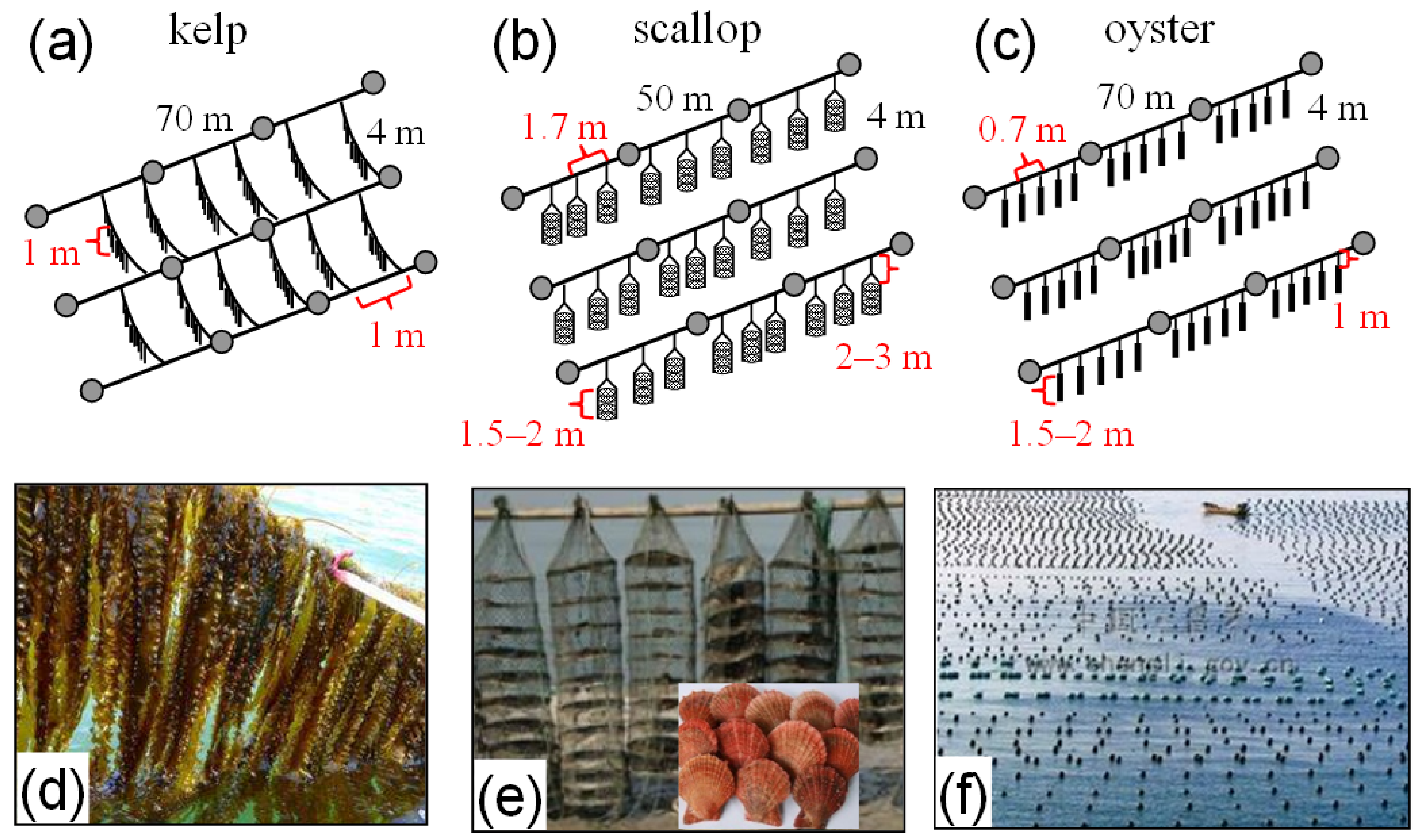
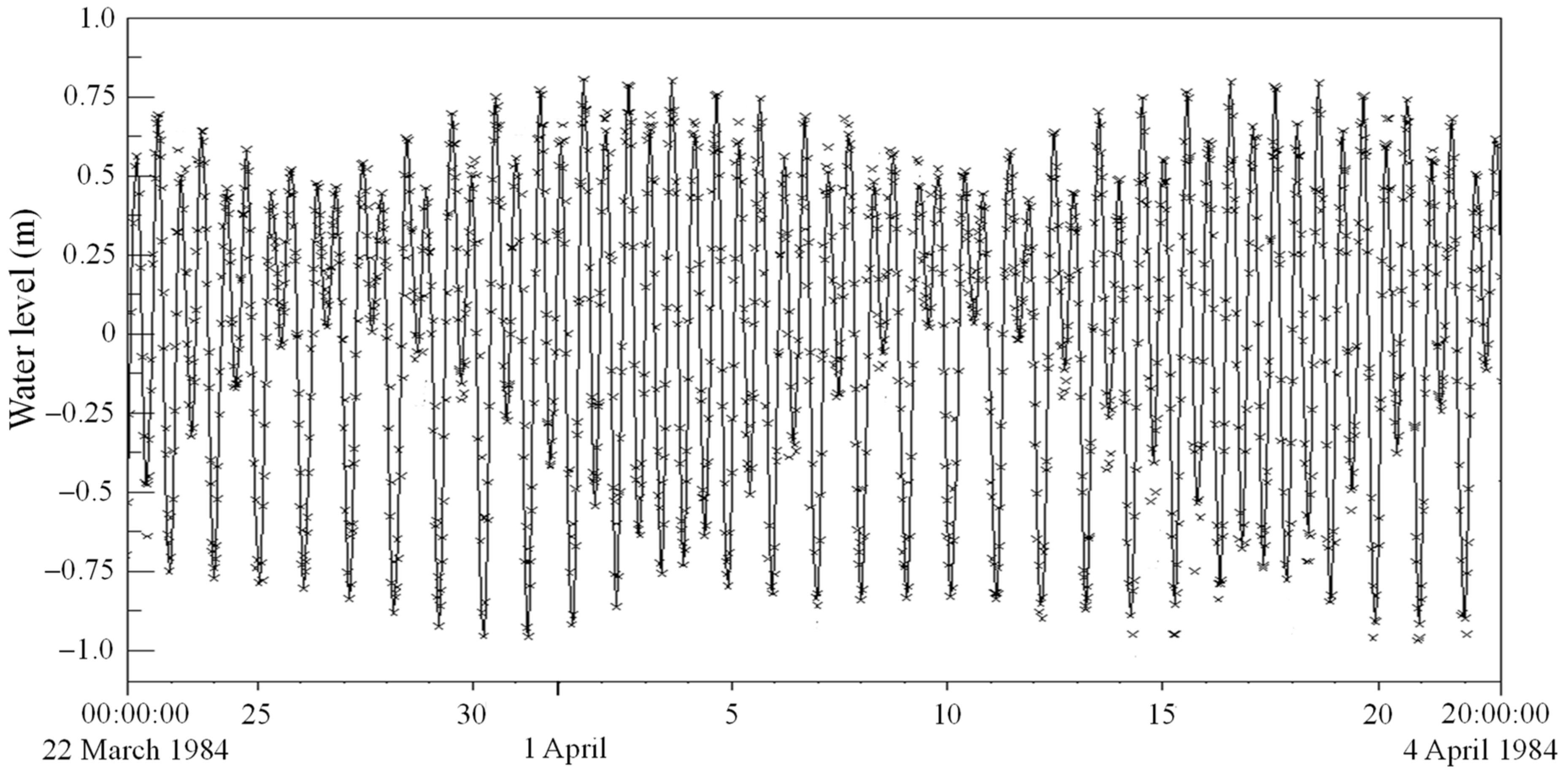
2.1. Field Observations
2.2. Method for Modeling Physical Process in the Aquaculture Bay
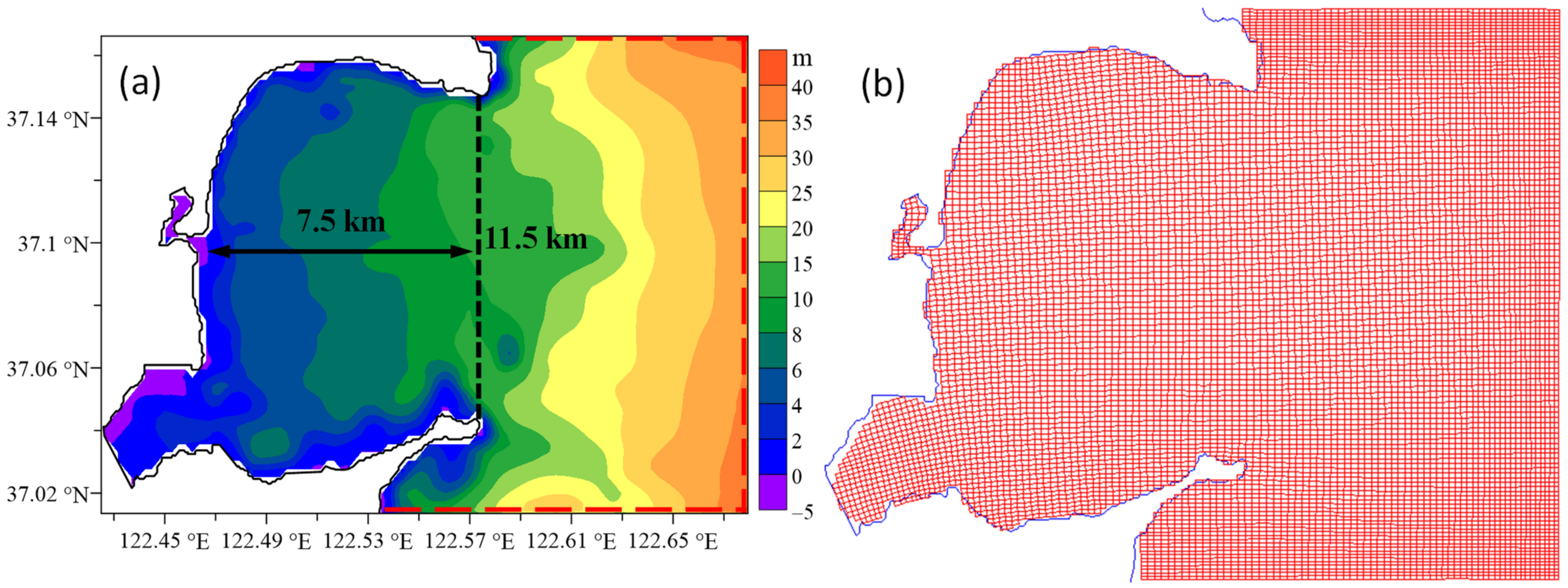
2.3. Model Configuration and Data Usage
2.4. Modeling of Water Exchange
3. Results
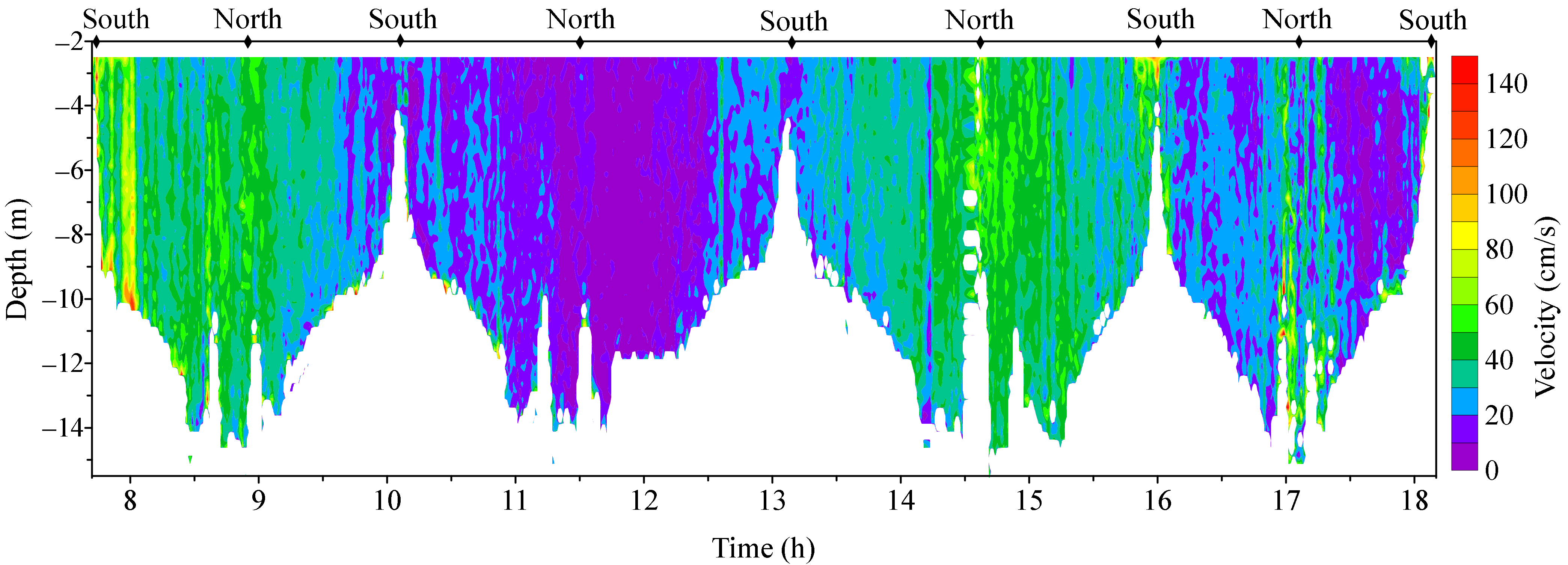
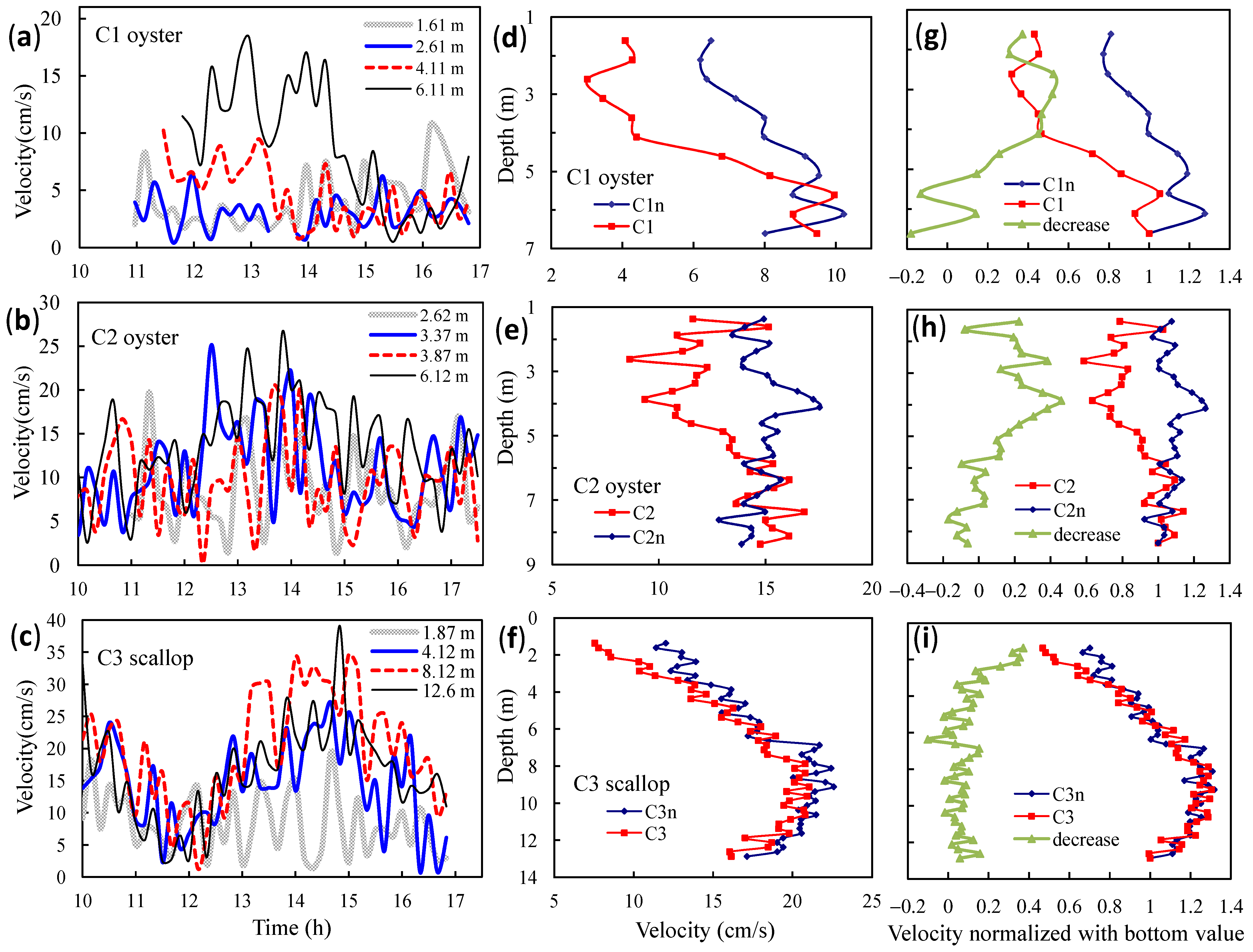
3.1. Observed Water Currents in Areas without Aquaculture
3.2. Observed Water Currents in Areas with Aquaculture
3.3. Modelled Water Levels for the Default Case of No Mariculture
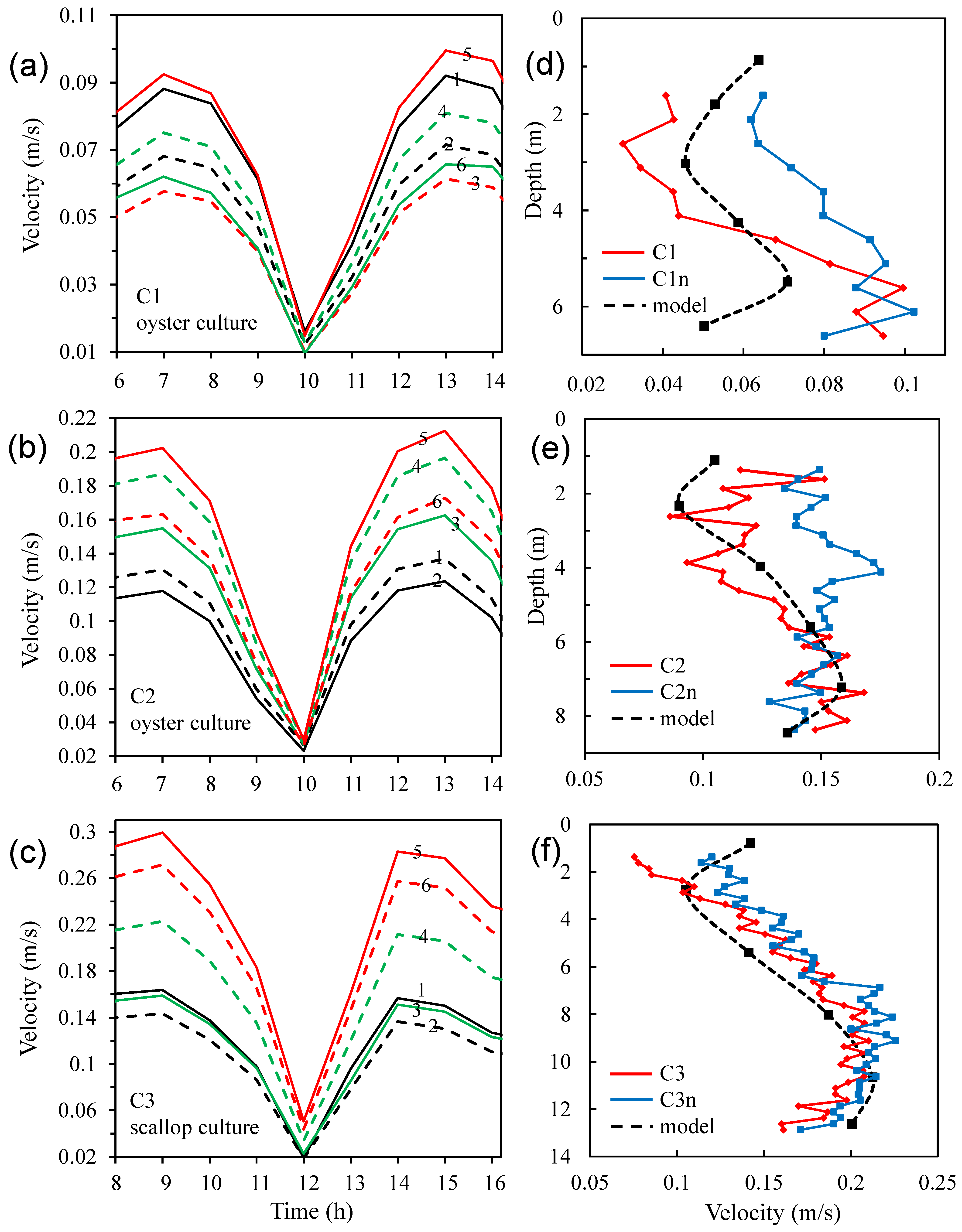
3.4. Modelled Water Currents for the Presence of Aquaculture
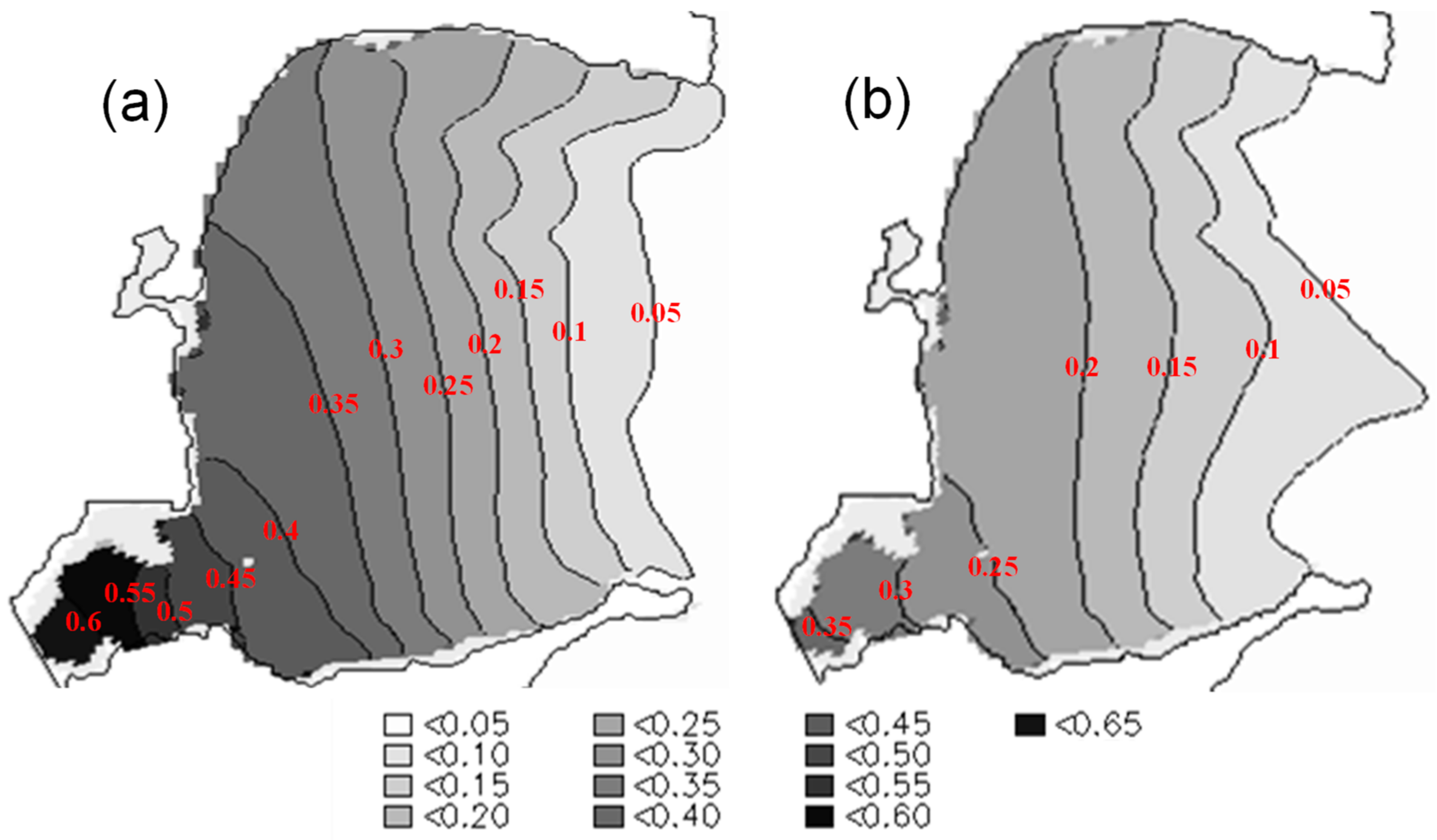
3.5. Effects of Aquaculture on Water Exchange
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Site | Error of Modeled Velocities at Each Layer (%) | Average Error (%) | RMSE (m/s) | SI | %Err (%) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |||||||
| 4.1 (O) 4.9 (S) | C1 | - | 29.2 | 30.4 | 13.5 | −19.6 | −43.8 | 1.9 | 0.3 | 0.015 | 0.113 | 9.8 |
| C2 | −11.2 | −4.3 | 18.9 | 1.4 | 0.6 | −7.5 | −0.4 | |||||
| C3 | - | 0.1 | −7.7 | −8.4 | 2.9 | 8.6 | −0.7 | |||||
| 4.0 (O) 4.0 (S) | C1 | - | 30.3 | 31.7 | 14.3 | −19.1 | −43.7 | 2.7 | 4.9 | 0.018 | 0.137 | 12.1 |
| C2 | −10.5 | −3.5 | 19.6 | 1.8 | 0.9 | −7.5 | 0.2 | |||||
| C3 | - | 19.0 | 7.2 | 2.3 | 12.8 | 17.3 | 11.7 | |||||
| 5.0 (O) 5.0 (S) | C1 | - | 25.3 | 26.1 | 11.1 | −20.0 | −41.5 | 0.2 | −1.5 | 0.015 | 0.113 | 9.7 |
| C2 | −14.9 | −8.6 | 15.7 | −0.3 | −0.2 | −6.7 | −2.5 | |||||
| C3 | - | −0.9 | −9.3 | −9.6 | 1.8 | 7.6 | −2.1 | |||||
| 6.0 (O) 7.5 (S) | C1 | - | 21.4 | 22.0 | 7.8 | −22.0 | −42.2 | −3.8 | −7.4 | 0.020 | 0.155 | 13.4 |
| C2 | −18.5 | −12.8 | 12.2 | −2.4 | −1.7 | −5.8 | −4.8 | |||||
| C3 | - | −18.5 | −24.2 | −20.4 | −8.4 | −1.8 | −14.7 | |||||
| 8.0 (O) 10.0 (S) | C1 | - | 16.2 | 16.3 | 4.1 | −23.7 | −40.6 | −5.5 | −12.0 | 0.026 | 0.201 | 17.1 |
| C2 | −23.1 | −18.3 | 8.1 | −4.6 | −2.9 | −4.4 | −7.5 | |||||
| C3 | - | −29.4 | −33.9 | −27.7 | −15.3 | −8.3 | −22.9 | |||||
| 20 (O) 25 (S) | C1 | - | 2.9 | 1.3 | −4.7 | −26.6 | −37.7 | −12.9 | −23.3 | 0.043 | 0.331 | 26.2 |
| C2 | −36.1 | −33.9 | −2.3 | −8.9 | −4.2 | −0.8 | −14.4 | |||||
| C3 | - | −55.7 | −56.9 | −44.5 | −31.6 | −23.9 | −42.5 | |||||
| 2.7 (O) 3.3 (S) | C1 | - | 37.7 | 39.4 | 19.4 | −17.5 | −44.5 | 6.9 | 8.8 | 0.021 | 0.156 | 14.4 |
| C2 | −3.6 | 4.6 | 26.2 | 5.7 | 3.1 | −8.8 | 4.5 | |||||
| C3 | - | 23.5 | 11.0 | 5.0 | 15.3 | 19.5 | 14.9 | |||||
| 2.0 (O) 2.5 (S) | C1 | - | 44.1 | 46.2 | 23.7 | −16.7 | −44.5 | 10.6 | 15.4 | 0.030 | 0.225 | 20.8 |
| C2 | 2.3 | 11.4 | 32.0 | 9.3 | 5.0 | −9.6 | 8.4 | |||||
| C3 | - | 41.7 | 25.9 | 15.6 | 24.8 | 27.7 | 27.1 | |||||
| 0.8 (O) 1.0 (S) | C1 | - | 66.5 | 70.2 | 39.2 | −11.3 | −45.4 | 23.9 | 38.2 | 0.067 | 0.512 | 44.3 |
| C2 | 21.7 | 33.4 | 50.7 | 20.0 | 9.9 | −11.5 | 20.7 | |||||
| C3 | - | 106.8 | 79.1 | 52.5 | 57.9 | 53.9 | 70.0 | |||||
References
- CIMA (Chinese Institute for Marine Affairs). China’s Ocean Development Report; Ocean Press: Beijing, China, 2013; p. 403.
- Jiang, Y.; Mu, Y.; Yao, L. A study on the contributions of inputs factors to the seawater mariculture output in China—Analysis based on the panel data by coastal province. Mar. Econ. 2013, 3, 32–37. [Google Scholar]
- FAO (Food and Agriculture Organization). The State of World Fisheries and Aquaculture 2018-Meeting the Sustainable Development Goals; Food and Agriculture Organization of the United Nations: Rome, Italy, 2018. [Google Scholar]
- Ferreira, J.G.; Andersson, H.C.; Corner, R.A.; Desmit, X.; Fang, Q.; Goede, E.D.; Groom, S.B.; Gu, H.; Gustafsson, B.G.; Hawkins, A.J.S.; et al. SPEAR: Sustainable Options for People Catchment and Aquatic Resources; Institute for Marine Research: Lisbon, Portugal, 2008; p. 180. [Google Scholar]
- Yang, Y.; Li, C.; Nie, X.; Tang, D.; Chuang, I. Development of mariculture and its impacts in Chinese coastal waters. Rev. Fish Biol. Fish. 2004, 14, 1–10. [Google Scholar]
- Ma, C.; Zhang, X.; Chen, W.; Zhang, G.; Duan, H.; Ju, M.; Li, H.; Yang, Z. China’s special marine protected area policy: Trade-off between economic development and marine conservation. Ocean. Coast. Manag. 2013, 76, 1–11. [Google Scholar] [CrossRef]
- Zhang, Z.; Huang, H.; Liu, Y.; Bi, H.; Yan, L. Numerical study of hydrodynamic conditions and sedimentary environments of the suspended kelp aquaculture area in Heini Bay. Estuar. Coast. Shelf Sci. 2020, 232, 106492. [Google Scholar] [CrossRef]
- Newell, C.R.; Richardson, J. The effects of ambient and aquaculture structure hydrodynamics on the food supply and demand of mussel rafts. J. Shellfish. Res. 2014, 33, 257–272. [Google Scholar] [CrossRef]
- Bacher, C.; Grant, J.; Hawkins, A.J.S.; Fang, J.; Zhu, M.; Besnard, M. Modelling the effect of food depletion on scallop growth in Sungo Bay (China). Aquat. Living Resour. 2003, 16, 10–24. [Google Scholar] [CrossRef]
- Duate, P.; Meneses, R.; Hawkins, A.J.S.; Zhu, M.; Fang, J.; Grant, J. Mathematical modeling to assess the carrying capacity for multi-species culture within coastal waters. Ecol. Model 2003, 168, 109–143. [Google Scholar]
- Nunes, J.P.; Ferreira, J.G.; Lencart-Silva, J.; Zhang, X.; Zhu, M.; Fang, J. A model for sustainable management of shellfish polyculture in coastal bays. Mariculture 2003, 219, 257–277. [Google Scholar] [CrossRef]
- Fan, X.; Wei, H.; Yuan, Y.; Zhao, L. The features of vertical structures of tidal current in a typical coastal mariculture area of China. Period. Ocean Univ. China 2009, 39, 181–186. [Google Scholar]
- Zeng, D.; Huang, D.; Qiao, X.; He, Y.; Zhang, T. Effect of suspended kelp culture on water exchange as estimated by in situ current measurement in Sanggou Bay, China. J. Mar. Syst. 2015, 149, 14–24. [Google Scholar] [CrossRef]
- Zhu, M.; Zhang, X.; Li, R.; Chen, S. Impacts of shellfish culture on the coastal ecosystem. J. Ocean. Univ. Qingdao 2000, 30, 53–57. [Google Scholar]
- Fang, J.; Strand, O.; Liang, X.; Zhang, J. Carrying capacity and optimizing measures for mariculture in Sungo Bay. Mar. Fish. Res. 2001, 22, 57–63. [Google Scholar]
- Plew, D.R.; Spigel, R.H.; Stevens, C.L.; Nokes, R.I.; Davidson, M.J. Stratified flow interactions with a suspended canopy. Environ. Fluid Mech. 2006, 6, 519–539. [Google Scholar] [CrossRef]
- Pilditch, C.A.; Grant, J.; Bryan, K.R. Seston supply to sea scallops (Placopecten magellanicus) in suspended culture. Can. J. Fish. Aquat. Sci. 2001, 58, 241–253. [Google Scholar] [CrossRef]
- Zhang, X.; Zhu, M.; Li, R.; Wang, Z. Simultaneous and consecutive multi-parameter monitoring of shellfish culture environment. Adv. Mar. Sci. 2004, 22, 340–346. [Google Scholar]
- Wang, T.; Khangaonkar, T.; Long, W.; Gill, G. Development of a Kelp-Type structure module in a coastal ocean model to assess the hydrodynamic impact of seawater uranium extraction technology. J. Mar. Sci. Eng. 2014, 2, 81–92. [Google Scholar] [CrossRef]
- Grant, J.; Bacher, C. A numerical model of flow modification induced by suspended mariculture in a Chinese bay. Can. J. Fish. Aquat. Sci. 2001, 58, 1003–1011. [Google Scholar] [CrossRef]
- Liu, X.; Pu, X.; Luo, D.; Lu, J.; Liu, Z. Model assessment of nutrient removal via planting Sesuvium portulacastrum in floating beds in eutrophic marine waters: The case of aquaculture areas of Dongshan Bay. Acta Oceanol. Sin. 2019, 38, 91–100. [Google Scholar] [CrossRef]
- Grant, J.; Stenton-Dozey, J.; Monteiro, P.; Pitcher, G.; Heasman, K. Shellfish culture in the Benguela system: A carbon budget of Saldanha Bay for raft culture of Mytilus galloprovincialis. J. Shellfish Res. 1998, 17, 41–49. [Google Scholar]
- O’Donncha, F.; Hartnett, M.; Nash, S. Physical and numerical investigation of the hydrodynamic implications of aquaculture farms. Aquacult. Eng. 2013, 52, 14–26. [Google Scholar] [CrossRef]
- Shi, J.; Wei, H. Simulation of hydrodynamic structures in a semi enclosed bay with dense raft culture. Period. Ocean Univ. China 2009, 39, 1181–1187. [Google Scholar]
- Fan, X.; Wei, H.; Yuan, Y.; Zhao, L. Vertical structure of tidal current in a typically coastal raft-culture area. Cont. Shelf Res. 2009, 29, 2345–2357. [Google Scholar] [CrossRef]
- Rickard, G. Three-dimensional hydrodynamic modelling of tidal flows interacting with aquaculture fish cages Graham Rickard. J. Fluid. Struct. 2020, 93, 102871. [Google Scholar] [CrossRef]
- Zhang, J.; Hansen, P.K.; Fang, J.; Wang, W.; Jiang, Z. Assessment of the local environmental impact of intensive marine shellfish and seaweed farming—application of the MOM system in the Sungo Bay, China. Aquaculture 2009, 287, 304–310. [Google Scholar] [CrossRef]
- Deltares. Delft3D-FLOW, Simulation of Multi-Dimensional Hydrodynamic Flows and Transport Phenomena, Including Sediments, User Manual, Version 3.15; Deltares: Delft, The Netherlands, 2021; Available online: https://oss.deltares.nl/web/delft3d/manuals (accessed on 28 March 2022).
- Bonamano, S.; Madonia, A.; Borsellino, C.; Stefann, C.; Caruso, G.; De Pasquale, F.; Piermattei, V.; Zappalt, G.; Marcelli, M. Modeling the dispersion of viable and total Escherichia coli cells in the artificial semi-enclosed bathing area of Santa Marinella (Latium, Italy). Mar. Pollut. Bull. 2015, 95, 141–154. [Google Scholar] [CrossRef]
- Bonamano, S.; Piazzolla, D.; Scanu, S.; Mancini, E.; Madonia, A.; Piermattei, V.; Marcelli, M. Modelling approach for the evaluation of burial and erosion processes on Posidonia oceanica meadows. Estuar. Coast. Shelf Sci. 2021, 254, 107321. [Google Scholar] [CrossRef]
- Bonamano, S.; Madonia, A.; Piazzolla, D.; de Mendoza, F.P.; Piermattei, V.; Scanu, S.; Marcelli, M. Development of a predictive tool to support environmentally sustainable management in Port Basins. Water 2017, 9, 898. [Google Scholar] [CrossRef] [Green Version]
- Chen, G. Marine Atlas of Bohai Sea, Yellow Sea and East China Sea: Hydrology; Ocean Press: Beijing, China, 1992; pp. 429–432. [Google Scholar]
- Li, F. Marine Hydrology Atlas of Shandong Coastal Sea; Shandong Atlas Press: Jinan, China, 1989; p. 42. [Google Scholar]
- Luff, R.; Pohlmann, T. Calculation of water exchange times in the ICES-boxes with an eulerian dispersion model using a half-life time approach. Dtsch. Hydrogr. Z. 1996, 47, 287–299. [Google Scholar] [CrossRef]
- Mellor, G.L. Users Guide for a Three-Dimensional, Primitive Equation, Numerical Ocean Model; Princeton University: Princeton, NJ, USA, 2004. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, X.; Zhang, X. Impacts of High-Density Suspended Aquaculture on Water Currents: Observation and Modeling. J. Mar. Sci. Eng. 2022, 10, 1151. https://doi.org/10.3390/jmse10081151
Liu X, Zhang X. Impacts of High-Density Suspended Aquaculture on Water Currents: Observation and Modeling. Journal of Marine Science and Engineering. 2022; 10(8):1151. https://doi.org/10.3390/jmse10081151
Chicago/Turabian StyleLiu, Xuehai, and Xuelei Zhang. 2022. "Impacts of High-Density Suspended Aquaculture on Water Currents: Observation and Modeling" Journal of Marine Science and Engineering 10, no. 8: 1151. https://doi.org/10.3390/jmse10081151
APA StyleLiu, X., & Zhang, X. (2022). Impacts of High-Density Suspended Aquaculture on Water Currents: Observation and Modeling. Journal of Marine Science and Engineering, 10(8), 1151. https://doi.org/10.3390/jmse10081151





