Experimental Study of Supercavitation Bubble Development over Bodies in a Free-Surface Flow
Abstract
:1. Introduction
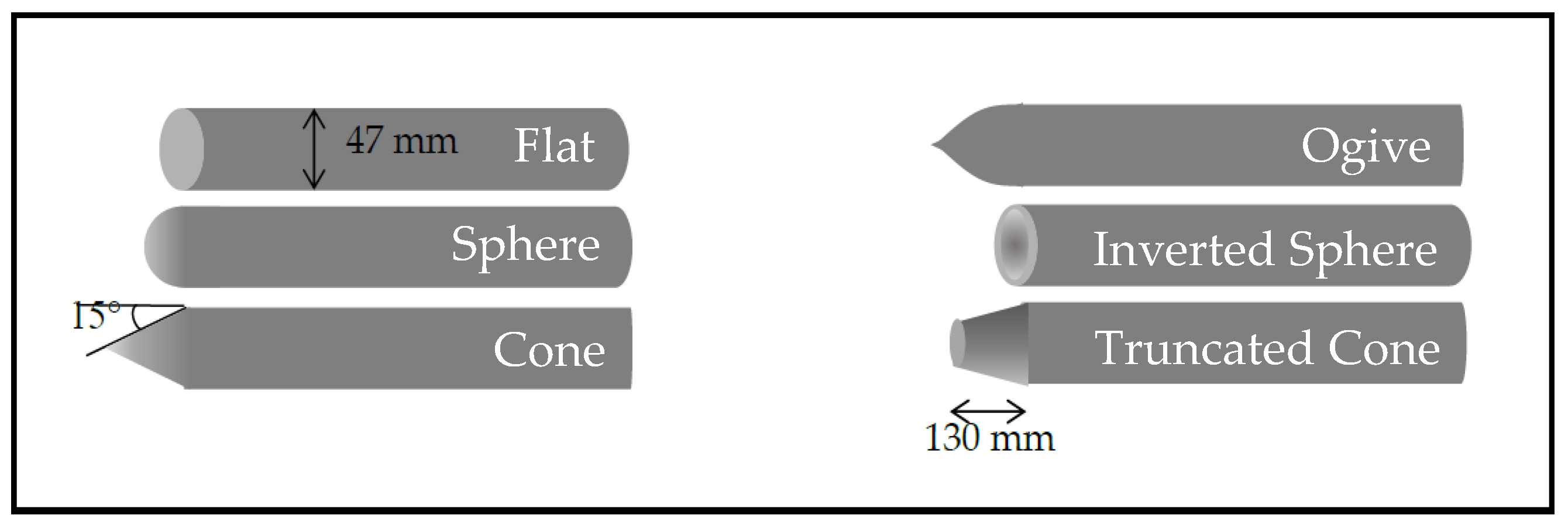
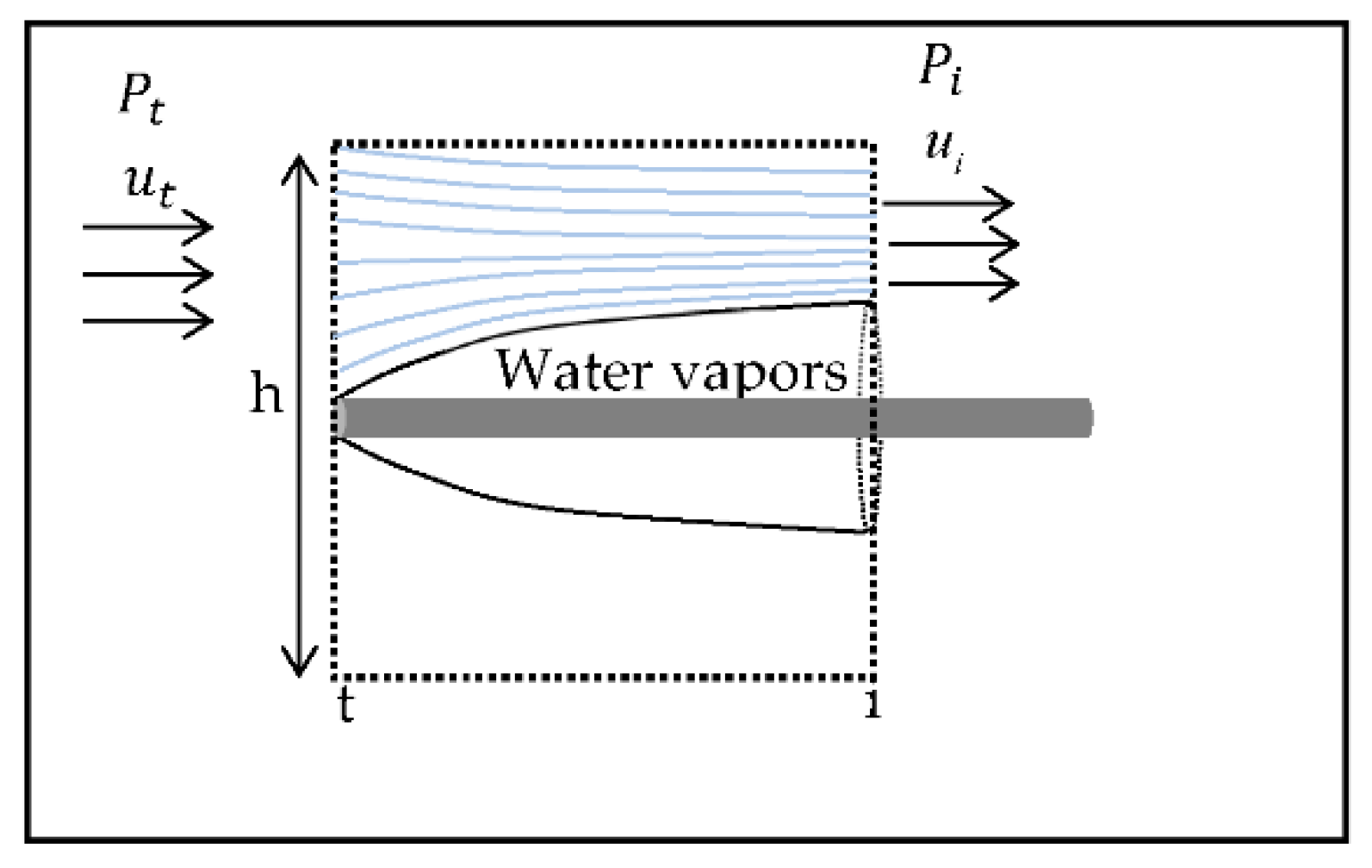
2. Problem Description
3. The Experimental System and Flow Conditions
4. Results
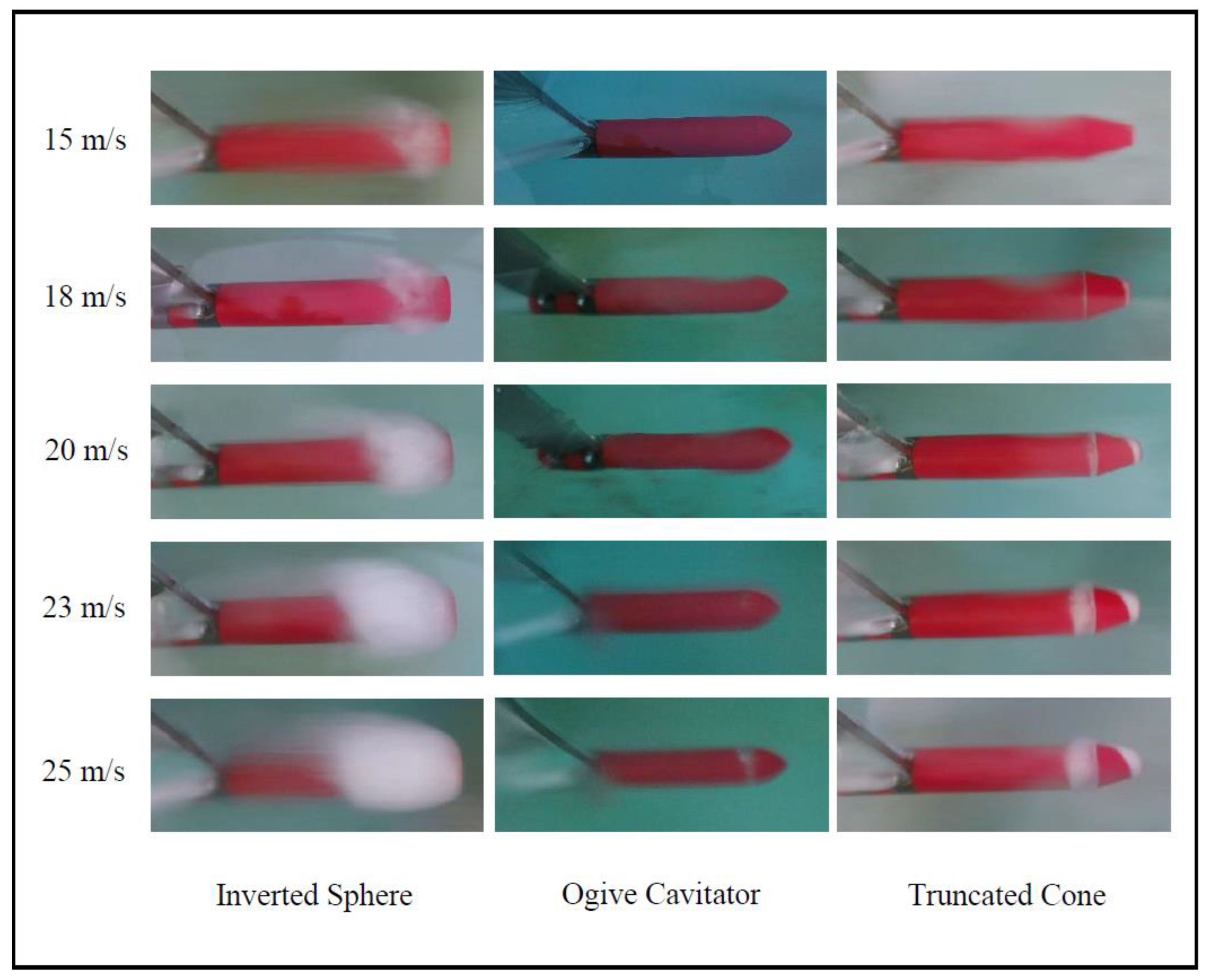
4.1. Stages of Bubble Development
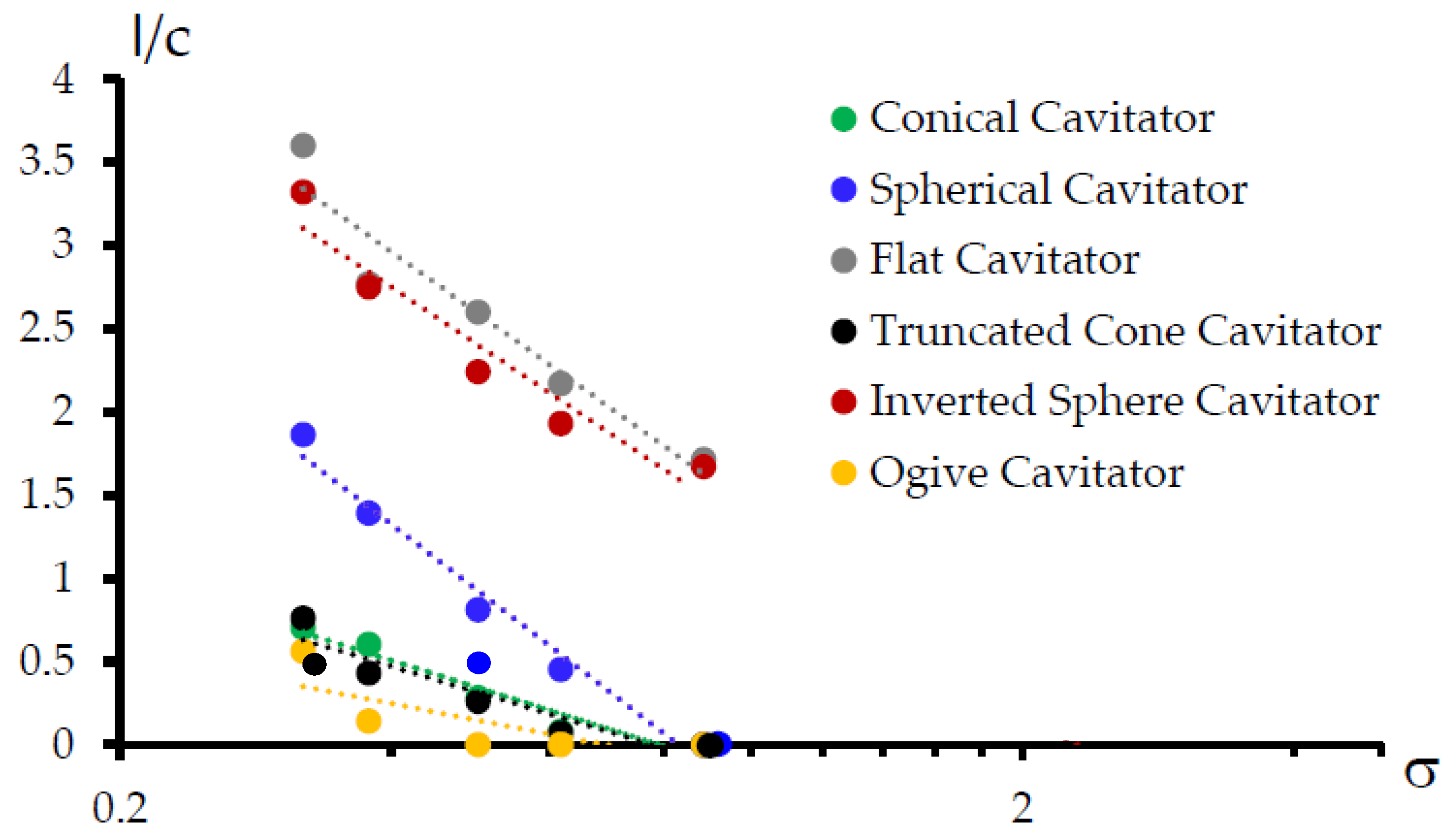
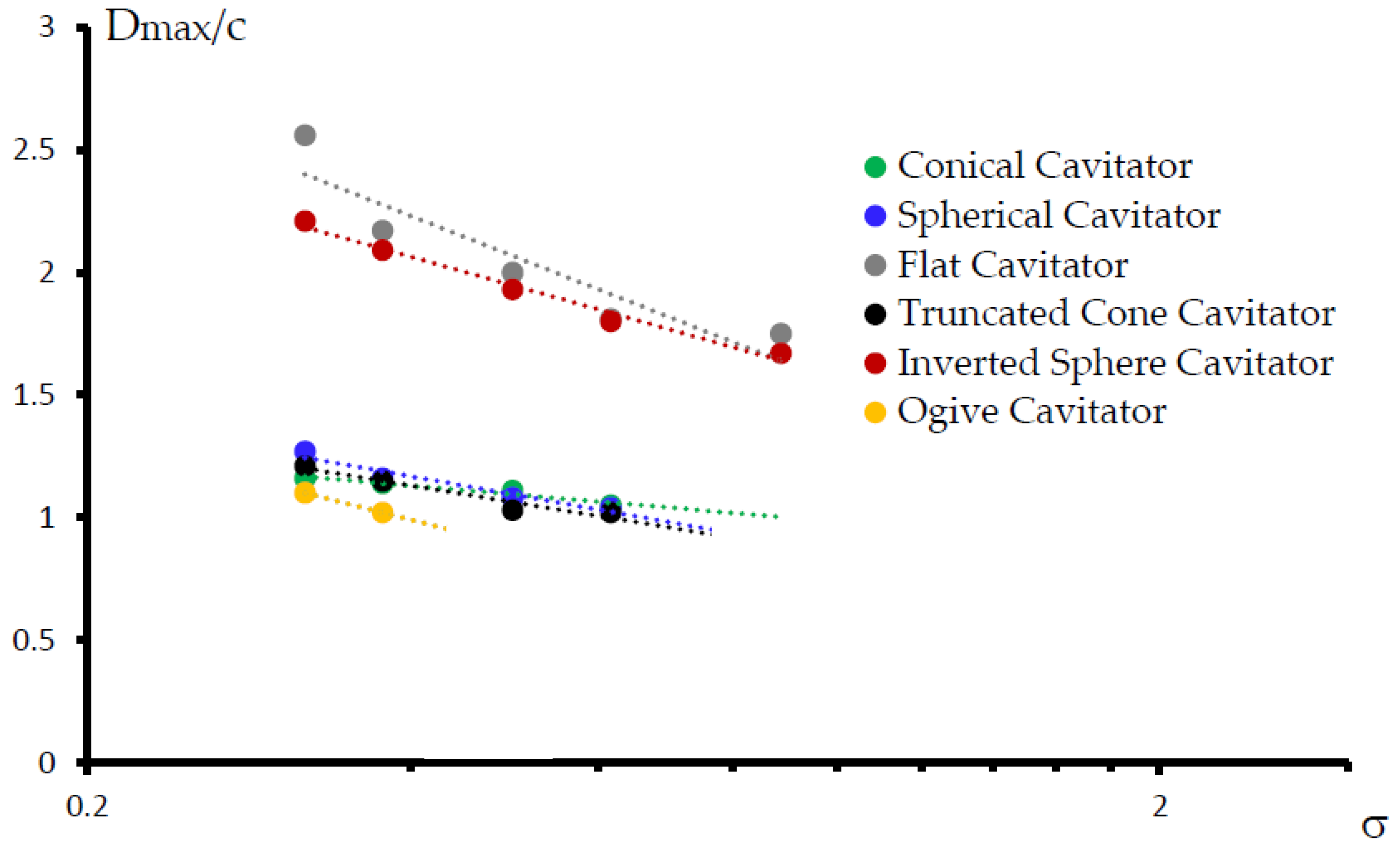
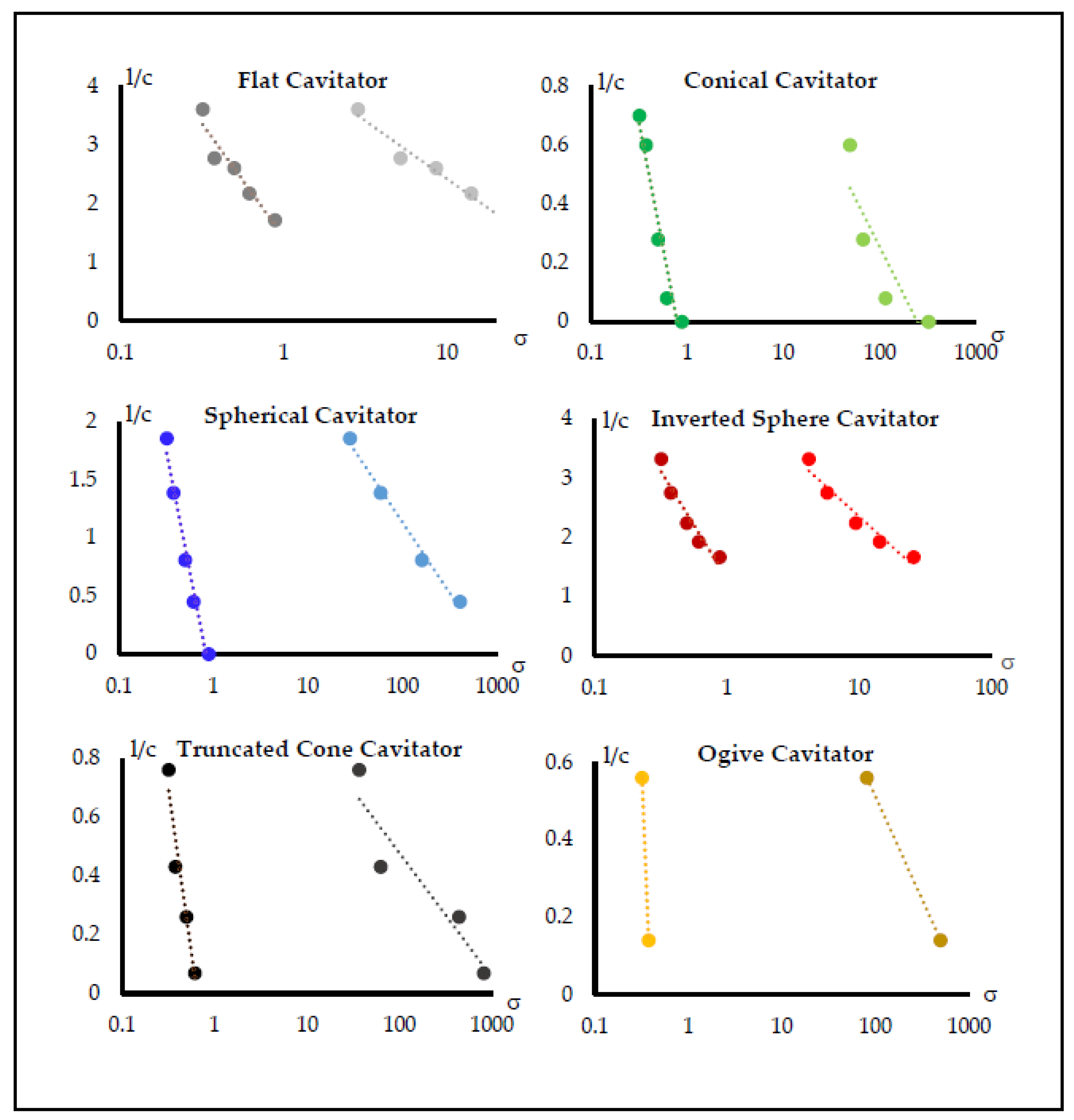
4.2. The Bubble Dimentions
4.3. The Pressure Difference and the Cavitation Number
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Logvinovich, G.V.; Serebryakov, V.V. On methods of calculating a shape of slender axisymmetric cavities. Hydromechanics 1975, 32, 47–54. [Google Scholar]
- Serebryakov, V.V. Asymptotic solutions of axisymmetric problems of the cavitational flow under slender body approximation. In Hydrodynamics of High Speeds; Chuvashian State University: Cheboksary, Russia, 1990; pp. 99–111. [Google Scholar]
- Serebryakov, V.V. The models of the supercavitation prediction for high-speed motion in water. In Proceedings of International Scientific School; HSH-2002: Chebocsary, Russia, 2002. [Google Scholar]
- Semenenko, V.N. Artificial Supercavitation. Physics and Calculation. In Proceedings of the RTO Lecture Series 005 on Supercavitating Flows, Brussels, Belgium, 12–16 February 2001. [Google Scholar]
- Savchenko, Y. Supercavitation-Problems and Perspectives. Available online: http://resolver.caltech.edu/cav2001:Lecture.003.2001 (accessed on 1 August 2022).
- Wu, T.Y.T.; Whitney, A.K.; Brennen, C. Cavity-flow wall effects and correction rules. J. Fluid Mech. 1971, 49, 223–256. [Google Scholar] [CrossRef]
- Ahn, B.K.; Lee, T.K.; Kim, H.T.; Lee, C.S. Experimental investigation of supercavitating flows. Int. J. Nav. Archit. Ocean. Eng. 2012, 4, 123–131. [Google Scholar] [CrossRef]
- Ahn, B.K.; Jeong, S.W.; Kim, J.H.; Shao, S.; Hong, J.; Arndt, R.E. An experimental investigation of artificial supercavitation generated by air injection behind disk-shaped cavitators. Int. J. Nav. Archit. Ocean Eng. 2017, 9, 227–237. [Google Scholar] [CrossRef]
- Fridman, G.M.; Achkinadze, A.S. Review of Theoretical Approaches to Nonlinear Supercavitating Flows; Saint Petersburg State Marine Technical University, Ship Theory Department: Saint Petersburg, Russia, 2001. [Google Scholar]
- Kirschner, I.I.; Chamberlin, R.; Arzoumanian, S.A. Simple approach to estimating three-dimensional supercavitating flow fields. In Proceedings of the 7th International Symposium on Cavitation CAV2009, Ann Arbor, MI, USA, 16–20 August 2009. [Google Scholar]
- Kwack, Y.K.; Ko, S.H. Numerical analysis for supercavitating flows around axisymmetric cavitators. Int. J. Nav. Archit. Ocean Eng. 2013, 5, 325–332. [Google Scholar] [CrossRef]
- Brennen, C. A numerical solution of axisymmetric cavity flows. J. Fluid Mech. 1969, 37, 671–688. [Google Scholar] [CrossRef]
- Kinnas, S.A. The prediction of unsteady sheet cavitation. In Proceedings of the 3rd International Symposium on Cavitation, Grenoble, France, 7–10 April 1998. [Google Scholar]
- Scardovelli, R.; Zaleski, S. Direct numerical simulation of free-surface and interfacial flow. Annu. Rev. Fluid Mech. 1999, 31, 567–603. [Google Scholar] [CrossRef]
- Vasin, A.D. The Principle of Independence of the Cavity Sections Expansion (Logvinovich’s Principle) as the Basis for Investigation on Cavitation Flows; Central Aerodynamics Institute (TSAGI): Moscow, Russia, 2001. [Google Scholar]
- Shi, H.H.; Wen, J.S.; Zhu, B.B.; Chen, B. Numerical simulation of the effect of different object nose shapes on hydrodynamic process in water entry. In Proceedings of the 10th International Symposium on Cavitation, CAV2018, Baltimore, MD, USA, 14–16 May 2018. [Google Scholar]
- Logvinovich, G.V. Hydrodynamics of Flows with Free Boundaries; Published by the National Aeronautics and Space Administration and the National Science Foundation: Washington, DC, USA, 1973. [Google Scholar]
- Ahn, B.K.; Jeong, S.W.; Park, S.T. An experimental investigation of artificial supercavitation with variation of the body shape. In Proceedings of the 10th International Symposium on Cavitation CAV2018, Baltimore, MD, USA, 19 October 2016. [Google Scholar]
- Franc, J.P.; Michel, J.M. Fundamentals of Cavitation; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2004. [Google Scholar]
- Arad Ludar, L.; Gany, A. Experimental study of supercavitation bubble development over bodies in a duct flow. J. Mar. Sci. Eng. 2020, 8, 28. [Google Scholar] [CrossRef]
- Gevari, M.T.; Ghorbani, M.; Svagan, A.J.; Grishenkov, D.; Kosar, A. Energy harvesting with micro scale hydrodynamic cavitation-thermoelectric generation coupling. AIP Adv. 2019, 9, 105012. [Google Scholar] [CrossRef] [Green Version]


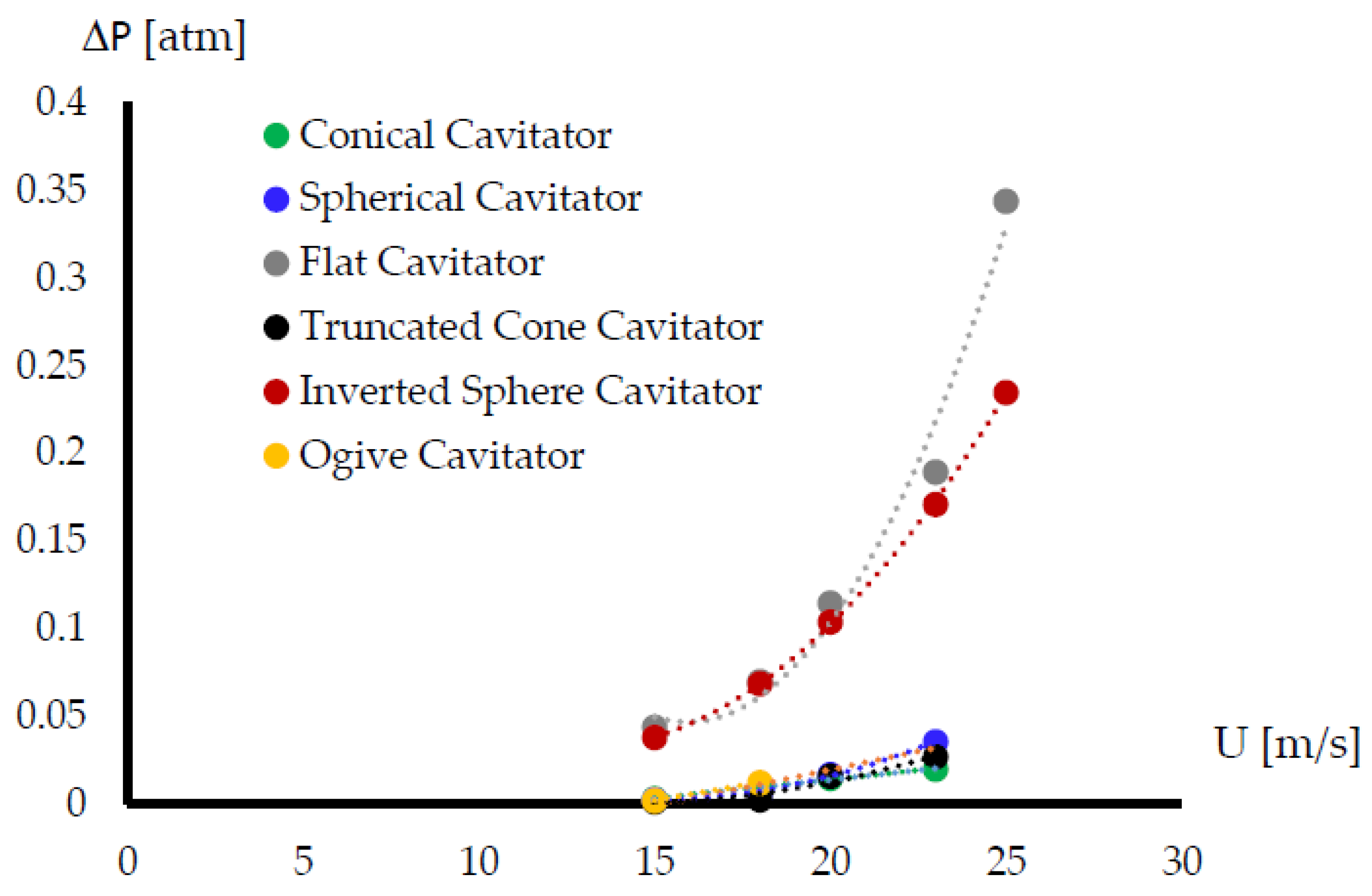
| 15 m/s | 18 m/s | 20 m/s | 23 m/s | 25 m/s | |
|---|---|---|---|---|---|
| Conical Cavitator | - | 0.08 | 0.28 | 0.6 | 0.7 |
| Spherical Cavitator | - | 0.45 | 0.81 | 1.39 | 1.86 |
| Flat Cavitator | 1.71 | 2.17 | 2.6 | 2.77 | 3.6 |
| Truncated Cone Cavitator | - | 0.07 | 0.26 | 0.43 | 0.76 |
| Inverted Sphere Cavitator | 1.67 | 1.93 | 2.24 | 2.75 | 3.32 |
| Ogive Cavitator | - | - | - | 0.14 | 0.56 |
| 15 m/s | 18 m/s | 20 m/s | 23 m/s | 25 m/s | |
|---|---|---|---|---|---|
| Conical Cavitator | - | 1.05 | 1.11 | 1.14 | 1.16 |
| Spherical Cavitator | - | 1.04 | 1.08 | 1.16 | 1.27 |
| Flat Cavitator | 1.75 | 1.81 | 2 | 2.17 | 2.56 |
| Truncated Cone Cavitator | - | 1.02 | 1.03 | 1.15 | 1.21 |
| Inverted Sphere Cavitator | 1.67 | 1.8 | 1.93 | 2.09 | 2.21 |
| Ogive Cavitator | - | - | - | 1.02 | 1.1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arad Ludar, L.; Gany, A. Experimental Study of Supercavitation Bubble Development over Bodies in a Free-Surface Flow. J. Mar. Sci. Eng. 2022, 10, 1244. https://doi.org/10.3390/jmse10091244
Arad Ludar L, Gany A. Experimental Study of Supercavitation Bubble Development over Bodies in a Free-Surface Flow. Journal of Marine Science and Engineering. 2022; 10(9):1244. https://doi.org/10.3390/jmse10091244
Chicago/Turabian StyleArad Ludar, Lotan, and Alon Gany. 2022. "Experimental Study of Supercavitation Bubble Development over Bodies in a Free-Surface Flow" Journal of Marine Science and Engineering 10, no. 9: 1244. https://doi.org/10.3390/jmse10091244
APA StyleArad Ludar, L., & Gany, A. (2022). Experimental Study of Supercavitation Bubble Development over Bodies in a Free-Surface Flow. Journal of Marine Science and Engineering, 10(9), 1244. https://doi.org/10.3390/jmse10091244







