CFD Method to Study Hydrodynamics Forces Acting on Ship Navigating in Confined Curved Channels with Current
Abstract
:1. Introduction
2. Computational Method
3. Simulation Cases and CFD Model
3.1. Ship Geometry
3.2. Simulation Cases
3.3. Computational Domain and Boundary Conditions
3.4. Mesh Generation and Sensitivity Analysis Test
- (a)
- refers to monotonic convergence
- (b)
- refers to oscillatory convergence
- (c)
- refers to divergence
3.5. Validation of the CFD Model
4. Results and Discussion
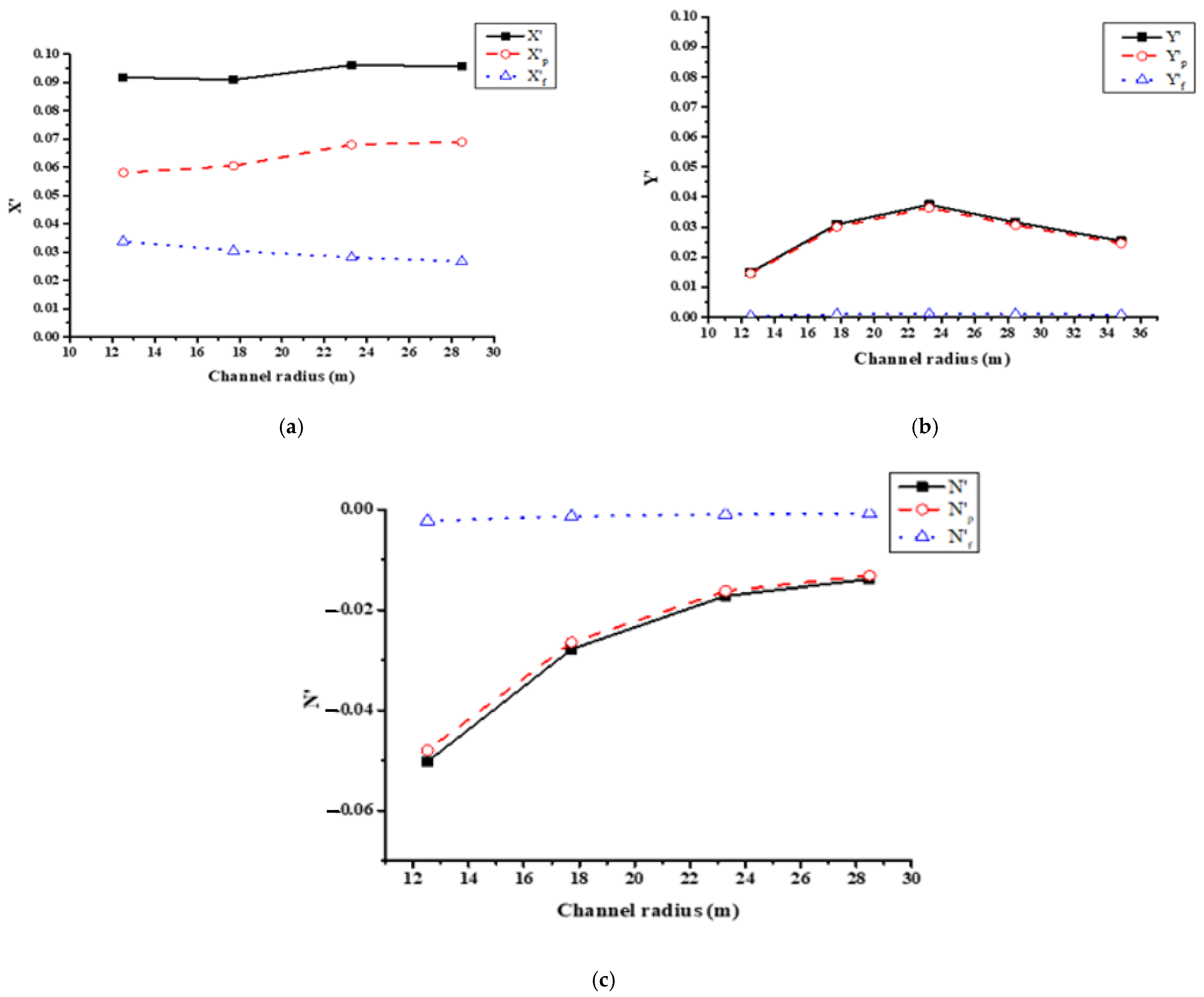
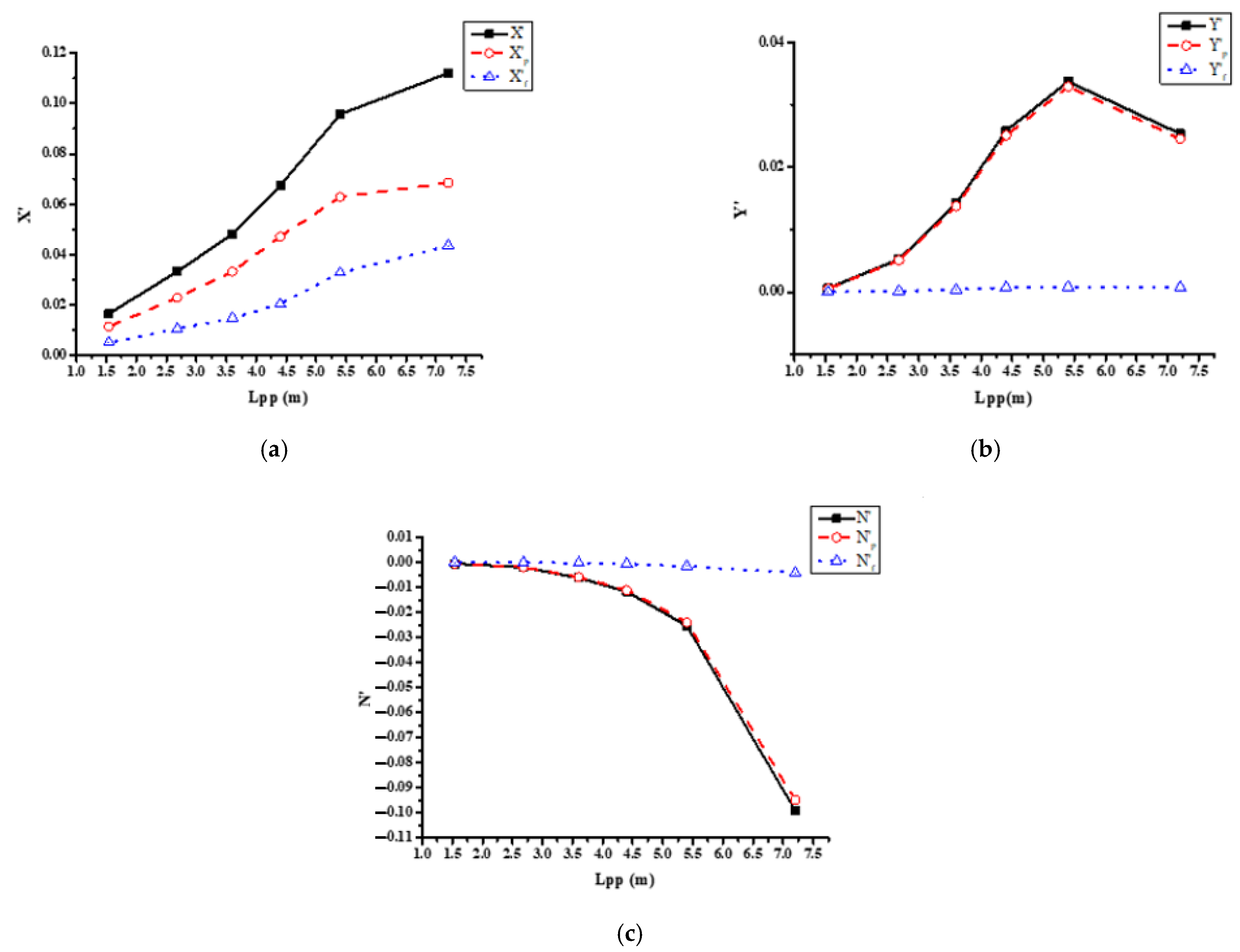
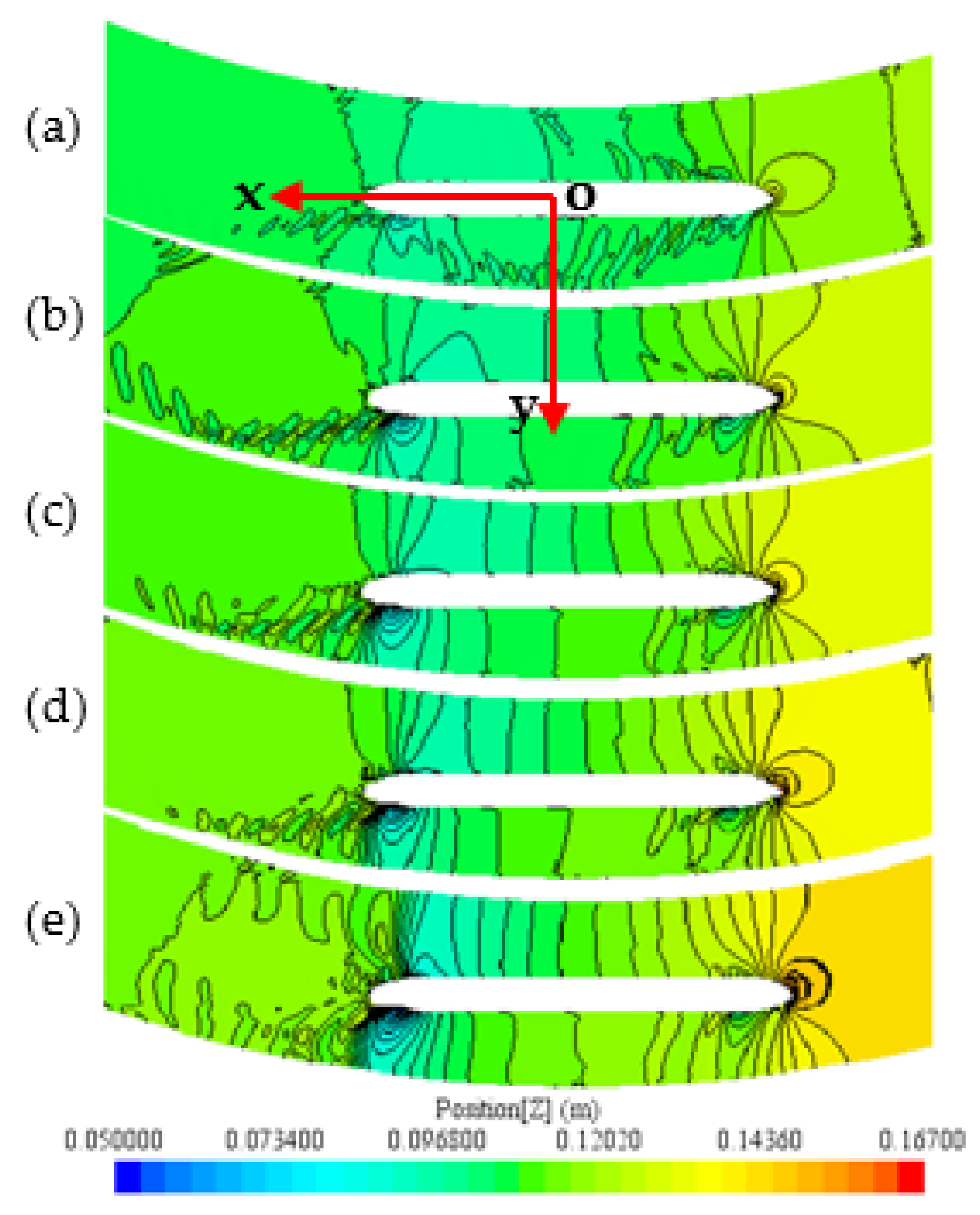
4.1. Effect of Channel Radius® on Flow Behavior and Hydrodynamic Forces and Moment of the Ship
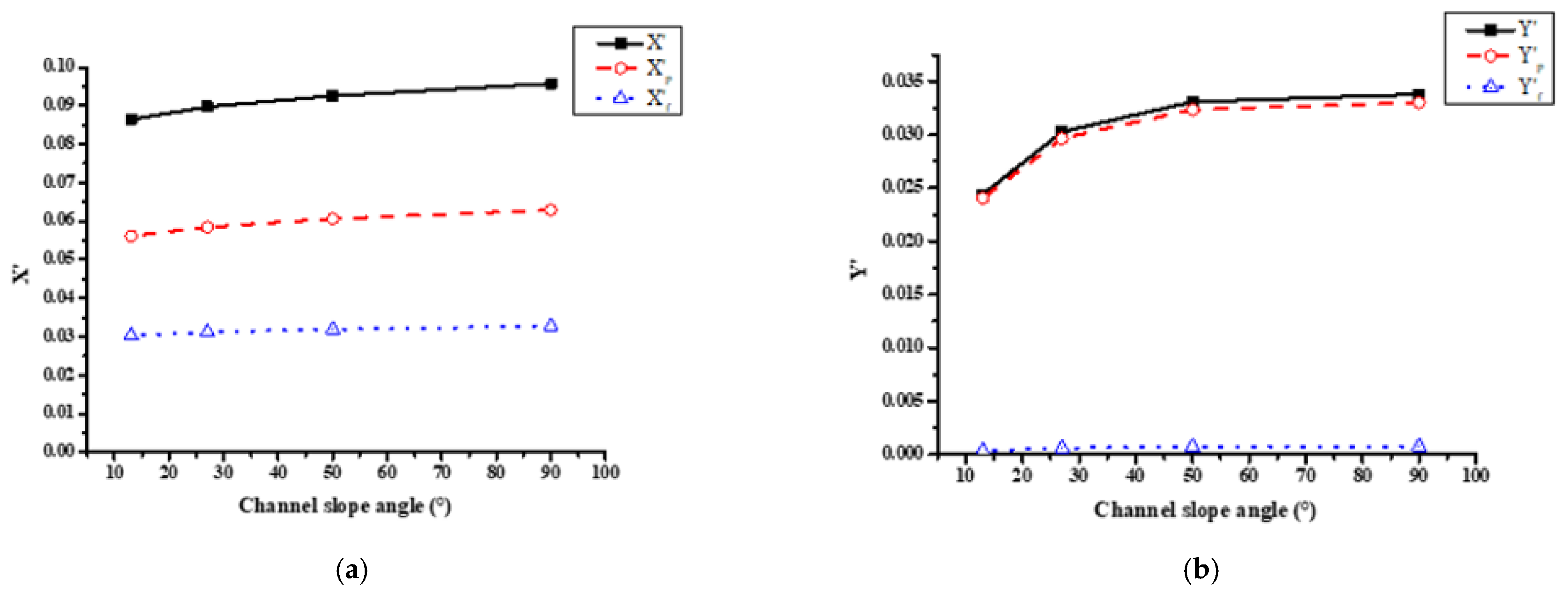
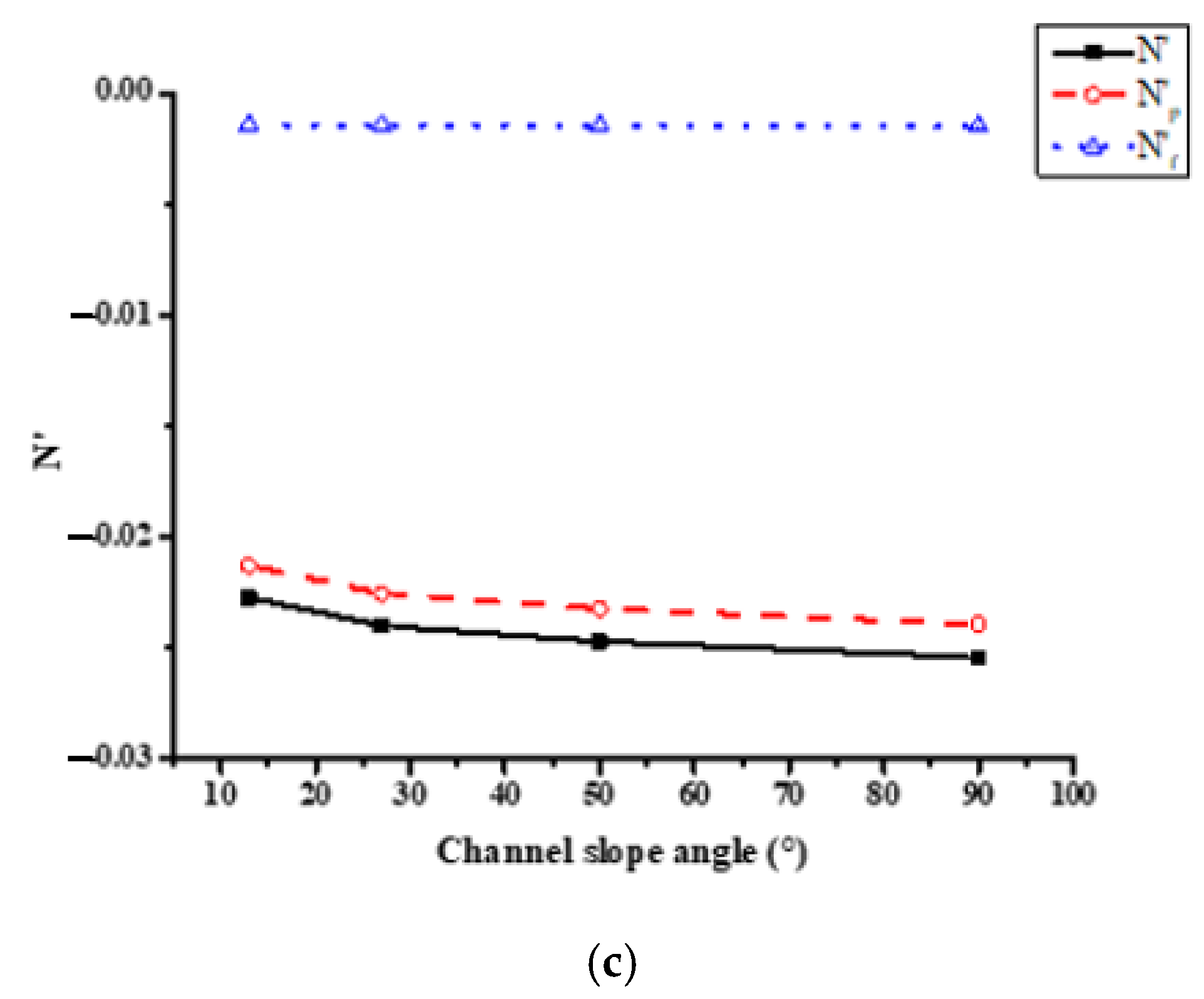
4.2. Effect of Bank Slope Angle(β) on Flow Behavior and Hydrodynamic Forces and Moment of the Ship
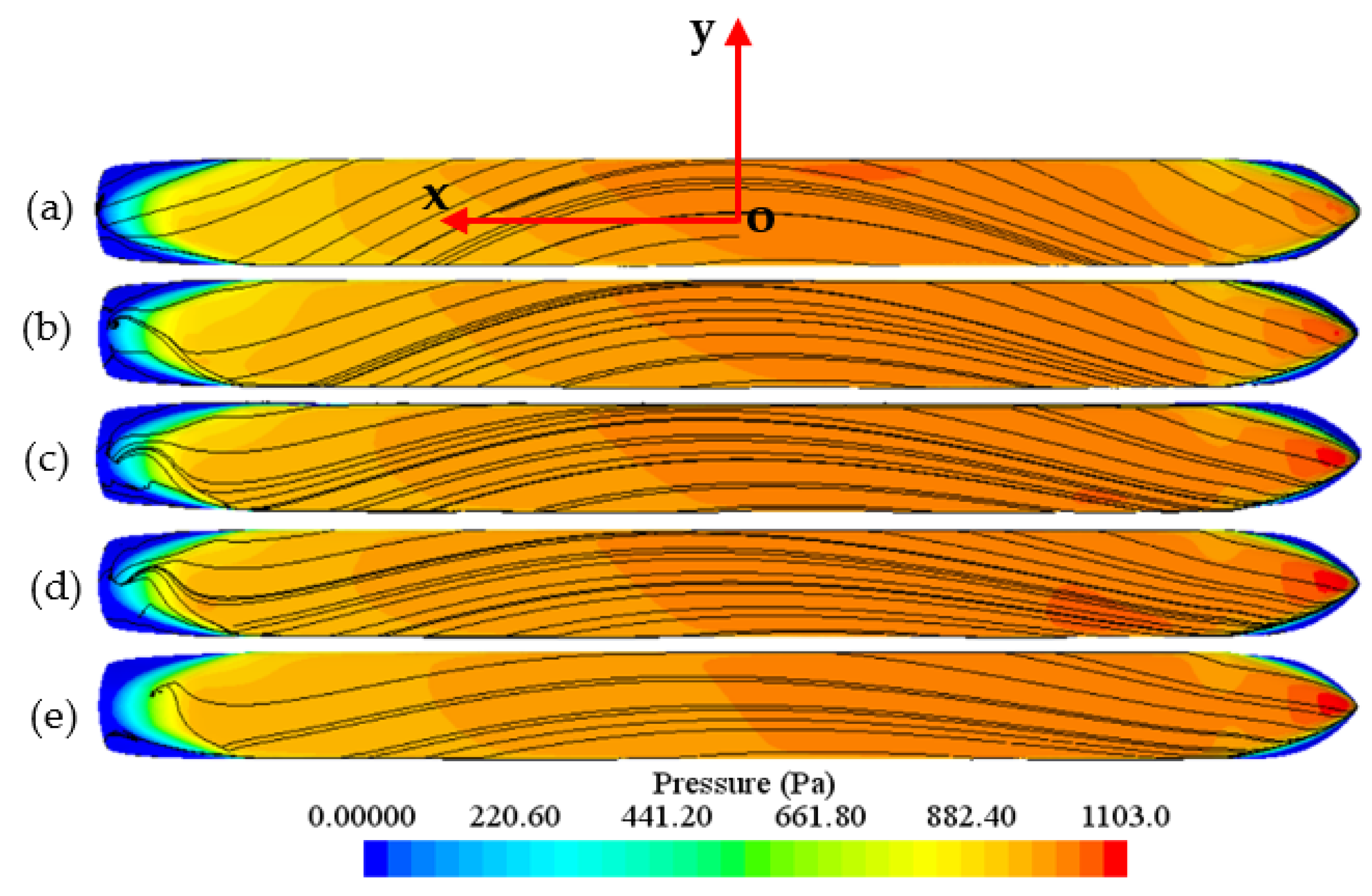
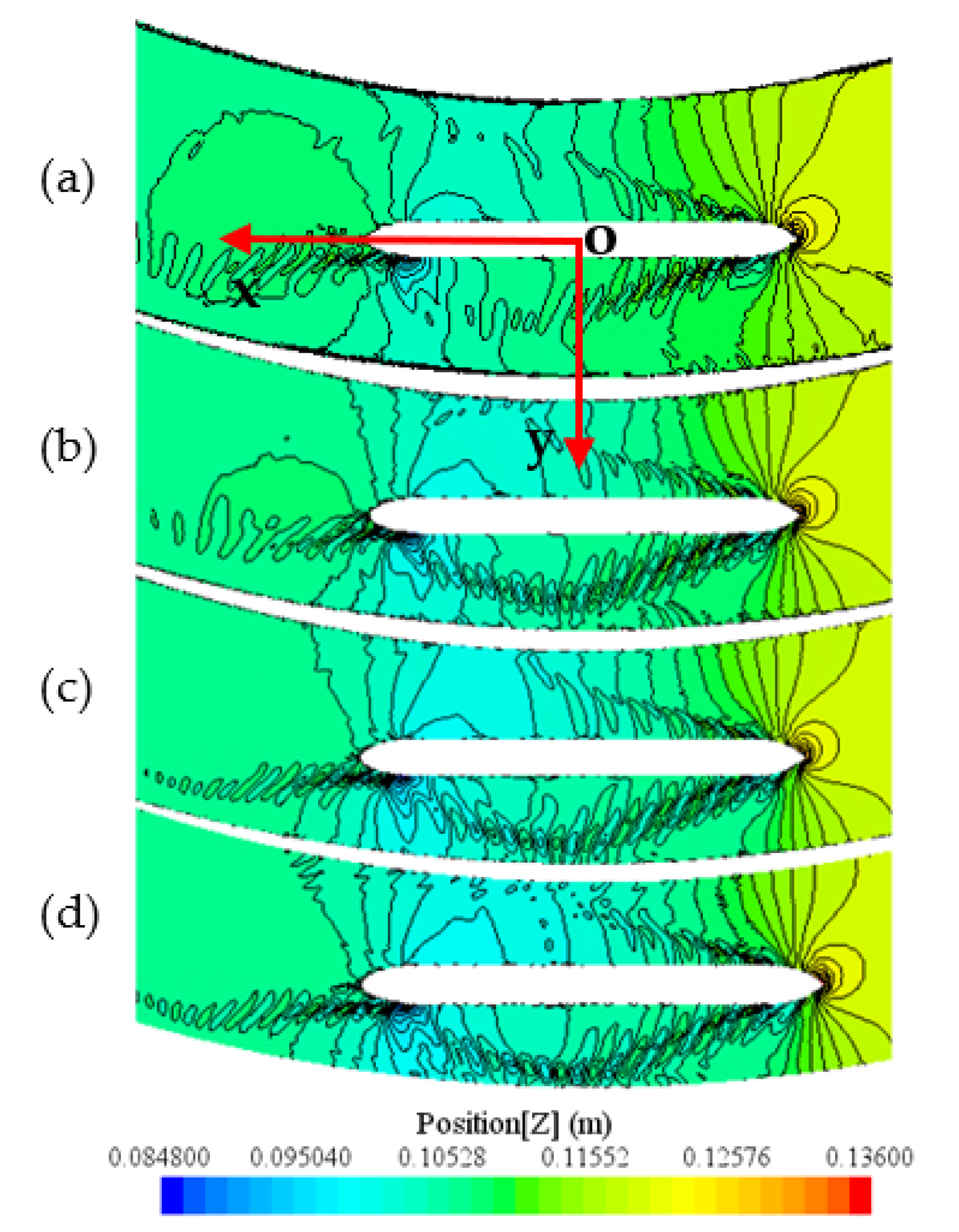
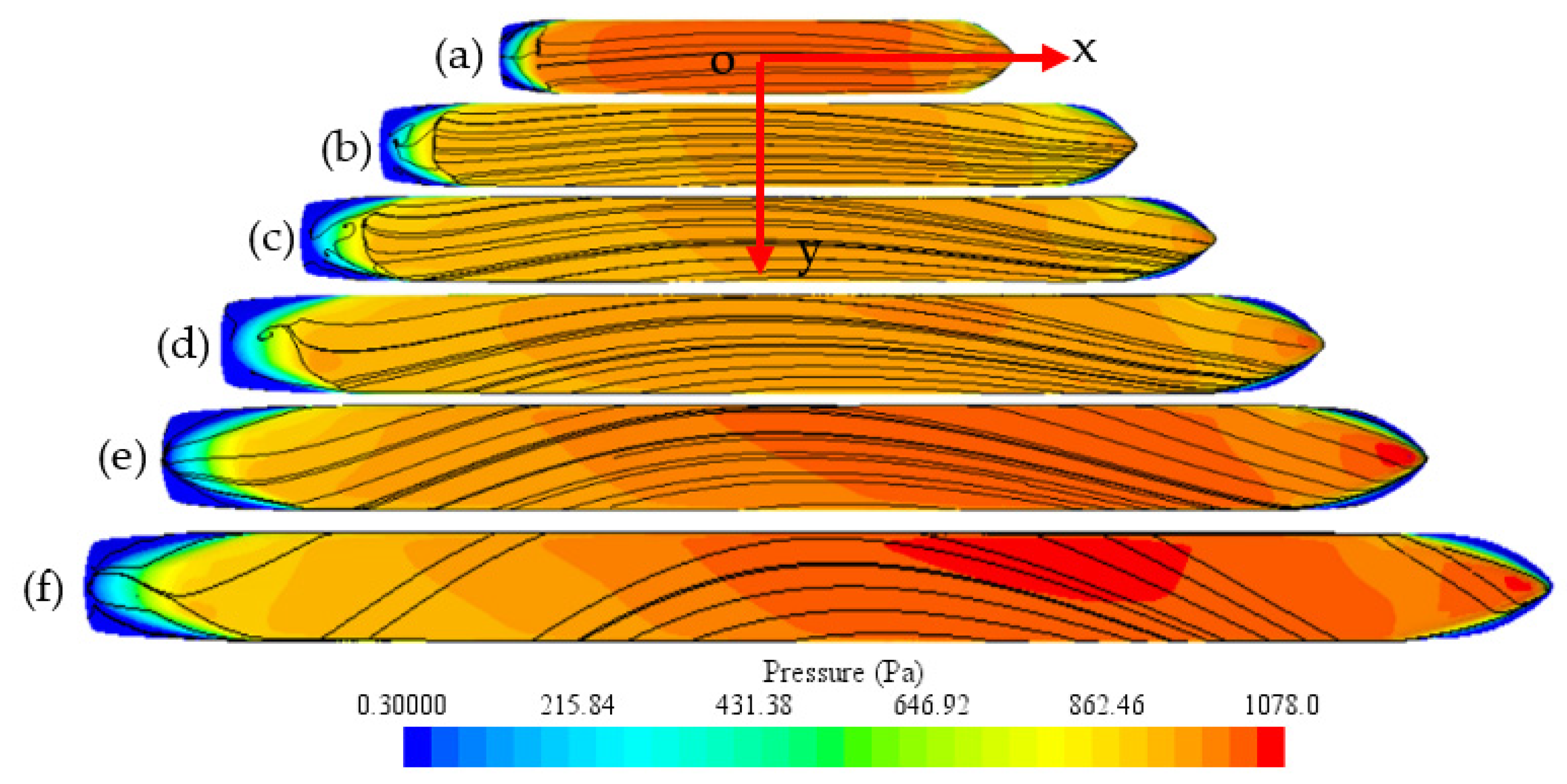
4.3. Effect of Ship Type on Flow Behavior and Hydrodynamic Forces and Moment of the Ship
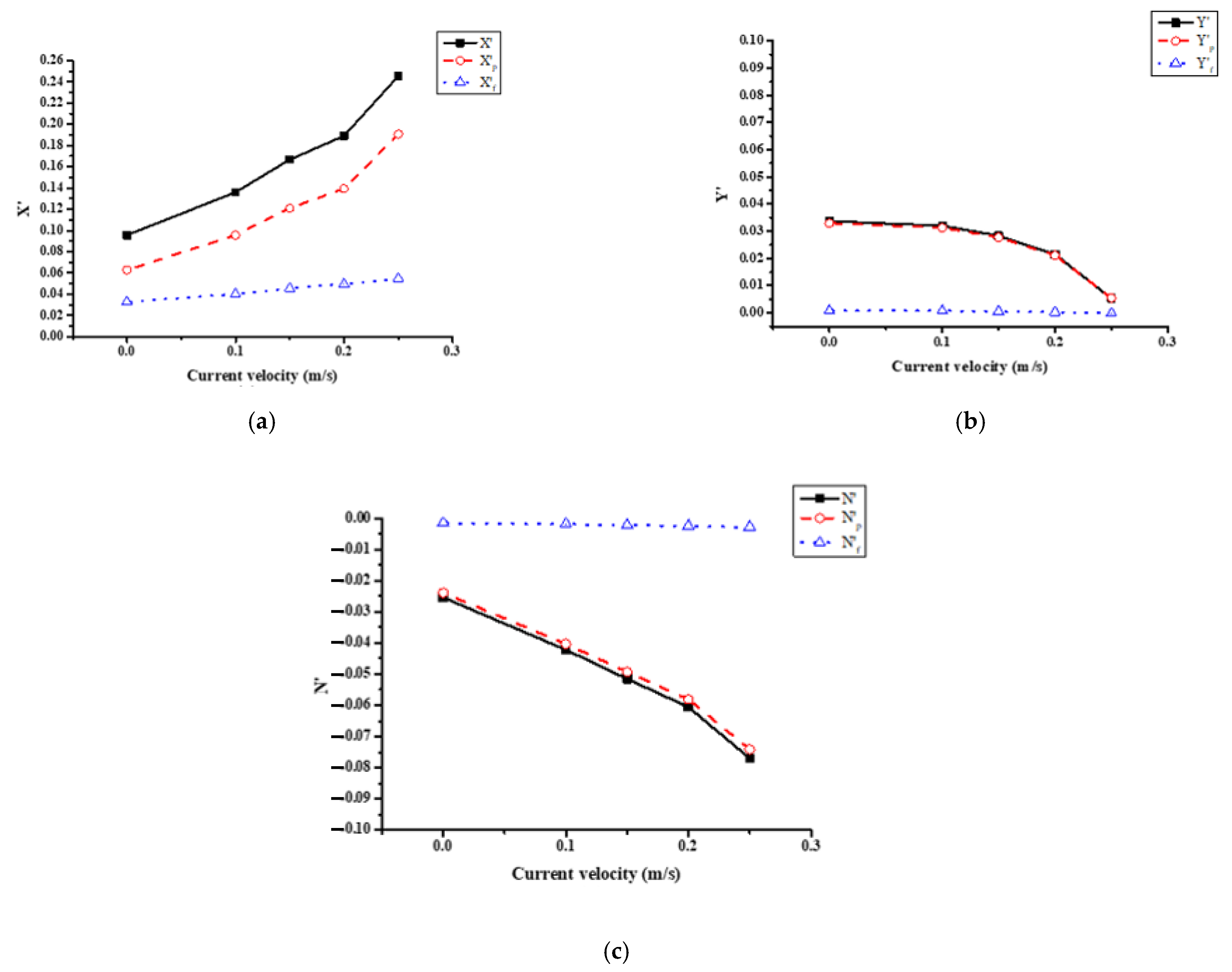
4.4. Current Effect on Flow Behavior and Hydrodynamic Forces and Moment of the Ship
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Eskinazi, S.; Yeh, H. An Investigation on Fully Developed Turbulent Flows in a Curved Channel. J. Aeronaut. Sci. 1956, 23, 23–34. [Google Scholar] [CrossRef]
- De Vriend, H.J. A Mathematical Model of Steady Flow in Curved Shallow Channels. J. Hydraul. Res. 1977, 15, 37–54. [Google Scholar] [CrossRef]
- Booij, R. Modelling the flow in curved tidal channels and rivers. In Proceedings of the International Conference on Estuaries and Coasts, Hangzhou, China, 9–11 November 2003. [Google Scholar]
- Blanckaert, K.; De Vriend, H.J. Nonlinear modeling of mean flow redistribution in curved open channels. Water Resour. Res. 2003, 39, 1375. [Google Scholar] [CrossRef]
- Kalkwijk, J.P.T.; De Vriend, H.J. Computation of the flow in shallow river bends. J. Hydraul. Res. 1980, 18, 327–342. [Google Scholar] [CrossRef]
- Blanckaert, K. Flow separation at convex banks in open channels. J. Fluid Mech. 2015, 779, 432–467. [Google Scholar] [CrossRef]
- Nguyen, V.T.; Nestmann, F. Applications of CFD in Hydraulics and River Engineering. Int. J. Comput. Fluid Dyn. 2004, 18, 165–174. [Google Scholar] [CrossRef]
- Aseperi, O. Dynamics of Flow in River Bends. Ph.D. Thesis, Colorado State University, Fort Collins, CO, USA, 2018. [Google Scholar]
- Huang, S.-L.; Jia, Y.-F.; Chan, H.-C.; Wang, S.S.Y. Three-Dimensional Numerical Modeling of Secondary Flows in a Wide Curved Channel. J. Hydrodyn. 2009, 21, 758–766. [Google Scholar] [CrossRef]
- Maslikova, O.Y.; Gritsuk, I.I.; Debol’Skaya, E.I. The effect of flow velocity distribution on matter transport in a curved channel segment with the effect of moving ships taken into account. IOP Conf. Series Earth Environ. Sci. 2019, 321, 012026. [Google Scholar] [CrossRef]
- Vujičić, S.; Mohović, R.; Tomaš, I. Methodology for Controlling the Ship’s Path during the Turn in Confined Waterways. Pomorstvo 2018, 32, 28–35. [Google Scholar] [CrossRef]
- Ai, W.Z.; Gan, X.Z. Analysis on Navigation Reliability of Curved Channel. Appl. Mech. Mater. 2013, 275–277, 2816–2820. [Google Scholar] [CrossRef]
- Ai, W.; Zhang, H.; Zhu, P.; Chi, H. A Study on Safe Ship Navigation in Curved Bridge Channel. J. Coast. Res. 2020, 109, 121–125. [Google Scholar] [CrossRef]
- Ai, W.; Zhu, P. Navigation Ship’s Drift Angle Determination Method in Curved Channel. J. Coast. Res. 2020, 109, 181–184. [Google Scholar] [CrossRef]
- Wang, C.H.; Cheng, X.B. Research on Navigable Ship Model Test in Curved Waterway. Appl. Mech. Mater. 2014, 580–583, 1918–1922. [Google Scholar] [CrossRef]
- Yang, B.; Kaidi, S.; Lefrançois, E. Numerical investigation of curvature effect on ship hydrodynamics in confined curved channels. In Proceedings of the 9th Conference on Computational Methods in Marine Engineering, Edinburgh, UK, 2–4 June 2021; Volume 1. [Google Scholar] [CrossRef]
- RoyChoudhury, S.; Dash, A.K.; Nagarajan, V.; Sha, O.P. CFD simulations of steady drift and yaw motions in deep and shallow water. Ocean Eng. 2017, 142, 161–184. [Google Scholar] [CrossRef]
- Bechthold, J.; Kastens, M. Robustness and quality of squat predictions in extreme shallow water conditions based on RANS-calculations. Ocean Eng. 2020, 197, 106780. [Google Scholar] [CrossRef]
- Shevchuk, I.; Kornev, N. A study of unsteady hydrodynamic effects in the stern area of river cruisers in shallow water. Ship Technol. Res. 2017, 64, 87–105. [Google Scholar] [CrossRef]
- Zou, L.; Larsson, L. Computational fluid dynamics (CFD) prediction of bank effects including verification and validation. J. Mar. Sci. Technol. 2013, 18, 310–323. [Google Scholar] [CrossRef]
- Kaidi, S.; Smaoui, H.; Sergent, P. CFD Investigation of Mutual Interaction between Hull, Propellers, and Rudders for an Inland Container Ship in Deep, Very Deep, Shallow, and Very Shallow Waters. J. Waterw. Port Coastal Ocean Eng. 2018, 144, 04018017. [Google Scholar] [CrossRef]
- Razgallah, I.; Kaidi, S.; Smaoui, H.; Sergent, P. The impact of free surface modelling on hydrodynamic forces for ship navigating in inland waterways: Water depth, drift angle, and ship speed effect. J. Mar. Sci. Technol. 2018, 24, 620–641. [Google Scholar] [CrossRef]
- Terziev, M.; Tezdogan, T.; Oguz, E.; Gourlay, T.; Demirel, Y.K.; Incecik, A. Numerical investigation of the behaviour and performance of ships advancing through restricted shallow waters. J. Fluids Struct. 2018, 76, 185–215. [Google Scholar] [CrossRef]
- Du, P.; Ouahsine, A.; Sergent, P.; Hu, H. Resistance and wave characterizations of inland vessels in the fully-confined waterway. Ocean. Eng. 2020, 210, 107580. [Google Scholar] [CrossRef]
- Du, P.; Ouahsine, A.; Toan, K.T.; Sergent, P. Simulation of ship maneuvering in a confined waterway using a nonlinear model based on optimization techniques. Ocean Eng. 2017, 142, 194–203. [Google Scholar] [CrossRef]
- Uncertainty Analysis in CFD Verification and Validation Methodology and Procedures. International Towing Tank Conference (ITTC), September 2017. 7.5-03-01-01, pp.1–13. Available online: https://www.ittc.info/media/8153/75-03-01-01.pdf (accessed on 25 July 2022).
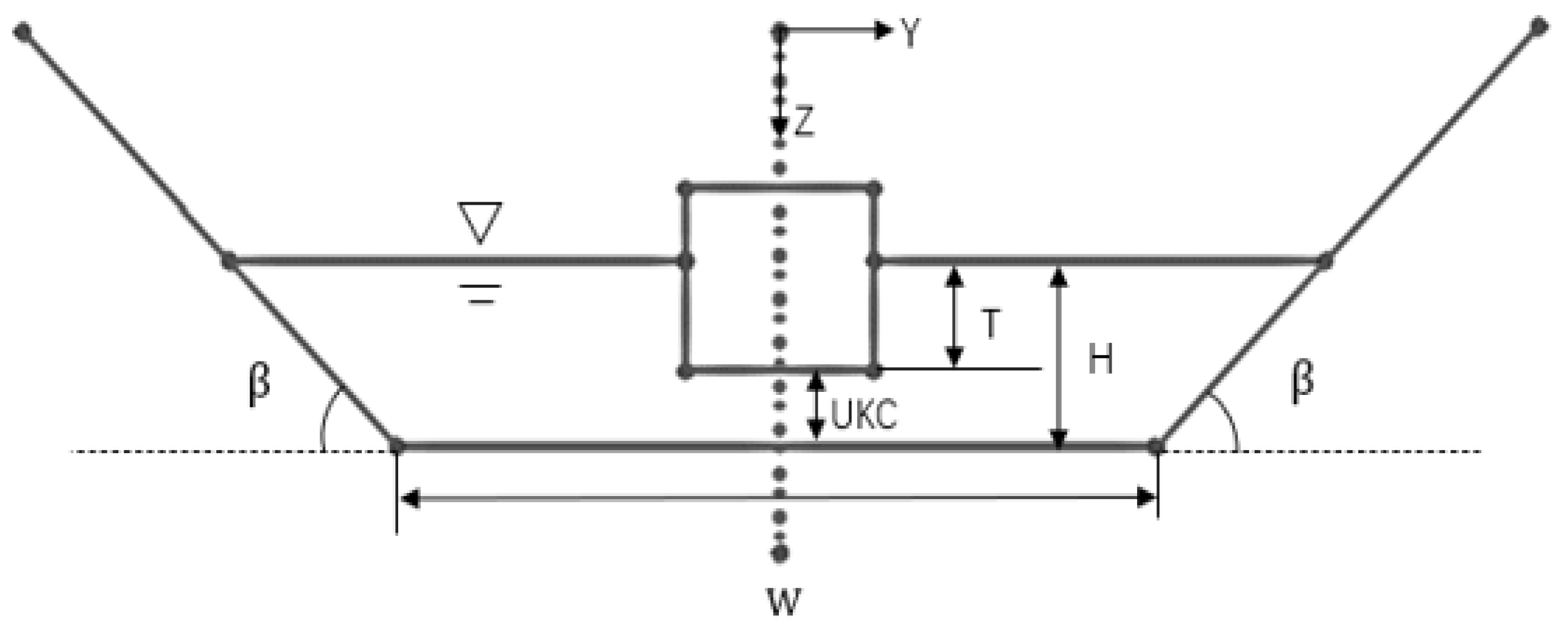
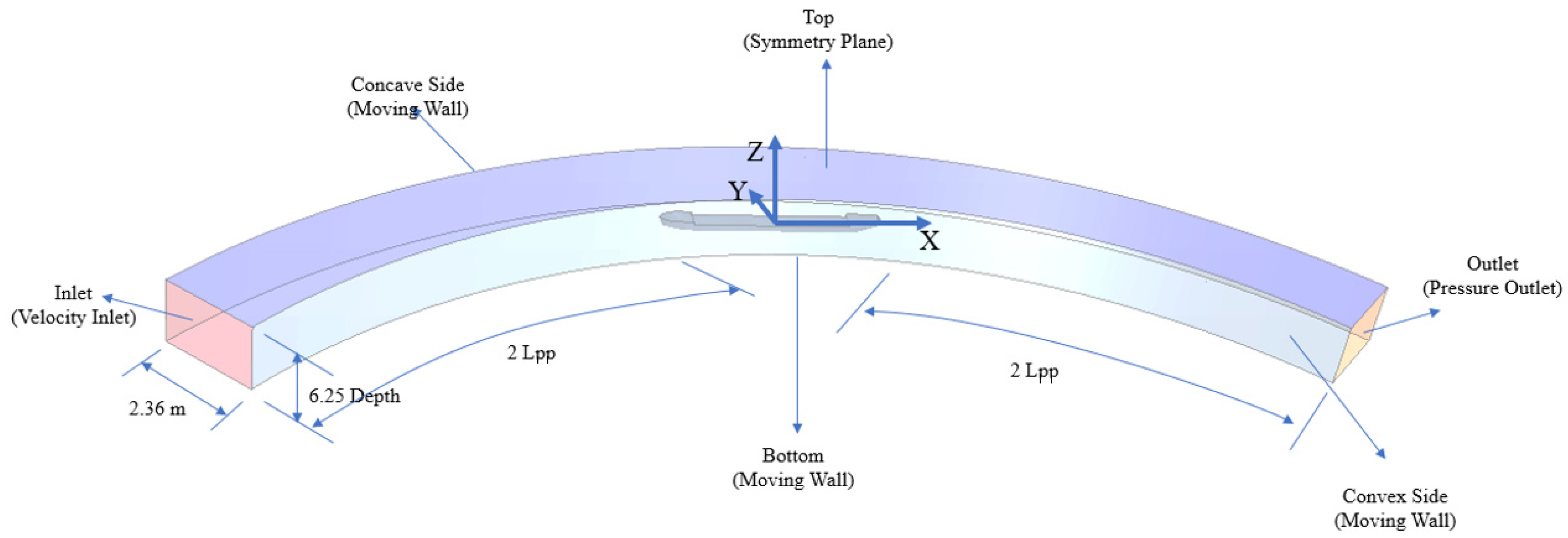


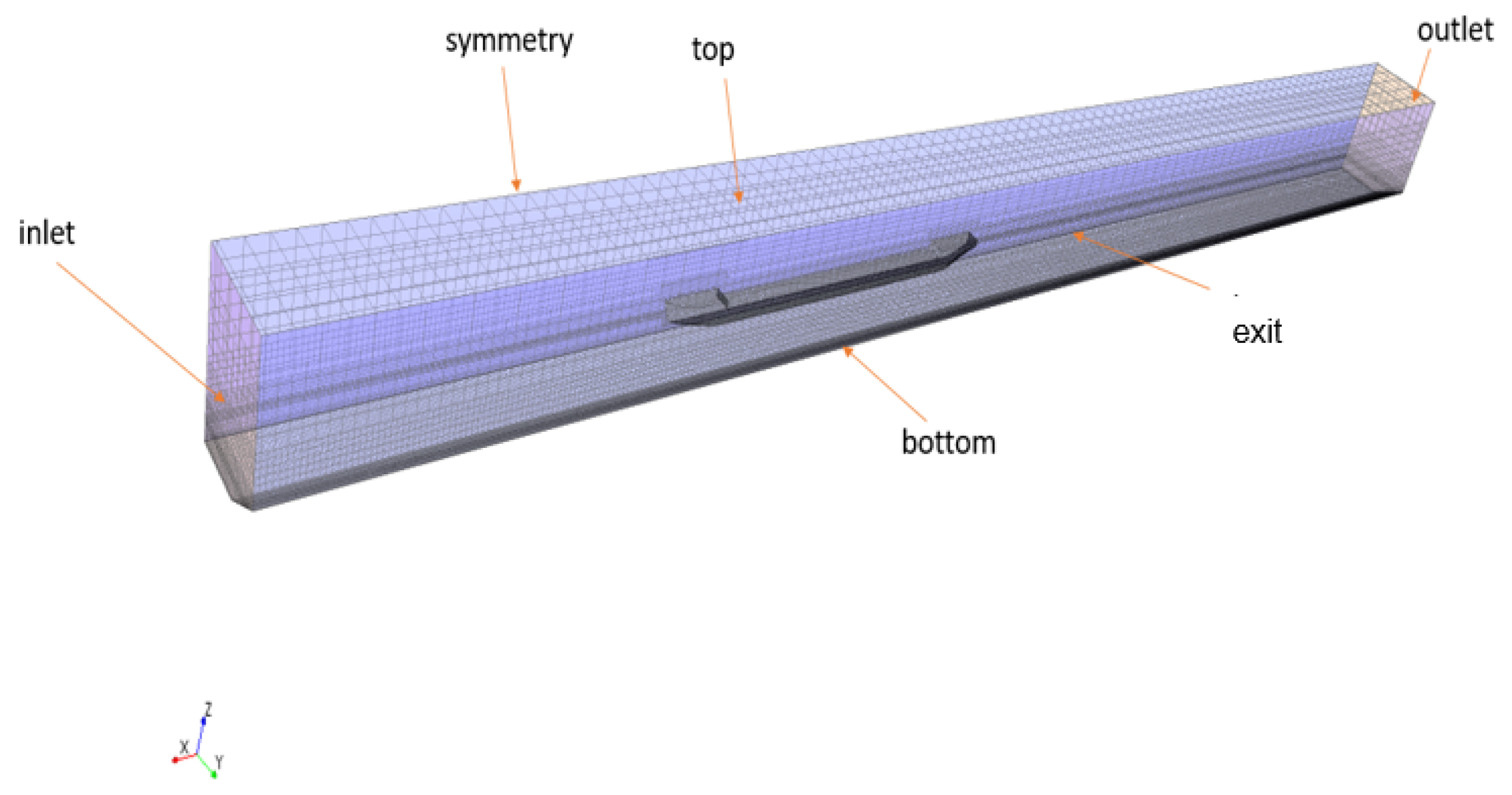

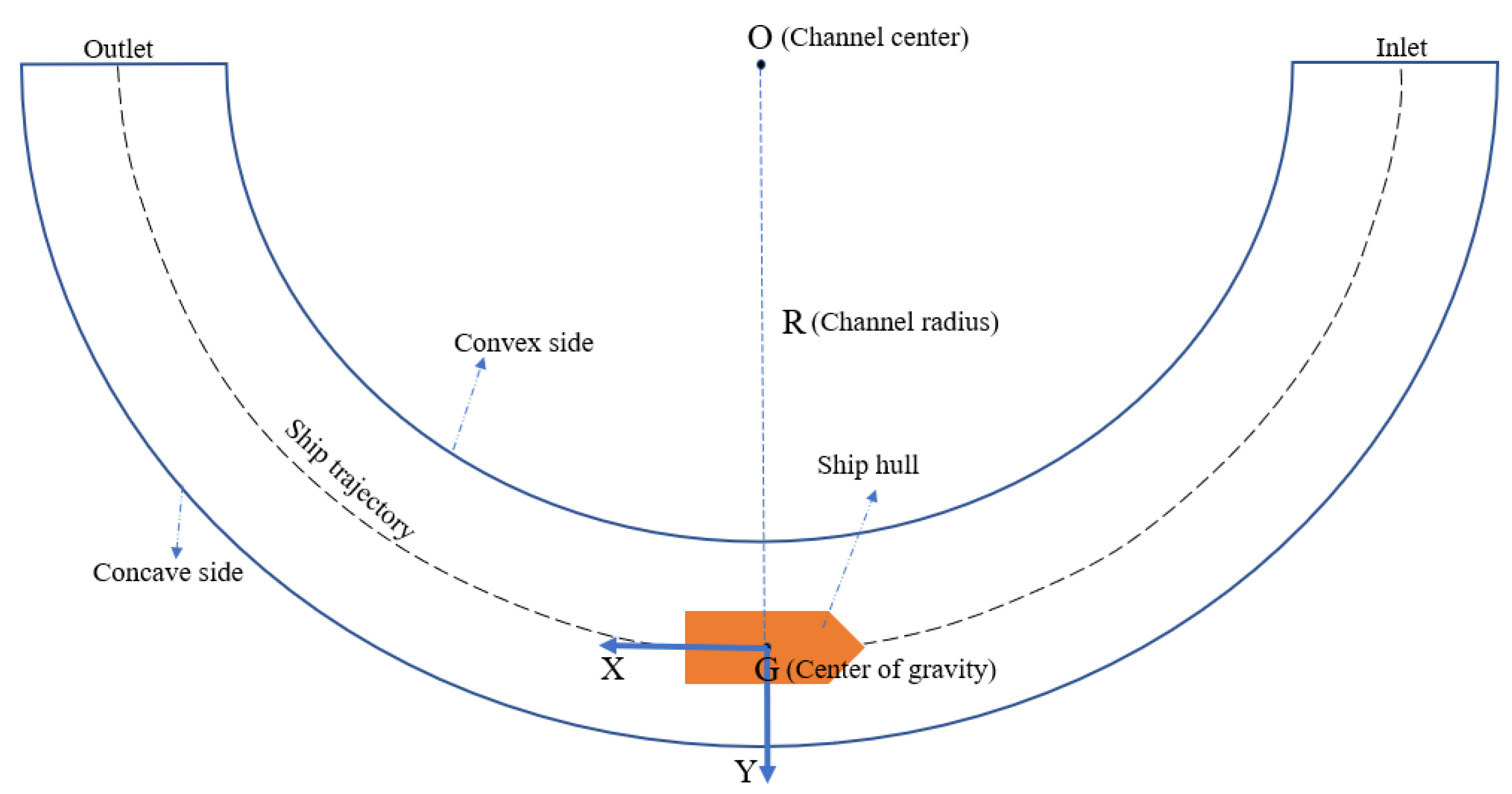





| Length between Perpendiculars, Lpp/m | Beam, B/m | Moulded Depth, H/m | Draft, T/m | Block Coefficient, | Wetted Surface, | Cross Area of Ship, | |
|---|---|---|---|---|---|---|---|
| full scale | 134.58 | 11.4 | 6 | 2.5 | 0.899 | 2104.8 | 34.114 |
| model scale | 5.4 | 0.45 | 0.24 | 0.1 | 0.899 | 3.367 | 0.045 |
| Config. A | Config. B | Config. C | Config. D | |
|---|---|---|---|---|
| Channel Radius Variation | Bank Slope Angle Variation | Ship Type Variation | Current Velocity Variation | |
| Total simulation case quantity | 4 | 4 | 5 | 8 |
| h/T | 1.2 | 1.2 | 1.2 | 1.2 |
| Channel radius, R/m | 12.52, 17.72, 23.28, 28.48 | 17.72 | 17.72 | 17.72 |
| Ship speed, | 0.6173 | 0.6173 | 0.6173 | 0.6173 |
| Channel bottom width, W/m | 2.36 | 2.36 | 2.36 | 2.36 |
| Bank slope, β/° | 90 | 13, 27, 50, 90 | 90 | 90 |
| Ship length, Lpp/m | 5.4 | 5.4 | 1.54, 2.68, 3.6, 4.4, 5.4, 7.2 | 5.4 |
| Ship beam, B/m | 0.45 | 0.45 | 0.202, 0.328, 0.38, 0.45, 0.45, 0.45 | 0.45 |
| Current velocity, | 0 | 0 | 0 | 0.1, 0.15, 0.2, 0.25 |
| No. | Elements | |||
|---|---|---|---|---|
| Grid 1 | 4,876,092 | 0.09395155 | 0.022136149 | −0.028939255 |
| Grid 2 | 1,371,356 | 0.094133305 | 0.029066149 | −0.030531812 |
| Grid 3 | 518,558 | 0.098757841 | 0.043988489 | −0.025078636 |
| 0.039302228 | 0.464404351 | −0.292042116 | ||
| Convergence condition | Monotonic | Monotonic | Oscillatory | |
| 24.47976382 | 1.15401605 | — | ||
| 7.42469 × | 0.006005115 | — | ||
| 9.34256 | 2.214058 | — | ||
| 0.000356084 | 0.007854884 | 0.002726588 |
| Ship Speed [m/s] | Resistance of Numerical Simulation [N] | Resistance of Experiment/2 [N] | Errors [%] |
|---|---|---|---|
| 0.335 | 0.690084 | 0.659 | 4.7168% |
| 0.4485 | 1.23664 | 1.194 | 3.5712% |
| 0.575 | 2.15804 | 2.124 | 1.6026% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, B.; Kaidi, S.; Lefrançois, E. CFD Method to Study Hydrodynamics Forces Acting on Ship Navigating in Confined Curved Channels with Current. J. Mar. Sci. Eng. 2022, 10, 1263. https://doi.org/10.3390/jmse10091263
Yang B, Kaidi S, Lefrançois E. CFD Method to Study Hydrodynamics Forces Acting on Ship Navigating in Confined Curved Channels with Current. Journal of Marine Science and Engineering. 2022; 10(9):1263. https://doi.org/10.3390/jmse10091263
Chicago/Turabian StyleYang, Bo, Sami Kaidi, and Emmanuel Lefrançois. 2022. "CFD Method to Study Hydrodynamics Forces Acting on Ship Navigating in Confined Curved Channels with Current" Journal of Marine Science and Engineering 10, no. 9: 1263. https://doi.org/10.3390/jmse10091263
APA StyleYang, B., Kaidi, S., & Lefrançois, E. (2022). CFD Method to Study Hydrodynamics Forces Acting on Ship Navigating in Confined Curved Channels with Current. Journal of Marine Science and Engineering, 10(9), 1263. https://doi.org/10.3390/jmse10091263







