Formation Coordination Control of Leaderless Multi-AUV System with Double Independent Communication Topology and Nonconvex Control Input Constraints
Abstract
:1. Introduction
- 1.
- The problem of formation coordination control of multi-AUV system is transformed into the problem of formation consensus of multi-AUV system, and the definition of formation consensus of leaderless multi-AUV system was given;
- 2.
- Under the condition that the communication delay of multi-AUV system formation with nonconvex control input constraints is bounded, a consensus constraint controller algorithm for discrete-time leaderless multi-AUV system formation with double independent position–velocity communication topology is proposed;
- 3.
- Combining the properties of the graph theory, random matrix and SIA matrix, it is proved that the formation of multi-AUV system can achieve the defined consensus objective by selecting the appropriate controller parameters and communication topology. On this basis, the unbounded communication delay of multi-AUV system formation is further studied.
2. Preliminaries
2.1. Notations
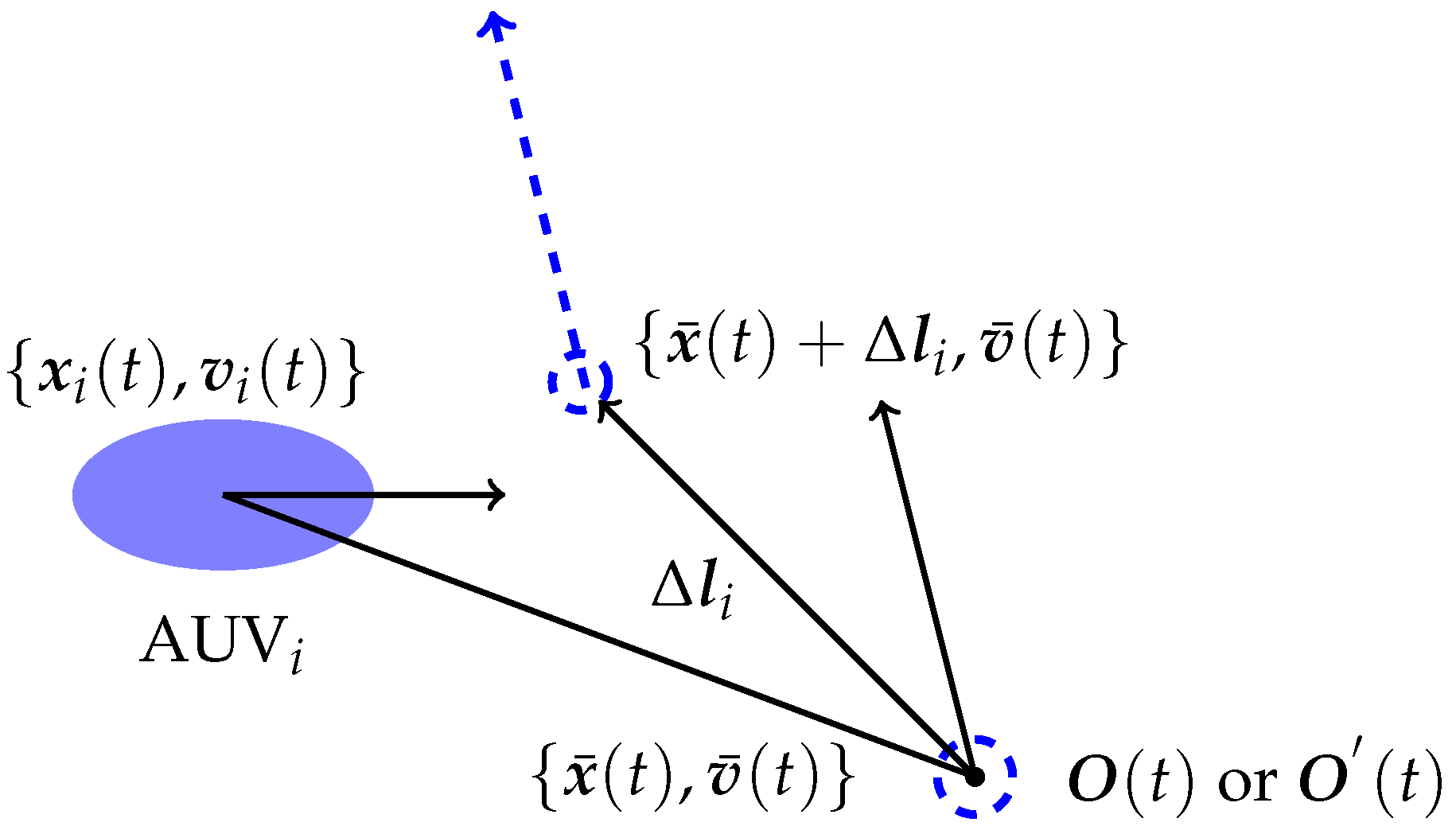
2.2. The Model of Multi-AUV System
- 1.
- For any , if there exists a constant such that , then the multi-AUV system is said to be no communication delayed.
- 2.
- For any , if there exists a positive integer N such that , then the multi-AUV system is said to be communication delay bounded. In this case, is valued as followswhere is a non-negative integer, and satisfies , , and .
- 3.
- If there is , for any positive integer N, , then the multi-AUV system is said to be communication delay unbounded.
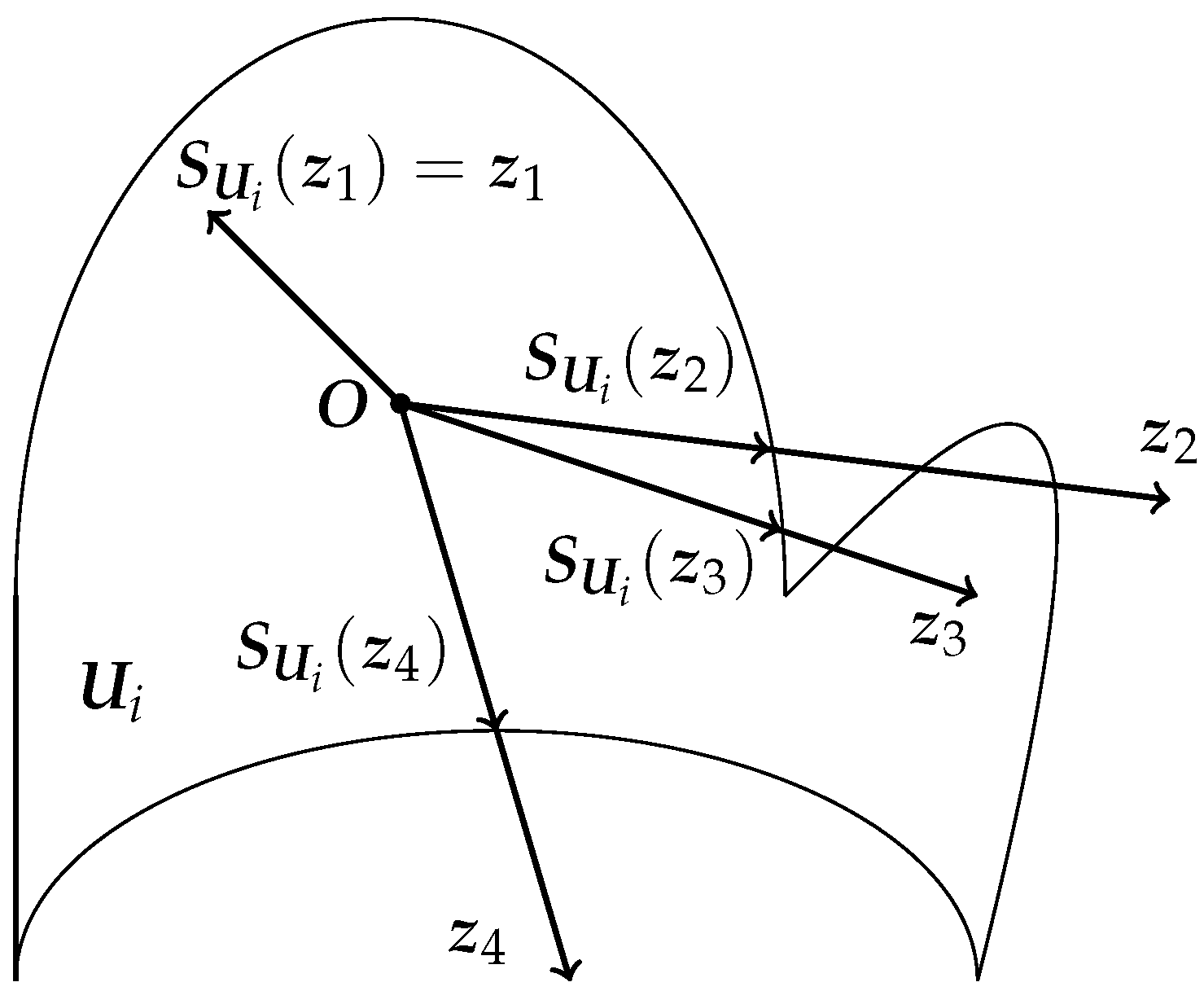
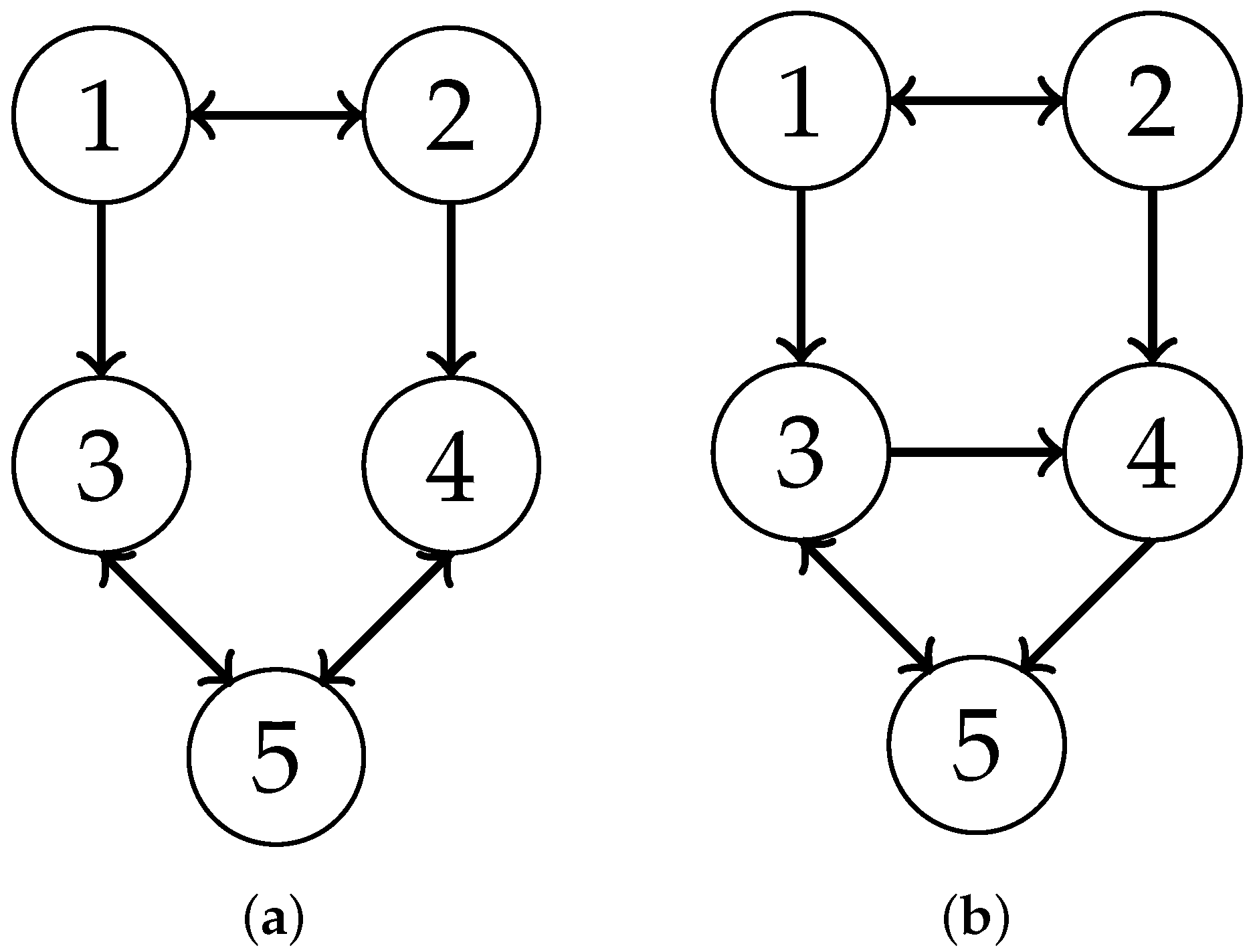
2.3. Graph Theory and Lemmas
3. Results
3.1. Formation Constrained Controller with Bounded Communication Delay
- 1.
- The position communication topology and speed communication topology have directed trees, respectively.
- 2.
- For all , , , where , , .
- 3.
- .
- 1.
- The union of position communication topologies the union of velocity communication topologies have directed trees, respectively,
- 2.
- For all , , , where , , .
- 3.
- .
3.2. Formation Constrained Controller with Unbounded Communication Delay
- 1.
- The union of position communication topologies the union of velocity communication topologies have directed trees, respectively,
- 2.
- For all , , , where , ,
- 3.
- .
- 1.
- when , are called the bounded communication delay of the multi-AUV formation system,
- 2.
- when , are called the unbounded communication delay of the multi-AUV formation system.
- 1.
- The union of position communication topologies the union of velocity communication topologies have directed trees, respectively,
- 2.
- For all , , , where , , .
- 3.
- .
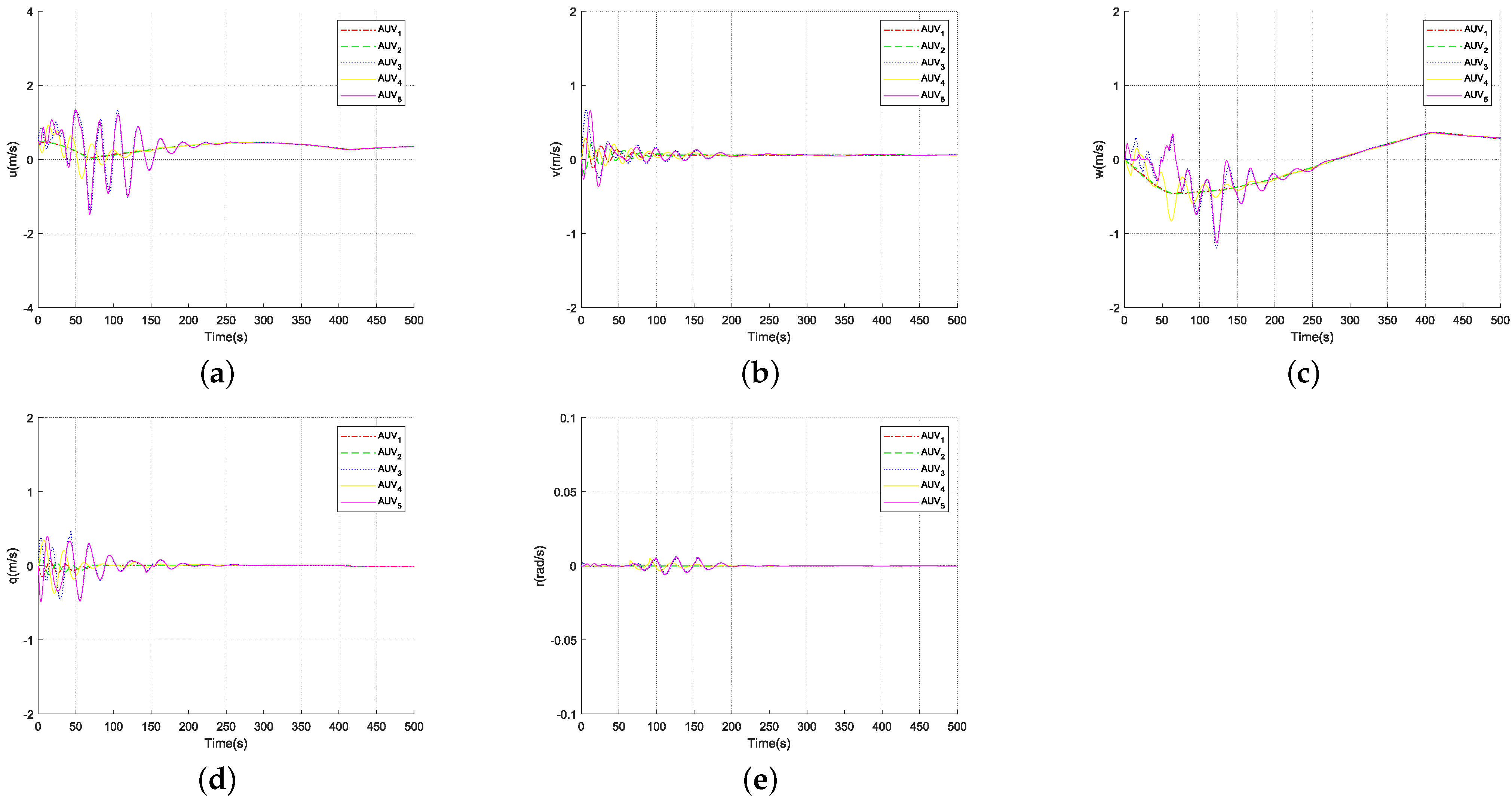
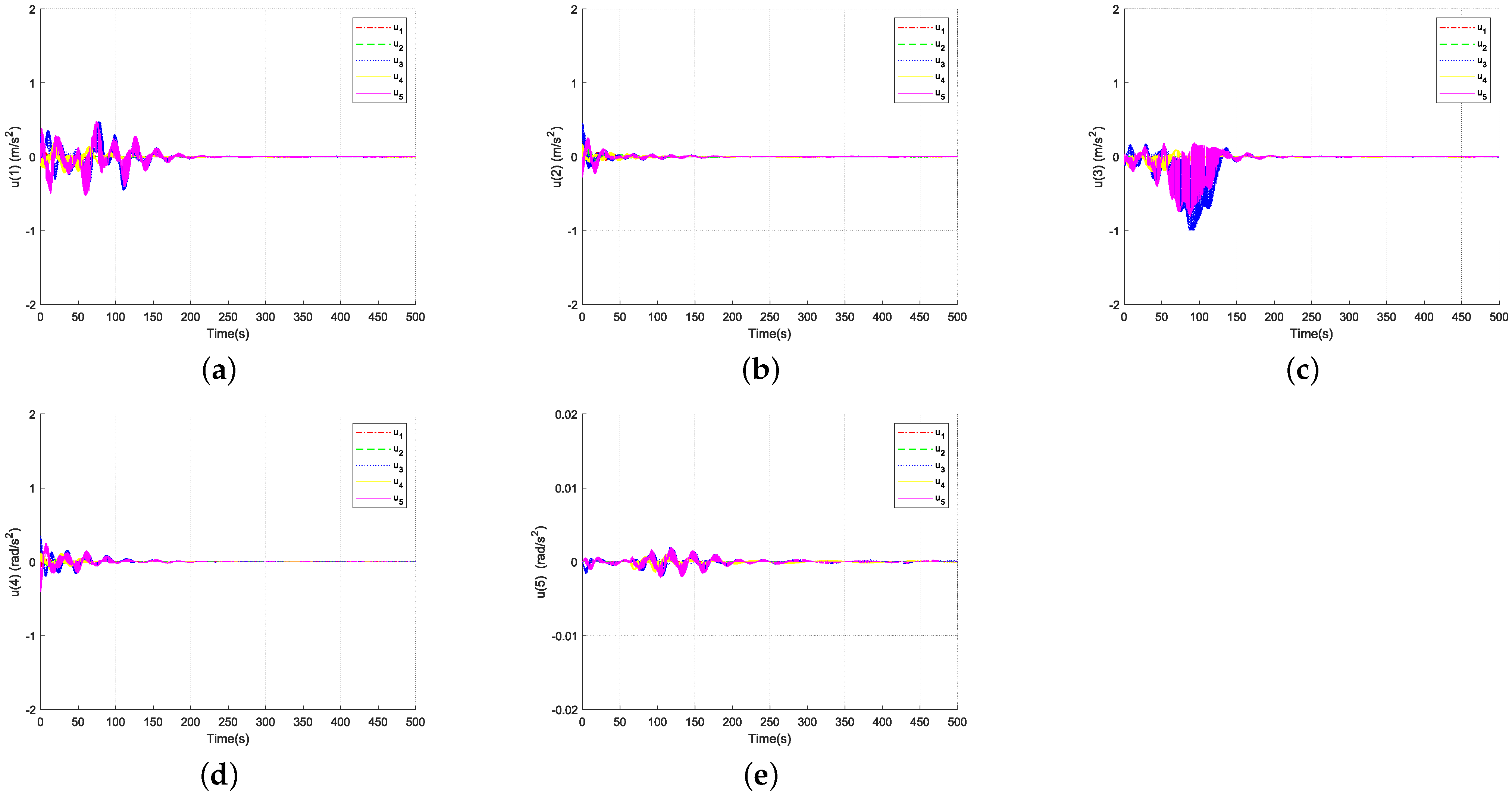
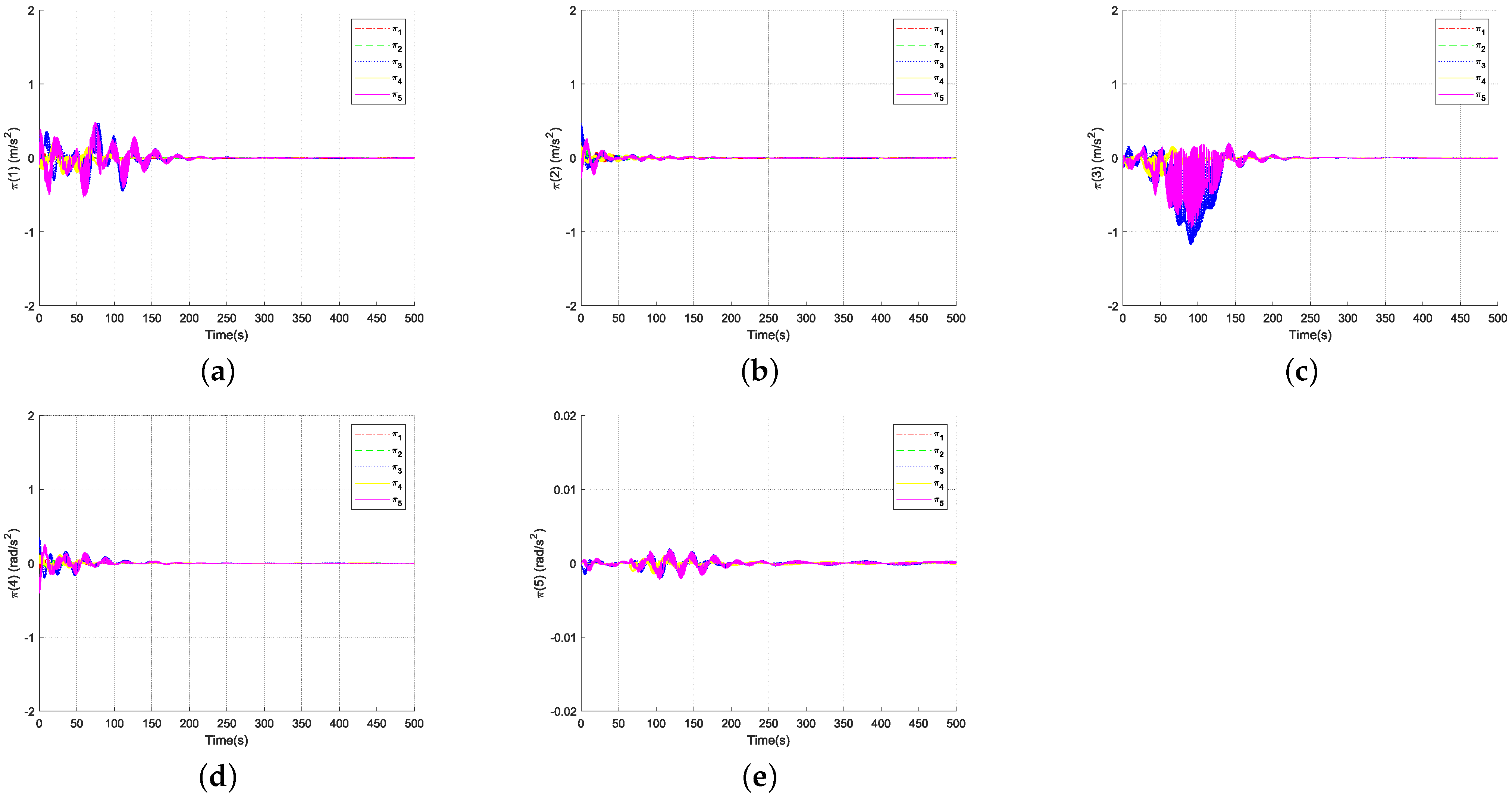
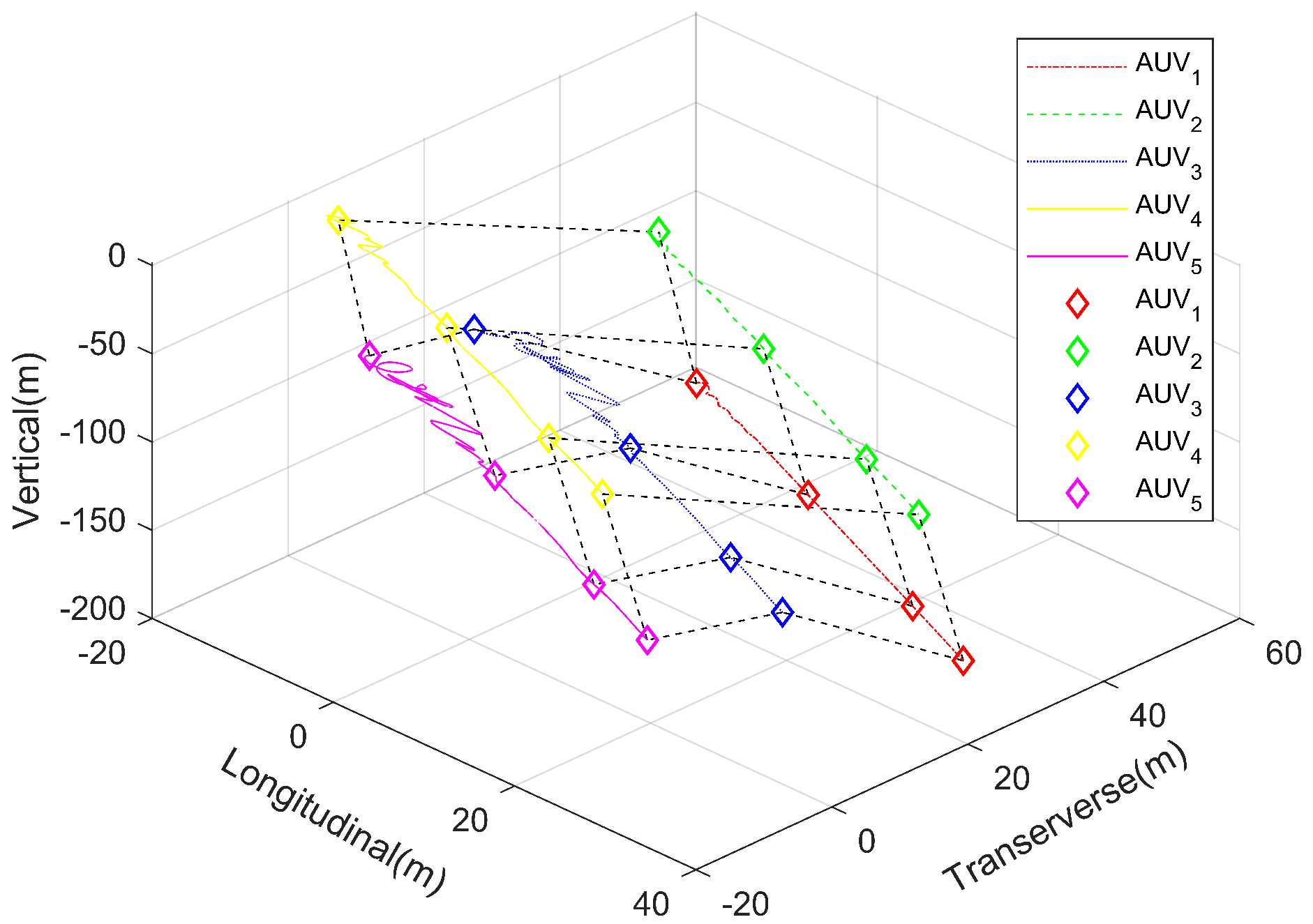
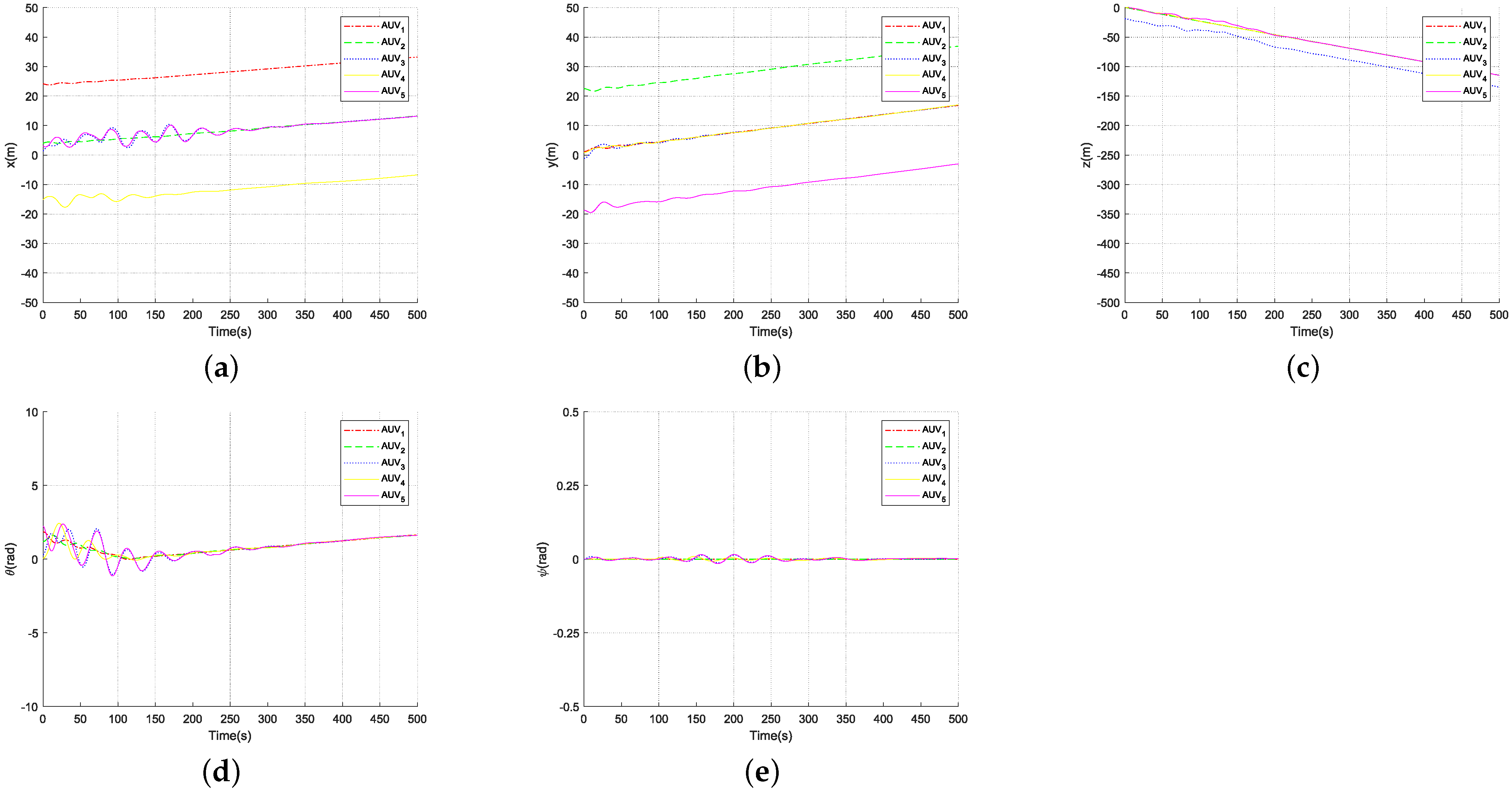
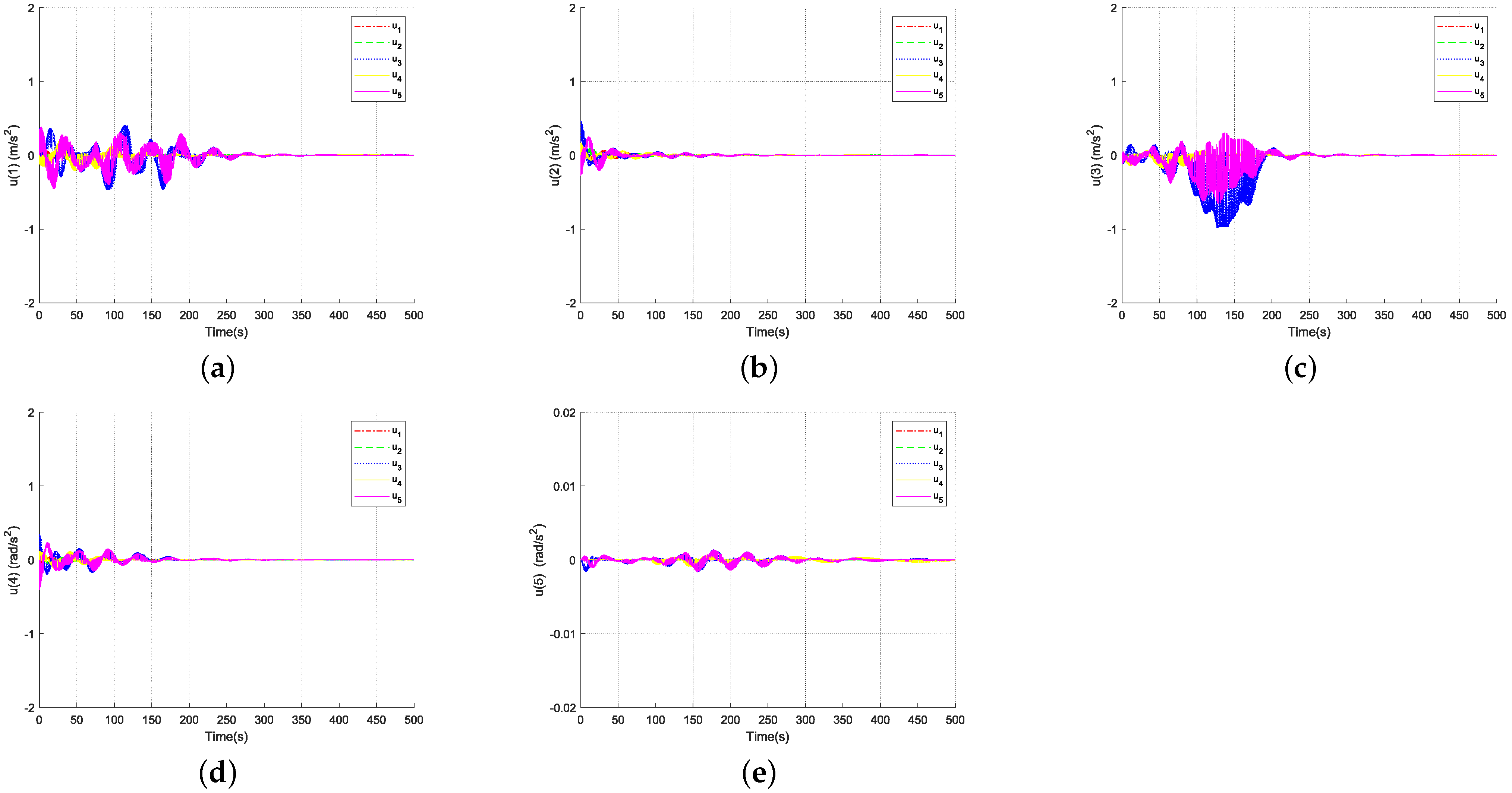
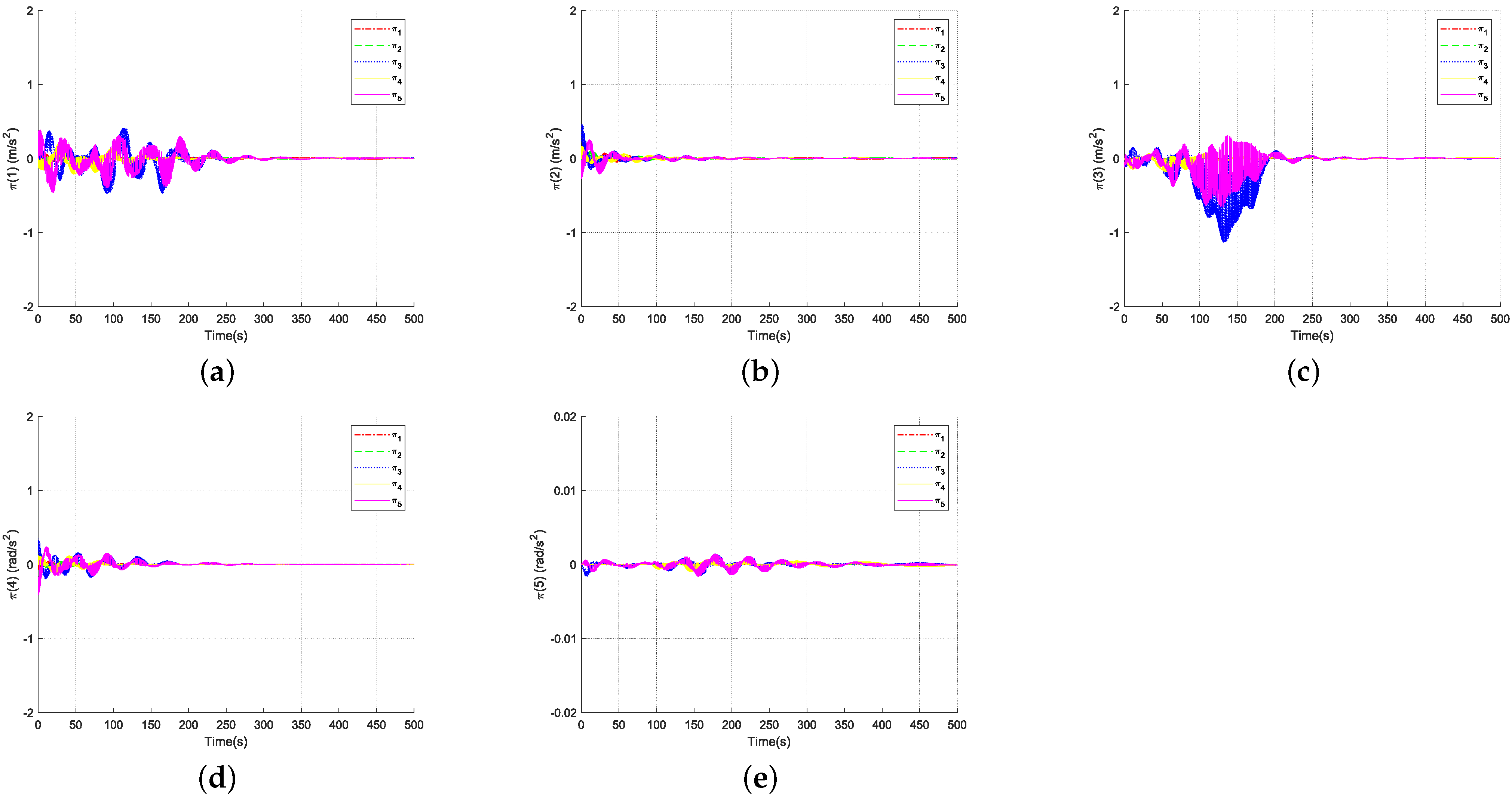
4. Simulation
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yang, Y.; Xiao, Y.; Li, T. A survey of autonomous underwater vehicle formation: Performance, formation control, and communication capability. IEEE Commun. Surv. Tutor. 2021, 23, 815–841. [Google Scholar] [CrossRef]
- Yan, Z.; Zhang, C.; Zhang, M.; Yan, J.; Tian, W. Distributed event-triggered formation control for multi-AUV system via asynchronous periodic sampling control approach. Ocean Eng. 2022, 256, 111561. [Google Scholar] [CrossRef]
- Wang, C.; Cai, W.; Lu, J.; Ding, X.; Yang, J. Design, Modeling, Control, and Experiments for Multiple AUVs Formation. IEEE Trans. Autom. Sci. Eng. 2021, 19, 2776–2787. [Google Scholar] [CrossRef]
- Gao, Z.; Guo, G. Fixed-time sliding mode formation control of AUVs based on a disturbance observer. IEEE/CAA J. Autom. Sin. 2020, 7, 539–545. [Google Scholar] [CrossRef]
- Yan, T.; Xu, Z.; Yang, S.X. Consensus Formation Control for Multiple AUVSystems Using Distributed Bioinspired Sliding Mode Control. IEEE Trans. Intell. Veh. 2022, 1. [Google Scholar] [CrossRef]
- Fang, Z.; Jiang, D.; Huang, J.; Cheng, C.; Sha, Q.; He, B.; Li, G. Autonomous underwater vehicle formation control and obstacle avoidance using multi-agent generative adversarial imitation learning. Ocean Eng. 2022, 262, 112182. [Google Scholar] [CrossRef]
- Wu, X.; Gao, Z.; Yuan, S.; Hu, Q.; Dang, Z. A Dynamic Task Allocation Algorithm for Heterogeneous UUV Swarms. Sensors 2022, 22, 2122. [Google Scholar] [CrossRef]
- Xia, G.; Zhang, Y.; Zhang, W.; Chen, X.; Yang, H. Dual closed-loop robust adaptive fast integral terminal sliding mode formation finite-time control for multi-underactuated AUV system in three dimensional space. Ocean Eng. 2021, 233, 108903. [Google Scholar] [CrossRef]
- Yang, H.; Wang, Y. Formation optimization and control for maneuvering target tracking by mobile sensing agents. IEEE Access 2019, 7, 32305–32314. [Google Scholar] [CrossRef]
- Xia, G.; Zhang, Y.; Zhang, W.; Zhang, K.; Yang, H. Robust adaptive super-twisting sliding mode formation controller for homing of multi-underactuated AUV recovery system with uncertainties. ISA Trans. 2022, 130, 136–151. [Google Scholar] [CrossRef]
- Hadi, B.; Khosravi, A.; Sarhadi, P. A review of the path planning and formation control for multiple autonomous underwater vehicles. J. Intell. Robot. Syst. 2021, 101, 67. [Google Scholar] [CrossRef]
- Li, J.; Zhang, Y.; Li, W. Formation Control of a Multi-Autonomous Underwater Vehicle Event-Triggered Mechanism Based on the Hungarian Algorithm. Machines 2021, 10, 346. [Google Scholar] [CrossRef]
- Du, J.; Li, J.; Lewis, F.L. Distributed 3D Time-Varying Formation Control of Underactuated AUVs With Communication Delays Based on Data-Driven State Predictor. IEEE Trans. Ind. Inform. 2022, 31, 6272–6287. [Google Scholar] [CrossRef]
- Zhao, Z.; Hu, Q.; Feng, H.; Feng, X.; Su, W. A Cooperative Hunting Method for Multi-AUV Swarm in Underwater Weak Information Environment with Obstacles. J. Mar. Sci. Eng. 2022, 9, 1266. [Google Scholar] [CrossRef]
- Li, L.; Li, Y.; Zhang, Y.; Xu, G.; Zeng, J.; Feng, X. Formation Control of Multiple Autonomous Underwater Vehicles under Communication Delay, Packet Discreteness and Dropout. J. Mar. Sci. Eng. 2022, 10, 920. [Google Scholar] [CrossRef]
- Xin, B.; Zhang, J.; Chen, J.; Wang, Q.; Qu, Y. Overview of research on transformation of multi-AUV formations. Complex Syst. Model. Simul. 2021, 1, 1–14. [Google Scholar] [CrossRef]
- Qi, X.; Cai, Z. Three-dimensional formation control based on nonlinear small gain method for multiple underactuated underwater vehicles. Ocean Eng. 2018, 151, 105–114. [Google Scholar] [CrossRef]
- Yan, Z.; Zhang, J.; Tang, J. Path planning for autonomous underwater vehicle based on an enhanced water wave optimization algorithm. Math. Comput. Simul. 2021, 181, 192–241. [Google Scholar] [CrossRef]
- Yan, Z.; Liu, Y.; Yu, C.; Zhou, J. Leader-following coordination of multiple UUVs formation under two independent topologies and time-varying delays. J. Cent. South Univ. 2017, 24, 382–393. [Google Scholar] [CrossRef]
- Yan, Z.; Zhang, M.; Zhang, C.; Zeng, J. Decentralized formation trajectory tracking control of multi-AUV system with actuator saturation. Ocean Eng. 2022, 255, 111423. [Google Scholar] [CrossRef]
- Yan, Z.; Zhang, C.; Tian, W.; Zhang, M. Formation trajectory tracking control of discrete-time multi-AUV in a weak communication environment. Ocean Eng. 2022, 245, 110495. [Google Scholar] [CrossRef]
- Yan, Z.; Yang, Z.; Yue, L.; Wang, L.; Jia, H.; Zhou, J. Discrete-time coordinated control of leader-following multiple AUVs under switching topologies and communication delays. Ocean Eng. 2019, 172, 361–372. [Google Scholar] [CrossRef]
- Yan, Z.; Pan, X.; Yang, Z.; Yue, L. Formation control of leader-following multi-UUVs with uncertain factors and time-varying delays. IEEE Access 2019, 7, 118792–118805. [Google Scholar] [CrossRef]
- Yan, Z.; Yang, Z.; Pan, X.; Zhou, J.; Wu, D. Virtual leader based path tracking control for Multi-UUV considering sampled-data delays and packet losses. Ocean Eng. 2020, 216, 108065. [Google Scholar] [CrossRef]
- Yan, Z.; Zhang, C.; Tian, W.; Cai, S.; Zhao, L. Distributed observer-based formation trajectory tracking method of leader-following multi-AUV system. Ocean Eng. 2022, 260, 112019. [Google Scholar] [CrossRef]
- Zhou, J.; Zhao, X.; Chen, T.; Yan, Z.; Yang, Z. Trajectory tracking control of an underactuated AUV based on backstepping sliding mode with state prediction. IEEE Access 2019, 7, 181983–181993. [Google Scholar] [CrossRef]
- Yan, Z.; Yue, L.; Yang, Z. Coordinated Control of Multiple AUVs with Nonconvex Control Input Constraints. In Proceedings of the 2022 41st Chinese Control Conference (CCC), Hefei, China, 25–27 July 2021; pp. 4849–4856. [Google Scholar]
- Wang, J.; Wang, C.; Wei, Y.; Zhang, C. Neuroadaptive sliding mode formation control of autonomous underwater vehicles with uncertain dynamics. IEEE Syst. J. 2019, 14, 3325–3333. [Google Scholar] [CrossRef]
- Zhang, Y.; Yang, F.; Li, Y.; Qiu, W. Design and numerical investigation of a multi-directional energy-harvesting device for UUVs. Energy 2021, 214, 118978. [Google Scholar] [CrossRef]
- Lin, X.; Tian, W.; Zhang, W.; Zeng, J.; Zhang, C. The leaderless multi-AUV system fault-tolerant consensus strategy under heterogeneous communication topology. Ocean Eng. 2021, 237, 109594. [Google Scholar] [CrossRef]
- Meng, C.; Zhang, X. Distributed leaderless formation control for multiple autonomous underwater vehicles based on adaptive nonsingular terminal sliding mode. Appl. Ocean. Res. 2021, 115, 102781. [Google Scholar] [CrossRef]
- Lin, P.; Ren, W.; Yang, C.; Gui, W. Distributed consensus of second-order multiagent systems with nonconvex velocity and control input constraints. IEEE Trans. Autom. Control 2017, 63, 1171–1176. [Google Scholar] [CrossRef]
- Ren, W.; Beard, R.W. Distributed Consensus in Multi-Vehicle Cooperative Control: Theory and Applications; Springer: London, UK, 2007. [Google Scholar]
- Wolfowitz, J. Products of indecomposable, aperiodic, stochastic matrices. Proc. Am. Math. Soc. 1963, 14, 733–737. [Google Scholar] [CrossRef]
- Jadbabaie, A.; Lin, J.; Morse, A.S. Coordination of groups of mobile autonomous agents using nearest neighbor rules. IEEE Trans. Autom. Control 2003, 48, 988–1001. [Google Scholar] [CrossRef] [Green Version]

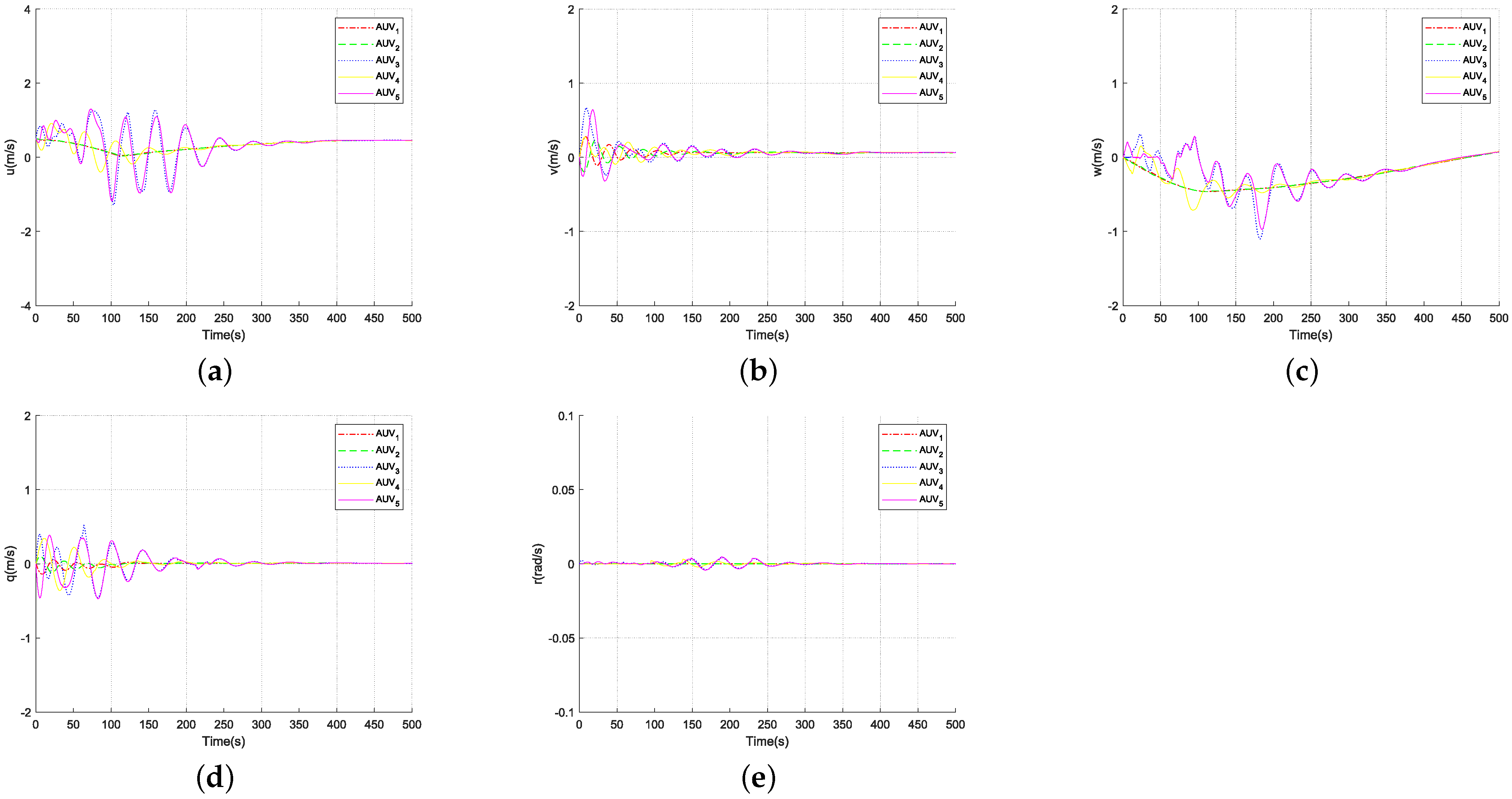

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, Z.; Yue, L.; Zhou, J.; Pan, X.; Zhang, C. Formation Coordination Control of Leaderless Multi-AUV System with Double Independent Communication Topology and Nonconvex Control Input Constraints. J. Mar. Sci. Eng. 2023, 11, 107. https://doi.org/10.3390/jmse11010107
Yan Z, Yue L, Zhou J, Pan X, Zhang C. Formation Coordination Control of Leaderless Multi-AUV System with Double Independent Communication Topology and Nonconvex Control Input Constraints. Journal of Marine Science and Engineering. 2023; 11(1):107. https://doi.org/10.3390/jmse11010107
Chicago/Turabian StyleYan, Zheping, Lidong Yue, Jiajia Zhou, Xiaoli Pan, and Chao Zhang. 2023. "Formation Coordination Control of Leaderless Multi-AUV System with Double Independent Communication Topology and Nonconvex Control Input Constraints" Journal of Marine Science and Engineering 11, no. 1: 107. https://doi.org/10.3390/jmse11010107
APA StyleYan, Z., Yue, L., Zhou, J., Pan, X., & Zhang, C. (2023). Formation Coordination Control of Leaderless Multi-AUV System with Double Independent Communication Topology and Nonconvex Control Input Constraints. Journal of Marine Science and Engineering, 11(1), 107. https://doi.org/10.3390/jmse11010107





