A Comparative Centrifuge Test Study on the Influence of Overlying Seawater on Seismic Response Spectrum
Abstract
:1. Introduction
2. Design of Dynamic Centrifugal Model Test
2.1. Centrifugal Model Test Equipment
2.2. Model Design Scheme
2.3. Model Similarity Rate
2.4. Inputting Ground Motion Form
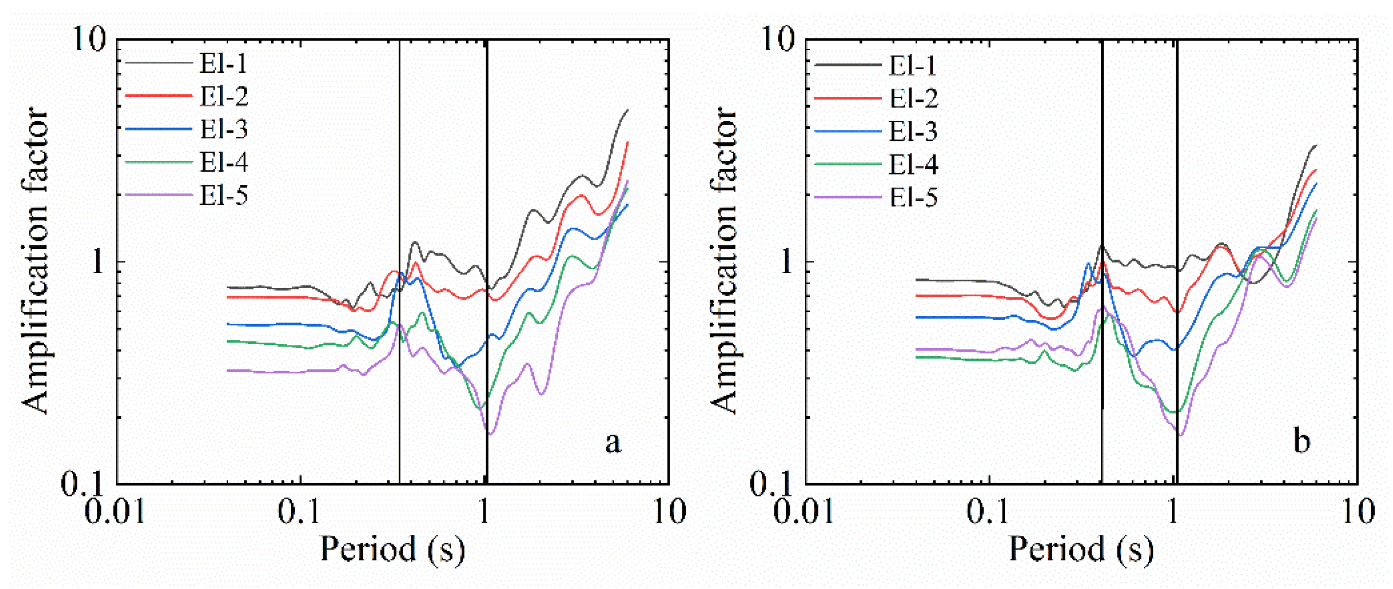
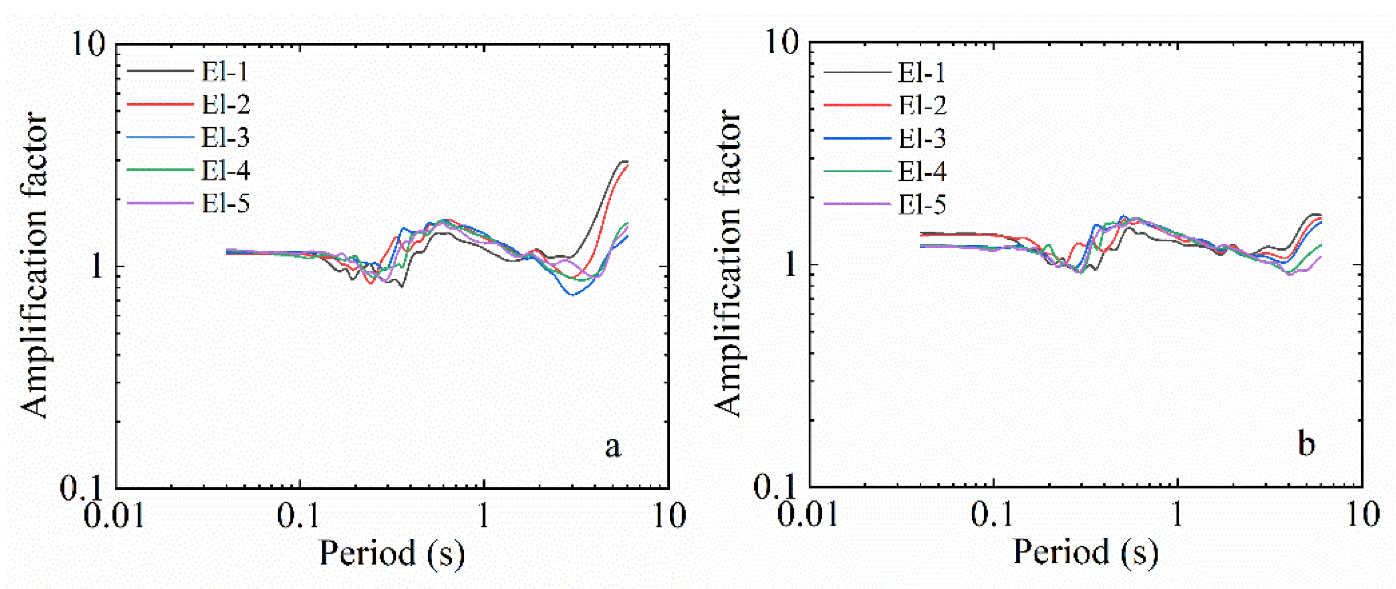
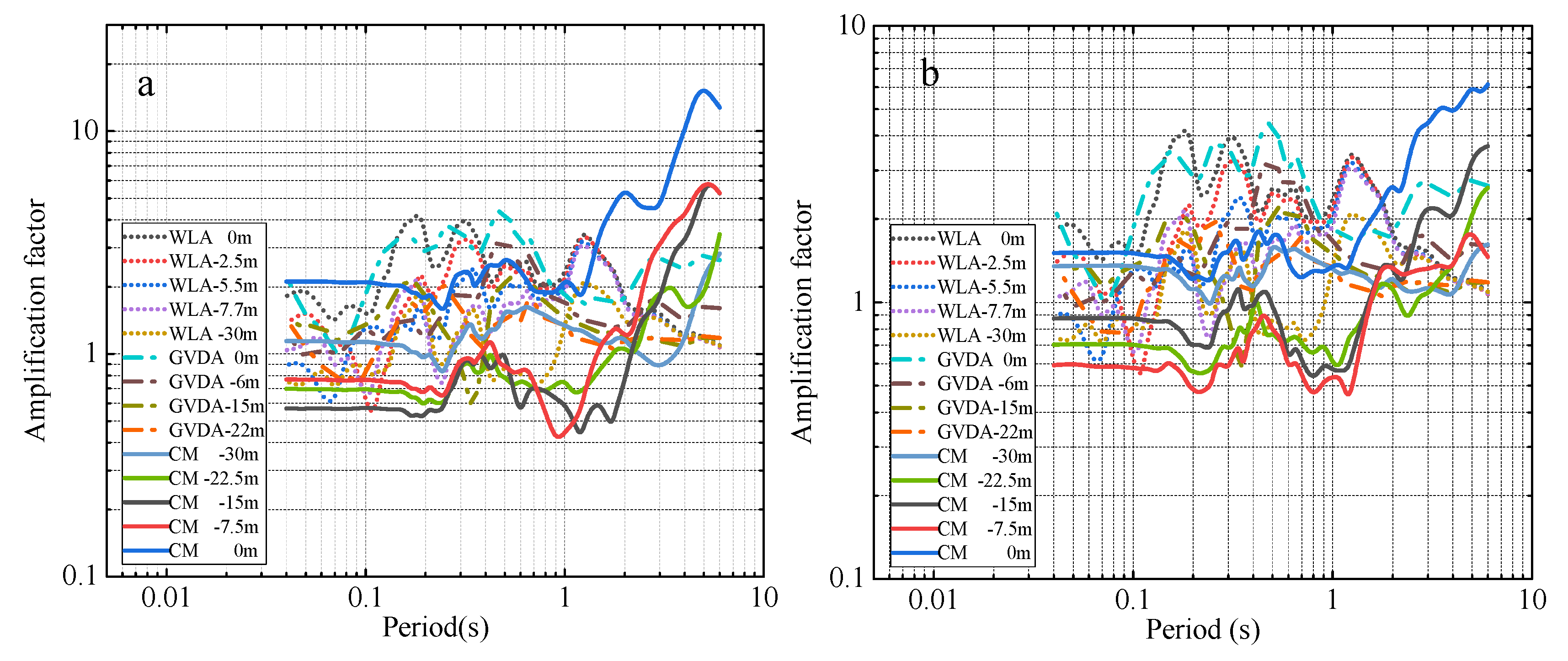
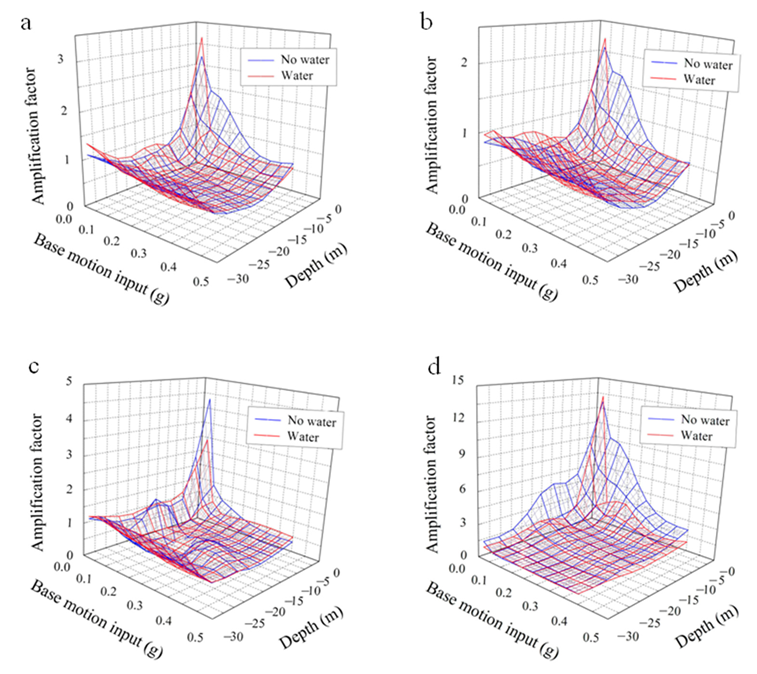
3. Analysis of Test Results
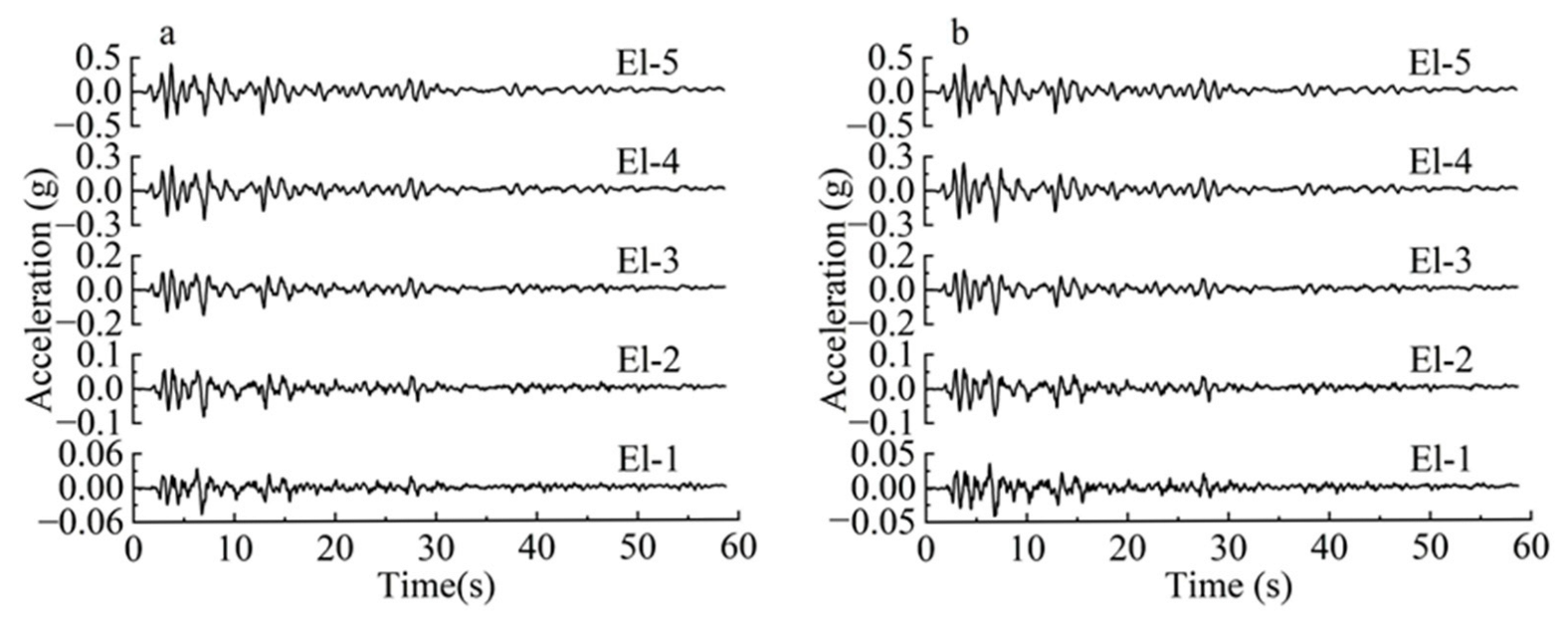
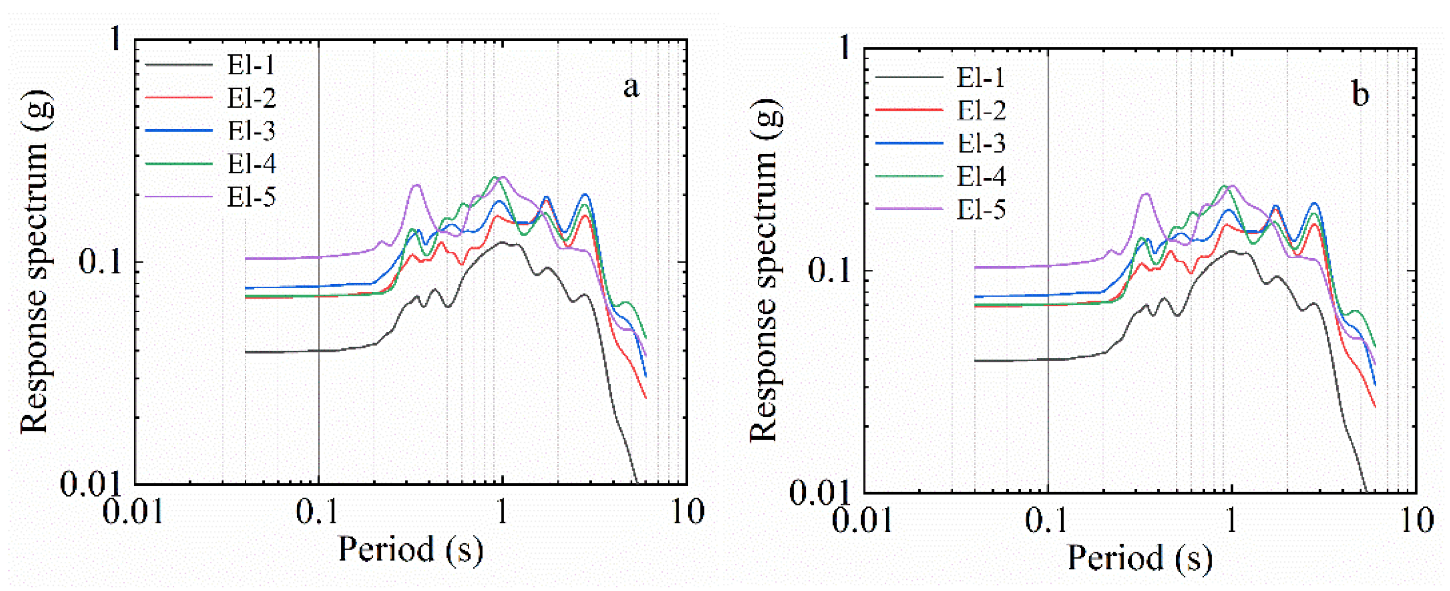
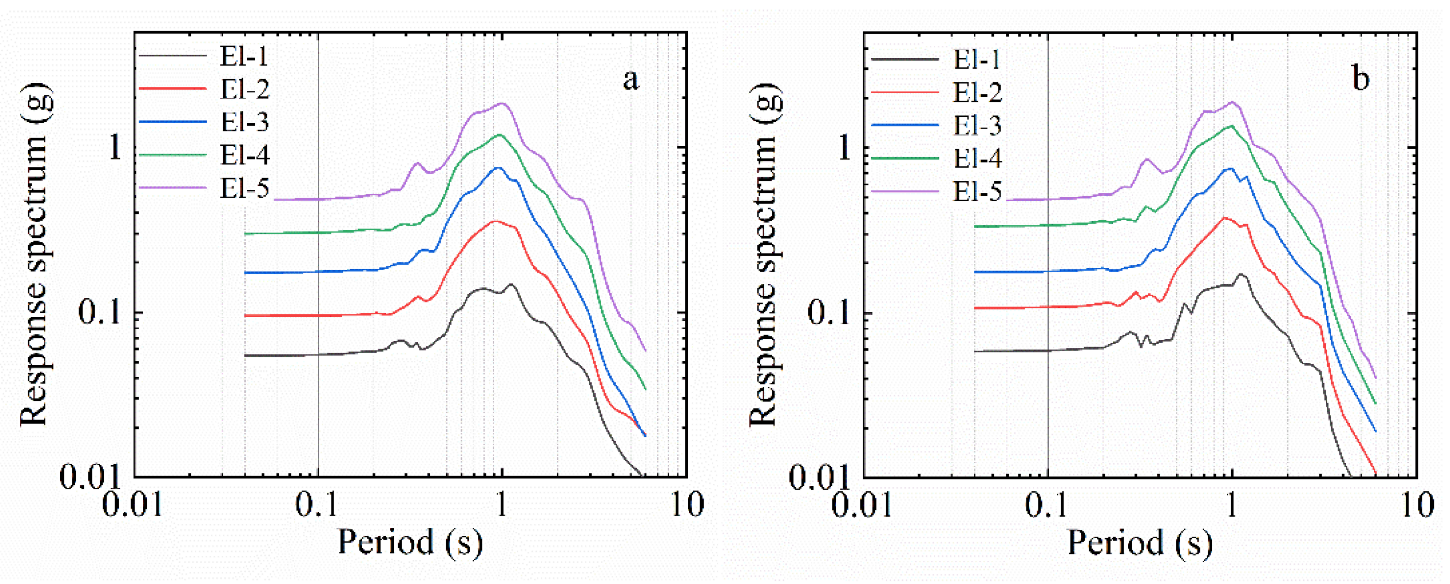
3.1. Effecting of Input Ground Motion on Response Spectrum
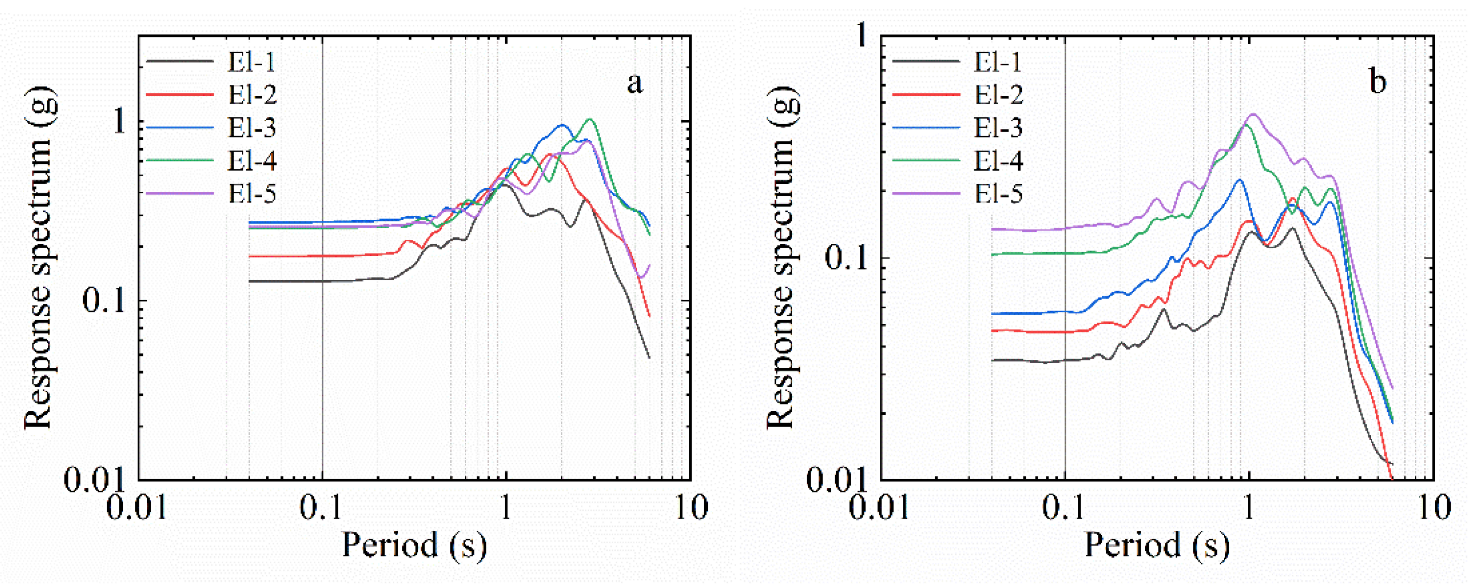
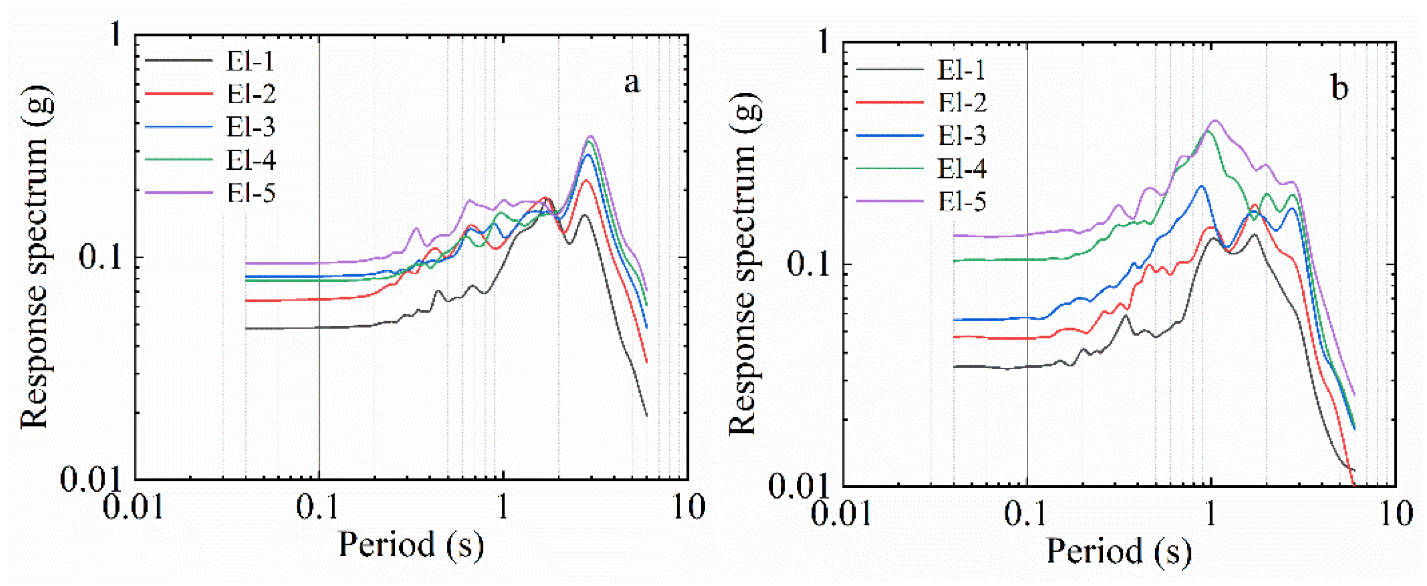
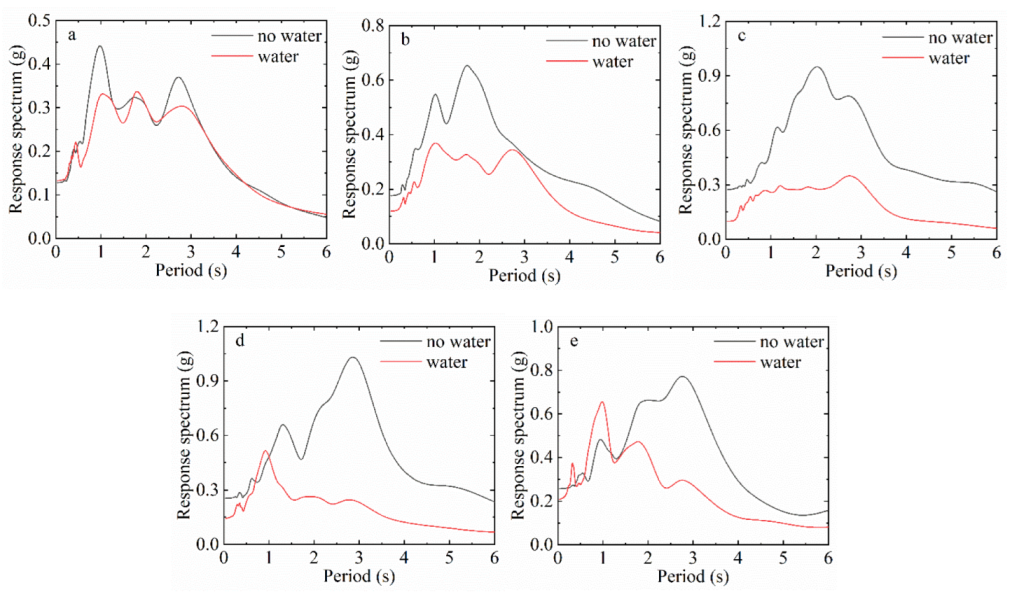
3.2. Comparative Analysis of Surface Response Spectra
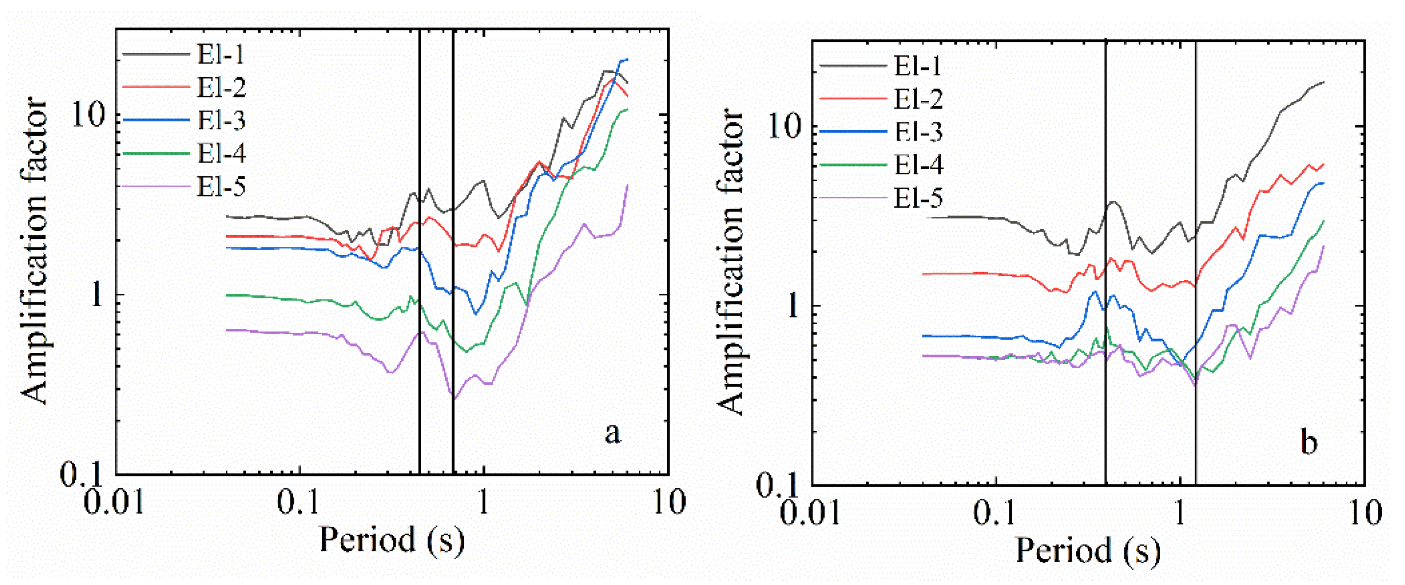
3.3. Amplification Factor of Response Spectrum at Specific Period Point
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kubo, H.; Nakamura, T.; Suzuki, W.; Dhakal, Y.P.; Kimura, T.; Kunugi, T.; Takahashi, N.; Aoi, S. Ground-Motion Characteristics and Nonlinear Soil Response Observed by DONET1 Seafloor Observation Network during the 2016 Southeast Off-Mie, Japan, Earthquake. Bull. Seismol. Soc. Am. 2019, 109, 976–986. [Google Scholar] [CrossRef]
- Boore, D.M.; Smith, C.E. Analysis of earthquake recordings obtained from the Seafloor Earthquake Measurement System (SEMS) instruments deployed off the coast of southern California. Bull. Seismol. Soc. Am. 1999, 89, 260–274. [Google Scholar] [CrossRef]
- Sleefe, G.E. The long-term measurement of strong-motion earthquakes offshore southern California. In Proceedings of the 22nd Annual Offshore Technology Conference, Houston, TX, USA, 7–10 May 1990; pp. 561–568. [Google Scholar]
- Chen, B.; Wang, D.; Li, H.; Sun, Z.; Li, C. Vertical-to-horizontal response spectral ratio for offshore ground motions: Analysis and simplified design equation. J. Cent. South Univ. 2017, 24, 203–216. [Google Scholar] [CrossRef]
- Diao, H.; Hu, J.; Xie, L. Effect of seawater on incident plane P and SV waves at ocean bottom and engineering characteristics of offshore ground motion records off the coast of southern California, USA. Earthq. Eng. Eng. Vib. 2014, 13, 181–194. [Google Scholar] [CrossRef]
- Zhu, J. Coupled motion of sea water and sea bed-soil under earthquake action. Earthq. Eng. Eng. Vib. 1988, 8, 37–43. (In Chinese) [Google Scholar]
- Zhu, J.; Zhou, J. A fluid mechanism basis for estimating undersea ground motion. Earthq. Eng. Eng. Vib. 1991, 11, 87–93. (In Chinese) [Google Scholar]
- Hatayama, K. Should We Consider Sea in Simulating Strong Ground Motion-Numerical Examination of Effects of Sea in the 2-D P-SV Wave Field. AGU Fall Meet. Abstr. 2003, 2003, S51E-0091. [Google Scholar]
- Nakamura, T.; Takenaka, H.; Okamoto, T.; Ohori, M.; Tsuboi, S. Long-period ocean-bottom motions in the source areas of large subduction earthquakes. Sci. Rep. 2015, 5, 16648. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Petukhin, A.; Iwata, T.; Kagawa, T. Study on the effect of the oceanic water layer on strong ground motion simulations. Earth Planets Space 2010, 62, 621–630. [Google Scholar] [CrossRef] [Green Version]
- Hu, J.; Zheng, X.; Hao, Y.; Xie, L. Characterization of strong motion of subduction earthquakes and its attenuation relationship. Chin. J. Geophys. 2017, 60, 1773–1787. [Google Scholar]
- Li, C.; Hao, H.; Li, H.; Bi, K. Theoretical modeling and numerical simulation of seismic motions at seafloor. Soil Dyn. Earthq. Eng. 2015, 77, 220–225. [Google Scholar] [CrossRef] [Green Version]
- Li, C.; Hao, H.; Li, H.; Bi, K.; Chen, B. Modeling and simulation of spatially correlated ground motions at multiple onshore and offshore sites. J. Earthq. Eng. 2017, 21, 359–383. [Google Scholar] [CrossRef] [Green Version]
- Fan, S.; Shi, Y.; Liu, C.; Li, W. Simulation of spatially varying seafloor ground motions with random seawater layer and complex terrain. Soil Dyn. Earthq. Eng. 2018, 111, 110–118. [Google Scholar] [CrossRef]
- Rong, M.; Yu, T.; Wang, J. Comparative study on site-effects of sea and land area based on strong earthquake observation. Build. Struct. 2018, 48, 345–349. (In Chinese) [Google Scholar]
- Lee, C.; Wei, Y.; Kuo, Y. Boundary effects of a laminar container in centrifuge shaking table tests. Soil Dyn. Earthq. Eng. 2012, 34, 37–51. [Google Scholar] [CrossRef]
- Building Seismic Safety Council. NEHRP Recommended Provisions for Seismic Regulations for New Buildings and Other Structures; 302/303, Part 1 and 2, 2009 Edition; Federal Emergency Management Agency: Washington, DC, USA, 2010. [Google Scholar]

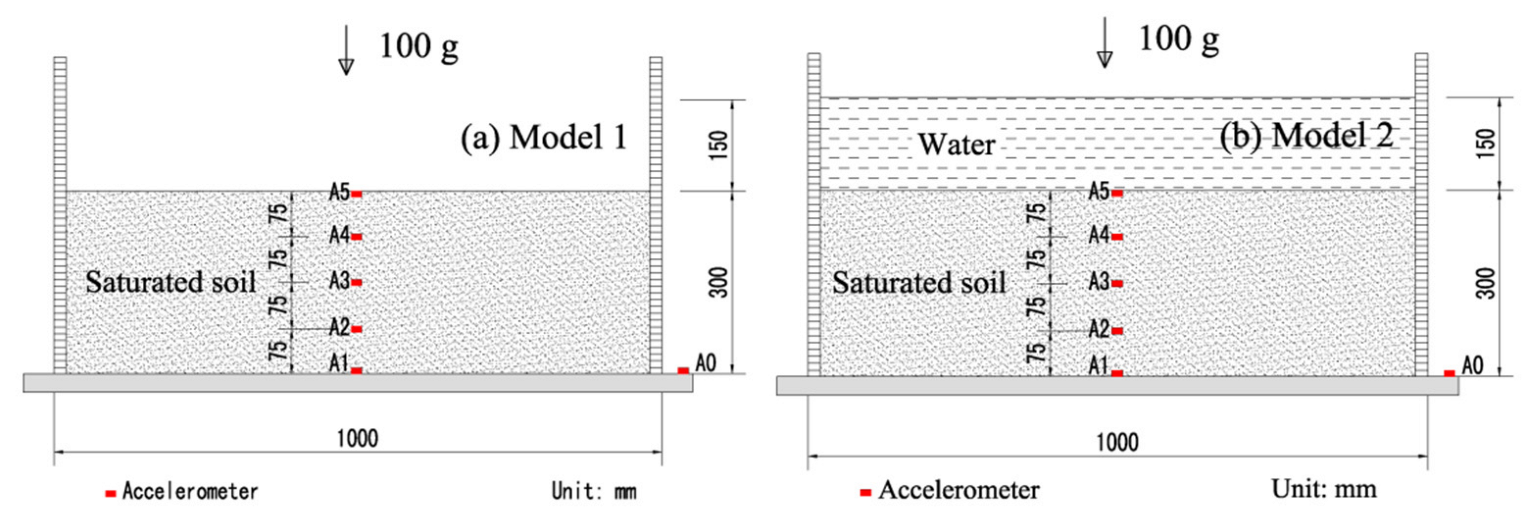



| Density ρ | Water Content ω | Plastic Limit | Liquid Limit | Void Ratio e |
|---|---|---|---|---|
| 1.61 g/m3 | 36% | 26% | 48% | 1.17 |
| Physical Quantity | Model | Prototype |
|---|---|---|
| Length | 1 | 100 |
| Inputting vibration time | 1 | 100 |
| Acceleration | 1 | 1/100 |
| Velocity` | 1 | 1 |
| Displacement | 1 | 100 |
| Vibration frequency | 1 | 1/100 |
| Seismic Wave Type | Working Condition | Amplitude (g) | Duration (s) | |
|---|---|---|---|---|
| No Water | Water | |||
| El Centro wave | El-1 | 0.047 | 0.041 | 60 |
| El-2 | 0.083 | 0.079 | ||
| El-3 | 0.150 | 0.146 | ||
| El-4 | 0.255 | 0.272 | ||
| El-5 | 0.403 | 0.395 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Wang, T.; Lan, J.; Song, X. A Comparative Centrifuge Test Study on the Influence of Overlying Seawater on Seismic Response Spectrum. J. Mar. Sci. Eng. 2023, 11, 167. https://doi.org/10.3390/jmse11010167
Liu J, Wang T, Lan J, Song X. A Comparative Centrifuge Test Study on the Influence of Overlying Seawater on Seismic Response Spectrum. Journal of Marine Science and Engineering. 2023; 11(1):167. https://doi.org/10.3390/jmse11010167
Chicago/Turabian StyleLiu, Juan, Ting Wang, Jingyan Lan, and Xijun Song. 2023. "A Comparative Centrifuge Test Study on the Influence of Overlying Seawater on Seismic Response Spectrum" Journal of Marine Science and Engineering 11, no. 1: 167. https://doi.org/10.3390/jmse11010167






