Angular Spectrum of Acoustic Pulses at Long Ranges
Abstract
:1. Introduction
2. Theory
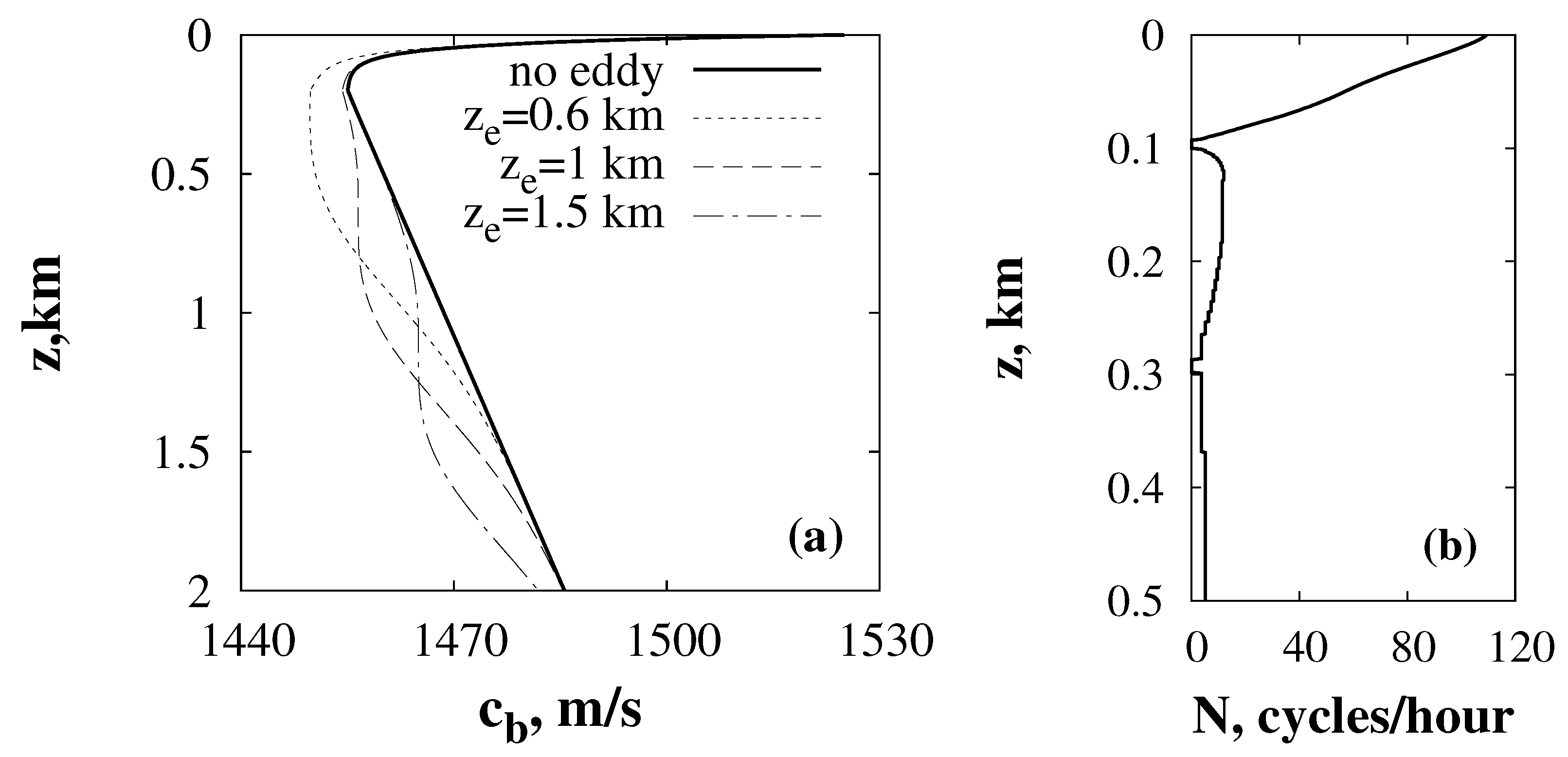
3. Model of a Waveguide
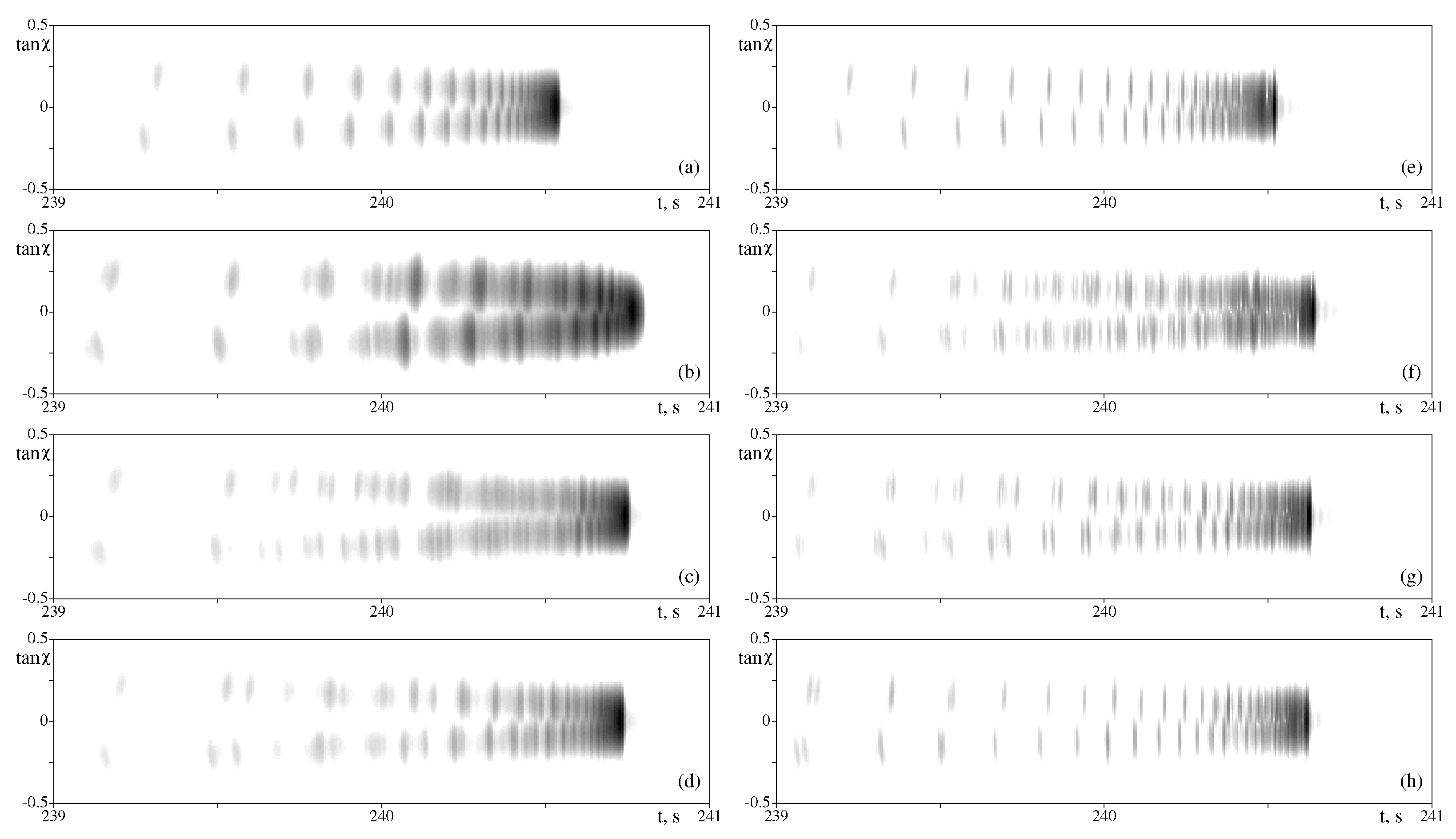
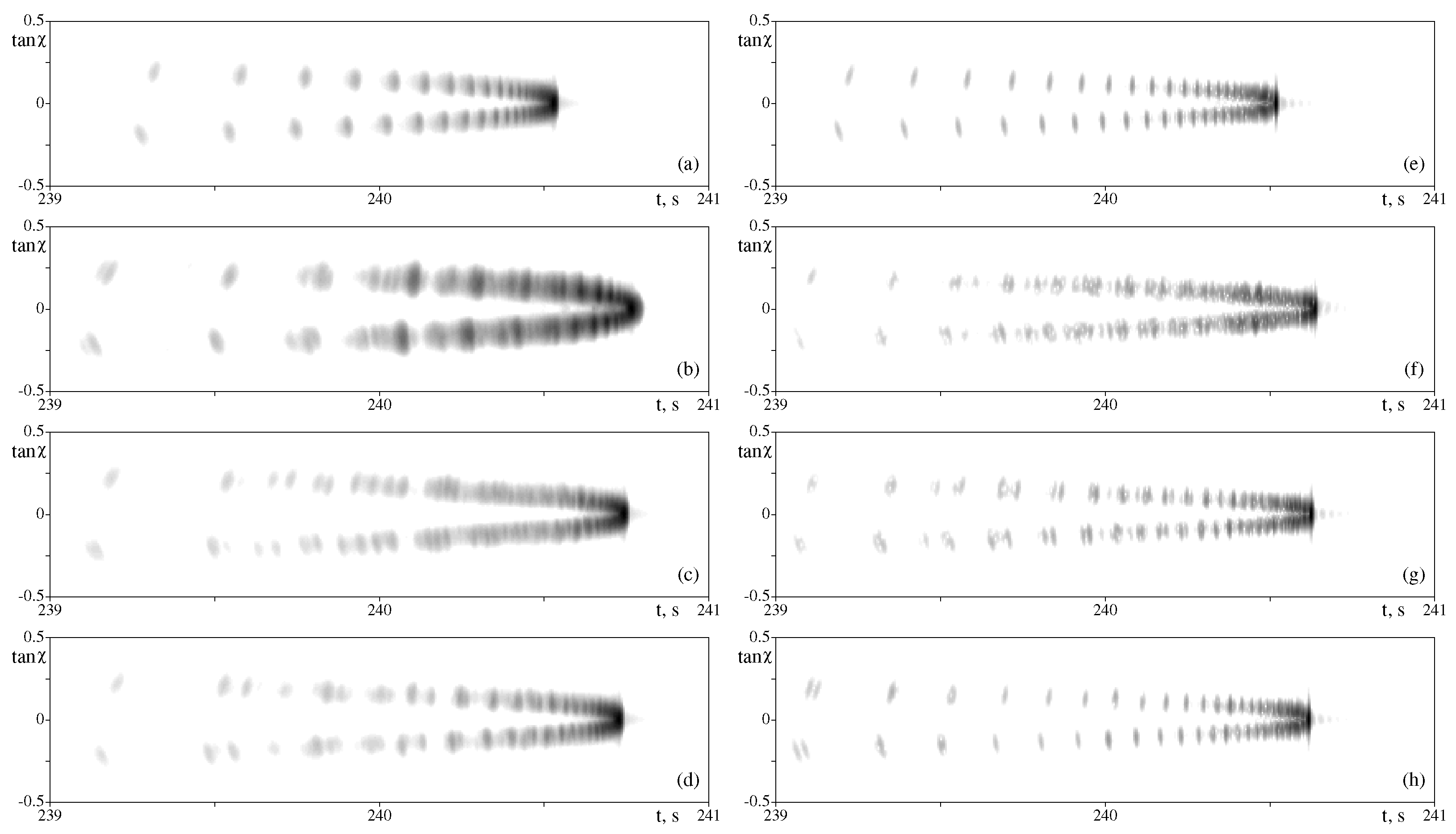
4. Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Makarov, D.; Prants, S.; Virovlyansky, A.; Zaslavsky, G. Ray and Wave Chaos in Ocean Acoustics: Chaos in Waveguides; Series on Complexity, Nonlinearity and Chaos; World Scientific: Singapore, 2010. [Google Scholar]
- Tappert, F.D.; Tang, X. Ray chaos and eigenrays. J. Acoust. Soc. Am. 1996, 99, 185–195. [Google Scholar] [CrossRef]
- Smirnov, I.P.; Virovlyansky, A.L.; Edelman, M.; Zaslavsky, G.M. Chaos-induced intensification of wave scattering. Phys. Rev. E 2005, 72, 026206. [Google Scholar] [CrossRef] [PubMed]
- Makarov, D.V.; Kon’kov, L.E.; Petrov, P.S. Influence of oceanic synoptic eddies on duration of modal acoustic pulses. Radiophys. Quantum Electron. 2016, 58, 1–15. [Google Scholar] [CrossRef]
- Virovlyansky, A.L.; Kazarova, A.Y.; Lyubavin, L.Y. Focusing of sound pulses using the time reversal technique on 100-km paths in a deep sea. Acoust. Phys. 2012, 58, 678–686. [Google Scholar] [CrossRef]
- Yao, H.; Wang, H.; Xu, Y.; Kurths, J. A recurrent plot based stochastic nonlinear ray propagation model for underwater signal propagation. New J. Phys. 2020, 22, 063025. [Google Scholar] [CrossRef]
- Makarov, D.V.; Komissarov, A.A. Modelling of sound propagation in the ocean using the matrix propagator. Proc. Meet. Acoust. 2020, 42, 055004. [Google Scholar] [CrossRef]
- Huang, J.; Diamant, R. Adaptive Modulation for Long-Range Underwater Acoustic Communication. IEEE Trans. Wirel. Commun. 2020, 19, 6844–6857. [Google Scholar] [CrossRef]
- Virovlyansky, A.L.; Kazarova, A.Y.; Kenigsberger, G.V.; Kolodiev, O.V.; Korotin, P.I.; Lyubavin, L.Y.; Moiseenkov, V.I.; Orlov, D.A.; Potapov, O.A.; Turchin, V.I. Experiment on estimating the coordinates of an emitter on the Black Sea shelf. Acoust. Phys. 2015, 61, 196–204. [Google Scholar] [CrossRef]
- Dubrovinskaya, E.; Kebkal, V.; Kebkal, O.; Kebkal, K.; Casari, P. Underwater Localization via Wideband Direction-of-Arrival Estimation Using Acoustic Arrays of Arbitrary Shape. Sensors 2020, 20, 3862. [Google Scholar] [CrossRef] [PubMed]
- Makarov, D. On measurement of acoustic pulse arrival angles using a vertical array. Acoust. Phys. 2017, 63, 673–680. [Google Scholar] [CrossRef]
- Makarov, D.V.; Kon’kov, L.E.; Uleysky, M.Y.; Petrov, P.S. Wave chaos in a randomly inhomogeneous waveguide: Spectral analysis of the finite-range evolution operator. Phys. Rev. E 2013, 87, 012911. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Virovlyanskii, A.L.; Okomel’kova, I.A. The ray approach to calculation of the local spectrum of a field in a waveguide smoothed over the angular and spatial scales. Radiophys. Quantum Electron. 1997, 40, 1039–1047. [Google Scholar] [CrossRef]
- Virovlyansky, A.L.; Zaslavsky, G.M. Evaluation of the smoothed interference pattern under conditions of ray chaos. Chaos Interdiscip. J. Nonlinear Sci. 2000, 10, 211–223. [Google Scholar] [CrossRef] [PubMed]
- Sundaram, B.; Zaslavsky, G.M. Wave analysis of ray chaos in underwater acoustics. Chaos 1999, 9, 483–492. [Google Scholar] [CrossRef] [PubMed]
- Smirnov, I.P.; Virovlyansky, A.L.; Zaslavsky, G.M. Wave chaos and mode–medium resonances at long-range sound propagation in the ocean. Chaos 2004, 14, 317–332. [Google Scholar] [CrossRef]
- Kon’kov, L.E.; Makarov, D.V.; Sosedko, E.V.; Uleysky, M.Y. Recovery of ordered periodic orbits with increasing wavelength for sound propagation in a range-dependent waveguide. Phys. Rev. E 2007, 76, 056212. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Makarov, D.V.; Kon’kov, L.E.; Uleysky, M.Y. Wave chaos in underwater acoustics. J. Sib. Fed. Univ. Math. Phys. 2010, 3, 336–348. [Google Scholar]
- Sugita, A.; Aiba, H. Second moment of the Husimi distribution as a measure of complexity of quantum states. Phys. Rev. E 2002, 65, 036205. [Google Scholar] [CrossRef] [Green Version]
- Arranz, F.J.; Seidel, L.; Giralda, C.G.; Benito, R.M.; Borondo, F. Onset of quantum chaos in molecular systems and the zeros of the Husimi function. Phys. Rev. E 2013, 87, 062901. [Google Scholar] [CrossRef] [Green Version]
- Oregi, I.; Arranz, F.J. Distribution of zeros of the Husimi function in systems with degeneracy. Phys. Rev. E 2014, 89, 022909. [Google Scholar] [CrossRef]
- Makarov, D.; Petrov, P. Full reconstruction of acoustic wavefields by means of pointwise measurements. Wave Motion 2022, 115, 103084. [Google Scholar] [CrossRef]
- Vadov, R.A. Point-source field in the underwater sound channel of the Sea of Japan. Acoust. Phys. 1998, 44, 516–523. [Google Scholar]
- Virovlyansky, A.L.; Kazarova, A.Y.; Lyubavin, L.Y. The possibility of using a vertical array for estimating the delays of sound pulses at multimegameter ranges. Acoust. Phys. 2008, 54, 486–494. [Google Scholar] [CrossRef]
- Virovlyansky, A.L.; Kazarova, A.Y.; Lyubavin, L.Y. Estimation of distortions in the sound field propagating through mesoscale inhomogeneities. Acoust. Phys. 2010, 56, 317–327. [Google Scholar] [CrossRef]
- Godin, O.; Zavorotny, V.; Voronovich, A.; Goncharov, V. Refraction of Sound in a Horizontally Inhomogeneous, Time-Dependent Ocean. IEEE J. Ocean. Eng. 2006, 31, 384–401. [Google Scholar] [CrossRef]
- Colosi, J.A.; Brown, M.G. Efficient numerical simulation of stochastic internal-wave-induced sound-speed perturbation fields. J. Acoust. Soc. Am. 1998, 103, 2232–2235. [Google Scholar] [CrossRef]
- Rostov, I.D.; Yurasov, G.I.; Rudykh, N.I.; Dmitrieva, E.V.; Rostov, V.I. Electronic oceanographic atlas of the Bering Sea and the Seas of Okhotsk and Japan. Oceanology 2004, 44, 439–444. [Google Scholar]
- Virovlyansky, A.L.; Makarov, D.V.; Prants, S.V. Ray and wave chaos in underwater acoustic waveguides. Phys.-Uspekhi 2012, 55, 18–46. [Google Scholar] [CrossRef]
- Makarov, D.V.; Kon’kov, L.E.; Uleysky, M.Y. The ray-wave correspondence and the suppression of chaos in long-range sound propagation in the ocean. Acoust. Phys. 2008, 54, 382–391. [Google Scholar] [CrossRef]
- Beron-Vera, F.J.; Brown, M.G.; Colosi, J.A.; Tomsovic, S.; Virovlyansky, A.L.; Wolfson, M.A.; Zaslavsky, G.M. Ray dynamics in a long-range acoustic propagation experiment. J. Acoust. Soc. Am. 2003, 114, 1226–1242. [Google Scholar] [CrossRef] [Green Version]
- Spindel, R.C.; Na, J.; Dahl, P.H.; Oh, S.; Eggen, C.; Kim, Y.G.; Akulichev, V.A.; Morgunov, Y.N. Acoustic tomography for monitoring the Sea of Japan: A pilot experiment. IEEE J. Ocean. Eng. 2003, 28, 297–302. [Google Scholar] [CrossRef]
- Bezotvetnykh, V.; Burenin, A.; Morgunov, Y.; Polovinka, Y. Experimental studies of pulsed signal propagation from the shelf to deep sea. Acoust. Phys. 2009, 55, 376–382. [Google Scholar] [CrossRef]
- Carey, W.M.; Evans, R.B. Ocean Ambient Noise: Measurement and Theory; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- McDonald, M.A.; Hildebrand, J.A.; Wiggins, S.M. Increases in deep ocean ambient noise in the Northeast Pacific west of San Nicolas Island, California. J. Acoust. Soc. Am. 2006, 120, 711–718. [Google Scholar] [CrossRef] [PubMed]
- D’Andrea, E.; Arena, M.; Viscardi, M.; Coppola, T. Bidimensional ray tracing model for the underwater noise propagation prediction. Fluids 2021, 6, 19. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Makarov, D.V.; Kon’kov, L.E. Angular Spectrum of Acoustic Pulses at Long Ranges. J. Mar. Sci. Eng. 2023, 11, 29. https://doi.org/10.3390/jmse11010029
Makarov DV, Kon’kov LE. Angular Spectrum of Acoustic Pulses at Long Ranges. Journal of Marine Science and Engineering. 2023; 11(1):29. https://doi.org/10.3390/jmse11010029
Chicago/Turabian StyleMakarov, Denis V., and Leonid E. Kon’kov. 2023. "Angular Spectrum of Acoustic Pulses at Long Ranges" Journal of Marine Science and Engineering 11, no. 1: 29. https://doi.org/10.3390/jmse11010029
APA StyleMakarov, D. V., & Kon’kov, L. E. (2023). Angular Spectrum of Acoustic Pulses at Long Ranges. Journal of Marine Science and Engineering, 11(1), 29. https://doi.org/10.3390/jmse11010029





