Persistency and Surface Convergence Evidenced by Two Maker Buoys in the Great Pacific Garbage Patch
Abstract
:1. Introduction
2. Materials and Methods
2.1. Characteristics of the Drifters and Trajectory Mapping
2.2. Post-Processing Steps
3. Results
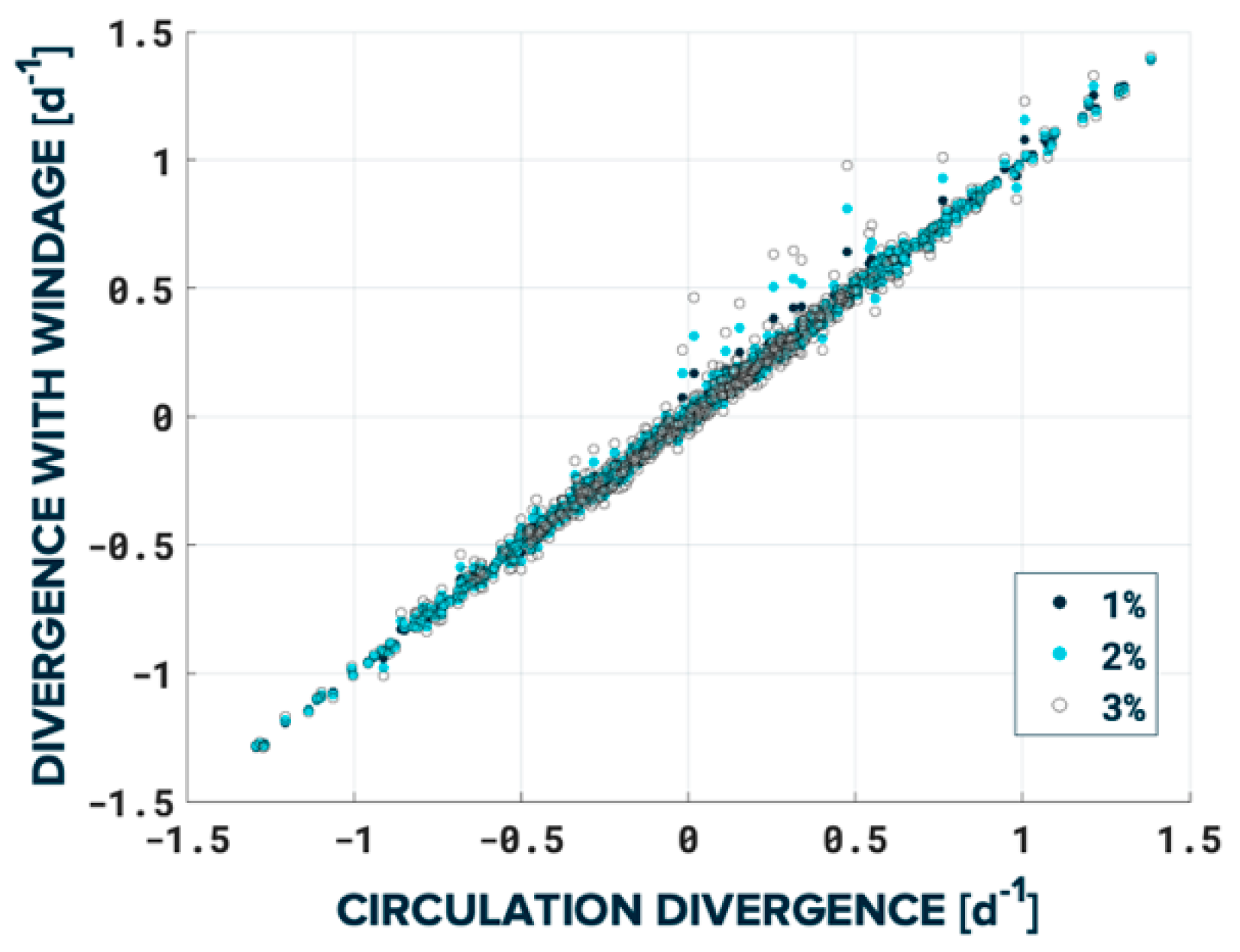
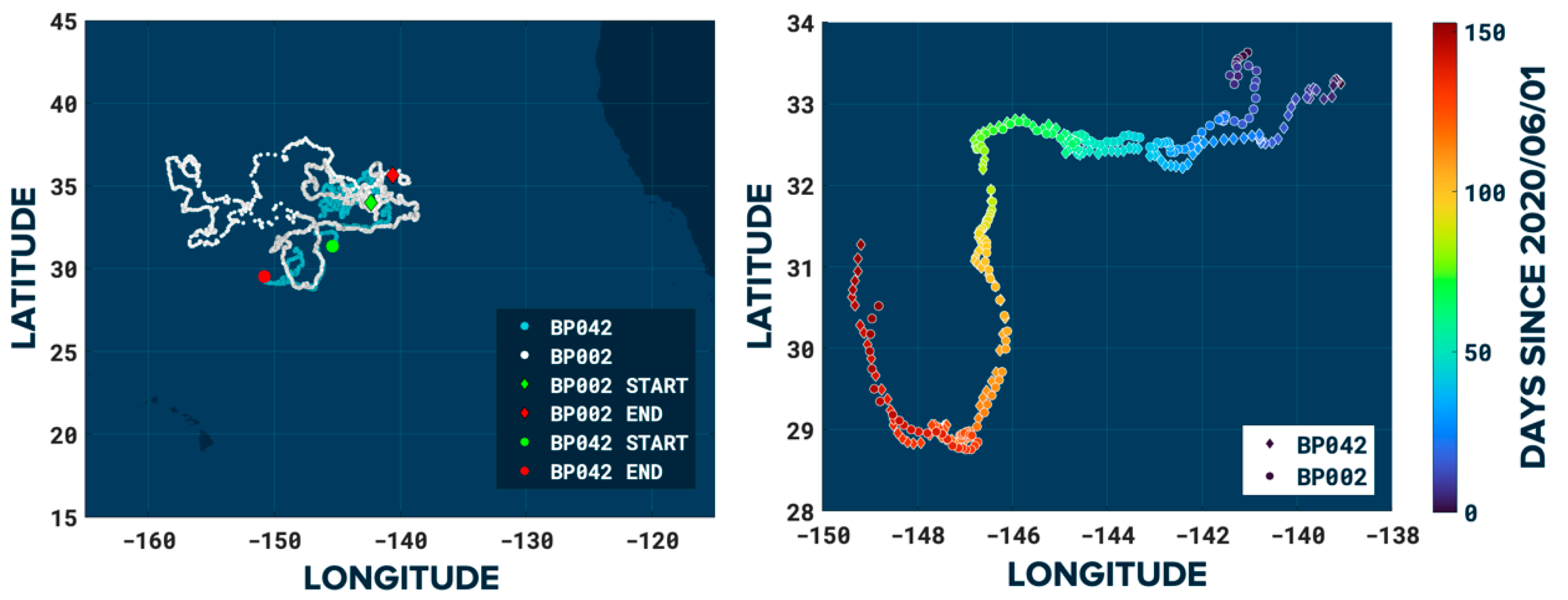
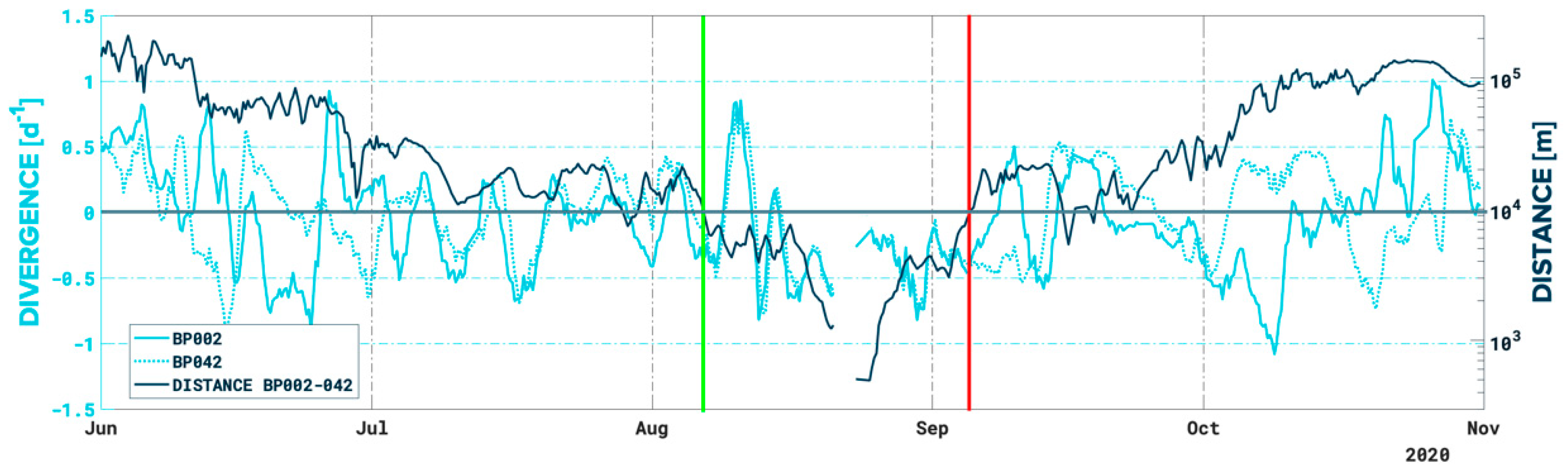
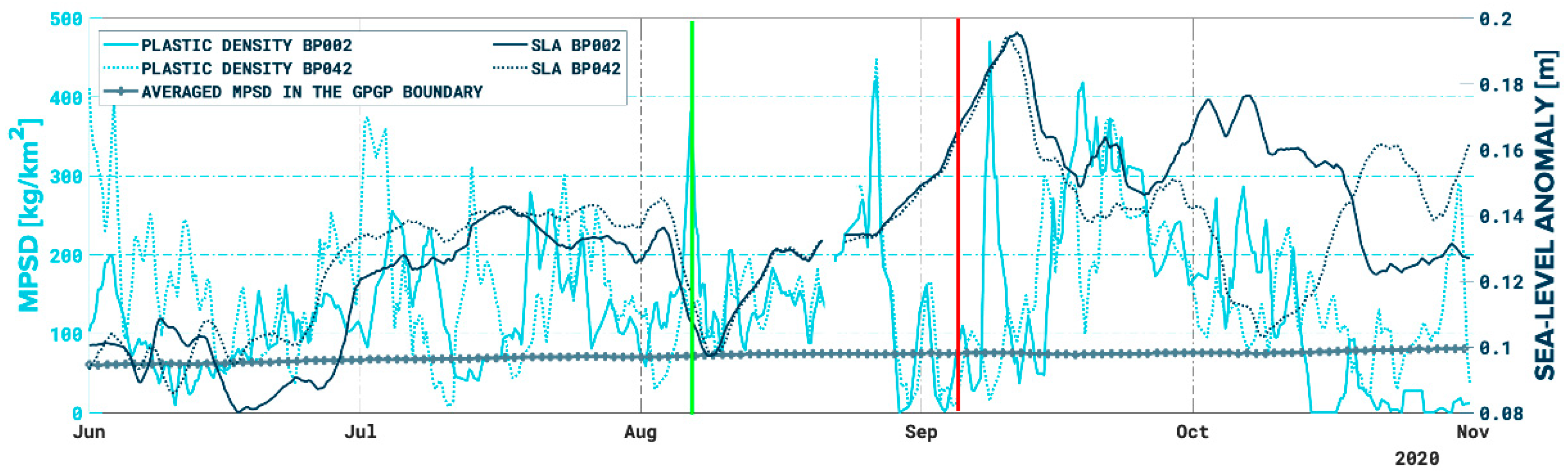
3.1. Convergent Event Analysis
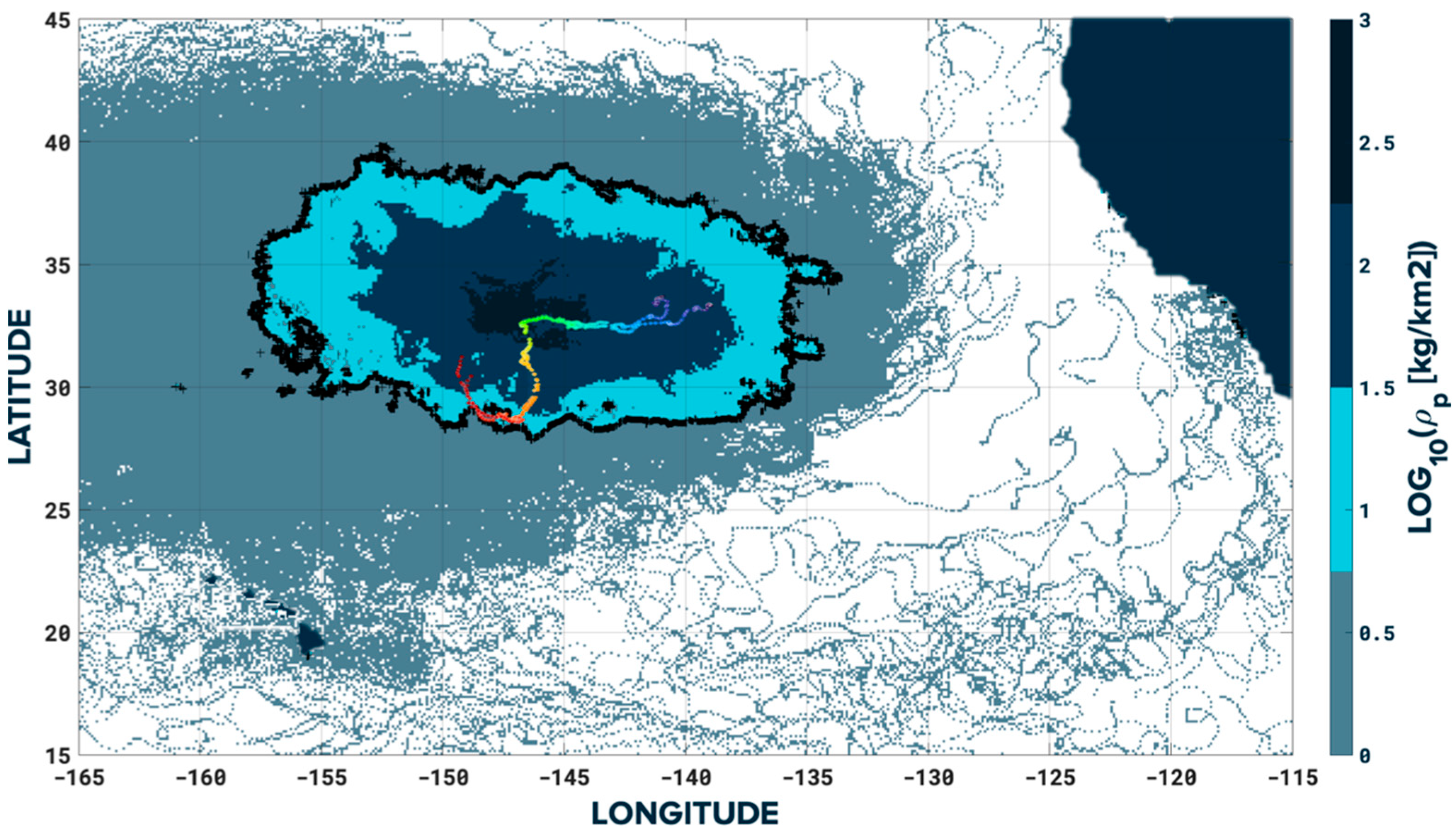
3.2. Persistency of BP002 in the GPGP
3.3. Comparison with SVP Undrogued Drifters
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- UNEP. From Pollution to Solution: A Global Assessment of Marine Litter and Plastic Pollution (Nairobi, 2021); UNEP: Nairobi, Kenya, 2021; ISBN 978-92-807-3881-0. [Google Scholar]
- Isobe, A.; Azuma, T.; Cordova, M.R.; Cózar, A.; Galgani, F.; Hagita, R.; Kanhai, L.D.; Imai, K.; Iwasaki, S.; Kako, S.; et al. A multilevel dataset of microplastic abundance in the world’s upper ocean and the Laurentian Great Lakes. Microplastics Nanoplastics 2021, 1, 16. [Google Scholar] [CrossRef]
- Meijer, L.J.J.; van Emmerik, T.; van der Ent, R.; Schmidt, C.; Lebreton, L. More than 1000 rivers account for 80% of global riverine plastic emissions into the ocean. Sci. Adv. 2021, 7, 1–14. [Google Scholar] [CrossRef] [PubMed]
- van der Mheen, M.; van Sebille, E.; Pattiaratchi, C. Beaching patterns of plastic debris along the Indian Ocean rim. Ocean Sci. Discuss. 2020, 16, 1317–1336. [Google Scholar] [CrossRef]
- Eriksen, M.; Lebreton, L.C.M.; Carson, H.S.; Thiel, M.; Moore, C.J.; Borerro, J.C.; Galgani, F.; Ryan, P.G.; Reisser, J. Plastic Pollution in the World’s Oceans: More than 5 Trillion Plastic Pieces Weighing over 250,000 Tons Afloat at Sea. PLoS ONE 2014, 9, e111913. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Available online: https://edition.cnn.com/travel/article/victor-vescovo-deepest-dive-pacific/index.html (accessed on 27 October 2022).
- Lacerda, A.L.D.F.; Rodrigues, L.D.S.; Van Sebille, E.; Rodrigues, F.L.; Ribeiro, L.; Secchi, E.R.; Kessler, F.; Proietti, M.C. Plastics in sea surface waters around the Antarctic Peninsula. Sci. Rep. 2019, 9, 3977. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Maximenko, N.; Corradi, P.; Law, K.L.; Van Sebille, E.; Garaba, S.P.; Lampitt, R.S.; Galgani, F.; Martinez-Vicente, V.; Goddijn-Murphy, L.; Veiga, J.M.; et al. Toward the Integrated Marine Debris Observing System. Front. Mar. Sci. 2019, 6, 447. [Google Scholar] [CrossRef] [Green Version]
- Jambeck, J.R.; Geyer, R.; Wilcox, C.; Siegler, T.R.; Perryman, M.; Andrady, A.; Narayan, R.; Law, K.L. Plastic waste inputs from land into the ocean. Science 2015, 347, 768–771. [Google Scholar] [CrossRef]
- Watson, R.A.; Cheung, W.W.; Anticamara, J.A.; Sumaila, R.U.; Zeller, D.; Pauly, D. Global marine yield halved as fishing intensity redoubles. Fish Fish. 2012, 14, 493–503. [Google Scholar] [CrossRef]
- van Sebille, E.; Aliani, S.; Law, K.L.; Maximenko, N.; Alsina, J.M.; Bagaev, A.; Bergmann, M.; Chapron, B.; Chubarenko, I.; Cózar, A.; et al. The physical oceanography of the transport of floating marine debris. Environ. Res. Lett. 2020, 15, 023003. [Google Scholar] [CrossRef] [Green Version]
- Available online: www.theoceancleanup.com (accessed on 27 October 2022).
- Lebreton, L.; Slat, B.; Ferrari, F.; Sainte-Rose, B.; Aitken, J.; Marthouse, R.; Hajbane, S.; Cunsolo, S.; Schwarz, A.; Levivier, A.; et al. Evidence that the Great Pacific Garbage Patch is rapidly accumulating plastic. Sci. Rep. 2018, 8, 4666. [Google Scholar] [CrossRef]
- Egger, M.; Nijhof, R.; Quiros, L.; Leone, G.; Royer, S.J.; McWhirter, A.C.; Kantakov, G.A.; Radchenko, V.I.; Pakhomov, E.A.; Hunt, B.P.; et al. A spatially variable scarcity of floating microplastics in the eastern North Pacific Ocean. Environ. Res. Lett. 2020, 15, 114056. [Google Scholar] [CrossRef]
- Reisser, J.; Slat, B.; Noble, K.; du Plessis, K.; Epp, M.; Proietti, M.; de Sonneville, J.; Becker, T.; Pattiaratchi, C. The vertical distribution of buoyant plastics at sea: An observational study in the North Atlantic Gyre. Biogeosciences 2015, 12, 1249–1256. [Google Scholar] [CrossRef] [Green Version]
- Egger, M.; Sulu-Gambari, F.; Lebreton, L. First evidence of plastic fallout from the North Pacific Garbage Patch. Sci. Rep. 2020, 10, 7495. [Google Scholar] [CrossRef] [PubMed]
- Sainte-Rose, B.; Wrenger, H.; Limburg, H.; Fourny, A.; Tjallema, A. Monitoring and performance evaluation of plastic cleanup systems (part I): Description of the experimental campaign. In Proceedings of the ASME 2020 39th International Conference on Ocean, Offshore and Arctic Engineering, Virtual, 3–7 August 2020; OMAE2020-18885; pp. 1–10. [Google Scholar] [CrossRef]
- Niiler, P.P.; Maximenko, N.A.; McWilliams, J.C. Dynamically balanced absolute sea level of the global ocean derived from near-surface velocity observations. Geophys. Res. Lett. 2003, 30, 3–6. [Google Scholar] [CrossRef] [Green Version]
- Lumpkin, R.; Centurioni, L.; Perez, R.C. Fulfilling observing system implementation requirements with the global drifter array. J. Atmos. Ocean. Technol. 2016, 33, 685–695. [Google Scholar] [CrossRef]
- Elipot, S.; Lumpkin, R.; Perez, R.C.; Lilly, J.M.; Early, J.J.; Sykulski, A.M. A global surface drifter data set at hourly resolution. J. Geophys. Res. Oceans 2016, 121, 2937–2966. [Google Scholar] [CrossRef]
- Mignac, D.; Tanajura, C.A.S.; Santana, A.N.; Lima, L.N.; Xie, J. Argo data assimilation into HYCOM with an EnOI method in the Atlantic Ocean. Ocean Sci. 2015, 11, 195–213. [Google Scholar] [CrossRef] [Green Version]
- Smit, P.; Houghton, I.; Jordanova, K.; Portwood, T.; Shapiro, E.; Clark, D.; Sosa, M.; Janssen, T. Assimilation of significant wave height from distributed ocean wave sensors. Ocean Model. 2021, 159, 101738. [Google Scholar] [CrossRef]
- Laxague, N.J.M.; Özgökmen, T.M.; Haus, B.K.; Novelli, G.; Shcherbina, A.; Sutherland, P.; Guigand, C.M.; Lund, B.; Mehta, S.; Alday, M.; et al. Observations of Near-Surface Current Shear Help Describe Oceanic Oil and Plastic Transport. Geophys. Res. Lett. 2018, 45, 245–249. [Google Scholar] [CrossRef]
- van Sebille, E.; Zettler, E.; Wienders, N.; Amaral-Zettler, L.; Elipot, S.; Lumpkin, R. Dispersion of Surface Drifters in the Tropical Atlantic. Front. Mar. Sci. 2021, 7, 607426. [Google Scholar] [CrossRef]
- Lumpkin, R.; Özgökmen, T.; Centurioni, L. Advances in the Application of Surface Drifters. Annu. Rev. Mar. Sci. 2017, 9, 59–81. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Van Sebille, E.; England, M.H.; Froyland, G. Origin, dynamics and evolution of ocean garbage patches from observed surface drifters. Environ. Res. Lett. 2012, 7, 044040. [Google Scholar] [CrossRef]
- Maximenko, N.; Hafner, J.; Niiler, P. Pathways of marine debris derived from trajectories of Lagrangian drifters. Mar. Pollut. Bull. 2012, 65, 51–62. [Google Scholar] [CrossRef] [PubMed]
- Dobler, D.; Maes, C.; Martinez, E.; Rahmania, R.; Gautama, B.G. On the Fate of Floating Marine Debris Carried to the Sea through the Main Rivers of Indonesia. J. Mar. Sci. Eng. 2022, 10, 1009. [Google Scholar] [CrossRef]
- Sainte-Rose, B.; Wrenger, H.; Soares, I.; Mosneron-Dupin, C.; Duval, C.; Planchat, A. Monitoring and performance evaluation of plastic cleanup systems (part II): Results and analysis. In Proceedings of the ASME 2020 39th International Conference on Ocean, Offshore and Arctic Engineering, Virtual, 3–7 August 2020; OMAE-18891; pp. 1–7. [Google Scholar] [CrossRef]
- Available online:. Available online: https://github.com/wjpavalko/Maker-Buoy (accessed on 10 November 2022).
- Carlson, D.F.; Pavalko, W.J.; Petersen, D.; Olsen, M.; Hass, A.E. Maker Buoy variants for water level monitoring and tracking drifting objects in remote areas of Greenland. Sensors 2020, 20, 1254. [Google Scholar] [CrossRef] [Green Version]
- Chassignet, E.P.; Hurlburt, H.E.; Metzger, E.J.; Smedstad, O.M.; Cummings, J.A.; Halliwell, G.R.; Bleck, R.; Baraille, R.; Wallcraft, A.J.; Lozano, C.; et al. US GODAE: Global Ocean Prediction with the HYbrid Coordinate Ocean Model (HYCOM). Oceanography 2009, 22, 64–75. [Google Scholar] [CrossRef] [Green Version]
- Available online:. Available online: https://www.hycom.org/dataserver/gofs-3pt1/analysis (accessed on 10 August 2022).
- Klink, D.; Peytavin, A.; Lebreton, L. Size Dependent Transport of Floating Plastics Modeled in the Global Ocean. Front. Mar. Sci. 2022, 9, 903134. [Google Scholar] [CrossRef]
- Lebreton, L.C.M.; Greer, S.D.; Borrero, J.C. Numerical modelling of floating debris in the world’s oceans. Mar. Pollut. Bull. 2012, 64, 653–661. [Google Scholar] [CrossRef]
- Available online:. Available online: https://www.hycom.org/dataserver/gofs-3pt1/reanalysis (accessed on 10 August 2022).
- Available online:. Available online: https://cds.climate.copernicus.eu/cdsapp#!/dataset/10.24381/cds.4c328c78?tab=overview (accessed on 10 November 2022).
- Lumpkin, R.; Pazos, M. Measuring surface currents with Surface Velocity Program drifters: The instrument, its data, and some recent results. In Lagrangian Analysis and Prediction of Coastal and Ocean Dynamics; Cambridge Core: Cambridge, UK, 2009; pp. 39–67. [Google Scholar]
- van Sebille, E.; Waterman, S.; Barthel, A.; Lumpkin, R.; Keating, S.R.; Fogwill, C.; Turney, C. Pairwise surface drifter separation in the western Pacific sector of the Southern Ocean. J. Geophys. Res. Oceans 2015, 120, 6769–6781. [Google Scholar] [CrossRef] [Green Version]
- McWilliams, J.C. Submesoscale currents in the ocean. Proc. R. Soc. A Math. Phys. Eng. Sci. 2016, 472, 20160117. [Google Scholar] [CrossRef] [Green Version]
- Thorpe, S.A. Langmuir circulation. Annu. Rev. Fluid Mech. 2004, 36, 55–79. [Google Scholar] [CrossRef]
- Serra, M.; Sathe, P.; Rypina, I.; Kirincich, A.; Ross, S.D.; Lermusiaux, P.; Allen, A.; Peacock, T.; Haller, G. Search and rescue at sea aided by hidden flow structures. Nat. Commun. 2020, 11, 2525. [Google Scholar] [CrossRef] [PubMed]
- Lebreton, L.; Royer, S.-J.; Peytavin, A.; Strietman, W.J.; Smeding-Zuurendonk, I.; Egger, M. Industrialised fishing nations largely contribute to floating plastic pollution in the North Pacific subtropical gyre. Sci. Rep. 2022, 12, 12666. [Google Scholar] [CrossRef] [PubMed]
- Maes, C.; Blanke, B.; Martinez, E. Origin and fate of surface drift in the oceanic convergence zones of the eastern Pacific. Geophys. Res. Lett. 2016, 43, 3398–3405. [Google Scholar] [CrossRef] [Green Version]
- Lebreton, L.; Andrady, A. Future scenarios of global plastic waste generation and disposal. Palgrave Commun. 2019, 5, 6. [Google Scholar] [CrossRef] [Green Version]
- Global Modeling and Assimilation Office (GMAO). inst3_3d_asm_Cp: MERRA-2 3D IAU State, Meteorology Instantaneous 3-Hourly (p-coord, 0.625x0.5L42), Version 5.12.4; Goddard Space Flight Center Distributed Active Archive Center (GSFC DAAC): Greenbelt, MD, USA, 2015. [Google Scholar] [CrossRef]
- Tamura, H.; Miyazawa, Y.; Oey, L.-Y. The Stokes drift and wave induced-mass flux in the North Pacific. J. Geophys. Res. Earth Surf. 2012, 117, C08021. [Google Scholar] [CrossRef]




| Dimension | Value (cm) |
|---|---|
| Topside height | 10 |
| Topside length | 20 |
| Topside width | 17 |
| Ballast tube height | 35 |
| Ballast tube diameter | 3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sainte-Rose, B.; Pham, Y.; Pavalko, W. Persistency and Surface Convergence Evidenced by Two Maker Buoys in the Great Pacific Garbage Patch. J. Mar. Sci. Eng. 2023, 11, 68. https://doi.org/10.3390/jmse11010068
Sainte-Rose B, Pham Y, Pavalko W. Persistency and Surface Convergence Evidenced by Two Maker Buoys in the Great Pacific Garbage Patch. Journal of Marine Science and Engineering. 2023; 11(1):68. https://doi.org/10.3390/jmse11010068
Chicago/Turabian StyleSainte-Rose, Bruno, Yannick Pham, and Wayne Pavalko. 2023. "Persistency and Surface Convergence Evidenced by Two Maker Buoys in the Great Pacific Garbage Patch" Journal of Marine Science and Engineering 11, no. 1: 68. https://doi.org/10.3390/jmse11010068
APA StyleSainte-Rose, B., Pham, Y., & Pavalko, W. (2023). Persistency and Surface Convergence Evidenced by Two Maker Buoys in the Great Pacific Garbage Patch. Journal of Marine Science and Engineering, 11(1), 68. https://doi.org/10.3390/jmse11010068







