Assessment of Ship Hull Ultimate Strength under Fire Conditions: The Fire Smith Method Approach
Abstract
:1. Introduction
2. Materials and Methods
2.1. Uniform Compression Thin Plate Model with Four Simply Supported Sides
2.2. Non-Uniform Compression Thin Plate Model with Three Simply Supported Sides and One Free Side
2.3. Uniform Compression Beam Model with Two Simply Supported Sides and Two Free Sides
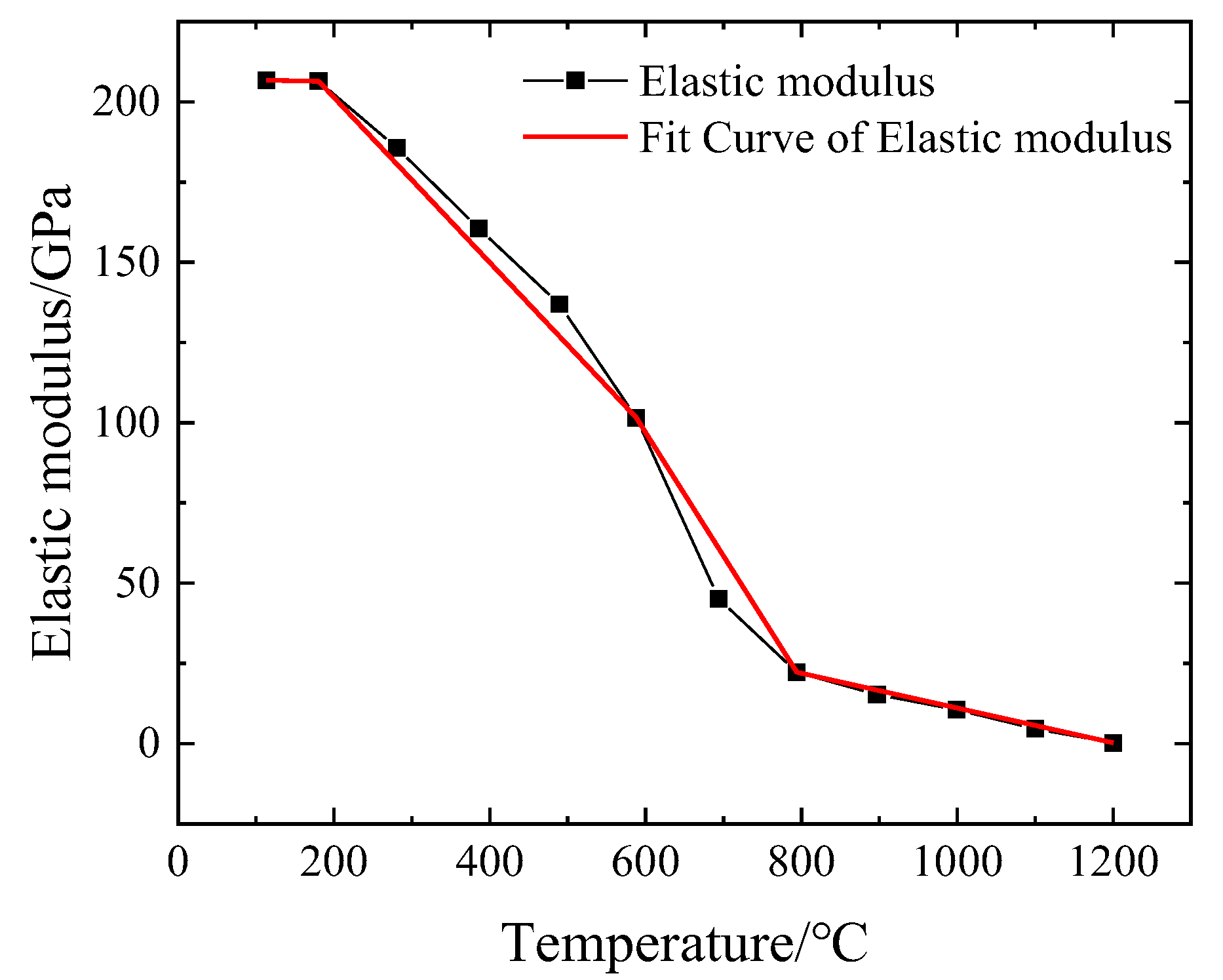
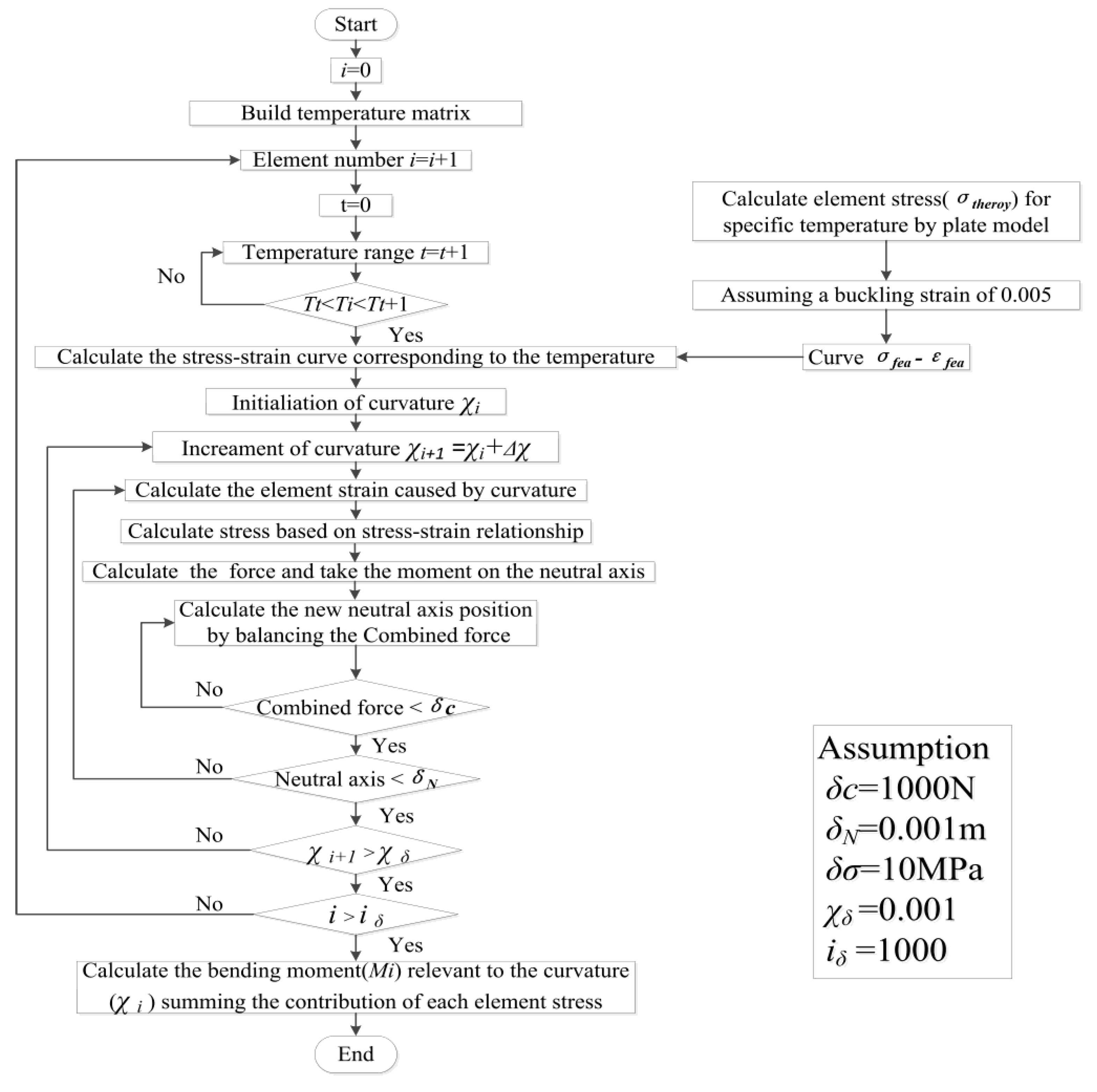
2.4. Ultimate Strength of Uniform and Non-Uniform Compression Plate Models under High-Temperature Conditions
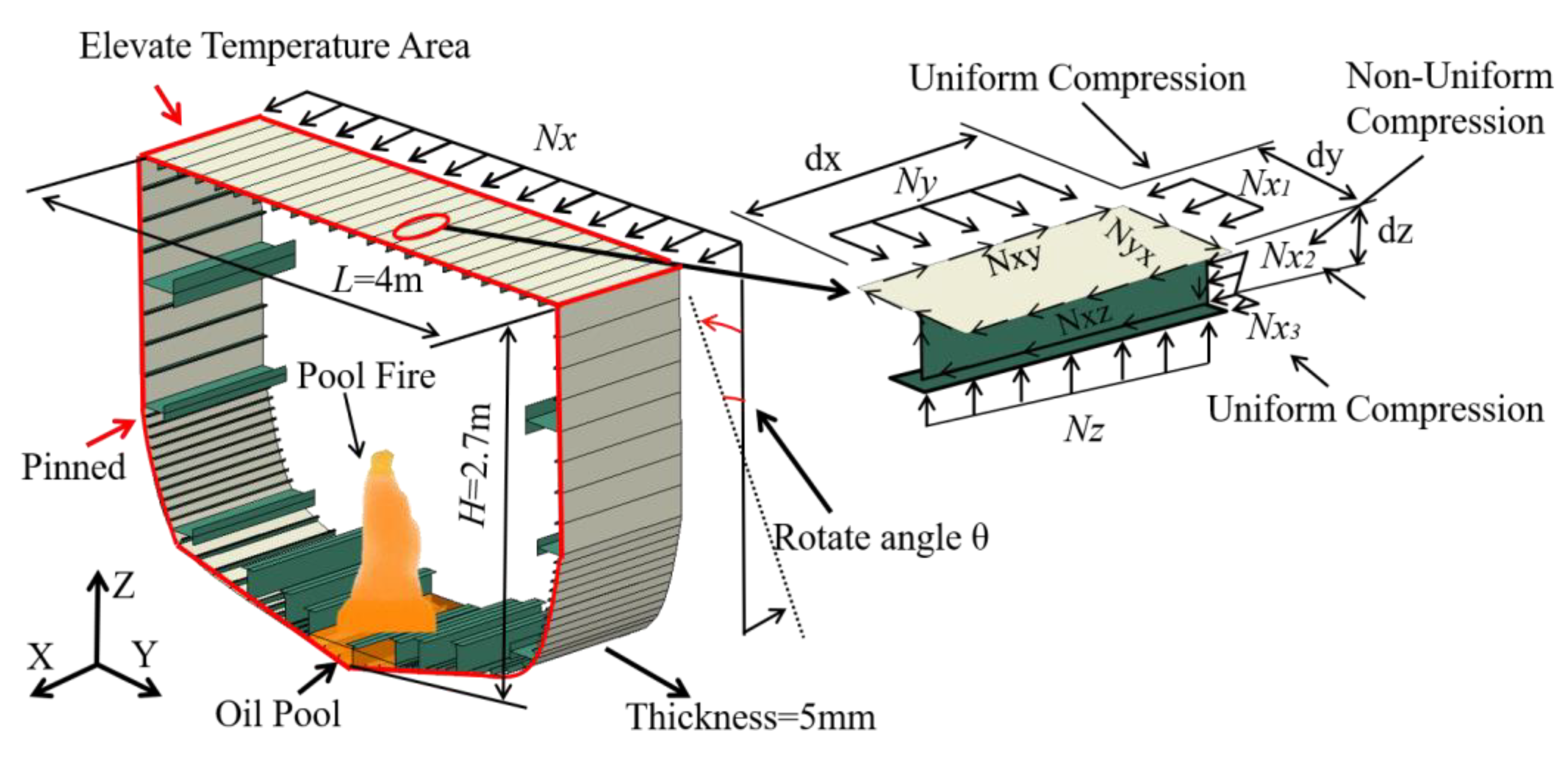
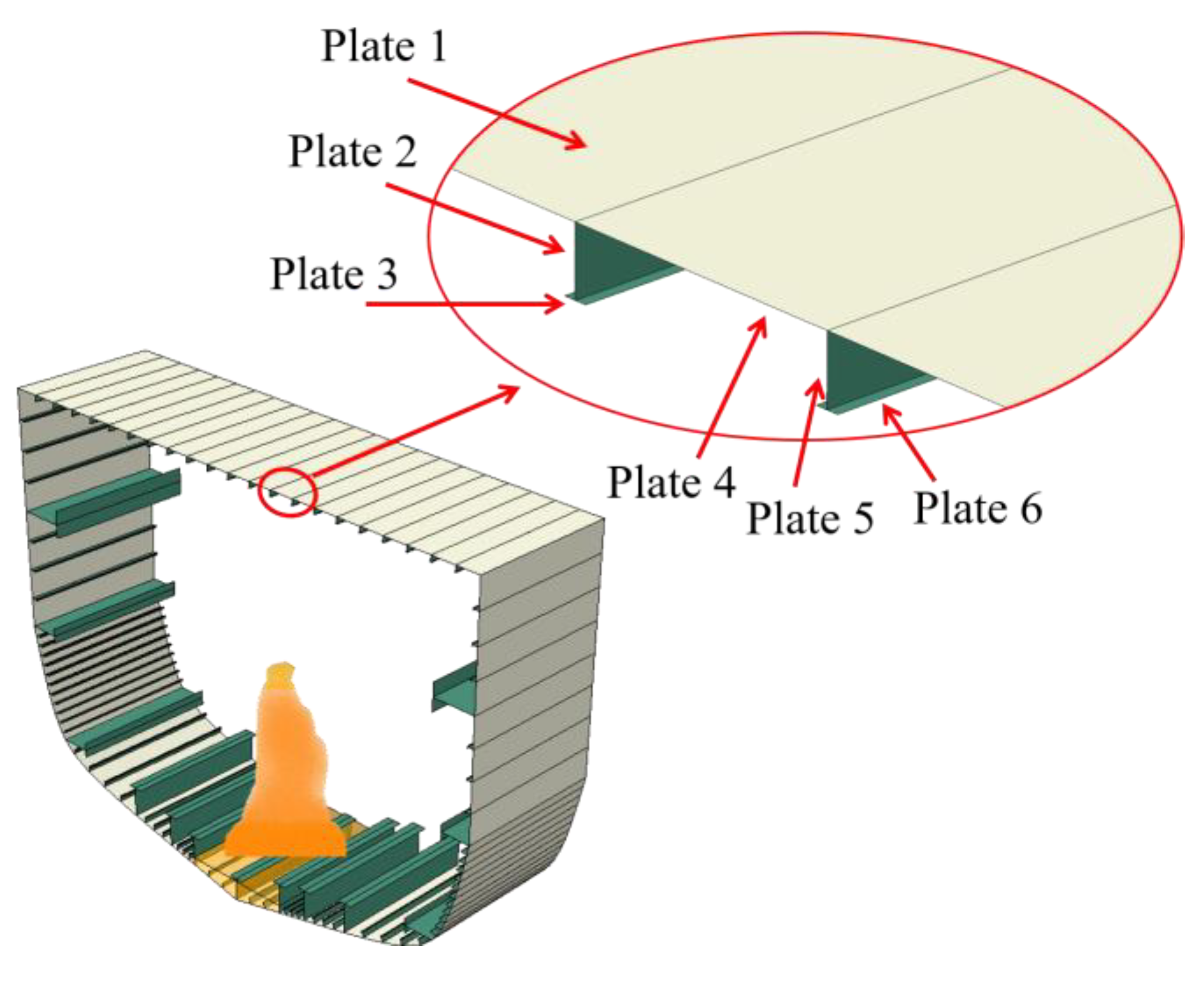
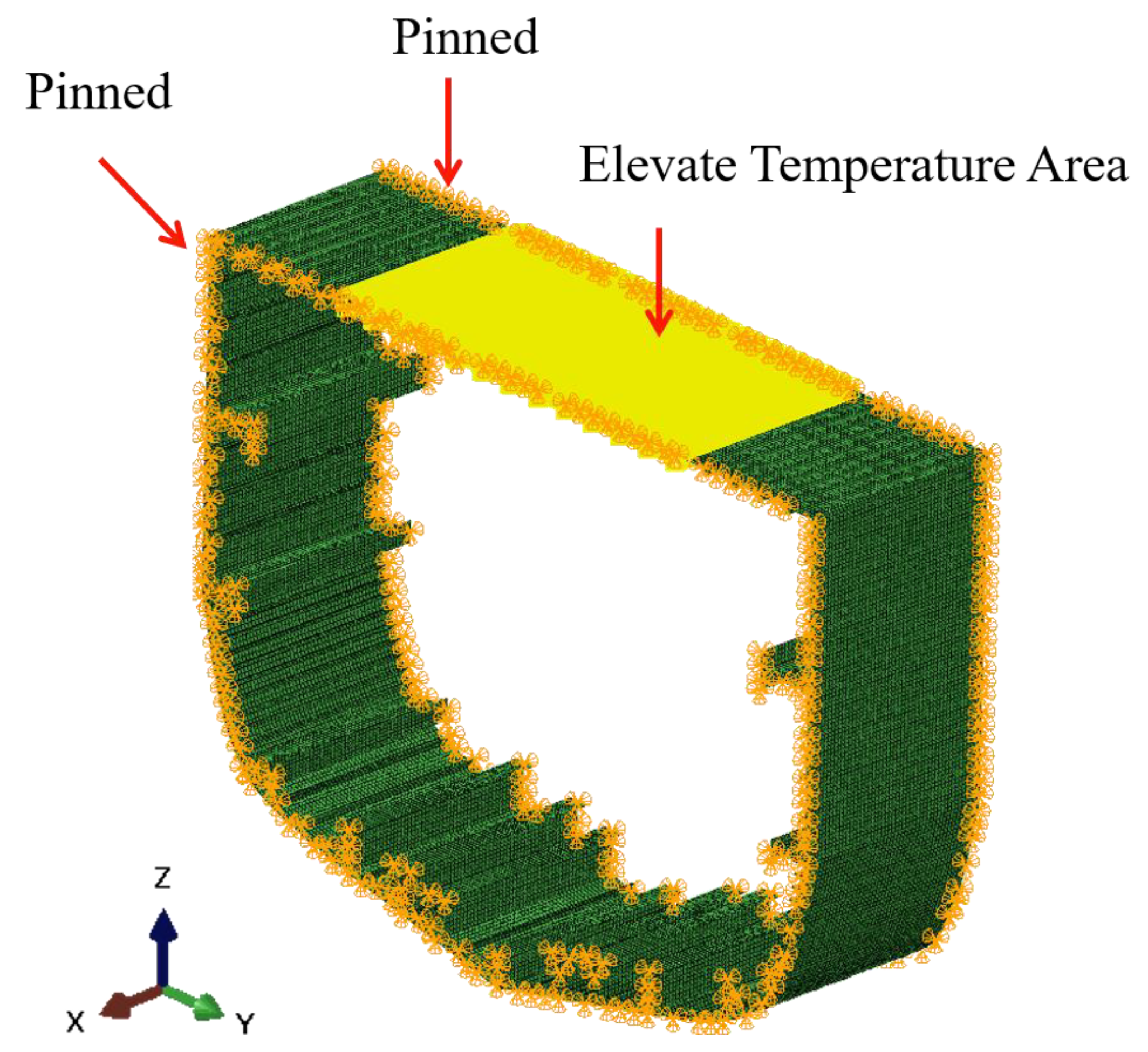
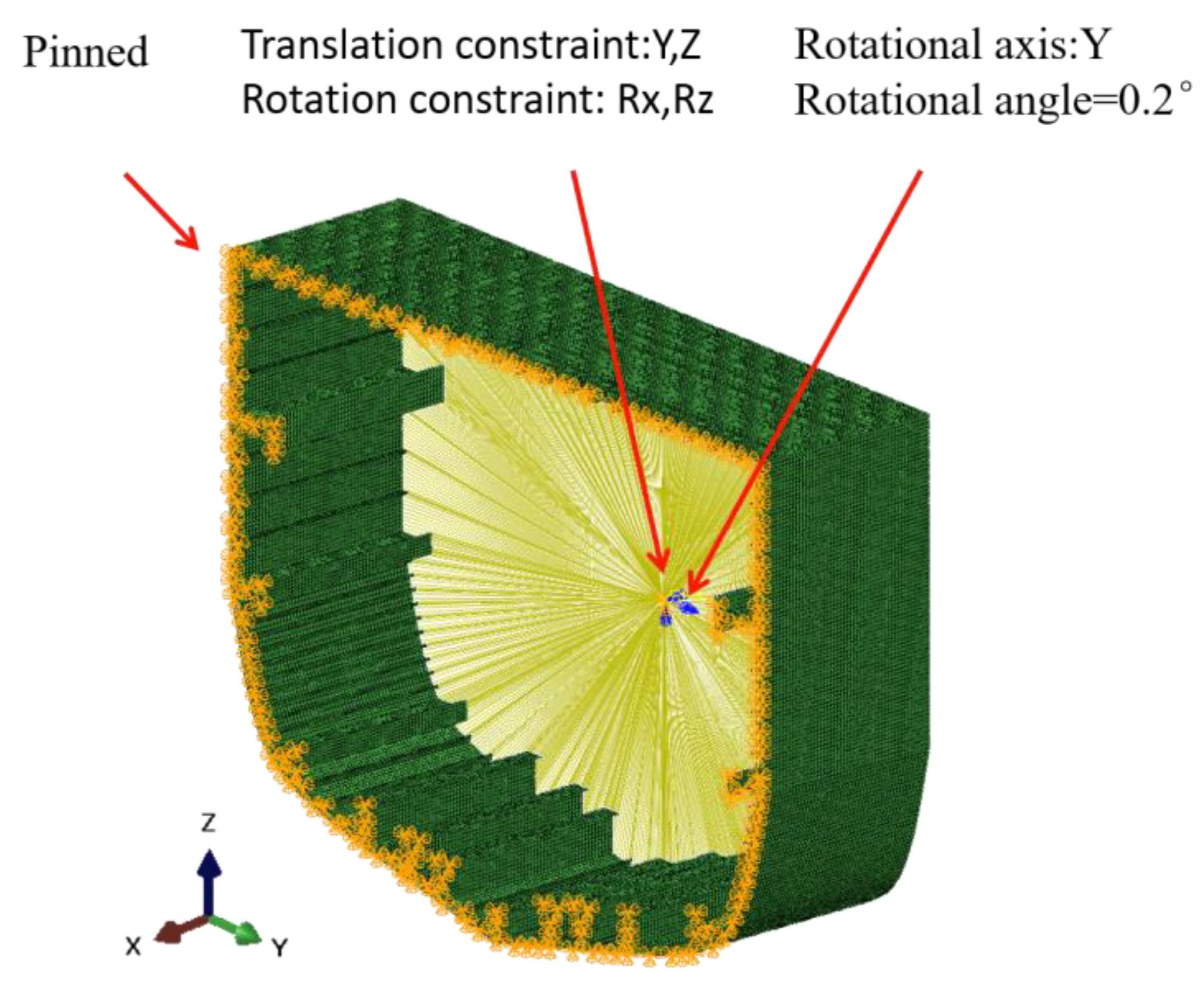
3. Simulation Setup
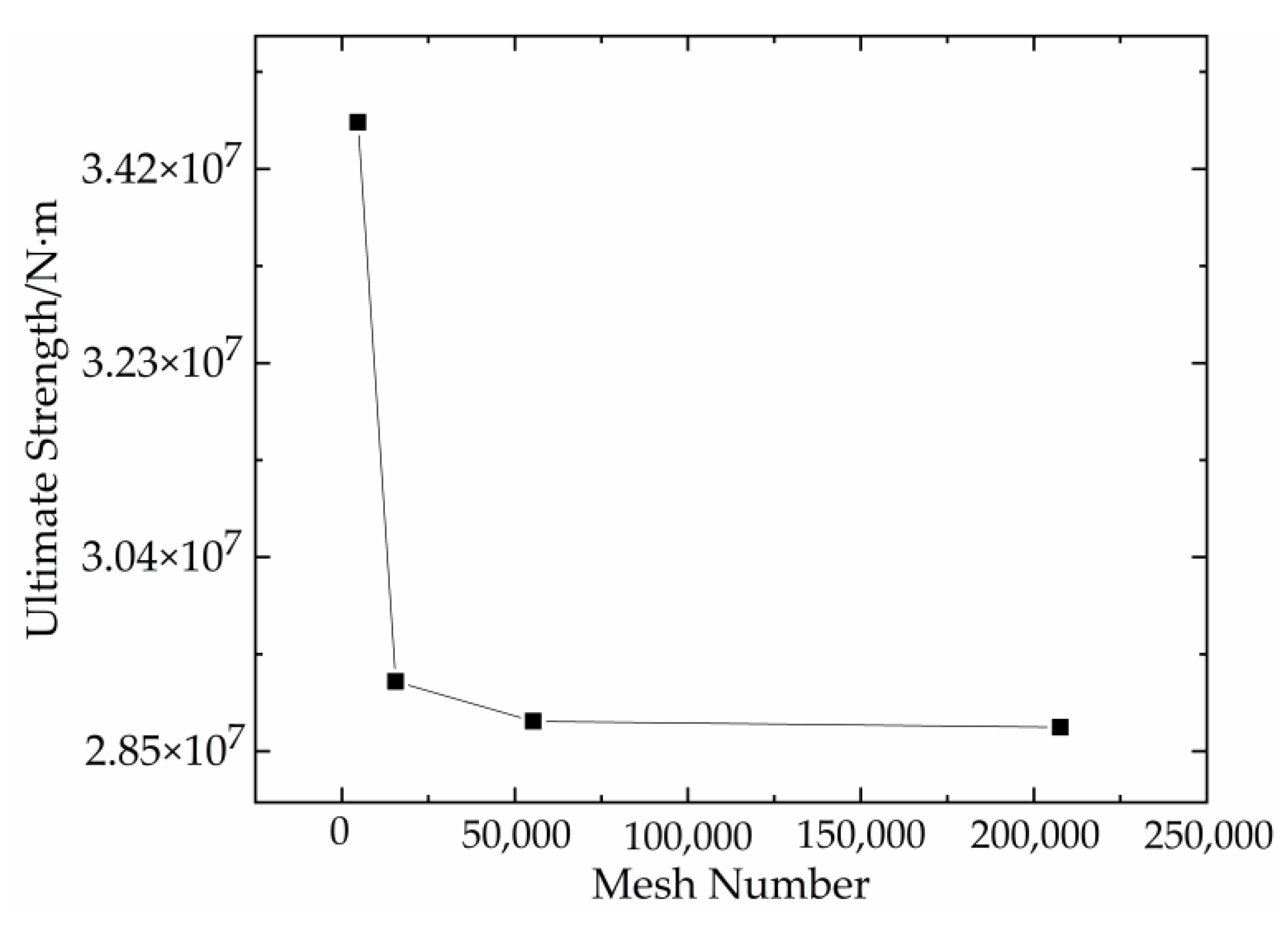
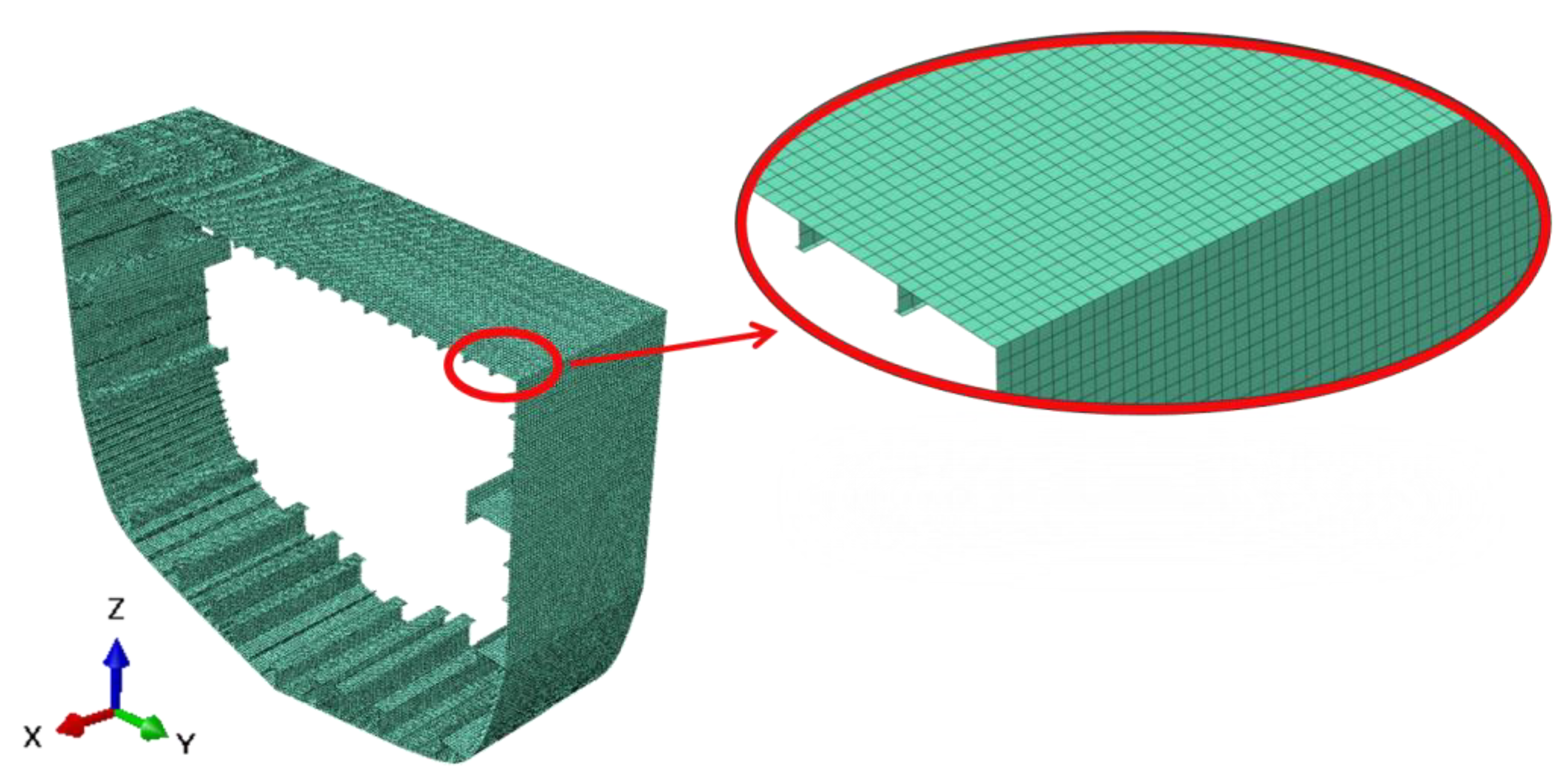
4. Mesh Sensitivity Analysis
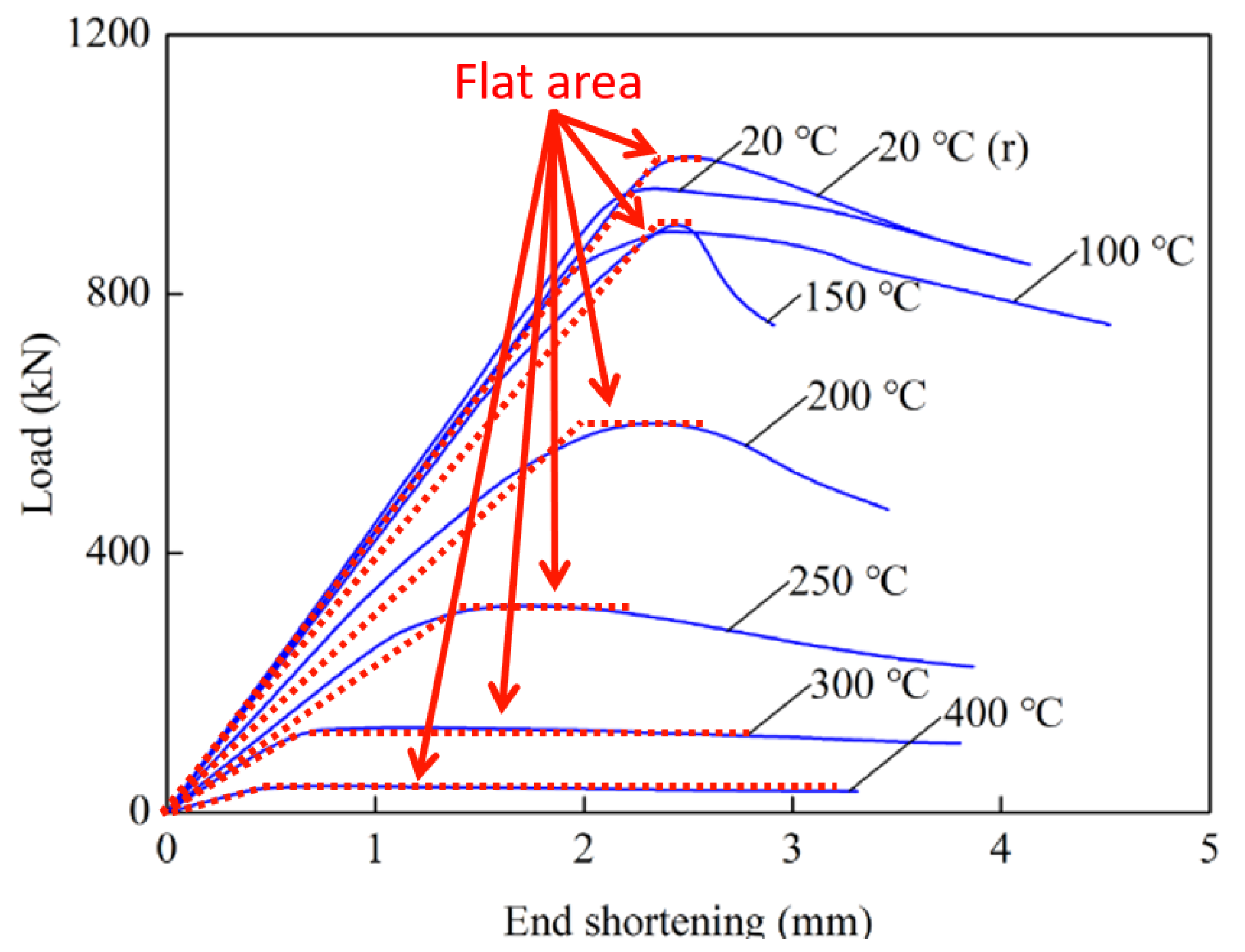
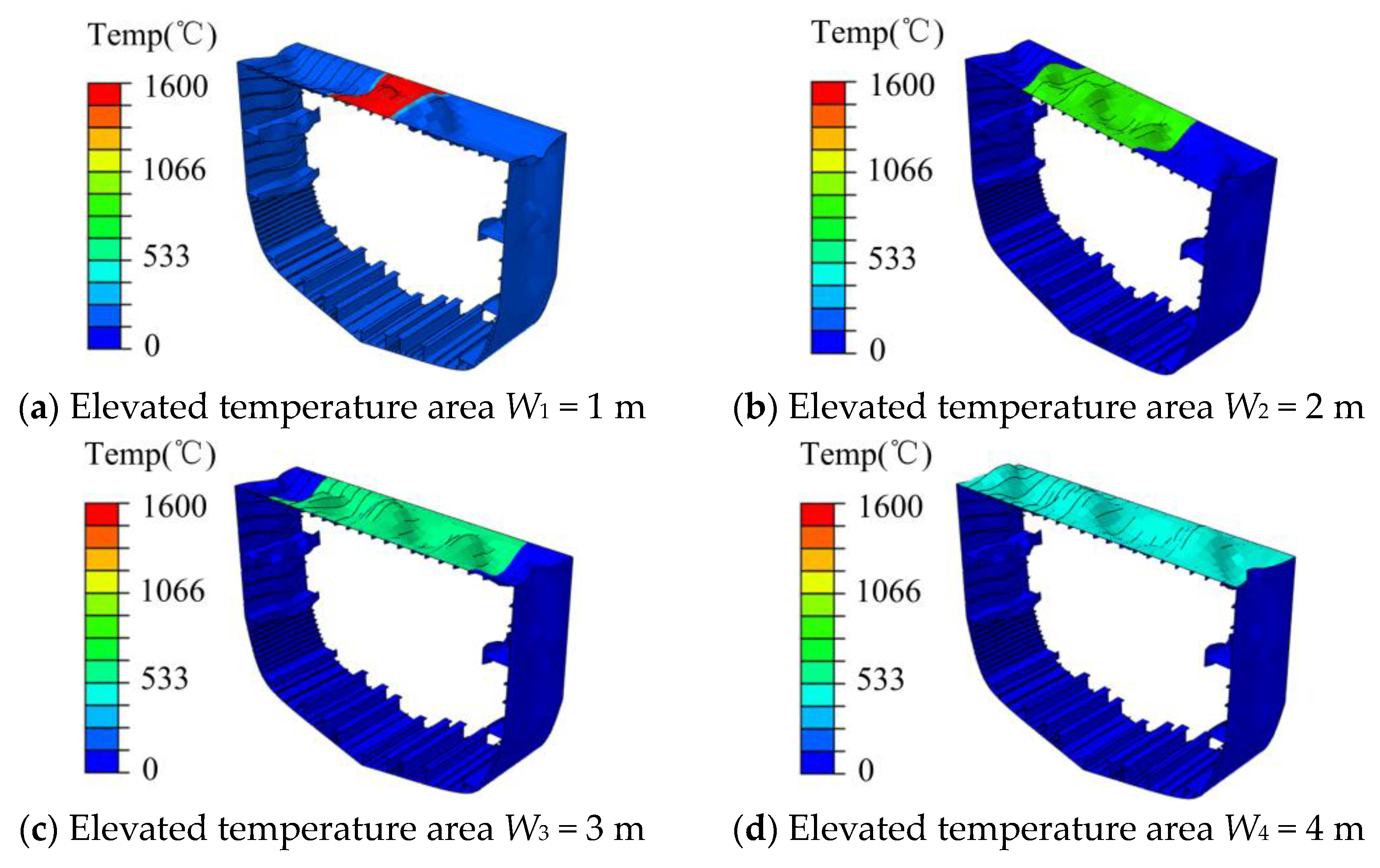
5. Results
6. Discussion
7. Conclusions
- (1)
- In order to quickly evaluate the ultimate strength of ship buckling under fire conditions, a method was proposed based on the Smith method and the plate model. Because there may be a phenomenon that the hull gradually changes from elastic buckling to plasticity, in order to avoid overestimating the ultimate strength of the hull under fire conditions, the elastic buckling equation is used to estimate the ultimate strength value. Although there is a 10% error, it can to some extent avoid overestimating the ultimate strength of the hull before the elastic transition to plasticity, making it safer to evaluate the ultimate strength of the hull in engineering.
- (2)
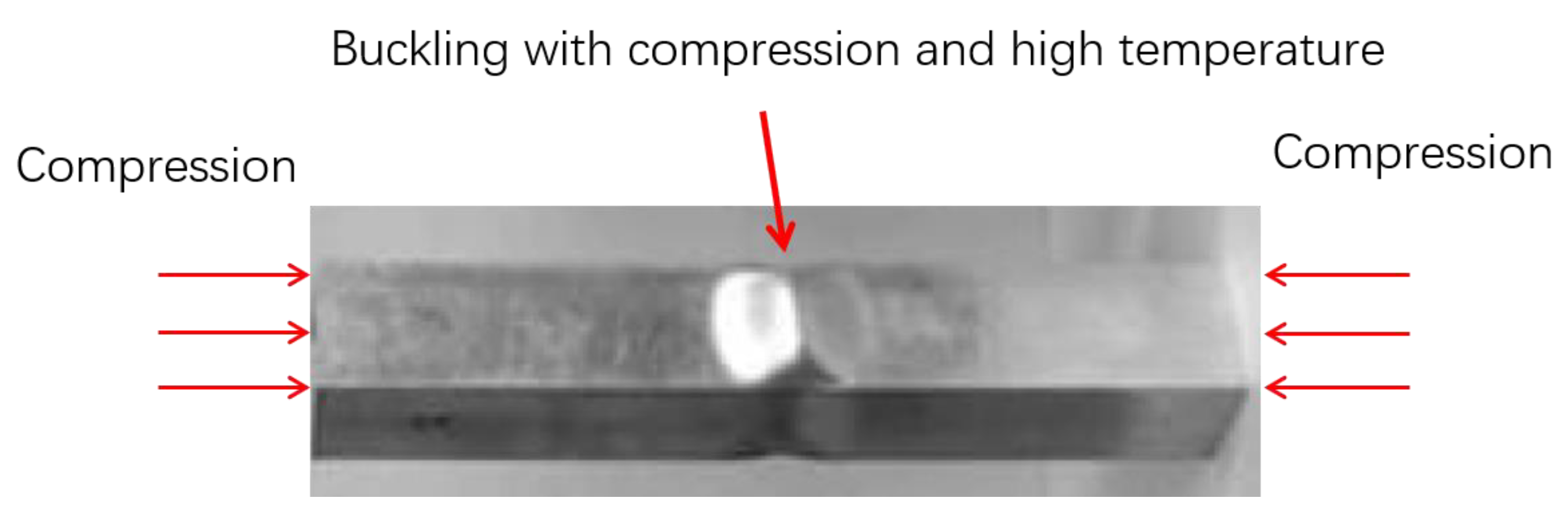
- Based on the principle of oxygen consumption, 64 simulations were carried out to study the ultimate strength of different high-temperature regions, and it was found that the high-temperature regions showed a “wavy” failure mode.
- (3)
- According to the simulation results, the ultimate strength characteristics of different high-temperature regions were obtained. The smaller the high-temperature region, the less oxygen required for the ultimate strength to begin to decrease. At the same time, the ultimate strength remains basically unchanged after the temperature reaches the threshold. The larger the high-temperature area, the more oxygen is required for the ultimate strength to decrease, but as the oxygen consumption coefficient increases, the ultimate strength increases.
- (4)
- Comparing the fire Smith method with the simulation results, we found that the trend was consistent, so the proposed method can be used as an alternative approach for evaluating the ultimate strength of a fire hull.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| D | stiffness coefficient of the plate |
| T | thickness, mm |
| L | ship width, m |
| Nx | buckling load along the x axes, N |
| Nxy | shear force per unit, N |
| m | half wave numbers in the x axes |
| Amn | undetermined constant |
| Nx,cr,min | smallest buckling load along the x axes, N |
| σx,cr,min | smallest buckling stress along the x axes, MPa |
| W1,2,3,4 | elevate temperature area, m |
| Tt | temperature range |
| Δχ | curvature increment |
| δN | tolerance of neutral axes |
| iδ | tolerance of element number |
| E | elastic modulus, GPa |
| μ | Poisson’s ratio |
| H | ship height, m |
| Ny | buckling load along the y axes, N |
| ω | buckling condition |
| n | half wave numbers in the y axes |
| k | buckling coefficient |
| ET | elasticity modulus function of temperature, GPa |
| T | temperature, °C |
| i | element number |
| χ | curvature |
| δc | tolerance of combined load |
| χδ | tolerance of curvature increment |
| Mi | bending moment/m |
References
- Roberts, S.E.; Pettit, S.J.; Marlow, P.B. Casualties and Loss of Life in Bulk Carriers from 1980 to 2010. Mar. Policy 2013, 42, 223–235. [Google Scholar] [CrossRef]
- Smith, S.C. Influence of Local Compressive Failure on Ultimate Longitudinal Strength of a Ship’s, Hull. In Proceedings of the International Symposium on Practical Design in Shipbuilding (PRADS), Tokyo, Japan, 17–21 October 1977; pp. 73–79. [Google Scholar]
- Rahman, M.K.; Chowdhury, M. Estimation of Ultimate Longitudinal Bending Moment of Ships and Box Girders. J. Ship Res. 1996, 40, 244–257. [Google Scholar] [CrossRef]
- Akpan, U.O.; Koko, T.S.; Ayyub, B.; Dunbar, T.E. Risk Assessment of Aging Ship Hull Structures in the Presence of Corrosion and Fatigue. Mar. Struct. 2002, 15, 211–231. [Google Scholar] [CrossRef]
- Ozguc, O.; Das, P.K.; Barltrop, N. A Comparative Study on the Structural Integrity of Single and Double Side Skin Bulk Carriers under Collision Damage. Mar. Struct. 2005, 18, 511–547. [Google Scholar] [CrossRef]
- Paik, J.K.; Satish Kumar, Y.V.; Lee, J.M. Ultimate Strength of Cracked Plate Elements under Axial Compression or Tension. Thin-Walled Struct. 2005, 43, 237–272. [Google Scholar] [CrossRef]
- Dexter, R.; Mahmoud, H. Predicting Stable Fatigue Crack Propagation in Stiffened Panels; National Aeronautics and Space Administration: Washington, DC, USA, 2004.
- Campanile, A.; Piscopo, V.; Scamardella, A. Comparative Analysis among Deterministic and Stochastic Collision Damage Models for Oil Tanker and Bulk Carrier Reliability. Int. J. Nav. Archit. Ocean Eng. 2018, 10, 21–36. [Google Scholar] [CrossRef]
- Campanile, A.; Piscopo, V.; Scamardella, A. Conditional Reliability of Bulk Carriers Damaged by Ship Collisions. Mar. Struct. 2018, 58, 321–341. [Google Scholar] [CrossRef]
- Amlashi, H.K.K.; Moan, T. Ultimate Strength Analysis of a Bulk Carrier Hull Girder under Alternate Hold Loading Condition—A Case Study. Mar. Struct. 2008, 21, 327–352. [Google Scholar] [CrossRef]
- Tanaka, Y.; Ogawa, H.; Tatsumi, A.; Fujikubo, M. Analysis Method of Ultimate Hull Girder Strength under Combined Loads. Ships Offshore Struct. 2015, 10, 587–598. [Google Scholar] [CrossRef]
- Kim, J.-H.; Kim, Y.; Kim, H.-S.; Jeong, S.-Y. Numerical Simulation of Ice Impacts on Ship Hulls in Broken Ice Fields. Ocean Eng. 2019, 182, 211–221. [Google Scholar] [CrossRef]
- Zhaka, V.; Bridges, R.; Riska, K.; Nilimaa, J.; Cwirzen, A. Observations of Snow–Slush–Snow Ice Transformation and Properties of Brash Ice in Ship Channels. Water 2023, 15, 2360. [Google Scholar] [CrossRef]
- Here Is What Happened to the USS Bonhomme Richard (2020) |CNN. Available online: https://edition.cnn.com/videos/world/2020/07/17/uss-bonhomme-richard-fire-lon-orig-tp.cnn (accessed on 27 June 2023).
- Larter, D. US Navy Orders General Dynamics Shipyard to Stop Work after Small Fire on the Warship Kearsarge. Available online: https://www.defensenews.com/naval/2020/07/18/us-navy-orders-to-general-dynamics-nassco-to-stop-work-after-fire-on-uss-kearsarge/ (accessed on 27 June 2023).
- CNN. Philippines Ferry Fire Kills Dozens as Passengers Jump into Sea to Escape. Available online: https://edition.cnn.com/2023/03/30/asia/philippine-ferry-fire-basilan-intl-hnk/index.html (accessed on 27 June 2023).
- Liu, Y.; Xue, H.; Zhou, J.; Tang, W. Numerical Analysis of Dynamical Thermal Response of Ship Cabin Structure in Fire Scenario. Ship Build. China 2018, 59, 161–169. [Google Scholar]
- Nassiraei, H.; Lotfollahi-Yaghin, M.A.; Neshaei, S.A.; Zhu, L. Structural Behavior of Tubular X-Joints Strengthened with Collar Plate under Axially Compressive Load at Elevated Temperatures. Mar. Struct. 2018, 61, 46–61. [Google Scholar] [CrossRef]
- Nassiraei, H.; Mojtahedi, A.; Lotfollahi-Yaghin, M.A.; Zhu, L. Capacity of Tubular X-Joints Reinforced with Collar Plates under Tensile Brace Loading at Elevated Temperatures. Thin-Walled Struct. 2019, 142, 426–443. [Google Scholar] [CrossRef]
- Li, C.F.; Zhang, K.; Wei, Z.Y.; Guo, Z.; Xu, W.J. Residual Strength of Hull Structures under Cabin Fire. J. Harbin Eng. Univ. 2019, 42, 610–617. [Google Scholar] [CrossRef]
- Paik, J.K.; Ryu, M.G.; He, K.; Lee, D.H.; Lee, S.Y.; Park, D.K.; Thomas, G. Full-Scale Fire Testing to Collapse of Steel Stiffened Plate Structures under Lateral Patch Loading (Part 1)—Without Passive Fire Protection. Ships Offshore Struct. 2020, 16, 227–242. [Google Scholar] [CrossRef]
- Paik, J.K.; Ryu, M.G.; He, K.; Lee, D.H.; Lee, S.Y.; Park, D.K.; Thomas, G. Full-Scale Fire Testing to Collapse of Steel Stiffened Plate Structures under Lateral Patch Loading (Part 2)—With Passive Fire Protection. Ships Offshore Struct. 2021, 16, 243–254. [Google Scholar] [CrossRef]
- ISO 834-1:1999; Fire-Resistance Tests Elements of Building Construction Part: 1: General Requirements. International Standard: Geneva, Switzerland, 1999.
- Liu, Y.; Guo, Z.; Jia, X.; Li, C.; Kang, J. Space Temperature Field and Structure Response of Multi-Chamber Cabin Subjected to Fire. Ocean Eng. 2022, 266, 112904. [Google Scholar] [CrossRef]
- Guo, Z. Residual Strength Prediction and Structural Response of a Multi-Chamber Cabin to a Fire. J. Mar. Eng. Technol. 2023, 22, 294–303. [Google Scholar] [CrossRef]
- Piscopo, V.; Scamardella, A. Modified Incremental-Iterative Method for Bulk Carriers under Alternate Hold Loading Conditions. Ships Offshore Struct. 2021, 16, 919–930. [Google Scholar] [CrossRef]
- Zhao, N.; Chen, B.-Q.; Zhou, Y.-Q.; Li, Z.-J.; Hu, J.-J.; Soares, C.G. Experimental and Numerical Investigation on the Ultimate Strength of a Ship Hull Girder Model with Deck Openings. Mar. Struct. 2022, 83, 103175. [Google Scholar] [CrossRef]
- Li, S.; Kim, D.K. A Comparison of Numerical Methods for Damage Index Based Residual Ultimate Limit State Assessment of Grounded Ship Hulls. Thin-Walled Struct. 2022, 172, 108854. [Google Scholar] [CrossRef]
- Xu, W.; Zhou, X.; Li, C.; Ren, H. Post-Ultimate Strength Behavior and Collapse Severity of Ship Hull Girder under Extreme Wave Load by an Analytical Method. Ships Offshore Struct. 2020, 17, 109627. [Google Scholar]
- Zhu, Z.; Ren, H.; Li, C.; Zhou, X. Ultimate Limit State Function and Its Fitting Method of Damaged Ship under Combined Loads. J. Mar. Sci. Eng. 2020, 8, 117. [Google Scholar] [CrossRef]
- Putranto, T.; Kõrgesaar, M.; Tabri, K. Application of Equivalent Single Layer Approach for Ultimate Strength Analyses of Ship Hull Girder. J. Mar. Sci. Eng. 2022, 10, 1530. [Google Scholar] [CrossRef]
- Cerik, B.C.; Choung, J. Progressive Collapse Analysis of Intact and Damaged Ships under Unsymmetrical Bending. J. Mar. Sci. Eng. 2020, 8, 988. [Google Scholar] [CrossRef]
- Guedes Soares, C.; Gordo, J.M.; Teixeira, A.P. Elasto-Plastic Behaviour of Plates Subjected to Heat Loads. J. Constr. Steel Res. 1998, 45, 179–198. [Google Scholar] [CrossRef]
- Guedes Soares, C.; Teixeira, A.P. Strength of Plates Subjected to Localised Heat Loads. J. Constr. Steel Res. 2000, 53, 335–358. [Google Scholar] [CrossRef]
- Gordo, J.M.; Guedes Soares, C.; Faulkner, D. Approximate Assessment of the Ultimate Longitudinal Strength of the Hull Girder. J. Ship Res. 1996, 40, 60–69. [Google Scholar] [CrossRef]
- Chen, B.-Q.; Guedes Soares, C. A Simplified Model for the Effect of Weld-Induced Residual Stresses on the Axial Ultimate Strength of Stiffened Plates. J. Mar. Sci. Appl. 2018, 17, 57–67. [Google Scholar] [CrossRef]
- Teixeira, A.P.; Guedes Soares, C. Reliability of load bearing steel plates subjected to localised heat loads. Int. J. Rel. Qual. Saf. Eng. 2006, 13, 97–113. [Google Scholar] [CrossRef]
- Guterl, F. Today’s Navies: Plying a Sea of Debate. IEEE Spectr. 1982, 19, 43–48. [Google Scholar] [CrossRef]
- Lake, J.S. The U.S. Navy: Can Ships Survive? IEEE Spectr. 1982, 19, 83–85. [Google Scholar] [CrossRef]
- Yang, K.C.; Lee, H.H. Experimental Study on Ultimate Strength of Steel Columns under Fire Load. Fire Saf. Sci. 2004, 6, 354–361. [Google Scholar]
- Yang, K.-C.; Lee, H.-H.; Chan, O. Performance of Steel H Columns Loaded under Uniform Temperature. J. Constr. Steel Res. 2006, 62, 262–270. [Google Scholar] [CrossRef]
- Han, Q.; Li, M.; Wang, Z.; Yun, X.; Ouyang, Y. Local Buckling Behaviour and Design of Aluminium Alloy Plates in Fire. Thin-Walled Struct. 2023, 189, 110886. [Google Scholar] [CrossRef]
- Han, Q.; Li, M.; Wang, Z. Testing of High Strength Aluminium Alloy SHS and RHS Stub Columns in Fire. Eng. Struct. 2023, 284, 115971. [Google Scholar] [CrossRef]
- Zhang, Y.; Huang, Y.; Wei, Y. Ultimate Strength Experiment of Hull Structural Plate with Pitting Corrosion Damage under Unaxial Compression. Ocean Eng. 2017, 130, 103–114. [Google Scholar] [CrossRef]
- NR467 Steel Ships, Part B Hull and Stability, Chapter 5 Design Loads, Section 2 Hull Girder Loads 2021. Available online: https://www.doc88.com/p-484420770866.html (accessed on 16 October 2023).
- GB 50018-2002; Technical Code of Cold-Formed Thin-Wall Steel Structures, Chapter 5 Calculation of Components, Section 6 Compression Plates in Components. Beijing China Planning Publishing House: Beijing, China, 2002; p. 27.
- BS EN 1993-1-5; Eurocode 3, Design of Steel Structure, Part 1–5: Plated Structural Elements. British Standard Institution: London, UK, 2006.
- AISC 36005 [S]; Specification for Structural Steel Buildings. American Institute of Steel Construction, Inc.: Chicago, IL, USA, 2005; p. 182.
- Nscort, A. Estimation of Rate of Heat Release by Means of Oxygen Consumption Measurements. Fire Mater. 1980, 4, 61–65. [Google Scholar]


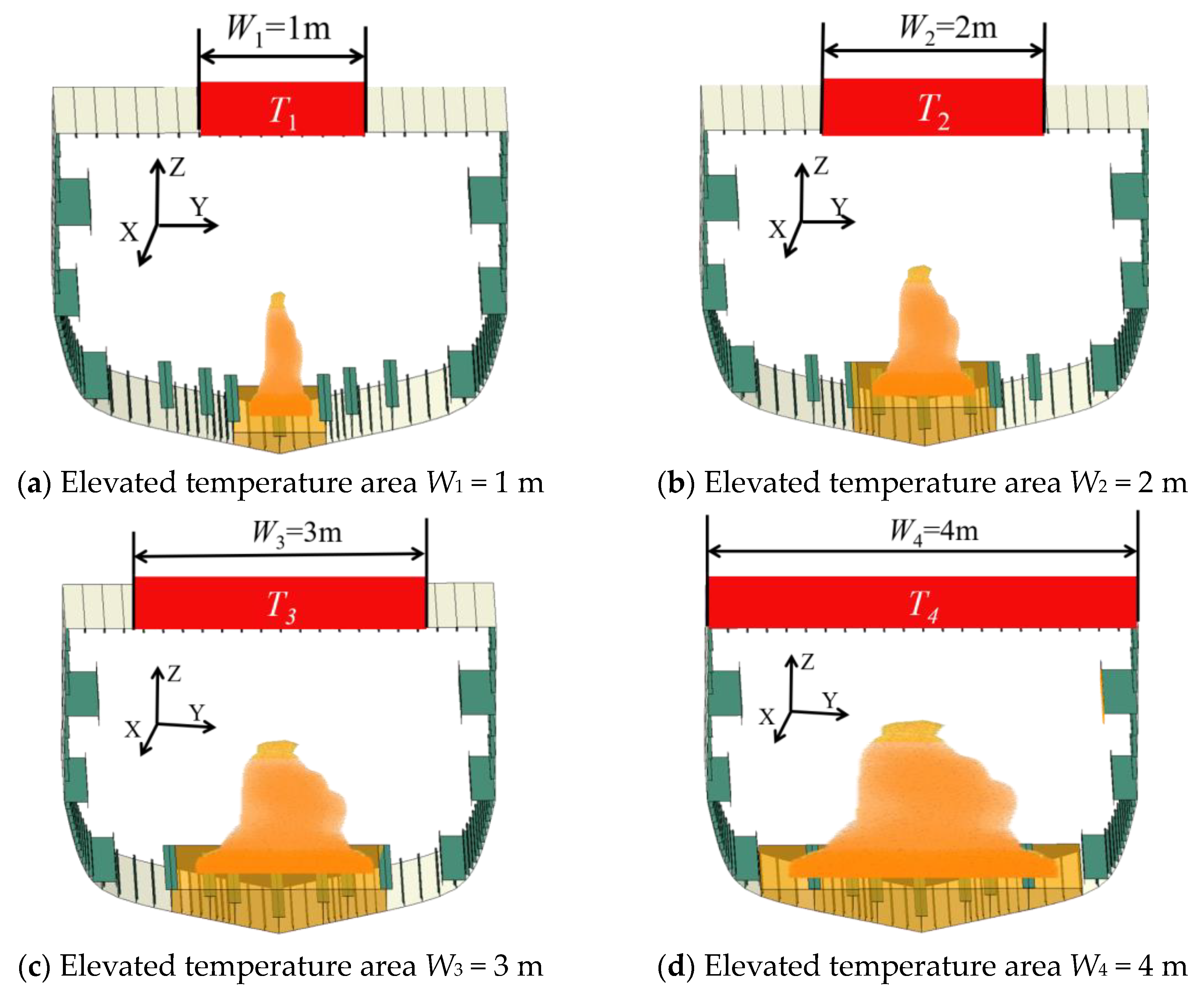

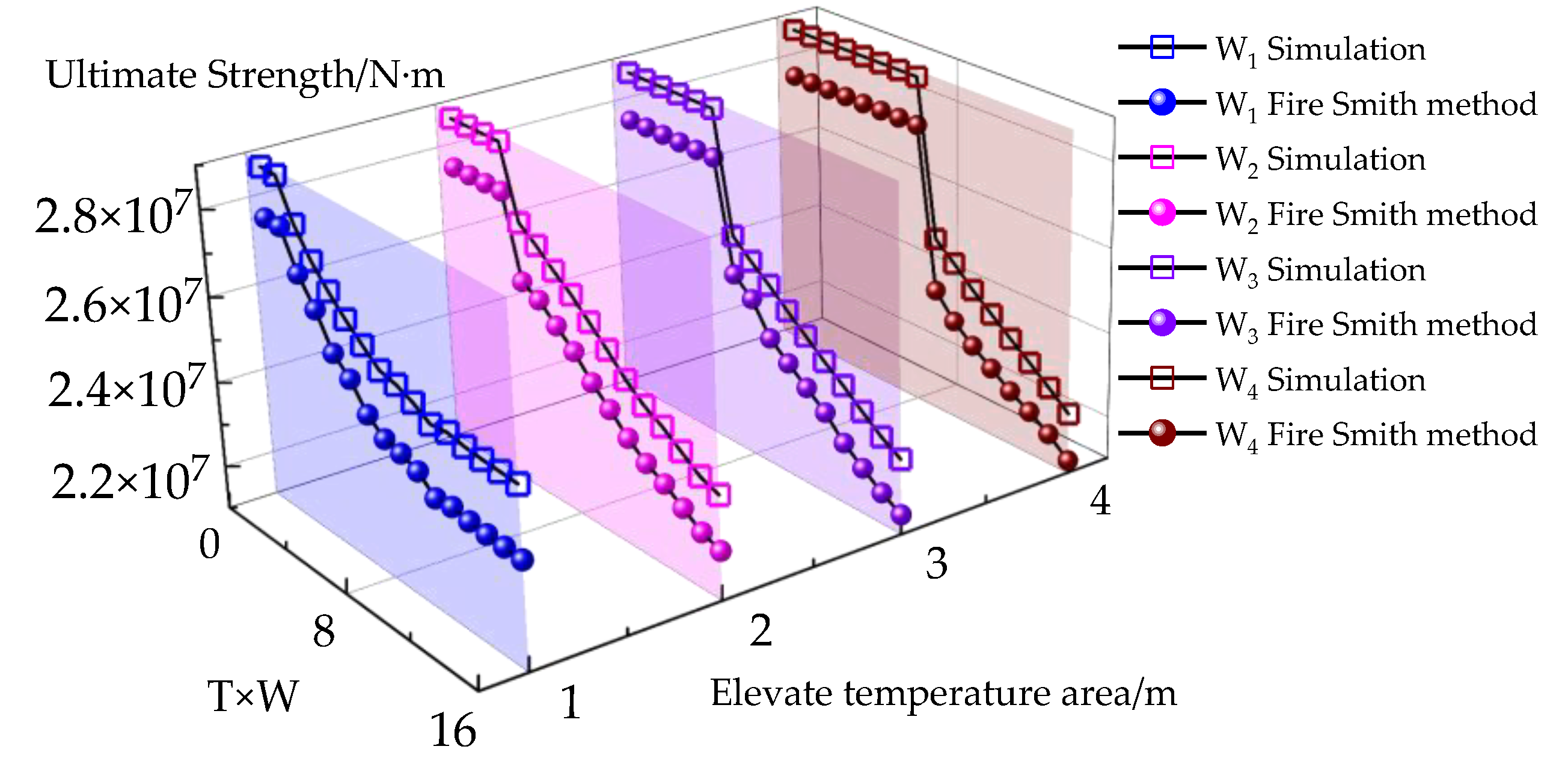
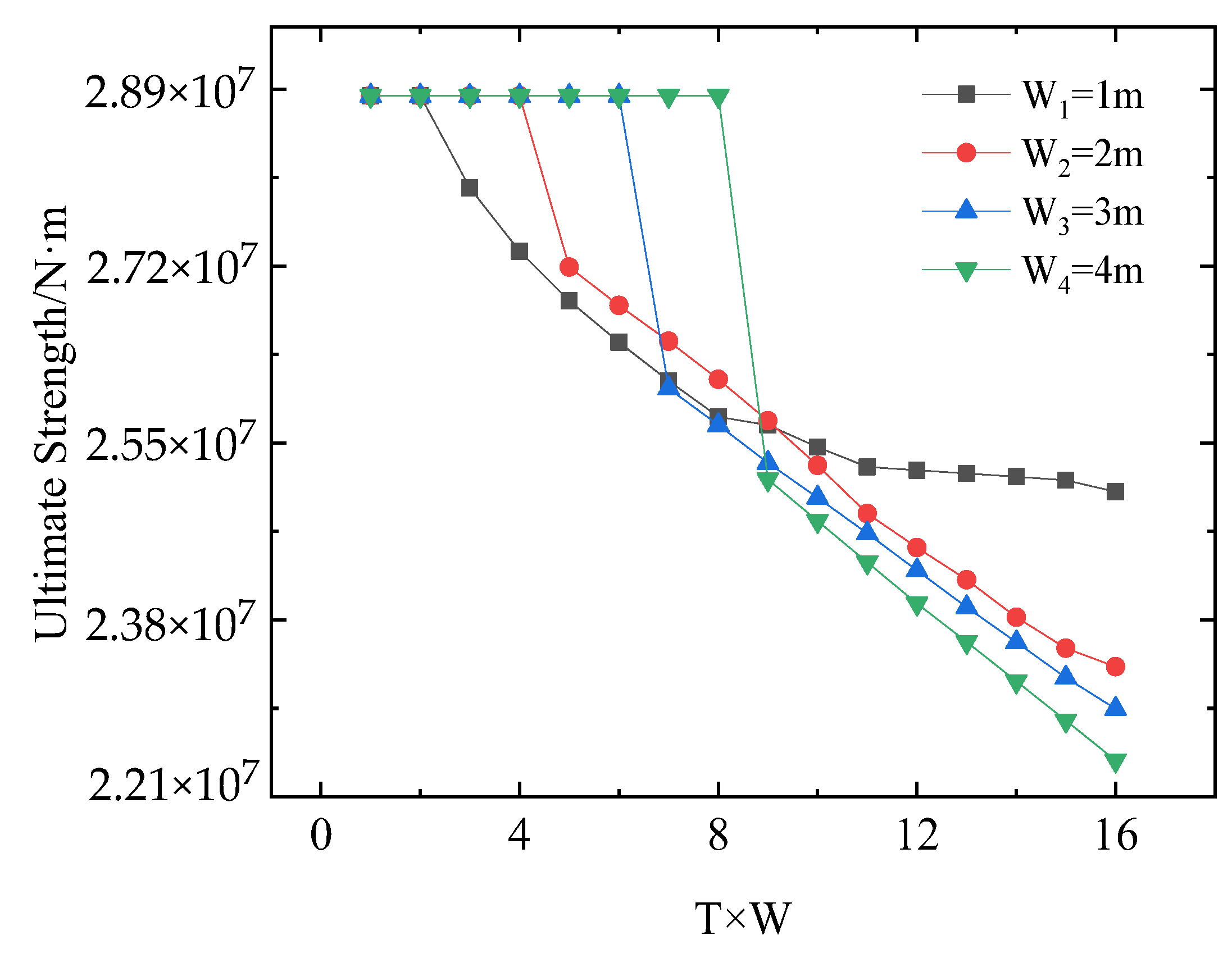
| T1 × W1 | T2 × W2 | T3 × W3 | T4 × W4 | |
|---|---|---|---|---|
| 1 | 100 × 1 | 50 × 2 | 33.3 × 3 | 25 × 4 |
| 2 | 200 × 1 | 100 × 2 | 66.6 × 3 | 50 × 4 |
| 3 | 300 × 1 | 150 × 2 | 99.9 × 3 | 75 × 4 |
| 4 | 400 × 1 | 200 × 2 | 133.3 × 3 | 100 × 4 |
| 5 | 500 × 1 | 250 × 2 | 166.6 × 3 | 125 × 4 |
| 6 | 600 × 1 | 300 × 2 | 199.9 × 3 | 150 × 4 |
| 7 | 700 × 1 | 350 × 2 | 233.3 × 3 | 175 × 4 |
| 8 | 800 × 1 | 400 × 2 | 266.6 × 3 | 200 × 4 |
| 9 | 900 × 1 | 450 × 2 | 299.9 × 3 | 225 × 4 |
| 10 | 1000 × 1 | 500 × 2 | 333.3 × 3 | 250 × 4 |
| 11 | 1100 × 1 | 550 × 2 | 366.6 × 3 | 275 × 4 |
| 12 | 1200 × 1 | 600 × 2 | 399.9 × 3 | 300 × 4 |
| 13 | 1300 × 1 | 650 × 2 | 433.3 × 3 | 325 × 4 |
| 14 | 1400 × 1 | 700 × 2 | 466.6 × 3 | 350 × 4 |
| 15 | 1500 × 1 | 750 × 2 | 499.9 × 3 | 375 × 4 |
| 16 | 1600 × 1 | 800 × 2 | 533.3 × 3 | 400 × 4 |
| No. | W1 = 1 m | W2 = 2 m | ||||
|---|---|---|---|---|---|---|
| Simulation | Fire Smith | Error (%) | Simulation | Fire Smith | Error (%) | |
| 1 | 2.88 × 107 | 2.65 × 107 | 7.82 | 2.88 × 107 | 2.65 × 107 | 7.82 |
| 2 | 2.88 × 107 | 2.65 × 107 | 7.82 | 2.88 × 107 | 2.65 × 107 | 7.82 |
| 3 | 2.79 × 107 | 2.57 × 107 | 7.82 | 2.88 × 107 | 2.65 × 107 | 7.82 |
| 4 | 2.73 × 107 | 2.51 × 107 | 7.96 | 2.88 × 107 | 2.65 × 107 | 7.82 |
| 5 | 2.68 × 107 | 2.46 × 107 | 8.09 | 2.71 × 107 | 2.50 × 107 | 7.92 |
| 6 | 2.64 × 107 | 2.42 × 107 | 8.23 | 2.68 × 107 | 2.46 × 107 | 8.01 |
| 7 | 2.60 × 107 | 2.39 × 107 | 8.37 | 2.64 × 107 | 2.43 × 107 | 8.11 |
| 8 | 2.57 × 107 | 2.35 × 107 | 8.50 | 2.61 × 107 | 2.39 × 107 | 8.21 |
| 9 | 2.56 × 107 | 2.34 × 107 | 8.64 | 2.57 × 107 | 2.35 × 107 | 8.31 |
| 10 | 2.54 × 107 | 2.32 × 107 | 8.78 | 2.52 × 107 | 2.31 × 107 | 8.40 |
| 11 | 2.52 × 107 | 2.30 × 107 | 8.92 | 2.48 × 107 | 2.27 × 107 | 8.50 |
| 12 | 2.52 × 107 | 2.29 × 107 | 9.05 | 2.44 × 107 | 2.23 × 107 | 8.60 |
| 13 | 2.52 × 107 | 2.28 × 107 | 9.19 | 2.41 × 107 | 2.20 × 107 | 8.70 |
| 14 | 2.51 × 107 | 2.28 × 107 | 9.33 | 2.38 × 107 | 2.17 × 107 | 8.79 |
| 15 | 2.51 × 107 | 2.27 × 107 | 9.42 | 2.35 × 107 | 2.14 × 107 | 8.87 |
| 16 | 2.50 × 107 | 2.26 × 107 | 9.47 | 2.33 × 107 | 2.12 × 107 | 8.95 |
| No. | W3 = 3 m | W4 = 4 m | ||||
| Simulation | Fire Smith | Error (%) | Simulation | Fire Smith | Error (%) | |
| 1 | 2.88 × 107 | 2.65 × 107 | 7.82 | 2.88 × 107 | 2.65 × 107 | 7.82 |
| 2 | 2.88 × 107 | 2.65 × 107 | 7.82 | 2.88 × 107 | 2.65 × 107 | 7.82 |
| 3 | 2.88 × 107 | 2.65 × 107 | 7.82 | 2.88 × 107 | 2.65 × 107 | 7.82 |
| 4 | 2.88 × 107 | 2.65 × 107 | 7.82 | 2.88 × 107 | 2.65 × 107 | 7.82 |
| 5 | 2.88 × 107 | 2.65 × 107 | 7.82 | 2.88 × 107 | 2.65 × 107 | 7.82 |
| 6 | 2.88 × 107 | 2.65 × 107 | 7.82 | 2.88 × 107 | 2.65 × 107 | 7.82 |
| 7 | 2.60 × 107 | 2.39 × 107 | 7.88 | 2.88 × 107 | 2.65 × 107 | 7.82 |
| 8 | 2.56 × 107 | 2.36 × 107 | 7.94 | 2.88 × 107 | 2.65 × 107 | 7.82 |
| 9 | 2.53 × 107 | 2.32 × 107 | 8.01 | 2.51 × 107 | 2.31 × 107 | 7.84 |
| 10 | 2.49 × 107 | 2.29 × 107 | 8.07 | 2.47 × 107 | 2.28 × 107 | 7.84 |
| 11 | 2.46 × 107 | 2.26 × 107 | 8.14 | 2.43 × 107 | 2.24 × 107 | 7.84 |
| 12 | 2.42 × 107 | 2.22 × 107 | 8.20 | 2.39 × 107 | 2.20 × 107 | 7.85 |
| 13 | 2.39 × 107 | 2.19 × 107 | 8.27 | 2.35 × 107 | 2.17 × 107 | 7.86 |
| 14 | 2.35 × 107 | 2.16 × 107 | 8.32 | 2.32 × 107 | 2.13 × 107 | 7.87 |
| 15 | 2.32 × 107 | 2.13 × 107 | 8.36 | 2.28 × 107 | 2.10 × 107 | 7.88 |
| 16 | 2.29 × 107 | 2.10 × 107 | 8.40 | 2.24 × 107 | 2.07 × 107 | 7.90 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, J.; Du, Z.; Yan, M.; Sun, X. Assessment of Ship Hull Ultimate Strength under Fire Conditions: The Fire Smith Method Approach. J. Mar. Sci. Eng. 2023, 11, 2055. https://doi.org/10.3390/jmse11112055
Wu J, Du Z, Yan M, Sun X. Assessment of Ship Hull Ultimate Strength under Fire Conditions: The Fire Smith Method Approach. Journal of Marine Science and Engineering. 2023; 11(11):2055. https://doi.org/10.3390/jmse11112055
Chicago/Turabian StyleWu, Jiaxin, ZhiPeng Du, Ming Yan, and Xingwei Sun. 2023. "Assessment of Ship Hull Ultimate Strength under Fire Conditions: The Fire Smith Method Approach" Journal of Marine Science and Engineering 11, no. 11: 2055. https://doi.org/10.3390/jmse11112055
APA StyleWu, J., Du, Z., Yan, M., & Sun, X. (2023). Assessment of Ship Hull Ultimate Strength under Fire Conditions: The Fire Smith Method Approach. Journal of Marine Science and Engineering, 11(11), 2055. https://doi.org/10.3390/jmse11112055









