Advanced State Estimation Approach for Partially Observable Shipboard Power Systems
Abstract
:1. Introduction
- (1)
- This paper presents a state estimation approach capable of rapidly and accurately locating fault positions within a partially observable SPS, thereby determining the current state of the system.
- (2)
- The state estimation approach is proposed based on distributed fault-tolerant control, which fully leverages the zonal distribution structure of SPS and ensures that subsystems do not enter invalid states.
- (3)
- Simulation cases are conducted to show that a state estimation approach significantly reduces computational workload and time, surpassing traditional fault localization methods by achieving a computational time reduction of two orders of magnitude, thus enhancing the efficacy of fault recovery strategies and overall system management.
2. Distributed Fault-Tolerant Control of an SPS
2.1. Distributed Control System
2.2. SPS Distributed Control Model
2.3. Fault-Tolerant Control Method
- Does not enter invalid states in the fault structure; or
- Recovers to the normal operating structure.
- ;
- Based on 1, it holds that .
3. State Estimation for the SPS
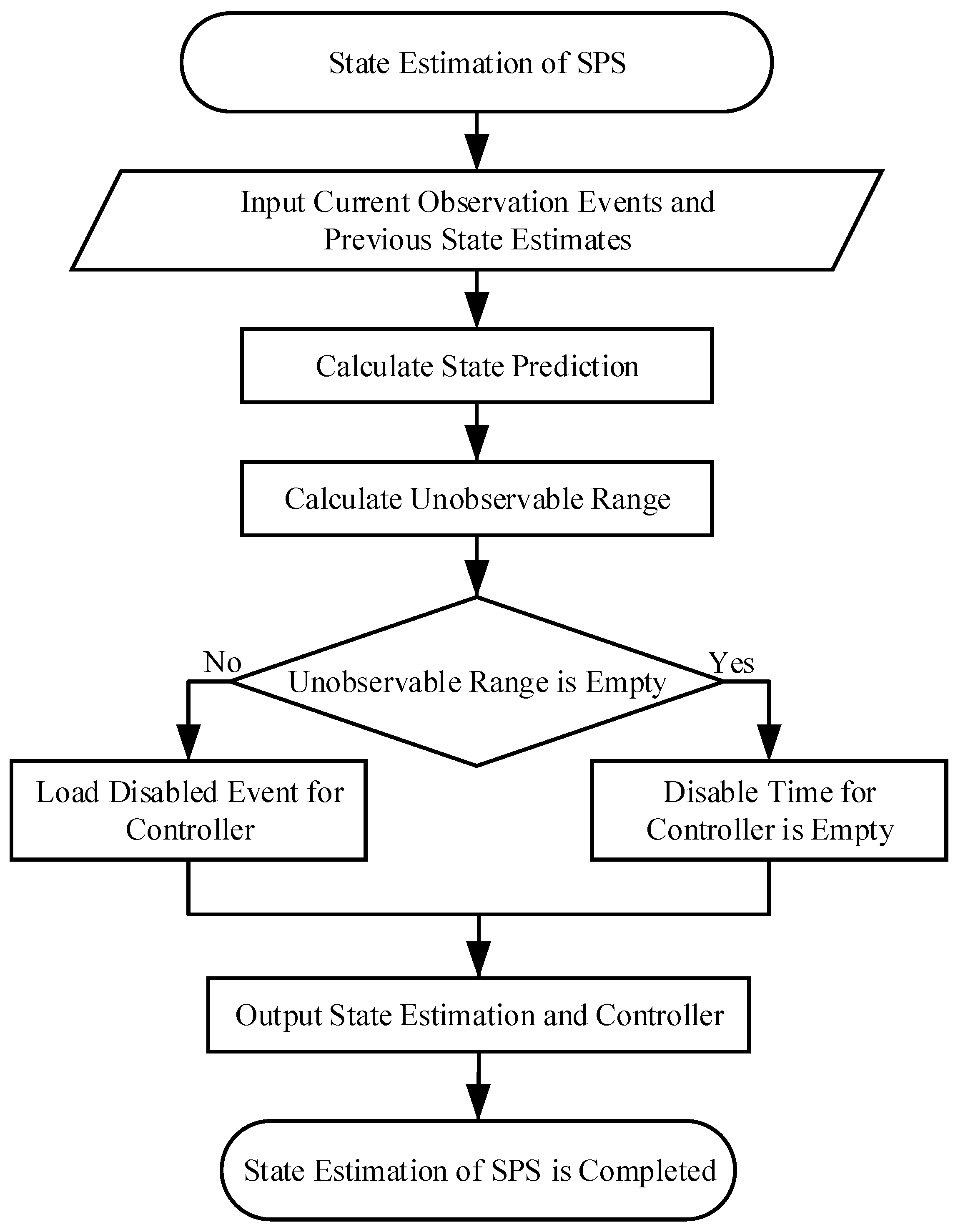
3.1. State Estimation Flowchart
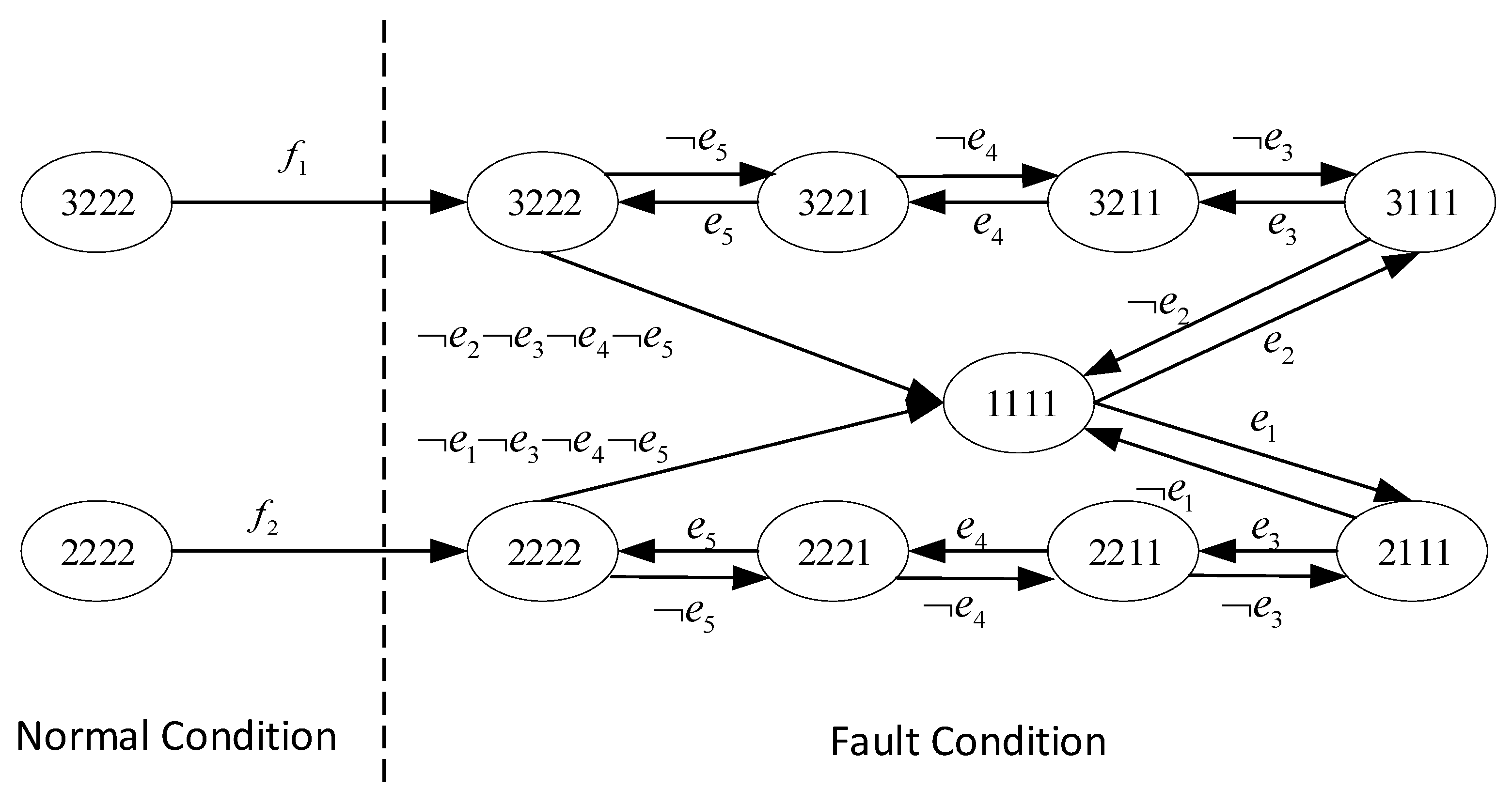
3.2. State Estimation under Partial Observability
- The system’s language is live, meaning that every state in the system has at least one corresponding state transition function;
- There are no closed-loop paths consisting solely of unobservable events in the system:
4. Simulation and Results Analysis
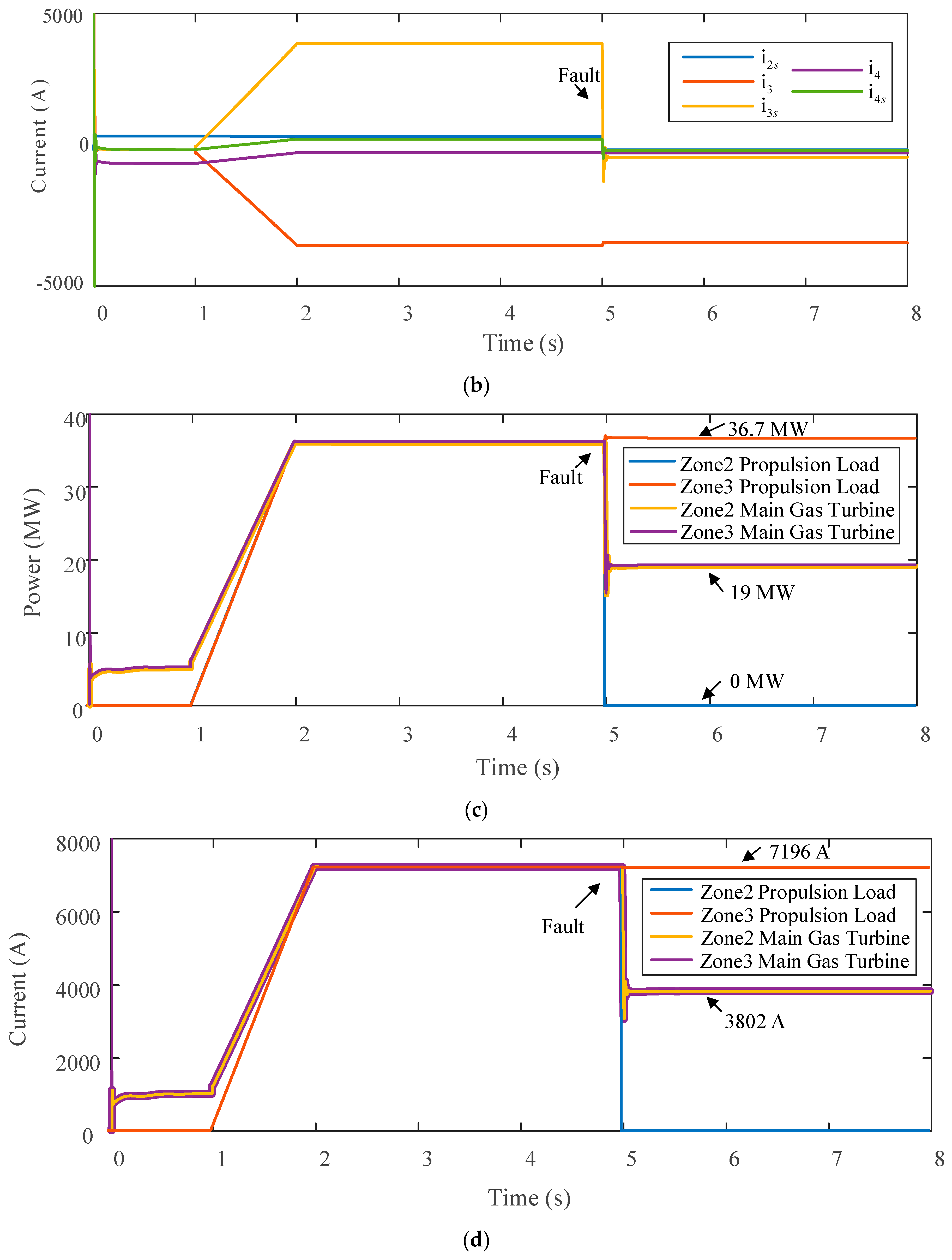
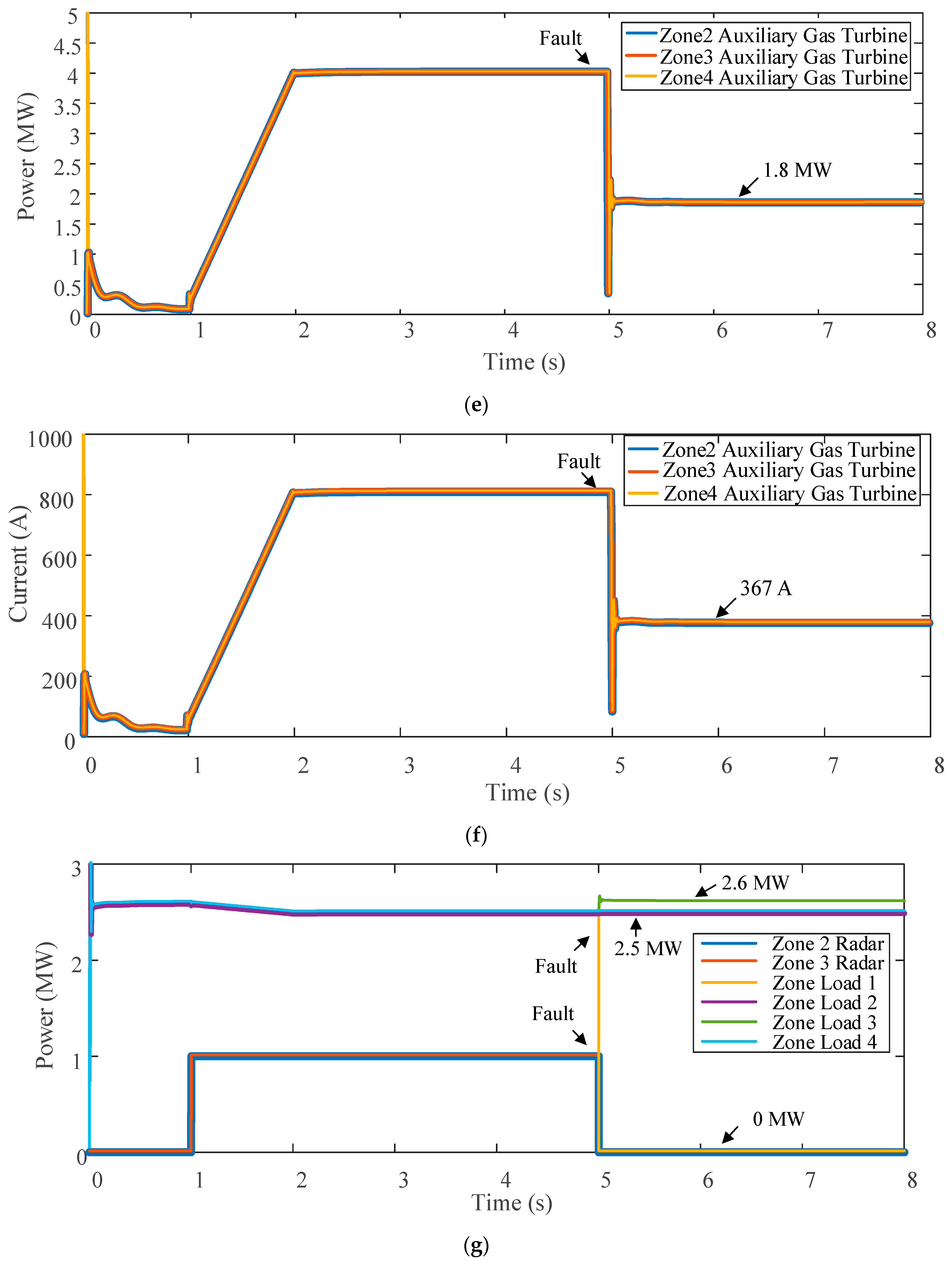
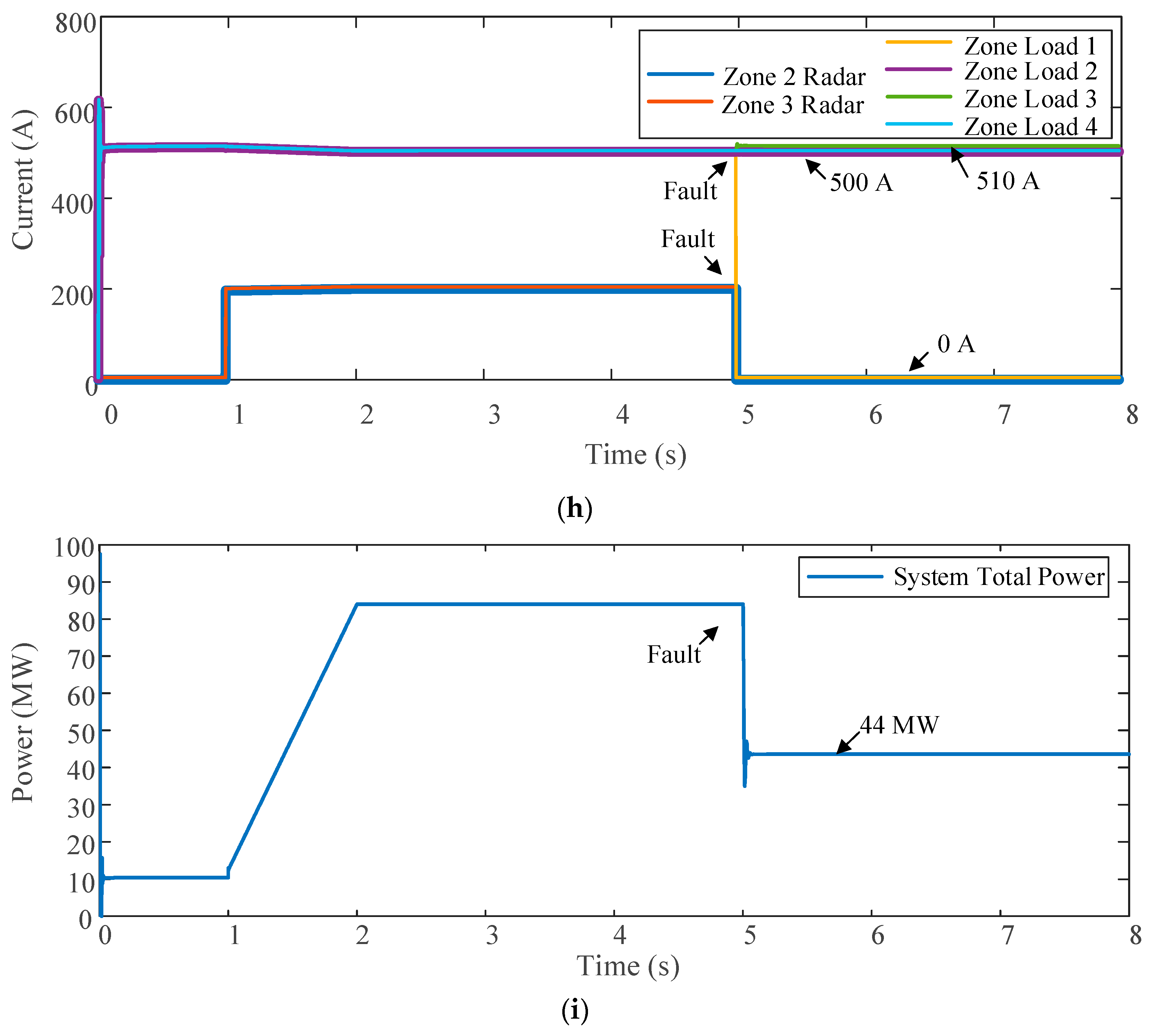
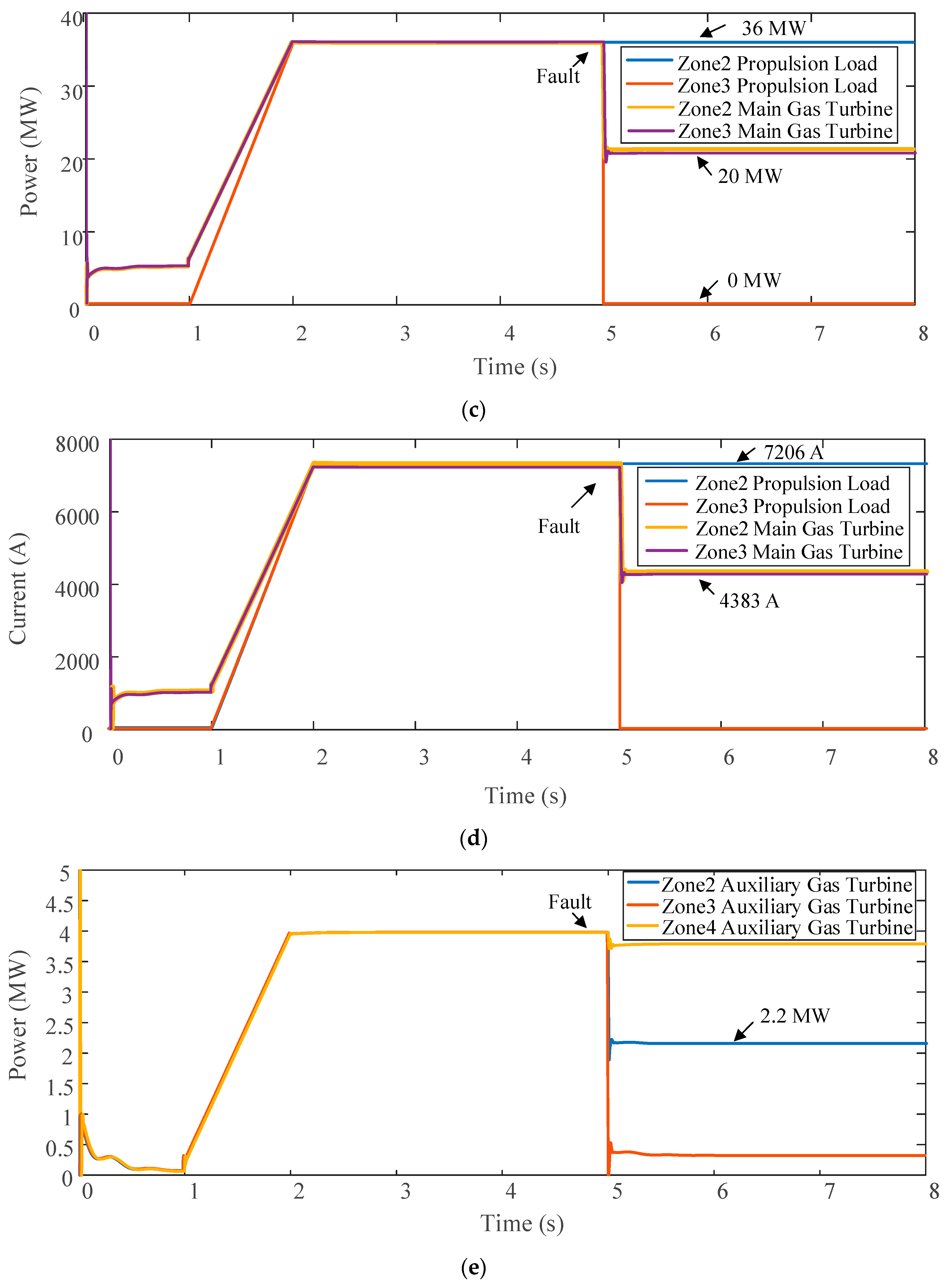
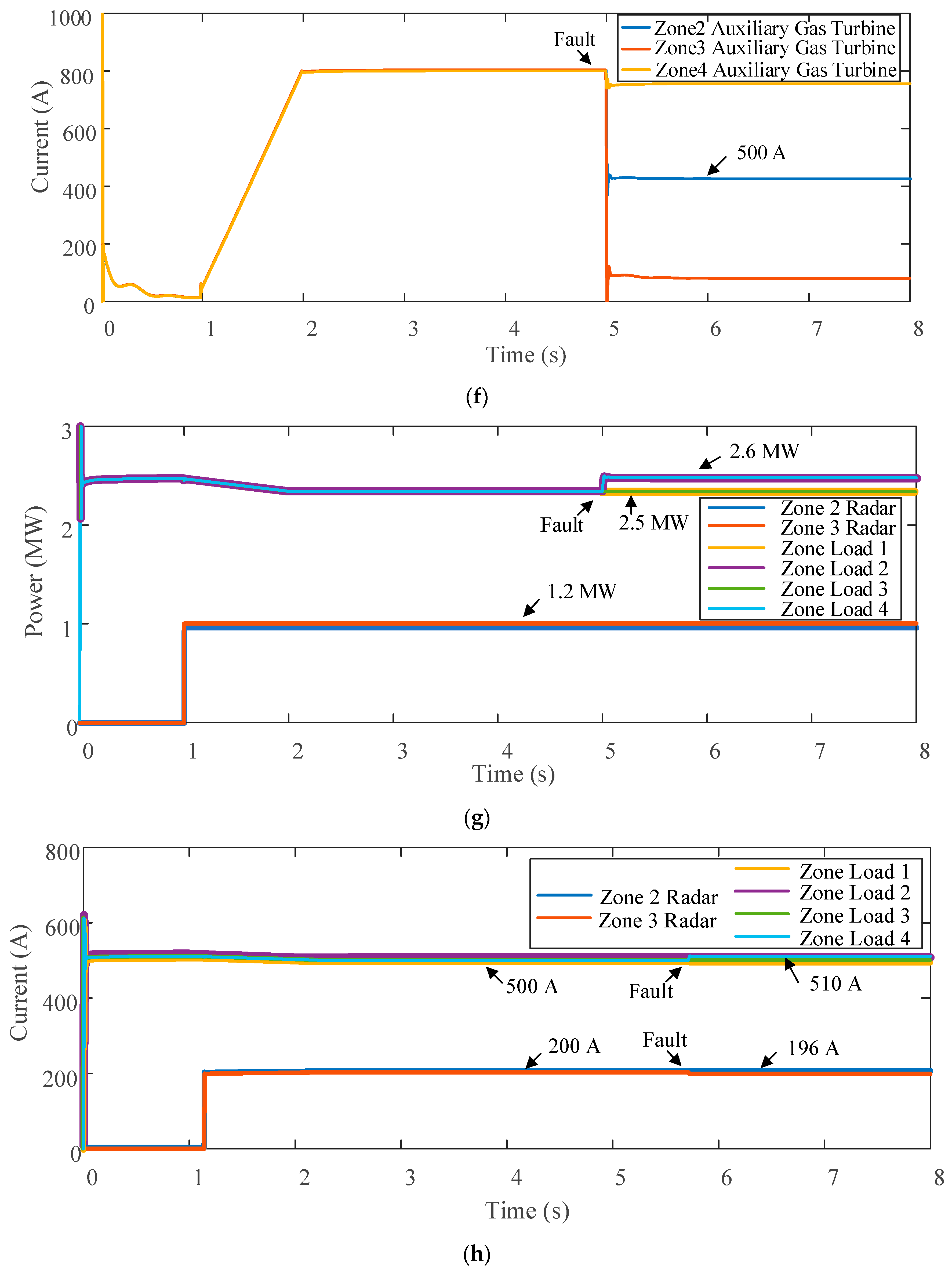
4.1. Case 1
4.2. Case 2
4.3. Comparison and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhu, X.; Wang, K.; Yang, J.; Huang, L.; Shen, B.; Sun, M. Research on the control strategy of grid connection between shore power supply and ship power grid. Energy Rep. 2022, 8, 638–647. [Google Scholar] [CrossRef]
- Yang, S. Research on Design, Detection and Realization of Monitoring System Based on Ship Power Grid Parameter. J. Phys. Conf. Ser. 2021, 2023, 012048. [Google Scholar] [CrossRef]
- Hannaford, E.; Maes, P.; Van Hassel, E. Autonomous ships and the collision avoidance regulations: A licensed deck officer survey. WMU J. Marit. Aff. 2022, 21, 233–266. [Google Scholar] [CrossRef]
- Gallo, M.; Kaza, D.; D’Agostino, F.; Cavo, M.; Zaccone, R.; Silvestro, F. Power plant design for all-electric ships considering the assessment of carbon intensity indicator. Energy 2023, 283, 129091. [Google Scholar] [CrossRef]
- Di, P.; Cheng, Y.; Pan, S.; Fan, X.; Zhan, W.; Gang, Y. Testability Modelling and Optimization Technology of Ship Electrical Equipment Based on Multi-Signal Flow Diagram. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1043, 022057. [Google Scholar] [CrossRef]
- Zhu, J.; Wang, L.; Zhang, D. Research on Ship Fault Diagnosis Based on Deep Learning. IOP Conf. Ser. Mater. Sci. Eng. 2020, 793, 012035. [Google Scholar] [CrossRef]
- Cossentino, M.; Sabatucci, L.; Zaffora, F. Safety Management in Smart Ships. In Proceedings of the Internet and Distributed Computing Systems: 12th International Conference, Naples, Italy, 10–12 October 2019; pp. 328–337. [Google Scholar]
- Ding, T.; Qu, M.; Wu, X.; Qin, B.; Yang, Y.; Blaabjerg, F. Defense strategy for resilient shipboard power systems considering sequential attacks. IEEE Trans. Inf. Forensics Secur. 2020, 15, 3443–3453. [Google Scholar] [CrossRef]
- Zhang, T.; Wu, D.; Li, L.; Yamashita, A.S.; Huang, S. A fault reconfiguration strategy based on adjustable space operator discrete state transition algorithm for ship microgrid system. Electr. Power Syst. Res. 2022, 205, 107707. [Google Scholar] [CrossRef]
- Zeng, C. Intelligent Retrieval System of Ship Fault Information Based on Big Data Analysis. J. Coast. Res. 2020, 103, 882–886. [Google Scholar] [CrossRef]
- Lou, H. Massive Ship Fault Data Retrieval Algorithm Supporting Complex Query in Cloud Computing. J. Coast. Res. 2019, 93, 1013–1018. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, Z.; Peng, H. Diagnostic Method for Short Circuit Faults at the Generator End of Ship Power Systems Based on MWDN and Deep-Gated RNN-FCN. J. Mar. Sci. Eng. 2023, 11, 1806. [Google Scholar] [CrossRef]
- Zhang, S. Large-scale Ship Fault Data Retrieval Algorithm Supporting Complex Query in Cloud Computing. J. Coast. Res. 2019, 97, 236–241. [Google Scholar] [CrossRef]
- Babaei, M.; Shi, J.; Abdelwahed, S. A survey on fault detection, isolation, and reconfiguration methods in electric ship power systems. IEEE Access 2018, 6, 9430–9441. [Google Scholar] [CrossRef]
- Zhang, Y.; Yang, T.; Tang, Z. Active fault-tolerant control for load frequency control in multi-area power systems with physical faults and cyber attacks. Int. Trans. Electr. Energy Syst. 2021, 31, e12906. [Google Scholar] [CrossRef]
- Ni, K.; Gan, C.; Peng, G.; Shi, H.; Hu, Y.; Qu, R. Power Compensation-Oriented SVM-DPC Strategy for a Fault-Tolerant Back-to-Back Power Converter Based DFIM Shipboard Propulsion System. IEEE Trans. Ind. Electron. 2021, 69, 8716–8726. [Google Scholar] [CrossRef]
- Ni, K.; Gan, C.; Hu, Y. Direct power control of fault-tolerant converter-based doubly-fed induction machine electric drivetrain for ship propulsion. In Proceedings of the 2020 23rd International Conference on Electrical Machines and Systems (ICEMS), Hamamatsu, Japan, 24–27 November 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1269–1274. [Google Scholar]
- Kuppusamy, S.; Joo, Y.H.; Kim, H.S. Fault-tolerant load frequency control for DFIG-based interconnected wind power systems. Inf. Sci. 2022, 582, 73–88. [Google Scholar] [CrossRef]
- Gao, J.; Yang, X.; Huang, J.; Peng, K. A data-driven fault detection and fault-tolerant control scheme for large-scale systems and its application on multi-area interconnected power systems. IET Control Theory Appl. 2023, 17, 400–418. [Google Scholar] [CrossRef]
- Zhu, W.; Shi, J.; Zhi, P.; Fan, L.; Lim, G.J. Distributed reconfiguration of a hybrid shipboard power system. IEEE Trans. Power Syst. 2021, 36, 4–16. [Google Scholar] [CrossRef]
- Lukas, K.; Astrid, B.; Richard, H. Optimal Design of a Distributed Ship Power System with Solid Oxide Fuel Cells under the Consideration of Component Malfunctions. Appl. Energy 2022, 316, 119052. [Google Scholar]
- Zhu, W.; Jin, C.; Liang, Z. Hybrid Modeling and Simulation for Shipboard Power System Considering High-Power Pulse Loads Integration. J. Mar. Sci. Eng. 2022, 10, 1507. [Google Scholar] [CrossRef]
- Zhu, W.; Shi, J.; Abdelwahed, S. End-to-end system level modeling and simulation for medium-voltage DC electric ship power systems. Int. J. Nav. Archit. Ocean Eng. 2018, 10, 37–47. [Google Scholar] [CrossRef]
- Alcala-Gonzalez, D.; García del Toro, E.M.; Más-López, M.I.; Pindado, S. Effect of distributed photovoltaic generation on short-circuit currents and fault detection in distribution networks: A practical case study. Appl. Sci. 2021, 11, 405. [Google Scholar] [CrossRef]
- Lv, X.; Yuan, L.; Cheng, Z.; Yin, B.; He, Y.; Ding, C. A subsystem-based fault location method in distribution grids by sparse measurement. IET Gener. Transm. Distrib. 2023, 17, 5016–5026. [Google Scholar] [CrossRef]
- Li, Y.; Wei, X.; Lin, J.; Niu, G. A robust fault location method for active distribution network based on self-adaptive switching function. Int. J. Electr. Power Energy Syst. 2023, 148, 109007. [Google Scholar] [CrossRef]
- Perez, R.; Vásquez, C.; Viloria, A. An intelligent strategy for faults location in distribution networks with distributed generation. J. Intell. Fuzzy Syst. 2019, 36, 1627–1637. [Google Scholar] [CrossRef]
- Cordova, J.; Faruque, M.O. Fault location identification in smart distribution networks with distributed generation. In Proceedings of the 2015 North American Power Symposium (NAPS), Charlotte, NC, USA, 4–6 October 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 1–7. [Google Scholar]

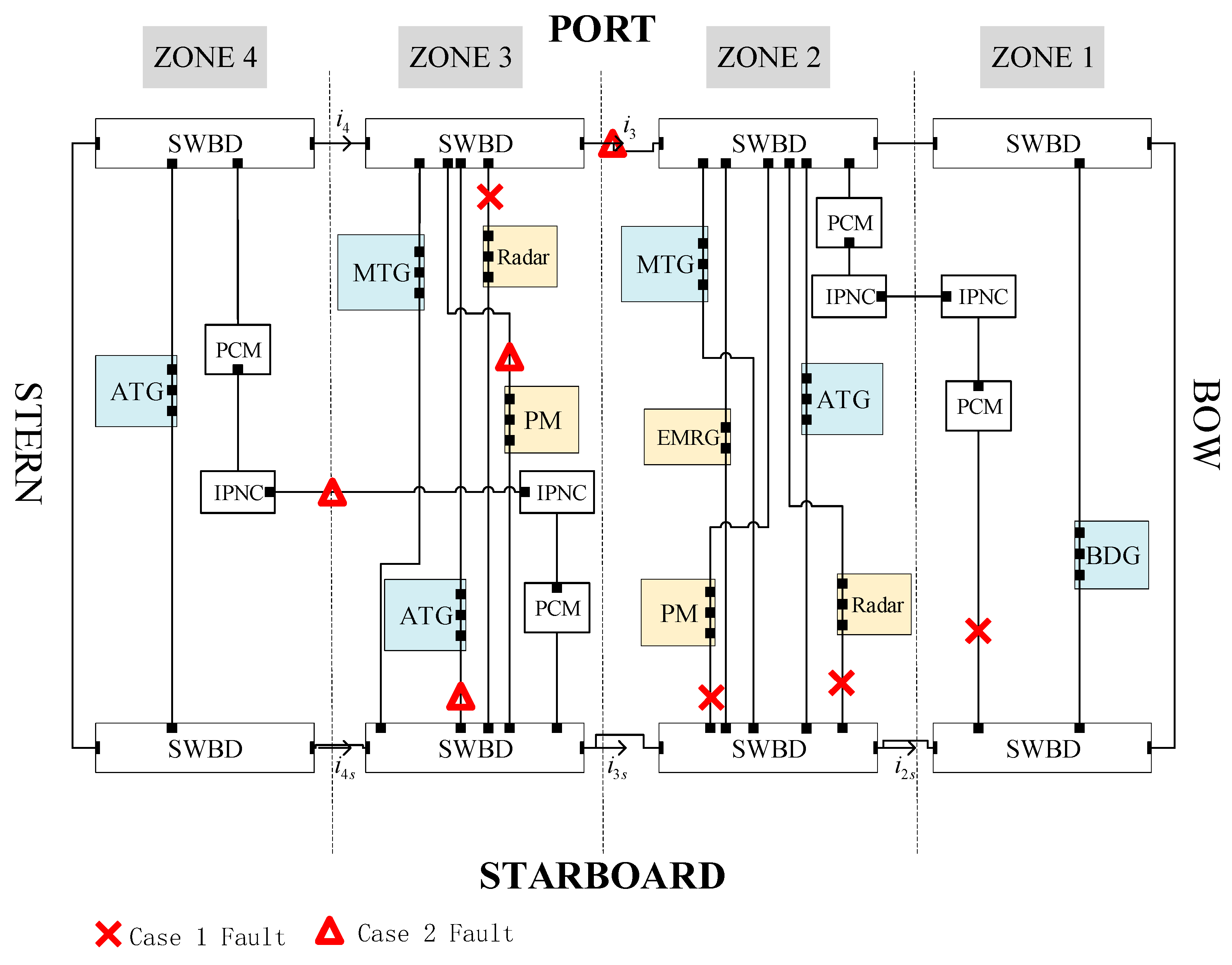



| Equipment | Zone 1 | Zone 2 | Zone 3 | Zone 4 |
|---|---|---|---|---|
| PGM | BDG 0.55 MW | ATG 4 WM MTG 36 MW | ATG 4 WM MTG 36 MW | ATG 4 MW |
| PMM | - | PM 36 MW | PM 36 MW | - |
| Mission load (ML) | - | Radar 1 MW EMRG 20 MW | Radar 1 MW | - |
| VL | 0.5 MW | 0.5 MW | 0.5 MW | 0.5 MW |
| SL | 1 MW | 1 MW | 1 MW | 1 MW |
| NL | 1 MW | 1 MW | 1 MW | 1 MW |
| Event | Initial State | Transferred State |
|---|---|---|
| e1 | 1111 | 2111 |
| e2 | 1111 | 3111 |
| e3 | 1111 | 1211 |
| e4 | 1111 | 1121 |
| e5 | 1111 | 1112 |
| Zone | System Status before Fault | State Estimation Result | Total Generator Power (MW) | Total Load Power (MW) | State Estimation Time (s) |
|---|---|---|---|---|---|
| 1 | 3222 | 1111 | 0 | 0 | 0.000434 |
| 2 | 44,332,222 | 44,112,222 | 40 | 2.5 | 0.001368 |
| 3 | 44,223,222 | 44,213,222 | 40 | 38.5 | 0.001291 |
| 4 | 42,222 | - | 4 | 2.5 | - |
| Zone | System Status before Fault | State Estimation Result | Total Generator Power (MW) | Total Load Power (MW) | State Estimation Time (s) |
|---|---|---|---|---|---|
| 1 | 3222 | - | 0 | 2.5 | - |
| 2 | 44,332,222 | - | 40 | 39.5 | - |
| 3 | 44,223,222 | 24,123,222 | 38 | 3.5 | 0.001063 |
| 4 | 42,222 | 42,222 | 4 | 2.5 | 0.000469 |
| Case | Node Status before the System Failure | Fault Location Result | Fault Location Result | Fault Location Time |
|---|---|---|---|---|
| 1 | 0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,1,−1,−1,1,0 | 0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,1,0 | 24 | 0.447650 s |
| 2 | 0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,1,1,1,−1,1 | 0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0, 0,0,0,0,1,0,0,0,0 | 21 | 0.438440 s |
| Research | Configuration | Fault Type | Number of Faults | Simulation Platform | Computation Time (s) |
|---|---|---|---|---|---|
| [24] | Centralized | Electrical faults | 2 | DIgSILENT | Above 0.3 |
| [25] | Centralized | Electrical faults | 136 | Matlab | 0.1 |
| [26] | Centralized | Communication faults | 6 | - | Above 2.4 |
| [27] | Distributed | Electrical faults | 11 | Matlab | - |
| [28] | Distributed | Electrical faults | 34 | OpenDSS | - |
| Our work | Distributed | Electrical + Communication faults | 4 | Matlab | About 0.001 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, W.; Gu, T.; Wu, J.; Liang, Z. Advanced State Estimation Approach for Partially Observable Shipboard Power Systems. J. Mar. Sci. Eng. 2023, 11, 2380. https://doi.org/10.3390/jmse11122380
Zhu W, Gu T, Wu J, Liang Z. Advanced State Estimation Approach for Partially Observable Shipboard Power Systems. Journal of Marine Science and Engineering. 2023; 11(12):2380. https://doi.org/10.3390/jmse11122380
Chicago/Turabian StyleZhu, Wanlu, Tianwen Gu, Jie Wu, and Zhengzhuo Liang. 2023. "Advanced State Estimation Approach for Partially Observable Shipboard Power Systems" Journal of Marine Science and Engineering 11, no. 12: 2380. https://doi.org/10.3390/jmse11122380
APA StyleZhu, W., Gu, T., Wu, J., & Liang, Z. (2023). Advanced State Estimation Approach for Partially Observable Shipboard Power Systems. Journal of Marine Science and Engineering, 11(12), 2380. https://doi.org/10.3390/jmse11122380





