Hydrodynamic Design of Fixed Hydrofoils for Planing Craft
Abstract
:1. Introduction
2. The Hydrofoil Technology
2.1. A Brief Historical Review
2.2. Application of Foils to Planing Craft and High-Speed Vessels
3. Wing Hydrodynamics
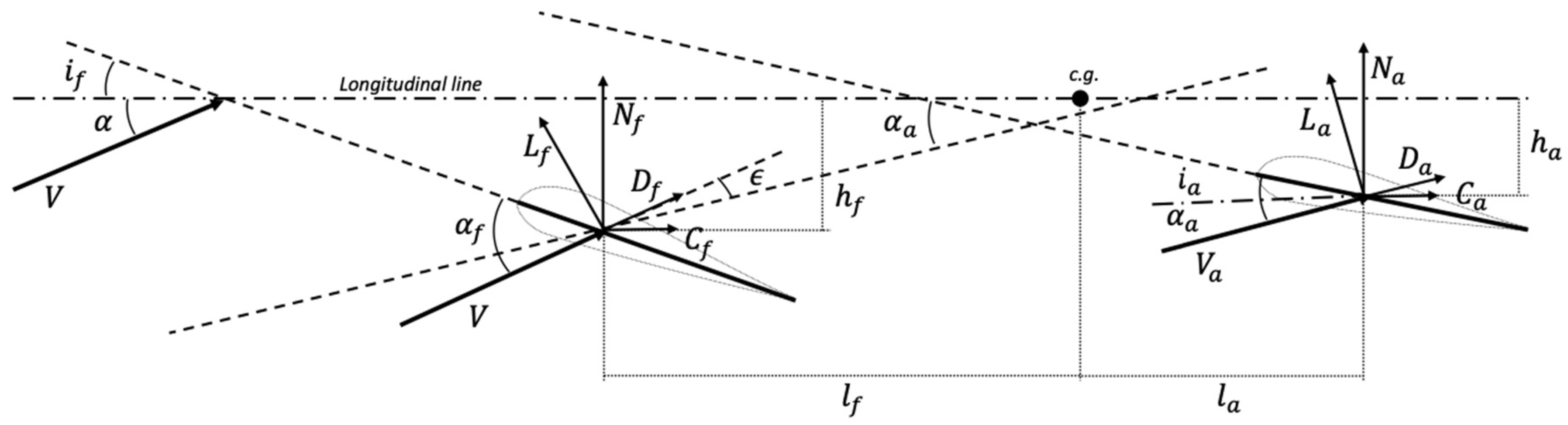
3.1. The Hydrodynamic Model
3.2. The Iterative Procedure for Wing Design
3.3. Seakeeping Equations
4. Reference Planing Craft
5. Case Study
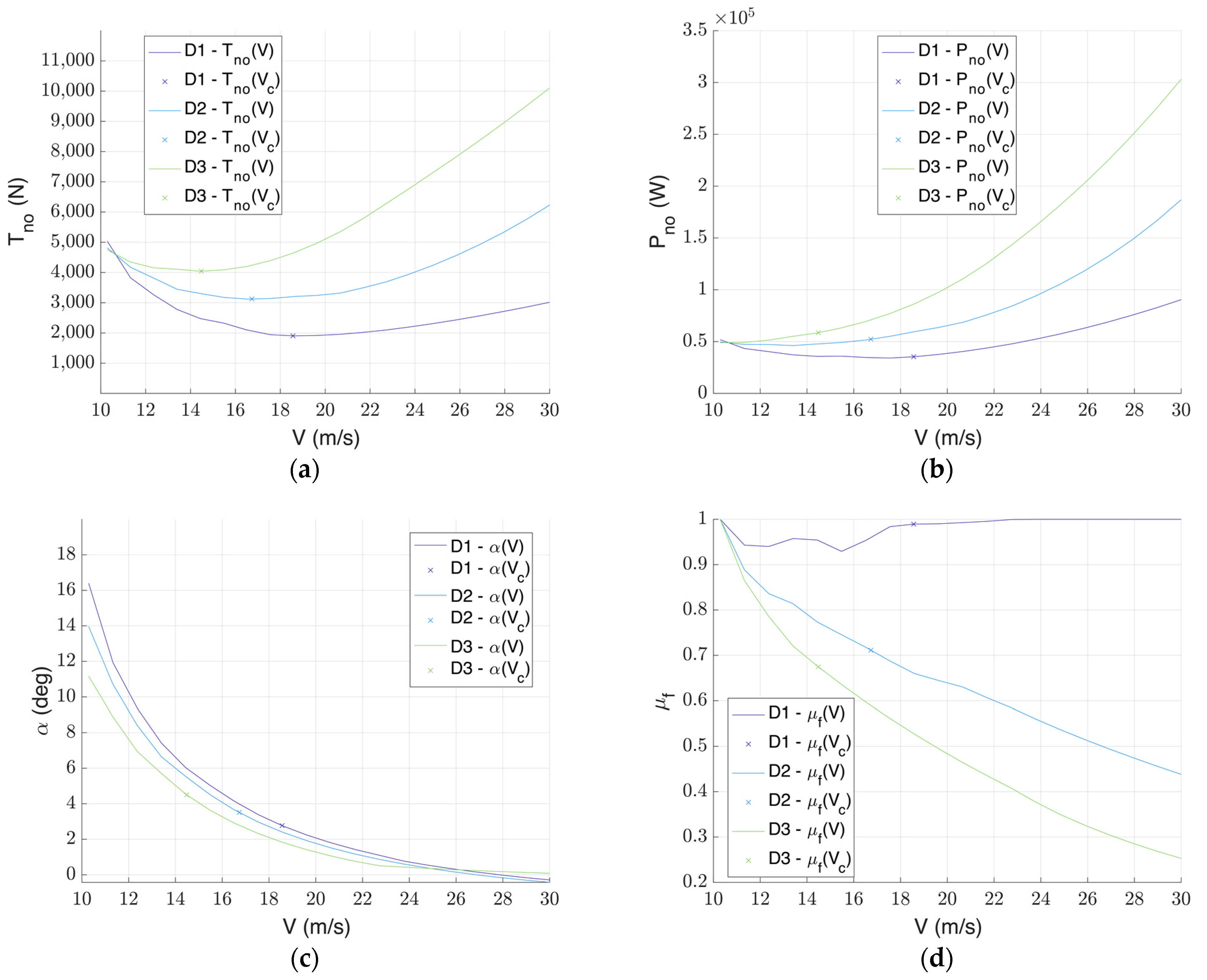
5.1. Wing Design and Selection
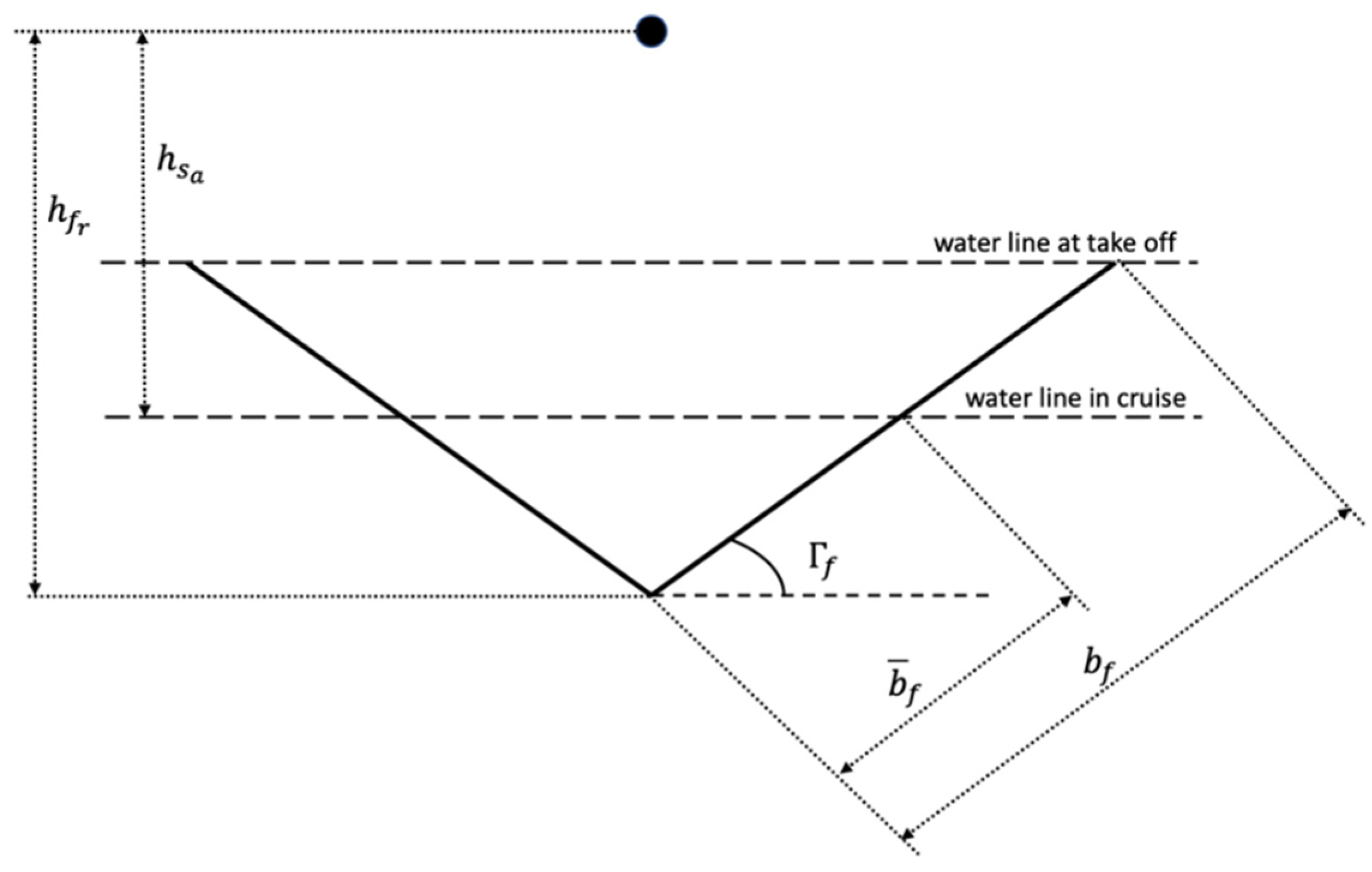
5.2. Assessment of Metacentric Height
5.3. Seakeeping Analysis
6. Conclusions
- i
- The iterative procedure for the wing design is revealed to be effective for the detection of the minimum thrust configuration, once the main parameters of the afterward and forward wings are selected;
- ii
- The heave-pitch seakeeping equations for the foil-borne mode are developed, including the restoring components due to the surface-piercing effect;
- iii
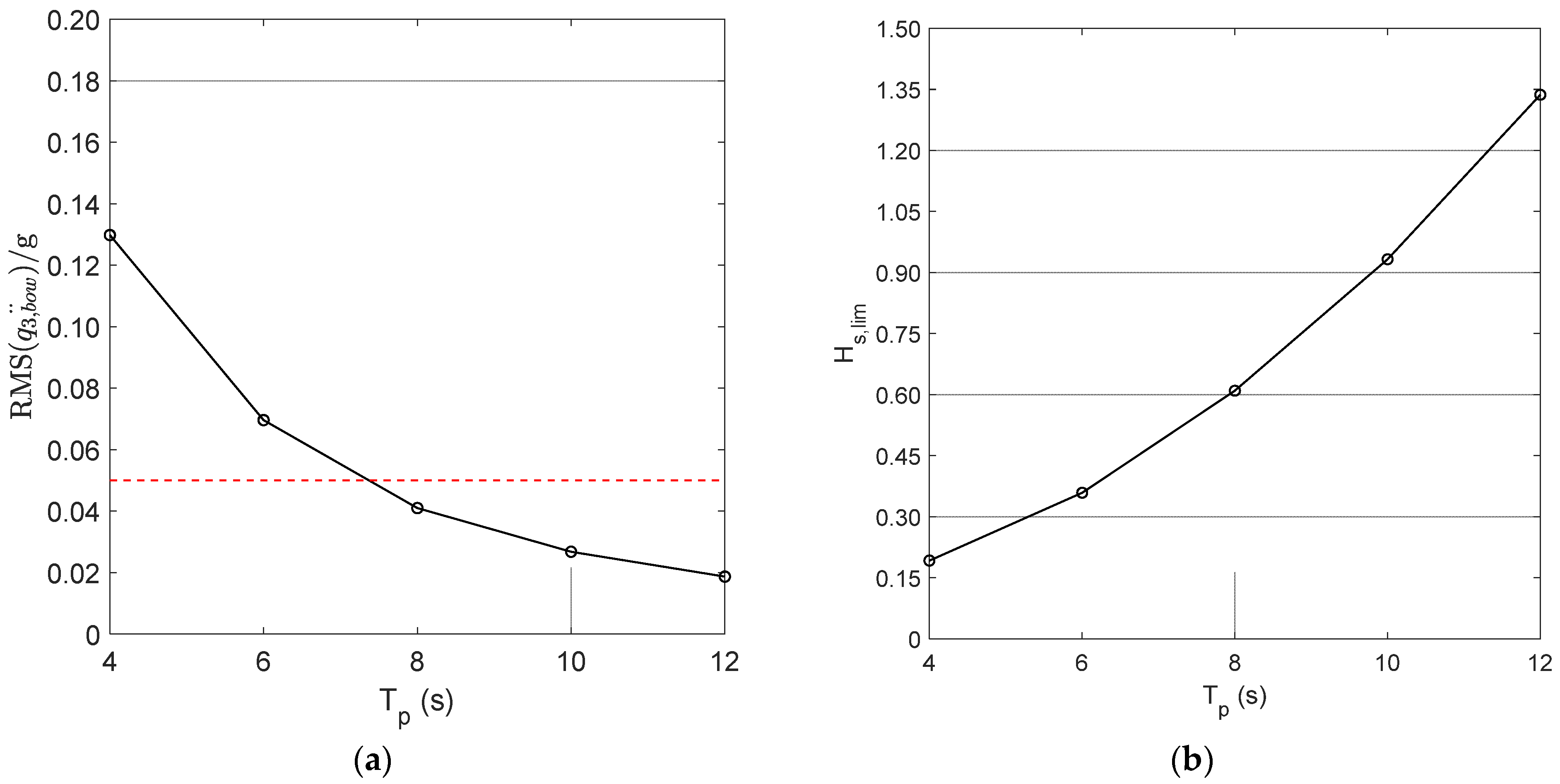
- The case study proves that the iterative procedure for wing design allows obtaining a set of wing configurations that need to be further analysed to ensure a satisfactory value of the metacentric height in the foil-borne mode. Besides, based on the results of seakeeping analysis the selected wing layout complies with the vertical acceleration limit criterion at the craft bow for 2 h exposure.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- MathWorks. Matlab User Guide R2022b; MathWorks: Natick, MA, USA, 2022. [Google Scholar]
- Meacham, W.M. Hydroplane boats: Latest type of high-speed craft. Sci. Am. 1906, 94, 188–189. [Google Scholar] [CrossRef] [Green Version]
- Von Schertel, A. Hydrofoils—The changing scene. Hover. Craft Hydrofoil 1963, 2, 13–16. [Google Scholar]
- Krack, R.C.; Gross, J.G. Experience with the hydrofoil craft Denison. In Proceedings of the SNAME Hydrofoil Symposium, Seattle, WA, USA, 13–14 May 1965; p. 2e. [Google Scholar]
- Ellsworth, W.M. The U.S. Navy Hydrofoil Development Program; Technical Note SDD-0H50-62; David Taylor Model Basin: Potomac, MD, USA, 1970. [Google Scholar]
- Kaplan, P.; Breslin, J.P. Evaluation of the theory for the flow pattern of a hydrofoil of finite span. J. Ship Res. 1960, 4, 13–29. [Google Scholar] [CrossRef]
- Johnson, R.S. Prediction of lift and cavitation characteristics of hydrofoil-strut arrays. Mar. Technol. 1965, 2, 57–69. [Google Scholar] [CrossRef]
- Plotkin, A. The Thin-hydrofoil thickness problem including leading-edge corrections. J. Ship Res. 1975, 19, 122–129. [Google Scholar] [CrossRef]
- Yeung, R.W.; Bouger, Y.C. A hybrid integral-equation method for steady two-dimensional ship waves. Int. J. Numer. Methods Eng. 1979, 14, 317–336. [Google Scholar] [CrossRef]
- Duncan, J.H. The breaking and non-breaking wave resistance of a two-dimensional hydrofoil. J. Fluid Mech. 1983, 126, 507–520. [Google Scholar] [CrossRef]
- Kennell, C.; Plotkin, A. A second order theory for the potential flow about thin hydrofoils. J. Ship Res. 1984, 28, 55–64. [Google Scholar] [CrossRef]
- Bai, K.J.; Han, J.H. Localized finite-element method for the nonlinear steady waves due to a two-dimensional hydrofoil. J. Ship Res. 1994, 38, 42–51. [Google Scholar] [CrossRef]
- Xie, N.; Vassalos, D. Performance analysis of 3D hydrofoil under free surface. Ocean Eng. 2007, 34, 1257–1264. [Google Scholar] [CrossRef]
- Sharma, A.; Sarwara, M.S.; Singh, H.; Swarup, L.; Sharma, R.K. CFD and real time analysis of a symmetric airfoil. Int. J. Res. Aeronaut. Mech. Eng. 2014, 2, 84–93. [Google Scholar]
- Liu, J.; Hekkenberg, R.G. Hydrodynamic characteristics of twin-rudders at small attack angles. In Proceedings of the 12th International Marine Design Conference, Tokyo, Japan, 11–14 May 2015; pp. 177–188. [Google Scholar]
- Kandil, M.A.F.; Elnady, A.O. CFD analysis of GOE 387 airfoil. IOSR J. Mech. Civ. Eng. 2017, 14, 80–85. [Google Scholar]
- Bai, J.; Kim, Y. Control of the vertical motion of a hydrofoil vessel. Ships Offshore Struct. 2010, 5, 189–198. [Google Scholar] [CrossRef]
- Liu, S.; Niu, H.; Zhang, L.; Xu, C. Modified adaptive complementary sliding mode control for the longitudinal motion stabilization of the fully-submerged hydrofoil craft. Int. J. Nav. Archit. Ocean Eng. 2019, 11, 584–596. [Google Scholar] [CrossRef]
- Deng, Y.; Xianku, Z.; Namkyun, I.; Kailey, L. Compound learning tracking control of a switched fully-submerged hydrofoil craft. Ocean Eng. 2021, 219, 108260. [Google Scholar] [CrossRef]
- Clement, E.P.; Blount, D.L. Resistance tests of a systematic series of planing hull form. SNAME Trans. 1963, 71, 491–579. [Google Scholar]
- Savitsky, D. Hydrodynamics design of planing hulls. Mar. Technol. 1964, 1, 71–95. [Google Scholar] [CrossRef]
- Hubble, E.N. Resistance of Hard-Chine, Stepless Planing Craft with Systematic Variation of Hull Form, Longitudinal Center of Gravity and Loading; Technical Report AD0779864; David Taylor Model Basin: West Bethesda, MD, USA, 1974. [Google Scholar]
- Weymouth, G.D.; Wilson, R.V.; Stern, F. RANS computational fluid dynamics predictions of pitch and heave ship motions in head seas. J. Ship Res. 2005, 49, 80–97. [Google Scholar] [CrossRef]
- Begovic, E.; Bertorello, C.; Pennino, S.; Piscopo, V.; Scamardella, A. Statistical analysis of planing hull motions and accelerations in irregular head sea. Ocean Eng. 2016, 112, 253–264. [Google Scholar] [CrossRef]
- De Luca, F.; Pensa, C. The Naples warped hard chine hulls systematic series. Ocean Eng. 2017, 139, 205–236. [Google Scholar] [CrossRef] [Green Version]
- De Luca, F.; Pensa, C. The Naples Systematic Series—Second part: Irregular waves, seakeeping in head sea. Ocean Eng. 2019, 194, 106620. [Google Scholar] [CrossRef]
- Pigazzini, R.; De Luca, F.; Pensa, C. An experimental assessment of nonlinear effects of vertical motions of Naples systematic series planing hulls in regular waves. Appl. Ocean Res. 2021, 111, 102546. [Google Scholar] [CrossRef]
- Sclavounos, P.D.; Borgen, H. Seakeeping analysis of a high-speed monohull with a motion-control bow hydrofoil. J. Ship Res. 2004, 48, 77–117. [Google Scholar] [CrossRef]
- Bi, X.; Shen, H.; Zhou, J.; Su, Y. Numerical analysis of the influence of fixed hydrofoil installation position on seakeeping of the planing craft. Appl. Ocean Res. 2019, 90, 101863. [Google Scholar] [CrossRef]
- Maram, M.A.; Ghafari, H.R.; Ghassemi, H.; Ghiasi, M. Numerical Study on the Tandem Submerged Hydrofoils Using RANS Solver. Math. Probl. Eng. 2021, 2021, 8364980. [Google Scholar] [CrossRef]
- Anderson, J.D.; Bowden, M.L. Introduction to Flight; McGraw-Hill Higher Education: New York, NY, USA, 2005; Volume 582. [Google Scholar]
- Matveev, K.I.; Kornev, N. Dynamics and stability of boats with aerodynamic support. J. Ship Prod. Des. 2013, 29, 17–24. [Google Scholar] [CrossRef]
- Matveev, K.I. Modeling of longitudinal motions of a hydroplane boat. Ocean Eng. 2012, 42, 1–6. [Google Scholar] [CrossRef]
- Abbott, I.H.; Von Doenhoff, A.E. Theory of Wing Sections: Including a Summary of Airfoil Data; Courier Corporation: Washington, DC, USA, 2012. [Google Scholar]
- Eppler, R. Wing sections for hydrofoils-Part 2: Nonsymmetrical profiles. J. Ship Res. 1981, 25, 191–200. [Google Scholar]
- Raymer, D.P. Aircraft Design: A Conceptual Approach; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2018. [Google Scholar]
- Cummins, W.E. The impulse response function and ship motions. Schiffstechnik 1962, 9, 101–109. [Google Scholar]
- Theodorsen, T. General Theory of Aerodynamic Instability and the Mechanism of Flutter; NACA Technical Report n. 496; Langley, Aeronautical Lab.: Langley Field, VA, USA, 1949; p. 24p. [Google Scholar]
- The International Maritime Organization. International Code of Safety for High-Speed Craft, 2021 edition; The International Maritime Organization: London, UK, 2000. [Google Scholar]
- Pennino, S.; Gaglione, S.; Innac, A.; Piscopo, V.; Scamardella, A. Development of a new ship adaptive weather routing model based on seakeeping analysis and optimization. J. Mar. Sci. Eng. 2020, 8, 270. [Google Scholar]

| Overall length | 11.00 m |
| Overall breadth | 3.12 m |
| Moulded depth | 1.30 m |
| Design draught | 0.53 m |
| Centre of gravity longitudinal position from the stern | 4.19 m |
| Centre of gravity vertical position from the baseline | 0.80 m |
| Propeller axis vertical position from the baseline | −0.30 m |
| Initial trim angle | 0.0 deg |
| Displacement at the full loaded condition | 8025 kg |
| Pitch moment of inertia | 60,000 kgm2 |
| Deadrise angle at the stern | 18 deg |
| Take-off speed | 20 kn |
| Maximum speed | 30 kn |
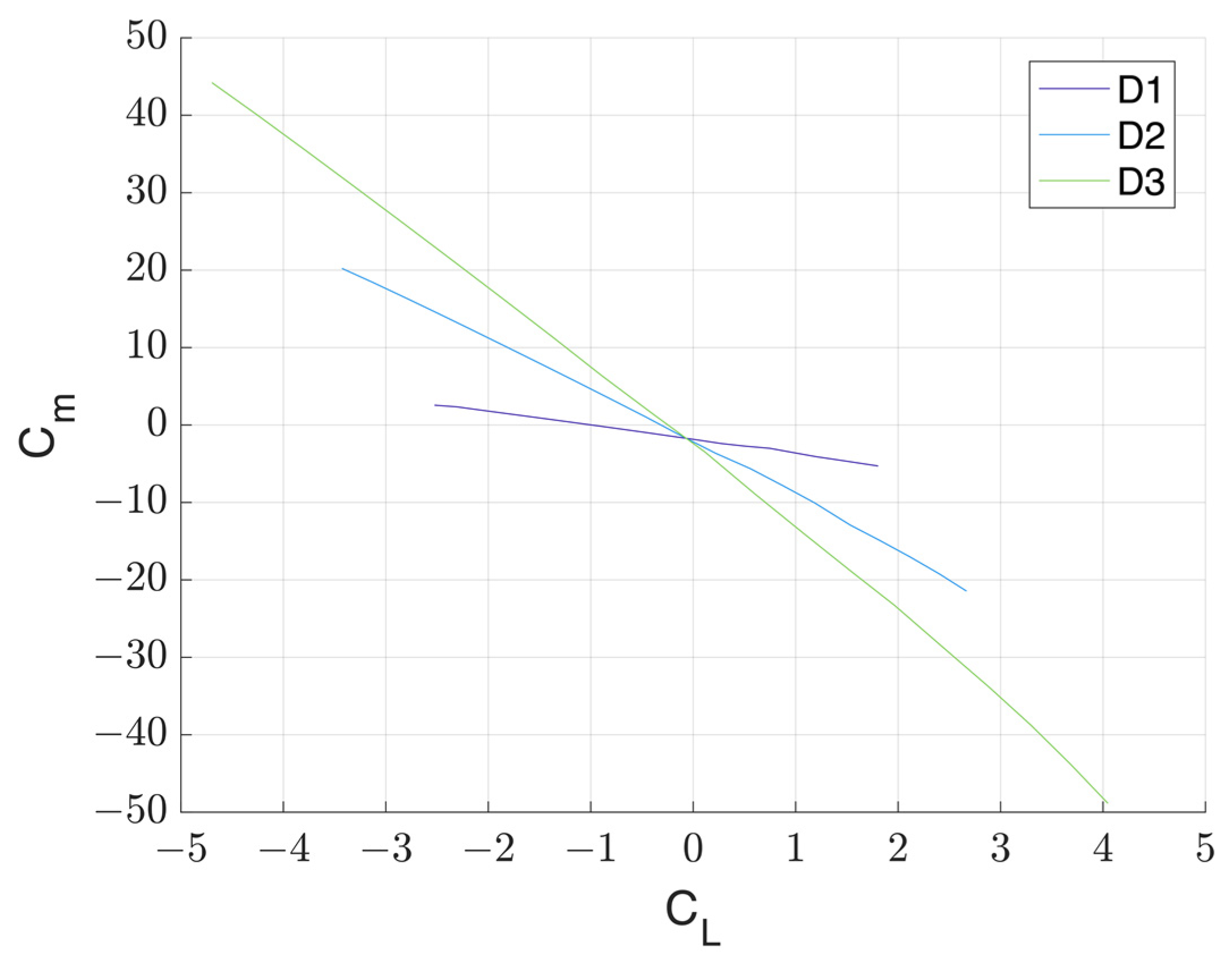
| Main Parameters | D1 | D2 | D3 |
|---|---|---|---|
| Forward foil span [m] | 3.12 | 3.12 | 3.12 |
| Forward foil aspect ratio | 21.46 | 21.02 | 20.60 |
| Forward foil surface [m2] | 0.453 | 0.463 | 0.472 |
| Forward foil incidence angle [deg] | 0.0 | 2.5 | 5.0 |
| Forward foil longitudinal distance from CG [m] | 3.50 | 3.50 | 3.50 |
| Forward foil dihedral angle [deg] | 25 | 25 | 25 |
| Afterward foil span [m] | 3.12 | 3.12 | 3.12 |
| Afterward foil aspect ratio | 15.91 | 14.36 | 11.86 |
| Afterward foil surface [m2] | 0.612 | 0.678 | 0.821 |
| Afterward foil incidence angle [deg] | 0.0 | 0.0 | 0.0 |
| Afterward foil longitudinal distance from CG [m] | 4.19 | 4.19 | 4.19 |
| Afterward foil dihedral angle [deg] | 10 | 10 | 10 |
| Reference Parameters | D2 | D3 |
|---|---|---|
| Cruise speed [m/s] | 17.0 | 14.5 |
| Lift coefficient of forward foil | 0.8338 | 1.1416 |
| Lift coefficient of afterward foil | 0.4474 | 0.4957 |
| Submergence ration of forward foil at cruise speed | 0.72 | 0.68 |
| Metacentric height [m] | 0.66 | 0.57 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
D’Amato, E.; Notaro, I.; Piscopo, V.; Scamardella, A. Hydrodynamic Design of Fixed Hydrofoils for Planing Craft. J. Mar. Sci. Eng. 2023, 11, 246. https://doi.org/10.3390/jmse11020246
D’Amato E, Notaro I, Piscopo V, Scamardella A. Hydrodynamic Design of Fixed Hydrofoils for Planing Craft. Journal of Marine Science and Engineering. 2023; 11(2):246. https://doi.org/10.3390/jmse11020246
Chicago/Turabian StyleD’Amato, Egidio, Immacolata Notaro, Vincenzo Piscopo, and Antonio Scamardella. 2023. "Hydrodynamic Design of Fixed Hydrofoils for Planing Craft" Journal of Marine Science and Engineering 11, no. 2: 246. https://doi.org/10.3390/jmse11020246
APA StyleD’Amato, E., Notaro, I., Piscopo, V., & Scamardella, A. (2023). Hydrodynamic Design of Fixed Hydrofoils for Planing Craft. Journal of Marine Science and Engineering, 11(2), 246. https://doi.org/10.3390/jmse11020246









