Application of Vortex Induced Vibration Systems to Improve Vertical Mixing and Create Light/Dark Cycles for Enhanced Algal Biomass Productivity in Raceway Ponds
Abstract
1. Introduction
2. Materials and Methods
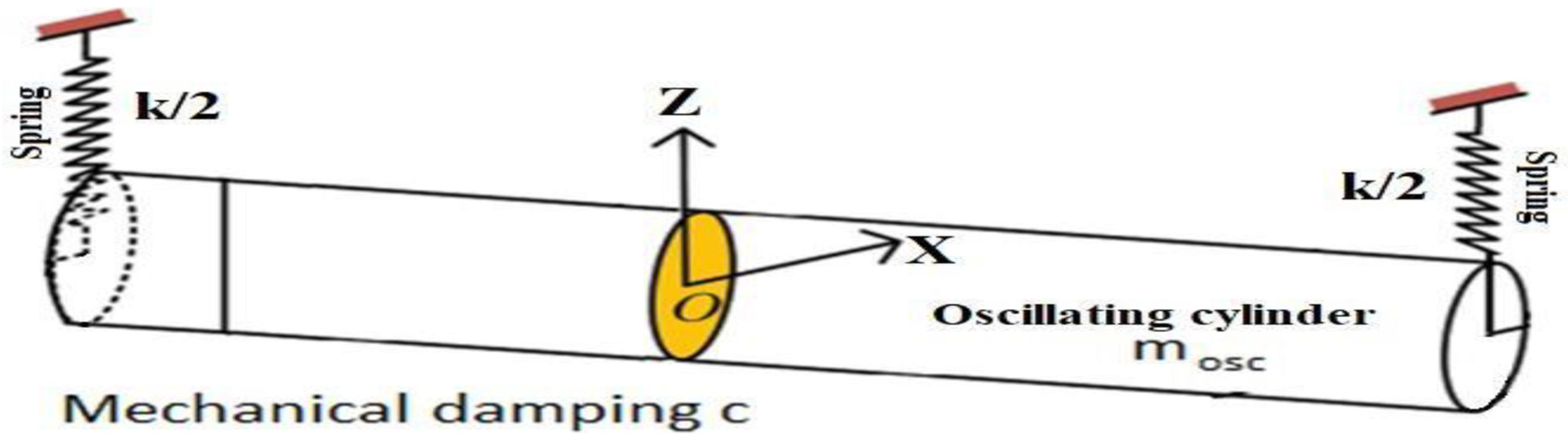
2.1. Experimental Methods and Setup
2.2. Numerical Implementation
2.2.1. Governing Equations
2.2.2. CFD Solution and Boundary
- -
- for validation of the VIV response of the cylinder obtained at the raceway pond experimentally
- -
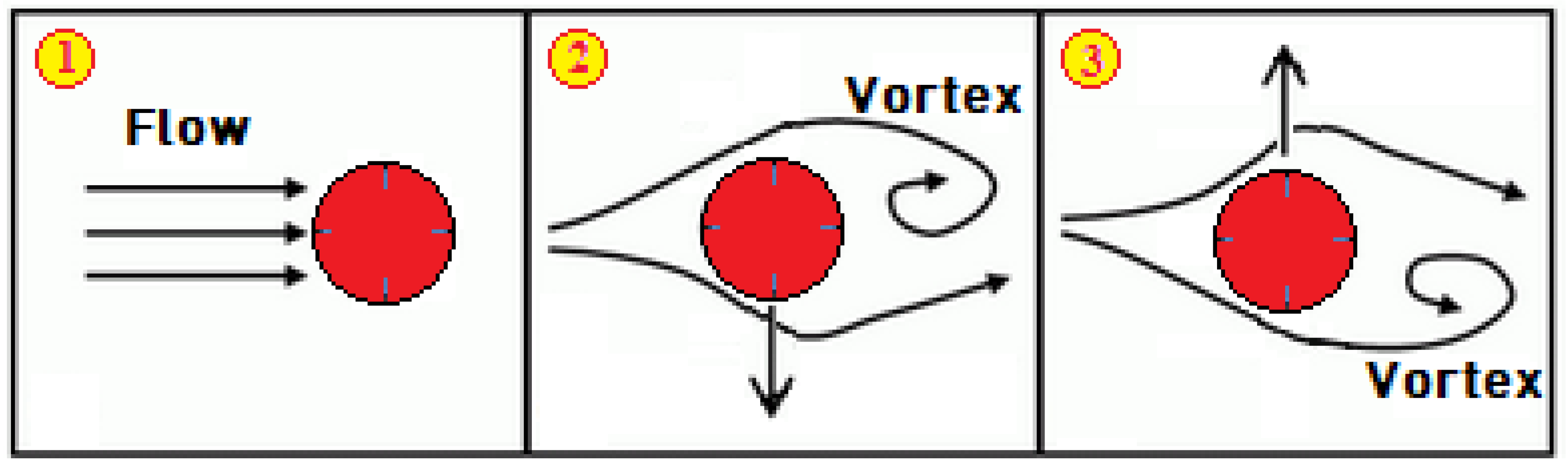
- to visualize the flow in order to gain insight into the vorticity field and flow velocities in the fluid domain.
- -
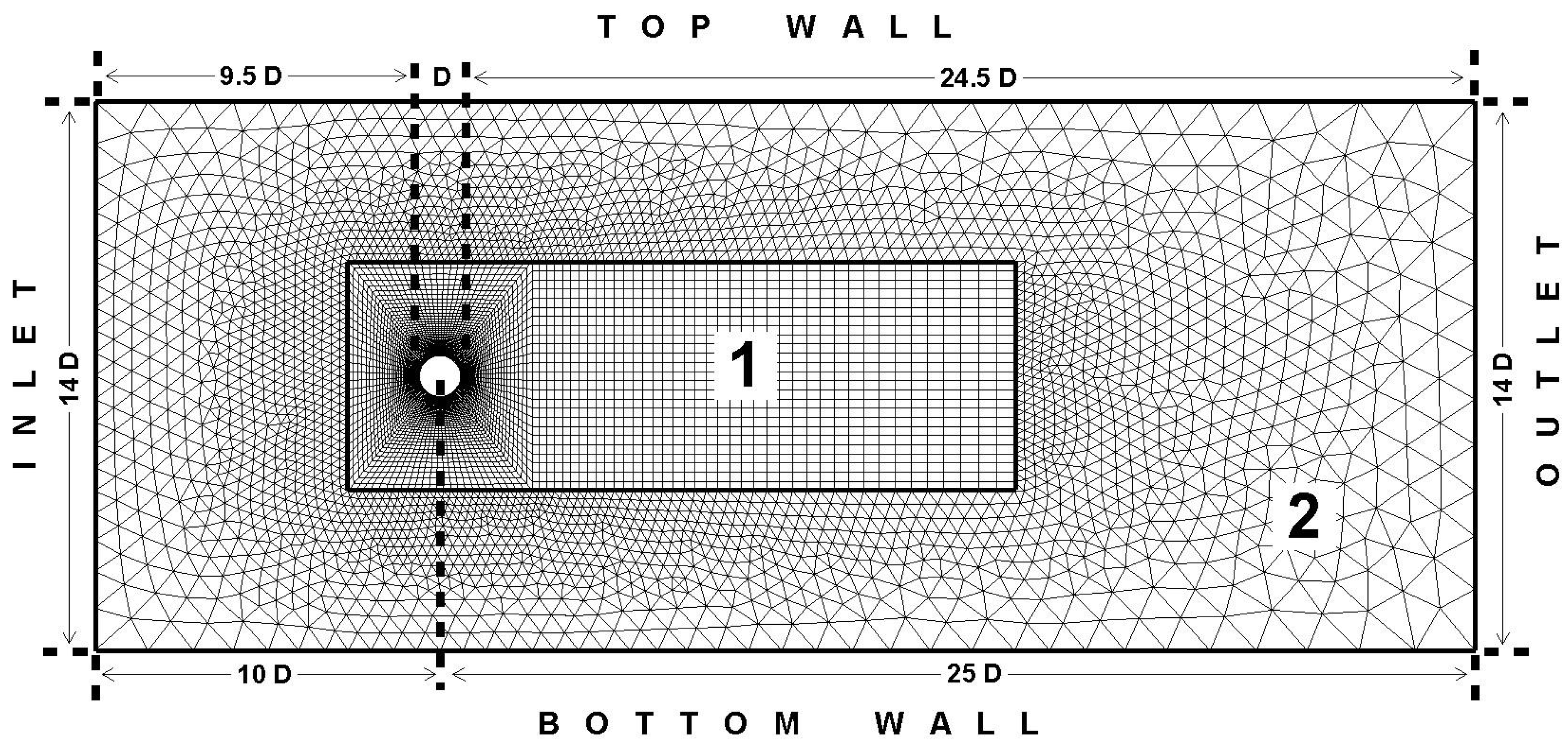
- The first domain is called the moving domain and surrounds the cylinder. The mesh is structured in this region and the elements are quadrilateral. The size of this inner rectangular domain is 17D × 6D. Number of elements in this region is around 7000.
- -
- The second domain is called the stationary domain and surrounds the moving domain. The mesh is unstructured in this region and the elements are triangular. This is the outer domain and covers the rest of the fluid domain. Number of elements in this region is around 5000.
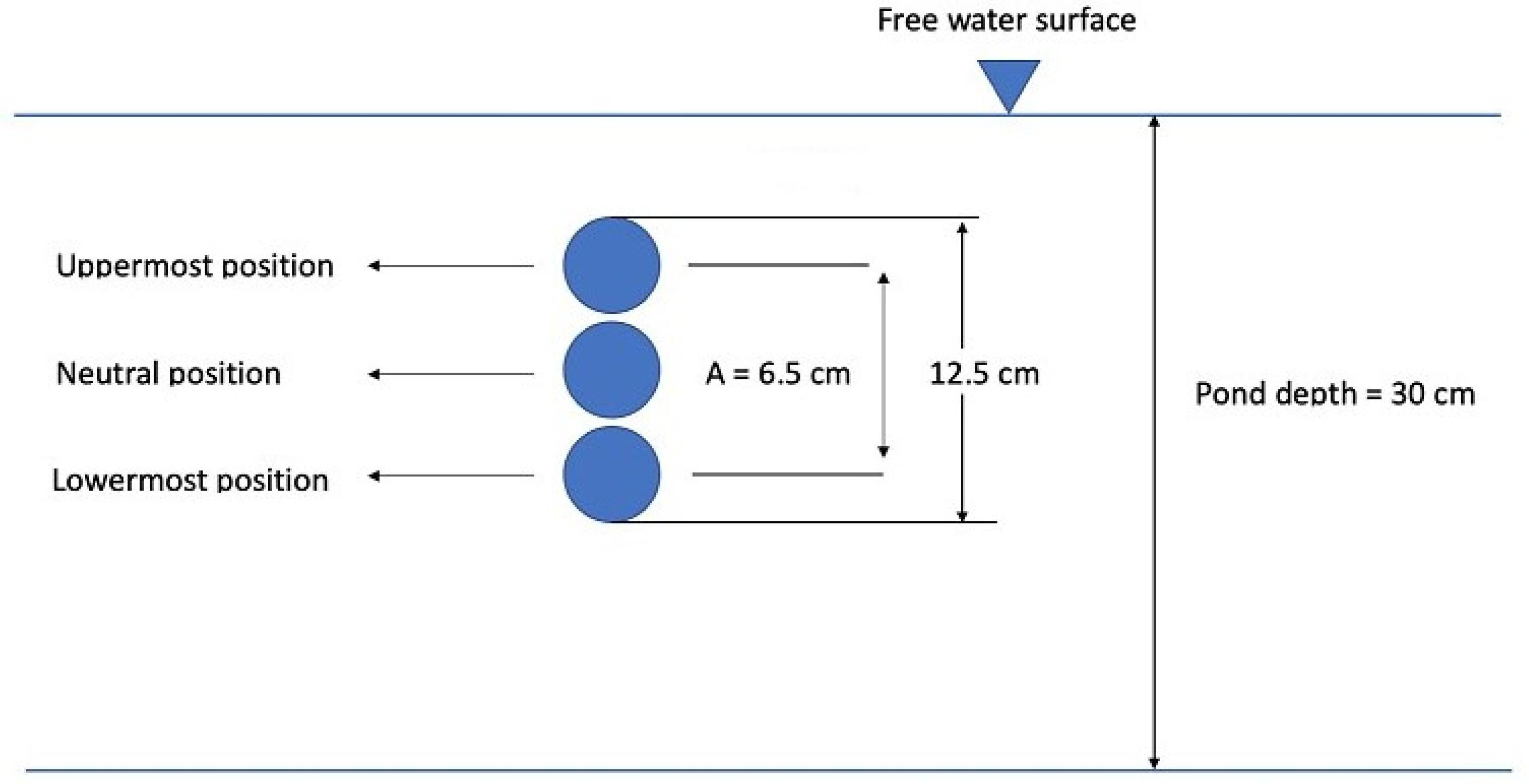
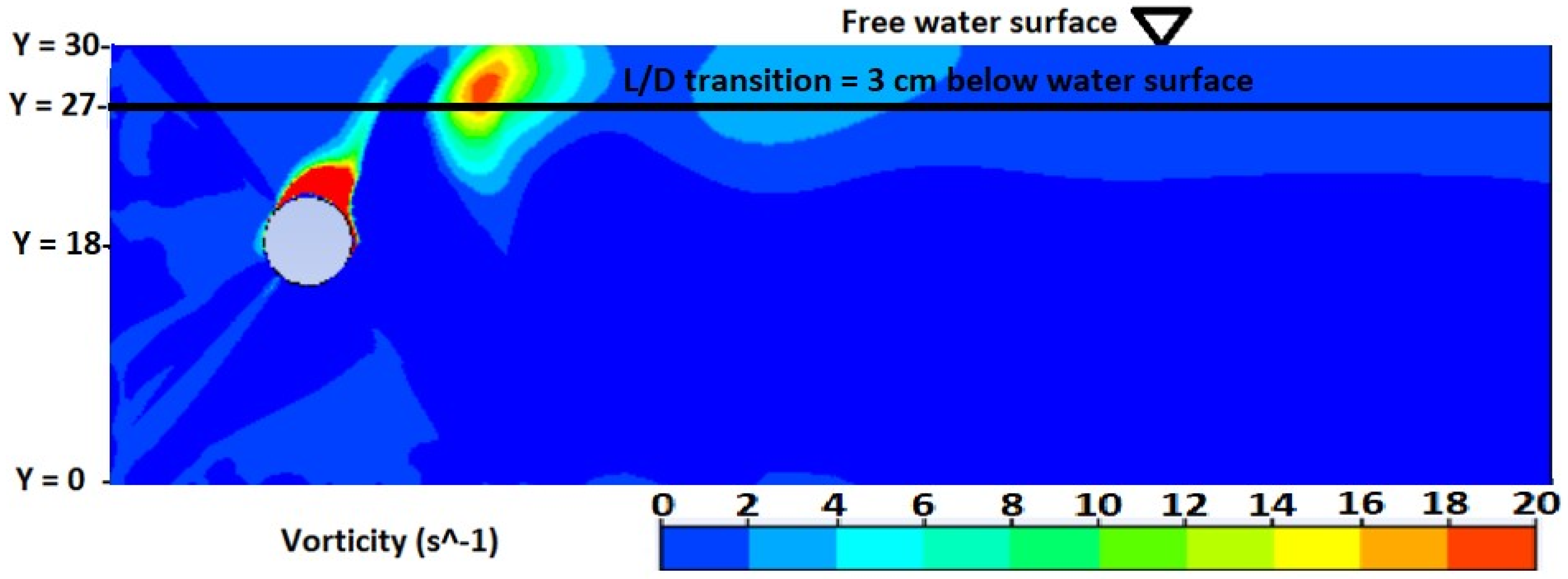
2.2.3. Evaluation of Vertical Mixing and L/D Cycles
2.2.4. Microalgae Growth Experiments with and without VIV System
3. Results and Discussion
3.1. Experimental Pilot Scale VIV Cylinder Oscillation
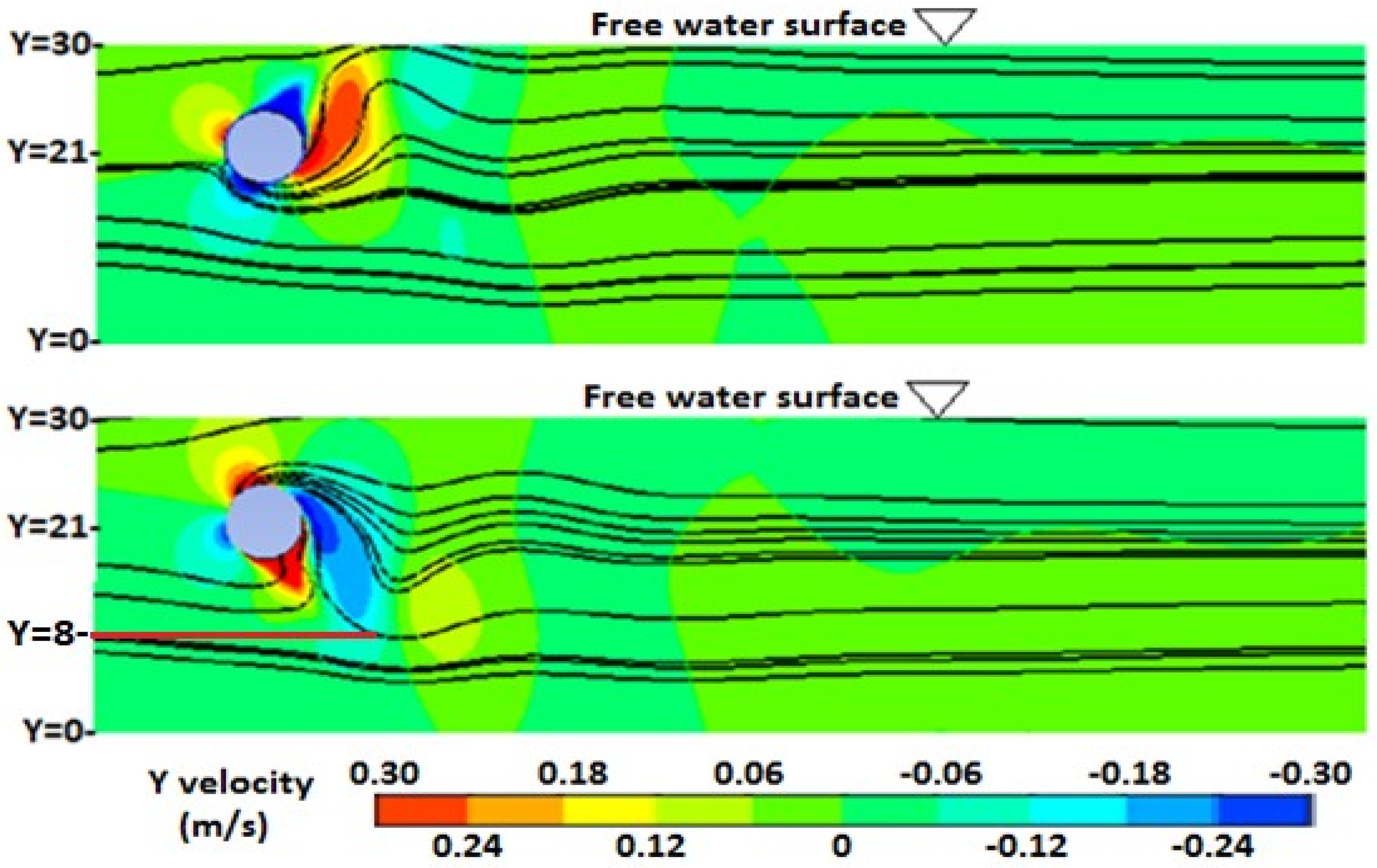
3.2. Numerical Investigation of Vertical Mixing and L/D Cycles
3.3. Enhanced Biomass Production in V—RWP
3.4. Concluding Remarks and Future Directions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| RWP | Raceway pond |
| CFD | Computational fluid Dynamics |
| L/W ratio | Length to width ratio |
| L/D cycle | Light/dark cycle |
| VIV | Vortex induced vibrations |
| mosc | Total oscillating mass |
| c | Mechanical damping |
| k | Spring stiffness |
| Ffluid | Force applied on cylinder by fluid |
| Fi | External (gravitational) force |
| m* | Mass ratio |
| fn,w | Natural frequency in still water |
| ζ | Damping ratio |
| md | Displaced mass |
| ma | Added mass |
| P | Power available in the fluid |
| Ca | Added mass coefficient |
| U | Flow velocity |
| U* | Reduced velocity |
| A | Amplitude |
| A* | Reduced amplitude |
| D | Cylinder diameter |
| f | Oscillation frequency |
| f* | Reduced oscillation frequency |
| fL/D | Light/dark cycle frequency |
| μ | Dynamic viscosity |
| p | Pressure |
| ρ | Fluid density |
| Ω | Angular velocity |
| ω | Vorticity magnitude |
| RANSE | Reynolds—averaged Navier—Stokes equations |
References
- Babcock, R.W.; Wellbrock, A.; Slenders, P.; Radway, J.C. Improving mass transfer in an inclined tubular photobioreactor. J. Appl. Phycol. 2016, 28, 2195–2203. [Google Scholar] [CrossRef]
- Wang, C.; Lan, C.Q. Effects of shear stress on microalgae-A review. Biotechnol. Adv. 2018, 36, 986–1002. [Google Scholar] [CrossRef]
- Zhang, Q.; Xue, S.; Yan, C.; Wu, X.; Wen, S.; Cong, W. Installation of flow deflectors and wing baffles to reduce dead zone and enhance flashing light effect in an open raceway pond. Bioresour. Technol. 2015, 198, 150–156. [Google Scholar] [CrossRef] [PubMed]
- Ghasemi, Y.; Rasoul-Amini, S.; Naseri, A.T.; Montazeri-Najafabady, N.; Mobasher, M.A.; Dabbagh, F. Microalgae Biofuel Potentials (Review). Appl. Biochem. Microbiol. 2012, 48, 126–144. [Google Scholar] [CrossRef]
- Mendoza, J.; Granados, M.; de Godos, I.; Acién, F.; Molina, E.; Banks, C.; Heaven, S. Fluid-dynamic characterization of real-scale raceway reactors for microalgae production. Biomass-Bioenergy 2013, 54, 267–275. [Google Scholar] [CrossRef]
- Hadiyanto, H.; Elmore, S.; Van Gerven, T.; Stankiewicz, A. Hydrodynamic evaluations in high rate algae pond (HRAP) design. Chem. Eng. J. 2013, 217, 231–239. [Google Scholar] [CrossRef]
- Sompech, K.; Chisti, Y.; Srinophakun, T. Design of raceway ponds for producing microalgae. Biofuels 2012, 3, 387–397. [Google Scholar] [CrossRef]
- Grobbelaar, J.U. Turbulence in mass algal cultures and the role of light/dark fluctuations. J. Appl. Phycol. 1994, 6, 331–335. [Google Scholar] [CrossRef]
- Xu, B.; Li, P.; Waller, P.; Huesemann, M. Evaluation of flow mixing in an ARID-HV algal raceway using statistics of temporal and spatial distribution of fluid particles. Algal Res. 2015, 9, 27–39. [Google Scholar] [CrossRef]
- Murphy, T.E.; Kapili, B.J.; Detweiler, A.M.; Bedout, B.M.; Prufert-Bedout, L.E. Vertical distribution of algal productivity in open raceways. Algal Res. 2015, 11, 334–342. [Google Scholar] [CrossRef]
- Borowitzka, M.A. Limits to Growth in Wastewater Treatment with Algae; Wong, Y.S., Tam, N.F.Y., Eds.; Springer: Berlin, Germany, 1998; pp. 203–226. [Google Scholar]
- Spierling, R.; Crowe, B.; Adler, N.; Poole, K.; Hutton, M.; Huesemann, M.; Lane, T.; Poorey, K.; Anderson, D.; Benemann, J.; et al. Final Report: Scale Up of Algal Biofuel Production Using Waste Nutrients; California Polytechnic Institute: San Luis Obispo, CA, USA, 2018. [Google Scholar]
- Sutherland, D.L.; Howard-Williams, C.; Turnbull, M.H.; Broady, P.A.; Craggs, R.J. Enhancing microalgal photosynthesis and productivity in wastewater treatment high rate algal ponds for biofuel production. Bioresour. Technol. 2015, 184, 222–229. [Google Scholar] [CrossRef] [PubMed]
- Cheng, J.; Guo, W.; Cai, C.; Ye, Q.; Zhou, J. Alternatively permutated conic baffles generate vortex flow field to improve microalgal productivity in a raceway pond. Bioresour. Technol. 2018, 249, 212–218. [Google Scholar] [CrossRef]
- Cheng, J.; Guo, W.; Song, Y.; Kumar, S.; Ali, K.A.; Zhou, J. Enhancing vorticity magnitude of turbulent flow to promote photochemical efficiency and trichome helix pitch of Arthosphira platensis in a raceway pond with conic baffles. Bioresour. Technol. 2018, 269, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Kumar, S.; Cheng, J.; Guo, W.; Ali, K.A.; Song, Y. Self rotary propellers with clockwise and counter-clockwise blades create spiral flow fields to improve mass transfer and promote microalgae growth. Bioresour. Technol. 2019, 286, 121384. [Google Scholar] [CrossRef] [PubMed]
- Chiaramonti, D.; Prussi, M.; Casini, D.; Tredici, M.R.; Rodolfi, L.; Bassi, N.; Zittelli, G.C.; Bondioli, P. Review of energy balance in raceway ponds for microalgae cultivation: Re-thinking a traditional system is possible. Appl. Energy 2013, 102, 101–111. [Google Scholar] [CrossRef]
- Cheng, J.; Yang, Z.; Ye, Q.; Zhou, J.; Cen, K. Enhanced flashing light effect with up-down chute baffles to improve microalgal growth in a raceway pond. Bioresour. Technol. 2015, 190, 29–35. [Google Scholar] [CrossRef] [PubMed]
- Yang, Z.; Cheng, J.; Ye, Q.; Liu, J.; Zhou, J.; Cen, K. Decrease in light/dark cycle of microalgal cells with computational fluid dynamics simulation to improve microalgal growth in a raceway pond. Bioresour. Technol. 2016, 220, 352–359. [Google Scholar] [CrossRef]
- Bernitsas, M.M.; Raghavan, K.; Ben-Simon, Y.; Garcia, E.M.H. VIVACE (Vortex Induced Vibration Aquatic Clean Energy): A New Concept in Generation of Clean and Renewable Energy From Fluid Flow. J. Offshore Mech. Arct. Eng. 2008, 130, 041101. [Google Scholar] [CrossRef]
- Govardhan, R.; Williamson, C.H.K. Modes of vortex formation and frequency response of a freely vibrating cylinder. J. Fluid Mech. 2000, 420, 85–130. [Google Scholar] [CrossRef]
- Wilcox, D. Formulation of k-ω turbulence model revisited. AIAA J. 2008, 46, 2823–2838. [Google Scholar] [CrossRef]
- Kinaci, O.K. 2-D Urans Simulations of Vortex Induced Vibrations of Circular Cylinder at Trsl3 Flow Regime. J. Appl. Fluid Mech. 2016, 9, 2537–2544. [Google Scholar] [CrossRef]
- Duranay, A.; Kinaci, O.K. Enhancing two-dimensional computational approach for vortex-induced vibrations by scaling lift force. Ocean Eng. 2020, 217, 107620. [Google Scholar] [CrossRef]
- Dobrucali, E.; Kinaci, O.K.; Academy, T.N. URANS-Based Prediction of Vortex Induced Vibrations of Circular Cylinders. J. Appl. Fluid Mech. 2017, 10, 957–970. [Google Scholar] [CrossRef]
- Chen, Z.; Zhang, X.; Jiang, Z.; Chen, X.; He, H.; Zhang, X. Light/dark cycle of microlgae cells in raceway ponds: Effects of paddlewheel rotational speeds and baffles installation. Bioresour. Technol. 2016, 219, 387–391. [Google Scholar] [CrossRef] [PubMed]
- Chiarini, A.; Quadrio, M. The light/dark cycle of microalgae in a thin-layer photobioreactor. J. Appl. Phycol. 2021, 33, 183–195. [Google Scholar] [CrossRef]
- Talley, L.D.; Pickard, G.L.; Emery, W.J.; Swift, J.H. Chapter 7-Dynamical processes for descriptive ocean circulation. In Descriptive Physical Oceanography, 6th ed.; Elsevier: Amsterdam, The Netherlands, 2011; pp. 187–221. [Google Scholar]
- Luhtana, H.; Tolvanen, H. Optimizing the use of Secchi depth as a proxy for euphotic depth in coastal waters: An empirical study for the Baltic sea. ISPRS Int. J. Geo-Inf. 2013, 2, 1153–1168. [Google Scholar] [CrossRef]
- Moberg, A.K.; Ellem, G.K.; Jameson, G.J.; Herbertson, J.G. Simulated cell trajectories in a stratified gas–liquid flow tubular photobioreactor. J. Appl. Phycol. 2011, 24, 357–363. [Google Scholar] [CrossRef]
- Pan, Z.; Cui, W.; Miao, Q. Numerical simulation of vortex-induced vibration of a circular cylinder at low mass-damping using RANS code. J. Fluids Struct. 2007, 23, 23–37. [Google Scholar] [CrossRef]
- Khalak, A.; Williamson, C.H.K. Dynamics of hydroelastic cylinder with very low mass and damping. J. Fluids Struct. 1996, 10, 455–472. [Google Scholar] [CrossRef]
- Wanderley, B.; Souza, G.; Sphaier, C.L.S.; Levi, C. Vortex induced vibration of an elastically mounted circular cylinder using an upwind TVD two-dimensional numerical scheme. Ocean. Eng. 2008, 35, 1533–1544. [Google Scholar] [CrossRef]
- Park, H.R.; Kumar, R.A.; Bernitsas, M.M. Enhancement of flow induced motions of rigid circular cylinder on springs by localized surface roughness at 3*104 < Re < 1.2*105. Ocean. Eng. 2013, 72, 403–415. [Google Scholar]
- Borowitkza, M.A.; Moheimani, N.R. Open pond culture systems. In Algae for Biofuels and Energy; Springer: Berlin/Heidelberg, Germany, 2013; pp. 133–152. [Google Scholar]
- Norsker, N.H.; Barbosa, M.J.; Vermue, M.H.; Wijffels, R.H. Micoalgal production-a close look at economics. Biotechnol. Adv. 2011, 29, 24–27. [Google Scholar] [CrossRef] [PubMed]
- Khoeyi, Z.A.; Seyfadabi, J.; Ramezanpour, Z. Effect of light intensity and photoperiod on biomass and fatty acid of the microalgae, Chlorella vulgaris. Aquac. Int. 2012, 20, 41–49. [Google Scholar] [CrossRef]
- Li, M.; Hu, D.; Liu, H. Photobioreactor with ideal light–dark cycle designed and built from mathematical modeling and CFD simulation. Ecol. Eng. 2014, 73, 162–167. [Google Scholar] [CrossRef]
- Brindley, C.; Fernández, F.A.; Fernández-Sevilla, J. Analysis of light regime in continuous light distributions in photobioreactors. Bioresour. Technol. 2010, 102, 3138–3148. [Google Scholar] [CrossRef] [PubMed]
- Laws, E.A.; Terry, K.L.; Wickman, J.; Chalup, M.S. A simple algal production system designed to utilize the flashing light effect. Biotechnol. Bioeng. 1983, 25, 2319–2335. [Google Scholar] [CrossRef]
- Grobbelaar, J.U.; Nedbal, L.; Tichý, V. Influence of high frequency light/dark fluctuations on photosynthetic characteristics of microalgae photoacclimated to different light intensities and implications for mass algal cultivation. J. Appl. Phycol. 1996, 8, 335–343. [Google Scholar] [CrossRef]






| Parameter | Symbol | Units | |
|---|---|---|---|
| Flow velocity | m s−1 | 0.3 | |
| Reduced flow velocity | U* | - | 5 |
| Oscillating mass | kg | 3.35 | |
| Displaced mass | kg | 1.16 | |
| Mass ratio | m* | - | 2.86 |
| Nat. frequency in still water | fn,w | - | 0.99 |
| Total spring stiffness | N m−1 | 178 | |
| Cylinder diameter | cm | 6 |
| Boundary/Domain | Dimensions | Boundary Condition (BC) or Mesh Technique (MT) | Elements | Moving | Deforming |
|---|---|---|---|---|---|
| Cylinder (boundary) | D | Wall (BC) | Line | Yes | No |
| Inlet (boundary) | 14D | Velocity Inlet (BC) | Line | No | No |
| Outlet (boundary) | 14D | Pressure Outlet (BC) | Line | No | No |
| Top Wall (boundary) | 35D | Wall (BC) | Line | No | No |
| Bottom Wall (boundary) | 35D | Wall (BC) | Line | No | No |
| 1 (domain) | 17D × 6D | Dynamic Mesh (MT) | Quadrilateral | Yes | No |
| 2 (domain) | The rest of the domain | Stationary Mesh (MT) | Triangular | No | Yes |
| Parameter | Symbol | Units | Experimental | Numerical | Deviation (%) | |
|---|---|---|---|---|---|---|
| Input | Mass ratio | - | 2.86 | - | ||
| Reduced velocity | - | 5 | - | |||
| Nat. freq. in still water | s−1 | 0.99 | - | |||
| Output | Reduced amplitude | - | 0.54 | 0.58 | 7.4 | |
| Oscillation frequency | s−1 | 1.24 | 1.30 | 4.8 | ||
| Distance from Cylinder | |||||||
|---|---|---|---|---|---|---|---|
| 10 | 20 | 30 | 40 | 50 | 60 | ||
| Cylinder position | Uppermost | 21.17 | 11.46 | 8.16 | 6.34 | 5.21 | 4.43 |
| Neutral | 5.28 | 3.48 | 2.69 | 2.19 | 1.89 | 1.66 | |
| Lowermost | 2.33 | 1.76 | 1.54 | 1.32 | 1.16 | 1.05 | |
| Method to Improve L/D Cyle Frequency | L/D Cycle Frequency (s−1) | Depth (m) | Method for Investigation of L/D Cycle Frequency | Reference |
|---|---|---|---|---|
| Vortex induced vibrations | 21.17–1.05 | 0.3 | Numerical | This study |
| Up—down chute baffles | 0.07–0.23 | 0.1 | Numerical | [2] |
| Foil wings * | 0.25–0.50 | 0.075 | Experimental | [40] |
| Flow deflector baffles | 0.33–0.57 | 0.3 | Numerical | [27] |
| Up—down chute baffles | 0.083–1 | 0.06 | Experimental | [18] |
| Up—down chute baffles | 0.3 | 0.06 | Numerical | [19] |
| Conic baffles * | 1.37 | 0.1 | Numerical | [14] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Akca, M.S.; Ceylan-Perver, G.; Duranay, A.; Kinaci, O.K.; Inanc, B. Application of Vortex Induced Vibration Systems to Improve Vertical Mixing and Create Light/Dark Cycles for Enhanced Algal Biomass Productivity in Raceway Ponds. J. Mar. Sci. Eng. 2023, 11, 245. https://doi.org/10.3390/jmse11020245
Akca MS, Ceylan-Perver G, Duranay A, Kinaci OK, Inanc B. Application of Vortex Induced Vibration Systems to Improve Vertical Mixing and Create Light/Dark Cycles for Enhanced Algal Biomass Productivity in Raceway Ponds. Journal of Marine Science and Engineering. 2023; 11(2):245. https://doi.org/10.3390/jmse11020245
Chicago/Turabian StyleAkca, Mehmet Sadik, Gamze Ceylan-Perver, Aytekin Duranay, Omer Kemal Kinaci, and Bulent Inanc. 2023. "Application of Vortex Induced Vibration Systems to Improve Vertical Mixing and Create Light/Dark Cycles for Enhanced Algal Biomass Productivity in Raceway Ponds" Journal of Marine Science and Engineering 11, no. 2: 245. https://doi.org/10.3390/jmse11020245
APA StyleAkca, M. S., Ceylan-Perver, G., Duranay, A., Kinaci, O. K., & Inanc, B. (2023). Application of Vortex Induced Vibration Systems to Improve Vertical Mixing and Create Light/Dark Cycles for Enhanced Algal Biomass Productivity in Raceway Ponds. Journal of Marine Science and Engineering, 11(2), 245. https://doi.org/10.3390/jmse11020245






