A Numerical Study on the Influence of Caterpillars to the Resistance Performance of an Amphibious Vehicle
Abstract
:1. Introduction
2. Numerical Simulation
2.1. Governing Equations
2.2. Computational Configuration
2.2.1. Simulation Object
2.2.2. Mesh Generation and Boundary Conditions
3. Result and Discussion
3.1. Numerical Simulation Results
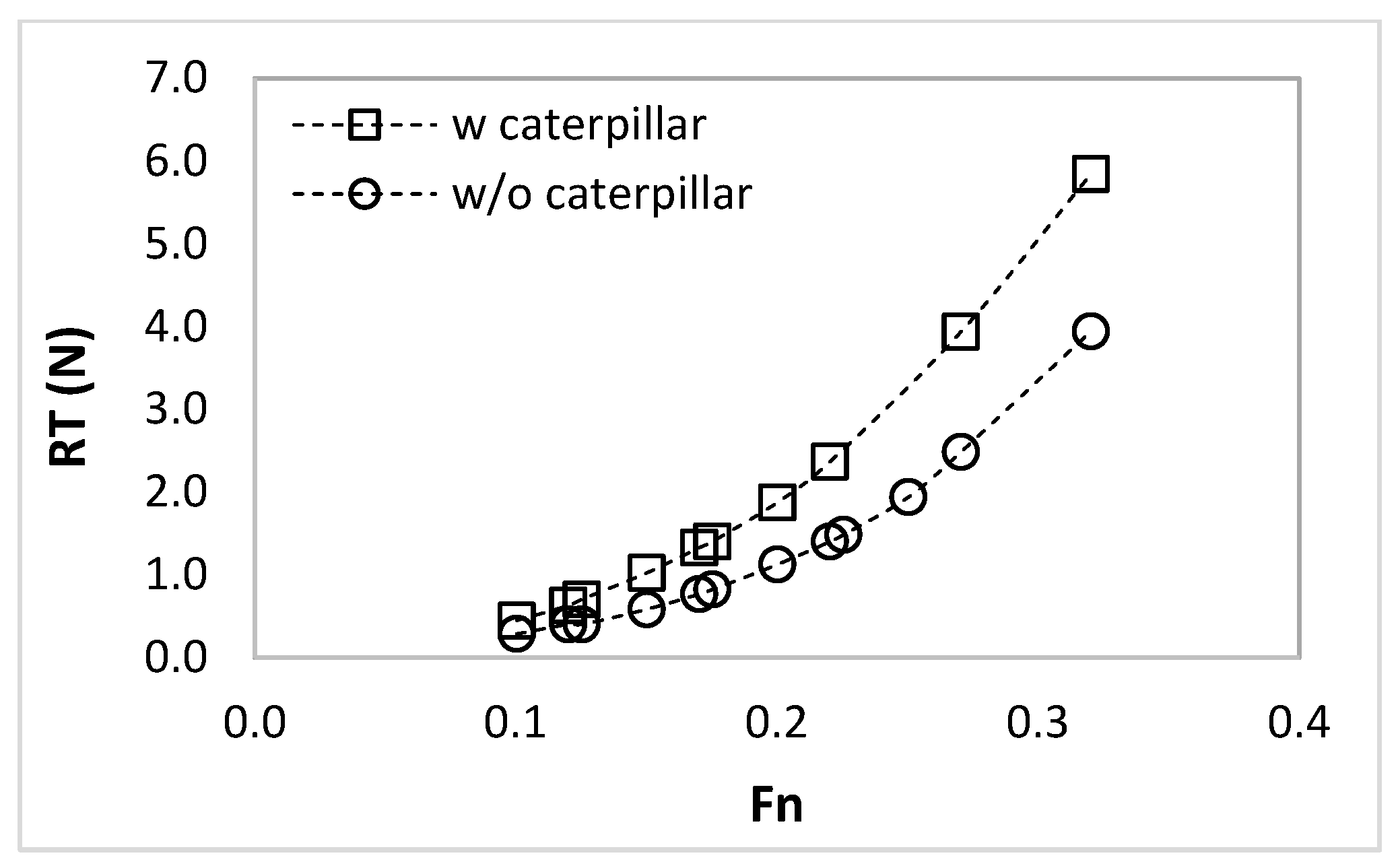
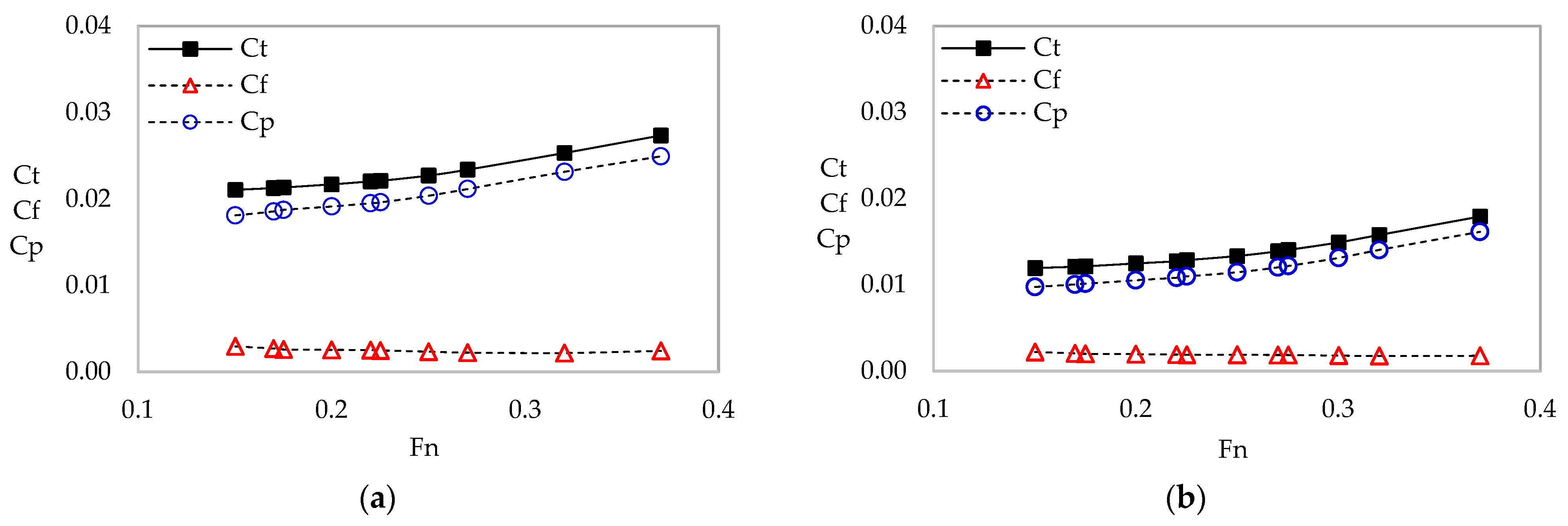
3.1.1. Components of Total Resistance
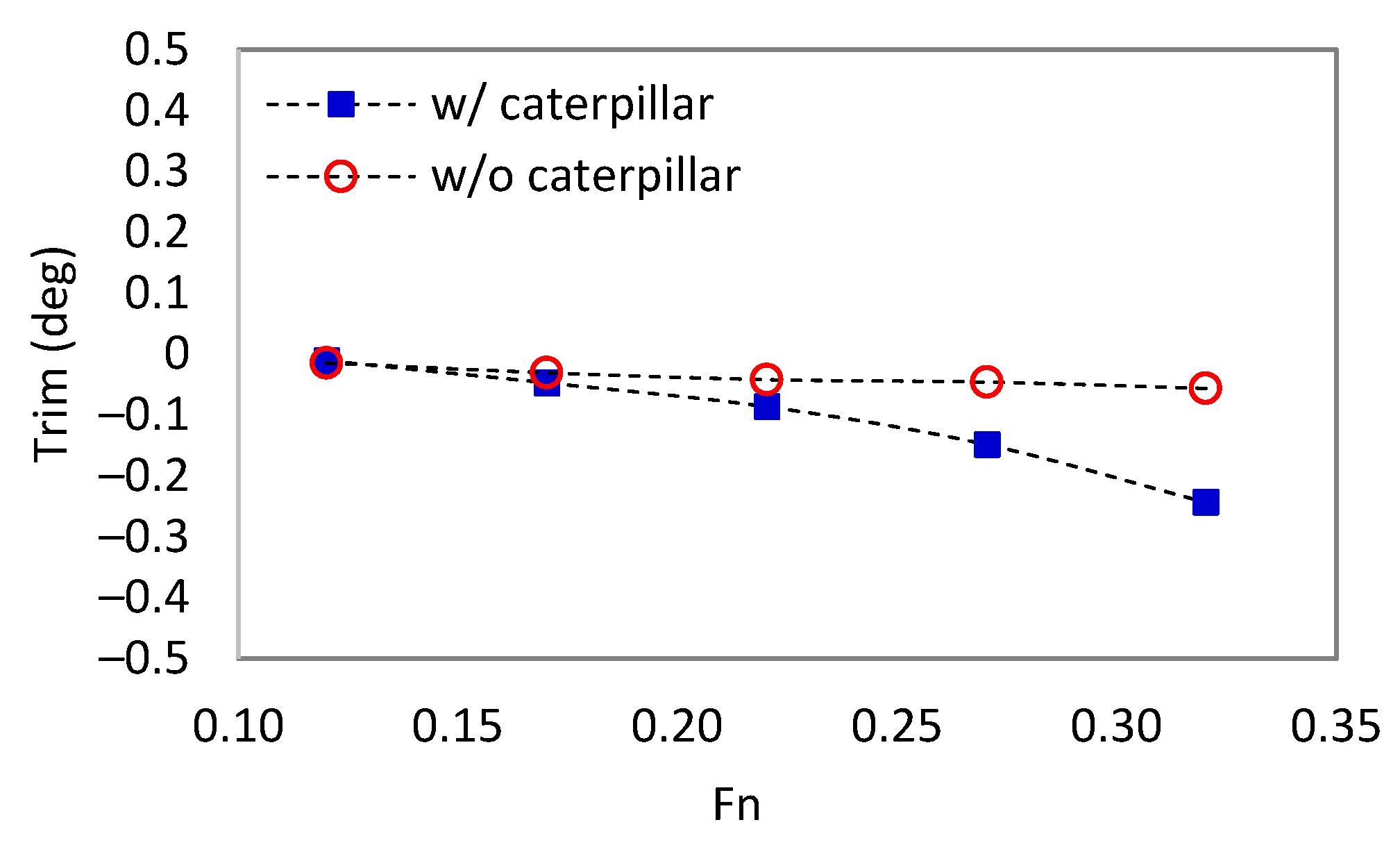
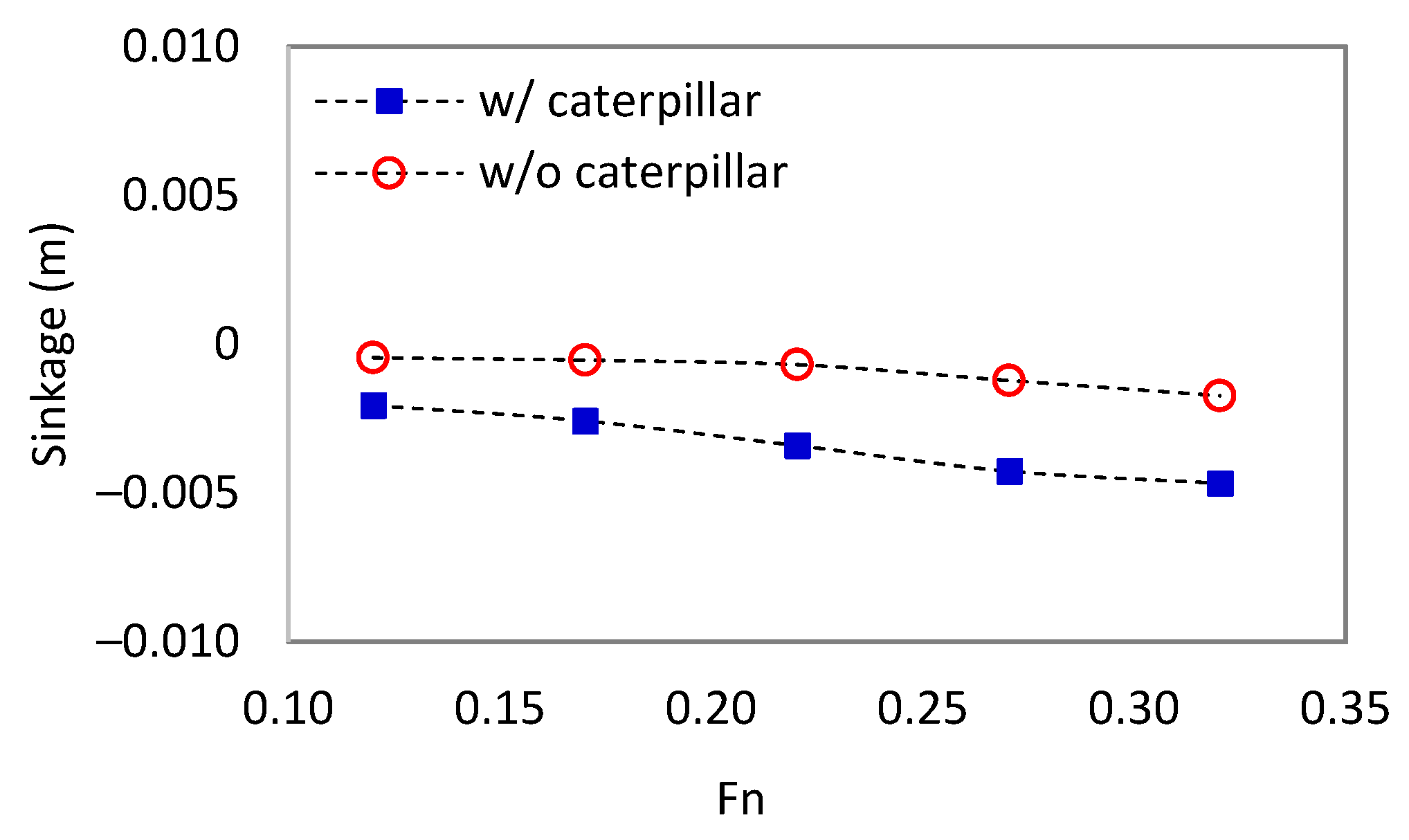
3.1.2. Trim and Sinkage
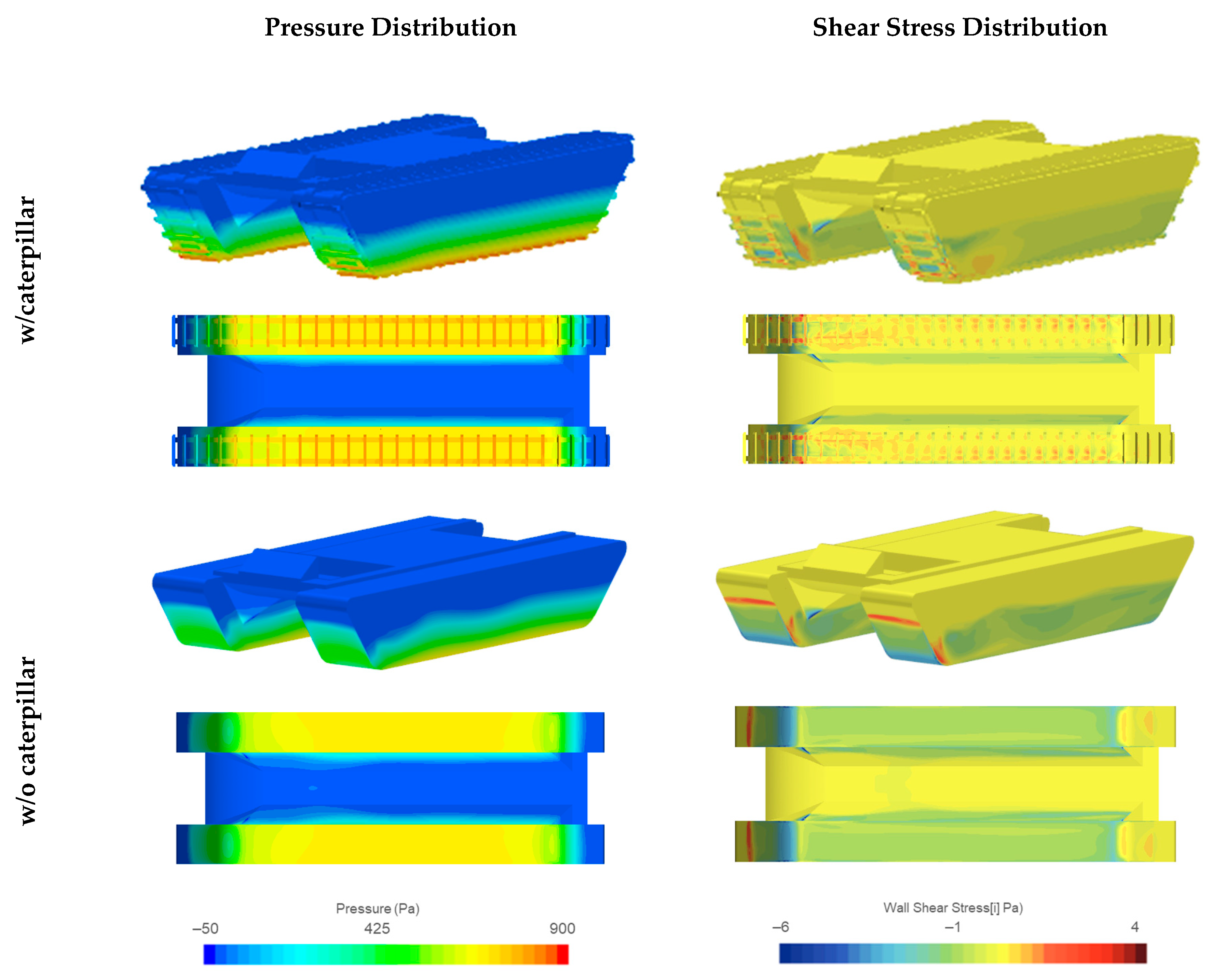
3.1.3. Pressure and Shear Stress Distribution
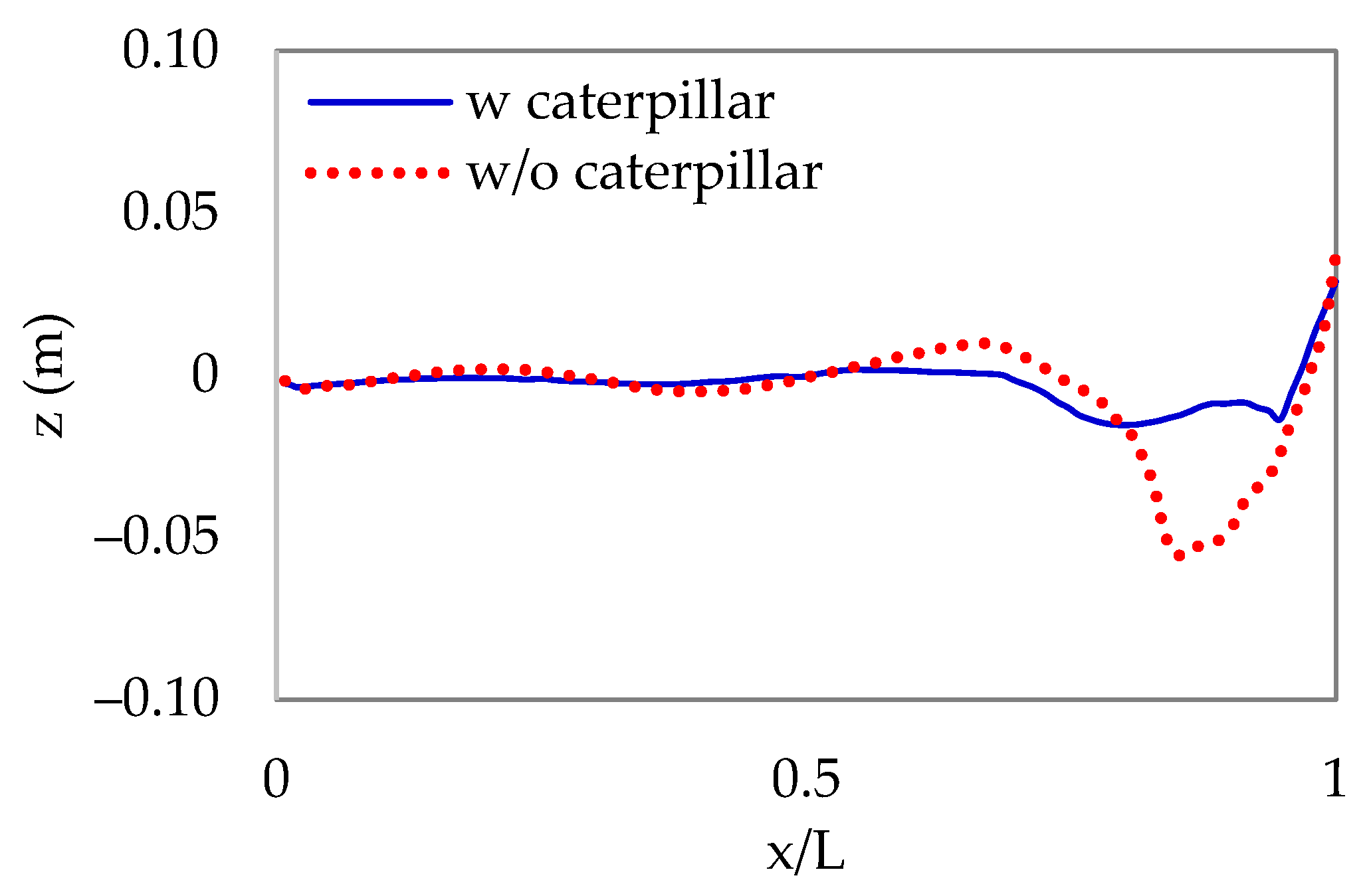
3.1.4. Wave Profile
3.1.5. Wave Configuration
3.2. Validation with Experiment
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kovačević, N.V. Influence of the Amphibious Transporter STM-M on Environment. Vojnoteh. Glas. 2014, 62, 187–200. [Google Scholar]
- Lepage, J.-D.G. German Military Vehicles of World War II: An Illustrated Guide to Cars, Trucks, Half-Tracks, Motorcycles, Amphibious Vehicles and Others; McFarland: Jefferson, NC, USA, 2007. [Google Scholar]
- Lee, C.-C. Track-Shoe of Amphibious Caterpillar Vehicle. U.S. Patent US20040239182A1, 2 December 2004. Available online: https://patents.google.com/patent/US20040239182A1/en (accessed on 28 November 2022).
- Lee, C.-C.; Lee, S.-S. Amphibious Caterpillar Vehicle. U.S. Patent US20220314720A1, 6 October 2022. Available online: https://patents.google.com/patent/US20220314720A1/en (accessed on 28 November 2022).
- Pan, X.; Yao, K.; Duan, L.; Hou, Z.; Tian, X.; Zhao, X. Simulation of Amphibious Vehicle Water Resistance Based on FLUENT. In Advances in Engineering Research, Proceedings of the 2015 International Conference on Materials Engineering and Information Technology Applications, Guilin, China, 30–31 August 2015; Atlantis Press: Amsterdam, The Netherlands, 2015; pp. 485–489. [Google Scholar] [CrossRef] [Green Version]
- Nakisa, M.; Maimun, A.; Ahmed, Y.M.; Behrouzi, F.; Tarmizi, A. RANS Simulation of Viscous Flow around Hull of Multipurpose Amphibious Vehicle. Int. J. Mech. Mechatron. Eng. 2014, 8, 298–302. [Google Scholar]
- Jaouad, H.; Vikram, P.; Balasubramanian, E.; Surendar, G. Computational Fluid Dynamic Analysis of Amphibious Vehicle. In Advances in Engineering Design and Simulation; Springer: Berlin, Germany, 2020; pp. 303–313. [Google Scholar]
- Yamashita, H.; Arnold, A.; Carrica, P.M.; Noack, R.W.; Martin, J.E.; Sugiyama, H.; Harwood, C. Coupled Multibody Dynamics and Computational Fluid Dynamics Approach for Amphibious Vehicles in the Surf Zone. Ocean. Eng. 2022, 257, 111607. [Google Scholar] [CrossRef]
- Sun, C.; Xu, X.; Wang, W.; Xu, H. Influence on Stern Flaps in Resistance Performance of a Caterpillar Track Amphibious Vehicle. IEEE Access 2020, 8, 123828–123840. [Google Scholar] [CrossRef]
- Jang, J.-Y.; Liu, T.-L.; Pan, K.-C.; Chu, T.-W. Numerical Investigation on the Hydrodynamic Performance of Amphibious Wheeled Armored Vehicles. J. Chin. Inst. Eng. 2019, 42, 700–711. [Google Scholar] [CrossRef]
- Du, Z.; Mu, X.; Zhu, H.; Han, M. Identification of Critical Parameters Influencing Resistance Performance of Amphibious Vehicles Based on a SM-SA Method. Ocean Eng. 2022, 258, 111770. [Google Scholar] [CrossRef]
- Sian, A.Y.; Maimun, A.; Priyanto, A.; Ahmed, Y.M. Assessment of Ship-Bank Interactions on LNG Tanker in Shallow Water. J. Teknol. 2014, 66, 3–4. [Google Scholar] [CrossRef] [Green Version]
- Nichols, B.D.; Hirt, C.W. Methods for Calculating Multidimensional, Transient Free Surface Flows Past Bodies. In Proceedings of the First International Conference on Numerical Ship Hydrodynamics, Gaithersburg, MD, USA, 20 October 1975; Volume 20. [Google Scholar]
- Hirt, C.W.; Nichols, B.D. Volume of Fluid (VOF) Method for the Dynamics of Free Boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Simcenter STAR-CCM+ Version 2022.1, News Part 1—Multiphase—Volupe Software. Available online: https://volupe.se/en/simcenter-star-ccm-version-2022-1-news-part-1-multiphase/ (accessed on 30 December 2022).
- ITTC. ITTC—Practical Guidelines for Ship CFD Applications; ITTC: Singapore, 2011. [Google Scholar]
- Rakowitz, M. Grid Refinement Study with a Uhca Wing-Body Configuration Using Richardson Extrapolation and Grid Convergence Index Gci. In New Results in Numerical and Experimental Fluid Mechanics III; Springer: Heidelberg, Germany, 2002; pp. 297–303. [Google Scholar]
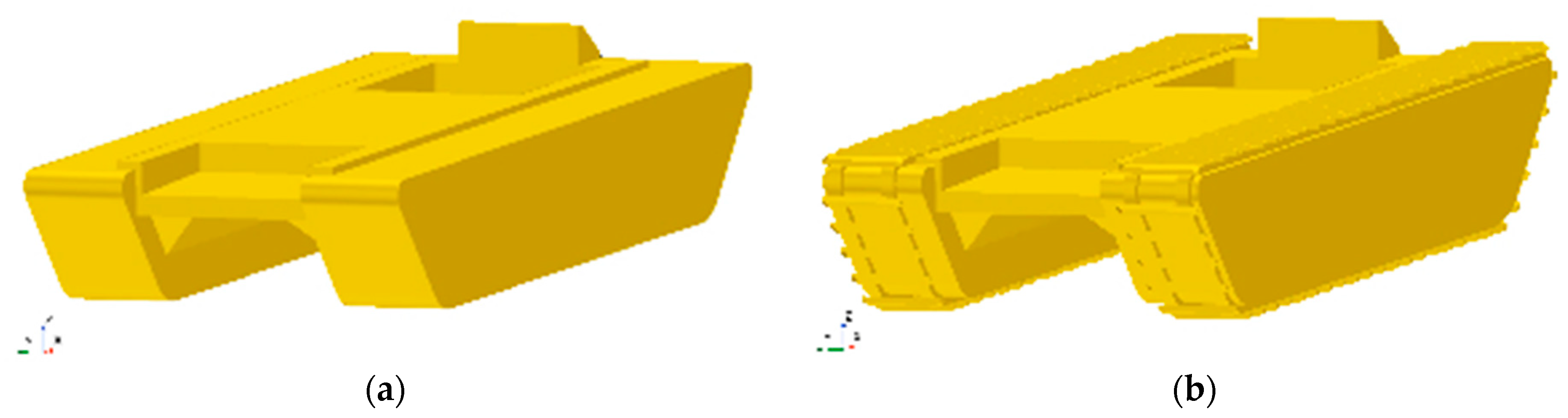
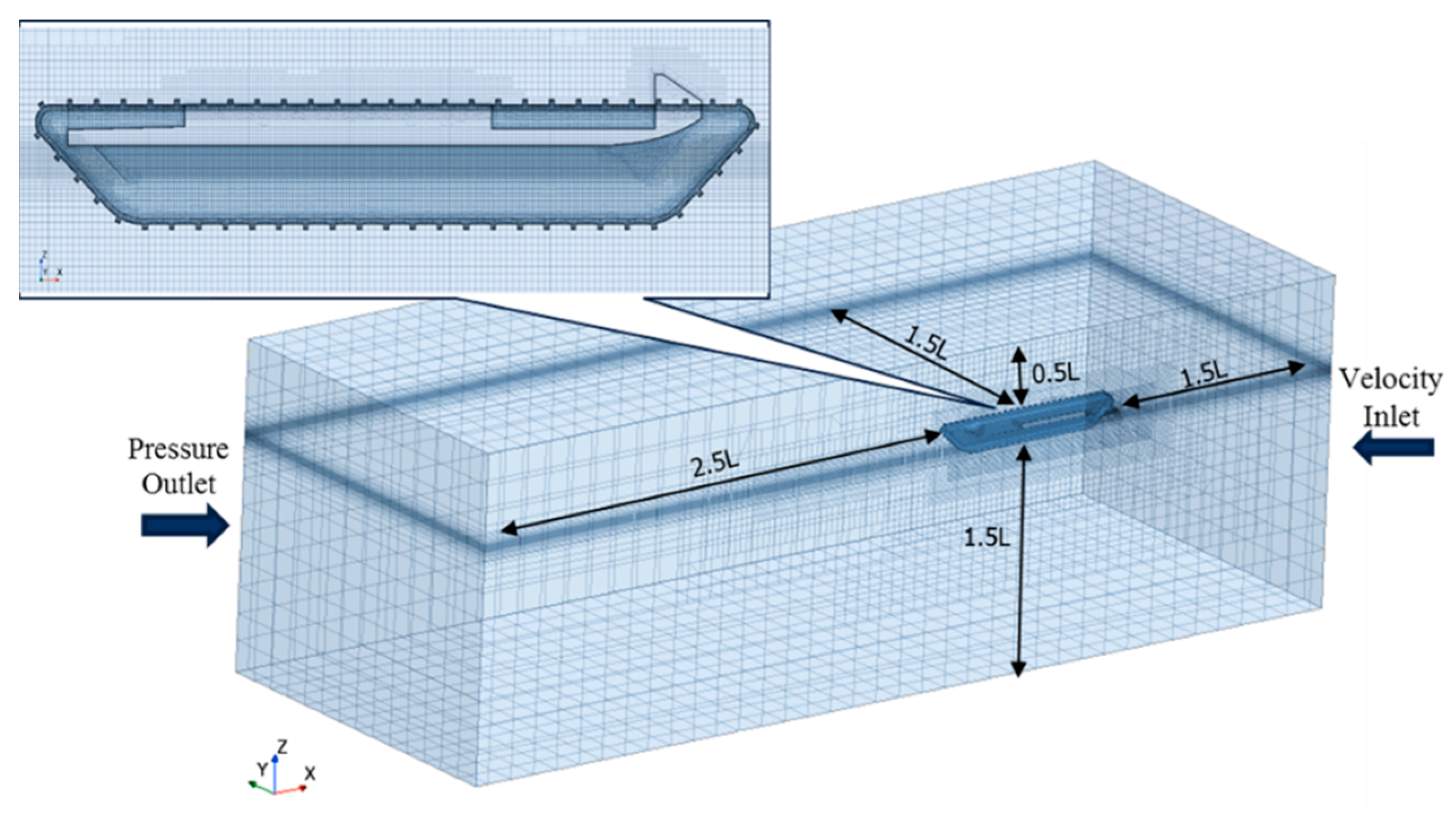




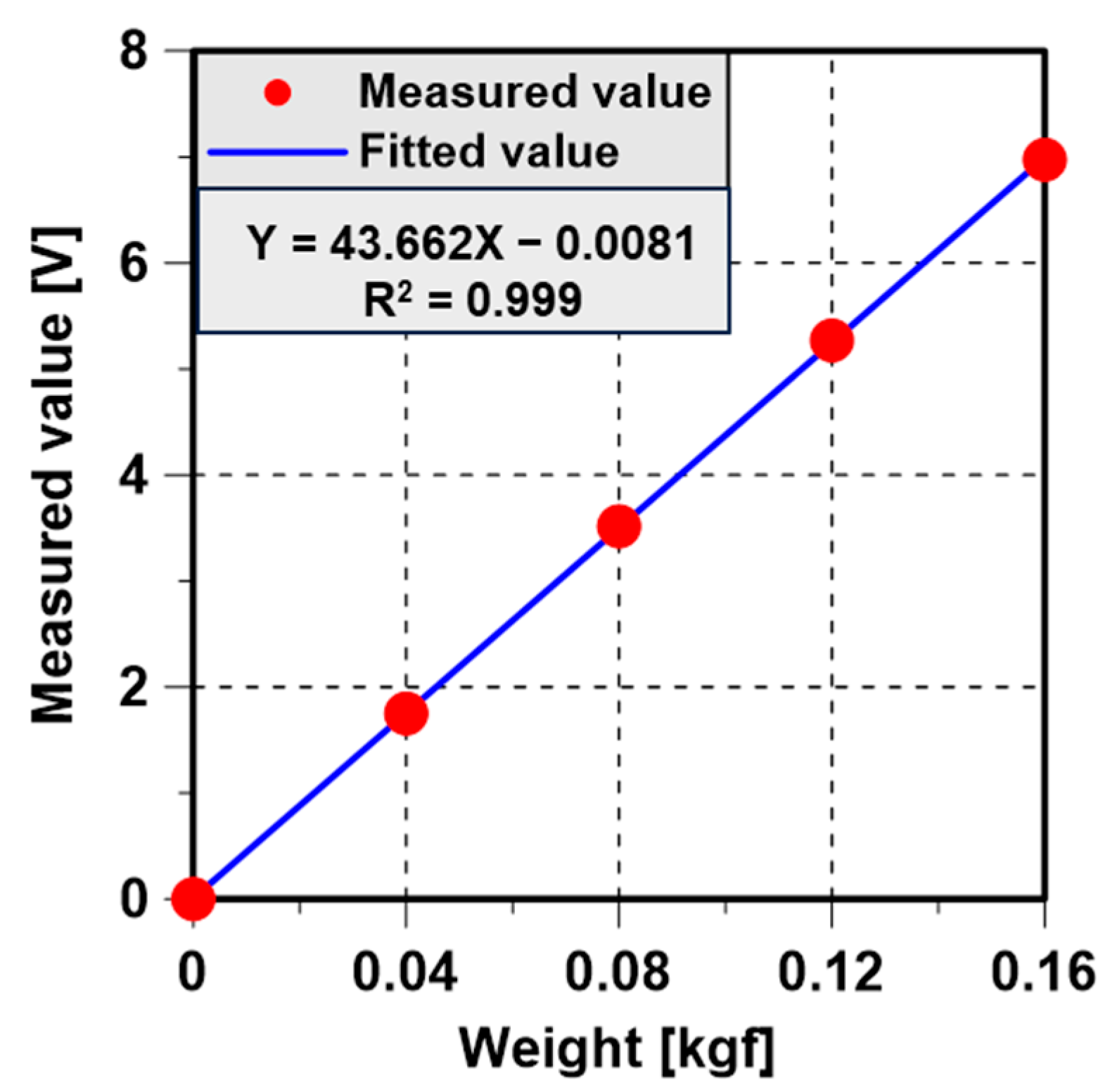

| Main Dimension | w/ Caterpillar | w/o Caterpillar | ||
|---|---|---|---|---|
| Full Scale | Model Scale | Full Scale | Model Scale | |
| Scale ratio | 1 | 1:10.767 | 1 | 1:10.767 |
| Length of Overall (LOA) [m] | 11.009 | 1.022 | 10.767 | 1 |
| Length of Waterline (LWL) [m] | 9.253 | 0.859 | 9.253 | 0.859 |
| Breadth, B [m] | 3.8 | 0.353 | 3.8 | 0.353 |
| Depth (D) [m] | 1.4 | 0.130 | 1.4 | 0.130 |
| Draft, T [m] | 0.75 | 0.07 | 0.74 | 0.069 |
| Displacement [kg] | 14,493.83 | 11.612 | 14,115.89 | 11.309 |
| Design Speed, V [knots] | 5.4 | 1.646 | 5.4 | 1.646 |
| Fn | 0.27 | 0.27 | 0.27 | 0.27 |
| Wetted Surface Area (S) [m2] | 66.53 | 0.57 | 49.68 | 0.42 |
| Mesh | 123 | 234 | 345 | 135 |
|---|---|---|---|---|
| 1.4142 | 1.4142 | 1.2910 | 1.8257 | |
| 2.3357 | 5.2177 | 7.3182 | 4.7219 | |
| 1.8663 | 1.8750 | 1.8750 | 1.8749 | |
| 0.7683 | 0.0308 | 0.0044 | 0.0112 | |
| 1.7130 | 0.1878 | 0.0287 | 0.1925 |
| Fn | Total Resistance (N) | Differences (%) | |
|---|---|---|---|
| w/ Caterpillars | w/o Caterpillars | ||
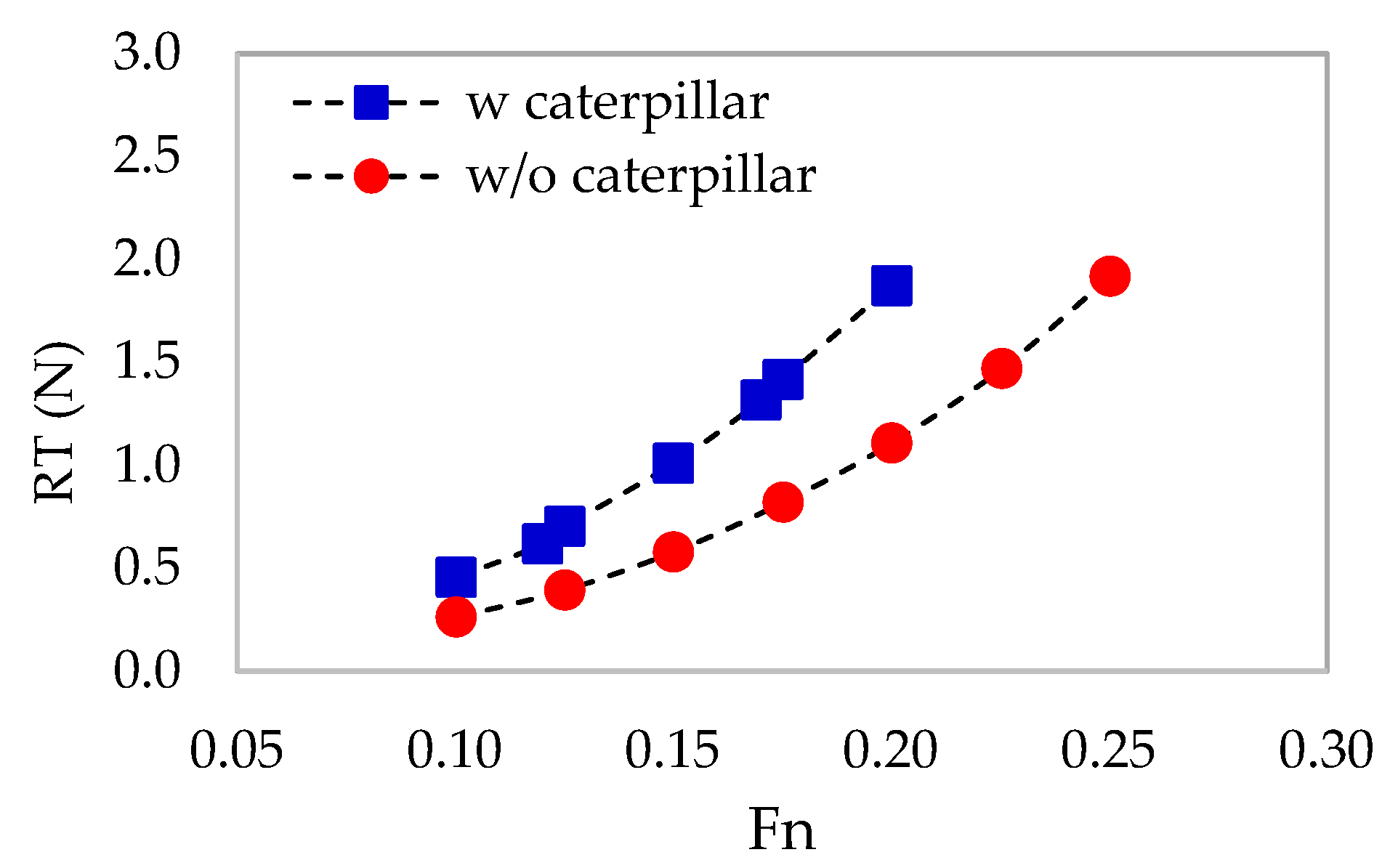
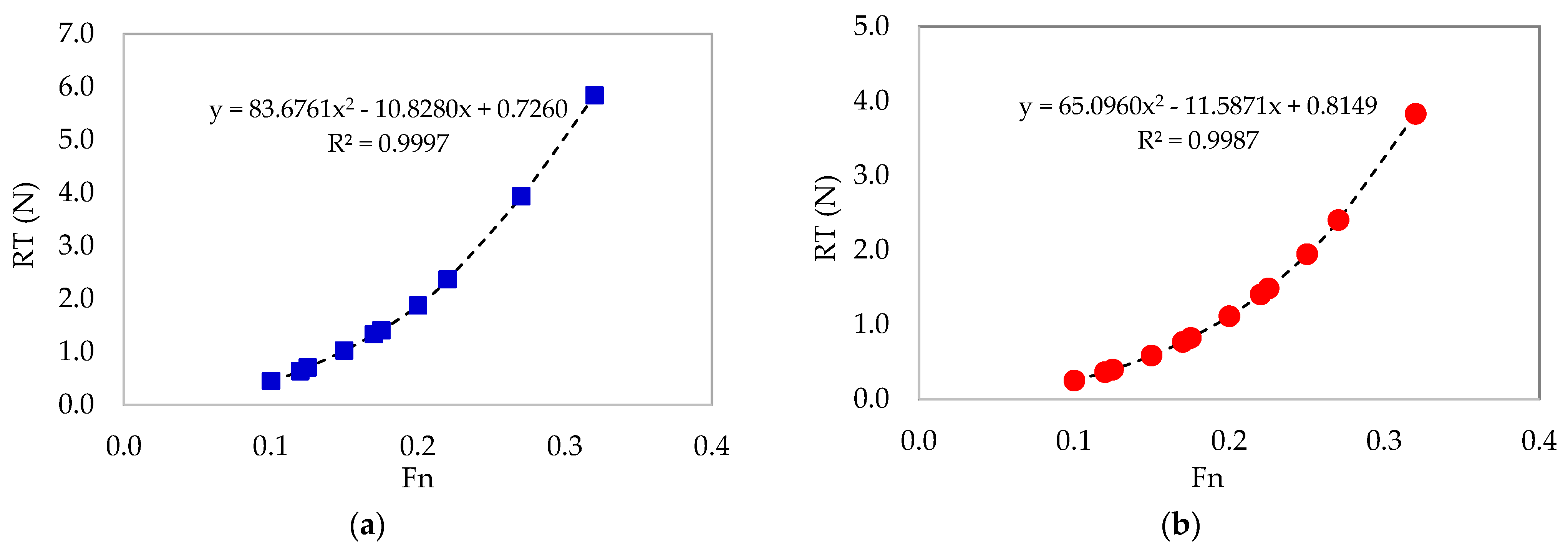
| 0.12 | 0.630 | 0.403 | 36.0% |
| 0.17 | 1.329 | 0.768 | 42.2% |
| 0.22 | 2.366 | 1.403 | 40.7% |
| 0.27 | 3.937 | 2.486 | 36.8% |
| 0.32 | 5.841 | 3.943 | 32.5% |
| Average | 39.2% | ||
| Fn | Ct | Cf | Cp | ||||||
|---|---|---|---|---|---|---|---|---|---|
| w | w/o | Diff. (%) | w | w/o | Diff. (%) | w | w/o | Diff. (%) | |
| 0.12 | 0.0213 | 0.0121 | 36.0% | 0.0027 | 0.0020 | 24.3% | 0.0186 | 0.0100 | 45.9% |
| 0.17 | 0.0220 | 0.0127 | 42.2% | 0.0025 | 0.0019 | 24.6% | 0.0195 | 0.0108 | 44.5% |
| 0.22 | 0.0234 | 0.0139 | 40.7% | 0.0022 | 0.0019 | 16.5% | 0.0212 | 0.0120 | 43.2% |
| 0.27 | 0.0253 | 0.0158 | 36.8% | 0.0022 | 0.0017 | 20.6% | 0.0231 | 0.0140 | 39.3% |
| 0.32 | 0.0273 | 0.0179 | 32.5% | 0.0024 | 0.0018 | 27.0% | 0.0249 | 0.0161 | 35.2% |
| Average | 39.2% | 22.6% | 43.0% | ||||||
| Total Resistance (N)—w/ Caterpillars | Total Resistance (N)—w/o Caterpillars | ||||||
|---|---|---|---|---|---|---|---|
| Fn | EFD | CFD | Error (%) | Fn | EFD | CFD | Error (%) |
| 0.10 | 0.455 | 0.448 | 1.60% | 0.10 | 0.263 | 0.266 | 1.27% |
| 0.12 | 0.617 | 0.630 | 1.98% | 0.13 | 0.394 | 0.400 | 1.66% |
| 0.13 | 0.703 | 0.704 | 0.18% | 0.15 | 0.580 | 0.585 | 0.88% |
| 0.15 | 1.009 | 1.024 | 1.47% | 0.18 | 0.820 | 0.823 | 0.30% |
| 0.17 | 1.316 | 1.329 | 0.95% | 0.20 | 1.108 | 1.126 | 1.59% |
| 0.18 | 1.418 | 1.403 | 1.06% | 0.23 | 1.470 | 1.486 | 1.07% |
| 0.20 | 1.873 | 1.875 | 0.12% | 0.25 | 1.918 | 1.945 | 1.43% |
| Average | 1.05% | 1.15% | |||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dhana, F.R.; Park, J.-C.; Yoon, H.-K. A Numerical Study on the Influence of Caterpillars to the Resistance Performance of an Amphibious Vehicle. J. Mar. Sci. Eng. 2023, 11, 286. https://doi.org/10.3390/jmse11020286
Dhana FR, Park J-C, Yoon H-K. A Numerical Study on the Influence of Caterpillars to the Resistance Performance of an Amphibious Vehicle. Journal of Marine Science and Engineering. 2023; 11(2):286. https://doi.org/10.3390/jmse11020286
Chicago/Turabian StyleDhana, Febriani Rohma, Jong-Chun Park, and Hyeon-Kyu Yoon. 2023. "A Numerical Study on the Influence of Caterpillars to the Resistance Performance of an Amphibious Vehicle" Journal of Marine Science and Engineering 11, no. 2: 286. https://doi.org/10.3390/jmse11020286
APA StyleDhana, F. R., Park, J.-C., & Yoon, H.-K. (2023). A Numerical Study on the Influence of Caterpillars to the Resistance Performance of an Amphibious Vehicle. Journal of Marine Science and Engineering, 11(2), 286. https://doi.org/10.3390/jmse11020286







