An Integrated Complete Ensemble Empirical Mode Decomposition with Adaptive Noise to Optimize LSTM for Significant Wave Height Forecasting
Abstract
:1. Introduction
2. Theories for CEEMDAN to Optimize LSTM
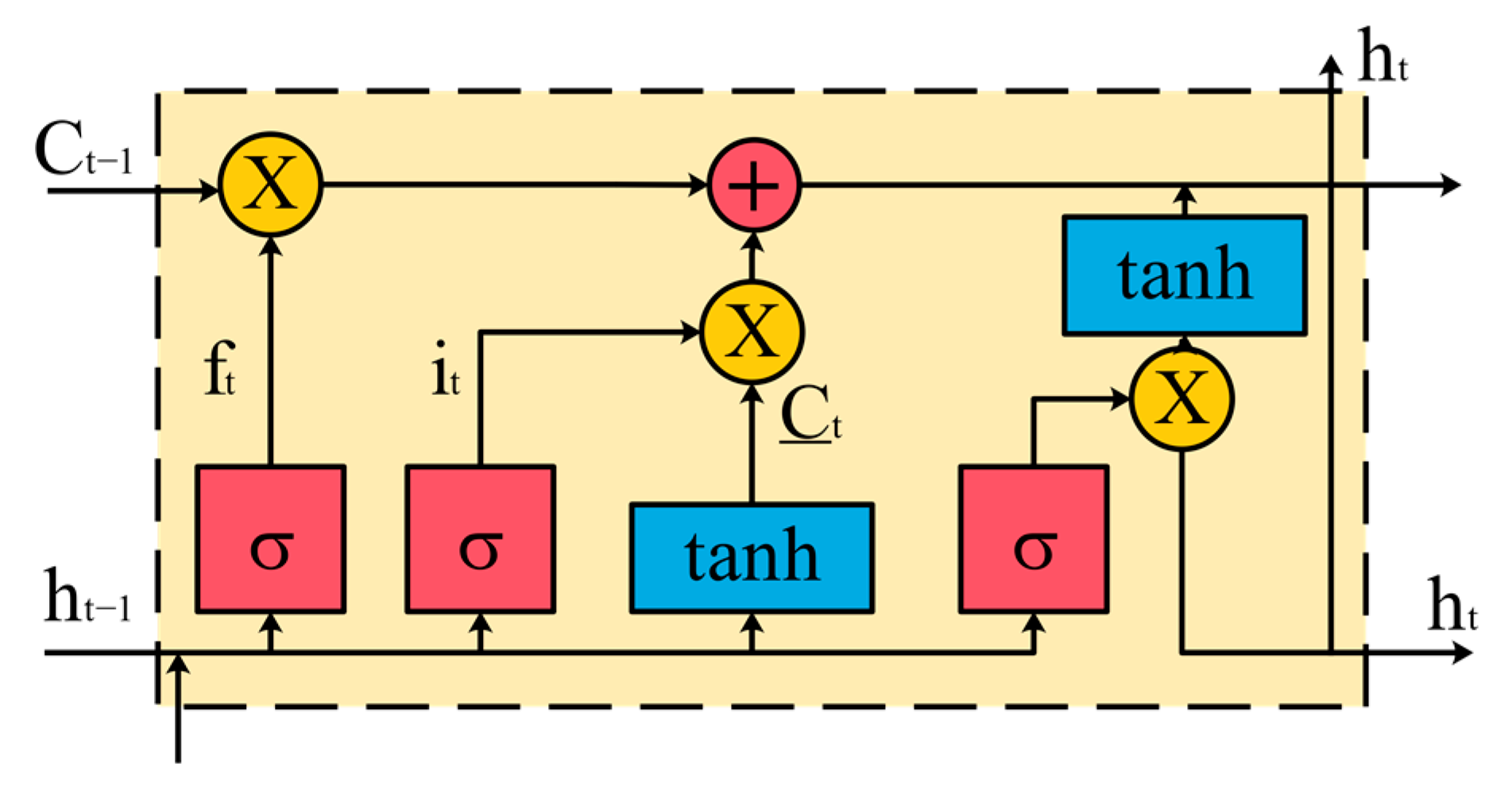
2.1. Long Short-Term Memory (LSTM)
2.2. Complete Ensemble Empirical Mode Decomposition with Adaptive Noise (CEEMDAN)
- Let be the original significant wave height (SWH) of ShiDao effective data, and add white noise to the load data to form a signal comprising the noise, as shown in Equation (3),where is various points in time, represents the white noise added to original data, is the standard noise deviation, is Gaussian white noise, is the newly generated signal.
- Decompose the by Equations (4) and (5) to obtain the IMF and calculate the corresponding residual .
- Gaussian white noise is added to the residual . The residual expression of adding white noise for the time is . The second-order IMF component is determined. EMD decomposes with white noise for the time to obtain . The is expressed as Equations (6) and (7).
- Similarly, the IMF of CEEMDAN and the residual can be obtained as Equations (8) and (9).
- The decomposition process will iterate until it reaches a point where the residual is a monotonic function that cannot be decomposed. Whereas is the final residual, as shown in Equation (10).
2.3. Numerical Algorithms of the Integrated CEEMDAN-LSTM Joint Model
2.4. Error Evaluation Indicators
3. Study Area and Data
3.1. Description of Study Area
3.2. Significant Wave Height Datasets Preprocessing
4. Research Results of the Integration Section
4.1. Novel Filter Formulation for SWH Outliers with Improved Violin-Box Plot
4.2. Decomposition Results of CEEMDAN
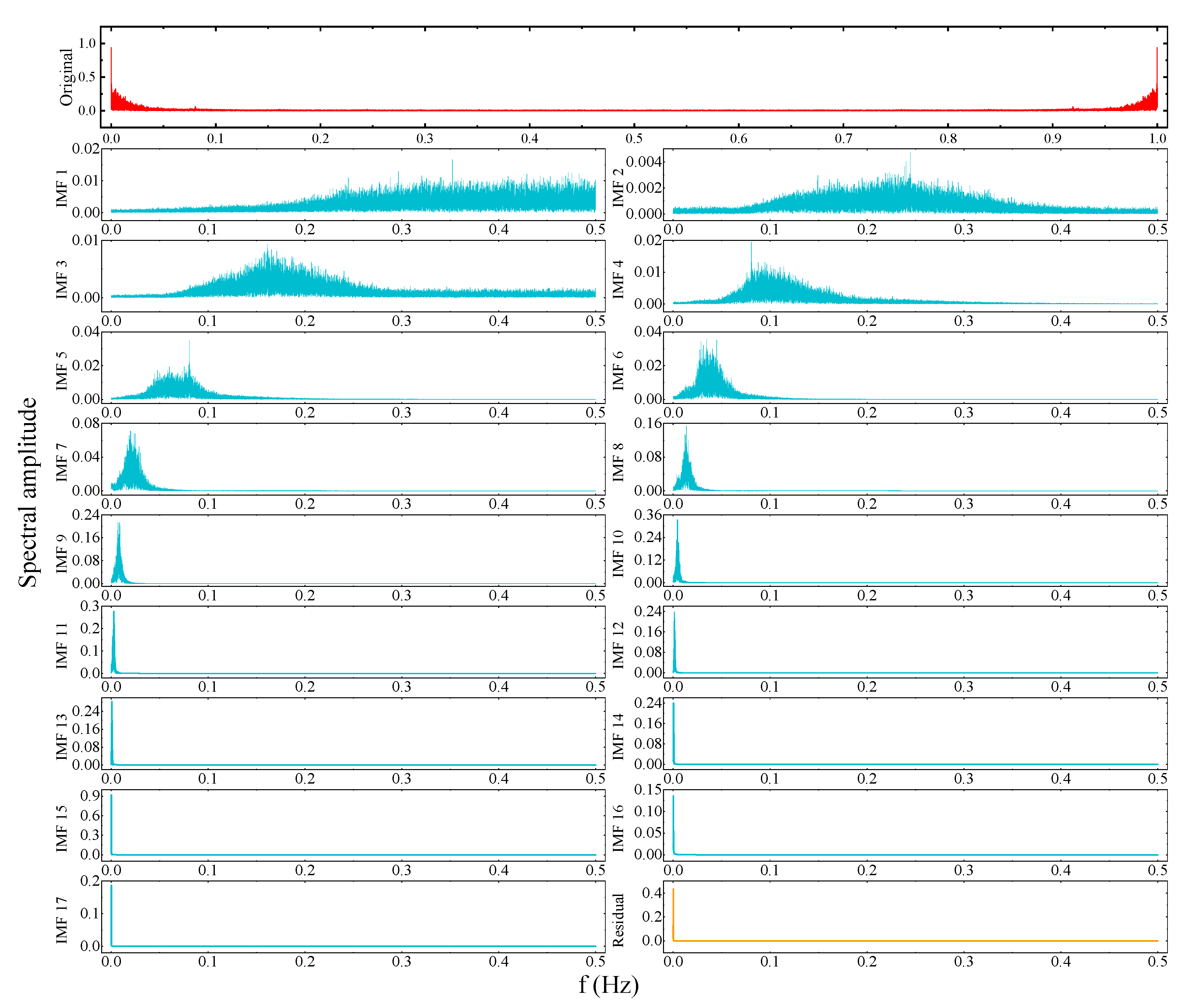
- In Figure 9, the CEEMDAN decomposition of IMF1-IMF7 contains high frequency sinusoidal intermittent signals. IMF8-IMF13 are intermediate frequency sinusoidal intermittent signals. IMF14-IMF17 and the residual are low frequency broad period signals. In this way the signals can be classified. Similarly, the EMD algorithm divides the IMFs components into IMF1-IMF8, IMF9-IMF14 and IMF15-IMF18, respectively.
- From IMF14 onwards, in Figure 9, the signal period increases and gets larger. Local signal surges from a global perspective disappear and the curve becomes increasingly smooth. It can be said that IMF14-IMF17 contain almost no noise at high and medium frequencies. This shows that CEEMDAN has a good processing effect on SWH sequences. A similar phenomenon is observed from IMF15 of EMD onwards. This indicates that CEEMDAN can obtain noise-free IMF components with fewer decomposition steps compared to EMD.
- For the EMD, divergence occurs at the end. For example, IMF13, IMF14 and IMF15 in Figure 8. Whereas, in Figure 9, on the other hand, this does not occur for all IMF components. This indicates that CEEMDAN handles data boundaries much better than EMD. Consider the fact that the upper (lower) envelope of the decomposition process is obtained from the local extremely large (small) values of the signal by three times spline interpolation. However, it is not possible for the endpoints of the signal to be at either a very large or a very small value at the same time. As a result, the upper and lower envelopes diverge at both ends of the data sequence and this divergence gradually increases as the operation proceeds, which is why divergence is a common problem with IMF14-16 in EMD. As the scatter in the decomposition makes the results less scientific, we suspect that this also has a negative impact on the accuracy of the prediction results. However, CEEMDAN does not suffer from such a shortcoming.
- The high frequency sinusoidal intermittent signals IMF1-IMF7 can reflect the essential characteristics of SWH data. For example, a tidal cycle (approximately 24 h and 50 min) is accompanied by a high tide and a low tide, which is reflected in one cycle of the high frequency sinusoidal interval signal.
- The intermediate frequency sinusoidal intermittent signals IMF8-IMF13 reflect the medium- and long-term meteorological influences of the monsoon and ocean currents on the SWH data, alternating between weekly and monthly cycles.
- In the modeling and analysis processes, the low frequency signals IMF14-IMF17 can be seen as a very small energy loss of the high frequency intermittent signals.
5. Analysis of Substantiation Results
5.1. Summary of Model Parameter Settings
5.2. Error Evaluation Indicators Quantify the Degree of Improvement
5.3. Statistical Tests of Prediction Results
5.4. Analysis of Substantiation Results through Data Visualization
5.5. Performance of SWH Predictions on Wave Energy
6. Comparison with the Work of Peers
7. Conclusions
- This paper proposes a novel filter formulation for SWH outliers based on an improved violin-box plot, which is able to filter SWH data with positive skewed distribution. It may also be applicable to SWH data from other regions along the eastern coast of China. In addition, the process proposed in this formulation is also of great interest for other nonlinear or nonstationary data.
- When the CEEMDAN-LSTM model is used for SWH forecasting, the forecasts show the general trend of the waves and better capture fluctuations in local peaks and troughs, and the forecast accuracy is greatly improved.
- Through the CEEMDAN algorithm, the original SWH data is decomposed into high frequency sinusoidal intermittent signals, intermediate frequency sinusoidal intermittent signals and low frequency broad period signals.
- The integrated CEEMDAN-LSTM joint model outperforms the LSTM in terms of accuracy, as CEEMDAN is able to decompose the original nonlinear and nonstationary SWH into various IMFs, thus enabling the LSTM to better capture changes in trends.
- When the forecast duration is 1 h, CEEMDAN-LSTM has the most significant improvement over LSTM, with 71.91% of RMSE, 68.46% of MAE and 6.80% of NSE, respectively.
- Even with a 24-h advance, CEEMDAN-LSTM still improves 53.44%, 40.31% and 7.91% over LSTM in terms of RMSE, MAE and NSE. CEEMDAN-LSTM is still substantially better than LSTM.
- Accurate SWH predictions are crucial for the development and commercial viability of wave energy conversion as a clean energy source. The results of the CEEMDAN-LSTM predictions have also been discussed for this paper, and the results were satisfactory.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Taylor, J.W.; Jeon, J. Probabilistic forecasting of wave height for offshore wind turbine maintenance. Eur. J. Oper. Res. 2018, 267, 877–890. [Google Scholar] [CrossRef]
- Guillou, N.; Lavidas, G.; Chapalain, G. Wave Energy Resource Assessment for Exploitation—A Review. J. Mar. Sci. Eng. 2020, 8, 705. [Google Scholar] [CrossRef]
- Wimalaratna, Y.P.; Hassan, A.; Afrouzi, H.N.; Mehranzamir, K.; Ahmed, J.; Siddique, B.M.; Liew, S.C. Comprehensive review on the feasibility of developing wave energy as a renewable energy resource in Australia. Clean. Energy Syst. 2022, 3, 100021. [Google Scholar] [CrossRef]
- Guillou, N.; Chapalain, G. Annual and seasonal variabilities in the performances of wave energy converters. Energy 2018, 165, 812–823. [Google Scholar] [CrossRef] [Green Version]
- Chen, C.; Sasa, K.; Prpić-Oršić, J.; Mizojiri, T. Statistical analysis of waves’ effects on ship navigation using high-resolution numerical wave simulation and shipboard measurements. Ocean. Eng. 2021, 229, 108757. [Google Scholar] [CrossRef]
- Saetre, C.; Tholo, H.; Hovdenes, J.; Kocbach, J.; Hageberg, A.A.; Klepsvik, I.; Aarnes, O.J.; Furevik, B.R.; Magnusson, A.K. Directional wave measurements from navigational buoys. Ocean. Eng. 2023, 268, 113161. [Google Scholar] [CrossRef]
- Figueiredo, R.; Fazeres-Ferradosa, T.; Chambel, J.; Rosa Santos, P.; Taveira Pinto, F. How does the selection of wave hindcast datasets and statistical models influence the probabilistic design of offshore scour protections? Ocean. Eng. 2022, 266, 113123. [Google Scholar] [CrossRef]
- Wu, M.; De Vos, L.; Arboleda Chavez, C.E.; Stratigaki, V.; Whitehouse, R.; Baelus, L.; Troch, P. A study of scale effects in experiments of monopile scour protection stability. Coast. Eng. 2022, 178, 104217. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, Y.; Qi, Z.; Wang, S.; Zhang, J.; Wang, F. A hybrid forecasting system with complexity identification and improved optimization for short-term wind speed prediction. Energy Convers. Manag. 2022, 270, 116221. [Google Scholar] [CrossRef]
- Zheng, C.-w.; Li, X.-h.; Azorin-Molina, C.; Li, C.-y.; Wang, Q.; Xiao, Z.-n.; Yang, S.-b.; Chen, X.; Zhan, C. Global trends in oceanic wind speed, wind-sea, swell, and mixed wave heights. Appl. Energy 2022, 321, 119327. [Google Scholar] [CrossRef]
- Fazeres-Ferradosa, T.; Taveira-Pinto, F.; Vanem, E.; Reis, M.T.; Neves, L.D. Asymmetric copula–based distribution models for met-ocean data in offshore wind engineering applications. Wind. Eng. 2018, 42, 304–334. [Google Scholar] [CrossRef] [Green Version]
- Fazeres-Ferradosa, T.; Welzel, M.; Schendel, A.; Baelus, L.; Santos, P.R.; Pinto, F.T. Extended characterization of damage in rubble mound scour protections. Coast. Eng. 2020, 158, 103671. [Google Scholar] [CrossRef]
- Duan, W.Y.; Han, Y.; Huang, L.M.; Zhao, B.B.; Wang, M.H. A hybrid EMD-SVR model for the short-term prediction of significant wave height. Ocean. Eng. 2016, 124, 54–73. [Google Scholar] [CrossRef]
- Ye, Y.; Wang, L.; Wang, Y.; Qin, L. An EMD-LSTM-SVR model for the short-term roll and sway predictions of semi-submersible. Ocean. Eng. 2022, 256, 111460. [Google Scholar] [CrossRef]
- Nie, Z.; Shen, F.; Xu, D.; Li, Q. An EMD-SVR model for short-term prediction of ship motion using mirror symmetry and SVR algorithms to eliminate EMD boundary effect. Ocean. Eng. 2020, 217, 107927. [Google Scholar] [CrossRef]
- Janssen, P.A.E.M. Progress in ocean wave forecasting. J. Comput. Phys. 2008, 227, 3572–3594. [Google Scholar] [CrossRef]
- Myrhaug, D.; Fouques, S. A joint distribution of significant wave height and characteristic surf parameter. Coast. Eng. 2010, 57, 948–952. [Google Scholar] [CrossRef]
- Sezer, A.; Asma, S. Statistical power of an information-based test and its application to wave height data. Comput. Geosci. 2010, 36, 1316–1324. [Google Scholar] [CrossRef]
- Nam, B.W.; Kim, J.-S.; Hong, S.Y. Numerical investigation on hopf bifurcation problem for nonlinear dynamics of a towed vessel in calm water and waves. Ocean. Eng. 2022, 266, 112661. [Google Scholar] [CrossRef]
- Zhao, L.; Li, Z.; Qu, L. Forecasting of Beijing PM2.5 with a hybrid ARIMA model based on integrated AIC and improved GS fixed-order methods and seasonal decomposition. Heliyon 2022, 8, e12239. [Google Scholar] [CrossRef]
- Yang, S.; Deng, Z.; Li, X.; Zheng, C.; Xi, L.; Zhuang, J.; Zhang, Z.; Zhang, Z. A novel hybrid model based on STL decomposition and one-dimensional convolutional neural networks with positional encoding for significant wave height forecast. Renew. Energy 2021, 173, 531–543. [Google Scholar] [CrossRef]
- Özger, M. Significant wave height forecasting using wavelet fuzzy logic approach. Ocean. Eng. 2010, 37, 1443–1451. [Google Scholar] [CrossRef]
- Shahabi, S.; Khanjani, M.J. Modelling of significant wave height using wavelet transform and GMDH. In Proceedings of the 36th IAHR World Congress, Hague, The Netherlands, 28 June 2015. [Google Scholar]
- Ali, M.; Prasad, R. Significant wave height forecasting via an extreme learning machine model integrated with improved complete ensemble empirical mode decomposition. Renew. Sustain. Energy Rev. 2019, 104, 281–295. [Google Scholar] [CrossRef]
- Kim, S.; Takeda, M.; Mase, H. GMDH-based wave prediction model for one-week nearshore waves using one-week forecasted global wave data. Appl. Ocean. Res. 2021, 117, 102859. [Google Scholar] [CrossRef]
- Camus, P.; Herrera, S.; Gutiérrez, J.M.; Losada, I.J. Statistical downscaling of seasonal wave forecasts. Ocean. Model. 2019, 138, 1–12. [Google Scholar] [CrossRef]
- Raj, N.; Brown, J. An EEMD-BiLSTM Algorithm Integrated with Boruta Random Forest Optimiser for Significant Wave Height Forecasting along Coastal Areas of Queensland, Australia. Remote Sens. 2021, 13, 1456. [Google Scholar] [CrossRef]
- Zilong, T.; Yubing, S.; Xiaowei, D. Spatial-temporal wave height forecast using deep learning and public reanalysis dataset. Appl. Energy 2022, 326, 120027. [Google Scholar] [CrossRef]
- Deka, P.C.; Prahlada, R. Discrete wavelet neural network approach in significant wave height forecasting for multistep lead time. Ocean. Eng. 2012, 43, 32–42. [Google Scholar] [CrossRef]
- Ma, J.; Xue, H.; Zeng, Y.; Zhang, Z.; Wang, Q. Significant wave height forecasting using WRF-CLSF model in Taiwan strait. Eng. Appl. Comput. Fluid Mech. 2021, 15, 1400–1419. [Google Scholar] [CrossRef]
- Gao, R.; Li, R.; Hu, M.; Suganthan, P.N.; Yuen, K.F. Dynamic ensemble deep echo state network for significant wave height forecasting. Appl. Energy 2023, 329, 120261. [Google Scholar] [CrossRef]
- Yao, J.; Wu, W. Wave height forecast method with multi-step training set extension LSTM neural network. Ocean. Eng. 2022, 263, 112432. [Google Scholar] [CrossRef]
- Li, X.; Cao, J.; Guo, J.; Liu, C.; Wang, W.; Jia, Z.; Su, T. Multi-step forecasting of ocean wave height using gate recurrent unit networks with multivariate time series. Ocean. Eng. 2022, 248, 110689. [Google Scholar] [CrossRef]
- Sun, Z.; Zhao, M.; Zhao, G. Hybrid model based on VMD decomposition, clustering analysis, long short memory network, ensemble learning and error complementation for short-term wind speed forecasting assisted by Flink platform. Energy 2022, 261, 125248. [Google Scholar] [CrossRef]
- Luo, Q.-R.; Xu, H.; Bai, L.-H. Prediction of significant wave height in hurricane area of the Atlantic Ocean using the Bi-LSTM with attention model. Ocean. Eng. 2022, 266, 112747. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, X.; Chen, G.; Dong, Q.; Guo, X.; Tian, X.; Lu, W.; Peng, T. Deterministic wave prediction model for irregular long-crested waves with Recurrent Neural Network. J. Ocean. Eng. Sci. 2022. [Google Scholar] [CrossRef]
- Ji, C.; Zhang, C.; Hua, L.; Ma, H.; Nazir, M.S.; Peng, T. A multi-scale evolutionary deep learning model based on CEEMDAN, improved whale optimization algorithm, regularized extreme learning machine and LSTM for AQI prediction. Environ. Res. 2022, 215, 114228. [Google Scholar] [CrossRef]
- Zhang, C.; Hua, L.; Ji, C.; Shahzad Nazir, M.; Peng, T. An evolutionary robust solar radiation prediction model based on WT-CEEMDAN and IASO-optimized outlier robust extreme learning machine. Appl. Energy 2022, 322, 119518. [Google Scholar] [CrossRef]
- Hu, C.; Zhao, Y.; Jiang, H.; Jiang, M.; You, F.; Liu, Q. Prediction of ultra-short-term wind power based on CEEMDAN-LSTM-TCN. Energy Rep. 2022, 8, 483–492. [Google Scholar] [CrossRef]
- Wang, N.; Nie, J.; Li, J.; Wang, K.; Ling, S. A compression strategy to accelerate LSTM meta-learning on FPGA. ICT Express 2022, 8, 322–327. [Google Scholar] [CrossRef]
- Mushtaq, E.; Zameer, A.; Umer, M.; Abbasi, A.A. A two-stage intrusion detection system with auto-encoder and LSTMs. Appl. Soft Comput. 2022, 121, 108768. [Google Scholar] [CrossRef]
- Huang, N.; Shen, Z.; Long, S.; Wu ML, C.; Shih, H.; Zheng, Q.; Yen, N.-C.; Tung, C.-C.; Liu, H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. London. Ser. A Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Wu, Z.; Huang, N.E. Ensemble Empirical Mode Decomposition: A Noise-Assisted Data Analysis Method. Adv. Data Sci. Adapt. Anal. 2009, 1, 1–41. [Google Scholar] [CrossRef]
- Xu, K.; Niu, H. Do EEMD based decomposition-ensemble models indeed improve prediction for crude oil futures prices? Technol. Forecast. Soc. Change 2022, 184, 121967. [Google Scholar] [CrossRef]
- Ran, P.; Dong, K.; Liu, X.; Wang, J. Short-term load forecasting based on CEEMDAN and Transformer. Electr. Power Syst. Res. 2023, 214, 108885. [Google Scholar] [CrossRef]
- Li, K.; Huang, W.; Hu, G.; Li, J. Ultra-short term power load forecasting based on CEEMDAN-SE and LSTM neural network. Energy Build. 2023, 279, 112666. [Google Scholar] [CrossRef]
- Vardaroglu, M.; Gao, Z.; Avossa, A.M.; Ricciardelli, F. Validation of a TLP wind turbine numerical model against model-scale tests under regular and irregular waves. Ocean. Eng. 2022, 256, 111491. [Google Scholar] [CrossRef]
- Koivu, A.; Kakko, J.-P.; Mäntyniemi, S.; Sairanen, M. Quality of randomness and node dropout regularization for fitting neural networks. Expert Syst. Appl. 2022, 207, 117938. [Google Scholar] [CrossRef]
- Röhmel, J. The permutation distribution of the Friedman test. Comput. Stat. Data Anal. 1997, 26, 83–99. [Google Scholar] [CrossRef]
- Ma, J.; Xia, D.; Wang, Y.; Niu, X.; Jiang, S.; Liu, Z.; Guo, H. A comprehensive comparison among metaheuristics (MHs) for geohazard modeling using machine learning: Insights from a case study of landslide displacement prediction. Eng. Appl. Artif. Intell. 2022, 114, 105150. [Google Scholar] [CrossRef]
- Berčič, G. The universality of Friedman’s isoconversional analysis results in a model-less prediction of thermodegradation profiles. Thermochim. Acta 2017, 650, 1–7. [Google Scholar] [CrossRef]
- Bozorgzadeh, L.; Bakhtiari, M.; Shani Karam Zadeh, N.; Esmaeeldoust, M. Forecasting of Wind-Wave Height by Using Adaptive Neuro-Fuzzy Inference System and Decision Tree. J. Soft Comput. Civ. Eng. 2019, 3, 22–36. [Google Scholar]
- Chen, S.-T.; Wang, Y.-W. Improving Coastal Ocean Wave Height Forecasting during Typhoons by using Local Meteorological and Neighboring Wave Data in Support Vector Regression Models. J. Mar. Sci. Eng. 2020, 8, 149. [Google Scholar] [CrossRef] [Green Version]
- Zhou, S.; Bethel, B.J.; Sun, W.; Zhao, Y.; Xie, W.; Dong, C. Improving Significant Wave Height Forecasts Using a Joint Empirical Mode Decomposition–Long Short-Term Memory Network. J. Mar. Sci. Eng. 2021, 9, 744. [Google Scholar] [CrossRef]
- Nasiri, H.; Ebadzadeh, M.M. MFRFNN: Multi-Functional Recurrent Fuzzy Neural Network for Chaotic Time Series Prediction. Neurocomputing 2022, 507, 292–310. [Google Scholar] [CrossRef]
- Nasiri, H.; Ebadzadeh, M.M. Multi-step-ahead Stock Price Prediction Using Recurrent Fuzzy Neural Network and Variational Mode Decomposition. arXiv 2022, arXiv:2212.14687. [Google Scholar]














| Monitoring Station | Positon | Data Duration | Dataset | Effective Data |
|---|---|---|---|---|
| ShiDao | 36.89° N 122.43° E | 2013.1.1–2022.7.31 | 73,819 | 68,068 |
| Forecast Durations (h) | LSTM | CEEMDAN-LSTM | Degree of Improvement | ||||||
|---|---|---|---|---|---|---|---|---|---|
| RMSE (m) | MAE (m) | NSE | RMSE (m) | MAE (m) | NSE | RMSE (%) | MAE (%) | NSE (%) | |
| 1 | 0.7693 | 0.1096 | 0.9312 | 0.2162 | 0.0346 | 0.9946 | 71.90% | 68.46% | 6.80% |
| 3 | 0.8297 | 0.1154 | 0.9234 | 0.2693 | 0.0430 | 0.9916 | 68.75% | 62.70% | 7.39% |
| 6 | 0.8940 | 0.1206 | 0.9167 | 0.3225 | 0.0515 | 0.9879 | 66.17% | 57.29% | 7.76% |
| 24 | 0.9720 | 0.1290 | 0.9016 | 0.4825 | 0.0770 | 0.9729 | 53.44% | 40.31% | 7.91% |
| Serial Number | Variable Name | Sample Size | Median | Standard Deviation | Statistical Quantities | p | Cohen’s f Value |
|---|---|---|---|---|---|---|---|
| ① | Measurement | 6806 | 5.000 | 2.934 | 6967.366 | 0.001 | 0.020 |
| ② | Prediction (1 h) | 6806 | 4.679 | 2.833 | |||
| ③ | Prediction (3 h) | 6806 | 4.645 | 2.824 | |||
| ④ | Prediction (6 h) | 6806 | 4.491 | 2.788 | |||
| ⑤ | Prediction (24 h) | 6806 | 4.541 | 2.711 |
| Pairing Variables | Median ± Standard Deviation | Statistical Quantities | p | Cohen’s d | ||
|---|---|---|---|---|---|---|
| Pairing 1 | Pairing 2 | Pairing Difference (Pairing 1–Pairing 2) | ||||
| ① pairing ② | 5.000 ± 2.934 | 4.679 ± 2.833 | 0.321 ± 0.101 | 51.686 | 0.001 | 0.015 |
| ① pairing ③ | 5.000 ± 2.934 | 4.645 ± 2.824 | 0.355 ± 0.109 | 25.375 | 0.001 | 0.009 |
| ① pairing ④ | 5.000 ± 2.934 | 4.491 ± 2.788 | 0.509 ± 0.146 | 60.732 | 0.001 | 0.041 |
| ① pairing ⑤ | 5.000 ± 2.934 | 4.541 ± 2.711 | 0.459 ± 0.223 | 10.234 | 0.001 | 0.010 |
| ② pairing ③ | 4.679 ± 2.833 | 4.645 ± 2.824 | 0.034 ± 0.009 | 26.311 | 0.001 | 0.007 |
| ② pairing ④ | 4.679 ± 2.833 | 4.491 ± 2.788 | 0.188 ± 0.045 | 112.418 | 0.001 | 0.058 |
| ② pairing ⑤ | 4.679 ± 2.833 | 4.541 ± 2.711 | 0.138 ± 0.123 | 41.452 | 0.001 | 0.026 |
| ③ pairing ④ | 4.645 ± 2.824 | 4.491 ± 2.788 | 0.154 ± 0.036 | 86.108 | 0.001 | 0.051 |
| ③ pairing ⑤ | 4.645 ± 2.824 | 4.541 ± 2.711 | 0.104 ± 0.114 | 15.141 | 0.001 | 0.020 |
| ④ pairing ⑤ | 4.491 ± 2.788 | 4.541 ± 2.711 | 0.050 ± 0.078 | 70.967 | 0.001 | 0.033 |
| Serial Number | Variable Name | Sample Size | Median | Standard Deviation | Statistical Quantities | p | Cohen’s f Value |
|---|---|---|---|---|---|---|---|
| ① | Measurement | 6806 | 5.000 | 2.934 | 6.223 | 0.183 | 0.001 |
| ② | Prediction (1 h) | 6806 | 4.752 | 2.922 | |||
| ③ | Prediction (3 h) | 6806 | 4.694 | 2.921 | |||
| ④ | Prediction (6 h) | 6806 | 4.65 | 2.921 | |||
| ⑤ | Prediction (24 h) | 6806 | 4.627 | 2.926 |
| Pairing Variables | Median ± Standard Deviation | Statistical Quantities | p | Cohen’s d | ||
|---|---|---|---|---|---|---|
| Pairing 1 | Pairing 2 | Pairing Difference (Pairing 1–Pairing 2) | ||||
| ① pairing ② | 5.000 ± 2.934 | 4.752 ± 2.922 | 0.248 ± 0.012 | 2.775 | 0.285 | 0.002 |
| ① pairing ③ | 5.000 ± 2.934 | 4.694 ± 2.921 | 0.306 ± 0.013 | 2.775 | 0.285 | 0.002 |
| ① pairing ④ | 5.000 ± 2.934 | 4.650 ± 2.921 | 0.350 ± 0.013 | 2.821 | 0.268 | 0.002 |
| ① pairing ⑤ | 5.000 ± 2.934 | 4.627 ± 2.926 | 0.373 ± 0.008 | 2.783 | 0.282 | 0.002 |
| ② pairing ③ | 4.752 ± 2.922 | 4.694 ± 2.921 | 0.058 ± 0.001 | 0.000 | 0.900 | 0.000 |
| ② pairing ④ | 4.752 ± 2.922 | 4.650 ± 2.921 | 0.102 ± 0.001 | 0.046 | 0.900 | 0.000 |
| ② pairing ⑤ | 4.752 ± 2.922 | 4.627 ± 2.926 | 0.125 ± 0.004 | 0.008 | 0.900 | 0.000 |
| ③ pairing ④ | 4.694 ± 2.921 | 4.650 ± 2.921 | 0.044 ± 0.000 | 0.046 | 0.900 | 0.000 |
| ③ pairing ⑤ | 4.694 ± 2.921 | 4.627 ± 2.926 | 0.067 ± 0.005 | 0.008 | 0.900 | 0.000 |
| ④ pairing ⑤ | 4.650 ± 2.921 | 4.627 ± 2.926 | 0.023 ± 0.005 | 0.038 | 0.900 | 0.000 |
| Source | Model | Forecast Durations (h) | RMSE (m) |
|---|---|---|---|
| The research work of Nasiri and Ebadzadeh | MFRFNN | 1 | 0.5493 |
| VMD-MFRFNN | 1 | 0.2182 | |
| Our research work | LSTM | 1 | 0.7693 |
| CEEMDAN-LSTM | 1 | 0.2163 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, L.; Li, Z.; Zhang, J.; Teng, B. An Integrated Complete Ensemble Empirical Mode Decomposition with Adaptive Noise to Optimize LSTM for Significant Wave Height Forecasting. J. Mar. Sci. Eng. 2023, 11, 435. https://doi.org/10.3390/jmse11020435
Zhao L, Li Z, Zhang J, Teng B. An Integrated Complete Ensemble Empirical Mode Decomposition with Adaptive Noise to Optimize LSTM for Significant Wave Height Forecasting. Journal of Marine Science and Engineering. 2023; 11(2):435. https://doi.org/10.3390/jmse11020435
Chicago/Turabian StyleZhao, Lingxiao, Zhiyang Li, Junsheng Zhang, and Bin Teng. 2023. "An Integrated Complete Ensemble Empirical Mode Decomposition with Adaptive Noise to Optimize LSTM for Significant Wave Height Forecasting" Journal of Marine Science and Engineering 11, no. 2: 435. https://doi.org/10.3390/jmse11020435
APA StyleZhao, L., Li, Z., Zhang, J., & Teng, B. (2023). An Integrated Complete Ensemble Empirical Mode Decomposition with Adaptive Noise to Optimize LSTM for Significant Wave Height Forecasting. Journal of Marine Science and Engineering, 11(2), 435. https://doi.org/10.3390/jmse11020435







