Comparison of Coherent to Incoherent Kirchhoff-Ray-Mode (KRM) Models in Predicting Backscatter by Swim-Bladder-Bearing Fish
Abstract
:1. Introduction
2. Theory and Method
2.1. Coherent and Incoherent KRM Models
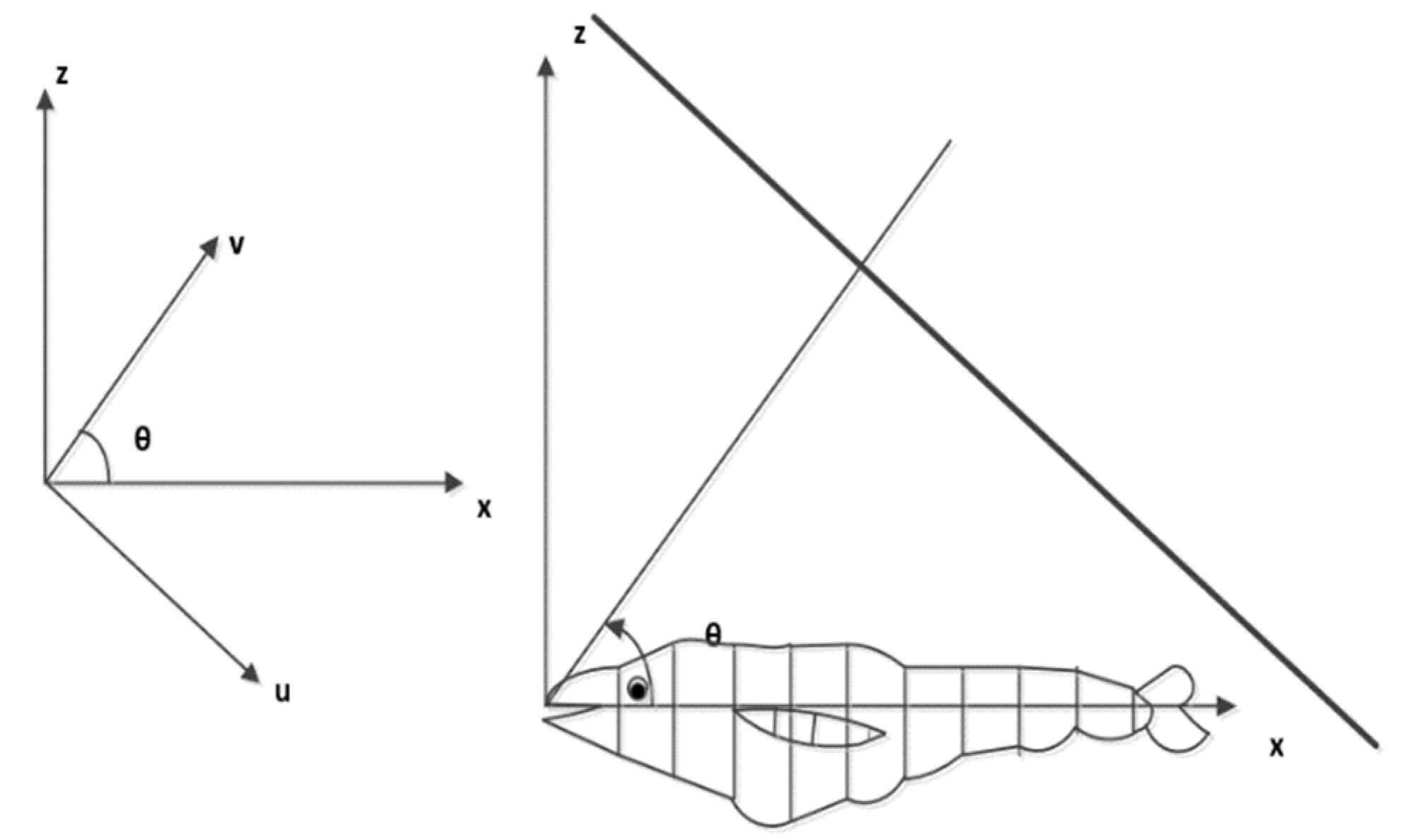
2.2. Digitized Fish Images and Scattering Computations
3. Results and Discussion
3.1. Comparison between Incoherent and Coherent TS Predictions of Individual Fish
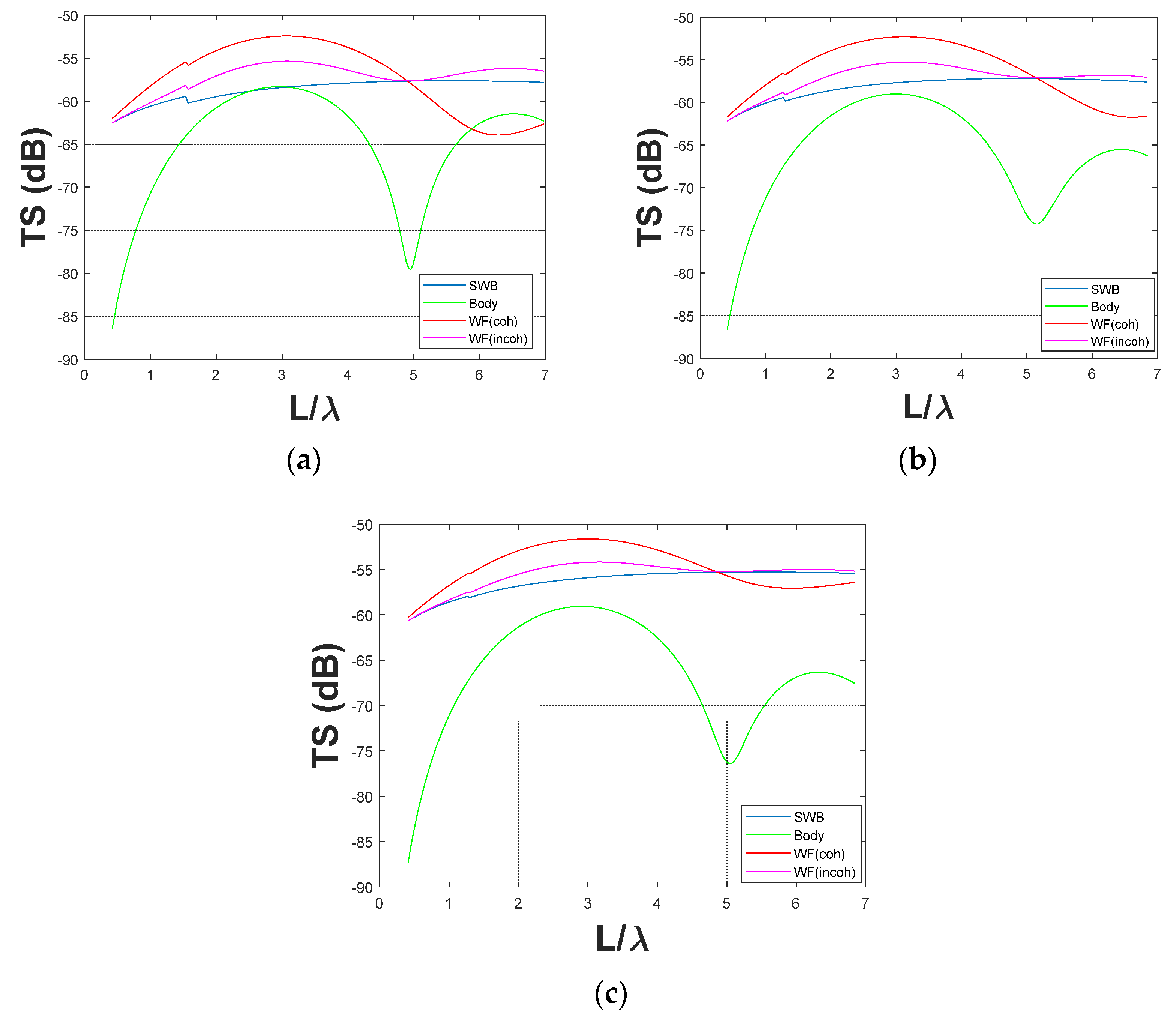
3.1.1. Small Fish (<60 mm TL)
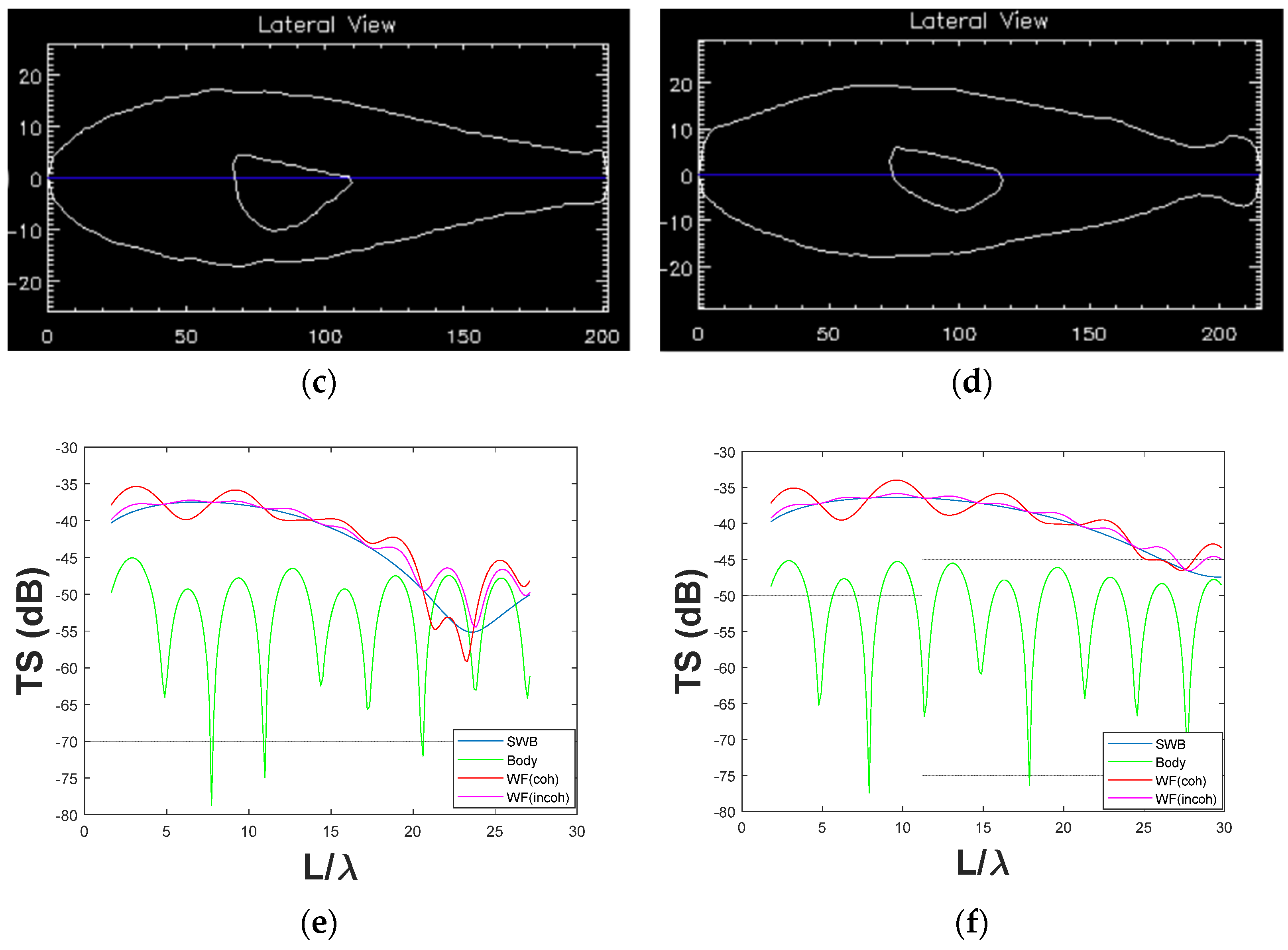
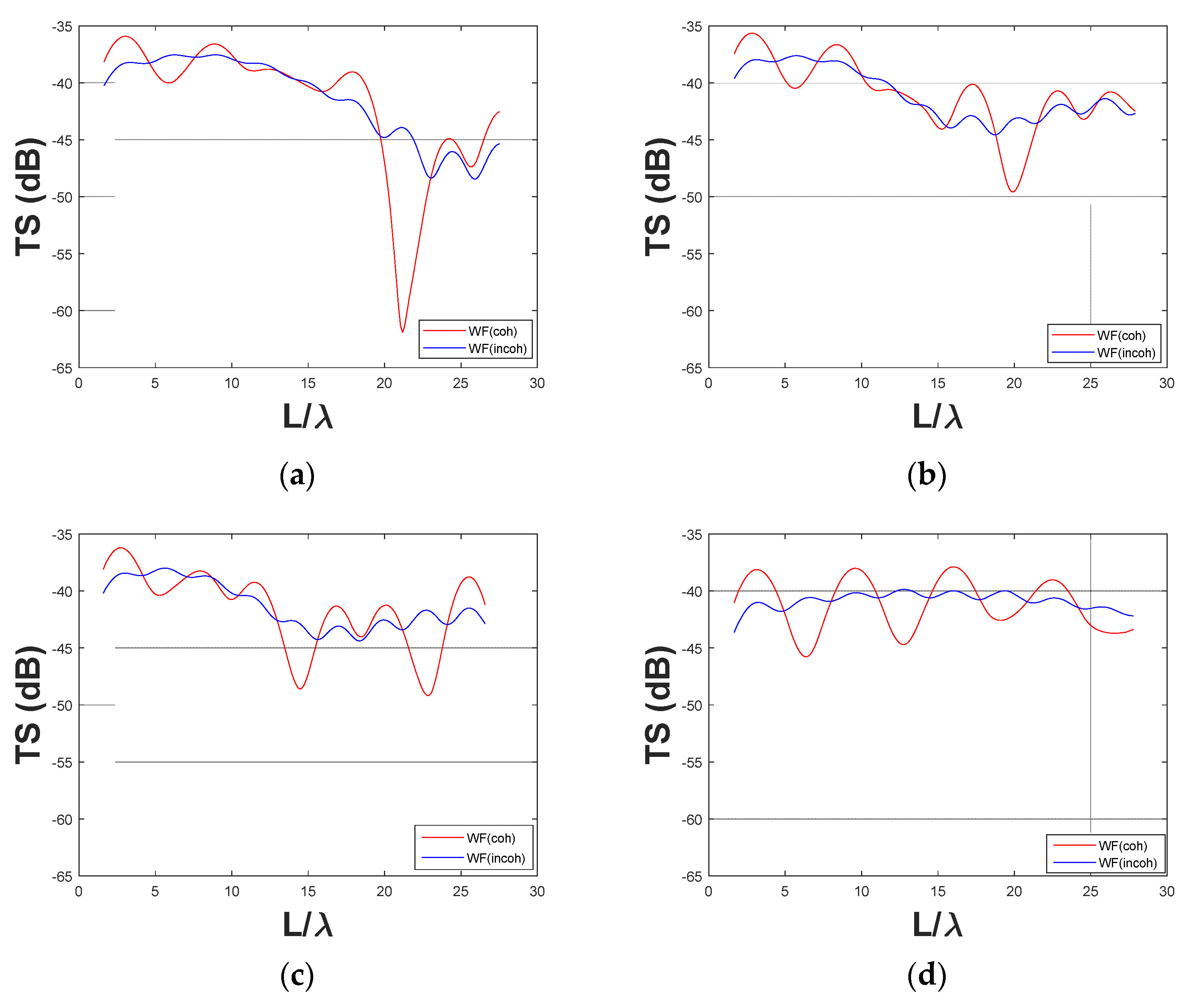
3.1.2. Large Fish (>200 mm)
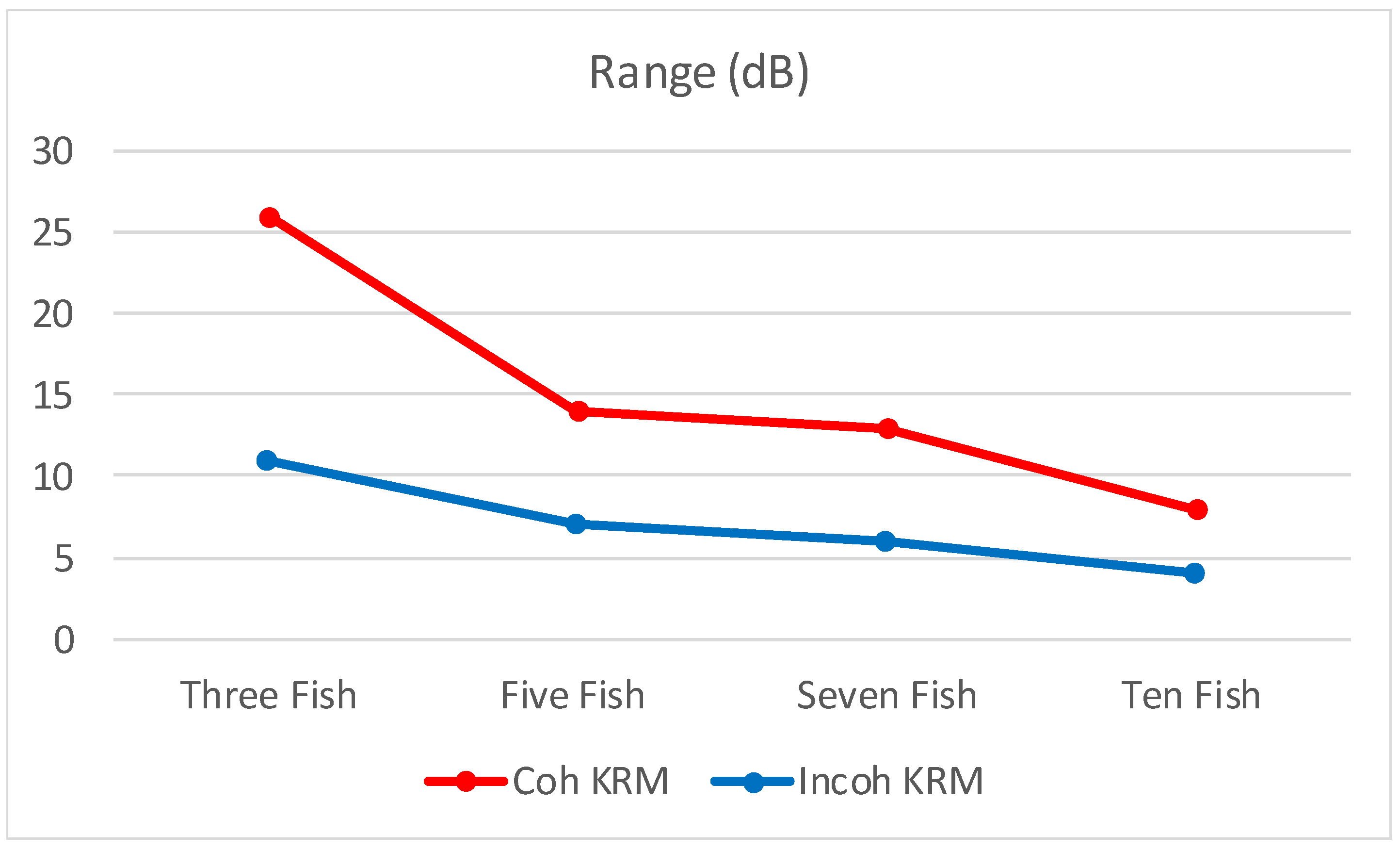
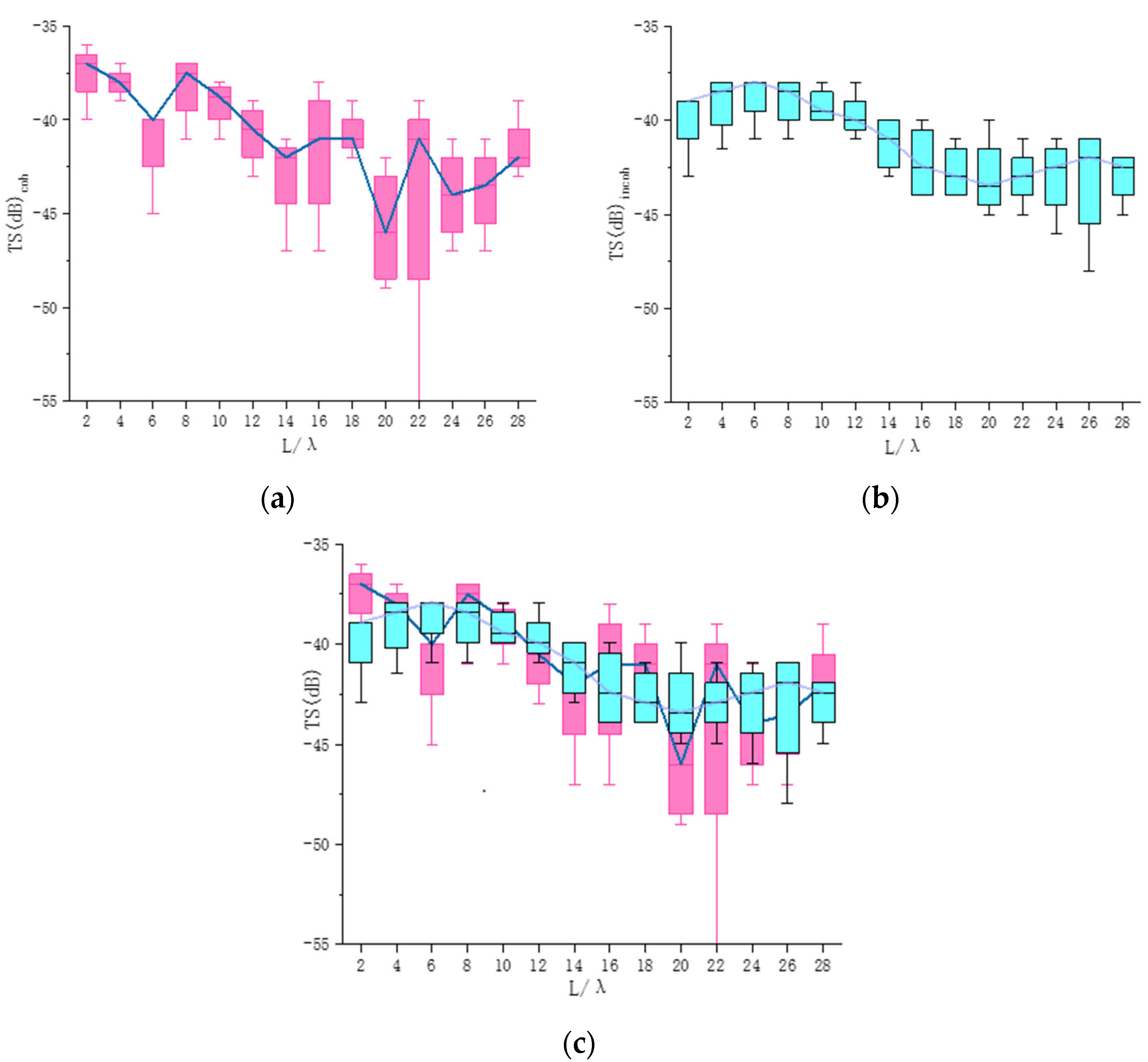
3.2. Comparison between Coherent and Incoherent TS Predictions with a Few Fish
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- MacLennan, D.N.; Simmonds, E.J. Fisheries Acoustics; Chapman & Hall: London, UK, 1992. [Google Scholar]
- MacLennan, D.N. Acoustical measurement of fish abundance. J. Acoust. Soc. Am. 1990, 87, 1–15. [Google Scholar] [CrossRef]
- Nakken, O.; Olsen, K. Target strength measurements of fish. Rapp. Proces-Verbaux Reun. Cons. Int. Pour L`Explor. Mer. 1977, 170, 52–69. [Google Scholar]
- Traynor, J.J. Target-strength measurements of walleye pollock (Theragra rhnkoprnrna) and Pacific whiting (Merlctccicts productus). ICES J. Mar. Sci. 1996, 53, 253–258. [Google Scholar] [CrossRef] [Green Version]
- Foote, K.G.; Traynor, J.J. Comparison of walleye pollock target strength estimates determined from in situ measurements and calculations based on swimbladder form. J. Acoust. Soc. Am. 1988, 83, 9–17. [Google Scholar] [CrossRef] [Green Version]
- Bertrand, A.; Josse, E.; Masse, J. In situ acoustic target strength measurement of bigeye (Thunnus obesus) and yellowfin tuna (Thunnus albacares) by coupling split-beam echosounder observations and sonic tracking. ICES J. Mar. Sci. 1999, 56, 51–60. [Google Scholar] [CrossRef]
- Sawada, K.; Ye, Z.; Kieser, R.; McFarlane, G.A.; Miyanohana, Y.; Furusawa, M. Target strength measurements and modelling of walleye pollock and Pacific hake. Fish. Sci. 1999, 65, 193–205. [Google Scholar] [CrossRef] [Green Version]
- Kang, D.; Hwang, D. Ex situ target strength of rockfish (Sebastes schlegeli) and red sea bream (Pagrus major) in the Northwest Pacific. ICES J. Mar. Sci. 2003, 60, 538–543. [Google Scholar] [CrossRef] [Green Version]
- Kang, D.; Hwang, D.; Na, J.; Kim, S. Target strength of red seabream (Pagrus major). In Proceedings of the International Symposium on Advanced Techniques of Sampling Gear and Acoustic Survey for Estimation of Fish Abundance and Behaviour (ACOUSTGEAR2000), Hakodate, Japan, 20–21 October 2000; Volume 1, pp. 17–24. [Google Scholar]
- Kang, D.; Sadayasu, K.; Mukai, T.; Iida, K.; Hwang, D.; Sawada, K.; Miyashita, K. Target strength estimation of black porgy Acanthopagrus schlegeli using acoustic measurements and a scattering model. Fish. Sci. 2004, 70, 819–828. [Google Scholar] [CrossRef]
- Reeder, D.B.; Stanton, T.K. Acoustic scattering by axisymmetric finite-length bodies: An extension of a two-dimensional conformal mapping method. J. Acoust. Soc. Am. 2004, 116, 729–746. [Google Scholar] [CrossRef]
- Henderson, M.J.; Horne, J.K. Comparison of in situ, situ, and backscatter model estimates of Pacific hake (Merluccius productus) target strength. Can. J. Fish. Aquat. Sci. 2007, 64, 1781–1794. [Google Scholar] [CrossRef] [Green Version]
- Nero, R.W.; Thompson, C.H.; Love, R.H. Low-frequency acoustic measurements of Pacific hake, Merluccius productus, off the west coast of the United States. Fish. Bull. 1998, 96, 329–343. [Google Scholar]
- Gauthier, S.; Horne, J.K. Acoustic characteristics of forage fish species in the Gulf of Alaska and Bering Sea based on Kirchhoff-approximation models. Can. J. Fish. Aquat. Sci. 2004, 61, 1839–1850. [Google Scholar] [CrossRef]
- Pena, H.; Foote, K.G. Modelling the target strength of Trachurus symmetricus murphyi based on high-resolution swimbladder morphometry using an MRI scanner. ICES J. Mar. Sci. 2008, 65, 1751–1761. [Google Scholar] [CrossRef]
- Jech, J.M.; Horne, J.K.; Chu, D.; Demer, D.A.; Francis, D.T.; Gorska, N.; Jones, B.; Lavery, A.C.; Stanton, T.K.; Macaulay, G.J.; et al. Comparisons among ten models of acoustic backscattering used in aquatic ecosystem research. J. Acoust. Soc. Am. 2015, 138, 3742–3764. [Google Scholar] [CrossRef] [Green Version]
- Love, R.H. Dorsal-aspect target strength of an individual fish. J. Acoust. Sci. Am. 1971, 49, 816–823. [Google Scholar] [CrossRef]
- Love, R.H. Resonant acoustic scattering by swimbladder-bearing fish. J. Acoust. Soc. Am. 1978, 64, 571–580. [Google Scholar] [CrossRef]
- Clay, C.S. Low-resolution acoustic scattering models: Fluid-filled cylinders and fish with swim bladders. J. Acoust. Soc. Am. 1991, 89, 2168–2179. [Google Scholar] [CrossRef]
- Clay, C.S. Composite ray-mode approximations for backscattered sound from gas-filled cylinders and swimbladders. J. Acoust. Soc. Am. 1992, 92, 2173–2180. [Google Scholar] [CrossRef]
- Gorska, N.; One, E. Modelling the effect of swimbladder compression on the acoustic backscattering from herring at normal or near-normal incidences. ICES J. Mar. Sci. 2003, 60, 1381–1391. [Google Scholar] [CrossRef]
- Love, R.H. Target strength of an individual fish at any aspect. J. Acoust. Soc. Am. 1977, 62, 1397–1403. [Google Scholar] [CrossRef]
- Foote, K.G. Effect of fish behaviour on echo energy: The need for measurements of orientation distributions. J. Cons. Int. Explor. Mer. 1980, 39, 193–201. [Google Scholar] [CrossRef]
- Foote, K.G. Rather-high-frequency sound scattering by swimbladdered fish. J. Acoust. Soc. Am. 1985, 78, 688–700. [Google Scholar] [CrossRef]
- Francis, D.T.I.; Foote, K.G. Depth-dependent target strength of gadoids by the boundary-element method. J. Acoust. Soc. Am. 2003, 114, 3136–3146. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ona, E. Physiological factors causing natural variations in acoustic target strength of fish. J. Mar. Biol. Assoc. 1990, 70, 107–127. [Google Scholar] [CrossRef]
- Horne, J.K. The influence of ontogeny, physiology, and behaviour on the target strength of walleye pollock (Theragra chalcogramma). ICES J. Mar. Sci. 2003, 60, 1063–1074. [Google Scholar] [CrossRef] [Green Version]
- Foote, K.G. Importance of the swimbladder in acoustic scattering by fish: A comparison of gadoid and mackerel target strengths. J. Acoust. Soc. Am. 1980, 67, 2084–2089. [Google Scholar] [CrossRef] [Green Version]
- Anderson, V.C. Sound Scattering from a Fluid Sphere. J. Acoust. Soc. Am. 1950, 22, 426–433. [Google Scholar] [CrossRef]
- Strasberg, M. The Pulsation Frequency of Nonspherical Gas Bubbles in Liquids. J. Acoust. Soc. Am. 1953, 25, 536–537. [Google Scholar] [CrossRef]
- Venkatarama, K. Probability and Random Processes; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2006; p. 259. [Google Scholar]
- Yeh, C. Scattering of Acoustic Waves by a Penetrable Prolate Spheroid. I. Liquid Prolate Spheroid. J. Acoust. Soc. Am. 1967, 42, 518–521. [Google Scholar] [CrossRef]
- Ye, Z. Acoustic scatter by prolate spheroidal fish swimbladders. J. Acoust. Soc. Am. 1995, 99, 785–792. [Google Scholar] [CrossRef]
- Furuswa, M.; Miyanohana, Y.; Ariji, M.; Sawada, Y. Prediction of Krill Target Strength by Liquid Prolate Spheroid Model. Fish. Sci. 1994, 60, 261–265. [Google Scholar] [CrossRef] [Green Version]
- Stanton, T.K. Sound scattering by cylinders of finite length. I. Fluid_cylinders. J. Acoust. Soc. Am. 1987, 83, 55–63. [Google Scholar] [CrossRef]
- Stanton, T.K. Sound scattering by cylinders of finite length. II. Elastic cylinders. J. Acoust. Soc. Am. 1987, 83, 64–67. [Google Scholar] [CrossRef]
- Stanton, T.K. Sound scattering by cylinder of finite length. III. Deformed cylinders. J. Acoust. Soc. Am. 1989, 86, 691–705. [Google Scholar] [CrossRef]
- Clay, C.S.; Horne, J.K. Acoustic models of fish The Atlantic cod (Gadus morhua). J. Acoust. Soc. Am. 1994, 96, 1661–1668. [Google Scholar] [CrossRef]
- Foote, K.G.; Francis, D.T.I. Comparing Kirchhoff-approximation and boundary-element models for computing gadoid target strengths. J. Acoust. Soc. Am. 2002, 111, 1644–1654. [Google Scholar] [CrossRef] [Green Version]
- Reeder, D.B.; Jech, J.M.; Stanton, T.K. Broadband acoustic backscatter and high-resolution morphology of fish: Measurement and modeling. J. Acoust. Soc. Am. 2004, 116, 747–761. [Google Scholar] [CrossRef] [Green Version]
- Horne, J.K.; Sawada, K.; Abe, K.; Kreisberg, R.B.; Barbee, D.H.; Sadayasu, K. Swimbladders under pressure: Anatomical and acoustic responses by walleye pollock. ICES J. Mar. Sci. 2009, 66, 1162–1168. [Google Scholar] [CrossRef] [Green Version]
- Grimmett, G.R.; Stirzaker, D.R. Probability and Random Processes, 2nd ed.; Clarendon Press: Oxford, UK, 1992; ISBN 0-19-853665-8. [Google Scholar]
- Medwin, H.; Clay, C.S. Fundamentals of Acoustical Oceanography (Applications of Modern Acoustics); Academic Press: New York, NY, USA, 1998. [Google Scholar]
- Foote, K.G. Linearity of fisheries acoustics, with addition theorems. J. Acoust. Soc. Am. 1983, 73, 1932–1940. [Google Scholar] [CrossRef]
- Simmonds, J.; MacLennan, D.N. Fisheries Acoustics: Theory and Practice; John Wiley & Sons: Hoboken, NJ, USA, 2005; 473p. [Google Scholar]
- Fischer, H. A History of the Central Limit Theorem; Springer: New York, NY, USA, 2010. [Google Scholar]


| FL (mm) | SWB L (mm) | |
|---|---|---|
| 1 | 191 | 28 |
| 2 | 198 | 42 |
| 3 | 200 | 38 |
| 4 | 198 | 35 |
| 5 | 202 | 43 |
| 6 | 208 | 43 |
| 7 | 205 | 46 |
| 8 | 203 | 42 |
| 9 | 205 | 41 |
| 10 | 210 | 42 |
| Mean | 202 | 40 |
| Std | 5.25 | 4.90 |
| Fish A (TSSWB ≈ TSfb) | Fish B (TSSWB > TSfb) (Little Larger) | Fish C (TSSWB > TSfb) (Much Larger) | ||||
|---|---|---|---|---|---|---|
| KRM (coh) | KRM (inc) | KRM (coh) | KRM (inc) | KRM (coh) | KRM (inc) | |
| TSfb (dB) | <−58> | <−59> | <−59> | |||
| TSSWB (dB) | <−58> | <−58> | <−55> | |||
| TSmax (dB) | −53 | −55 | −53 | −55 | −52 | −54 |
| TSmin (dB) | −64 | −58 | −62 | −58 | −60 | −60 |
| Span (dB) | 11 | 3 | 9 | 3 | 8 | 6 |
| Fish A | Fish B | |||
|---|---|---|---|---|
| Coherent KRM | Incoherent KRM | Coherent KRM | Incoherent KRM | |
| TS max (dB) | −35 | −37 | −34 | −36 |
| TS min (dB) | −59 | −54 | −46 | −46 |
| Range (dB) | 24 | 17 | 12 | 10 |
| mean (dB) | −42 | −42 | −39 | −39 |
| median (dB) | −40 | −40 | −39 | −38 |
| Std | 6.003 | 4.858 | 3.402 | 3.151 |
| Three Fish | Five Fish | Seven Fish | Ten Fish | |||||
|---|---|---|---|---|---|---|---|---|
| Coh KRM | Incoh KRM | Coh KRM | Incoh KRM | Coh KRM | Incoh KRM | Coh KRM | Incoh KRM | |
| TS max (dB) | −36 | −37 | −36 | −38 | −36 | −38 | −46 | −40 |
| TS min (dB) | −62 | −48 | −50 | −45 | −49 | −44 | −38 | −44 |
| Range (dB) | 26 | 11 | 14 | 7 | 13 | 6 | 8 | 4 |
| Mean (dB) | −42 | −41 | −41 | −41 | −42 | −41 | −41 | −41 |
| Median (dB) | −40 | −40 | −41 | −42 | −41 | −42 | −41 | −41 |
| Std (dB) | 14.786 | 9.634 | 13.91 | 6.939 | 12.96 | 6.393 | 7.891 | 3.781 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, C.; Chu, D.; Horne, J.; Li, H. Comparison of Coherent to Incoherent Kirchhoff-Ray-Mode (KRM) Models in Predicting Backscatter by Swim-Bladder-Bearing Fish. J. Mar. Sci. Eng. 2023, 11, 473. https://doi.org/10.3390/jmse11030473
Li C, Chu D, Horne J, Li H. Comparison of Coherent to Incoherent Kirchhoff-Ray-Mode (KRM) Models in Predicting Backscatter by Swim-Bladder-Bearing Fish. Journal of Marine Science and Engineering. 2023; 11(3):473. https://doi.org/10.3390/jmse11030473
Chicago/Turabian StyleLi, Chao, Dezhang Chu, John Horne, and Haisen Li. 2023. "Comparison of Coherent to Incoherent Kirchhoff-Ray-Mode (KRM) Models in Predicting Backscatter by Swim-Bladder-Bearing Fish" Journal of Marine Science and Engineering 11, no. 3: 473. https://doi.org/10.3390/jmse11030473
APA StyleLi, C., Chu, D., Horne, J., & Li, H. (2023). Comparison of Coherent to Incoherent Kirchhoff-Ray-Mode (KRM) Models in Predicting Backscatter by Swim-Bladder-Bearing Fish. Journal of Marine Science and Engineering, 11(3), 473. https://doi.org/10.3390/jmse11030473







