A Numerical Study on the Effects of Ship-Generated Waves on a Moored Ship in Restricted Waterways Considering Initial Acceleration Process
Abstract
:1. Introduction
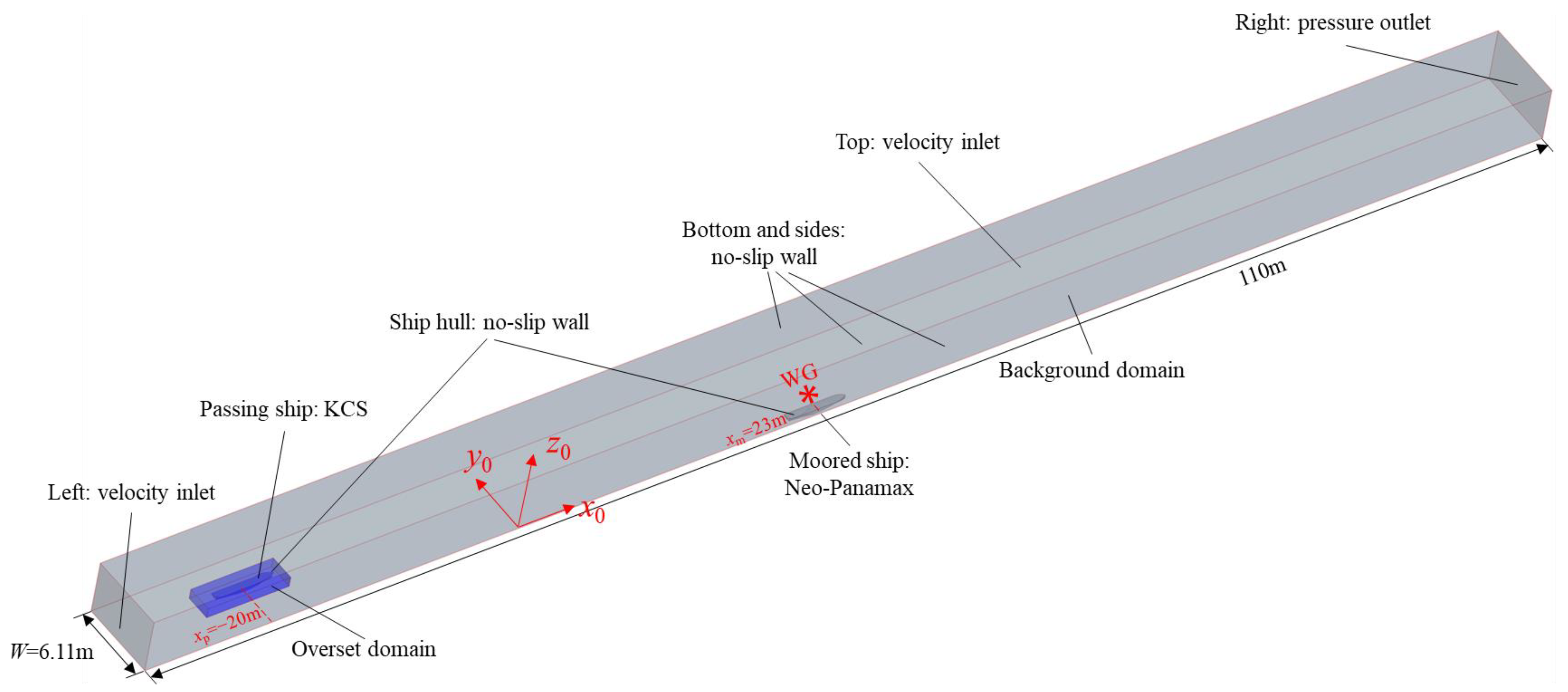
2. Problem Description
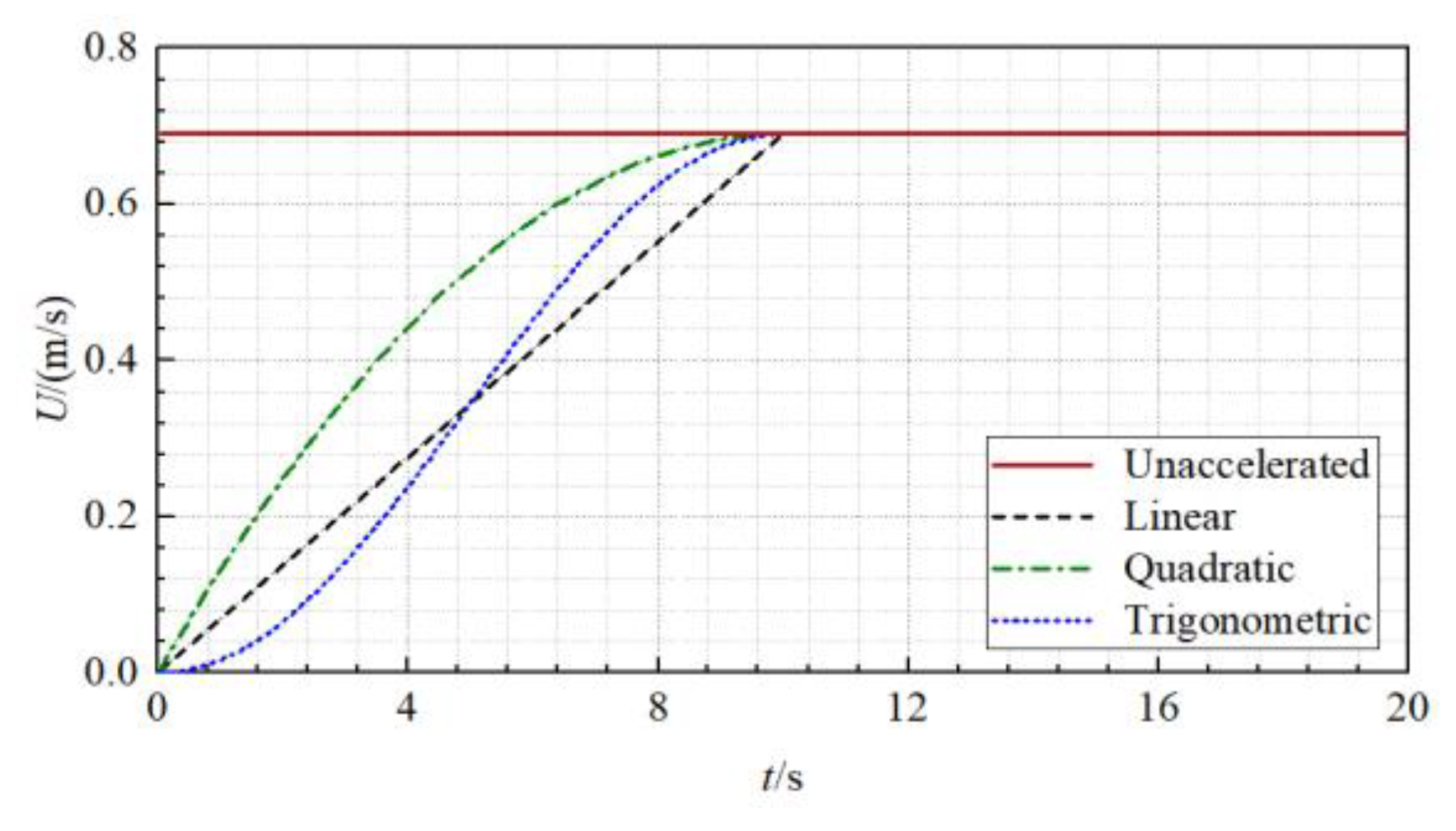
- Acceleration process: starting from the static state, the passing ship is accelerated to the specified passing speed U by a carriage.
- Constant-speed process: the passing ship passes the moored ship with the constant speed U.
- Deceleration process: after the passing ship has moved away from the moored ship, it is decelerated to zero speed.
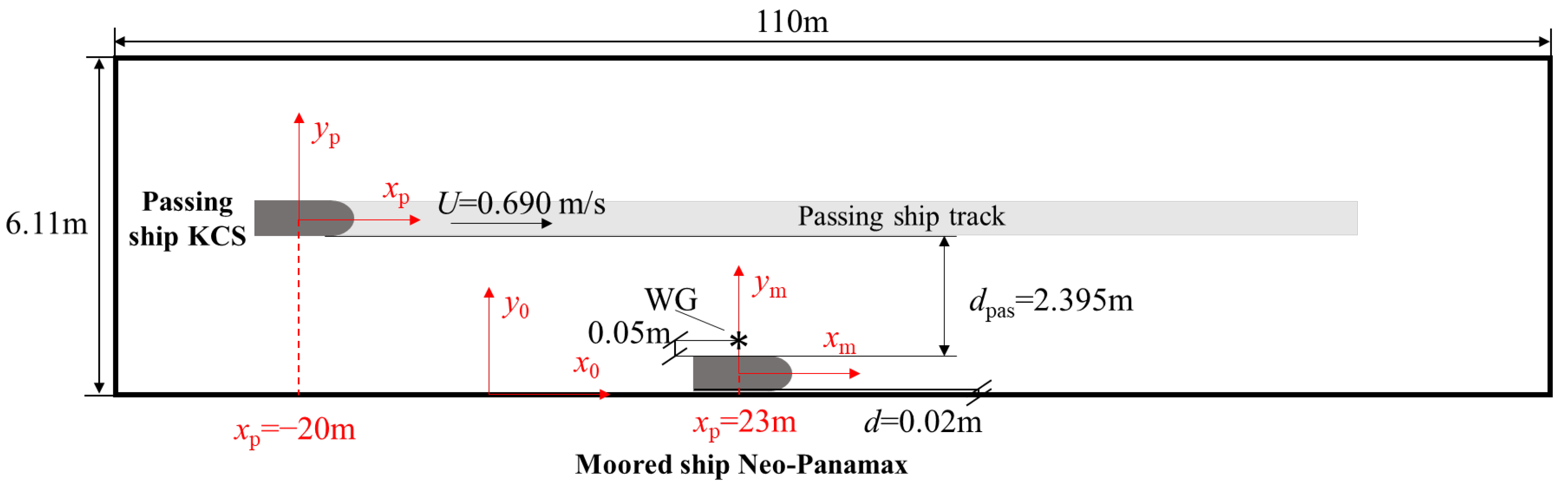
| Main Particulars | Symbol | Units | Value |
|---|---|---|---|
| Water depth | h | m | 0.285 |
| Under keel clearance | UKC | - | 50% |
| Tank width | W | m | 6.11 |
| Passing speed | U | m/s | 0.690 |
| Froude number based on the passing ship length | Fr | - | 0.1055 |
| Froude number based on water depth | Frh | - | 0.4128 |
| Passing distance | dpas | m | 2.395 |
3. Governing Equations and Numerical Methods
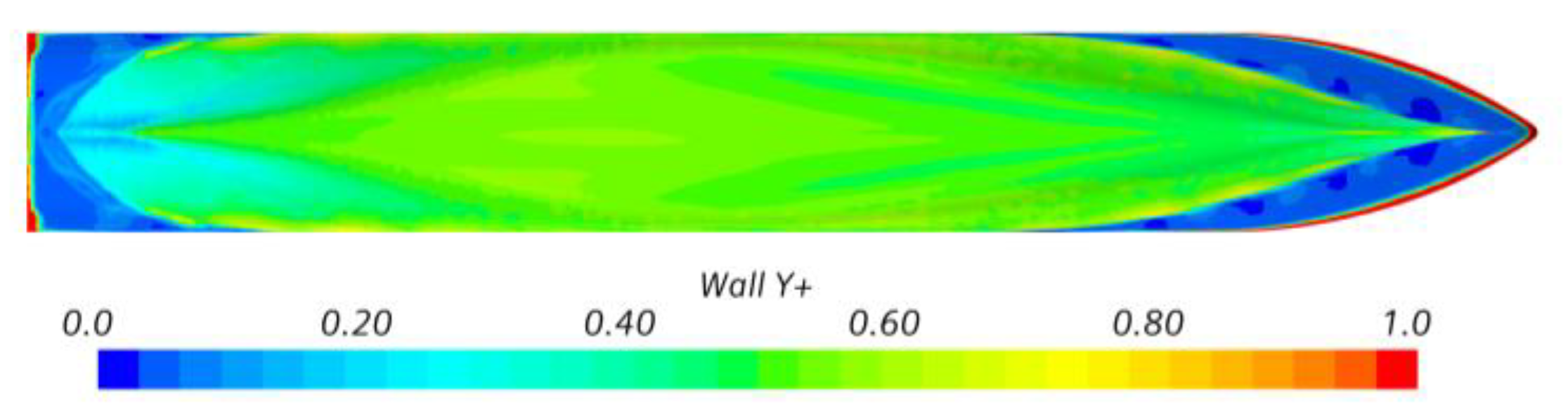
3.1. Governing Equations and Turbulence Model
3.2. Dynamic Overset Meth Technique
3.3. Numerical Settings
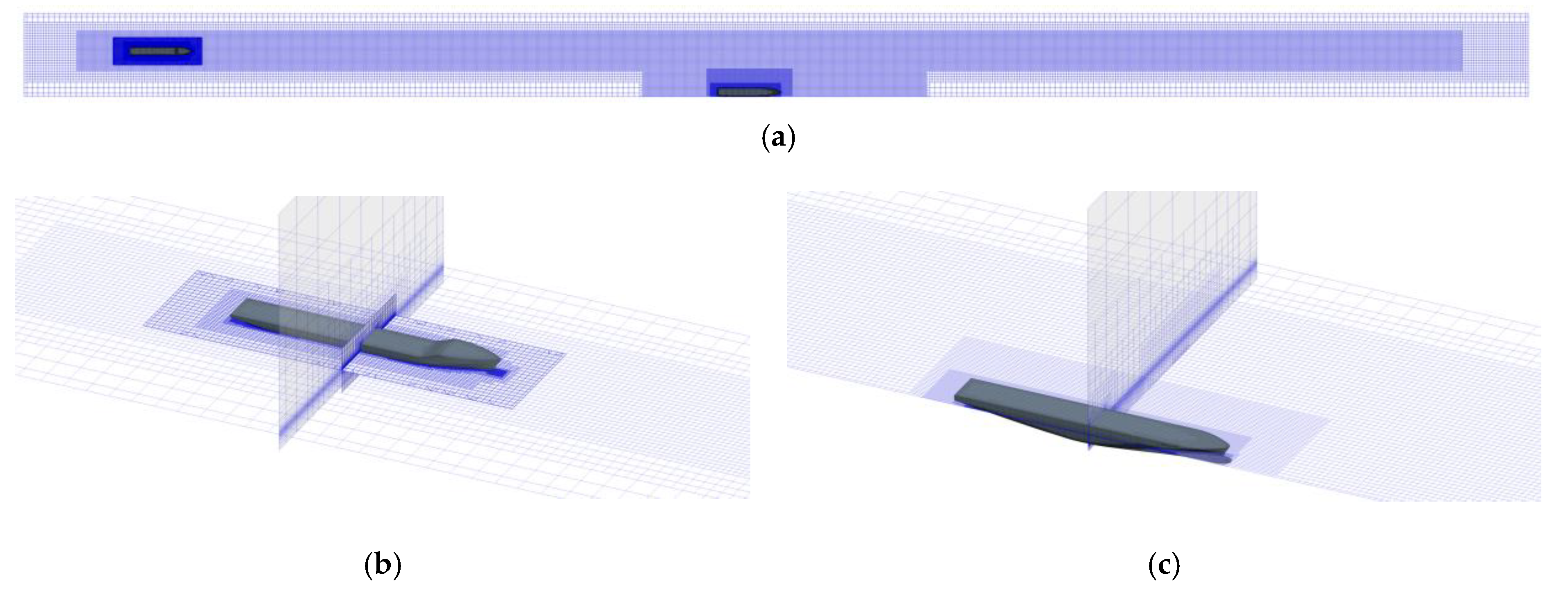
3.4. Mesh Generation
4. Mesh Convergence Study
5. Numerical Results
5.1. Effects of Ship-Generated Waves
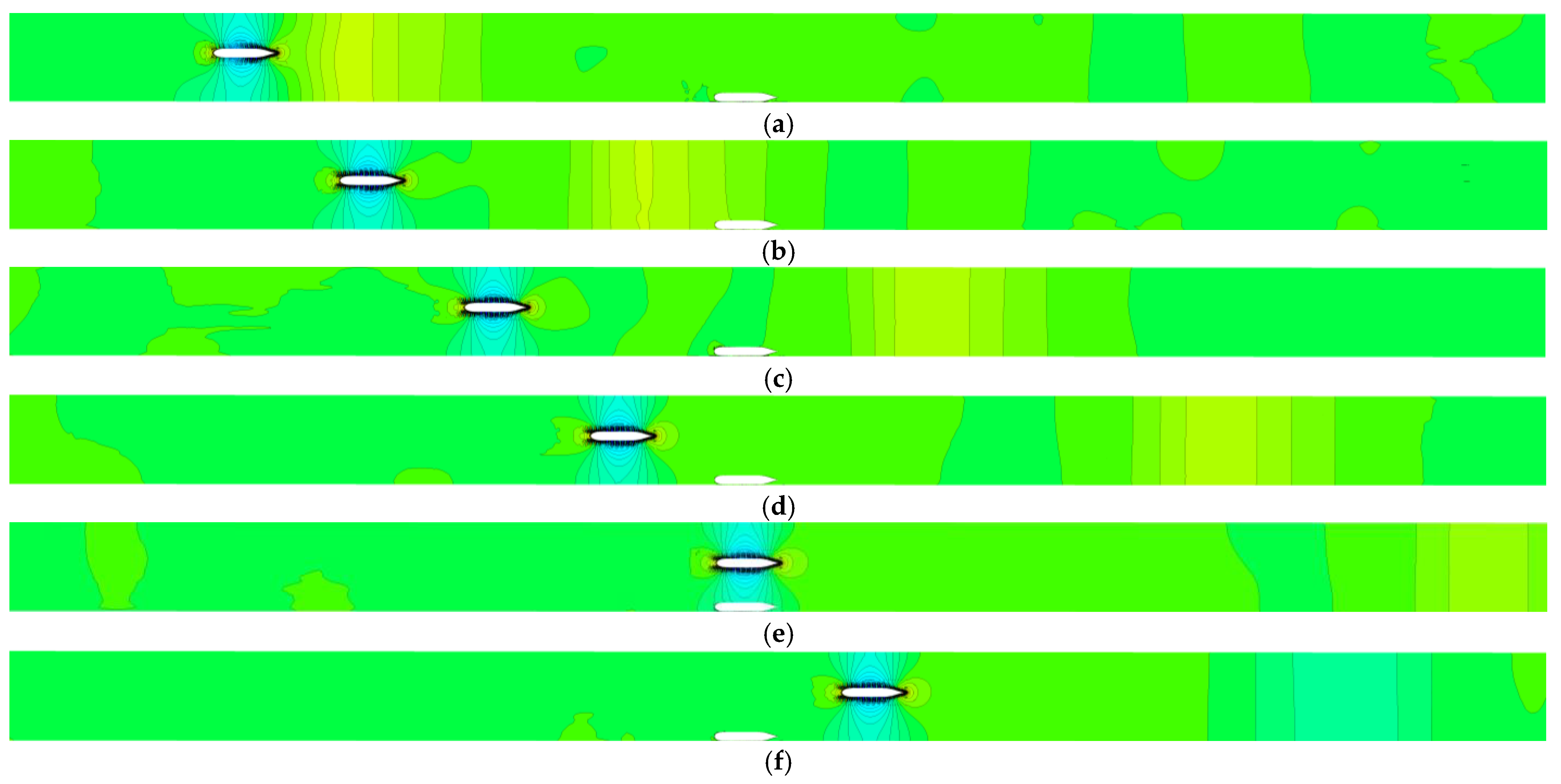
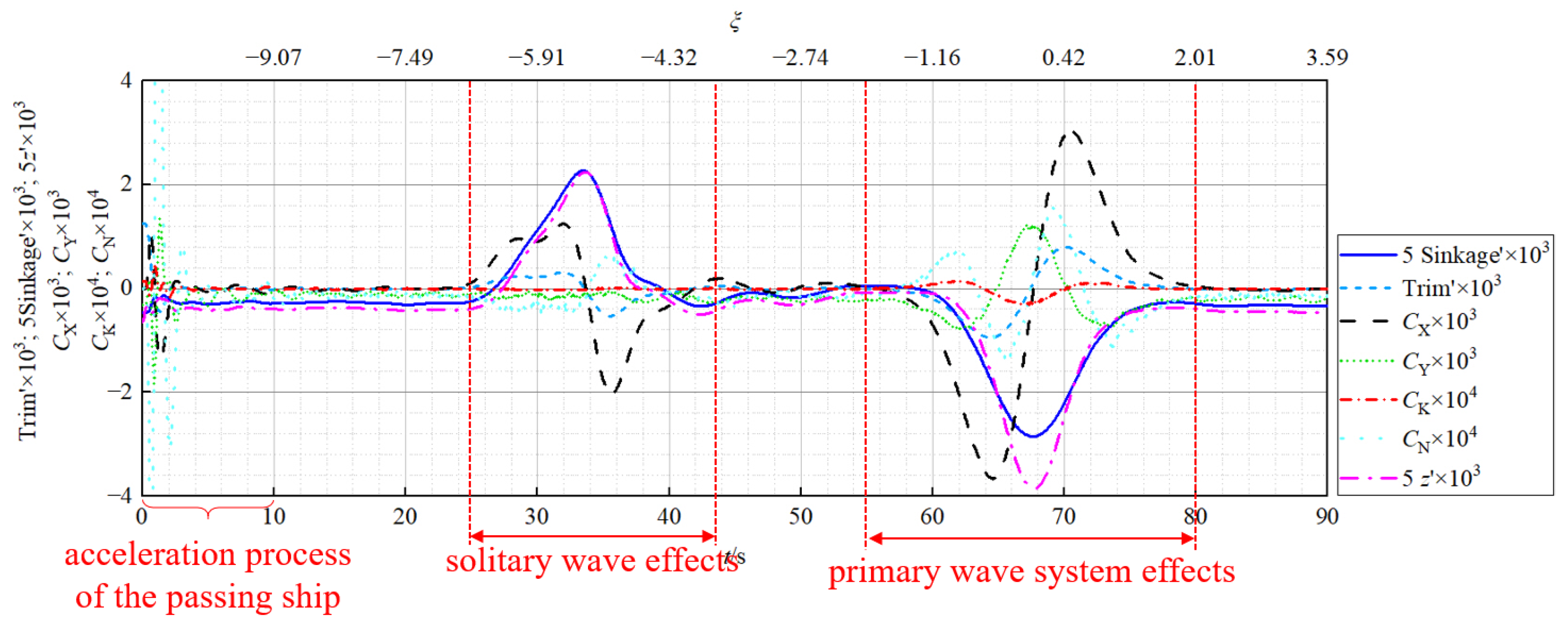
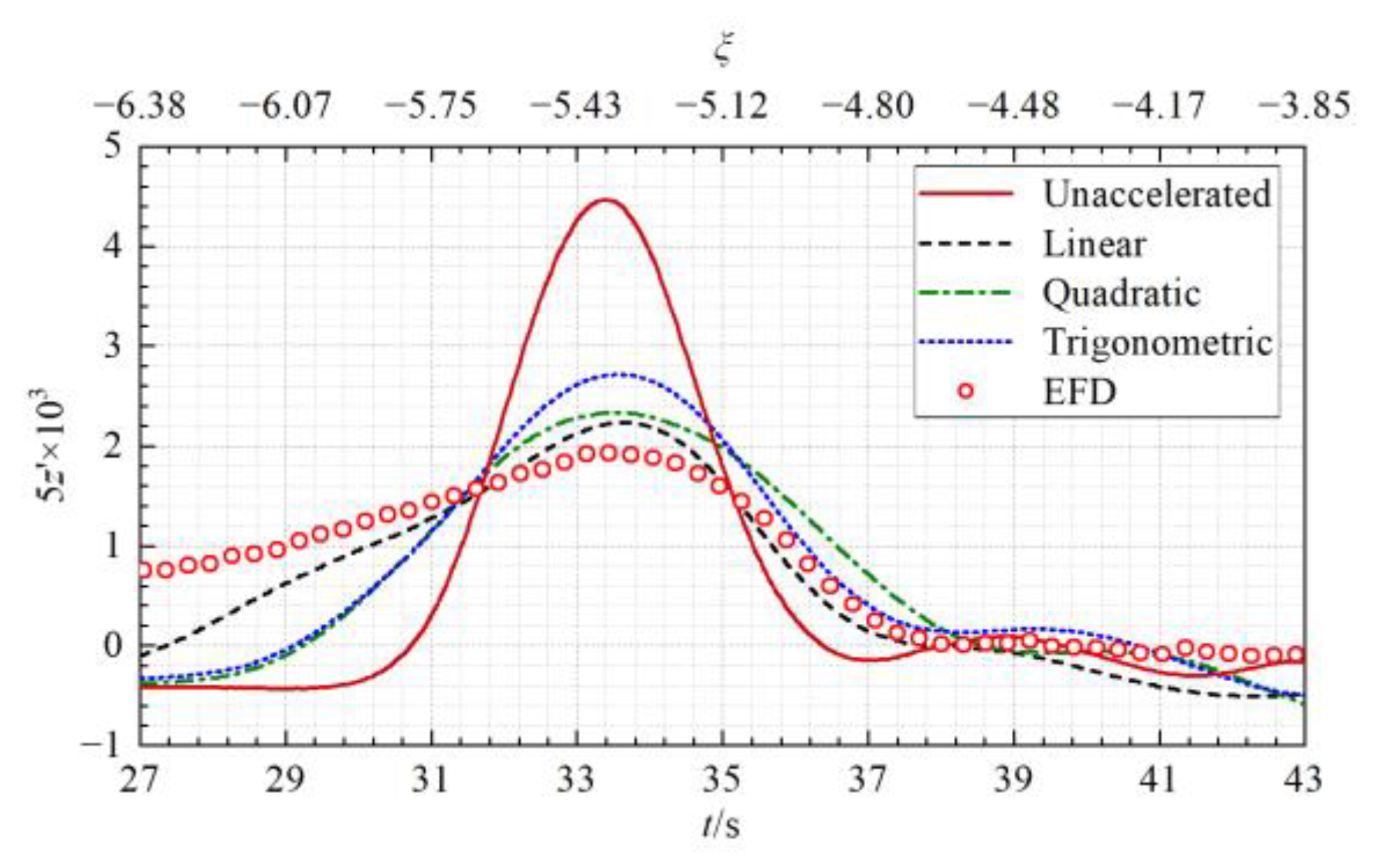
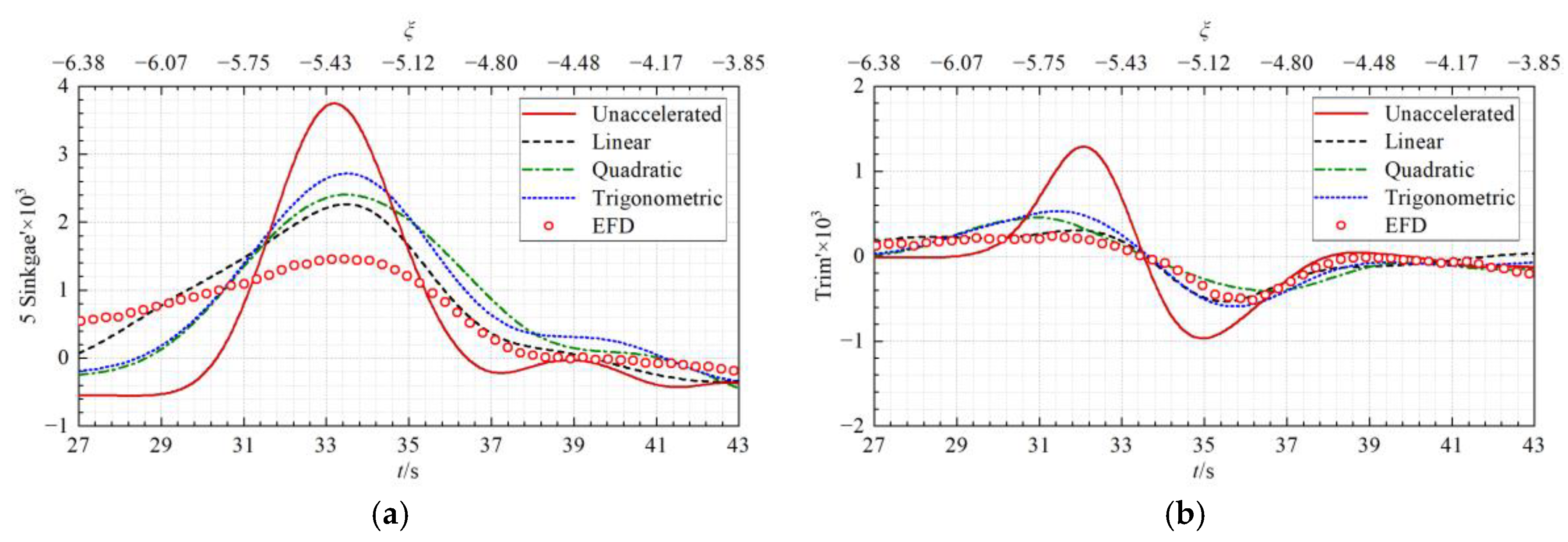
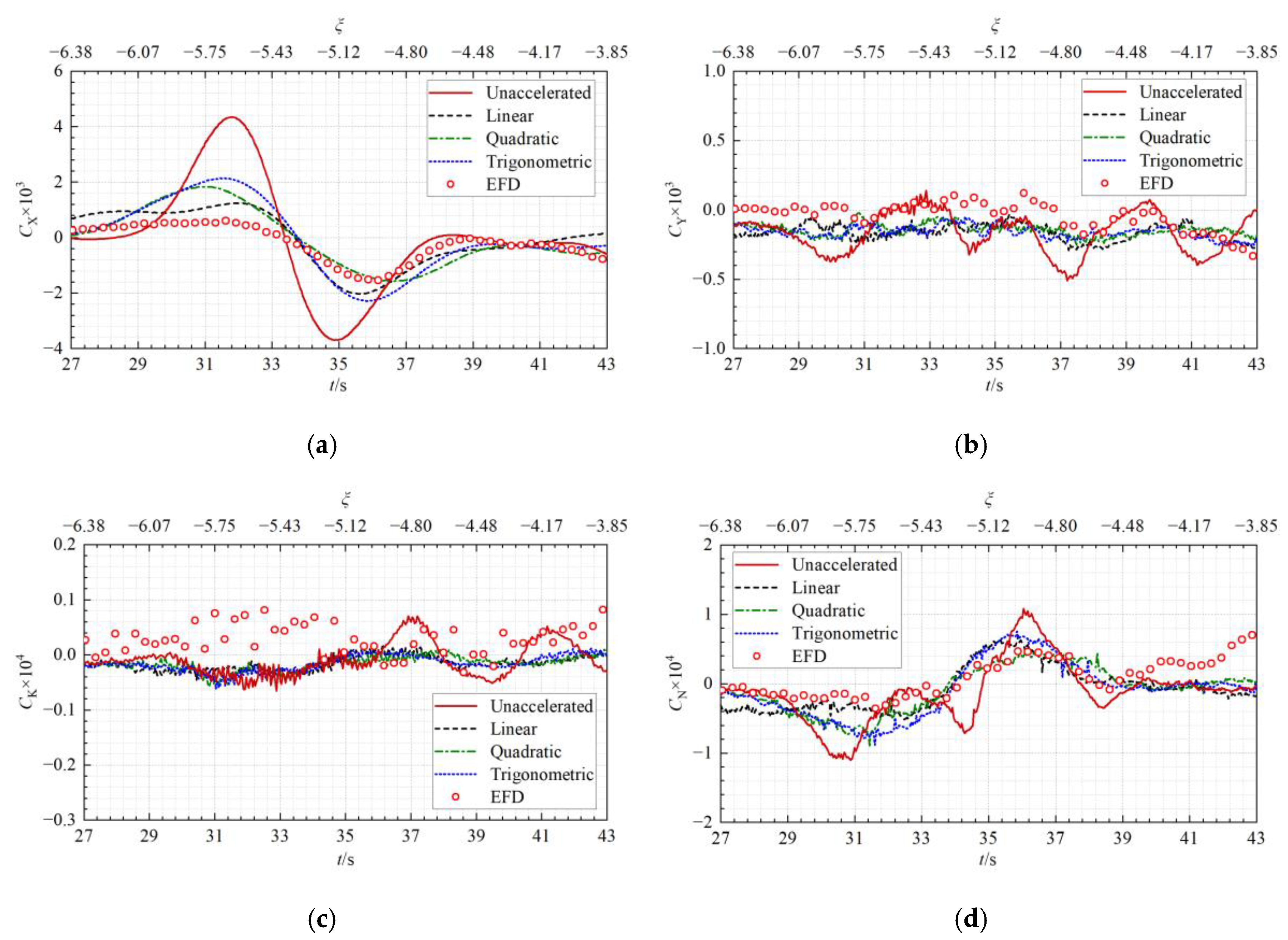
- Solitary wave effects: During the initial passing process, a solitary wave induced by the passing ship propagates steadily from the ship through the tank. This phenomenon was also recorded in the model tests by van Zwijnsvoorde et al. [13]. When the solitary wave is passing the moored ship (27 s < t < 43 s or −6.38 < ξ < −3.85), there is still a long distance between the two ships (27.82~16.78 m, about 6.39~3.86 times the moored ship length), and the moored ship obviously rises and the longitudinal force X on it varies significantly. After the solitary wave travels away from the moored ship (t > 50 s), the attitudes and the hydrodynamic quantities of the moored ship return to zero.
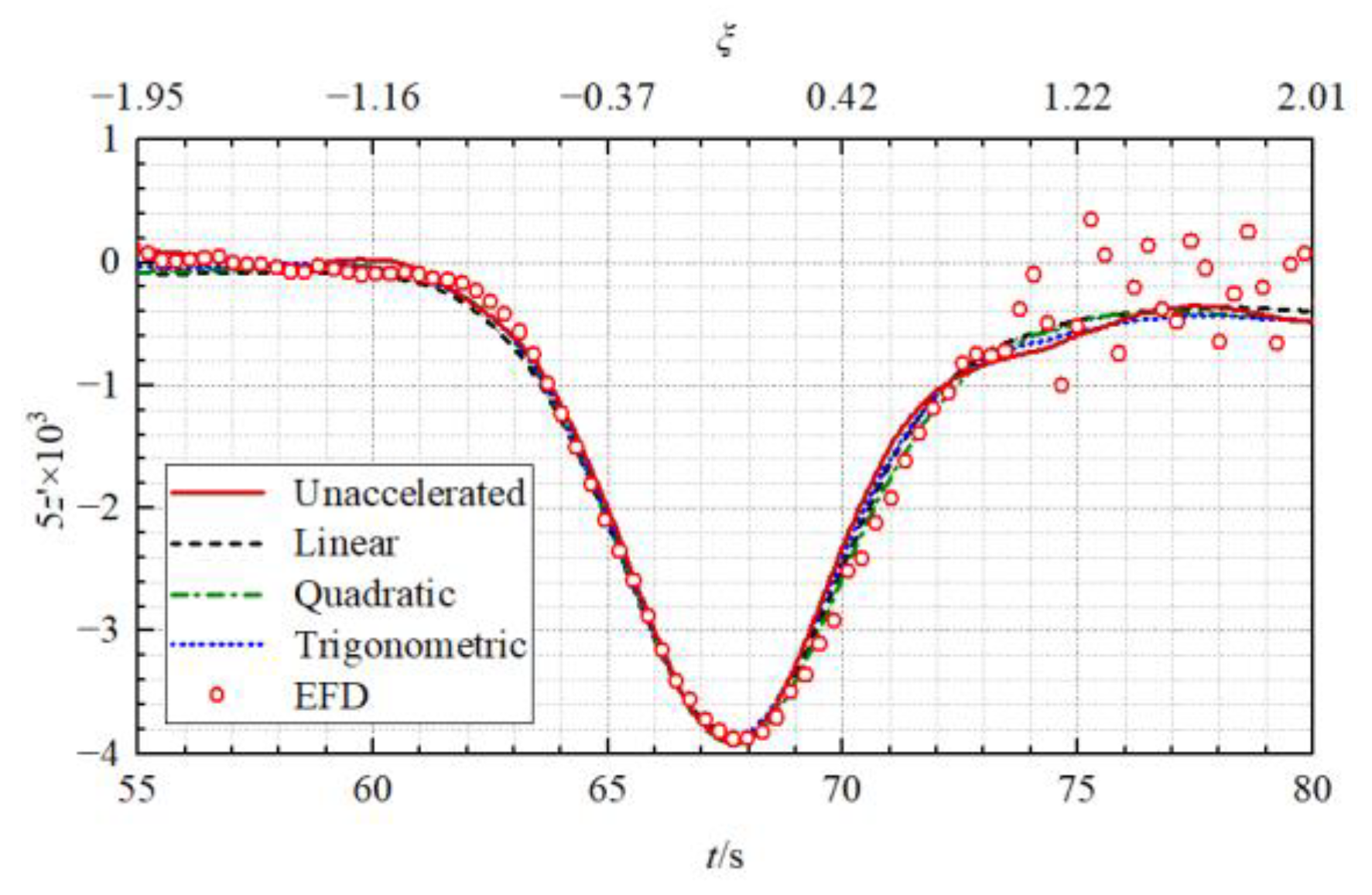
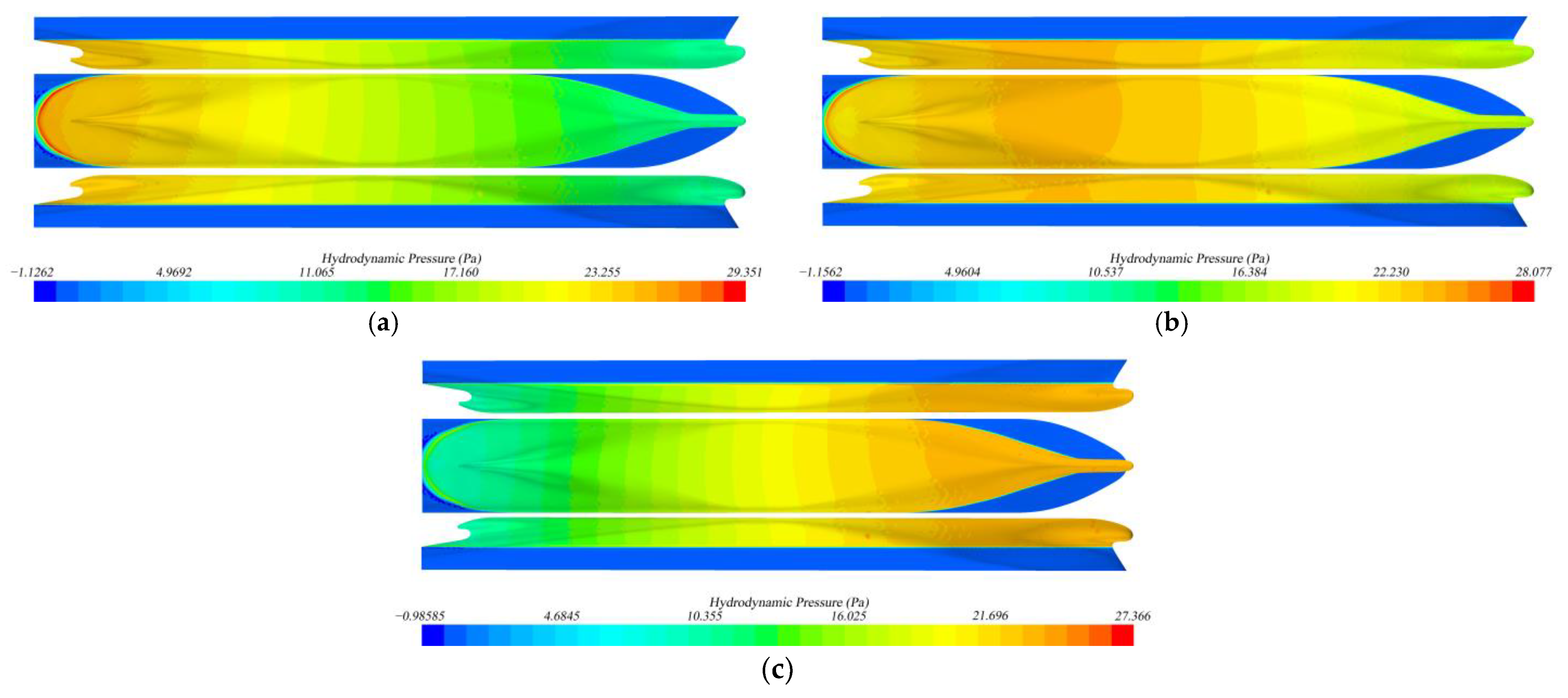
- Primary wave system effects: The wave systems generated by a moving ship are typically classified into the near-field part and the far-field part [5,7]. The former is attributed to the primary wave system resulting from low-frequency pressure variations due to the presence of the passing ship, which is the dominant part at low speeds, especially under the impacts of confined water effects, while the latter is associated with the high-frequency free waves (Kelvin wave or secondary wave system) generated by the passing ship at higher speeds. It should be noted that the primary wave system is often a major concern for passing ship problems in confined waterways, because it usually causes significant impacts on the ships in the vicinity, while the far-field disturbances by the Kelvin wave system are not negligible when the passing ship is at a high speed. As can be seen from the simulated wave patterns in Figure 7, at a low speed (Fr = 0.1055) of the passing ship, the Kelvin wave system is not evident, while the primary wave system is more prominent. Thus, the impact of the Kelvin wave is negligible. Besides, the primary wave system travels with the passing ship all the time. When the ship is passing the moored ship (55 s < t < 80 s or −2 < ξ < 2), the primary wave system has pronounced hydrodynamic impacts on the moored ship, which generates additional motions of the moored ship, namely more remarkable variations of the ship attitudes, and also more pronounced hydrodynamic forces and moments on the ship.

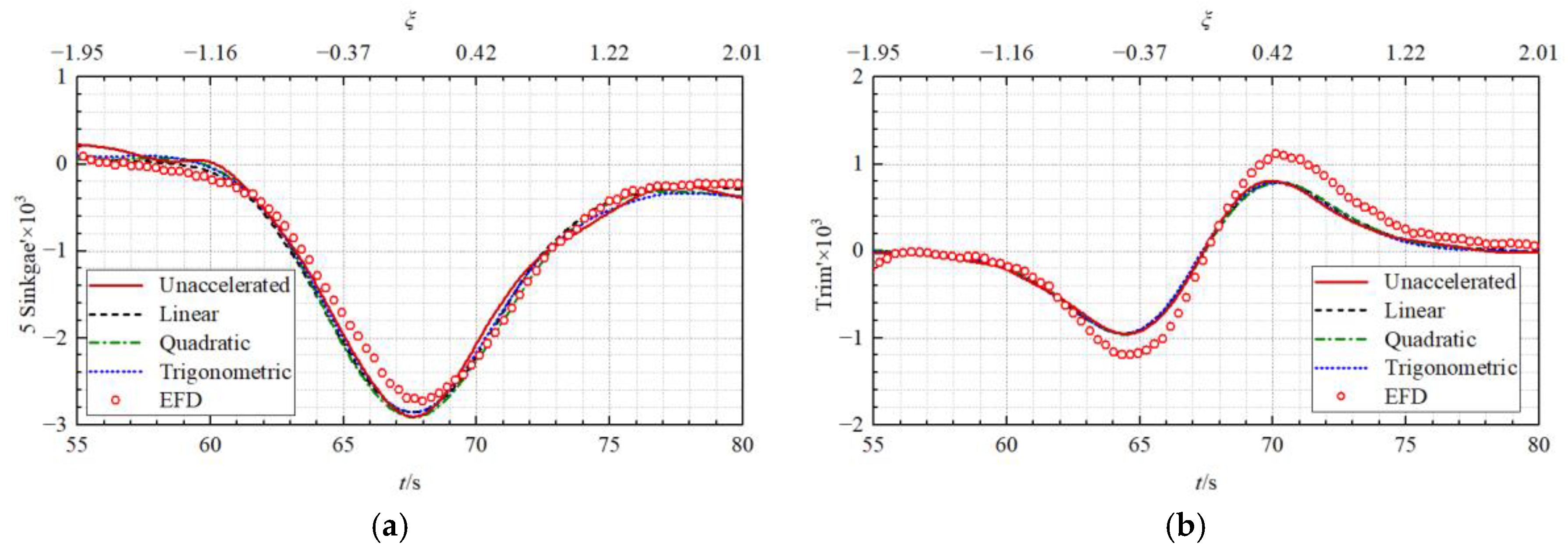
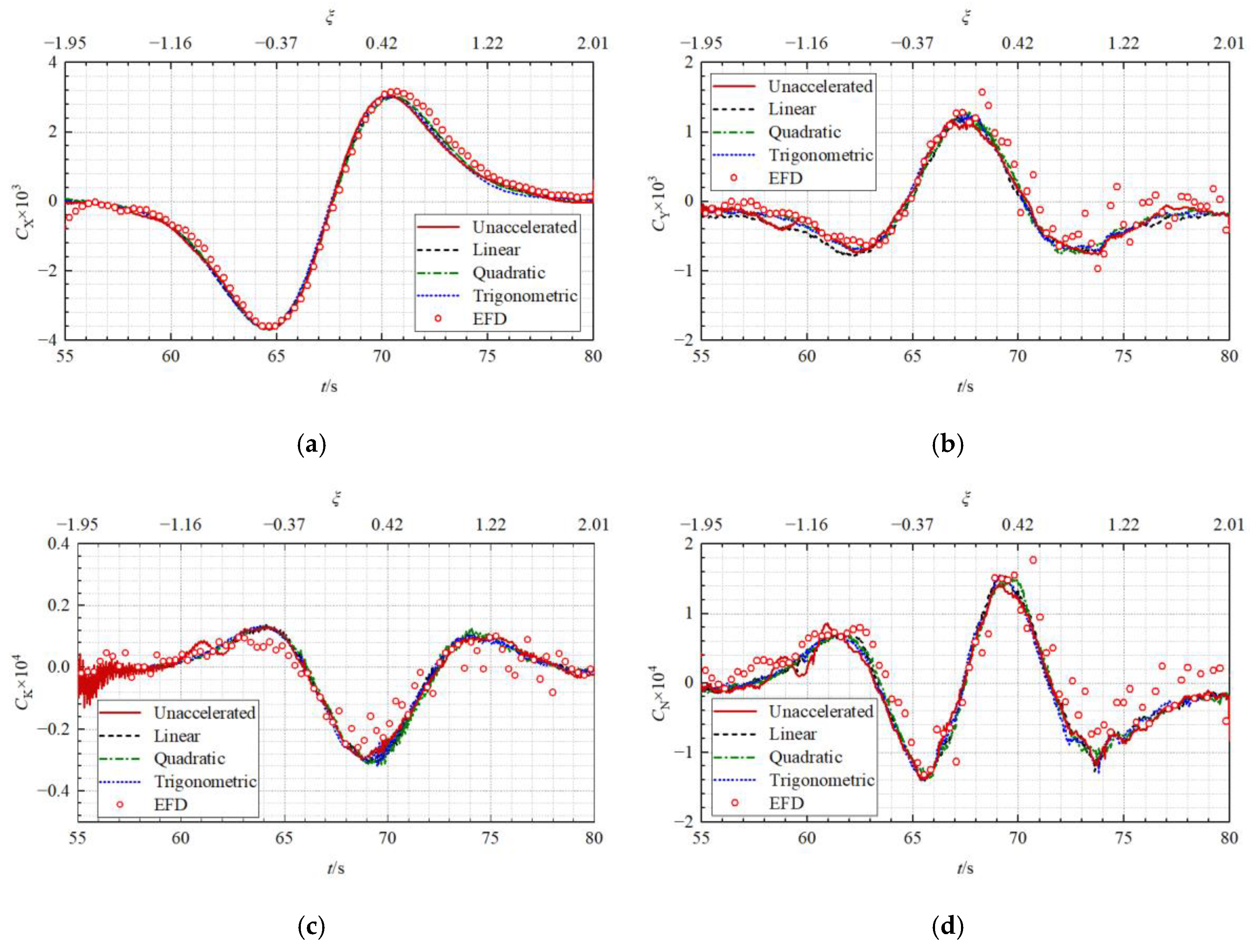
5.2. Influences of Acceleration Process
5.2.1. Accuracy of the Predicted Solitary Wave
5.2.2. Accuracy of the Predicted Primary Wave System
5.3. Physical Mechanism Analyses
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pinkster, J.A.; Keuning, J.A. Prediction of the effects of fast passing vessels on moored vessels. In Proceedings of the 32nd International Conference on Ocean, Offshore and Arctic Engineering, New York, NY, USA, 9–14 June 2013. [Google Scholar]
- Pinkster, J.A.; Ruijter, M.N. The influence of passing ships on ships moored in restricted waters. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 3–6 May 2004. [Google Scholar]
- Almström, B.; Larson, M. Measurements and analysis of primary ship waves in the Stockholm Archipelago, Sweden. J. Mar. Sci. Eng. 2020, 8, 743. [Google Scholar] [CrossRef]
- Göransson, G.; Larson, M.; Althage, J. Ship-generated waves and induced turbidity in the Göta Älv River in Sweden. J. Waterw. Port Coast. Ocean Eng. 2014, 140, 04014004. [Google Scholar] [CrossRef]
- Pinkster, J.A.; Rotterdam, B.V. Suction, seiche and wash effects of passing ships in ports. In Proceedings of the SNAME Maritime Convention, Rotterdam, The Netherlands, 21 October 2009; pp. 99–124. [Google Scholar]
- Pinkster, J.A.; Naaijien, P. Predicting the effect of passing ships. In Proceedings of the 18th International Workshop on Water Waves and Floating Bodies, Le Croisic, France, 6–9 April 2003. [Google Scholar]
- Zhou, L.; Abdelwahab, H.S.; Guedes Soares, C. Experimental and CFD investigation of the effects of a high-speed passing ship on a moored container ship. Ocean Eng. 2021, 228, 108914. [Google Scholar] [CrossRef]
- Maneuvering Committee of International Towing Tank Conference. Final Report and Recommendations to the 29th ITTC. In Proceedings of the 29th International Towing Tank Conference, Virtual, 13–18 June 2021.
- Remery, G.F. Mooring forces induced by passing ships. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 5–7 May 1974. [Google Scholar]
- Vantorre, M.; Verzhbitskaya, E.; Laforce, E. Model test based formulations of ship-ship interaction forces. Ship Technol. Res. 2002, 49, 124–141. [Google Scholar]
- Duffy, J.T.; Renilson, M.R. The importance of the form of time domain forces and moments on berthed ship interaction. In Proceedings of the 2nd International Conference on Ship Manoeuvering in Shallow and Confined Water: Ship to Ship Interactions, Trondheim, Norway, 18–20 May 2011; pp. 107–116. [Google Scholar]
- Lataire, E.; Vantorre, M.; Vandenbroucke, J.; Eloot, K. Ship to ship interaction forces during lightering operations. In Proceedings of the 2nd International Conference on Ship Manoeuvring in Shallow and Confined Water: Ship to Ship Interaction, Trondheim, Norway, 18–20 May 2011; pp. 211–221. [Google Scholar]
- Van Zwijnsvoorde, T.; Delefortrie, G.; Lataire, E. Passing ship effects in shallow and confined water: Open model test data for validation purposes. In Proceedings of the 6th MASHCON International Conference on Ship Manoeuvring in Shallow and Confined Water, Glasgow, UK, 22–26 May 2022; pp. 255–283. [Google Scholar]
- Van der Molen, W.; Moes, J.; Swiegers, P.B.; Vantorre, M. Calculation of forces on moored ships due to passing ships in shallow water. In Proceedings of the 2nd International Conference on Ship Manoeuvring in Shallow and Confined Water: Ship to Ship Interaction, Trondheim, Norway, 18–20 May 2011; pp. 369–374. [Google Scholar]
- Talstra, H.; Bliek, A.J. Loads on moored ships due to passing ship in a straight harbour channel. In Proceedings of the 33rd PIANC International Navigation Congress, San Francisco, CA, USA, 1–5 June 2014; pp. 206–224. [Google Scholar]
- Yuan, Z.M.; Li, L.; Yeung, R.W. Free-surface effects on interaction of multiple ships moving at different speeds. J. Ship Res. 2019, 63, 251–267. [Google Scholar] [CrossRef]
- Degrieck, A.; Uyttersprot, B.; Sutulo, S.; Guedes Soares, C.; Van Hoydonck, W.; Vantorre, M.; Lataire, E. Hydrodynamic ship-ship and ship-bank interaction: A comparative numerical study. Ocean Eng. 2021, 230, 108970. [Google Scholar] [CrossRef]
- Sadat-Hosseini, H.; Wu, P.C.; Toda, Y.; Carrica, P.; Stern, F. URANS studies of ship-ship interactions in shallow water. In Proceedings of the 2nd International Conference on Ship Manoeuvring in Shallow and Confined Water: Ship to Ship Interaction, Trondheim, Norway, 18–20 May 2011; pp. 299–308. [Google Scholar]
- Zou, L.; Larsson, L. Numerical predictions of ship-to-ship interaction in shallow water. Ocean Eng. 2013, 72, 386–402. [Google Scholar] [CrossRef]
- Kwon, C.; Yeon, S. A study on the numerical captive model tests for ships in shallow and confined waters using CFD: Comparative study for PESCA (passing effects in shallow and confined areas) project. In Proceedings of the 6th MASHCON International Conference on Ship Manoeuvring in Shallow and Confined Water, Glasgow, UK, 22–26 May 2022; pp. 119–127. [Google Scholar]
- Yu, J.; Liu, L.; Zhang, Z.; Yao, C.; Feng, D.; Wang, X. Numerical investigation of passing ship effects in shallow and confined water using Ship-HUST code. In Proceedings of the 6th MASHCON International Conference on Ship Manoeuvring in Shallow and Confined Water, Glasgow, UK, 22–26 May 2022; pp. 310–318. [Google Scholar]
- Zheng, Z.Q.; Zou, L.; Zou, Z.J. A numerical investigation on the ship-ship interaction between a passing ship and a moored ship in restricted waterways. In Proceedings of the 6th MASHCON International Conference on Ship Manoeuvring in Shallow and Confined Water, Glasgow, UK, 22–26 May 2022; pp. 344–355. [Google Scholar]
- Denehy, S.P. Modelling of Berthed Ship-Passing Ship Interaction Forces and Moments in Shallow and Confined Water. Ph.D. Thesis, University of Tasmania, Tasmania, Australia, 2022. [Google Scholar]
- Pawar, R.; Bhar, A.; Dhavalikar, S. Numerical prediction of hydrodynamic forces on a moored ship due to a passing ship. Proc. Inst. Mech. Eng. Part M J. Eng. Marit. Environ. 2019, 233, 575–585. [Google Scholar] [CrossRef]
- Alisal, S.M. Some experimental results with ship model acceleration waves. J. Ship Res. 1981, 25, 181–190. [Google Scholar] [CrossRef]
- Mao, L.; Li, X.; Chen, Y. Numerical investigation of ship waves and associated hydrodynamics over a sloping bed with a non-hydrostatic model. J. Offshore Mech. Arct. Eng. 2022, 145, 031201. [Google Scholar] [CrossRef]
- Terziev, M.; Zhao, G.; Tezdogan, T.; Yuan, Z.M.; Incecik, A. Virtual replica of a towing tank experiment to determine the Kelvin half-angle of a ship in restricted water. J. Mar. Sci. Eng. 2020, 8, 258. [Google Scholar] [CrossRef] [Green Version]
- Li, M.; Yuan, Z.M.; Yeung, R.W. Unsteady wave-making resistance of an accelerating ship. In Proceedings of the 39th International Conference on Ocean, Offshore and Arctic Engineering, Virtual Online, 3–7 August 2020. [Google Scholar]
- Lungu, A. CFD prediction of ship-bank interaction. In Proceedings of the 7th Conference of the Sustainable Solutions for Energy and Environment, Virtual Online, 21–24 October 2020. [Google Scholar]
- Shih, T.H.; Liou, W.W.; Shabbir, A.; Yang, Z.; Zhu, J. A new k-ε eddy viscosity model for high Reynolds number turbulent flows. Comput. Fluids 1995, 24, 227–238. [Google Scholar] [CrossRef]
- Wnęk, A.D.; Sutulo, S.; Guedes Soares, C. CFD analysis of ship-to-ship hydrodynamic interaction. J. Mar. Sci. Appl. 2018, 17, 21–37. [Google Scholar] [CrossRef]
- Hadzic, H. Development and Application of Finite Volume Method for the Computation of Flows around Moving Bodies on Unstructured, Overlapping Grids. Ph.D. Thesis, Technische Universität Hamburg, Hamburg, Germany, 2005. [Google Scholar]
- Ohmori, T. Finite-volume simulation of flows about a ship in maneuvering motion. J. Mar. Sci. Technol. 1998, 3, 82–93. [Google Scholar] [CrossRef]
- Maneuvering Committee of International Towing Tank Conference. Final Report and Recommendations to the 28th ITTC. In Proceedings of the 28th International Towing Tank Conference, Wuxi, China, 17–22 September 2017.
- Celik, I.B.; Ghia, U.; Roache, P.J.; Freitas, C.J.; Coleman, H.; Raad, P.E. Procedure for estimation and reporting of uncertainty due to discretization in CFD applications. J. Fluids Eng. 2008, 130, 078001. [Google Scholar]

| Main Particulars | Symbol | Units | KCS | Neo-Panamax |
|---|---|---|---|---|
| Scale ratio | λ | - | 1/80 | 1/80 |
| Length between perpendiculars | Lpp | m | 4.367 | 4.350 |
| Breadth | B | m | 0.611 | 0.610 |
| Draft | T | m | 0.190 | 0.190 |
| Ship mass | m | kg | 320.6 | 326.2 |
| Wetted surface area | S | m2 | 3.304 | 3.361 |
| Longitudinal centre of gravity | xG | m | −0.048 | −0.114 |
| Vertical centre of gravity | zG | m | 0.003 | −0.002 |
| Inertia moment around x-axis | Ixx | kgm2 | 11.9 | 11.2 |
| Inertia moment around y-axis | Iyy | kgm2 | 367.4 | 396.6 |
| Inertia moment around z-axis | Izz | kgm2 | 385.8 | 376.1 |
| Mesh Set | Basic Size (m) | Number of Mesh Cells (Million) | ||
|---|---|---|---|---|
| Background | Overset | Total | ||
| Coarse | 0.1189 | 1.47 | 0.83 | 2.29 |
| Medium | 0.1 | 2.41 | 1.12 | 3.53 |
| Fine | 0.0841 | 3.80 | 1.61 | 5.41 |
| CX | CY | CK | CN | |
|---|---|---|---|---|
| ϕ1 | −3.745 × 10−3 | 1.332 × 10−3 | −0.305 × 10−4 | −1.399 × 10−4 |
| ϕ2 | −3.667 × 10−3 | 1.224 × 10−3 | −0.316 × 10−4 | −1.403 × 10−4 |
| ϕ3 | −3.552 × 10−3 | 1.484 × 10−3 | −0.337 × 10−4 | −1.610 × 10−4 |
| R | 0.68 | −0.41 | 0.56 | 0.02 |
| Convergence type | Mon. Con. | Osc. Con. | Mon. Con. | Mon. Con. |
| ϕ0 | −3.908 × 10−3 | 1.408 × 10−3 | −0.290 × 10−4 | −1.399 × 10−4 |
| e1 | 4.17% | 5.42% | 5.04% | 0.01% |
| e2 | 6.16% | 13.09% | 9.02% | 0.36% |
| GCI | 5.44% | 7.17% | 5.99% | 0.01% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, Z.; Zou, L.; Zou, Z. A Numerical Study on the Effects of Ship-Generated Waves on a Moored Ship in Restricted Waterways Considering Initial Acceleration Process. J. Mar. Sci. Eng. 2023, 11, 483. https://doi.org/10.3390/jmse11030483
Zheng Z, Zou L, Zou Z. A Numerical Study on the Effects of Ship-Generated Waves on a Moored Ship in Restricted Waterways Considering Initial Acceleration Process. Journal of Marine Science and Engineering. 2023; 11(3):483. https://doi.org/10.3390/jmse11030483
Chicago/Turabian StyleZheng, Ziqiang, Lu Zou, and Zaojian Zou. 2023. "A Numerical Study on the Effects of Ship-Generated Waves on a Moored Ship in Restricted Waterways Considering Initial Acceleration Process" Journal of Marine Science and Engineering 11, no. 3: 483. https://doi.org/10.3390/jmse11030483
APA StyleZheng, Z., Zou, L., & Zou, Z. (2023). A Numerical Study on the Effects of Ship-Generated Waves on a Moored Ship in Restricted Waterways Considering Initial Acceleration Process. Journal of Marine Science and Engineering, 11(3), 483. https://doi.org/10.3390/jmse11030483






