Assessment of Using Artificial Neural Network and Support Vector Machine Techniques for Predicting Wave-Overtopping Discharges at Coastal Structures
Abstract
:1. Introduction
2. Materials and Methods
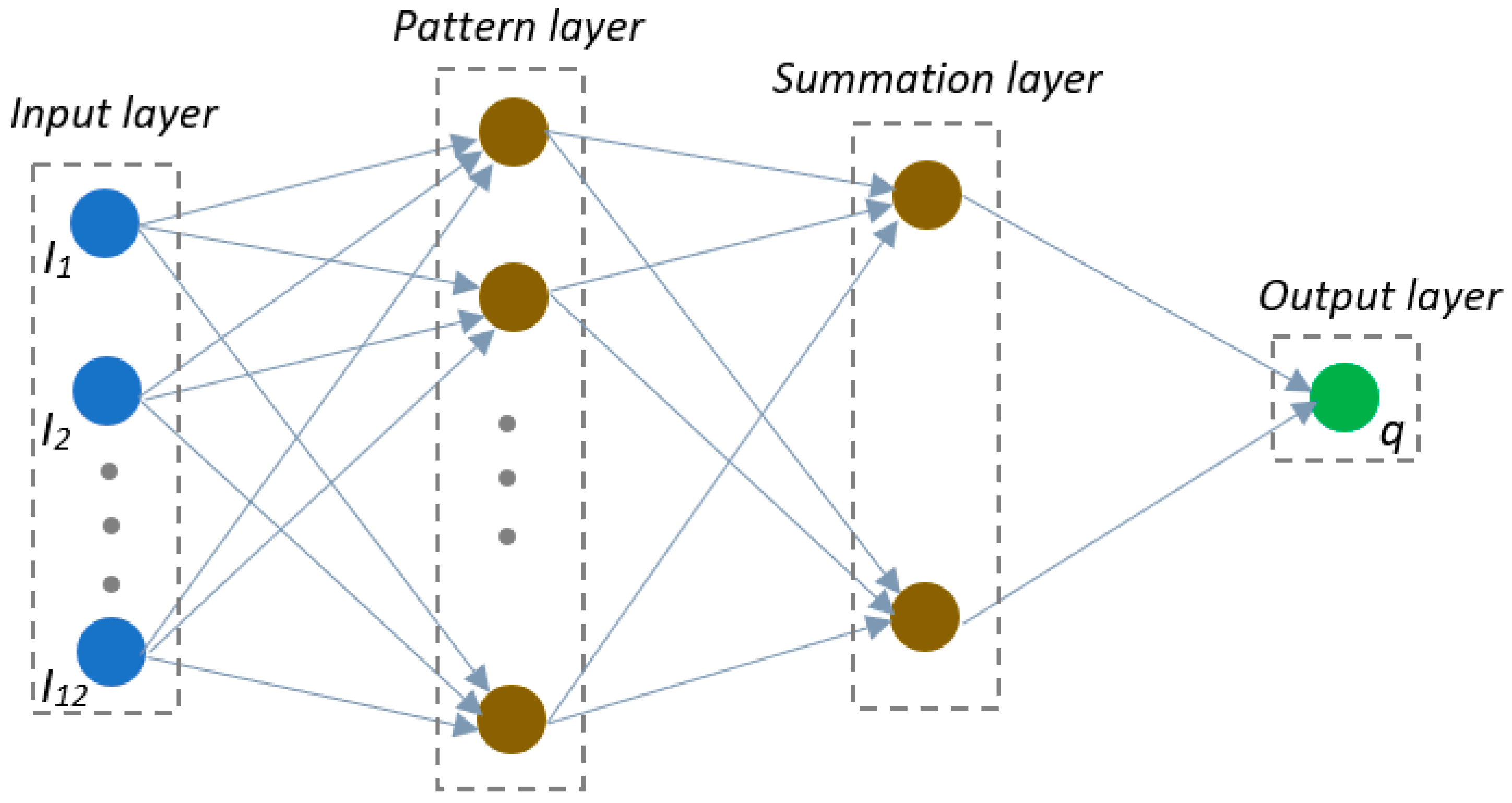
2.1. ANN Methods
2.2. SVM Method
2.3. Data
3. Results and Discussion
3.1. ANN Models
3.2. SVM Model
3.3. Comparison between the ANN and SVM Models
3.4. Comparison of the GRNN Model with the van Gent et al. (2007) Model
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dong, S.; Abolfathi, S.; Salauddin, M.; Tan, Z.H.; Pearson, J.M. Enhancing climate resilience of vertical seawall with retrofitting-A physical modelling study. Appl. Ocean. Res. 2020, 103, 102331. [Google Scholar] [CrossRef]
- Salauddin, M.; O’Sullivan, J.J.; Abolfathi, S.; Peng, Z.; Dong, S.; Pearson, J.M. New insights in the probability distributions of wave-by-wave overtopping volumes at vertical breakwaters. Sci. Rep. 2022, 12, 16228. [Google Scholar] [CrossRef] [PubMed]
- Mehrabani, M.B.; Chen, H.-P.; Stevenson, M.W. Overtopping failure analysis of coastal flood defences affected by climate change. J. Phys. Conf. Ser. 2015, 628, 12049. [Google Scholar] [CrossRef] [Green Version]
- De Rouck, J.; Van de Walle, B.; Geeraerts, J. Crest level assessment of coastal structures by full scale monitoring, neural network prediction adn hazard analysis on permissible wave overtopping-(CLASH). Proc. Eurocean 2004, 2004, 1–4. [Google Scholar]
- Pullen, T.; Allsop, N.W.H.; Bruce, T.; Kortenhaus, A.; Schüttrumpf, H.; Van der Meer, J.W. EurOtop Wave Overtopping of sea Defences and Related Structures: Assessment Manual. 2007. Available online: http://www.overtopping-manual.com/assets/downloads/EAK-K073_EurOtop_2007.pdf (accessed on 14 December 2022).
- van Gent, M.R.A.; van den Boogaard, H.F.P.; Pozueta, B.; Medina, J.R. Neural network modelling of wave overtopping at coastal structures. Coast Eng. 2007, 54, 586–593. [Google Scholar] [CrossRef] [Green Version]
- EurOtop, Manual on Wave Overtopping of Sea Defences and Related Structures, 2nd ed. 2018. Available online: http://www.overtopping-manual.com/assets/downloads/EurOtop_II_2018_Final_version.pdf (accessed on 14 December 2022).
- Dong, S.; Salauddin, M.; Abolfathi, S.; Pearson, J. Wave impact loads on vertical seawalls: Effects of the geometrical properties of recurve retrofitting. Water 2021, 13, 2849. [Google Scholar] [CrossRef]
- Zanuttigh, B.; Formentin, S.M.; Briganti, R. A neural network for the prediction of wave reflection from coastal and harbor structures. Coast Eng. 2013, 80, 49–67. [Google Scholar] [CrossRef]
- Zanuttigh, B.; Formentin, S.M.; Van der Meer, J.W. Advances in Modelling Wave-Structure Interaction Through Artificial Neural Networks. Coast Eng. Proc. 2014, 1, 69. [Google Scholar] [CrossRef] [Green Version]
- Formentin, S.M.; Zanuttigh, B.; Van Der Meer, J.W. A neural network tool for predicting wave reflection, overtopping and transmission. Coast Eng. J. 2017, 59, 1750006-1–1750006-31. [Google Scholar] [CrossRef]
- Zanuttigh, B.; Formentin, S.M.; van der Meer, J.W. Prediction of extreme and tolerable wave overtopping discharges through an advanced neural network. Ocean. Eng. 2016, 127, 7–22. [Google Scholar] [CrossRef]
- Molines, J.; Medina, J.R. Explicit wave overtopping formula for mound breakwaters with crown walls using CLASH neural network-derived data. J. Waterw. Port. Coast. Ocean Eng. 2016, 142, 4015024. [Google Scholar] [CrossRef] [Green Version]
- Lee, S.B. Derivation of Wave Overtopping Formulas for Vertical and Inclined Seawalls Using GMDH Algorithm. Master’s Thesis, Seoul National University, Seoul, Republic of Korea, 2018. [Google Scholar]
- Lee, S.B.; Suh, K.-D. Development of wave overtopping formulas for inclined seawalls using GMDH algorithm. KSCE J. Civ. Eng. 2019, 23, 1899–1910. [Google Scholar] [CrossRef]
- den Bieman, J.P.; van Gent, M.R.A.; van den Boogaard, H.F.P. Wave overtopping predictions using an advanced machine learning technique. Coast Eng. 2021, 166, 103830. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. Xgboost: A scalable tree boosting system. In Proceedings of the 22nd Acm Sigkdd International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Hosseinzadeh, S.; Etemad-Shahidi, A.; Koosheh, A. Prediction of mean wave overtopping at simple sloped breakwaters using kernel-based methods. J. Hydroinform. 2021, 23, 1030–1049. [Google Scholar] [CrossRef]
- Oliver, J.M.; Esteban, M.D.; López-Gutiérrez, J.-S.; Negro, V.; Neves, M.G. Optimizing wave overtopping energy converters by ANN modelling: Evaluating the overtopping rate forecasting as the first step. Sustainability 2021, 13, 1483. [Google Scholar] [CrossRef]
- Habib, M.A.; O’Sullivan, J.; Salauddin, M. Comparison of machine learning algorithms in predicting wave overtopping discharges at vertical breakwaters. In Proceedings of the EGU General Assembly 2022, Vienna, Austria, 23–27 May 2022. [Google Scholar]
- Elbisy, M.S.; Osra, F.A.; Alyafei, Y.S. Soft computing techniques for predicting wave overtopping discharges at vertical coastal structures. GEOMATE J. 2022, 23, 205–211. [Google Scholar] [CrossRef]
- Sasikumar, H.; Mane, V.; Rao, S. Estimation of Wave Overtopping Discharge at Quarter Circle Breakwater Using LSSVM. In Proceedings of 2nd International Conference on Artificial Intelligence: Advances and Applications: ICAIAA 2021; Springer: Berlin/Heidelberg, Germany, 2022; pp. 399–405. [Google Scholar]
- Habib, M.A.; O’Sullivan, J.J.; Salauddin, M. Prediction of Wave Overtopping Characteristics at Coastal Flood Defences Using Machine Learning Algorithms: A Systematic Rreview. In IOP Conference Series: Earth and Environmental Science; IOP Publishing: Philadelphia, PA, USA, 2022; p. 12003. [Google Scholar]
- Swingler, K. Applying Neural Networks: A Practical Guide. In Morgan Kaufmann; Morgan Kaufman Publishers: San Francisco, CA, USA, 1996. [Google Scholar]
- Fahlman, S.; Lebiere, C. The cascade-correlation learning architecture. Adv. Neural. Inf. Process Syst. 1989, 2, 524–532. [Google Scholar]
- Song, J.; Romero, C.E.; Yao, Z.; He, B. A globally enhanced general regression neural network for on-line multiple emissions prediction of utility boiler. Knowl. Based Syst. 2017, 118, 4–14. [Google Scholar] [CrossRef]
- Specht, D.F. A general regression neural network. IEEE Trans. Neural. Netw. 1991, 2, 568–576. [Google Scholar] [CrossRef] [Green Version]
- Ye, H.; Ren, Q.; Hu, X.; Lin, T.; Shi, L.; Zhang, G.; Li, X. Modeling energy-related CO2 emissions from office buildings using general regression neural network. Resour. Conserv. Recycl. 2018, 129, 168–174. [Google Scholar] [CrossRef]
- Antanasijević, D.Z.; Ristić, M.Đ.; Perić-Grujić, A.A.; Pocajt, V.V. Forecasting human exposure to PM10 at the national level using an artificial neural network approach. J. Chemom. 2013, 27, 170–177. [Google Scholar] [CrossRef]
- Ni, Y.Q.; Li, M. Wind pressure data reconstruction using neural network techniques: A comparison between BPNN and GRNN. Measurement 2016, 88, 468–476. [Google Scholar] [CrossRef]
- Kisi, O.; Tombul, M.; Kermani, M.Z. Modeling soil temperatures at different depths by using three different neural computing techniques. Theor. Appl. Climatol. 2015, 121, 377–387. [Google Scholar] [CrossRef]
- Barzegar, R.; Asghari Moghaddam, A. Combining the advantages of neural networks using the concept of committee machine in the groundwater salinity prediction. Model. Earth Syst. Environ. 2016, 2, 26. [Google Scholar] [CrossRef] [Green Version]
- Vapnik, V.; Golowich, S.; Smola, A. Support vector method for function approximation, regression estimation and signal processing. Adv. Neural. Inf. Process Syst. 1996, 9, 1–7. [Google Scholar]
- Efron, B.; Tibshirani, R.J. An Introduction to the Bootstrap; CRC Press: Boca Raton, FL, USA, 1994. [Google Scholar]
- James, G.; Witten, D.; Hastie, T.; Tibshirani, R. An Introduction to Statistical Learning; Springer: Berlin/Heidelberg, Germany, 2013; Volume 112. [Google Scholar]
- van der Meer, J.W.; Verhaeghe, H.; Steendam, G.J. The new wave overtopping database for coastal structures. Coast Eng. 2009, 56, 108–120. [Google Scholar] [CrossRef]













| Features | Definition | Description |
|---|---|---|
| MSE | Mean squared error | |
| MAE | Mean absolute error | |
| RMSE | Root mean square error | |
| SI | Scatter index | |
| R | Correlation coefficient | |
| EF | Model performance |
| Parameter. | Unit | Definition | Type | Min | Max | Mean | Std. Dev. |
|---|---|---|---|---|---|---|---|
| m | [-] | Foreshore slope, 1: m | structural | 6 | 1000 | 499.271 | 467.885 |
| β | [°] | Angle of wave attack | hydraulic | 0 | 80 | 3.827 | 11.730 |
| h | [m] | Water depth at the structure toe | structural | 0.029 | 5.01 | 0.463 | 0.412 |
| Hm,0,t | [m] | Significant wave height at the structure toe. | hydraulic | 0.017 | 1.48 | 0.127 | 0.079 |
| ht | [m] | Toe submergence | structural | 0.029 | 5.01 | 0.443 | 0.416 |
| Bt | [m] | Toe width | structural | 0 | 0.8 | 0.052 | 0.118 |
| cotα | [-] | Cotangent of the structure with a horizontal | structural | 0 | 7 | 2.358 | 1.201 |
| γf | [-] | Roughness factor | structural | 0.38 | 1 | 0.712 | 0.277 |
| D | [m] | Average size of the structure elements in the run-up/down area | structural | 0 | 0.1 | 0.025 | 0.026 |
| Rc | [m] | Crest height with respect to sea water level (SWL) | structural | 0 | 2.5 | 0.169 | 0.157 |
| Ac | [m] | (Armor) crest freeboard without crown wall | structural | −0.03 | 2.5 | 0.162 | 0.158 |
| Gc | [m] | Crest width or promenade width | structural | 0 | 0.94 | 0.119 | 0.149 |
| q | [m3/s per m] | Wave-overtopping discharge | output | 0.000001 | 0.0256 | 0.001 | 0.002 |
| Parameter | Type | Min | Max | Mean | Std Dev | Upper 95% Mean | Lower 95% Mean |
|---|---|---|---|---|---|---|---|
| m | Geometry | 6 | 1000 | 499.271 | 467.885 | 467.885 | 513.098 |
| β | Wave conditions | 0 | 80 | 3.827 | 11.730 | 11.730 | 4.174 |
| h/Lm-1,0,t | Wave conditions | 0.0002 | 0.774 | 0.133 | 0.103 | 0.136 | 0.130 |
| Hm,0,t/Lm-1,0,t | Wave conditions | 0.0001 | 0.085 | 0.033 | 0.014 | 0.034 | 0.033 |
| ht/Lm-1,0,t | Geometry | 0.0002 | 0.774 | 0.127 | 0.104 | 0.130 | 0.124 |
| Bt/Lm-1,0,t | Geometry | 0 | 0.761 | 0.017 | 0.05 | 0.019 | 0.016 |
| cotα | Geometry | 0 | 7 | 2.358 | 1.201 | 2.394 | 2.323 |
| γf | Structure characteristics | 0.38 | 1 | 0.712 | 0.277 | 0.72 | 0.704 |
| D/Hm, 0, t | Structure characteristics | 0 | 2.682 | 0.202 | 0.219 | 0.028 | 0.195 |
| Rc/Hm,0,t | Geometry | 0 | 4.586 | 0.133 | 0.644 | 1.347 | 1.309 |
| Ac/Hm,0,t | Geometry | −0.368 | 4.587 | 1.268 | 0.651 | 1.287 | 1.249 |
| Gc/Lm-1,0,t | Geometry | 0 | 0.425 | 0.033 | 0.045 | 0.035 | 0.032 |
| Sq | Output | 0.000004 | 0.241 | 0.006 | 0.014 | 0.006 | 0.006 |
| Model | Parameters |
|---|---|
| MPNN | Training method: conjugate gradient algorithm. Transfer function: sigmoid for the hidden layer and linear for the output layer. Architecture of MPNN: 12, 20, and 1 Validation method: cross-validation, and number of cross-validation folds = 10. |
| CCNN | Training method: conjugate gradient algorithm. Size of CCNN: 12–20-1 (sigmoid neurons = 3, and Gaussian neurons = 17) Transfer function: sigmoid and Gaussian functions and linear function for the hidden and output layers, respectively. Validation method: cross-validation method |
| GRNN | Training method: conjugate gradient algorithm. Kernel function: Gaussian; sigma (σ) = 0.0001:10 Validation method: leave-one-out |
| SVM | Type of SVM model: Epsilon-SVR Kernel function: radial basis function (RBF) Free parameters of kernel function: = 0.001, C = 0.1, = 50, and P = 0.0001 Validation method: cross-validation, and number of cross-validation folds = 10 |
| m | Β | h/Lm-1,0,t | Hm,0,t/Lm-1,0,t | ht/ Lm-1,0,t | Bt/ Lm-1,0,t | cot α | γf | D/ Hm, 0, t | Rc/Hm,0,t | Ac/Hm,0,t | Gc/ Lm-1,0,t | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| σ | 0.252 | 0.264 | 0.089 | 0.076 | 0.087 | 0.465 | 0.458 | 0.264 | 0.272 | 0.148 | 0.229 | 0.270 |
| Eigenvalue | Percentage of Variance (%) | Cumulative (%) | |
|---|---|---|---|
| 1 | 4.842 | 96.835 | 96.835 |
| 2 | 0.127 | 2.542 | 99.376 |
| 3 | 0.023 | 0.451 | 99.827 |
| 4 | 0.009 | 0.173 | 100 |
| 5 | 1.31423 × 10−13 | 2.62846 × 10−12 | 100 |
| Coefficients of PC1 | Coefficients of PC2 | |
|---|---|---|
| q (actual) | 0.448 | −0.396 |
| q(GRNN) | 0.449 | −0.348 |
| q(MPNN) | 0.441 | 0.679 |
| q(CCNN) | 0.450 | 0.397 |
| q(SVM) | 0.448 | −0.322 |
| ANN Models | Error Statistics | |||||
|---|---|---|---|---|---|---|
| MSE | MAE | RMSE | SI | Ef | R | |
| MPNN | 0.000001 | 0.001 | 0.001 | 1.068 | 0.843 | 0.922 |
| CCNN | 0.000001 | 0.0004 | 0.0007 | 0.791 | 0.913 | 0.958 |
| GRNN | 0.0000001 | 0.0001 | 0.0003 | 0.353 | 0.983 | 0.991 |
| SVM | 0.0000002 | 0.0003 | 0.0005 | 0.585 | 0.953 | 0.981 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alshahri, A.H.; Elbisy, M.S. Assessment of Using Artificial Neural Network and Support Vector Machine Techniques for Predicting Wave-Overtopping Discharges at Coastal Structures. J. Mar. Sci. Eng. 2023, 11, 539. https://doi.org/10.3390/jmse11030539
Alshahri AH, Elbisy MS. Assessment of Using Artificial Neural Network and Support Vector Machine Techniques for Predicting Wave-Overtopping Discharges at Coastal Structures. Journal of Marine Science and Engineering. 2023; 11(3):539. https://doi.org/10.3390/jmse11030539
Chicago/Turabian StyleAlshahri, Abdullah H., and Moussa S. Elbisy. 2023. "Assessment of Using Artificial Neural Network and Support Vector Machine Techniques for Predicting Wave-Overtopping Discharges at Coastal Structures" Journal of Marine Science and Engineering 11, no. 3: 539. https://doi.org/10.3390/jmse11030539





