Wave Runup Prediction and Alongshore Variability on a Pocket Gravel Beach under Fetch-Limited Wave Conditions
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Site
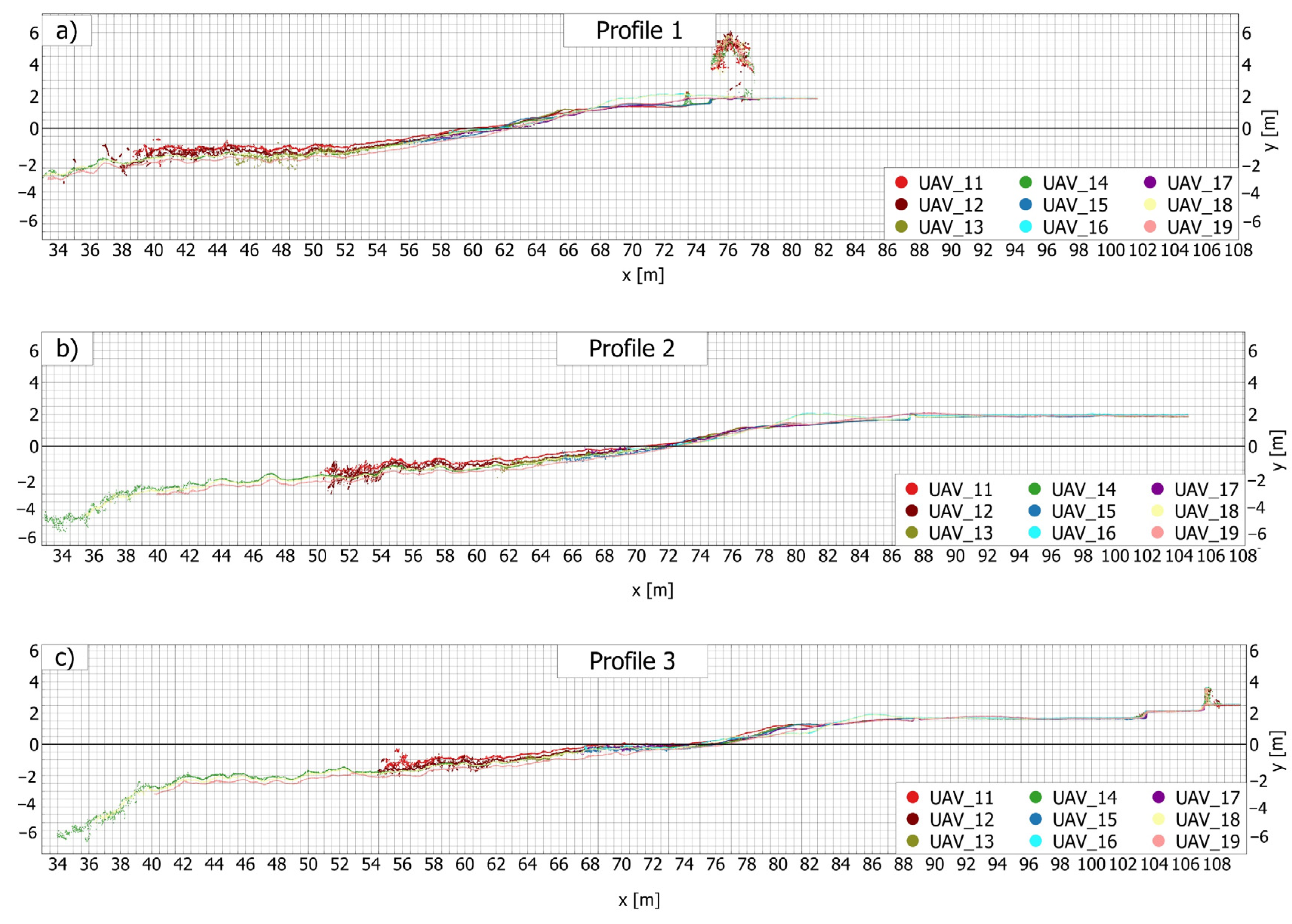
2.2. Data Collection
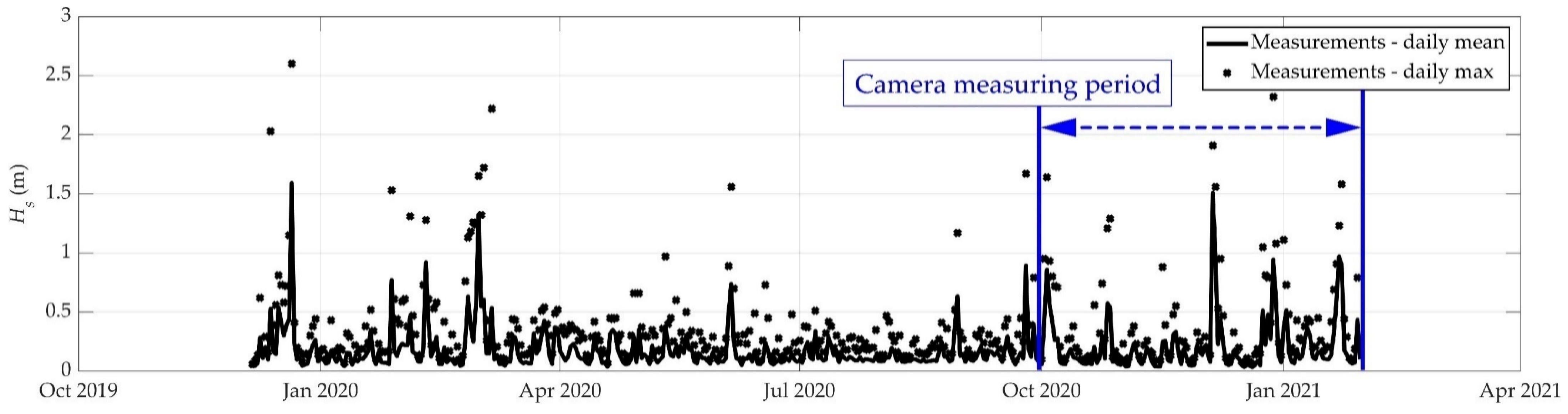
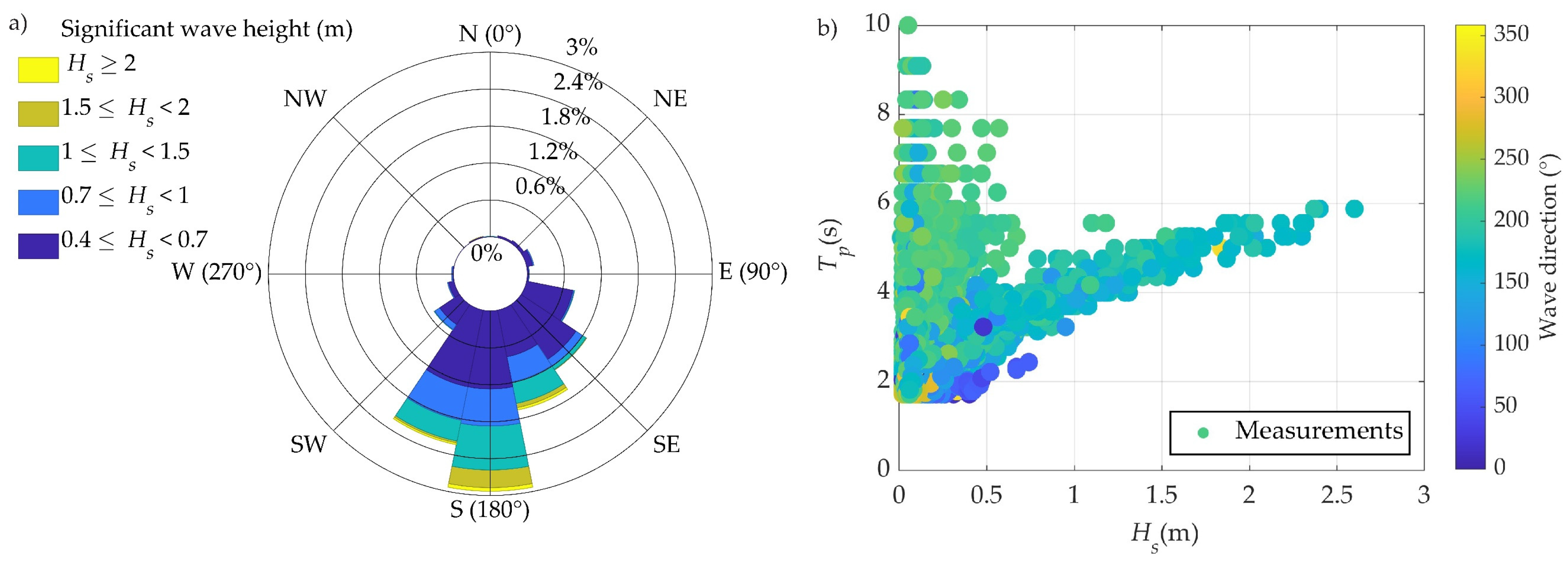
2.3. Evironmental Conditions
2.4. Wave Runup Models and Error Metrics
3. Results
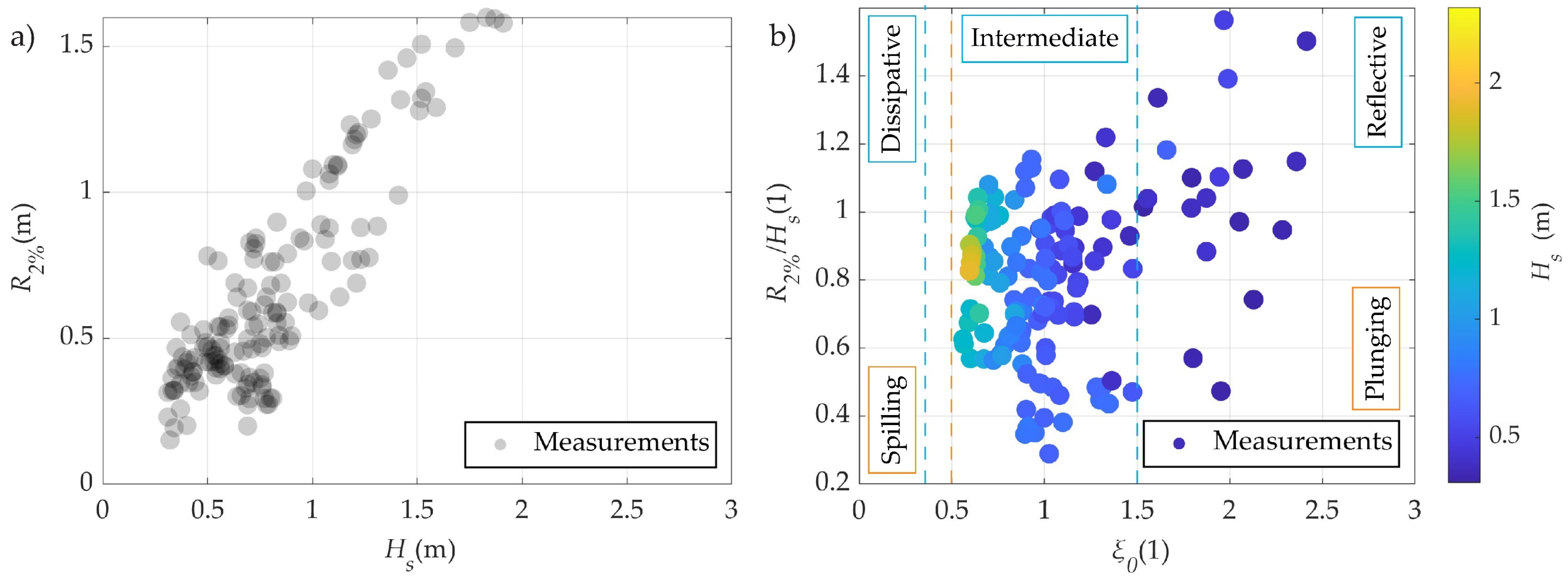
3.1. Description of Field Measurements for the Centerline Profile (Profile 2)
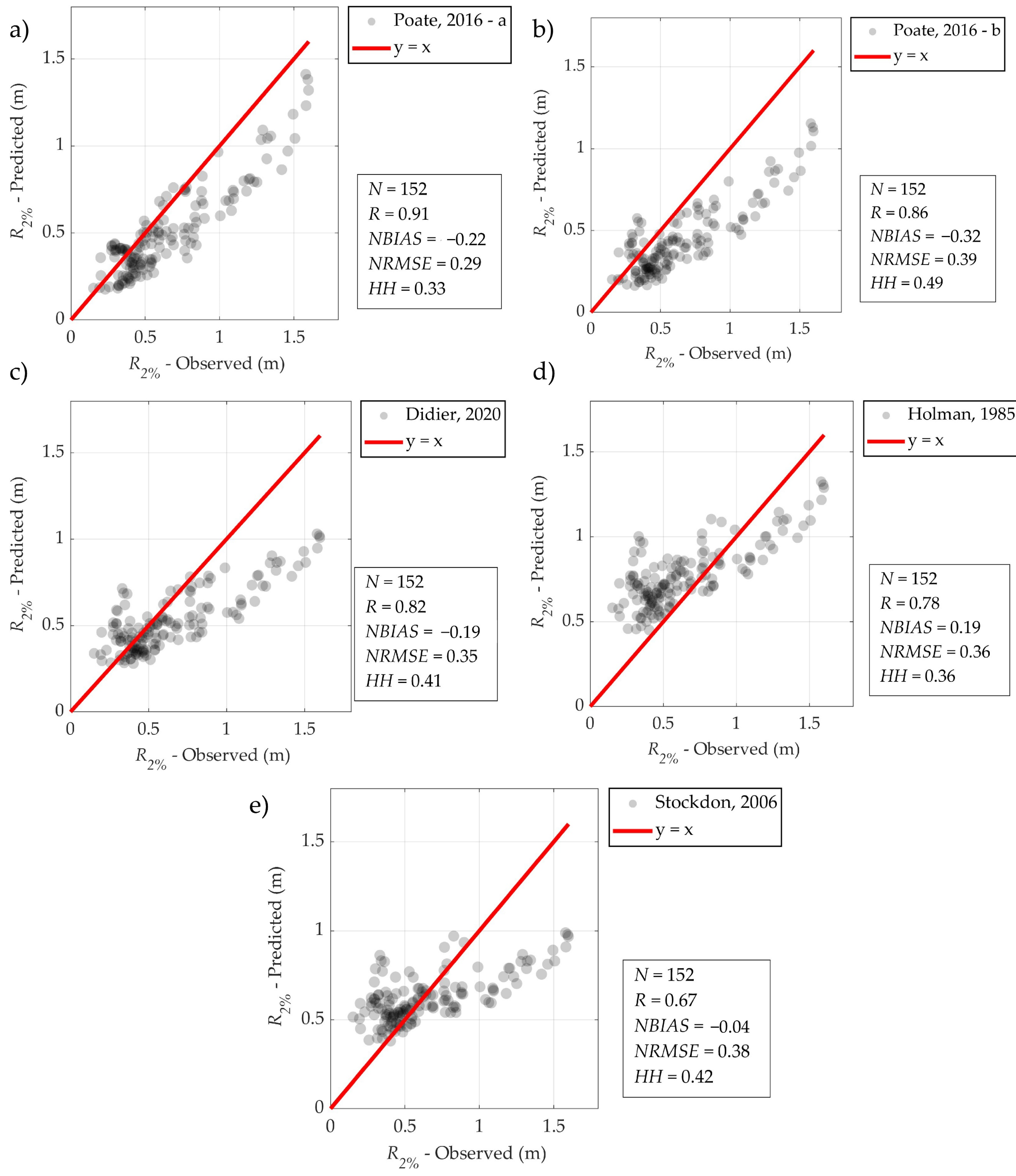
3.2. Comparison with Existing Wave Runup Equations for the Centerline Profile (Profile 2)
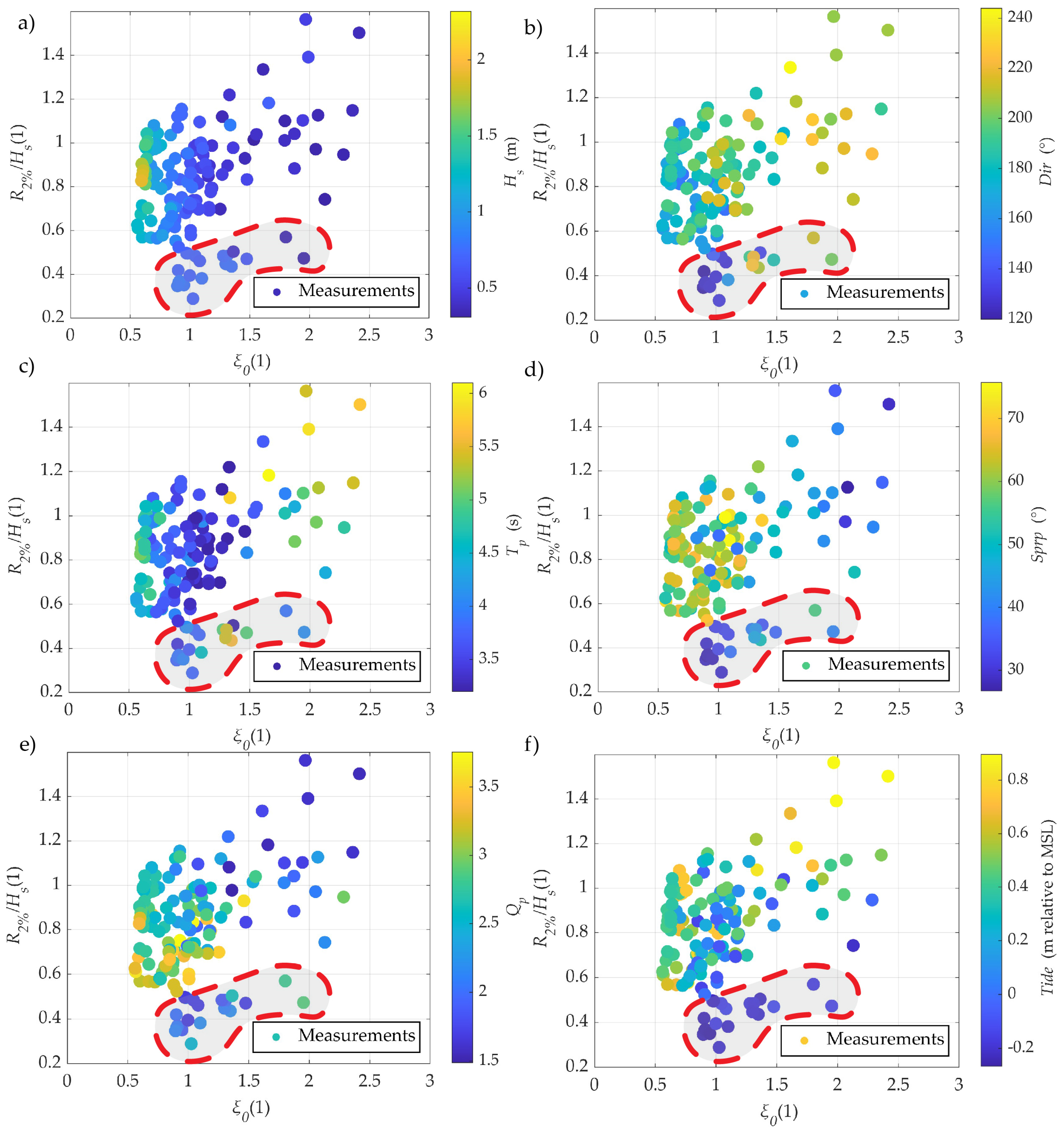
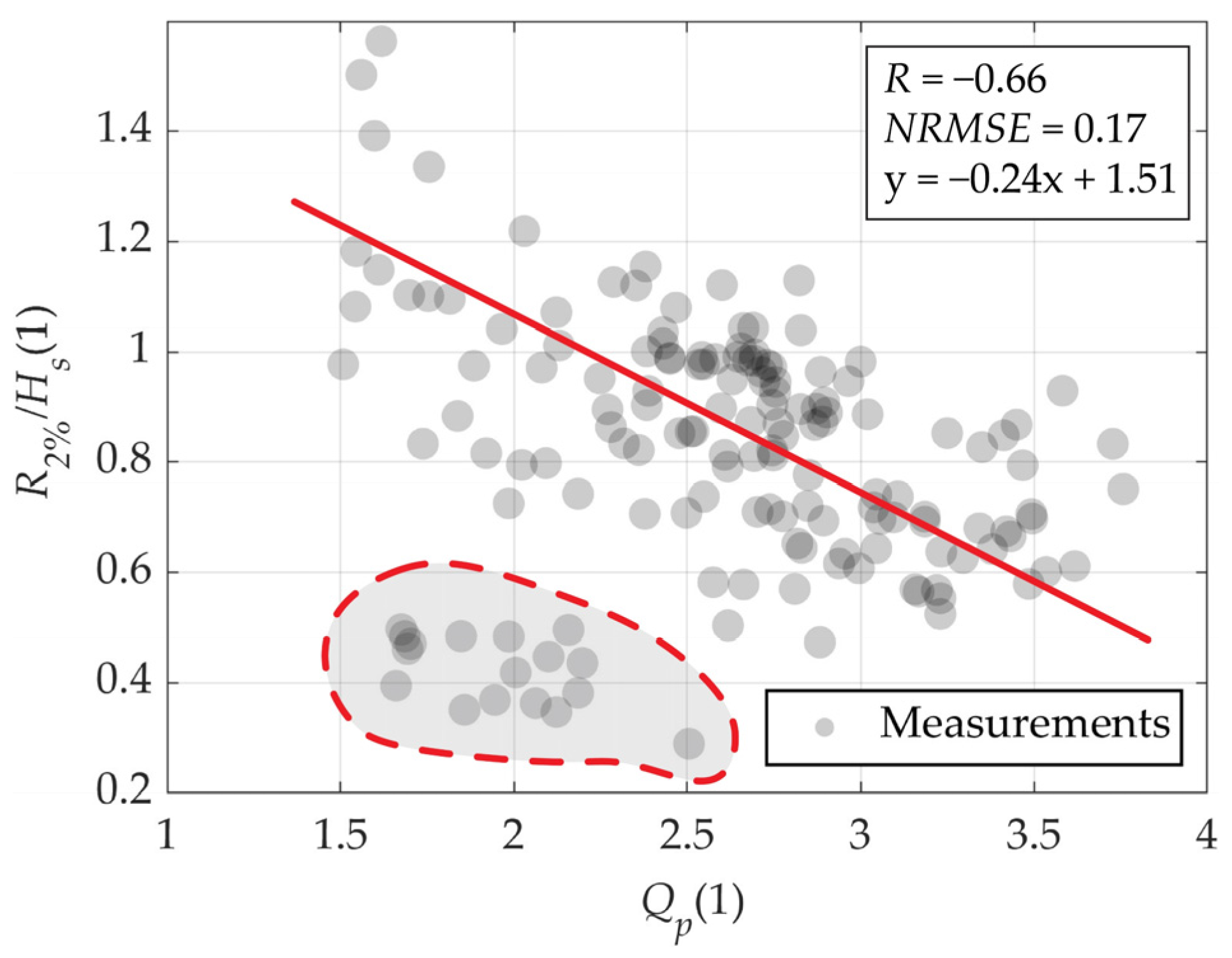
3.3. Influence of Offshore Wave Spectra Parameters on Wave Runup for the Centerline Profile (Profile 2)
3.4. Alongshore Variability of Wave Runup
4. Discussion
4.1. Wave Runup
4.2. Application of Existing Wave Runup Equations
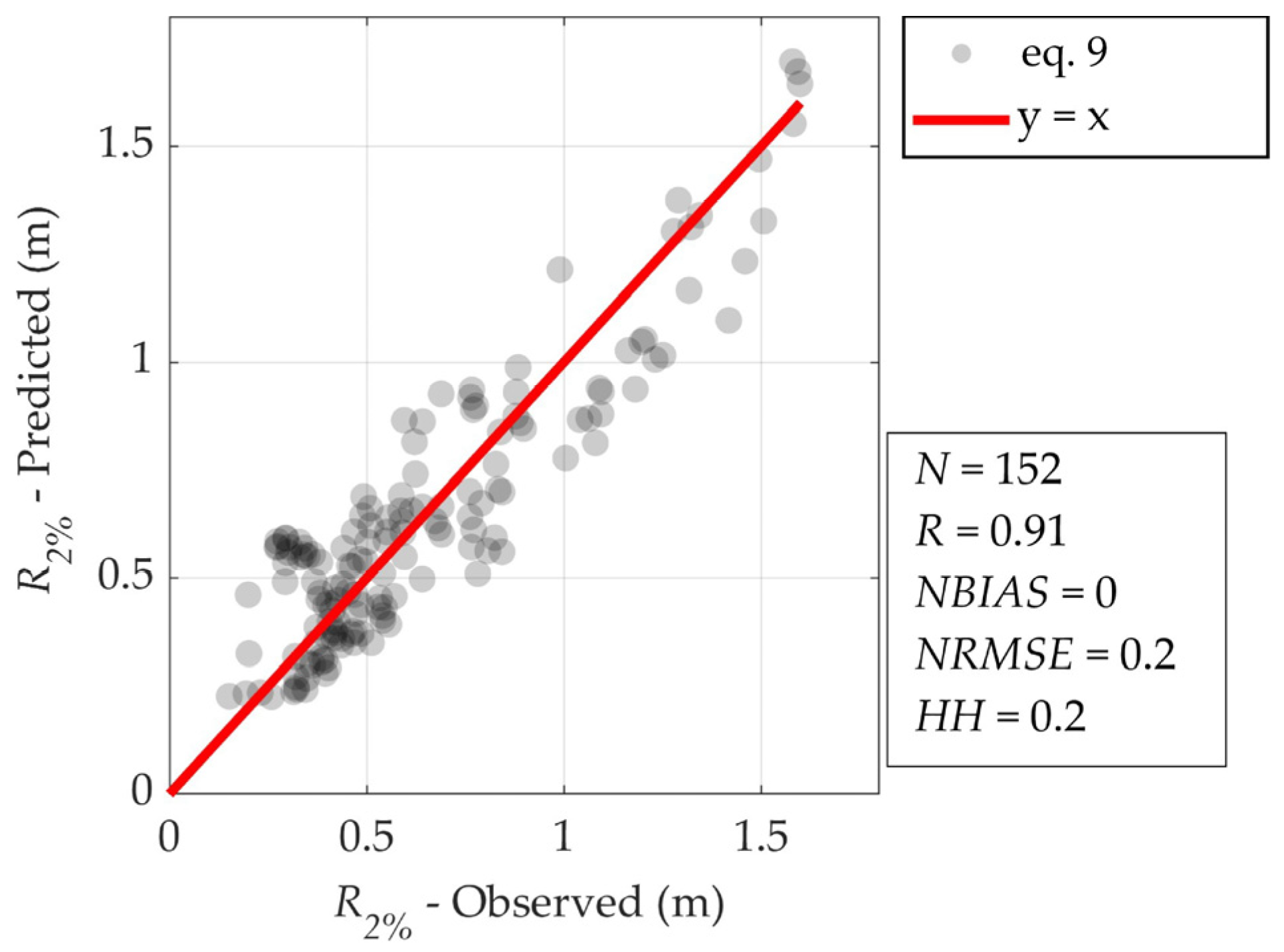
4.3. Derivation of the New Runup Equation for Fetch-Limited Gravel Pocket Beach Cases
4.4. Effects of Tides and Groundwater Dynamics
4.5. Alongshore Wave Runup Variability
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Survey Label | Date | Number of Images | Flying Altitude (m) | Ground Res. (mm/pix) | Coverage Area (km²) | Reprojection Error (pix) |
|---|---|---|---|---|---|---|
| UAV_11 | 1.10.2020 | 535 | 28.1 | 7.53 | 0.0177 | 0.772 |
| UAV_12 | 6.10.2020. | 492 | 28.6 | 7.18 | 0.0199 | 0.826 |
| UAV_13 | 13.10.2020. | 538 | 28.5 | 7.12 | 0.0181 | 0.79 |
| UAV_14 | 2.11.2020. | 208 | 103 | 19.5 | 0.0802 | 0.733 |
| UAV_15 | 24.11.2020. | 278 | 20.5 | 5.08 | 0.00797 | 0.515 |
| UAV_16 | 10.12.2020. | 600 | 24.3 | 6.05 | 0.0172 | 0.315 |
| UAV_17 | 14.12.2020. | 560 | 26.7 | 6.62 | 0.0162 | 0.318 |
| UAV_18 | 14.1.2021. | 269 | 100 | 19.1 | 0.06 | 0.724 |
| UAV_19 | 26.2.2021. | 290 | 101 | 19.6 | 0.06 | 0.791 |
Appendix B
| Reference | Equation | Range of Conditions | Measurement and Beach Type |
|---|---|---|---|
| Stockdon, et al. [4] | Field measurements—sandy beach | ||
| Poate, et al. [17] | Field measurements—gravel beach | ||
| Didier, et al. [64] | Field measurements—sandy, mixed and gravel beach | ||
| Holman and Sallenger [43] | Field measurements—sandy beach |
References
- Longuet-Higgins, M.S.; Stewart, R.W. Radiation stresses in water waves; a physical discussion, with applications. Deep Sea Res. Oceanogr. 1964, 11, 529–562. [Google Scholar] [CrossRef]
- Miche, M. Le Povoir Réfléchissant des Ouvrages Maritimes Exposés à L’action de la Houle. Ann. Ponts Chaussées 1951, 121, 285–319. [Google Scholar]
- Gomes da Silva, P.; Coco, G.; Garnier, R.; Klein, A.H.F. On the prediction of runup, setup and swash on beaches. Earth-Sci. Rev. 2020, 204, 103148. [Google Scholar] [CrossRef]
- Stockdon, H.F.; Holman, R.A.; Howd, P.A.; Sallenger, A.H. Empirical parameterization of setup, swash, and runup. Coast. Eng. 2006, 53, 573–588. [Google Scholar] [CrossRef]
- Ruiz de Alegria-Arzaburu, A.; Masselink, G. Storm response and beach rotation on a gravel beach, Slapton Sands, UK. Mar. Geol. 2010, 278, 77–99. [Google Scholar] [CrossRef]
- Coco, G.; Senechal, N.; Rejas, A.; Bryan, K.R.; Capo, S.; Parisot, J.P.; Brown, J.A.; MacMahan, J.H.M. Beach response to a sequence of extreme storms. Geomorphology 2014, 204, 493–501. [Google Scholar] [CrossRef] [Green Version]
- Tomás, A.; Méndez, F.J.; Medina, R.; Jaime, F.F.; Higuera, P.; Lara, J.L.; Ortiz, M.D.; Álvarez de Eulate, M.F. A methodology to estimate wave-induced coastal flooding hazard maps in Spain. J. Flood Risk Manag. 2016, 9, 289–305. [Google Scholar] [CrossRef]
- Butt, T.; Russell, P. Hydrodynamics and cross-shore sediment transport in the swash-zone of natural beaches. J. Coast. Res. 2000, 16, 255–268. [Google Scholar]
- Elfrink, B.; Baldock, T. Hydrodynamics and sediment transport in the swash zone: A review and perspectives. Coast. Eng. 2002, 45, 149–167. [Google Scholar] [CrossRef]
- Van der Meer, J.W.; Stam, C.J.M. Wave runup on smooth and rocky slopes of coastal structures. J. Waterw. Port Coast. Ocean Eng. 1992, 118, 534–550. [Google Scholar] [CrossRef]
- Madsen, P.A.; Sørensen, O.R.; Schäffer, H.A. Surf zone dynamics simulated by a Boussinesq type model. Part II: Surf beat and swash oscillations for wave groups and irregular waves. Coast. Eng. 1997, 32, 289–319. [Google Scholar] [CrossRef]
- Lange, A.M.Z.; Fiedler, J.W.; Becker, J.M.; Merrifield, M.A.; Guza, R.T. Estimating runup with limited bathymetry. Coast. Eng. 2021, 172, 104055. [Google Scholar] [CrossRef]
- Gao, J.L.; Ma, X.Z.; Dong, G.H.; Chen, H.Z.; Liu, Q.; Zang, J. Investigation on the effects of Bragg reflection on harbor oscillations. Coast. Eng. 2021, 170, 103977. [Google Scholar] [CrossRef]
- Liang, D.; Gotoh, H.; Khayyer, A. Boussinesq modelling of solitary wave and N-wave runup on coast. Appl. Ocean Res. 2013, 42, 144–154. [Google Scholar] [CrossRef]
- Henderson, C.S.; Fiedler, J.W.; Merrifield, M.A.; Guza, R.T.; Young, A.P. Phase resolving runup and overtopping field validation of SWASH. Coast. Eng. 2022, 175, 104128. [Google Scholar] [CrossRef]
- Tsung, W.S.; Hsiao, S.C.; Lin, T.C. Numerical simulation of solitary wave run-up and overtopping using Boussinesq-type model. J. Hydrodyn. Ser. B 2012, 24, 899–913. [Google Scholar] [CrossRef]
- Poate, T.G.; McCall, R.T.; Masselink, G. A new parameterisation for runup on gravel beaches. Coast. Eng. 2016, 117, 176–190. [Google Scholar] [CrossRef] [Green Version]
- Lashley, C.; Bertin, X.; Roelvink, D. Field measurements and numerical modelling of wave run-up and overwash in the pertuis Breton embayment, France. In Proceedings of the 7th International Conference on the Application of Physical Modelling in Coastal and Port Engineering and Science (Coastlab18), Santander, Spain, 22–26 May 2018; pp. 1–10. [Google Scholar]
- Nicolae Lerma, A.; Pedreros, R.; Robinet, A.; Senechal, N. Simulating wave setup and runup during storm conditions on a complex barred beach. Coast. Eng. 2017, 123, 29–41. [Google Scholar] [CrossRef]
- Mase, H. Random wave runup height on gentle slope. J. Waterw. Port Coast. Ocean Eng. 1989, 115, 649–661. [Google Scholar] [CrossRef]
- Melby, J.A.; Nadal-Caraballo, N.C.; Kobayashi, N. Wave RunUp prediction for flood mapping. Coast. Eng. 2012, 33. [Google Scholar] [CrossRef] [Green Version]
- Roberts, T.M.; Wang, P.; Kraus, N.C. Limits of wave runup and corresponding beach-profile change from large-scale laboratory data. J. Coast. Res. 2010, 261, 184–198. [Google Scholar] [CrossRef]
- Atkinson, A.L.; Power, H.E.; Moura, T.; Hammond, T.; Callaghan, D.P.; Baldock, T.E. Assessment of runup predictions by empirical models on non-truncated beaches on the south-east Australian coast. Coast. Eng. 2017, 119, 15–31. [Google Scholar] [CrossRef] [Green Version]
- Gomes da Silva, P.; Medina, R.; Gonzalez, M.; Garnier, R. Infragravity swash parameterization on beaches: The role of the profile shape and the morphodynamic beach state. Coast. Eng. 2018, 136, 41–55. [Google Scholar] [CrossRef]
- Holman, R. Extreme value statistics for wave run-up on a natural beach. Coast. Eng. 1986, 9, 527–544. [Google Scholar] [CrossRef]
- Power, H.E.; Gharabaghi, B.; Bonakdari, H.; Robertson, B.; Atkinson, A.L.; Baldock, T.E. Prediction of wave runup on beaches using Gene-Expression Programming and empirical relationships. Coast. Eng. 2019, 144, 47–61. [Google Scholar] [CrossRef]
- Ruggiero, P.; Komar, P.D.; McDougal, W.G.; Marra, J.J.; Reggie, A. Wave runup, extreme water levels and the erosion of properties backing beaches. J. Coast. Res. 2001, 17, 407–419. [Google Scholar]
- Vousdoukas, M.I.; Wziatek, D.; Almeida, L.P. Coastal vulnerability assessment based on video wave run-up observations at a mesotidal, steep-sloped beach. Ocean Dyn. 2012, 62, 123–137. [Google Scholar] [CrossRef]
- Guza, R.T.; Thornton, E.B. Swash oscillations on a natural beach. J. Geophys. Res. 1982, 87, 483–491. [Google Scholar] [CrossRef]
- Nielsen, P.; Hanslow, D.J. Wave runup distributions on natural beaches. J. Coast. Res. 1991, 7, 1139–1152. [Google Scholar]
- Ruessink, B.G.; Kleinhans, M.G.; Van Den Beukel, P.G.L. Observations of swash under highly dissipative conditions. J. Geophys. Res. 1998, 103, 3111–3118. [Google Scholar] [CrossRef]
- Gallien, T.W.; Sanders, B.F.; Flick, R.E. Urban coastal flood prediction: Integrating wave overtopping, flood defenses and drainage. Coast. Eng. 2014, 91, 18–28. [Google Scholar] [CrossRef]
- Didier, D.; Bernatchez, P.; Boucher-Brossard, G.; Lambert, A.; Fraser, C.; Barnett, R.; Van-Wierts, S. Coastal flood assessment based on field debris measurements and wave runup empirical model. J. Mar. Sci. Eng. 2015, 3, 560–590. [Google Scholar] [CrossRef]
- Ramirez, J.A.; Lichter, M.; Coulthard, T.J.; Skinner, C. Hyper-resolution mapping of regional storm surge and tide flooding: Comparison of static and dynamic models. Nat. Hazards 2016, 82, 571–590. [Google Scholar] [CrossRef]
- Vousdoukas, M.I.; Voukouvalas, E.; Mentaschi, L.; Dottori, F.; Giardino, A.; Bouziotas, D.; Bianchi, A.; Salamon, P.; Feyen, L. Developments in large-scale coastal flood hazard mapping. Nat. Hazards Earth Syst. Sci. 2016, 16, 1841–1853. [Google Scholar] [CrossRef] [Green Version]
- Johnson, C.N. Rubble beaches versus rubble revetments. In Proceedings ASCE Conference on Coastal Sediments 1987; American Society of Civil Engineers: Reston, VA, USA, 1987; pp. 1216–1231. [Google Scholar]
- Aminti, P.; Cipriani, L.E.; Pranzini, E. Back to the beach: Converting seawalls into gravel beaches. Coast. Syst. Cont. Margins 2003, 7, 261–274. [Google Scholar]
- Almeida, L.P.; Masselink, G.; McCall, R.; Russell, P. Storm overwash of a gravel barrier: Field measurements and XBeach-G modelling. Coast. Eng. 2017, 120, 22–35. [Google Scholar] [CrossRef] [Green Version]
- Austin, M.J.; Masselink, G. Observations of morphological change and sediment transport on a steep gravel beach. Mar. Geol. 2006, 229, 59–77. [Google Scholar] [CrossRef]
- Austin, M.J.; Buscombe, D. Morphological change and sediment dynamics of the beach step on a macrotidal gravel beach. Mar. Geol. 2008, 249, 167–183. [Google Scholar] [CrossRef]
- Ivamy, M.C.; Kench, P.S. Hydrodynamics and morphological adjustment of a mixed sand and gravel beach, Torere, Bay of Plenty, New Zealand. Mar. Geol. 2006, 228, 137–152. [Google Scholar] [CrossRef]
- Masselink, G.; Scott, T.; Poate, T.; Russell, P.; Davidson, M.; Conley, D. The extreme 2013/14 winter storms: Hydrodynamic forcing and coastal response along the southwest coast of England. Earth Surf. Process. Landf. 2016, 41, 378–391. [Google Scholar] [CrossRef] [Green Version]
- Holman, R.A.; Sallenger, A.H. Setup and swash on a natural beach. J. Geophys. Res. 1985, 90, 945–953. [Google Scholar] [CrossRef]
- Senechal, N.; Coco, G.; Plant, N.; Bryan, K.R.; Brown, J.; MacMahan, J.H.M. Field Observations of Alongshore Runup Variability Under Dissipative Conditions in the Presence of a Shoreline Sandwave. J. Geophys. Res. Ocean. 2018, 123, 6800–6817. [Google Scholar] [CrossRef]
- Palmer, T.; Nicholls, R.J.; Wells, N.C.; Saulter, A.; Mason, T. Identification of ‘energetic’ swell waves in a tidal strait. Cont. Shelf Res. 2014, 88, 203–215. [Google Scholar] [CrossRef]
- Jackson, N.L.; Nordstrom, K.F.; Farrell, E.J. Longshore sediment transport and foreshore change in the swash zone of an estuarine beach. Mar. Geol. 2017, 386, 88–97. [Google Scholar] [CrossRef]
- Jackson, N.L.; Nordstrom, K.F.; Eliot, I.; Masselink, G. “Low energy” sandy beaches in marine and estuarine environments a review. Geomorphology 2002, 48, 147–162. [Google Scholar] [CrossRef]
- Sayol, J.M.; Marcos, M. Assessing flood risk under sea level rise and extreme Sea Levels scenarios: Application to the ebro delta (Spain). J. Geophys. Res. Ocean. 2018, 123, 794–811. [Google Scholar] [CrossRef] [Green Version]
- Bernatchez, P.; Fraser, C.; Lefaivre, D.; Dugas, S. Integrating anthropogenic factors, geomorphological indicators and local knowledge in the analysis of coastal flooding and erosion hazards. Ocean Coast. Manag. 2011, 54, 621–632. [Google Scholar] [CrossRef]
- Moftakhari, H.R.; AghaKouchak, A.; Sanders, B.F.; Matthew, R.A. Cumulative hazard: The case of nuisance flooding. Earth’s Future 2017, 5, 214–223. [Google Scholar] [CrossRef]
- Serafin, K.A.; Ruggiero, P.; Stockdon, H.F. The relative contribution of waves, tides, and nontidal residuals to extreme total water levels on U.S. West Coast sandy beaches. Geophys. Res. Lett. 2017, 44, 1839–1847. [Google Scholar] [CrossRef]
- Hegge, B.; Eliot, I.; Hsu, J. Sheltered sandy beaches of southwestern Australia stable. J. Coast. Res. 1996, 12, 748–760. [Google Scholar]
- Masselink, G.; Pattiaratchi, C.B. Seasonal changes in beach morphology along the sheltered coastline of Perth, Western Australia. Mar. Geol. 2001, 172, 243–263. [Google Scholar] [CrossRef]
- Senechal, N.; Coco, G.; Bryan, K.; Macmahan, J.; Brown, J.; Holman, R. Tidal Effects on Runup in Presence of Complex 3D Morphologies under Dissipative Surf Zone Conditions. Coastal Dynamics. 2013, pp. 1483–1494. Available online: https://www.semanticscholar.org/paper/Tidal-effects-on-runup-in-presence-of-complex-3D-S%C3%A9n%C3%A9chal-Coco/eb414c2aae0b742c1471a1bf13384066b9896123 (accessed on 1 January 2023).
- Ruggiero, P.; Holman, R.A.; Beach, R.A. Wave run-up on a high-energy dissipative beach. J. Geophys. Res. 2004, 109. [Google Scholar] [CrossRef] [Green Version]
- Guedes, R.M.C.; Bryan, K.R.; Coco, G. Observations of alongshore variability of swash motions on an intermediate beach. Cont. Shelf Res. 2012, 48, 61–74. [Google Scholar] [CrossRef]
- Tadić, A.; Ružić, I.; Krvavica, N.; Ilić, S. Post-Nourishment Changes of an Artificial Gravel Pocket Beach Using UAV Imagery. J. Mar. Sci. Eng. 2022, 10, 358. [Google Scholar] [CrossRef]
- Suanez, S.; Cancouet, R.; Floc’h, F.; Blaise, E.; Ardhuin, F.; Filipot, J.F.; Cariolet, J.M. Observations and predictions of wave runup, extreme water levels, and medium-term dune erosion during storm conditions. J. Mar. Sci. Eng. 2015, 3, 674–698. [Google Scholar] [CrossRef] [Green Version]
- Orford, J.D.; Jennings, S.C.; Pethick, J. Extreme storm effect on gravel-dominated barriers. Mar. Geol. 2011, 290. [Google Scholar] [CrossRef]
- Orford, J.D.; Carter, R.W.G.; Forbes, D.L. Crestal overtop and washover sedimentation on a fringing sandy gravel barrier coast Carnsore Point, SE Ireland. J. Coast. Res. 1991, 7, 477–488. [Google Scholar]
- Bouguet, J.Y. Camera Calibration Toolbox for Matlab; CaltechDATA: Pasadena, CA, USA, 2022. [Google Scholar]
- Bruder, B.L.; Brodie, K.L. CIRN Quantitative Coastal Imaging Toolbox. SoftwareX 2020, 12, 100582. [Google Scholar] [CrossRef]
- Holland, K.T.; Raubenheimer, B.; Guza, R.T.; Holman, R.A. Runup kinematics on a natural beach. J. Geophys. Res. Ocean. 1995, 100, 4985–4993. [Google Scholar] [CrossRef]
- Didier, D.; Caulet, C.; Bandet, M.; Bernatchez, P.; Dumont, D.; Augereau, E.; Floc’h, F.; Delacourt, C. Wave runup parameterization for sandy, gravel and platform beaches in a fetch-limited, large estuarine system. Cont. Shelf Res. 2020, 192, 104024. [Google Scholar] [CrossRef]
- Holman, R.A.; Guza, R.T. Measuring run-up on a natural beach. Coast. Eng. 1984, 8, 129–140. [Google Scholar] [CrossRef]
- HHI. Peljar za Male Brodove—Drugi Dio: Sedmovraće—Rt. Oštra; Hrvatski Hidrografski Institut: Split, Croatia, 2020; p. 312. [Google Scholar]
- Masselink, G.; Short, A.D. The effect of tide range on beach morphodynamics and morphology: A conceptual beach model. J. Coast. Res. 1993, 9, 785–800. [Google Scholar]
- Short, A.D. Australian beach systems—Nature and distribution. J. Coast. Res. 2006, 221, 11–27. [Google Scholar] [CrossRef]
- Medugorac, I.; Pasaric, M.; Orlic, M. Severe flooding along the eastern Adriatic coast: The case of 1 December 2008. Ocean Dyn. 2015, 65, 817–830. [Google Scholar] [CrossRef]
- Battjes, J.A. Run-up distributions of waves breaking on slopes. J. Waterw. Harb. Coast. Eng. Div. 1971, 97, 91–114. [Google Scholar] [CrossRef]
- Roos, A.; Battjes, J.A. Characteristics of Flow in Run-Up of Periodic Waves. Coast. Eng. 1976, 1, 781–795. [Google Scholar] [CrossRef] [Green Version]
- Montaño, J.K.; Blossier, B.; Osorio, A.F.; Winter, C. The role of frequency spread on swash dyanamics. Geo-Marine Lett. 2020, 40, 243–254. [Google Scholar] [CrossRef]
- Polidoro, A.; Dornbusch, U.; Pullen, T. Wave Run-Up on Shingle Beaches—A New Method; HR Wallingford: Oxfordshire, UK, 2014. [Google Scholar]
- Polidoro, A.; Dornbusch, U.; Pullen, T. Improved maximum run-up formula for mixed beaches based on field data. In Proceedings of the ICE Coasts, Marine Structures and Breakwaters Conference, Edinburgh, UK, 18–20 September 2013; pp. 389–398. [Google Scholar]
- Conn, A.R.; Gould, N.I.M.; Toint, P.L. A Globally Convergent Augmented Lagrangian Algorithm for Optimization with General Constraints and Simple Bounds. Siam J. Numer. Anal. 1991, 28, 545–572. [Google Scholar] [CrossRef] [Green Version]
- Goldberg, D. Genetic Algorithms in Search Optimization and Machine Learning; Pearson: Upper Saddle River, NJ, USA, 2013. [Google Scholar]
- Guza, R.T.; Thornton, E.B.; Holman, R.A. Swash on steep and shallow beaches. In Proceedings of the 19th International Conference on Coastal Engineering, Houston, TX, USA, 3–7 September 1984; pp. 708–723. [Google Scholar]
- Guza, R.T.; Bowen, A.J. Resonant interactions for waves breaking on a beach. In Proceedings of the 15th International Conference on Coastal Engineering, Honolulu, HI, USA, 11–17 July 1976; pp. 560–579. [Google Scholar]
- Didier, D.; Bernatchez, P.; Marie, G.; Boucher-Brossard, G. Wave runup estimations on platform-beaches for coastal flood hazard assessment. Nat. Hazards 2016, 83, 1443–1467. [Google Scholar] [CrossRef]
- Baldock, T.E.; Cox, D.; Maddux, T.; Killian, J.; Fayler, L. Kinematics of breaking tsunami wavefronts: A data set from large scale laboratory experiments. Coast. Eng. 2009, 56, 506–516. [Google Scholar] [CrossRef]
- Plant, N.G.; Stockdon, H.F. How well can wave runup be predicted? Comment on Laudier et al. (2011) and Stockdon et al. (2006). Coast. Eng. 2015, 102, 44–48. [Google Scholar] [CrossRef] [Green Version]
- Guedes, R.M.C.; Bryan, K.R.; Coco, G. Observations of wave energy fluxes and swash motions on a low-sloping, dissipative beach. J. Geophys. Res. Ocean. 2013, 118, 3651–3669. [Google Scholar] [CrossRef]
- Guedes, R.M.C.; Bryan, K.R.; Coco, G.; Holman, R.A. The Effects of Tides on Swash Statistics on an Intermediate Beach. J. Geophys. Res. 2011, 116. Available online: https://researchcommons.waikato.ac.nz/handle/10289/5559 (accessed on 1 January 2023). [CrossRef] [Green Version]
- Didier, D.; Bernatchez, P.; Augereau, E.; Caulet, C.; Dumont, D.; Bismuth, E.; Cormier, L.; Floc’h, F.; Delacourt, C. LiDAR validation of a video-derived beachface topography on a tidal flat. Remote Sens. 2017, 9, 826. [Google Scholar] [CrossRef] [Green Version]
- Paprotny, D.; Andrzejewski, P.; Terefenko, P.; Furmańczyk, K. Application of empirical wave run-up formulas to the Polish Baltic Sea coast. PLoS ONE 2014, 9, e105437. [Google Scholar] [CrossRef] [Green Version]
- Villarroel-Lamb, D.; Hammeken, A.; Simons, R. Quantifying the effect of bed permeability on maximum wave runup. In Proceedings of the 19th International Conference on Coastal Engineering, Seoul, Republic of Korea, 15–20 June 2014. [Google Scholar]
- Kobayashi, N.; Cox, D.T.; Wurjanto, A. Permeability effects on irregular wave runup and reflection. J. Coast. Res. 1991, 7, 127–136. [Google Scholar]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bujak, D.; Ilic, S.; Miličević, H.; Carević, D. Wave Runup Prediction and Alongshore Variability on a Pocket Gravel Beach under Fetch-Limited Wave Conditions. J. Mar. Sci. Eng. 2023, 11, 614. https://doi.org/10.3390/jmse11030614
Bujak D, Ilic S, Miličević H, Carević D. Wave Runup Prediction and Alongshore Variability on a Pocket Gravel Beach under Fetch-Limited Wave Conditions. Journal of Marine Science and Engineering. 2023; 11(3):614. https://doi.org/10.3390/jmse11030614
Chicago/Turabian StyleBujak, Damjan, Suzana Ilic, Hanna Miličević, and Dalibor Carević. 2023. "Wave Runup Prediction and Alongshore Variability on a Pocket Gravel Beach under Fetch-Limited Wave Conditions" Journal of Marine Science and Engineering 11, no. 3: 614. https://doi.org/10.3390/jmse11030614
APA StyleBujak, D., Ilic, S., Miličević, H., & Carević, D. (2023). Wave Runup Prediction and Alongshore Variability on a Pocket Gravel Beach under Fetch-Limited Wave Conditions. Journal of Marine Science and Engineering, 11(3), 614. https://doi.org/10.3390/jmse11030614







