Natural Frequency Analysis of Monopile Supported Offshore Wind Turbines Using Unified Beam-Column Element Model
Abstract
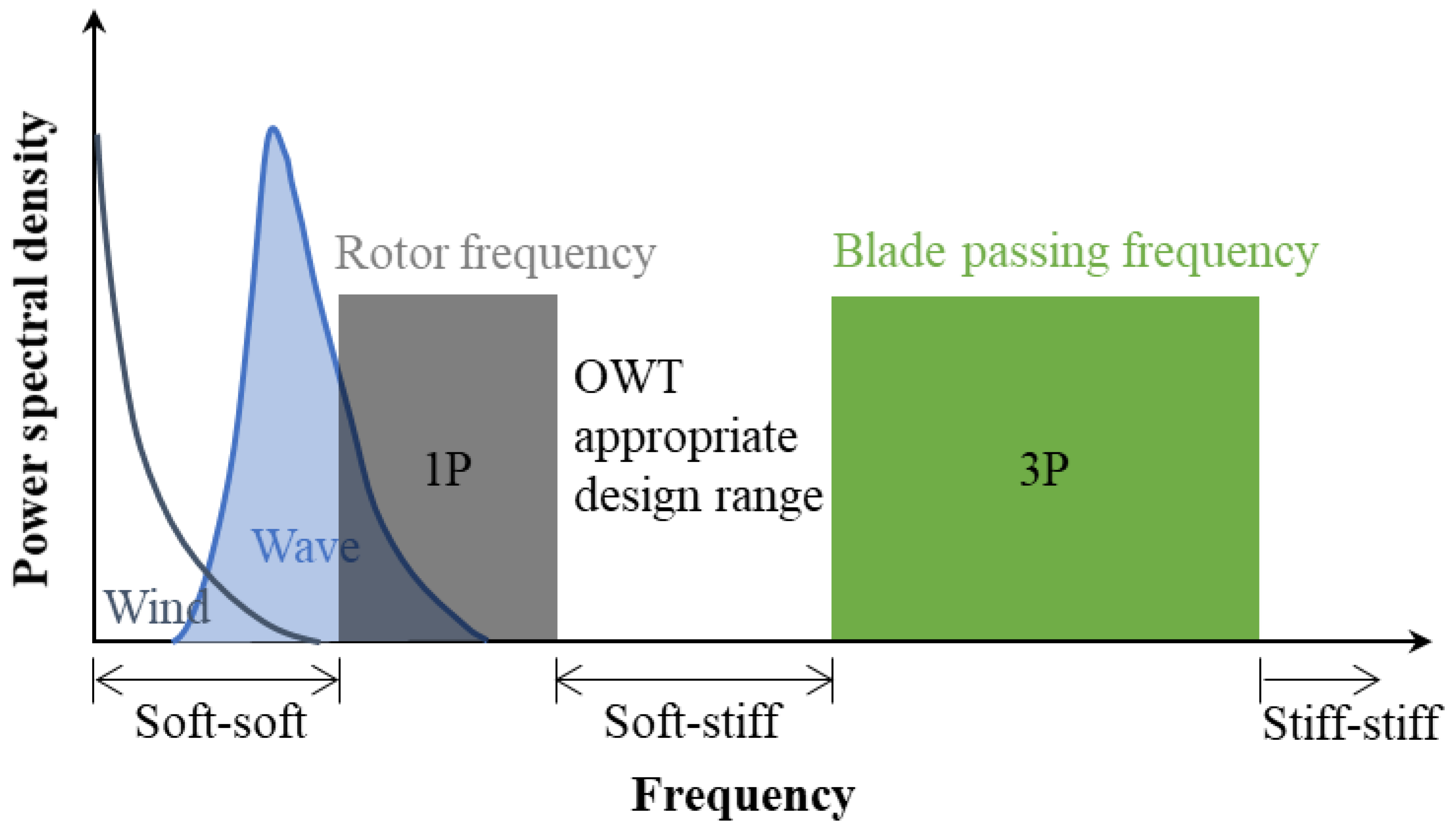
:1. Introduction
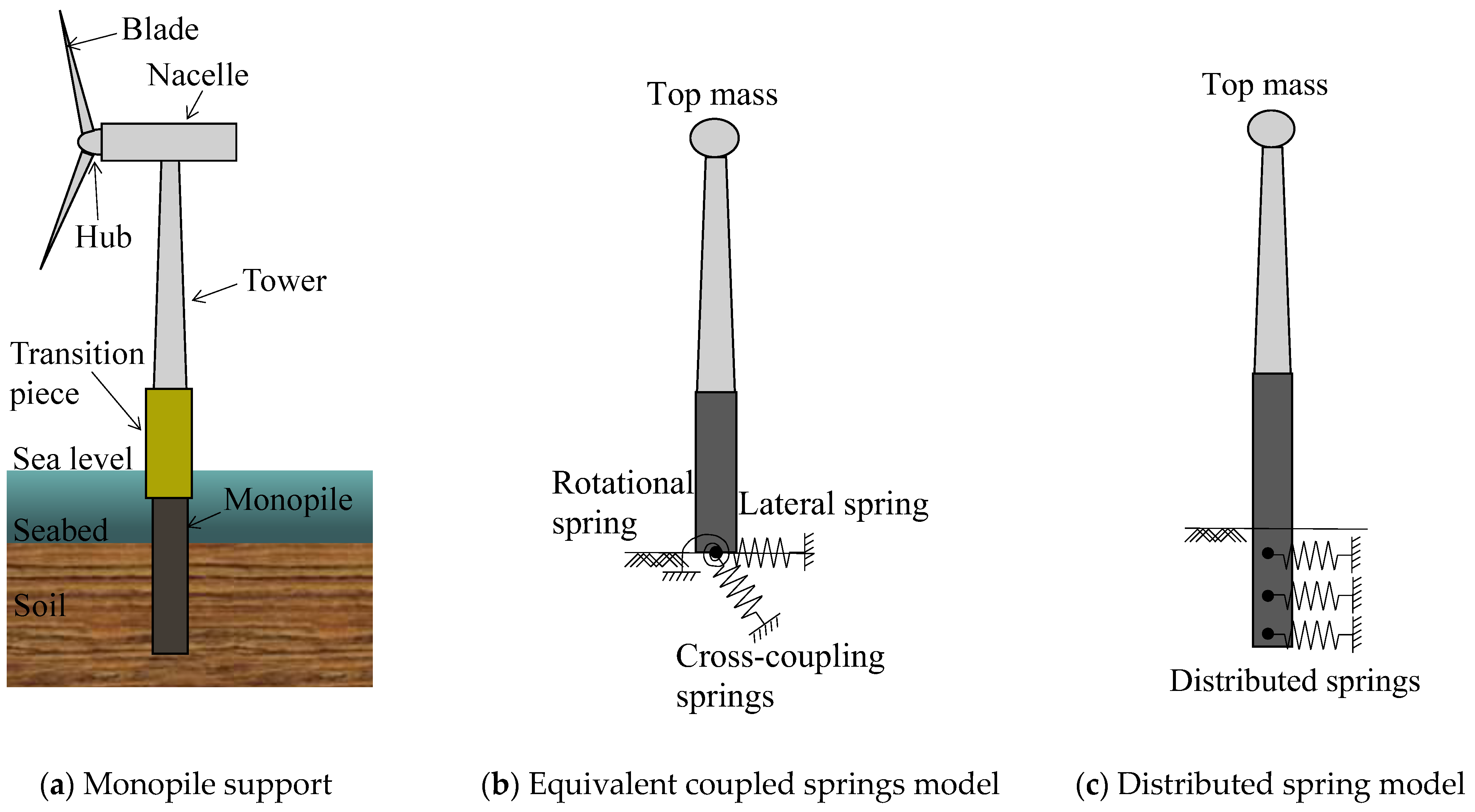
2. Structural Model of the OWT
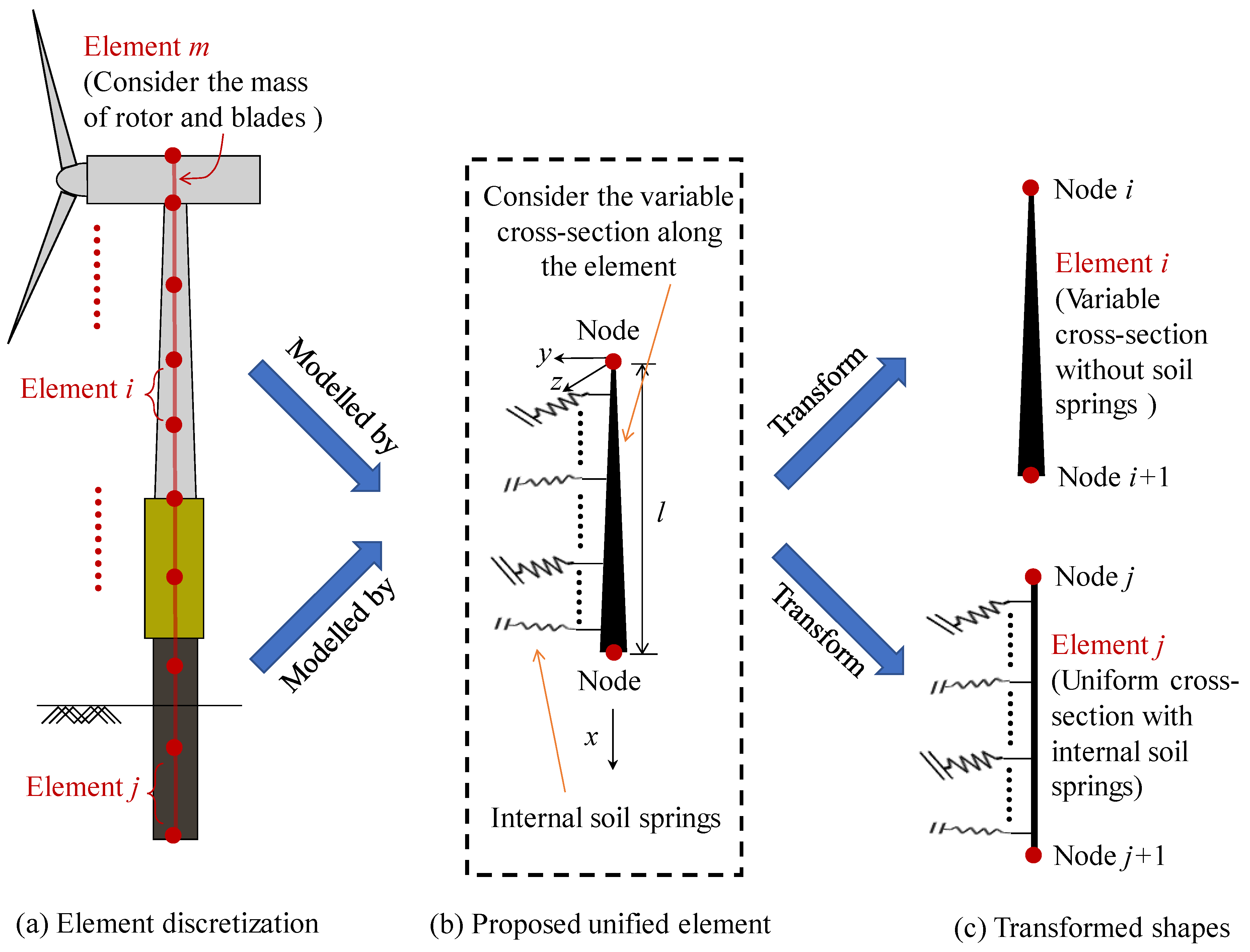
3. Element Formulations
3.1. Tangent Stiffness Matrix
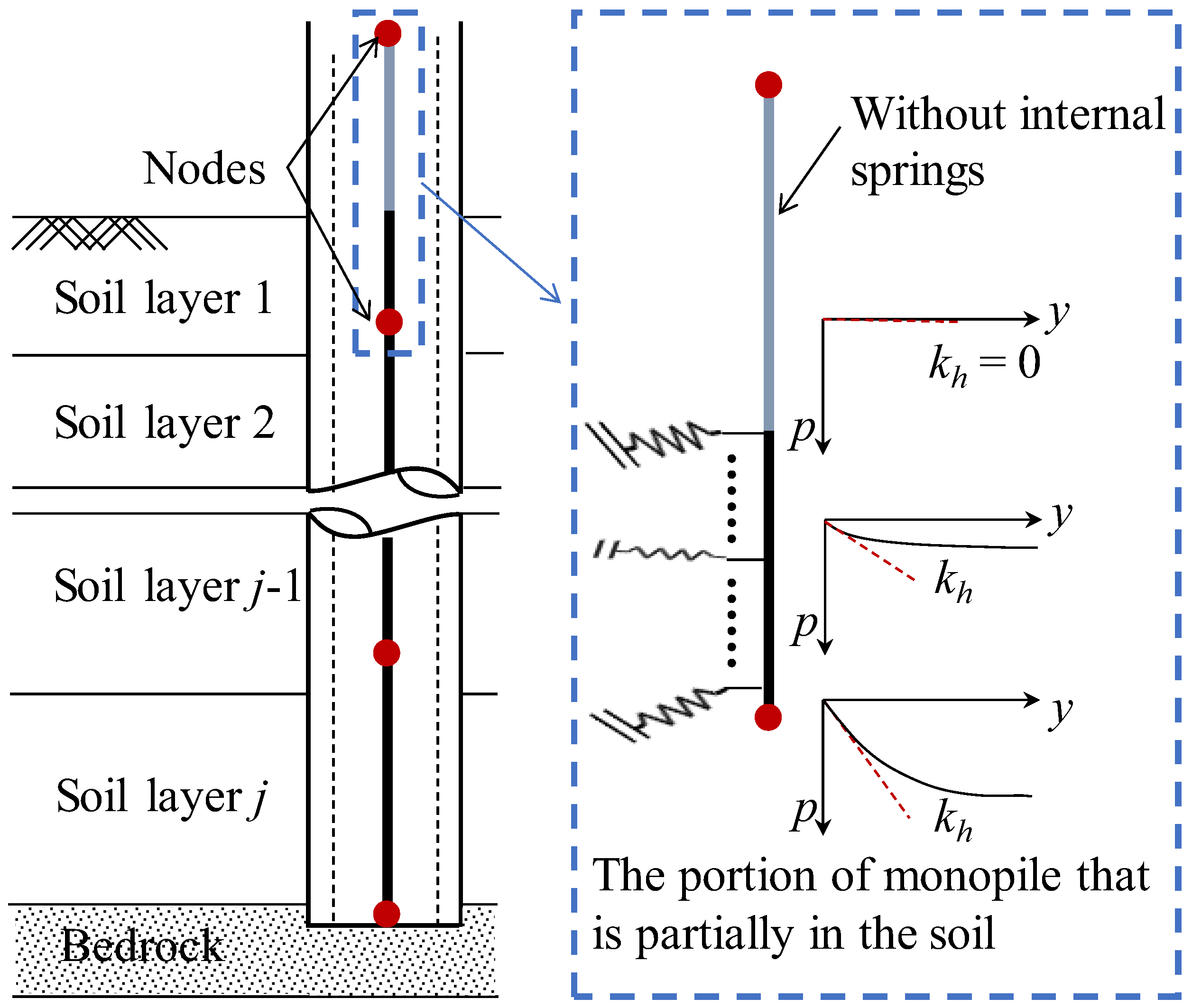
3.2. Internal Zero-Length Soil Springs
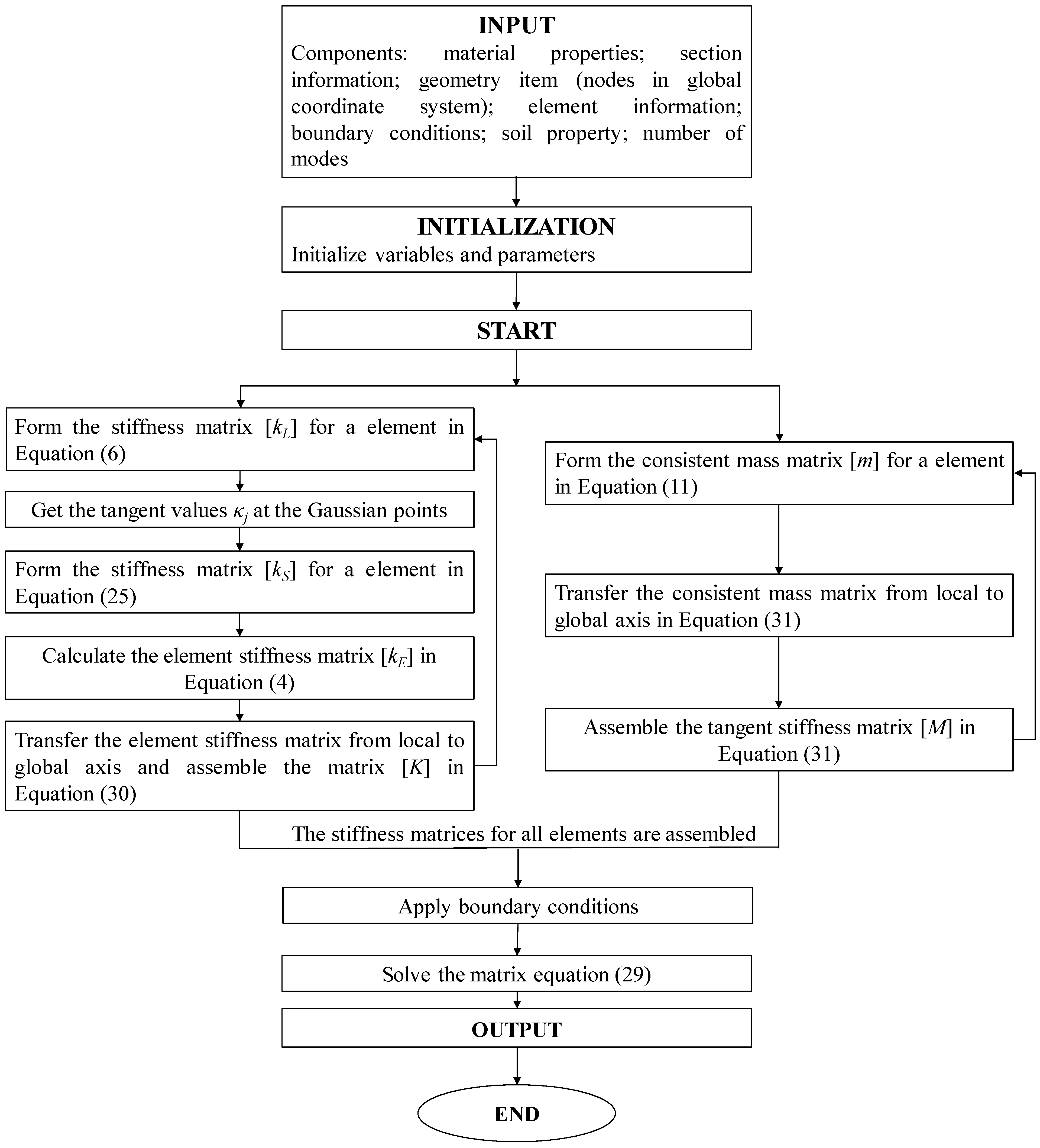
4. Numerical Analysis Procedure
5. Model Validation
5.1. Compare with Closed-Form Solutions
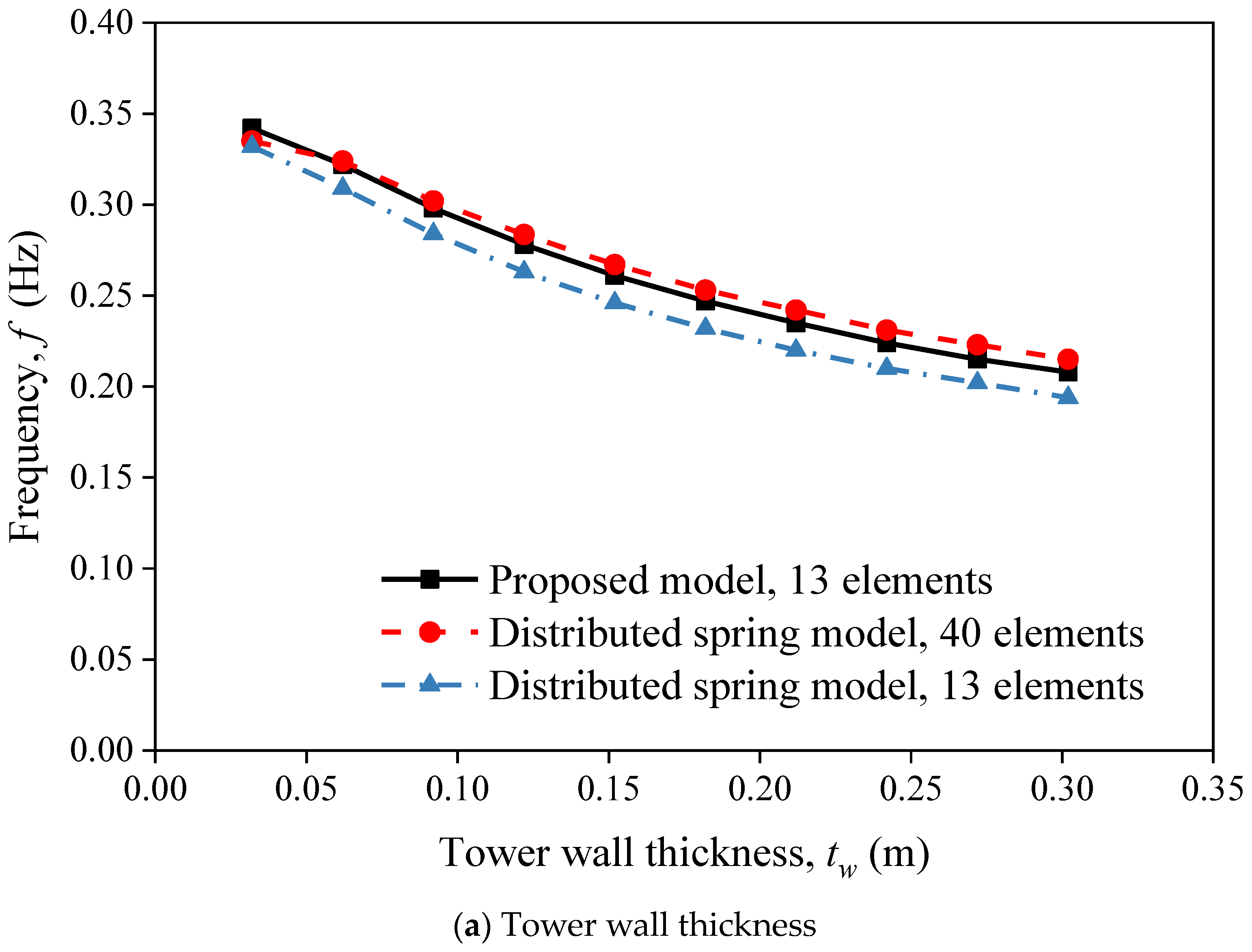
5.2. Compare with the Distributed Spring Model
5.3. Compare with the Field Measurements
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| D | Diameter |
| xi | Coordinate of the x-axis at the ith node |
| tw | Wall thickness |
| Iy | Moment of inertia about the y-axes |
| Iz | Moment of inertia about the z-axes |
| A | Cross-sectional area |
| [kL] | Linear stiffness matrix |
| [kS] | Soil stiffness matrix for representing the lateral restraint from soils |
| E | Young’s modulus |
| l | Element length |
| [m] | Local consistent mass matrix |
| ρ | Material density |
| ξq,j | Integration parameter in Gauss-Legendre integration method |
| κj | Tangent values on the soil resistance versus lateral deflection curves |
| n | Number of Gaussian points |
| {U} | Displacement vector at all degrees of freedom |
| Acceleration vectors at all degrees of freedom | |
| [M] | Global consistent mass matrix |
| [K] | Global element stiffness matrix |
| {F} | Force vector at the corresponding degrees of freedom |
| {A} | Vector of the amplitude of motion |
| ω | Circular natural frequency |
| ς | Phase angle |
| NELE | Total number of elements |
| [γ]i | Local to global transformation matrix |
| MT | Top concentrated mass |
| L | Total length |
| kh | Modulus of horizontal subgrade reaction |
| nh | Coefficient of subgrade reaction |
| f | Frequency |
| γ′ | Submerged unit weight |
| Asoil | Soil coefficient |
References
- Snyder, B.; Kaiser, M.J. A comparison of offshore wind power development in Europe and the U.S.: Patterns and drivers of development. Appl. Energy 2009, 86, 1845–1856. [Google Scholar] [CrossRef]
- Yang, C.; Wang, R.; Zhang, J. A simplified method for analyzing the fundamental frequency of monopile supported offshore wind turbine system design. Earthq. Eng. Eng. Vib. 2018, 17, 893–901. [Google Scholar] [CrossRef]
- Zhao, L.; Xue, L.; Li, Z.; Wang, J.; Yang, Z.; Xue, Y. Progress on Offshore Wind Farm Dynamic Wake Management for Energy. J. Mar. Sci. Eng. 2022, 10, 1395. [Google Scholar] [CrossRef]
- Shi, Y.; Yao, W.; Yu, G. Dynamic Analysis on Pile Group Supported Offshore Wind Turbine under Wind and Wave Load. J. Mar. Sci. Eng. 2022, 10, 1024. [Google Scholar] [CrossRef]
- Chen, M.; Yuan, G.; Li, C.B.; Zhang, X.; Li, L. Dynamic Analysis and Extreme Response Evaluation of Lifting Operation of the Offshore Wind Turbine Jacket Foundation Using a Floating Crane Vessel. J. Mar. Sci. Eng. 2022, 10, 2023. [Google Scholar] [CrossRef]
- Malekjafarian, A.; Jalilvand, S.; Doherty, P.; Igoe, D. Foundation damping for monopile supported offshore wind turbines: A review. Mar. Struct. 2021, 77, 102937. [Google Scholar] [CrossRef]
- AlHamaydeh, M.; Hussain, S. Optimized frequency-based foundation design for wind turbine towers utilizing soil–structure interaction. J. Frankl. Inst. 2011, 348, 1470–1487. [Google Scholar] [CrossRef]
- Zaaijer, M.B. Foundation modelling to assess dynamic behaviour of offshore wind turbines. Appl. Ocean Res. 2006, 28, 45–57. [Google Scholar] [CrossRef]
- Bisoi, S.; Haldar, S. Dynamic analysis of offshore wind turbine in clay considering soil–monopile–tower interaction. Soil Dyn. Earthq. Eng. 2014, 63, 19–35. [Google Scholar] [CrossRef]
- Arshad, M.; O’Kelly, B.C. Offshore wind-turbine structures: A review. Proc. Inst. Civ. Eng. Energy 2013, 166, 139–152. [Google Scholar] [CrossRef]
- Bhattacharya, S.; Cox, J.A.; Lombardi, D.; Muir Wood, D. Dynamics of offshore wind turbines supported on two foundations. Proc. Inst. Civ. Eng. Geotech. Eng. 2013, 166, 159–169. [Google Scholar] [CrossRef] [Green Version]
- Lombardi, D.; Bhattacharya, S.; Muir Wood, D. Dynamic soil–structure interaction of monopile supported wind turbines in cohesive soil. Soil Dyn. Earthq. Eng. 2013, 49, 165–180. [Google Scholar] [CrossRef]
- Fei, C.; Wang, N.; Zhou, B.; Chen, C. Dynamic Performance Investigation for Large-Scale Wind Turbine Tower. In Proceedings of the 2005 International Conference on Electrical Machines and Systems, Nanjing, China, 27–29 September 2005; pp. 996–999. [Google Scholar]
- Van Der Tempel, J. Design of Support Structures for Offshore Wind Turbines. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 2006. [Google Scholar]
- Arany, L.; Bhattacharya, S.; Macdonald, J.H.G.; Hogan, S.J. Closed form solution of Eigen frequency of monopile supported offshore wind turbines in deeper waters incorporating stiffness of substructure and SSI. Soil Dyn. Earthq. Eng. 2016, 83, 18–32. [Google Scholar] [CrossRef] [Green Version]
- Alkhoury, P.; Soubra, A.H.; Rey, V.; Aït-Ahmed, M. A full three-dimensional model for the estimation of the natural frequencies of an offshore wind turbine in sand. Wind Energy 2020, 24, 699–719. [Google Scholar] [CrossRef]
- Adhikari, S.; Bhattacharya, S. Dynamic analysis of wind turbine towers on flexible foundations. Shock Vib. 2012, 19, 408493. [Google Scholar] [CrossRef]
- Arany, L.; Bhattacharya, S.; Adhikari, S.; Hogan, S.J.; Macdonald, J.H.G. An analytical model to predict the natural frequency of offshore wind turbines on three-spring flexible foundations using two different beam models. Soil Dyn. Earthq. Eng. 2015, 74, 40–45. [Google Scholar] [CrossRef] [Green Version]
- Amar Bouzid, D.; Bhattacharya, S.; Otsmane, L. Assessment of natural frequency of installed offshore wind turbines using nonlinear finite element model considering soil-monopile interaction. J. Rock Mech. Geotech. Eng. 2018, 10, 333–346. [Google Scholar] [CrossRef]
- Ko, Y. A simplified structural model for monopile-supported offshore wind turbines with tapered towers. Renew. Energy 2020, 156, 777–790. [Google Scholar] [CrossRef]
- Cao, Q.; Li, H.; Tang, G.; Wang, B.; Lu, L. Dynamic analysis of monopile OWTs with viscoelastic dampers based on pole-residue method. Ocean Eng. 2022, 266, 113167. [Google Scholar] [CrossRef]
- Andersen, L.V.; Vahdatirad, M.J.; Sichani, M.T.; Sørensen, J.D. Natural frequencies of wind turbines on monopile foundations in clayey soils—A probabilistic approach. Comput. Geotech. 2012, 43, 1–11. [Google Scholar] [CrossRef]
- Shirgir, V.; Ghanbari, A.; Shahrouzi, M. Natural frequency of single pier bridges considering soil-structure interaction. J. Earthq. Eng. 2015, 20, 611–632. [Google Scholar] [CrossRef]
- Darvishi-Alamouti, S.; Bahaari, M.-R.; Moradi, M. Natural frequency of offshore wind turbines on rigid and flexible monopiles in cohesionless soils with linear stiffness distribution. Appl. Ocean Res. 2017, 68, 91–102. [Google Scholar] [CrossRef]
- Roy, J.; Kumar, A.; Choudhury, D. Natural frequencies of piled raft foundation including superstructure effect. Soil Dyn. Earthq. Eng. 2018, 112, 69–75. [Google Scholar] [CrossRef]
- De Risi, R.; Bhattacharya, S.; Goda, K. Seismic performance assessment of monopile-supported offshore wind turbines using unscaled natural earthquake records. Soil Dyn. Earthq. Eng. 2018, 109, 154–172. [Google Scholar] [CrossRef]
- Plodpradit, P.; Dinh, V.; Kim, K.D. Coupled analysis of offshore wind turbine jacket structures with pile-soil-structure interaction using FAST v8 and X-SEA. Appl. Sci. 2019, 9, 1633. [Google Scholar] [CrossRef] [Green Version]
- Williams, S.A.; Pelecanos, L.; Darby, A.P. A Winkler model of monopile ratcheting under long-term dynamic cyclic loading. Ocean Eng. 2022, 266, 112625. [Google Scholar] [CrossRef]
- Sunday, K.; Brennan, F. Influence of soil–structure modelling techniques on offshore wind turbine monopile structural response. Wind Energy 2022, 25, 998–1012. [Google Scholar] [CrossRef]
- Chiou, J.S.; Lin, C.L.; Chen, C.H. Exploring influence of sectional flexural yielding on experimental pile response analysis and applicability of distributed plastic hinge model in inelastic numerical simulation for laterally loaded piles. Comput. Geotech. 2014, 56, 40–49. [Google Scholar] [CrossRef]
- Carswell, W.; Arwade, S.R.; DeGroot, D.J.; Lackner, M.A. Soil-structure reliability of offshore wind turbine monopile foundations. Wind Energy 2015, 18, 483–498. [Google Scholar] [CrossRef]
- Li, X.y.; Wan, J.h.; Liu, S.w.; Zhang, L.m. Numerical formulation and implementation of Euler-Bernoulli pile elements considering soil-structure-interaction responses. Int. J. Numer. Anal. Methods Geomech. 2020, 44, 1903–1925. [Google Scholar] [CrossRef]
- Banerjee, J.; Williams, F. Exact Bernoulli–Euler dynamic stiffness matrix for a range of tapered beams. Int. J. Numer. Methods Eng. 1985, 21, 2289–2302. [Google Scholar] [CrossRef]
- Bai, R.; Liu, S.W.; Chan, S.L. Finite-element implementation for nonlinear static and dynamic frame analysis of tapered members. Eng. Struct. 2018, 172, 358–381. [Google Scholar] [CrossRef]
- El Gendy, O.; Sallam, E.; Mohamedien, M.A. Finite element formulation of Timoshenko tapered beam-column element for large displacement analysis based on the exact shape functions. Aust. J. Struct. Eng. 2022, 23, 269–288. [Google Scholar] [CrossRef]
- Wan, J.H.; Liu, S.W.; Li, X.Y.; Zhang, L.M.; Zhao, H.P. Buckling analysis of tapered piles using non-prismatic beam-column element model. Comput. Geotech. 2021, 139, 104370. [Google Scholar] [CrossRef]
- Gautschi, W. Numerical Analysis; Springer Science & Business Media: Berlin, Germany, 2011. [Google Scholar]
- Hutton, D.V. Fundamentals of Finite Element Analysis; McGraw-Hill Science Engineering: New York, NY, USA, 2003. [Google Scholar]
- Paz, M.; Kim, Y.H. Structural Dynamics: Theory and Computation, 6th ed.; Springer International Publishing: Cham, Switzerland, 2019. [Google Scholar]
- DNV, G. DNV-OS-J101–Design of offshore wind turbine structures. DNV GL Oslo Nor. 2014. [Google Scholar]
- Jeong, S.; Kim, Y.; Kim, J. Influence on lateral rigidity of offshore piles using proposed p–y curves. Ocean Eng. 2011, 38, 397–408. [Google Scholar] [CrossRef]
- Sun, Y.; Xu, C.; Du, X.; El Naggar, M.H.; Zhang, X.; Jia, J. Nonlinear lateral response of offshore large-diameter monopile in sand. Ocean Eng. 2020, 216, 108013. [Google Scholar] [CrossRef]
- Li, X.Y.; Wan, J.H.; Zhao, H.P.; Liu, S.W. Three-Dimensional analysis of nonlinear pile–soil interaction responses using 3D pile element model. Int. J. Geomech. 2021, 21, 04021129. [Google Scholar] [CrossRef]
- Van Rossum, G.; Drake, F. Python 3 Reference Manual; Createspace: Scotts Valley, CA, USA, 2009. [Google Scholar]
- Clough, R.W.; Penzien, J. Dynamics of Structures, Computers & Structures; Computers & Structures, Inc.: New York, NY, USA, 1995. [Google Scholar]
- Eskandari, H.; Nik, M.G.; Pakzad, A. Foundation analyzing of centrifugal ID fans in cement plants. Alex. Eng. J. 2016, 55, 1563–1572. [Google Scholar] [CrossRef] [Green Version]
- Bhartiya, P.; Chakraborty, T.; Basu, D. Nonlinear subgrade modulus of sandy soils for analysis of piled raft foundations. Comput. Geotech. 2020, 118, 103350. [Google Scholar] [CrossRef]
- Kallehave, D.; Thilsted, C.L.; Liingaard, M.A. Modification of the API p-y formulation of initial stiffness of sand. In Proceedings of the Offshore Site Investigation and Geotechnics: Integrated Technologies-Present and Future, London, UK, 12 September 2012. [Google Scholar]
- Chaudhuri, D. Liquefaction and Lateral Soil Movement Effects on Piles; Cornell University: Ithaca, NY, USA, 1998. [Google Scholar]
- Terzaghi, K. Evalution of conefficients of subgrade reaction. Geotechnique 1955, 5, 297–326. [Google Scholar] [CrossRef]
- Zekkos, A.; Woods, R.; Grizi, A. Effect of Pile-Driving Induced Vibrations on Nearby Structures and Other Assets; University of Michigan: Ann Arbor, MI, USA, 2013. [Google Scholar]
- Thieken, K.; Achmus, M.; Lemke, K. A new static p-y approach for piles with arbitrary dimensions in sand. Geotechnik 2015, 38, 267–288. [Google Scholar] [CrossRef]
- May, J. Post-construction results from the North Hoyle offshore wind farm. In Proceedings of the Copenhagen Offshore Wind International Conference, Copenhagen, Denmark, 26 September 2005; pp. 1–10. [Google Scholar]

| OWT Component Dimension (Unit) | Gunfleet Sands | Irene Vorrink | Kentish Flats | Lely A2 | North Hoyle | Walney 1 |
|---|---|---|---|---|---|---|
| Mass of the rotor and blades (ton) | 234.5 | 35.7 | 130.8 | 32 | 100 | 234.5 |
| Material density of tower and monopile (g/cm3) | 7.86 | 7.86 | 7.86 | 7.86 | 7.86 | 7.86 |
| Tower length (m) | 60 | 44.5 | 60.06 | 37.9 | 67 | 67.3 |
| Tower Young’s modulus (GPa) | 210 | 210 | 210 | 210 | 210 | 210 |
| Tower top diameter (m) | 3 | 1.7 | 2.3 | 1.9 | 2.3 | 3 |
| Tower bottom diameter (m) | 5 | 3.5 | 4.45 | 3.2 | 4 | 5 |
| Tower wall thickness (mm) | 33 | 13 | 22 | 13 | 35 | 40 |
| Platform length from pile head to tower bottom (m) | 28 | 5.2~6 | 16 | 12.1 | 7 | 37.3 |
| Platform diameter (m) | 5 | 3.5 | 4.3 | 3.2 | 4 | 6 |
| Platform wall thickness (mm) | 50 | 28 | 45 | 35 | 50 | 80 |
| Monopile diameter (m) | 5 | 3.5 | 4.3 | 3.2 | 4 | 6 |
| Monopile wall thickness (mm) | 94 | 28 | 45 | 35 | 50 | 80 |
| Total length of monopile (m) | 38 | 24.6 | 29.5 | 13.5 | 33 | 23.5 |
| Length of monopile in soil (m) | 27 | 19 | 25 | 30 | 33 | 23.5 |
| Monopile Young’s modulus (GPa) | 210 | 210 | 210 | 210 | 210 | 210 |
| Wind Farm Name | Soil Conditions [15,53] | Asoil [50] | γ′ (kN/m3) [52] | m [42] | n [42] |
|---|---|---|---|---|---|
| Gunfleet Sands | Cross-bedded Holocene sand with intermittent layers of soft clay | 600 | 9.76 | 0.5 | 0.6 |
| Irene Vorrink | Soft layers of silt and clay in the upper seabed to dense sand and very dense sand below | 600 | 9.76 | 0.5 | 0.6 |
| Kentish Flats | Layers of dense sand and firm clay | 1500 | 10 | 0.5 | 0.5 |
| Lely A2 | Soft clay in the uppermost layer to dense and very dense sand layers below | 600 | 9.76 | 0.5 | 0.6 |
| North Hoyle | Sand and sandy gravels with varying amounts of stone and minor clay/silt content | 600 | 9.76 | 0.5 | 0.6 |
| Walney 1 | Medium and dense sand layers | 1500 | 10 | 0.5 | 0.5 |
| Wind Farm Name | Measured Frequency (Hz) | Predicted Frequency (Hz) | Difference (%) |
|---|---|---|---|
| Gunfleet Sands | 0.314 | 0.317 | 1.0 |
| Irene Vorrink | 0.546~0.563 | 0.557~0.564 | 0.2~2.0 |
| Kentish Flats | 0.339 | 0.338 | 0.3 |
| Lely A2 | 0.634 | 0.641 | 1.1 |
| North Hoyle | 0.350 | 0.362 | 3.4 |
| Walney 1 | 0.350 | 0.335 | 4.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wan, J.-H.; Bai, R.; Li, X.-Y.; Liu, S.-W. Natural Frequency Analysis of Monopile Supported Offshore Wind Turbines Using Unified Beam-Column Element Model. J. Mar. Sci. Eng. 2023, 11, 628. https://doi.org/10.3390/jmse11030628
Wan J-H, Bai R, Li X-Y, Liu S-W. Natural Frequency Analysis of Monopile Supported Offshore Wind Turbines Using Unified Beam-Column Element Model. Journal of Marine Science and Engineering. 2023; 11(3):628. https://doi.org/10.3390/jmse11030628
Chicago/Turabian StyleWan, Jian-Hong, Rui Bai, Xue-You Li, and Si-Wei Liu. 2023. "Natural Frequency Analysis of Monopile Supported Offshore Wind Turbines Using Unified Beam-Column Element Model" Journal of Marine Science and Engineering 11, no. 3: 628. https://doi.org/10.3390/jmse11030628
APA StyleWan, J.-H., Bai, R., Li, X.-Y., & Liu, S.-W. (2023). Natural Frequency Analysis of Monopile Supported Offshore Wind Turbines Using Unified Beam-Column Element Model. Journal of Marine Science and Engineering, 11(3), 628. https://doi.org/10.3390/jmse11030628








