Effect of Wave Phases and Heights on Supercavitation Flow Field and Dynamic Characteristics of Successively Fired High-Speed Projectiles
Abstract
:1. Introduction
2. Numerical Methods and Theoretical Model
2.1. Governing Equations
2.2. Wave Model
2.3. Numerical Methods and Boundary Conditions
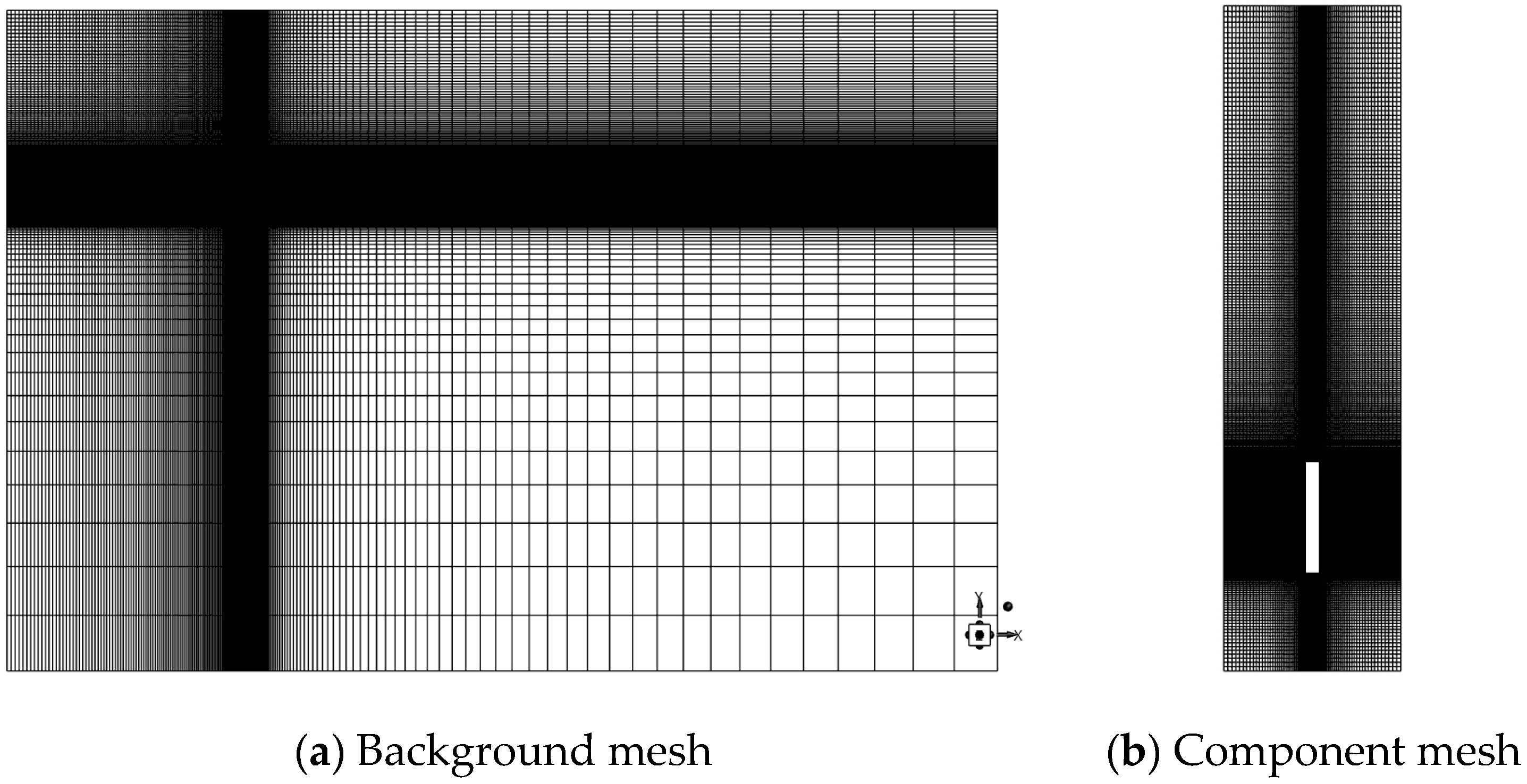
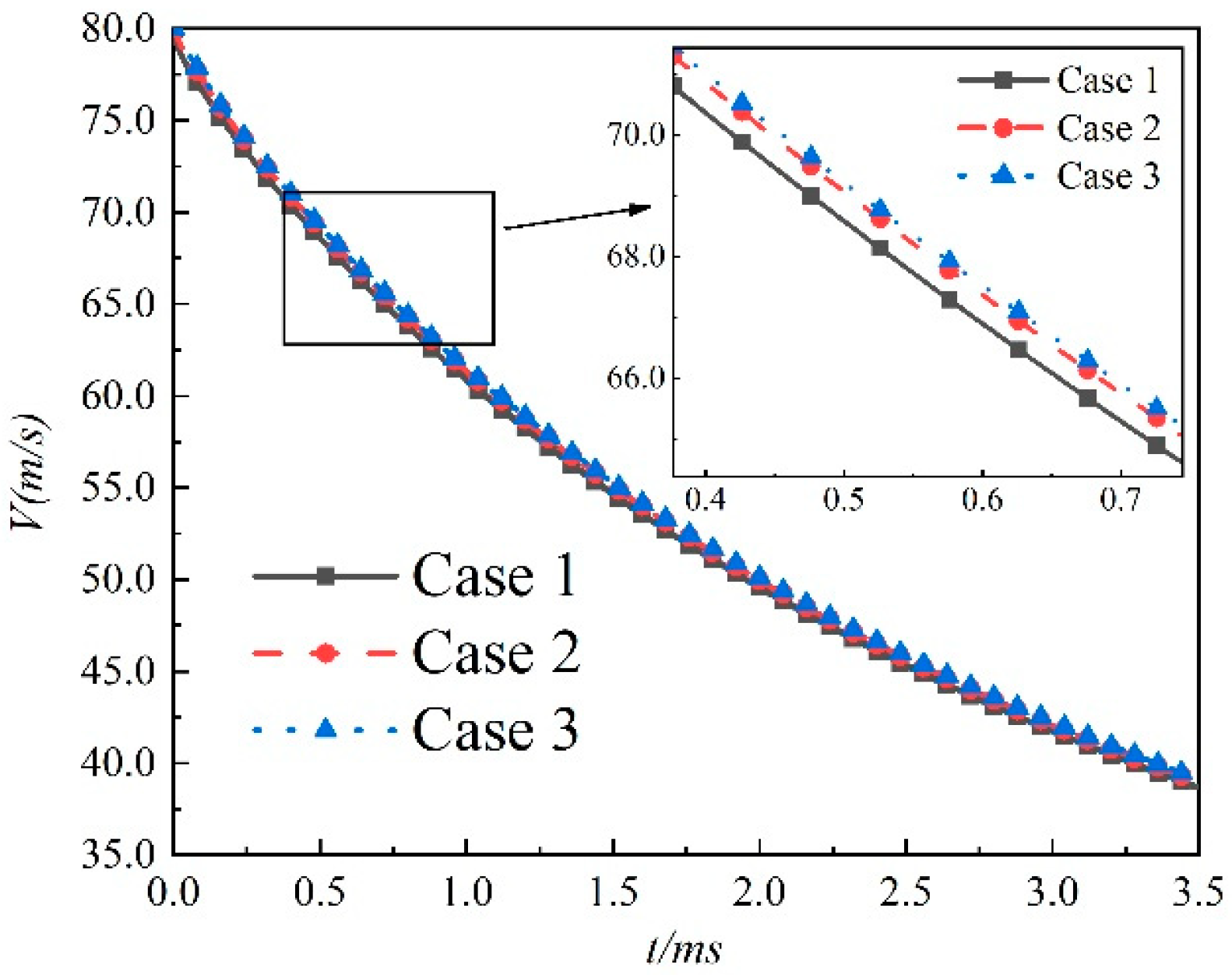
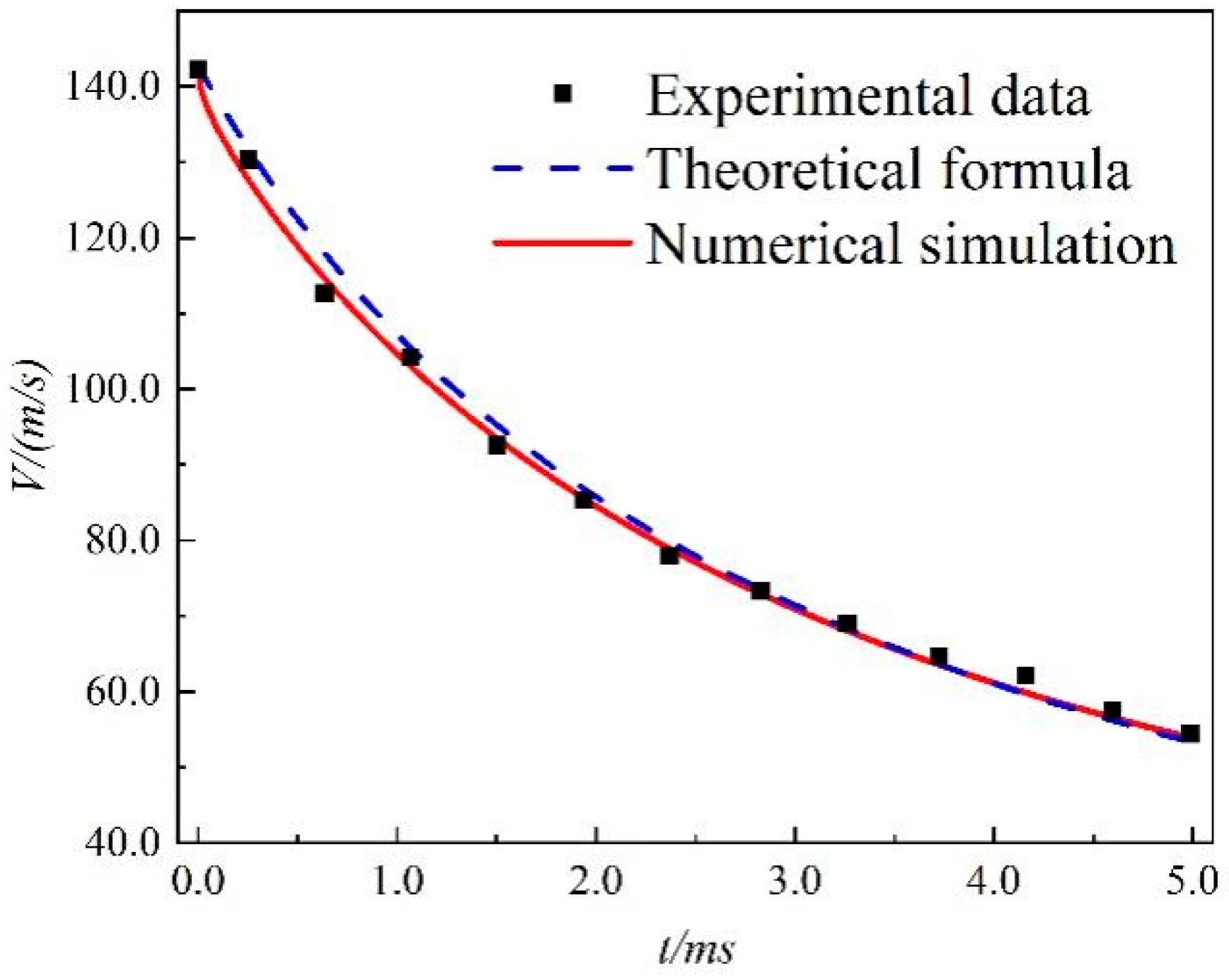
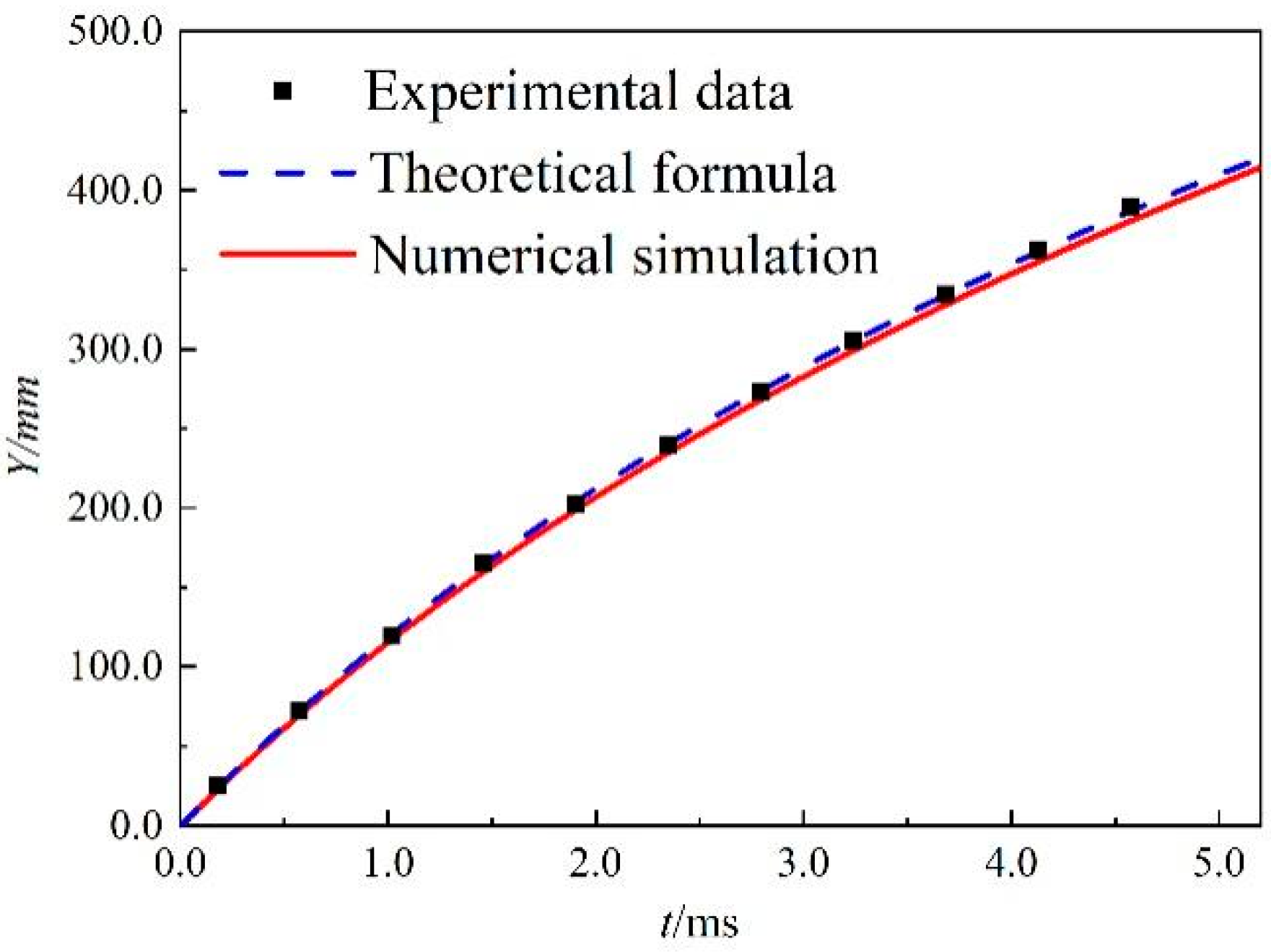
3. Mesh Independence and Numerical Methods Validation
4. Results and Discussion
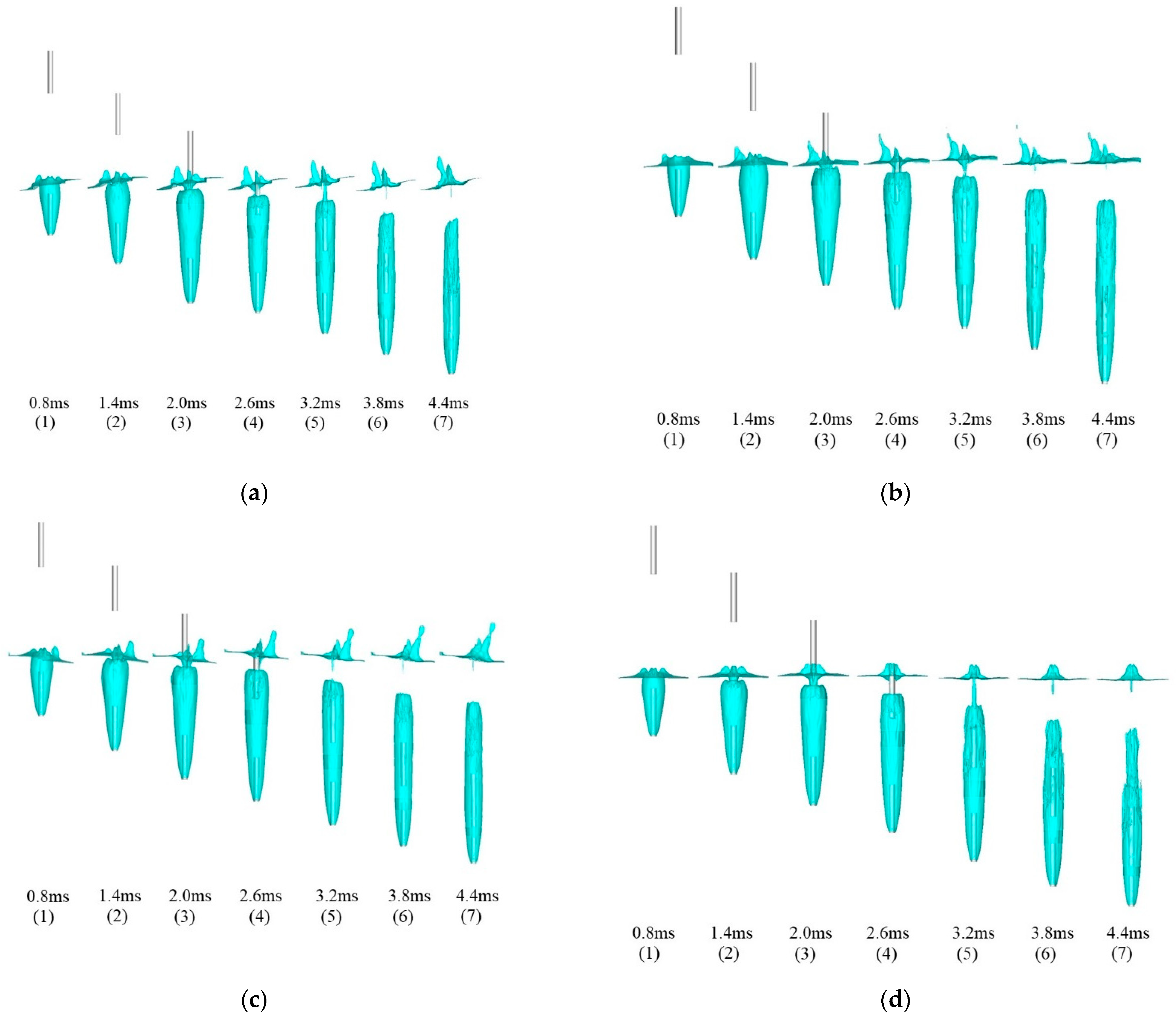
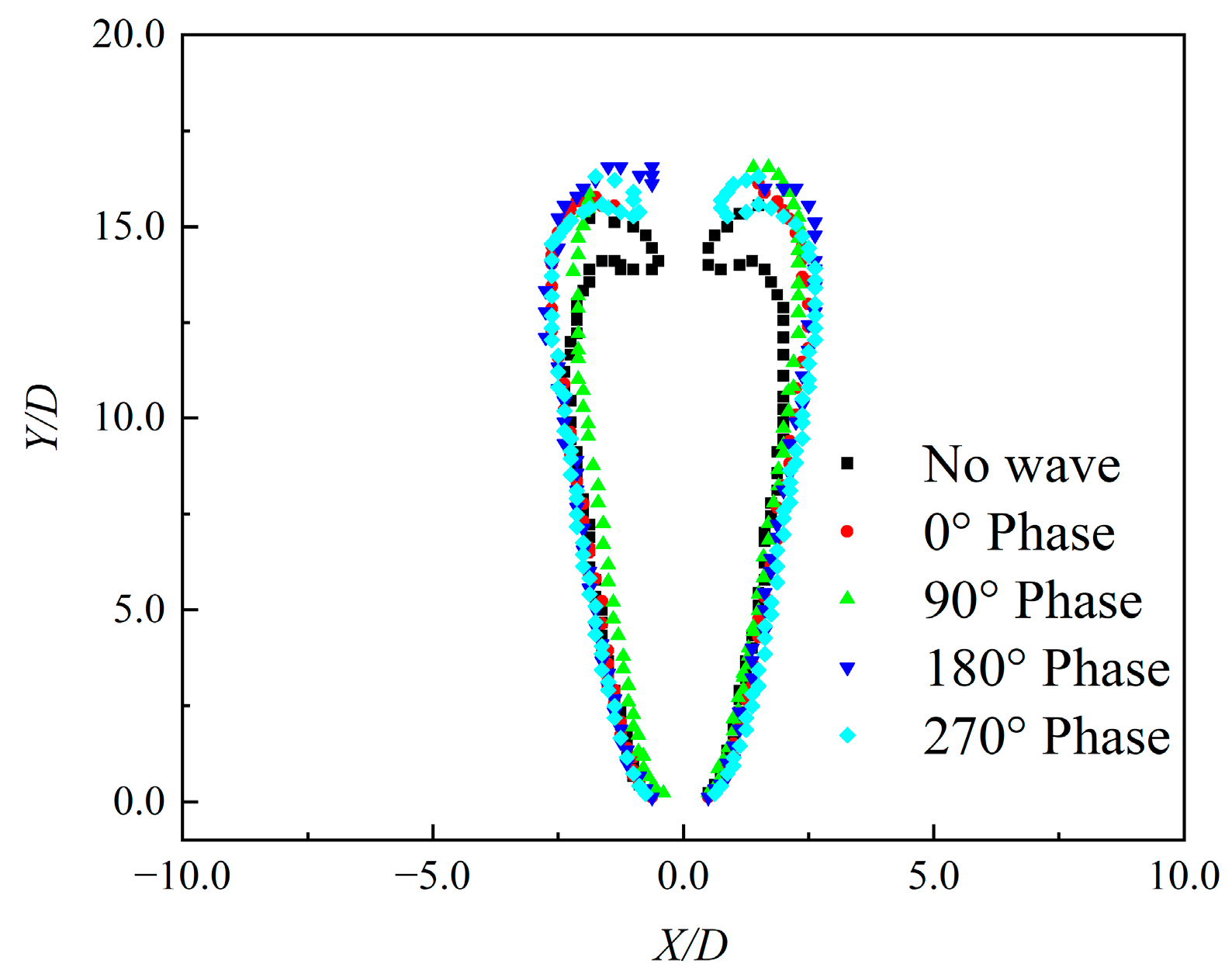
4.1. Water Entry of Successively Fired Projectiles in Different Wave Phases
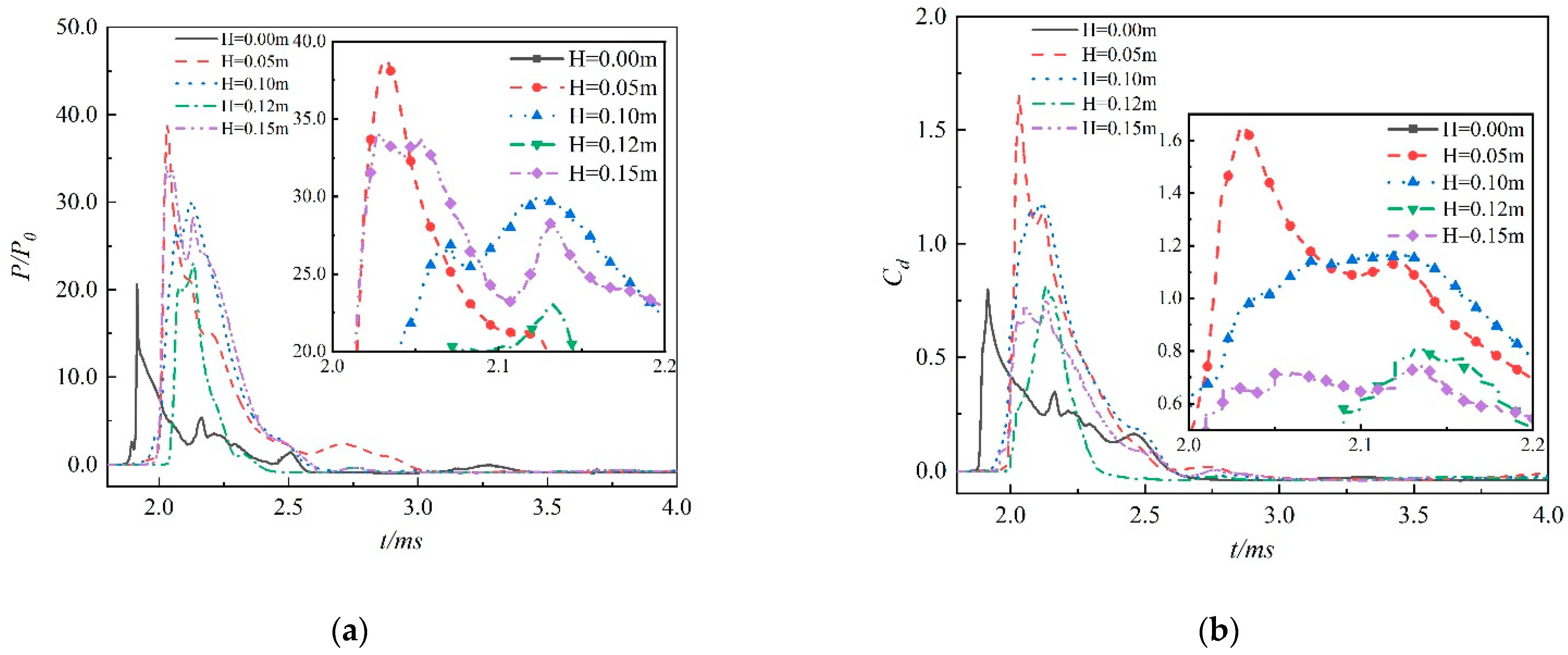
4.2. Water Entry of Successively Fired Projectiles in Different Wave Heights
5. Discussion
6. Conclusions
- The wave phase has an effect on the cavitation shape and has a significant effect on the water splash. The length of the cavitation around the first projectile under wave conditions is increased by about 15% compared with that under the no-wave condition. At the 0° phase, the splash on the left side is stronger than that on the right side, while at the 180° phase, the splash on the right side is higher than that on the left side. The asymmetry of the water splash may be caused by the difference in the thickness of the water layer on the left and right sides of the head of the projectile vertically entering the water.
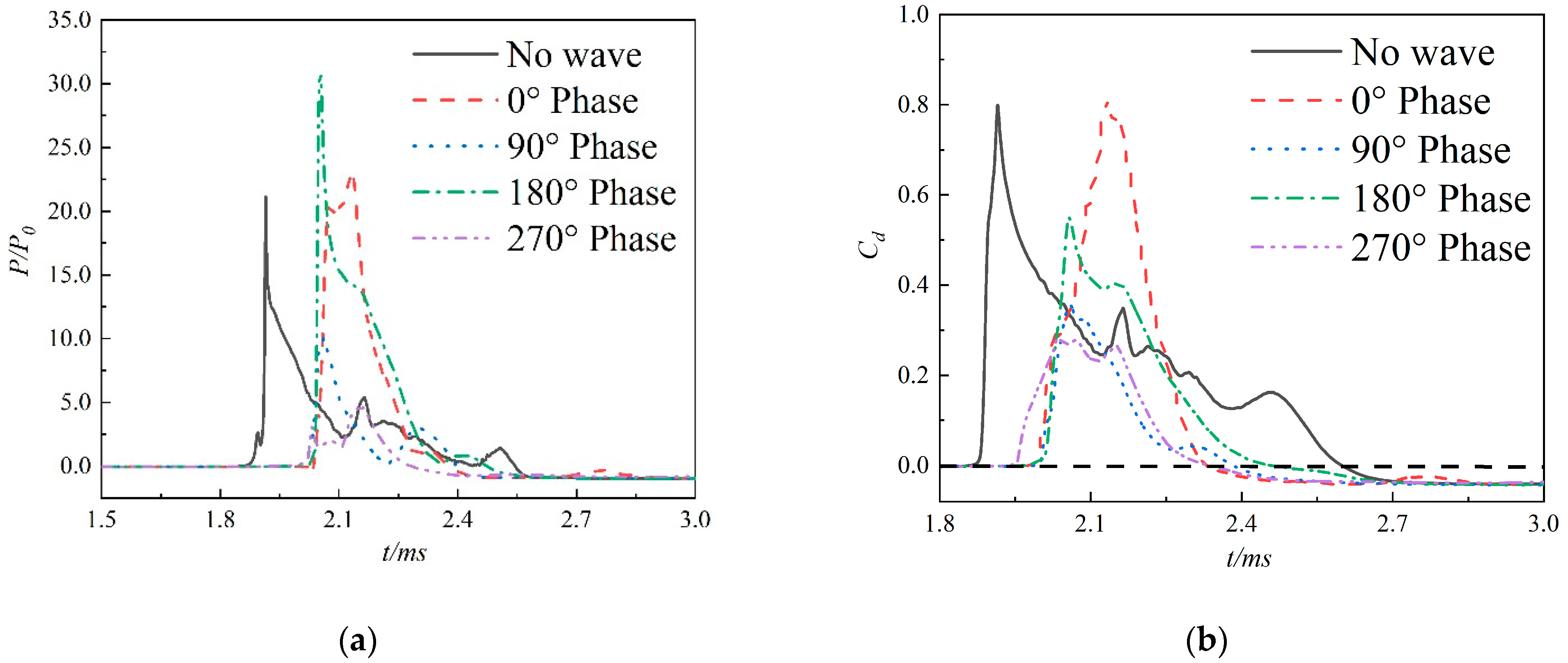
- For the first projectile, the peak of the drag force coefficient under wave conditions is about 50% compared with that under the no-wave condition. The wave phases have an effect on the peak of the drag coefficient. The peak value of the drag coefficient of the first projectile is the largest for the 0° phase; while for 180° phase, the peak value is the minimum. The peak under the condition of the 180° phase is about 40% lower than that of the 0° phase.
- The peak of the drag force coefficient of the first projectile decreases with the increase in the wave height. When the wave height increases from 0 m to 0.05 m, the peak value of the drag coefficient decreases by about 45%. When the wave height continues to increase, the downward trend of the peak value slows down. The peak value of the drag coefficient decreases only by about 13% when the wave height increases from 0.05 m to 0.15 m.
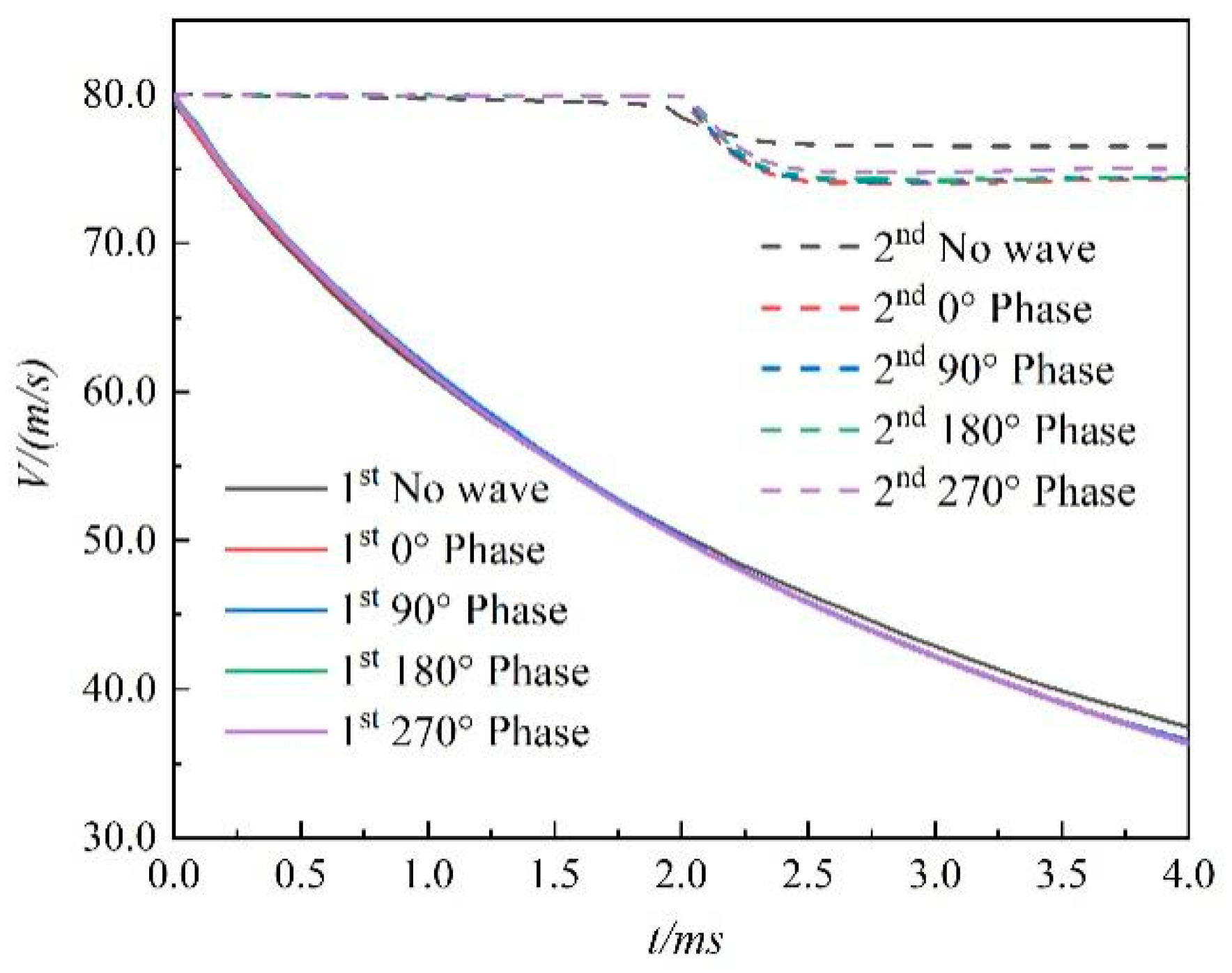
- For different conditions, the peak of the drag of the second projectile can be reduced by about 85–95% compared with that of the first one. That is, the peak on the second one is far less than that of the first one. Correspondingly, the decrease in the velocity of the second one is much slower than that of the front one.
- When the second projectile enters the cavity of the first one, a negative value of the drag coefficient is observed on the second projectile.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Laberteaux, K.R.; Ceccio, S.L. Partial cavity flows. Part 1. Cavities forming on models without spanwise variation. J. Fluid Mech. 2001, 431, 1–41. [Google Scholar] [CrossRef]
- Koukouvinis, P.; Naseri, H.; Gavaises, M. Performance of turbulence and cavitation models in prediction of incipient and developed cavitation. Int. J. Engine Res. 2017, 18, 333–350. [Google Scholar] [CrossRef]
- Ghorbani, M.; Sadaghiani, A.K.; Villanueva, L.G.; Koşar, A. Hydrodynamic cavitation in microfluidic devices with roughened surfaces. J. Micromech. Microeng. 2018, 28, 075016. [Google Scholar] [CrossRef]
- Truscott, T.T.; Techet, A.H. Water entry of spinning spheres. J. Fluid Mech. 2009, 625, 135–165. [Google Scholar] [CrossRef] [Green Version]
- Truscott, T.T. Cavity Dynamics of Water Entry for Spheres and Ballistic Projectiles. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2009. [Google Scholar]
- Yao, E.; Wang, H.R.; Pan, L.; Wang, X.B.; Woding, R.H. Vertical Water-Entry of Bullet-Shaped Projectiles. J. Appl. Math. Phys. 2014, 02, 323–334. [Google Scholar] [CrossRef] [Green Version]
- Shi, H.H.; Takami, T. Hydrodynamic behavior of an underwater moving body after water entry. Acta Mech. Sin. 2001, 17, 35–44. [Google Scholar]
- Shi, H.H.; Takami, T. Some progress in the study of the water entry phenomenon. Exp. Fluids 2001, 30, 475–477. [Google Scholar] [CrossRef]
- Chen, T.; Huang, W.; Zhang, W.; Qi, Y.F.; Guo, Z.T. Experimental investigation on trajectory stability of high-speed water entry projectiles. Ocean Eng. 2019, 175, 16–24. [Google Scholar] [CrossRef]
- Nair, V.V.; Bhattacharyya, S.K. Water entry and exit of axisymmetric bodies by CFD approach. J. Ocean. Eng. Sci. 2018, 3, 156–174. [Google Scholar] [CrossRef]
- Kozelkov, A.; Kurkin, A.; Pelinovskiĭ, E.N. Effect of the angle of water entry of a body on the generated wave heights. Fluid Dyn. 2016, 51, 288–298. [Google Scholar] [CrossRef]
- Kamath, A.; Bihs, H.; Arntsen, Ø.A. Study of Water Impact and Entry of a Free Falling Wedge Using Computational Fluid Dynamics Simulations. J. Offshore Mech. Arct. Eng. 2017, 139, 031802. [Google Scholar] [CrossRef]
- Nguyen, V.T.; Ha, C.T.; Park, W.G. Multiphase flow simulation of water-entry and -exit of axisymmetric bodies. In ASME International Mechanical Engineering Congress and Exposition; American Society of Mechanical Engineers: New York, NY, USA, 2013. [Google Scholar]
- Neaves, M.D.; Edwards, J.R. All-Speed Time-Accurate Underwater Projectile Calculations Using a Preconditioning Algorithm. J. Fluids Eng.-Trans. ASME 2006, 128, 284–296. [Google Scholar] [CrossRef]
- Chen, Y.; Lu, C.J.; Chen, X.; Li, J.; Gong, Z.X. An approach for the numerical prediction of the compressible supercavitating flows over ultrahigh-speed underwater object. Eng. Comput. 2016, 33, 2356–2376. [Google Scholar] [CrossRef]
- Zhou, D.H.; Shi, H.H.; Jia, H.X. Characteristics of the multiphase flow field with super-cavitation induced by successively fired projectiles under-water and cross-medium. J. Mech. Sci. Technol. 2022, 36, 247–258. [Google Scholar] [CrossRef]
- Jiang, Y.H.; Li, Y.; Guo, J.; Yang, L.L.; Wang, H.B. Numerical simulations of series and parallel water entry of supersonic projectiles in compressible flow. Ocean. Eng. 2021, 235, 109155. [Google Scholar] [CrossRef]
- Wang, K.; Ma, X.; Bai, W.; Lin, Z.B.; Li, Y.B. Numerical simulation of water entry of a symmetric/asymmetric wedge into waves using OpenFOAM. Ocean. Eng. 2021, 227, 108923. [Google Scholar] [CrossRef]
- Sun, S.L.; Liu, B.C.; Zhang, A.M. On the fully nonlinear water entry of a cone in Stokes wave. Eng. Anal. Bound. Elem. 2019, 98, 232–242. [Google Scholar] [CrossRef]
- Hu, X.Z.; Jiang, Y.Y.; Cai, D.J. Numerical Modeling and Simulation of Wave Impact of a Circular Cylinder during the Submergence Process. Model. Simul. Eng. 2017, 2017, 2197150. [Google Scholar] [CrossRef] [Green Version]
- Hu, X.Z.; Liu, S.J. Numerical investigation of water-entry of flatted-bottom seafloor mining tool in ocean waves. J. Cent. South Univ. 2014, 21, 3071–3078. [Google Scholar] [CrossRef]
- Hu, X.Z.; Liu, S.J. Numerical Investigation of Wave Slamming of Flat Bottom Body during Water Entry Process. Math. Probl. Eng. 2014, 2014, 821689. [Google Scholar] [CrossRef] [Green Version]
- Xiang, G.; Li, X.; Yu, X.C.; Luo, Y.; Cao, Y. Motion dynamics of dropped cylindrical objects in flows after water entry. Ocean Eng. 2019, 173, 659–671. [Google Scholar] [CrossRef]
- Zhang, G.Y.; Hou, Z.; Sun, T.Z.; Wei, H.P.; Li, N.; Zhou, B.; Gao, Y.X. Numerical simulation of the effect of waves on cavity dynamics for oblique water entry of a cylinder. J. Hydrodyn. 2020, 32, 1178–1190. [Google Scholar] [CrossRef]
- Wang, W.H.; Wang, Y.Y. An essential solution of water entry problems and its engineering applications. J. Mar. Sci. Appl. 2010, 9, 268–273. [Google Scholar] [CrossRef]
- Wang, W.H.; Wang, Y.Y. Numerical Study on Cylinder Entering Water in Wave. J. Shanghai Jiaotong Univ. 2010, 44, 1393. [Google Scholar]
- Zhou, L.J.; Wang, Z.W. Numerical Simulation of Cavitation Around a Hydrofoil and Evaluation of a RNG κ-ε Model. J. Fluids Eng.-Trans. ASME 2008, 130, 011302. [Google Scholar] [CrossRef]
- Singhal, A.K.; Athavale, M.M.; Li, H.Y.; Jiang, Y. Mathematical Basis and Validation of the Full Cavitation Model. J. Fluids Eng.-Trans. ASME 2002, 124, 617–624. [Google Scholar] [CrossRef]
- Dean, R.G.; Dalrymple, R.A. Water Wave Mechanics for Engineers and Scientists; World Scientific Publishing Company: Singapore, 1983. [Google Scholar]
- Guo, B.J.; Sverre, S. Comparison of Numerical Methods for Wave Generation by VOF-Based Numerical Wave Tank. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering, Rotterdam, The Netherlands, 19–24 June 2011. [Google Scholar]
- Guo, Z.T.; Zhang, W.; Xiao, X.K.; Wei, G.; Ren, P. An investigation into horizontal water entry behaviors of projectiles with different nose shapes. Int. J. Impact Eng. 2012, 49, 43–60. [Google Scholar] [CrossRef]
- Chuang, S.L. Experiments on Flat-Bottom Slamming. J. Ship Res. 1966, 10, 10–17. [Google Scholar] [CrossRef]
- Rabbi, R.; Speirs, N.B.; Kiyama, A.; Belden, J.; Truscott, T.T. Impact force reduction by consecutive water entry of spheres. J. Fluid Mech. 2021, 915, A55. [Google Scholar] [CrossRef]
- Jia, H.X.; Wang, Z.K.; Zhou, D.H.; Shi, H.H. Effect of Wave Phases on Supercavitation Flow Field and Dynamic Characteristics of High-speed Projectiles. BMCSF 2022, 7308, 1–6. [Google Scholar]








Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, L.; Wang, Z.; Jia, H. Effect of Wave Phases and Heights on Supercavitation Flow Field and Dynamic Characteristics of Successively Fired High-Speed Projectiles. J. Mar. Sci. Eng. 2023, 11, 629. https://doi.org/10.3390/jmse11030629
Zhang L, Wang Z, Jia H. Effect of Wave Phases and Heights on Supercavitation Flow Field and Dynamic Characteristics of Successively Fired High-Speed Projectiles. Journal of Marine Science and Engineering. 2023; 11(3):629. https://doi.org/10.3390/jmse11030629
Chicago/Turabian StyleZhang, Lite, Zhuokai Wang, and Huixia Jia. 2023. "Effect of Wave Phases and Heights on Supercavitation Flow Field and Dynamic Characteristics of Successively Fired High-Speed Projectiles" Journal of Marine Science and Engineering 11, no. 3: 629. https://doi.org/10.3390/jmse11030629




