Analysis of Water Resonance in the Inner Domain of a Large Fixed Floating Tourist Platform Based on a 3D Non-Hydrostatic Model
Abstract
1. Introduction
2. Numerical Model
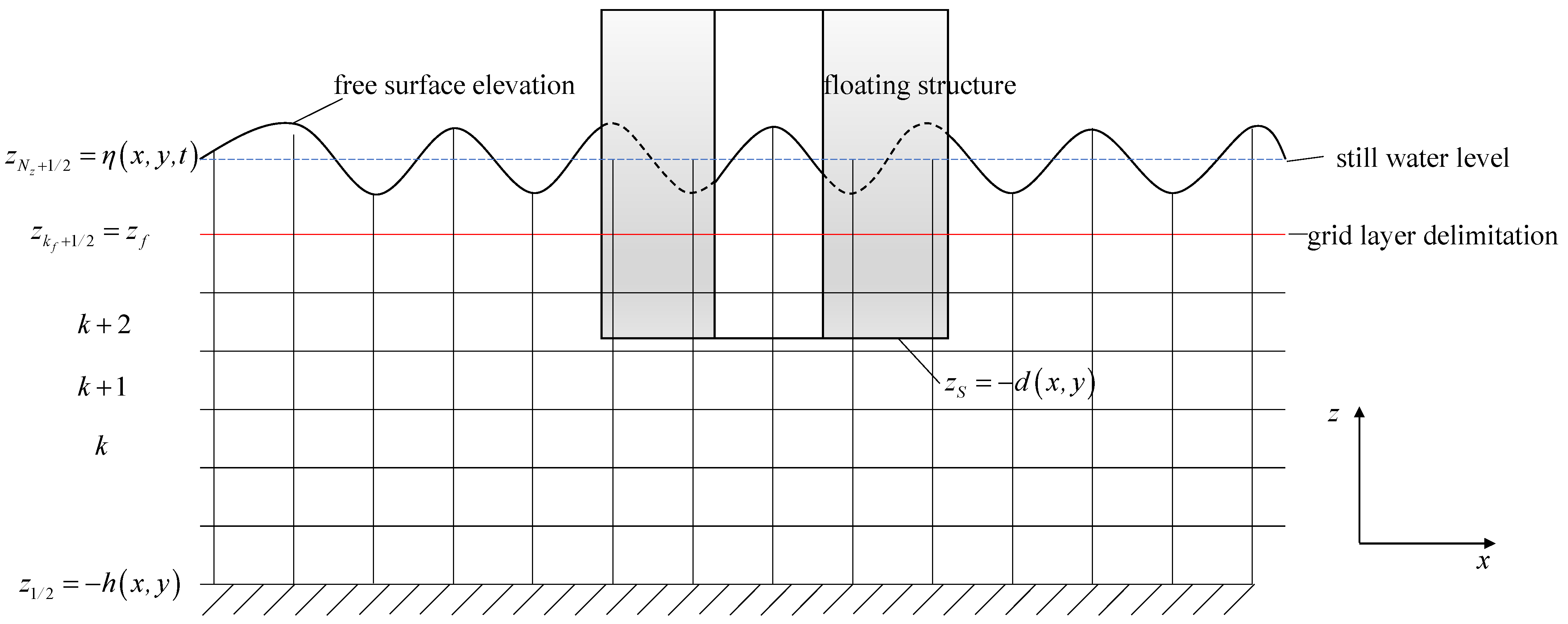
2.1. Governing Equations
2.2. Boundary Conditions
2.3. Numerical Algorithms
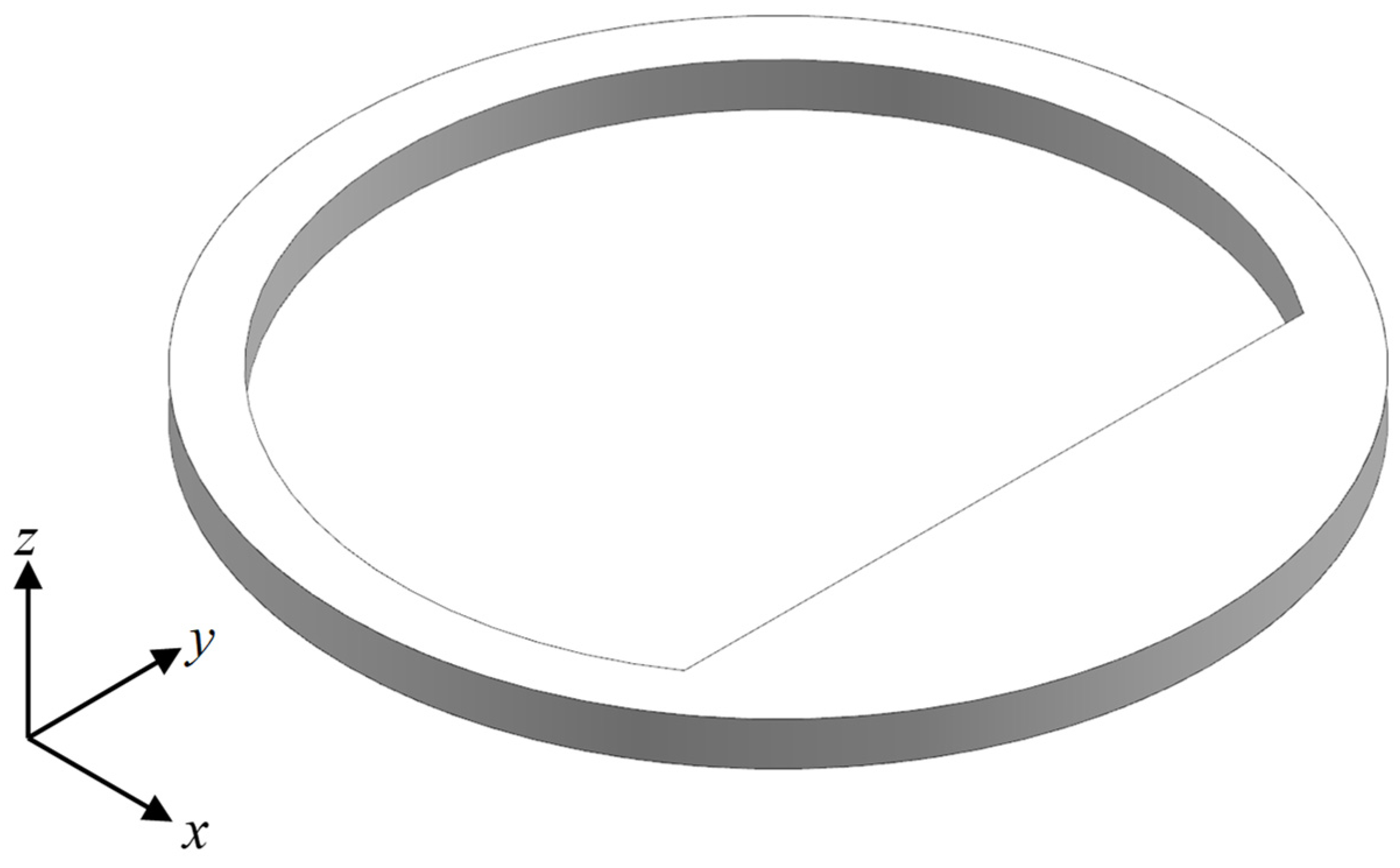
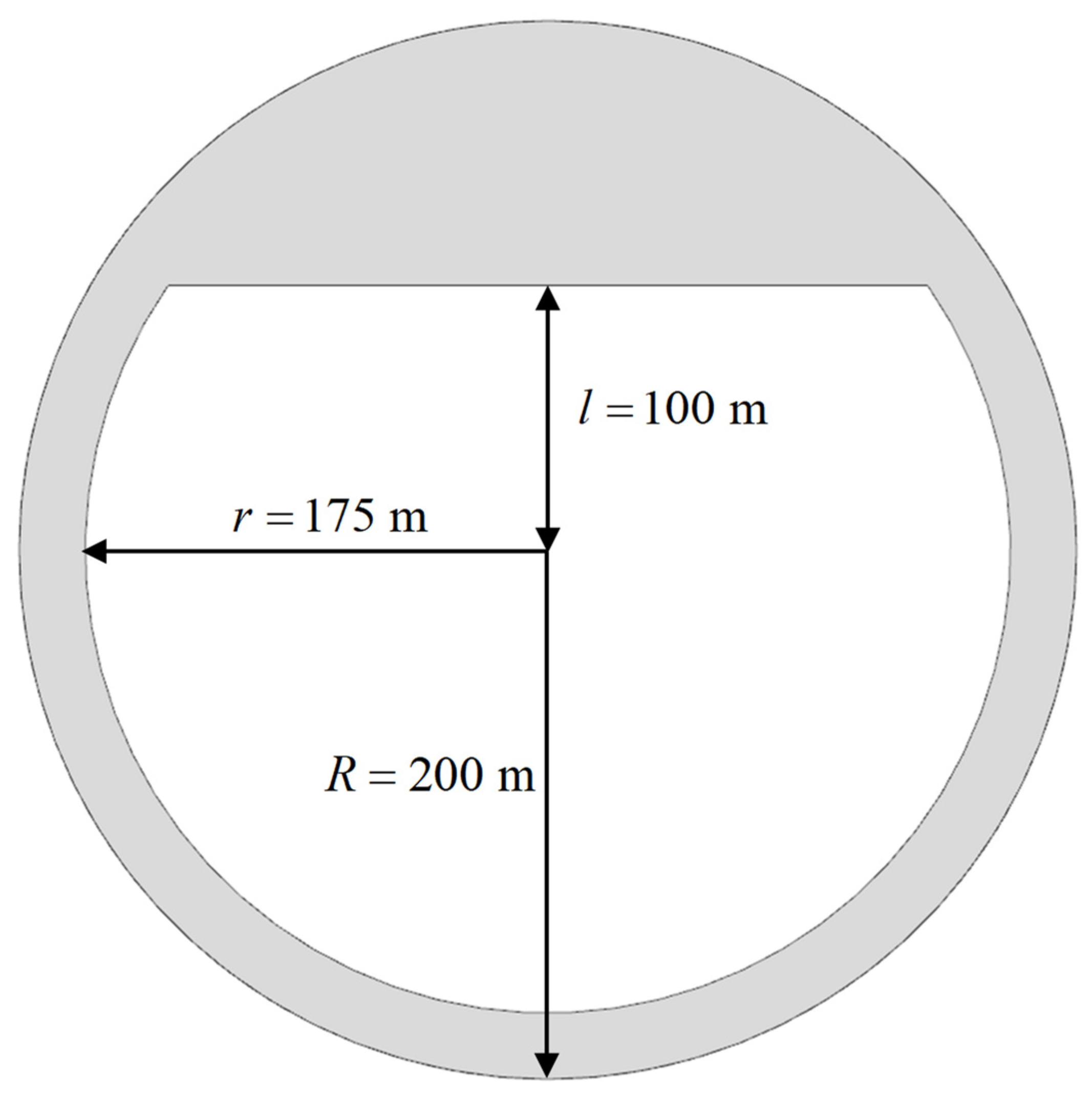
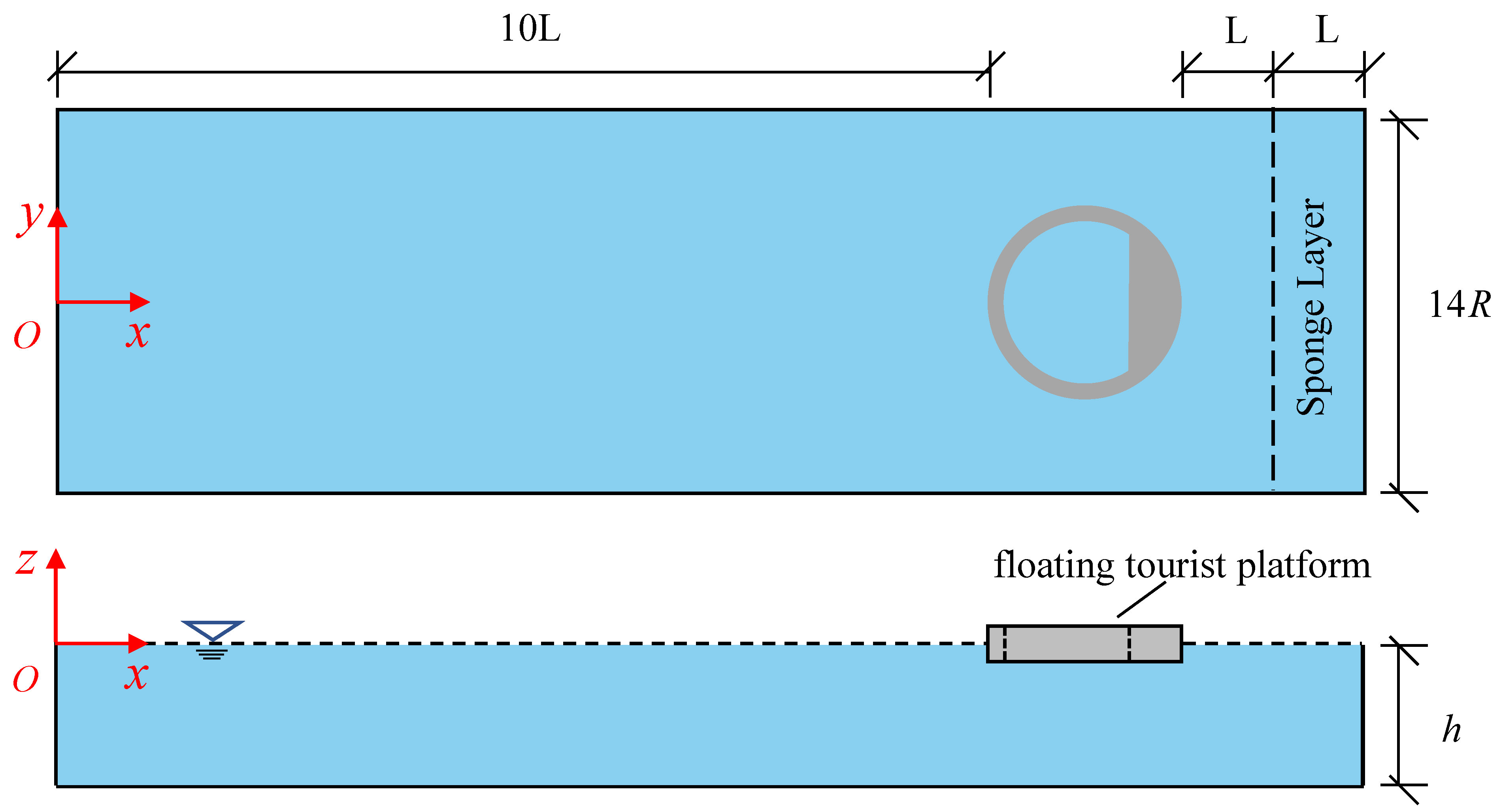
2.4. Description of the Tourist Platform
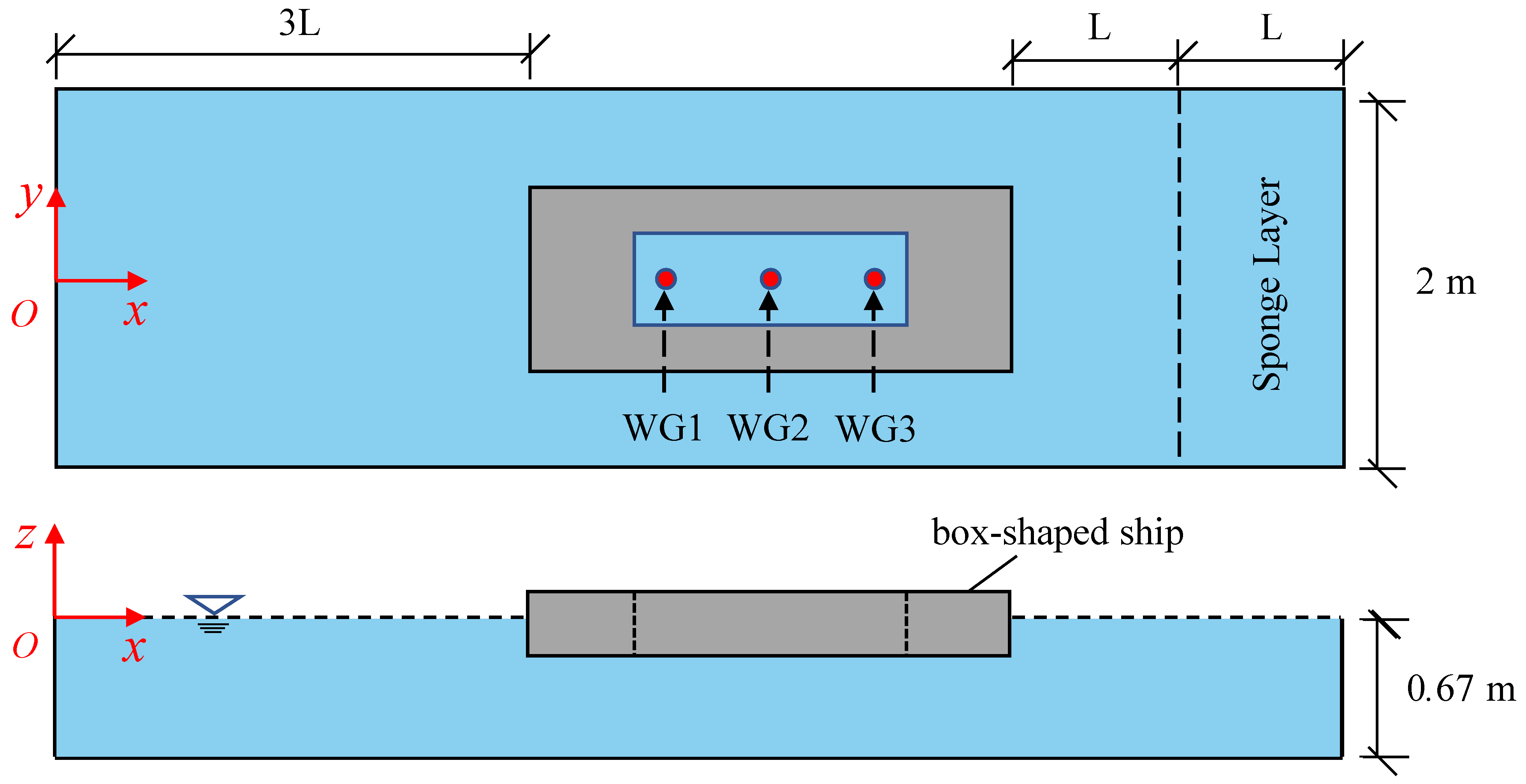
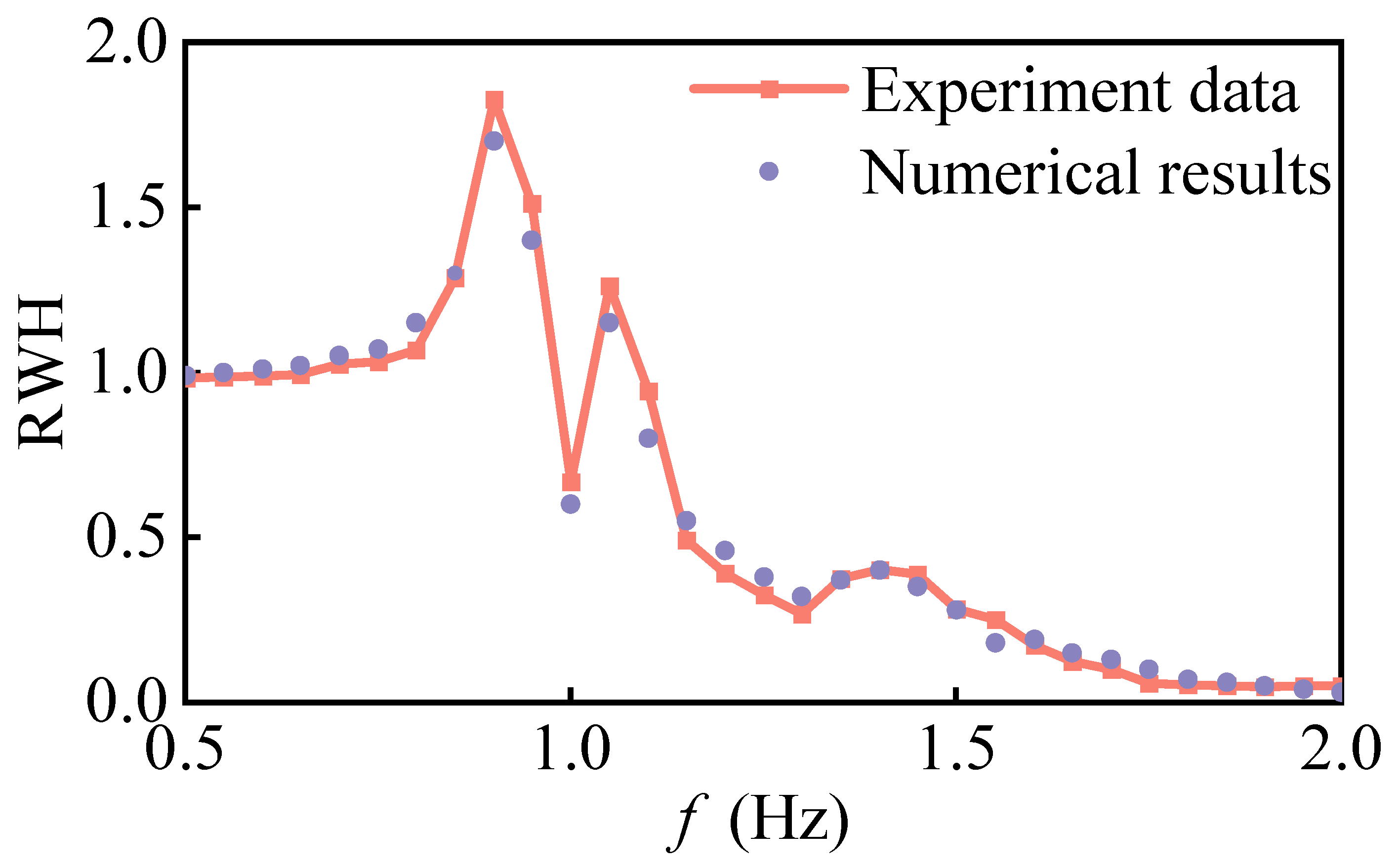
3. Model Validation
4. Water Resonance in the Inner Domain of the Floating Tourist Platform
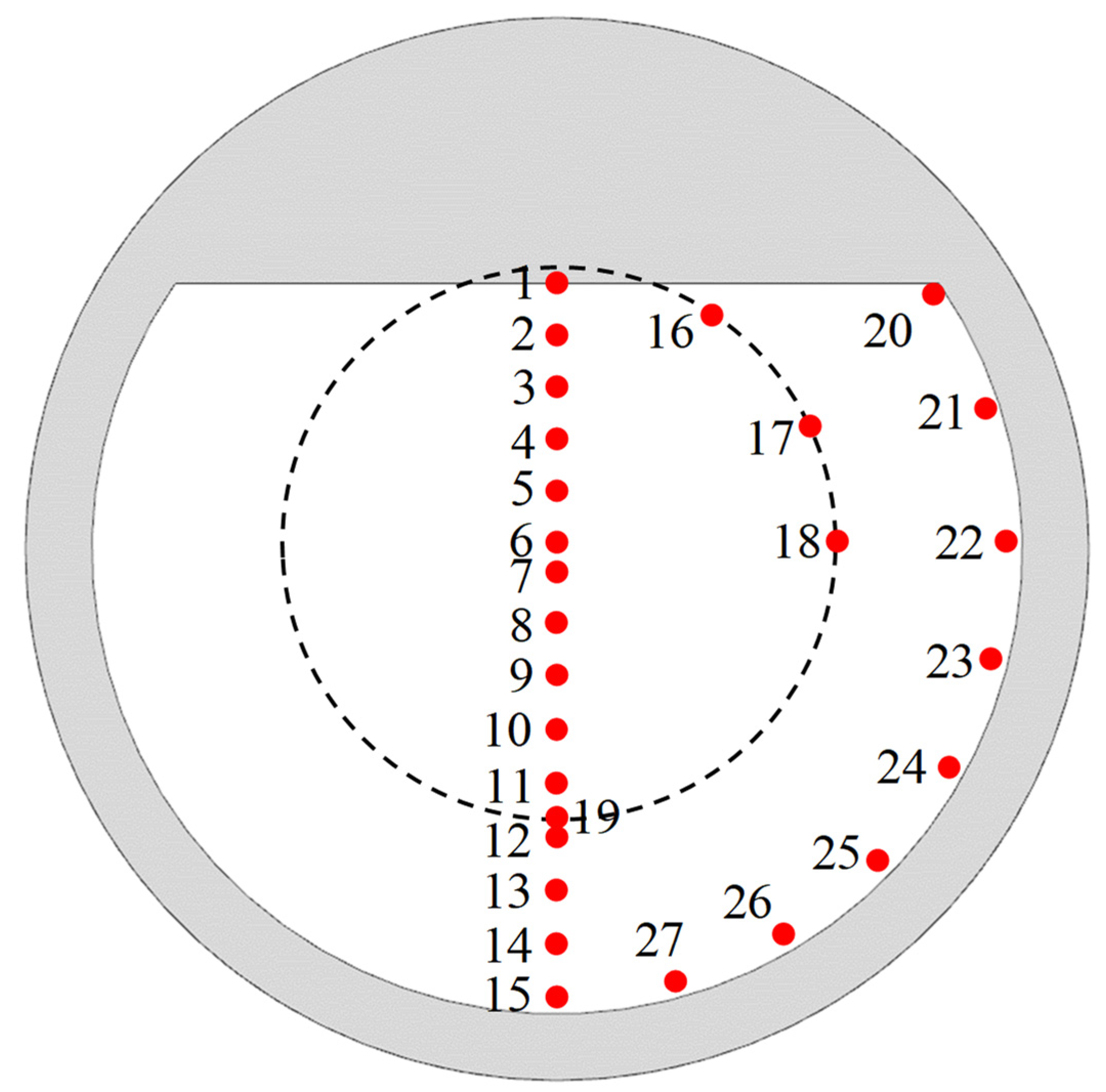
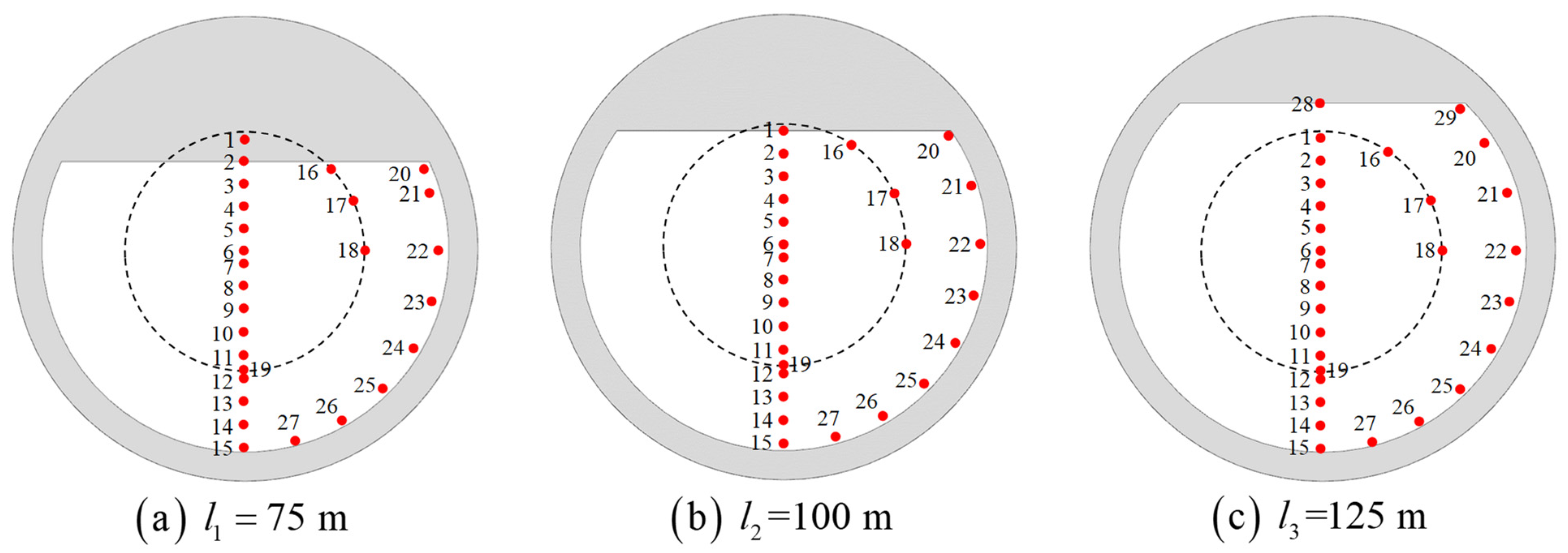
4.1. Numerical Setup
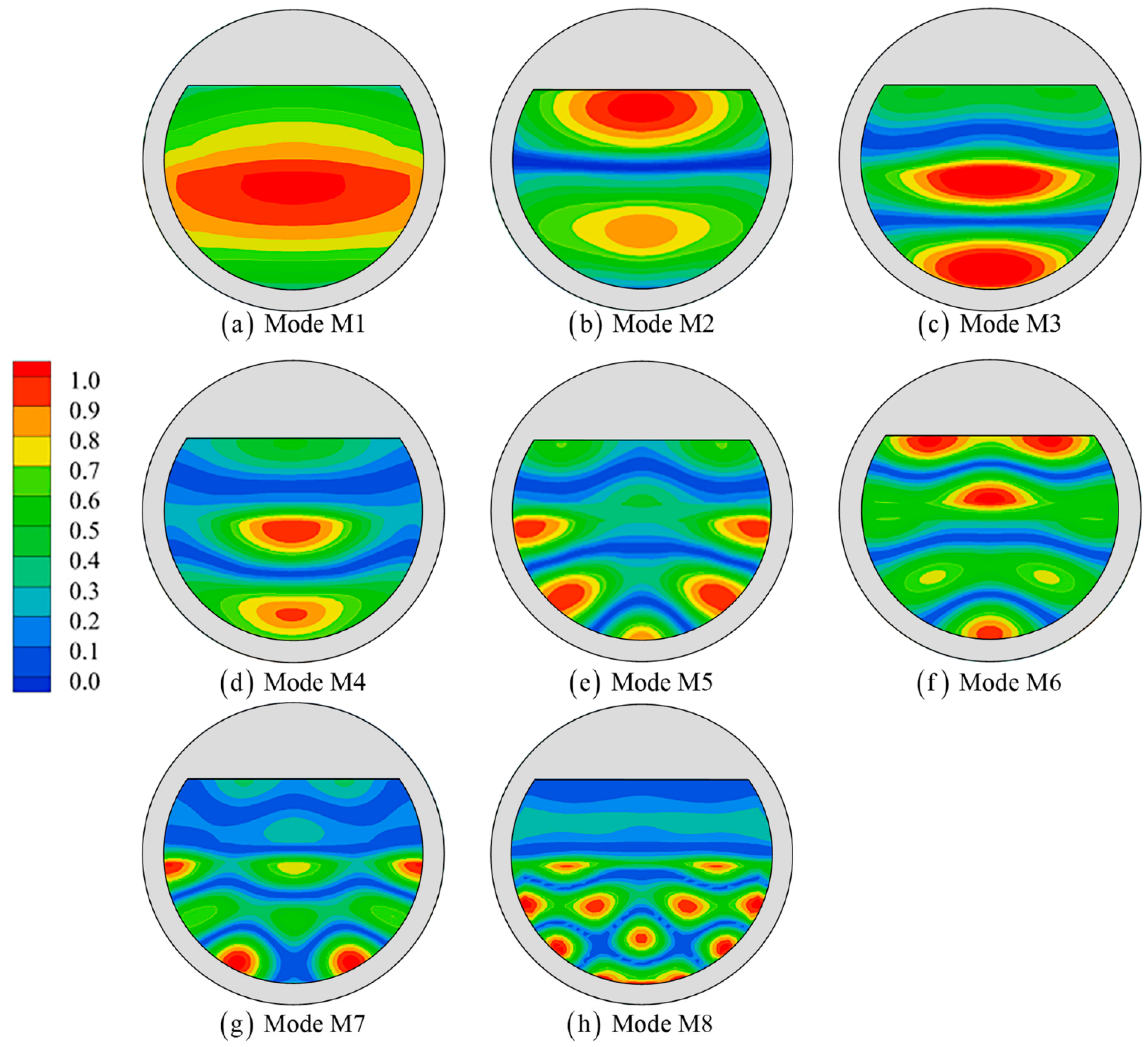
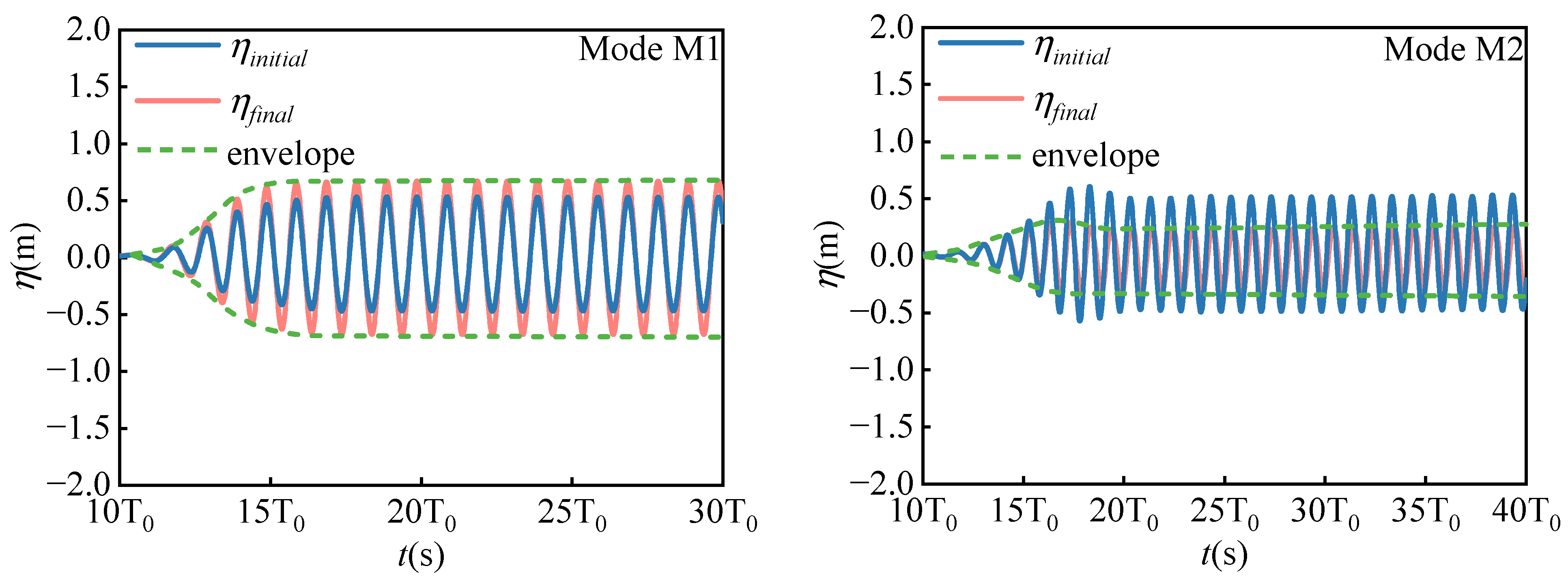
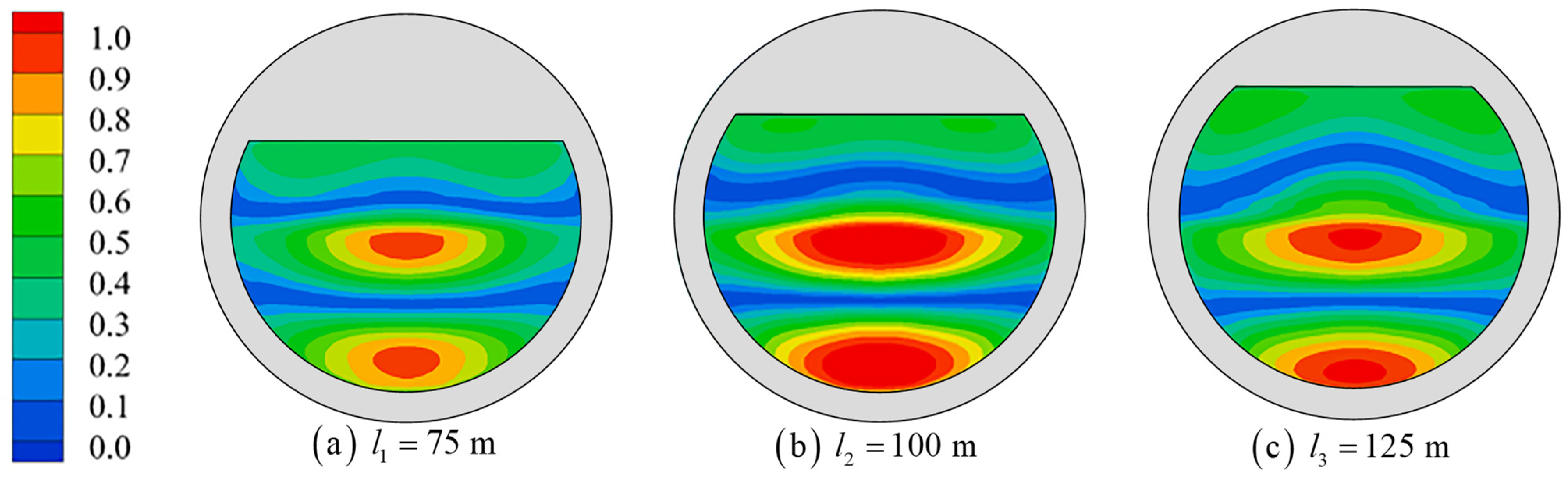
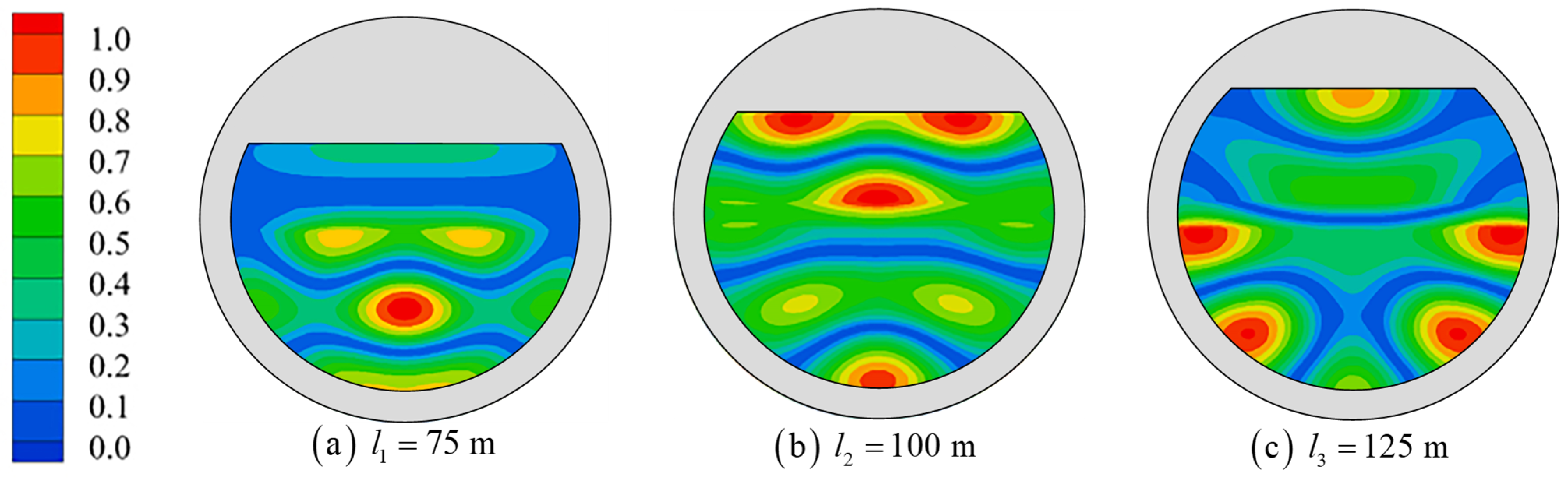
4.2. Resonant Frequencies and Modes
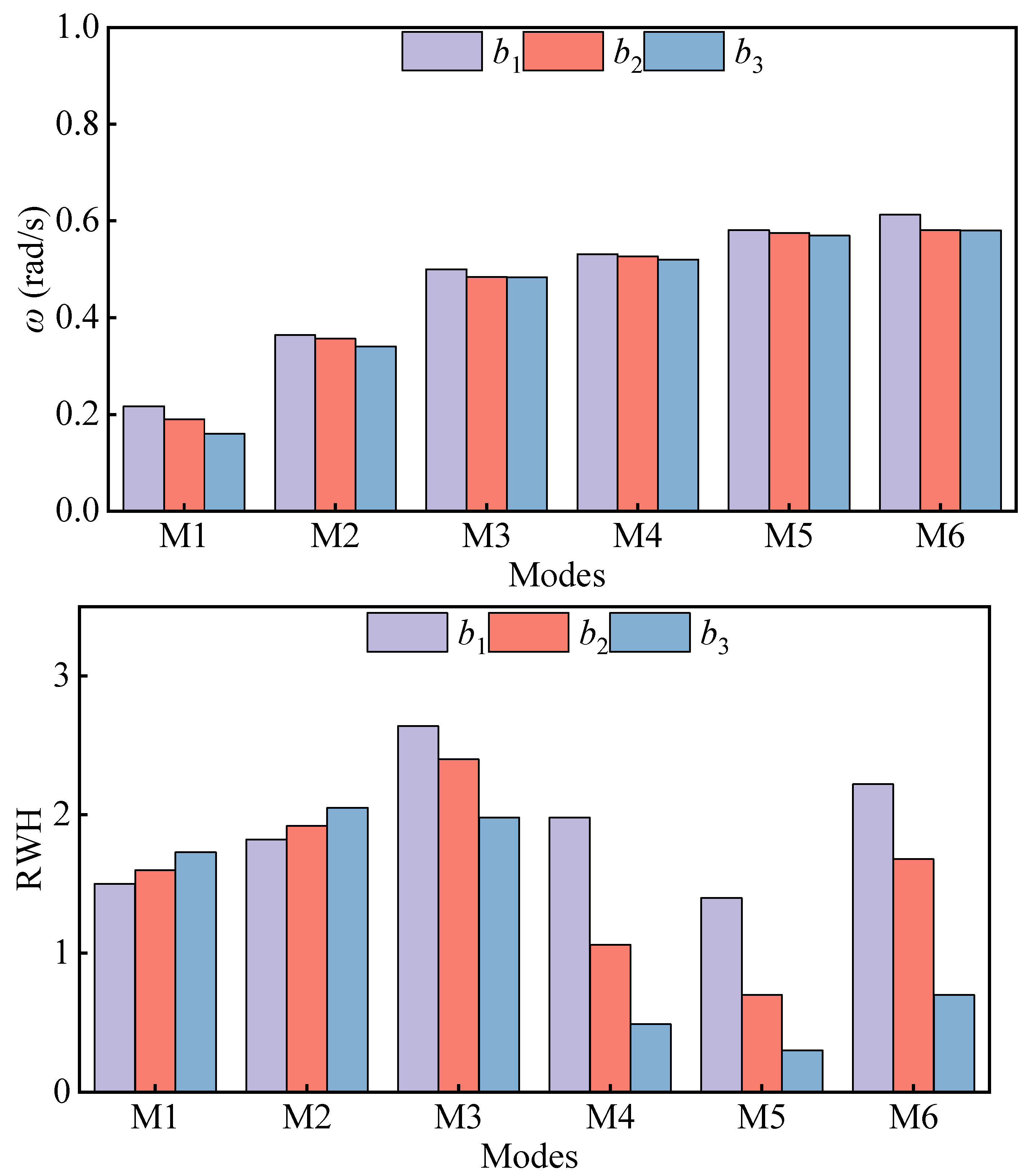
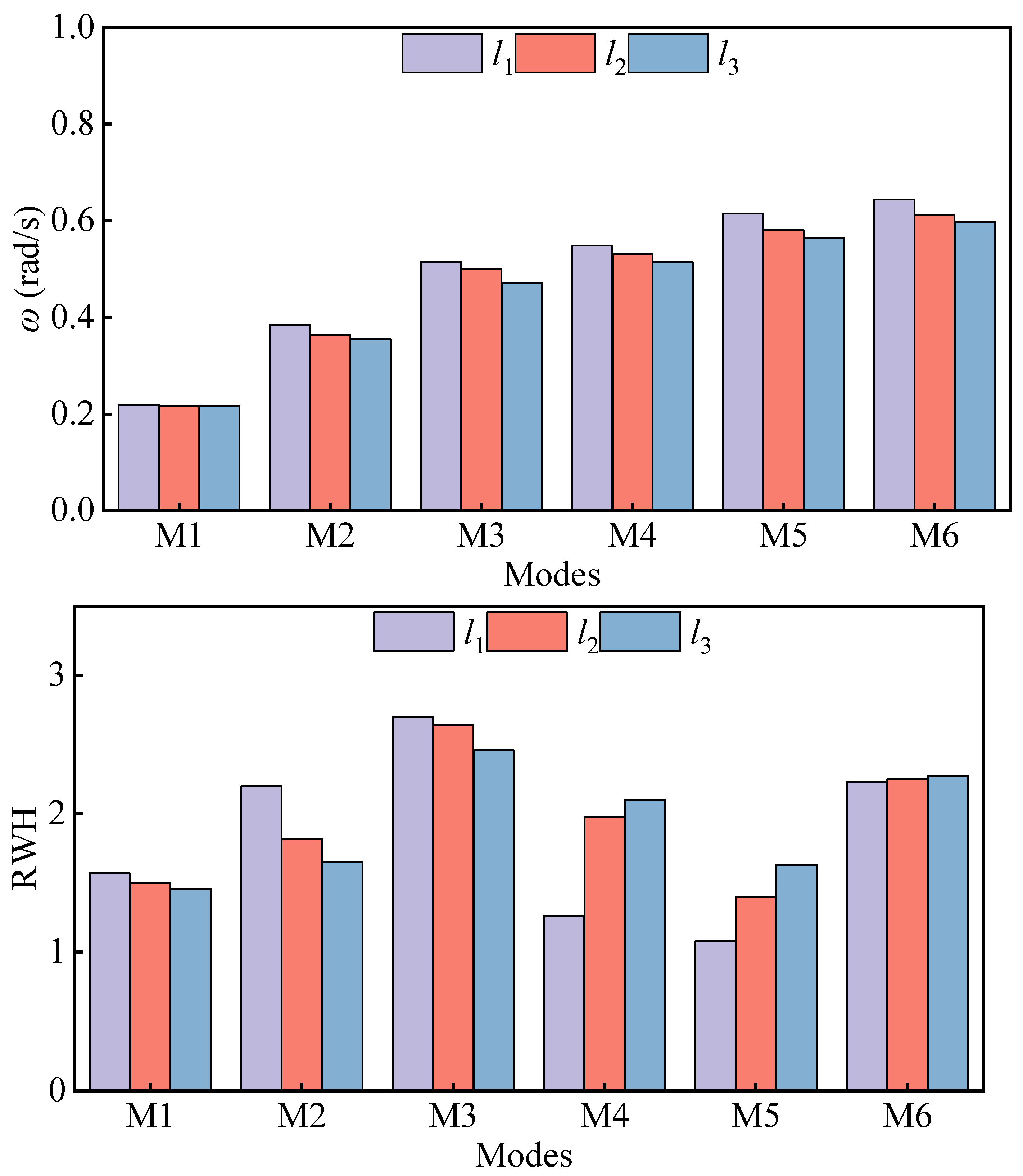
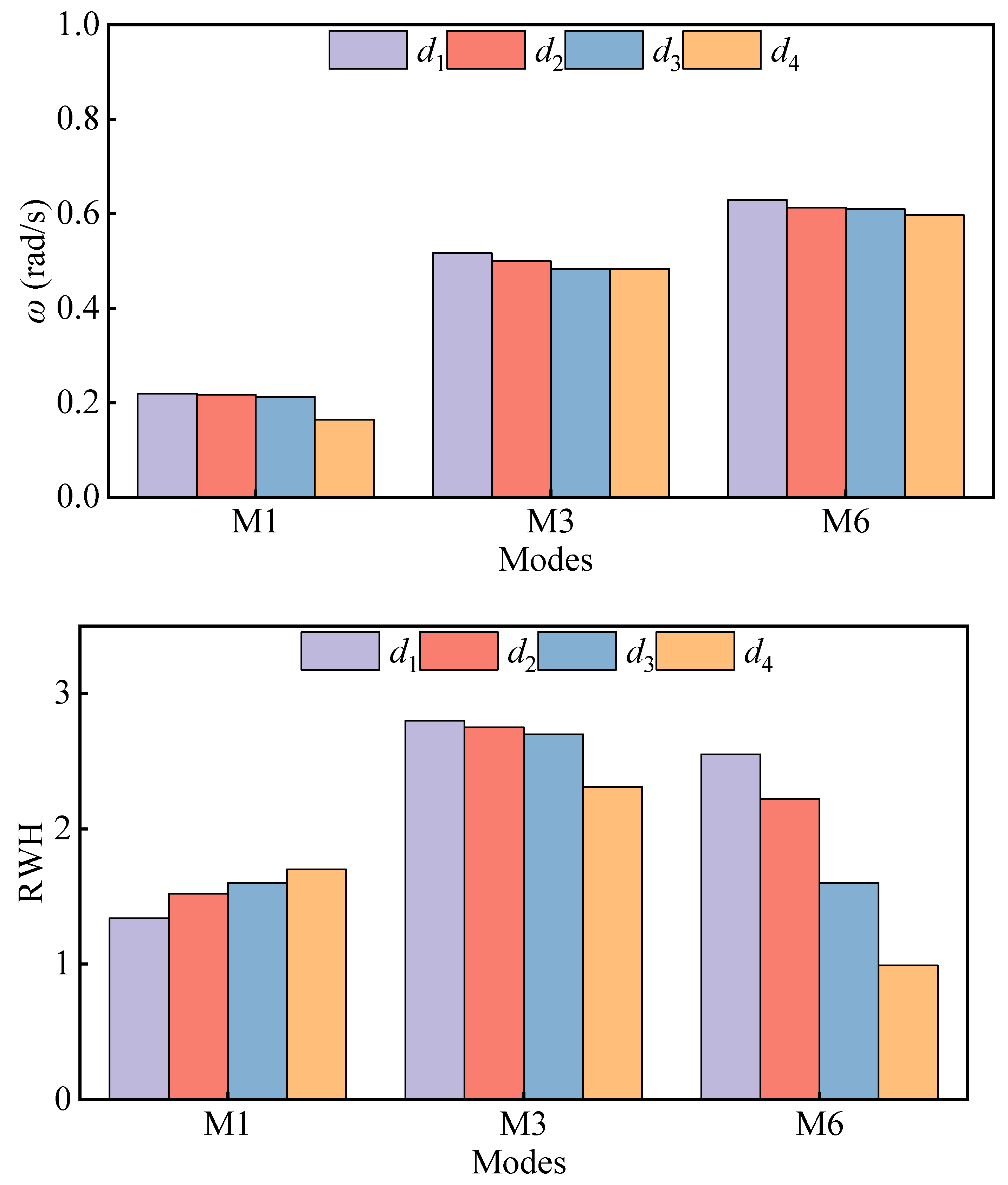
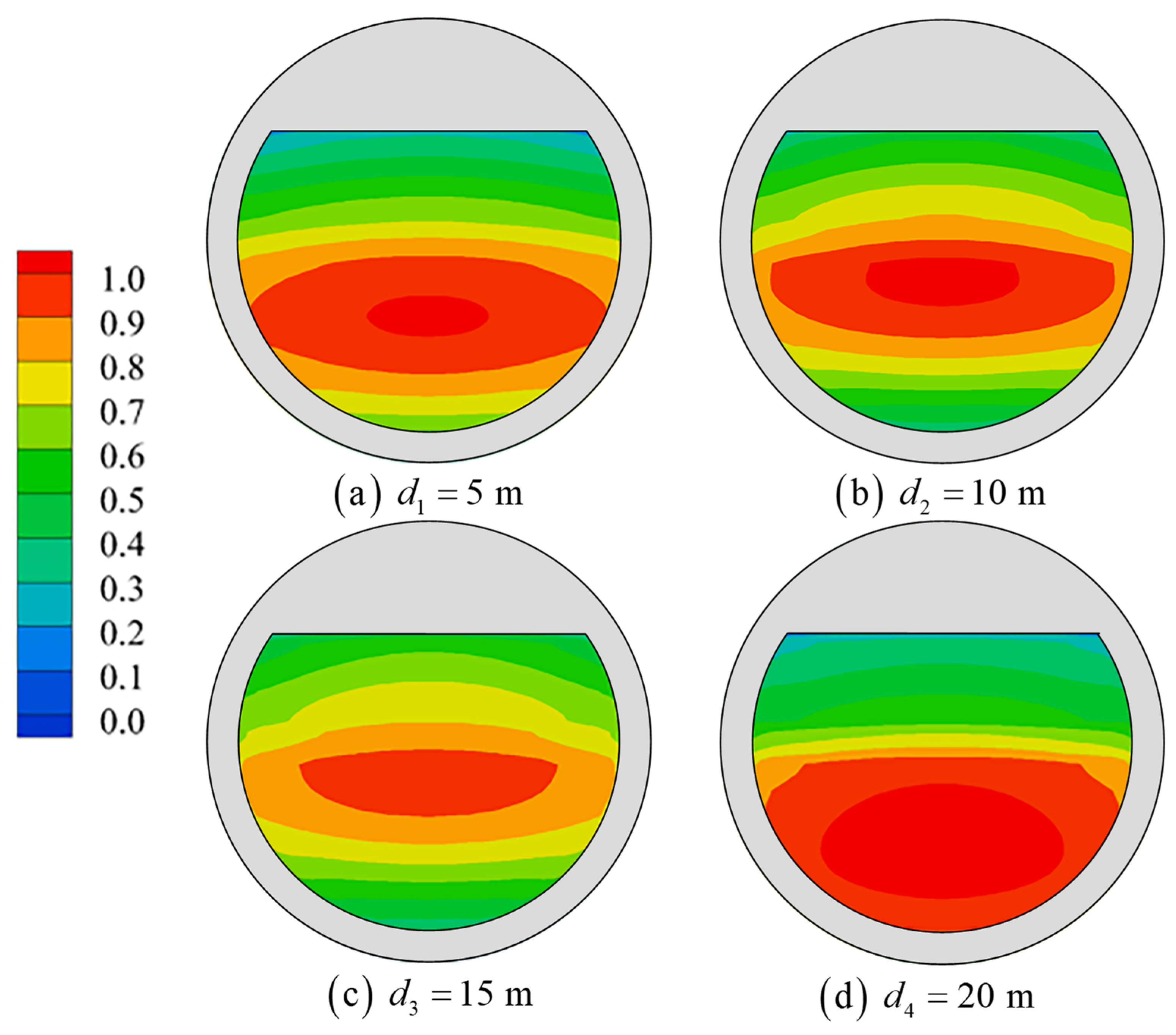
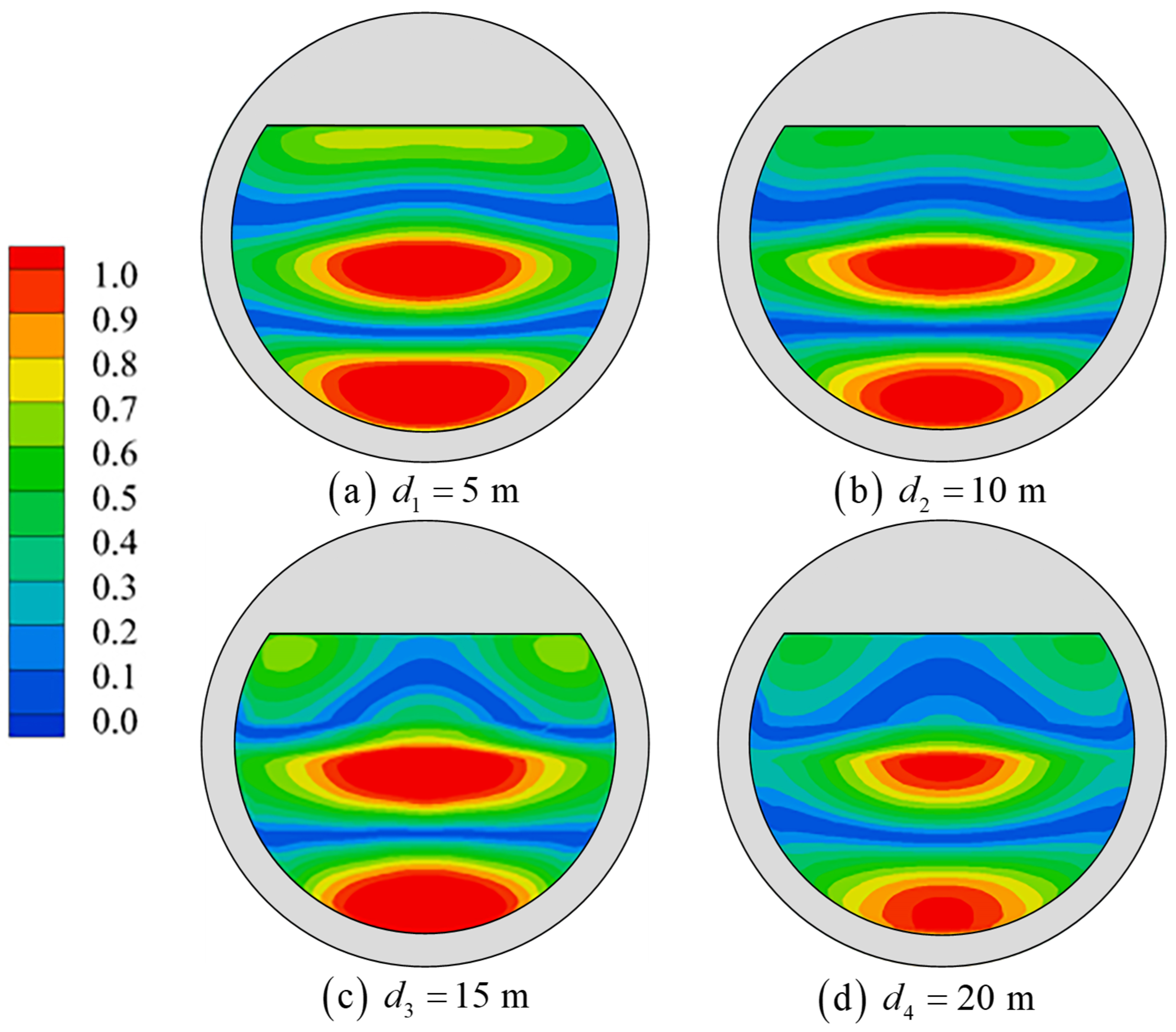
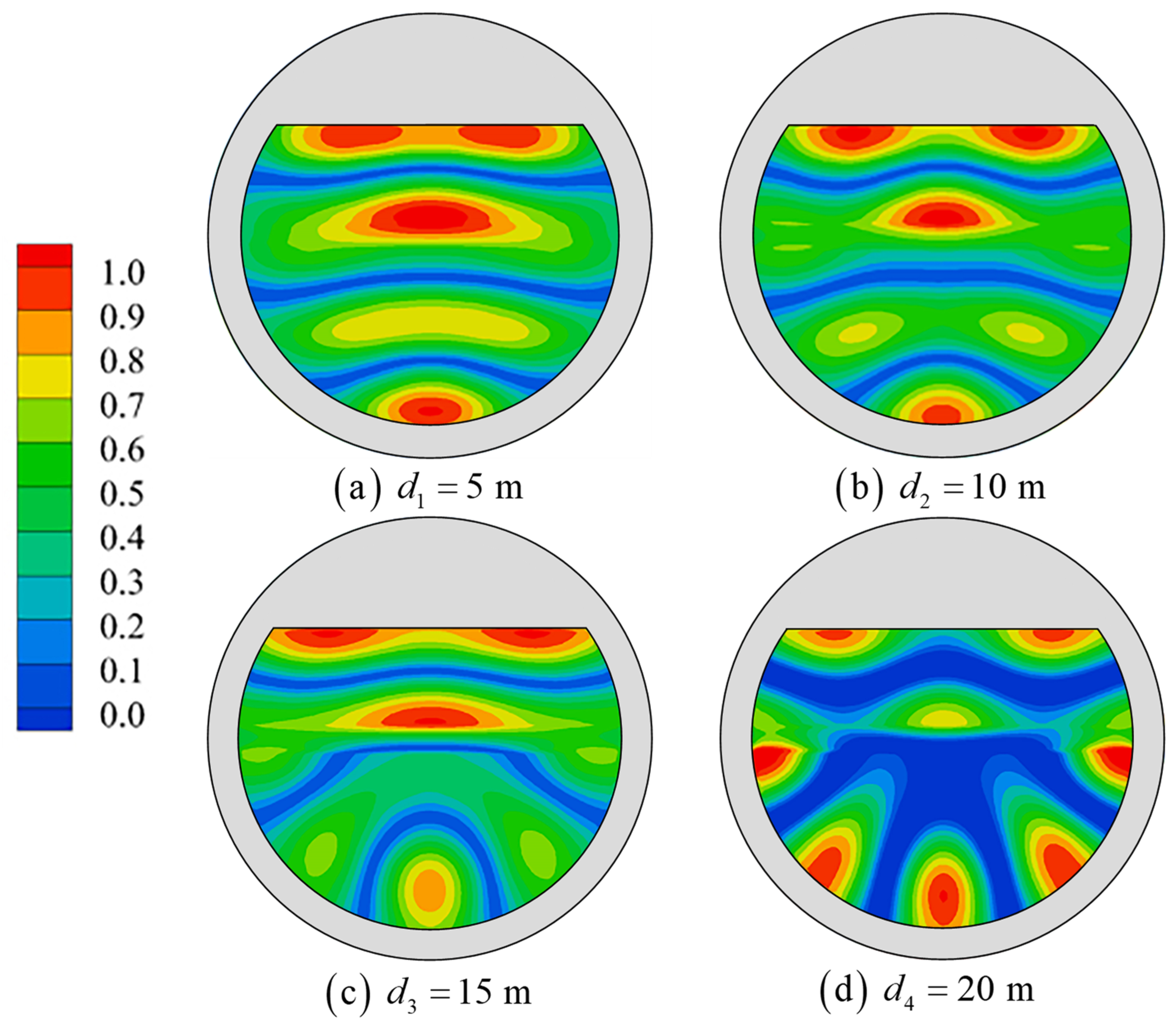
5. Analysis of Resonance Influencing Factors
- (a)
- Influence of the platform’s wall thickness
- (b)
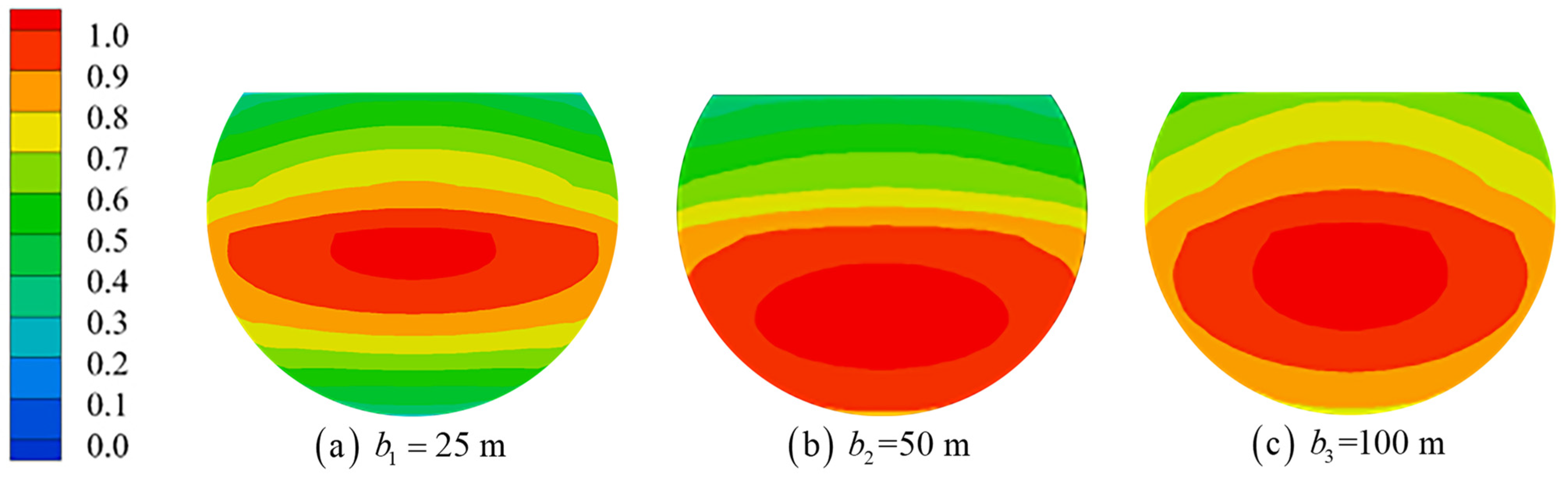
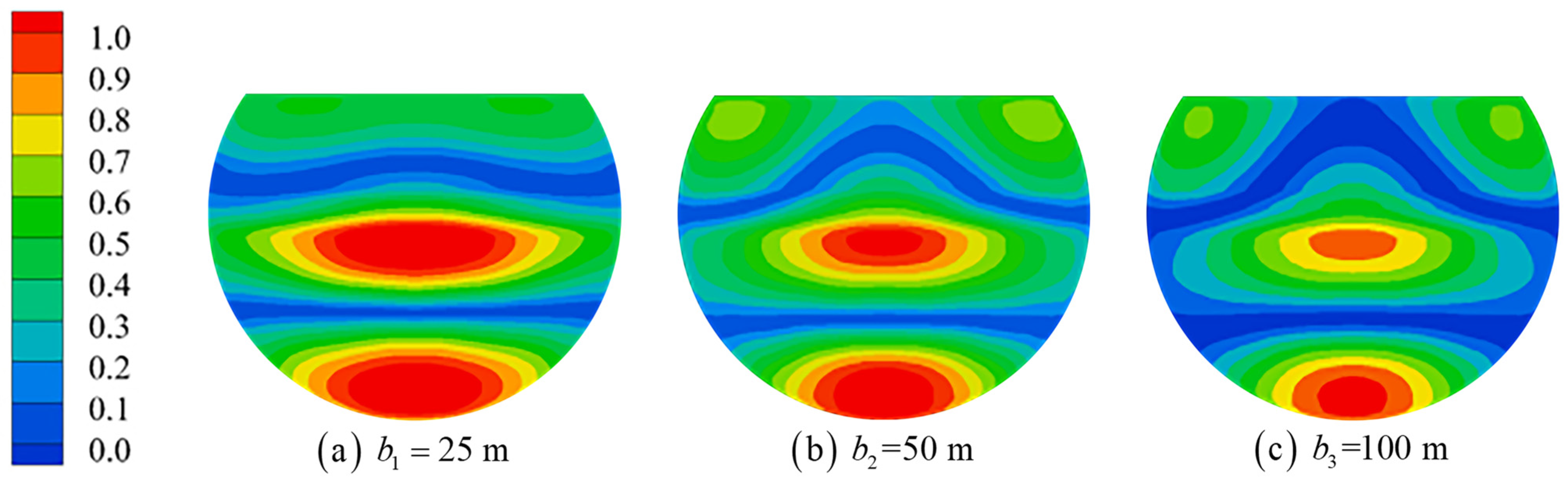
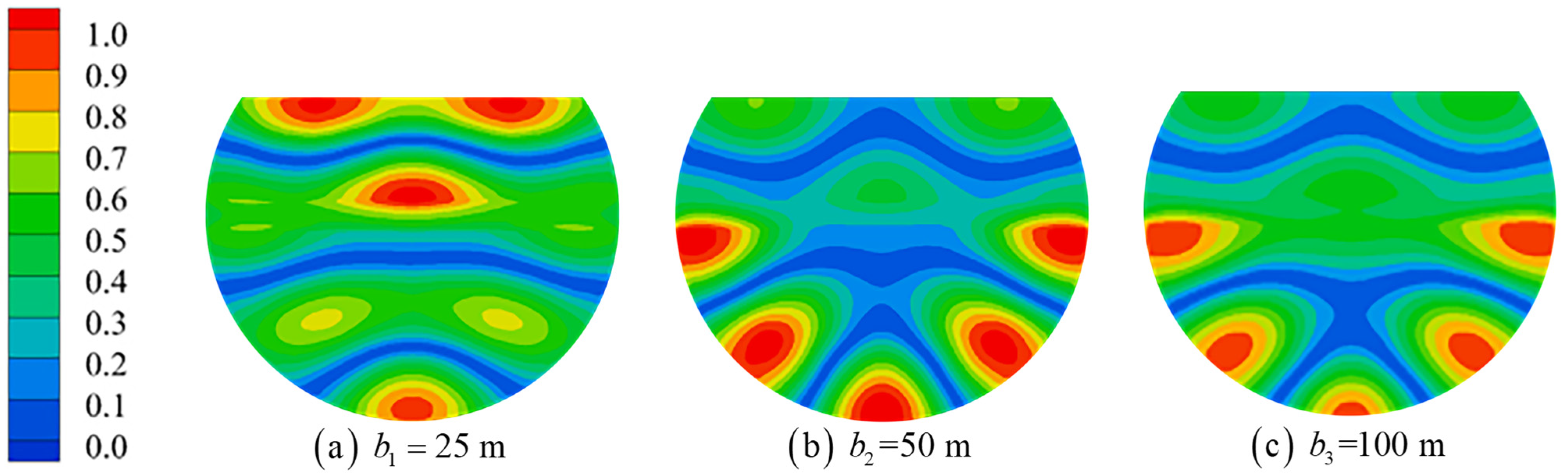
- Influence of the platform chord distance
- (c)
- Influence of platform drafts
6. Conclusions
- The floating tourist platform has six resonant modes, one piston mode, and five sloshing modes, in which higher-order sloshing modes exist. All resonant modes have an , and the resonance is most obvious when the wave frequency is , and the second-order sloshing mode (M3) is .
- For a large floating tourist platform, its resonant response is characterized by a wide range of resonant frequency distributions, the piston mode needs to be excited by long-period waves, and the wobble mode can be excited by waves of common frequency in ocean engineering. The largest wave surface elevation among the modes is the second-order sloshing mode, not the piston mode, which differs from the moonpool and harbor oscillations.
- The wall thickness, chordal distance and draft increase of the floating tourist platform will cause the resonant frequency of each mode to move in the low-frequency direction. The effects on wave surface elevation are different because of the different mechanisms of action of the three, but the effects on the higher-order sloshing modes are greater.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ravinthrakumar, S.; Kristiansen, T.; Molin, B.; Ommani, B. Coupled vessel and moonpool responses in regular and irregular waves. Appl. Ocean. Res. 2020, 96, 102010. [Google Scholar] [CrossRef]
- Molin, B.; Zhang, X.; Huang, H.; Remy, F. On natural modes in moonpools and gaps in finite depth. J. Fluid Mech. 2018, 840, 530–554. [Google Scholar] [CrossRef]
- Molin, B. On the piston and sloshing modes in moonpools. J. Fluid Mech. 2001, 430, 27–50. [Google Scholar] [CrossRef]
- Aalbers, A. The water motions in a moonpool. Ocean Eng. 1984, 11, 557–579. [Google Scholar] [CrossRef]
- Faltinsen, O.M.; Rognebakke, O.F.; Timokha, A.N. Two-dimensional resonant piston-like sloshing in a moonpool. J. Fluid Mech. 2007, 575, 359–397. [Google Scholar] [CrossRef]
- Ravinthrakumar, S.; Kristiansen, T.; Molin, B.; Ommani, B. A two-dimensional numerical and experimental study of piston and sloshing resonance in moonpools with recess. J. Fluid Mech. 2019, 877, 142–166. [Google Scholar] [CrossRef]
- Price, W.G.; Magee, A.; Feng, A. Experimental and Numerical Study for Drillship Moonpool Gap Resonances in Stationary and Transit Conditions in Wave Flume. J. Offshore Mech. Arct. Eng. 2020, 142, 021205. [Google Scholar] [CrossRef]
- Xu, X.; Zhang, X.; Chu, B.; Huang, H. On natural frequencies of three-dimensional moonpool of vessels in the fixed and free-floating conditions. Ocean Eng. 2020, 195, 106656. [Google Scholar] [CrossRef]
- Casulli, V.; Stelling, G.S. Numerical simulation of 3D quasi-hydrostatic, free-surface flows. J. Hydraul. Eng. 1998, 124, 678–686. [Google Scholar] [CrossRef]
- Stansby, P.; Zhou, J. Shallow-water flow solver with non-hydrostatic pressure: 2D vertical plane problems. Int. J. Numer. Methods Fluids 1998, 28, 541–563. [Google Scholar] [CrossRef]
- Ai, C.; Jin, S.; Lv, B. A new fully non-hydrostatic 3D free surface flow model for water wave motions. Int. J. Numer. Methods Fluids 2011, 66, 1354–1370. [Google Scholar] [CrossRef]
- Ai, C.; Ding, W.; Jin, S. A general boundary-fitted 3D non-hydrostatic model for nonlinear focusing wave groups. Ocean Eng. 2014, 89, 134–145. [Google Scholar] [CrossRef]
- Ai, C.; Ma, Y.; Yuan, C.; Dong, G. Development and assessment of semi-implicit nonhydrostatic models for surface water waves. Ocean Model. 2019, 144, 101489. [Google Scholar] [CrossRef]
- Ma, G.; Shi, F.; Kirby, J.T. Shock-capturing non-hydrostatic model for fully dispersive surface wave processes. Ocean Model. 2012, 43–44, 22–35. [Google Scholar] [CrossRef]
- Zijlema, M.; Stelling, G.; Smit, P. SWASH: An operational public domain code for simulating wave fields and rapidly varied flows in coastal waters. Coast. Eng. 2011, 58, 992–1012. [Google Scholar] [CrossRef]
- Ai, C.; Jin, S. A multi-layer non-hydrostatic model for wave breaking and run-up. Coast. Eng. 2012, 62, 1–8. [Google Scholar] [CrossRef]
- Smit, P.; Zijlema, M.; Stelling, G. Depth-induced wave breaking in a non-hydrostatic, near-shore wave model. Coast. Eng. 2013, 76, 1–16. [Google Scholar] [CrossRef]
- Yamazaki, Y.; Kowalik, Z.; Cheung, K.F. Depth-integrated, non-hydrostatic model for wave breaking and run-up. Int. J. Numer. Methods Fluids 2009, 61, 473–497. [Google Scholar] [CrossRef]
- Ai, C.; Jin, S. Non-hydrostatic finite volume model for non-linear waves interacting with structures. Comput. Fluids 2010, 39, 2090–2100. [Google Scholar] [CrossRef]
- Ai, C.; Ma, Y.; Yuan, C.; Dong, G. A 3D non-hydrostatic model for wave interactions with structures using immersed boundary method. Comput. Fluids 2019, 186, 24–37. [Google Scholar] [CrossRef]
- Ai, C.; Ma, Y.; Yuan, C.; Xie, Z.; Dong, G.; Stoesser, T. An efficient 3D non-hydrostatic model for predicting nonlinear wave interactions with fixed floating structures. Ocean Eng. 2022, 248, 110810. [Google Scholar] [CrossRef]
- Ai, C.; Ma, Y.; Yuan, C.; Xie, Z.; Dong, G.; Stoesser, T. Vortex shedding and evolution induced by the interactions between a solitary wave and a submerged horizontal plate. J. Hydraul. Res. 2022, 60, 311–325. [Google Scholar] [CrossRef]
- Wu, C.H.; Yuan, H. Efficient non-hydrostatic modelling of surface waves interacting with structures. Appl. Math. Model. 2007, 31, 687–699. [Google Scholar] [CrossRef]
- Li, C.W.; Zhang, M.L. 3D modelling of hydrodynamics and mixing in a vegetation field under waves. Comput. Fluids 2010, 39, 604–614. [Google Scholar] [CrossRef]
- Ma, G.; Kirby, J.T.; Su, S.-F.; Figlus, J.; Shi, F. Numerical study of turbulence and wave damping induced by vegetation canopies. Coast. Eng. 2013, 80, 68–78. [Google Scholar] [CrossRef]
- Yamazaki, Y.; Cheung, K.F.; Kowalik, Z. Depth-integrated, non-hydrostatic model with grid nesting for tsunami generation, propagation, and run-up. Int. J. Numer. Methods Fluids 2011, 67, 2081–2107. [Google Scholar] [CrossRef]
- Ai, C.; Ma, Y.; Yuan, C.; Dong, G. Semi-implicit non-hydrostatic model for 2D nonlinear wave interaction with a floating/suspended structure. Eur. J. Mech.-B/Fluids 2018, 72, 545–560. [Google Scholar] [CrossRef]
- Ma, G.; Farahani, A.A.; Kirby, J.T.; Shi, F. Modeling wave-structure interactions by an immersed boundary method in a σ-coordinate model. Ocean Eng. 2016, 125, 238–247. [Google Scholar] [CrossRef]
- Zijlema, M.; Stelling, G.S. Further experiences with computing non-hydrostatic free-surface flows involving water waves. Int. J. Numer. Methods Fluids 2005, 48, 169–197. [Google Scholar] [CrossRef]
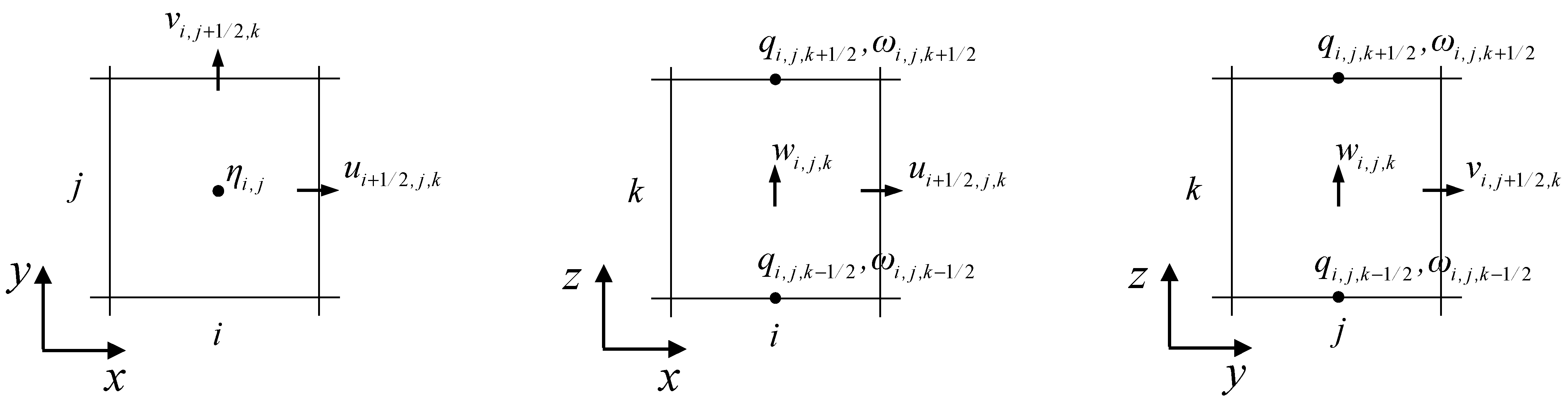
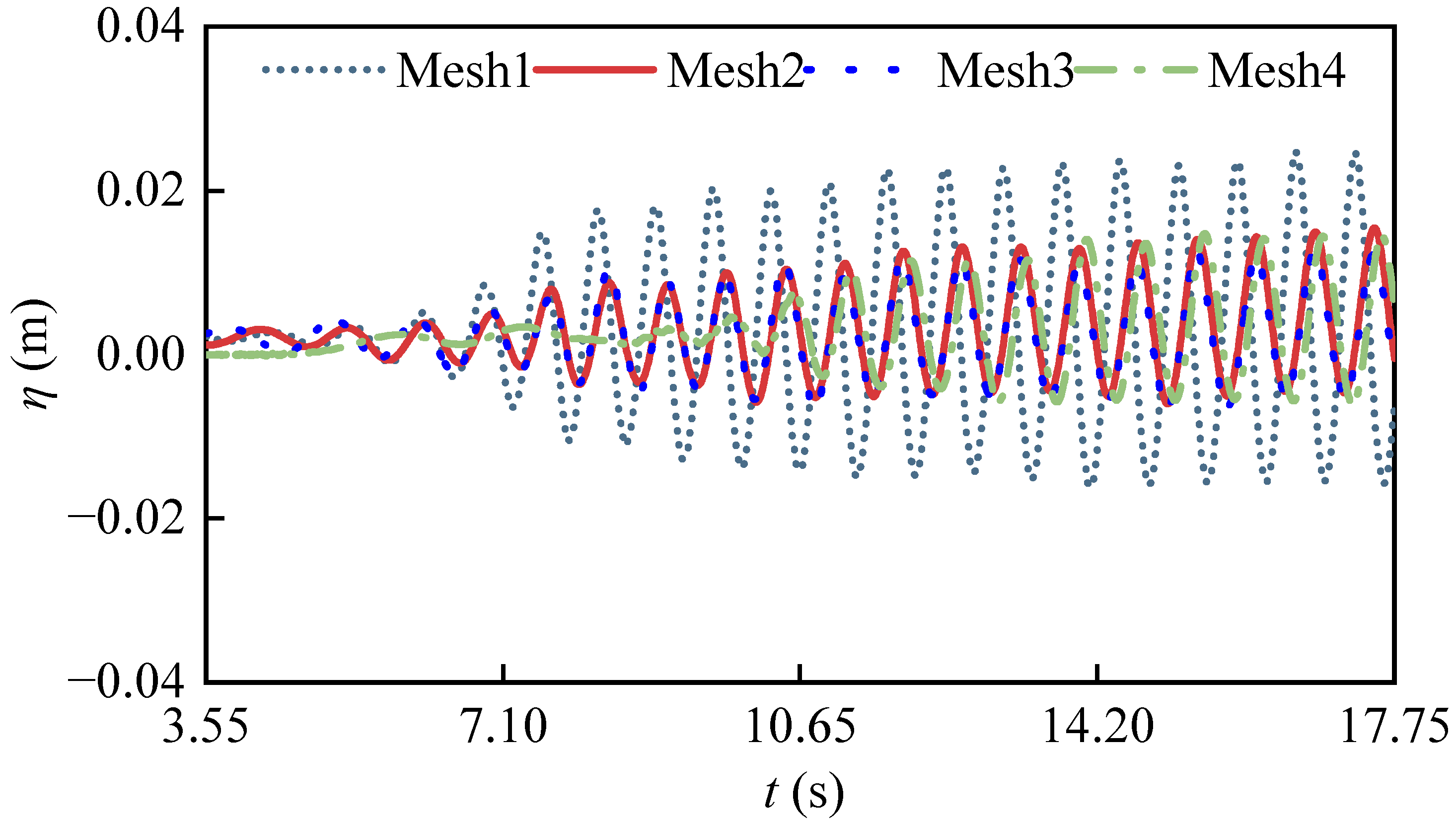



| Mesh | Mesh1 | Mesh2 | Mesh3 | Mesh4 |
|---|---|---|---|---|
| 0.02 | 0.01 | 0.01 | 0.005 | |
| 24 | 24 | 28 | 24 | |
| −0.16 | −0.16 | −0.16 | −0.16 | |
| used in the vertical grid system | 12 | 12 | 12 | 12 |
| Mode | Period (s) | RWH | |
|---|---|---|---|
| M1 | 0.217 | 28.95 | 1.50 |
| M2 | 0.364 | 17.26 | 2.15 |
| M3 | 0.500 | 12.57 | 2.75 |
| M4 | 0.531 | 11.83 | 1.98 |
| M5 | 0.581 | 10.81 | 1.90 |
| M6 | 0.613 | 10.25 | 2.22 |
| M7 | 0.693 | 9.07 | 1.00 |
| M8 | 0.757 | 8.30 | 0.80 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Z.; Mao, Y.; Ding, J.; Tian, C.; Wang, S.; Ai, C.; Ma, X.; Dong, G. Analysis of Water Resonance in the Inner Domain of a Large Fixed Floating Tourist Platform Based on a 3D Non-Hydrostatic Model. J. Mar. Sci. Eng. 2023, 11, 649. https://doi.org/10.3390/jmse11030649
Liu Z, Mao Y, Ding J, Tian C, Wang S, Ai C, Ma X, Dong G. Analysis of Water Resonance in the Inner Domain of a Large Fixed Floating Tourist Platform Based on a 3D Non-Hydrostatic Model. Journal of Marine Science and Engineering. 2023; 11(3):649. https://doi.org/10.3390/jmse11030649
Chicago/Turabian StyleLiu, Zhiqiang, Yanjun Mao, Jun Ding, Chao Tian, Siyu Wang, Congfang Ai, Xiaozhou Ma, and Guohai Dong. 2023. "Analysis of Water Resonance in the Inner Domain of a Large Fixed Floating Tourist Platform Based on a 3D Non-Hydrostatic Model" Journal of Marine Science and Engineering 11, no. 3: 649. https://doi.org/10.3390/jmse11030649
APA StyleLiu, Z., Mao, Y., Ding, J., Tian, C., Wang, S., Ai, C., Ma, X., & Dong, G. (2023). Analysis of Water Resonance in the Inner Domain of a Large Fixed Floating Tourist Platform Based on a 3D Non-Hydrostatic Model. Journal of Marine Science and Engineering, 11(3), 649. https://doi.org/10.3390/jmse11030649






