Experimental Study of the Hydrodynamic Characteristics of a Submerged Floating Tunnel under Freak Wave (II: Time-Frequency Domain Study)
Abstract
1. Introduction
2. Experiments
2.1. Experimental Equipment and Instruments
2.2. Model Parameters and Layout
2.3. Experimental Parameters and Methods
2.3.1. Experimental Parameters
2.3.2. Experimental Method
2.3.3. Wavelet Analysis Method
3. Results and Discussions
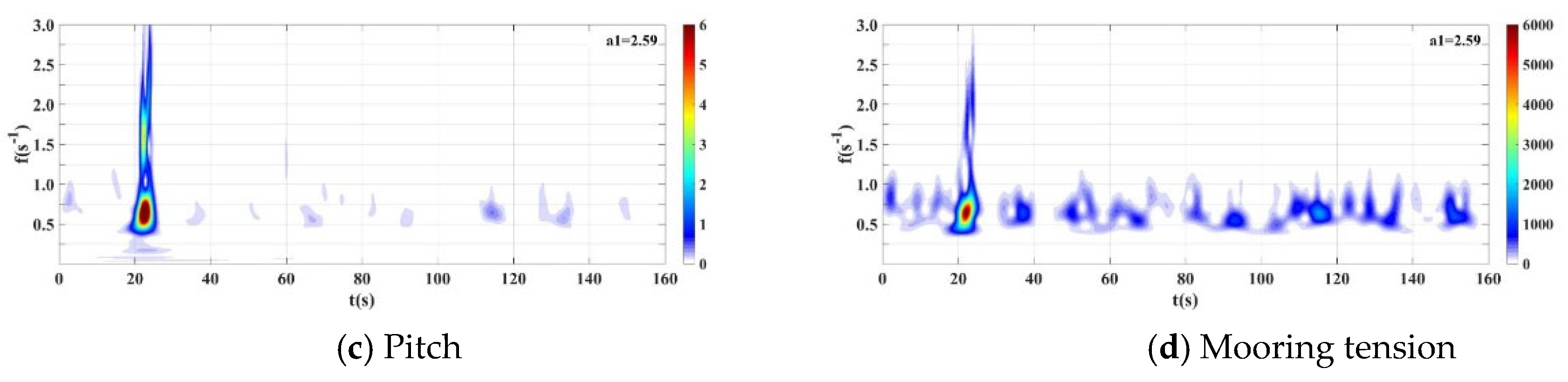
3.1. Time-Frequency Spectra Characteristics of Dynamic Response
3.2. Time-Frequency Structure Analysis of Dynamic Response
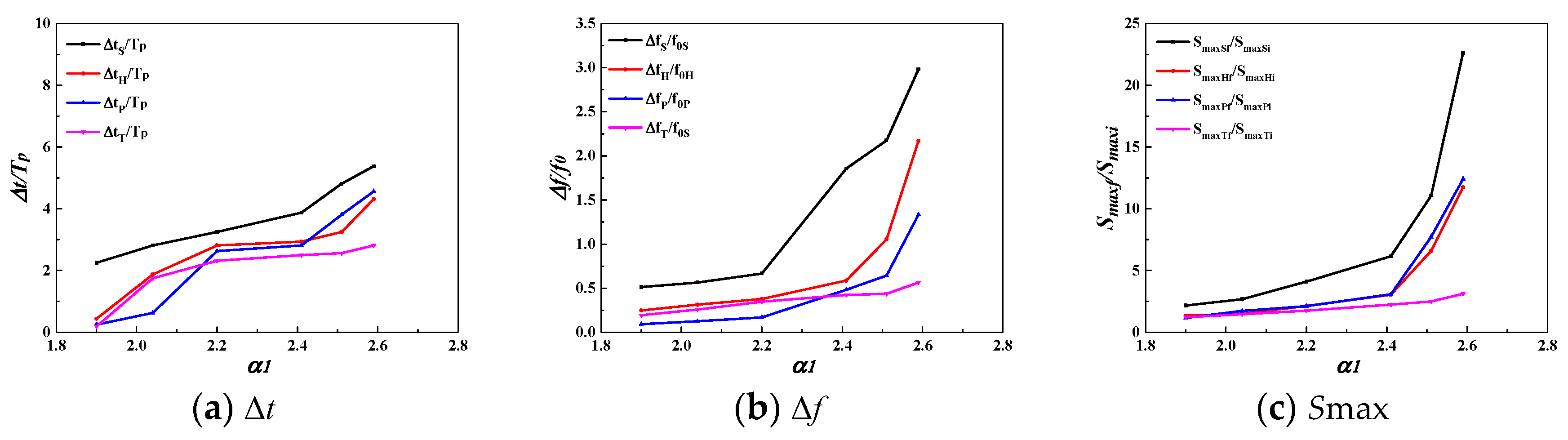
3.2.1. Time-Frequency Spectrum Parameter Analysis
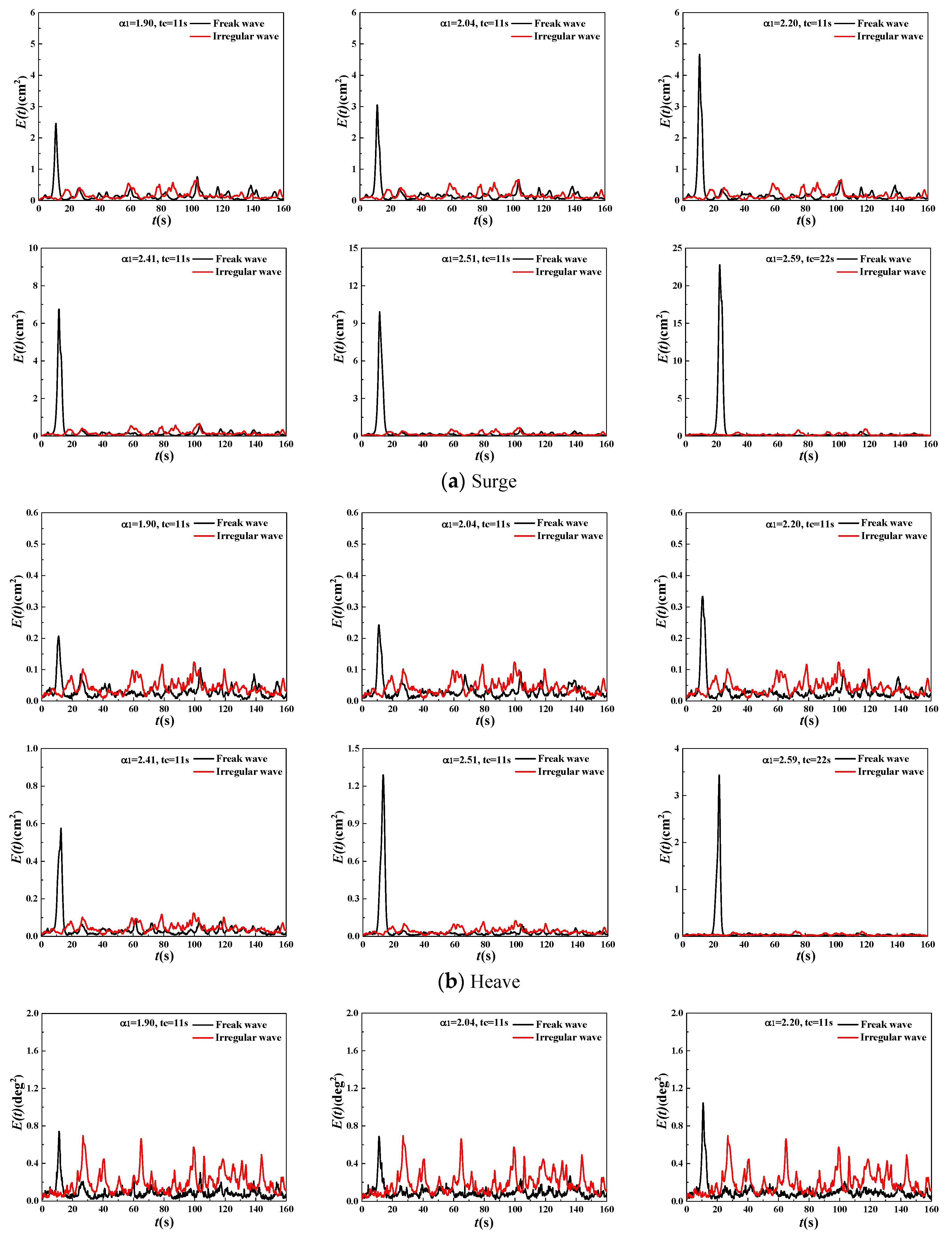
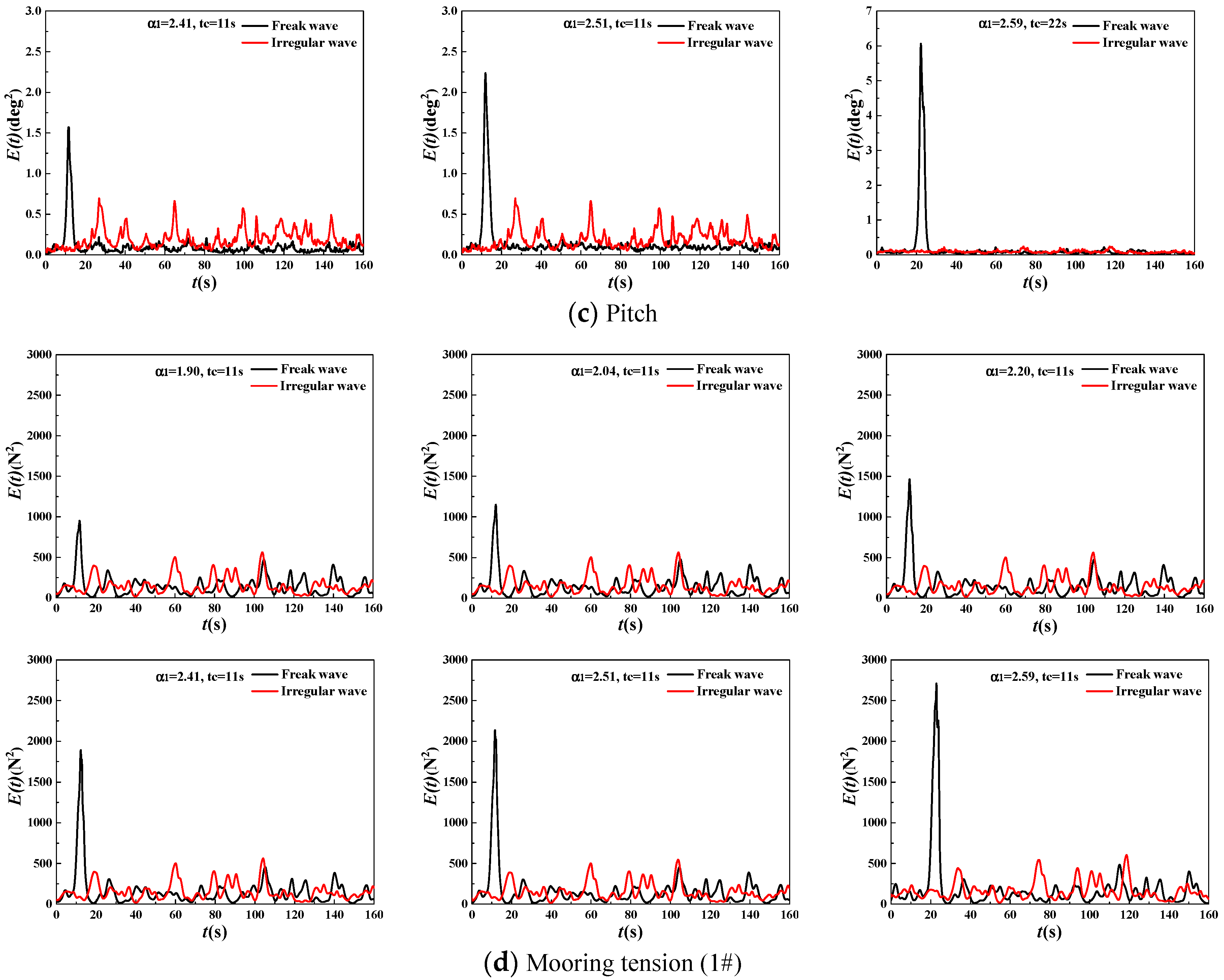
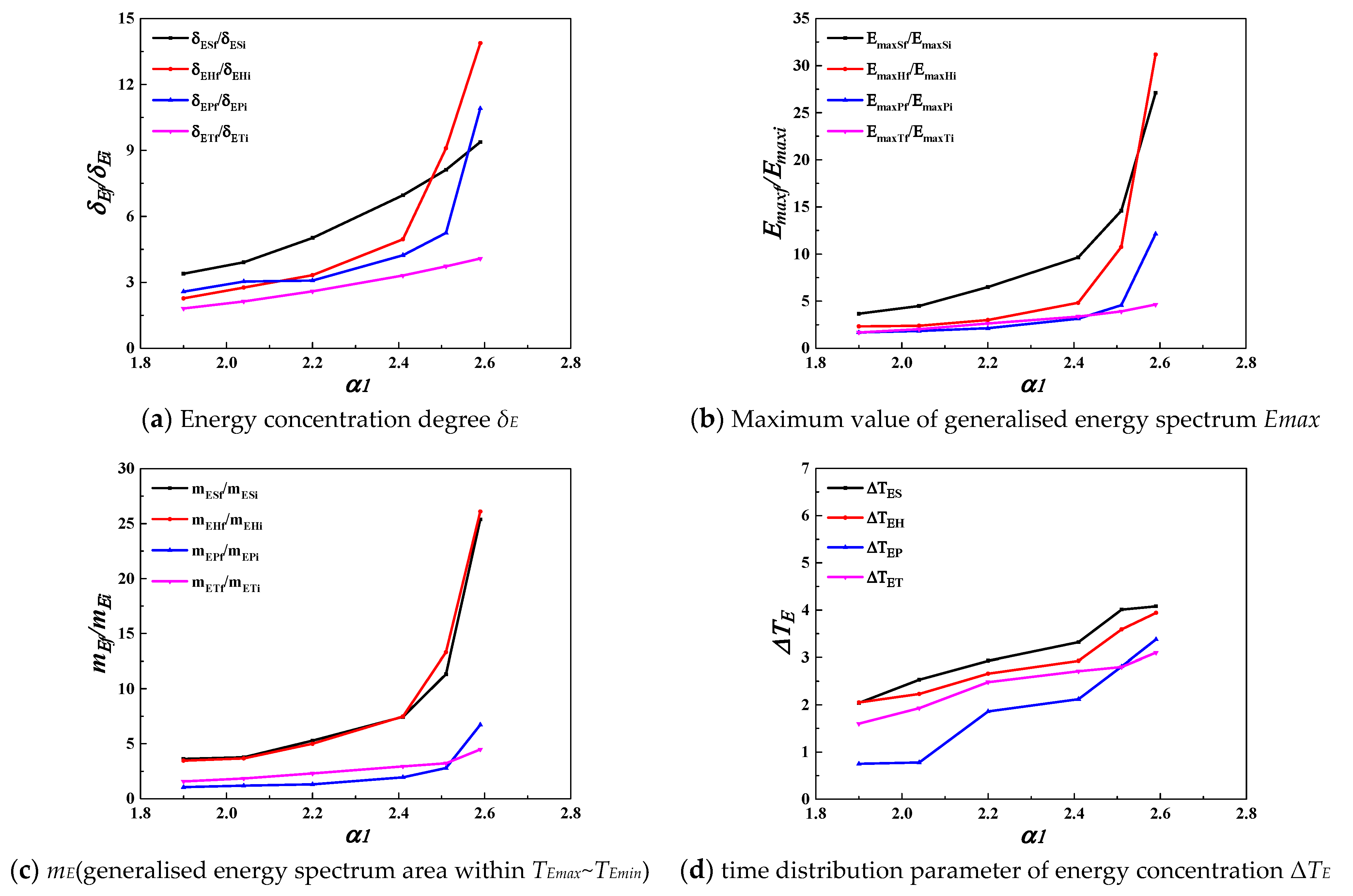
3.2.2. Generalized Energy Spectrum and Spectral Parameter Analysis
- (1)
- Basic characteristics of the generalized energy spectrum
- (2)
- Generalised energy spectrum parameters
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kharif, C.; Pelinovsky, E. Physical mechanisms of the rogue wave phenomenon. Eur. J. Mech. B Fluids 2003, 22, 603–634. [Google Scholar] [CrossRef]
- Kimura, A.; Ohta, T. Probability of the freak wave appearance in a 3-dimensional sea condition. In Proceedings of the 24th International Conference on Coastal Engineering, Kobe, Japan, 23–28 October 1994; Part 1 (of 3). ASCE: New York, NY, USA; Kobe, Japan, 1995; pp. 356–369, ISBN 08938717. [Google Scholar]
- Fochesato, C.; Grilli, S.; Dias, F. Numerical modeling of extreme rogue waves generated by directional energy focusing. Wave Mot. 2007, 44, 395–416. [Google Scholar] [CrossRef]
- Pelinovsky, E.; Talipova, T.; Kharif, C. Nonlinear-dispersive mechanism of the freak wave formation in shallow water. Phys. D Nonlinear Phenom. 2000, 147, 83–94. [Google Scholar] [CrossRef]
- Cui, C.; Pan, W.-B. Experimental Study on the Wavelengths of Two-Dimensional and Three-Dimensional Freak Waves. China Ocean Eng. 2023, 37, 154–164. [Google Scholar] [CrossRef]
- Gibson, R.S.; Swan, C. The evolution of large ocean waves: The role of local and rapid spectral changes. Proc. R. Soc. A Math. Phys. Eng. Sci. 2007, 463, 21–48. [Google Scholar] [CrossRef]
- Akhmediev, N.; Ankiewicz, A.; Soto-Crespo, J.M.; Dudley, J.M. Rogue wave early warning through spectral measurements? Phys. Lett. Sect. A Gen. Solid State Phys. 2011, 375, 541–544. [Google Scholar] [CrossRef]
- Clauss, G.F.; Schmittner, C.E.; Stutz, K. Freak wave impact on semisubmersibles-time-domain analysis of motions and forces. In Proceedings of the 13th International Offshore and Polar Engineering Conference, Honolulu, HI, USA, 25–30 May 2003; International Society of Offshore and Polar Engineers: Honolulu, HI, USA, 2003. [Google Scholar]
- Rudman, M.; Leontini, J.; Cleary, P.; Sinnott, M.; Prakash, M. Rogue wave impact on a semi-submersible offshore platform. In Proceedings of the 27th International Conference on Offshore Mechanics and Arctic Engineering, OMAE 2008, Estoril, Portugal, 15–20 June 2008; OMAE: Estoril, Portugal, 2008; pp. 887–894, ISBN 9780791848227. [Google Scholar]
- Paul, P.W.; Rudman, M. Extreme wave interaction with a floating oil rig: Prediction using SPH. Prog. Comput. Fluid Dyn. 2009, 9, 332–344. [Google Scholar]
- Rudman, M.; Cleary, P.W. Rogue wave impact on a tension leg platform: The effect of wave incidence angle and mooring Line tension. Ocean Eng. 2013, 61, 123–138. [Google Scholar] [CrossRef]
- Bennett, S.S.; Hudson, D.A.; Temarel, P. The influence of forward speed on ship motions in abnormal waves: Experimental measurements and numerical predictions. J. Fluids Struct. 2013, 39, 154–172. [Google Scholar] [CrossRef]
- Pan, W.; Zhang, N.; Huang, G.; Ma, X. Experimental study on motion responses of a moored rectangular cylinder under freak waves (I: Time-domain study). Ocean Eng. 2018, 153, 268–281. [Google Scholar] [CrossRef]
- Shen, Y.G.; Yang, J.M.; Li, X. Numerical investigation on the motion response of semisubmersible platform under extreme waves. Ocean. Eng. 2013, 31, 9–17. (In Chinese) [Google Scholar]
- Chandrasekaran, S.; Koshti, Y. Dynamic analysis of a tension Leg platform under extreme waves. J. Nav. Archit. Mar.Eng. 2013, 10, 59–68. [Google Scholar] [CrossRef]
- Pan, W.; Liang, C.; Zhang, N.; Huang, G. Experimental study on hydrodynamic characteristics of a moored square cylinder under freak wave (II: Frequency-domain study). Ocean Eng. 2021, 219, 108452. [Google Scholar] [CrossRef]
- Pan, W.; Zhang, N.; Zeng, F.; Huang, G. Time-frequency domain characteristics on the dynamic response of a moored floater under a freak wave by wavelet analysis. Int. J. Offshore Polar Eng. 2021, 31, 160–168. [Google Scholar] [CrossRef]
- Klinting, P.; Sand, S. Analysis of prototype freak waves. In Coastal Hydrodynamic; ASCE: New York, NY, USA, 1987; pp. 618–632. [Google Scholar]
- Pei, Y.G. The Generation of Freak Waves and Its Behaviors; Dalian University of Technology: Dalian, China, 2008. [Google Scholar]
- Abroug, I.; Abcha, N.; Jarno, A.; Marin, F. Laboratory study of non-linear wave-wave interactions of extreme focused waves in the nearshore zone. Nat. Hazards Earth Syst. Sci. 2020, 20, 3279–3291. [Google Scholar] [CrossRef]
- Gao, J.; Ma, X.; Zang, J.; Dong, G.; Zhu, Y.; Zhou, L. Numerical investigation of harbor oscillations induced by focused transient wave groups. Coast. Eng. 2020, 158, 103670. [Google Scholar] [CrossRef]
- Cui, C.; Zhang, N.C.; Yu, Y.X.; Li, J.B. Numerical study on the effects of uneven bottom topography on freak waves. Ocean Eng. 2012, 54, 132–141. [Google Scholar] [CrossRef]
- Grinsted, A.; Moore, J.C.; Jevrejeva, S. Application of the cross wavelet transform and wavelet coherence to geophysical time series. Nonlinear Process. Geophys. 2004, 11, 561–566. [Google Scholar] [CrossRef]
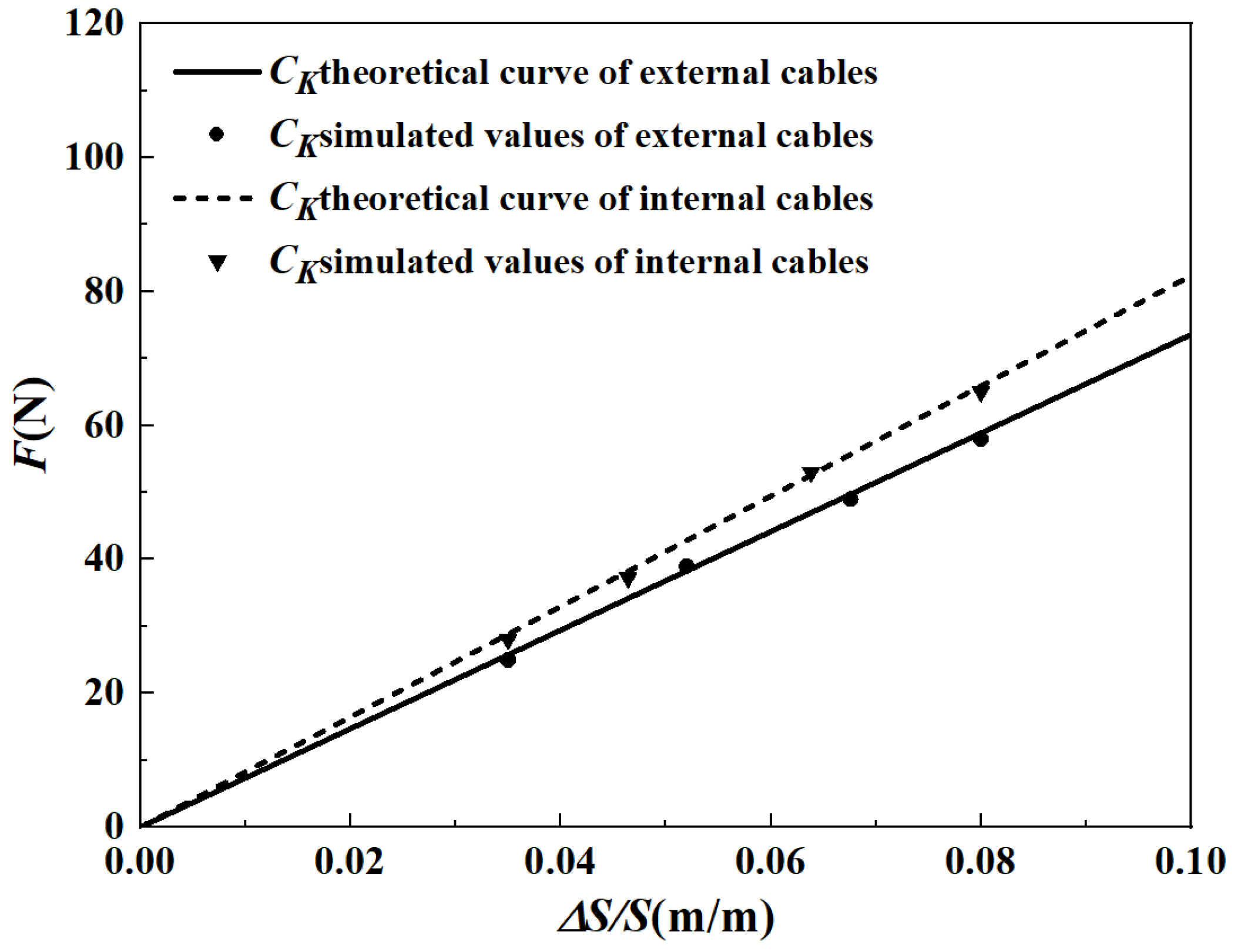



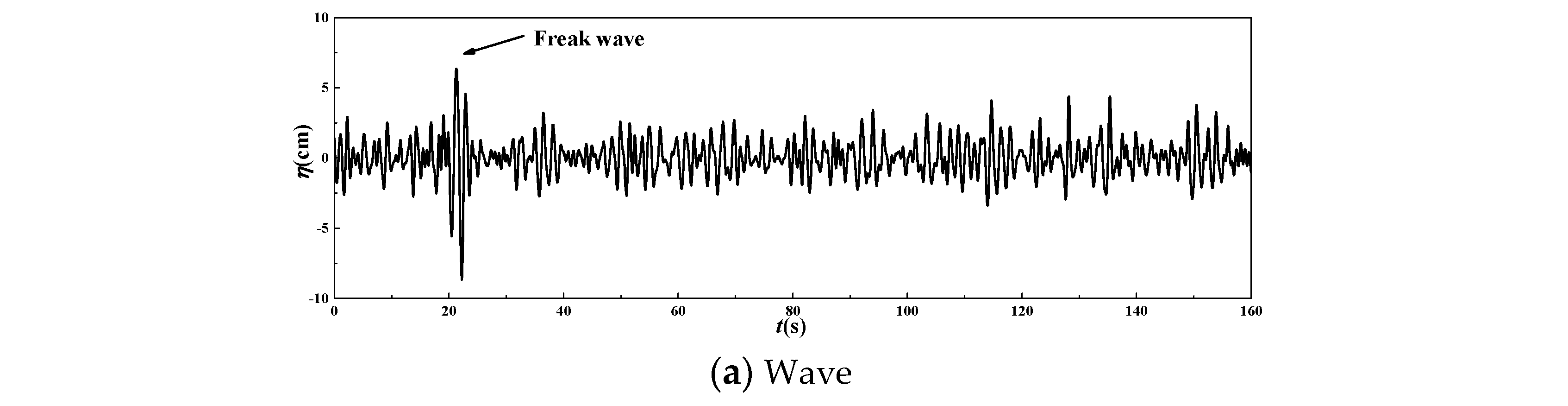
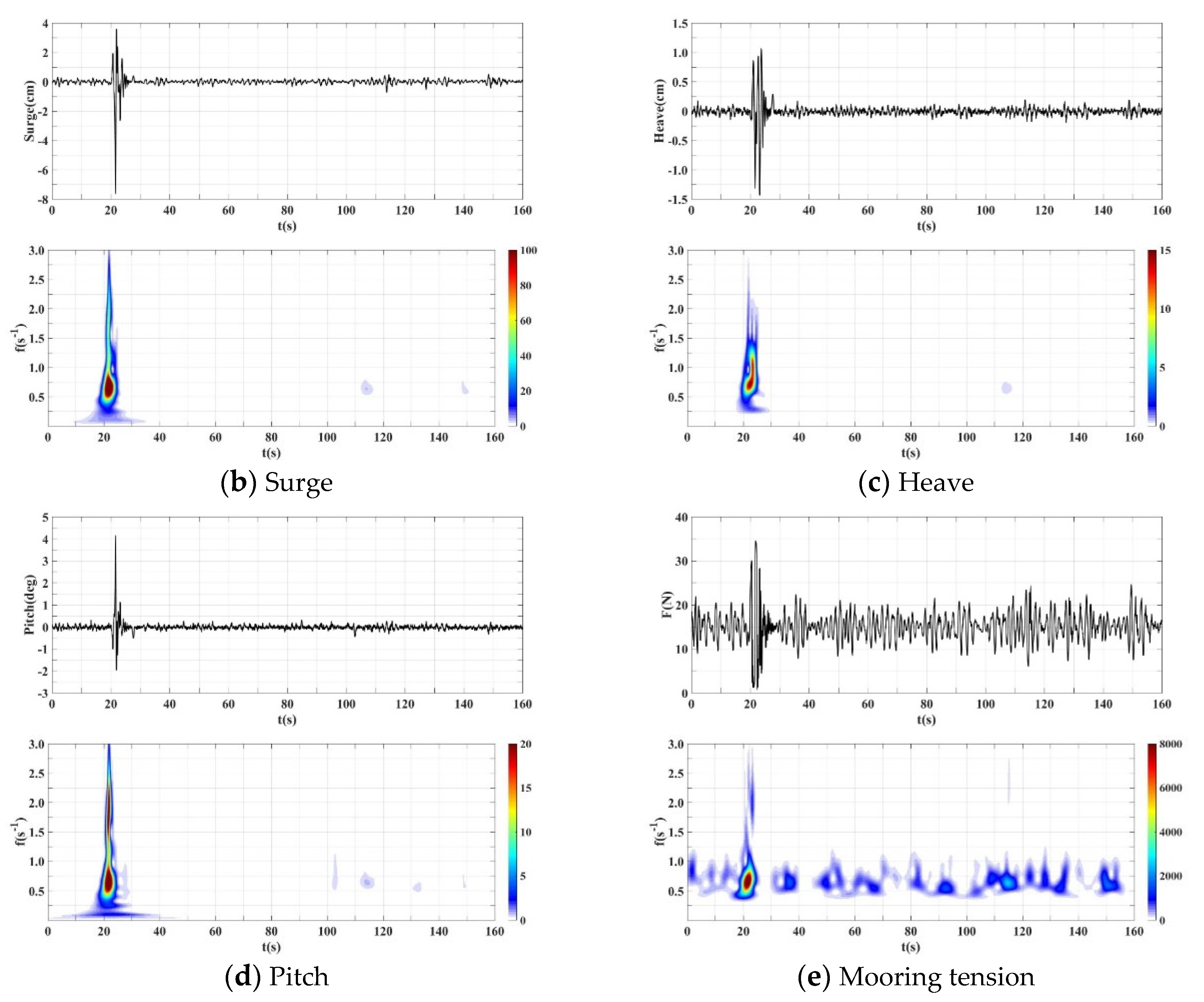

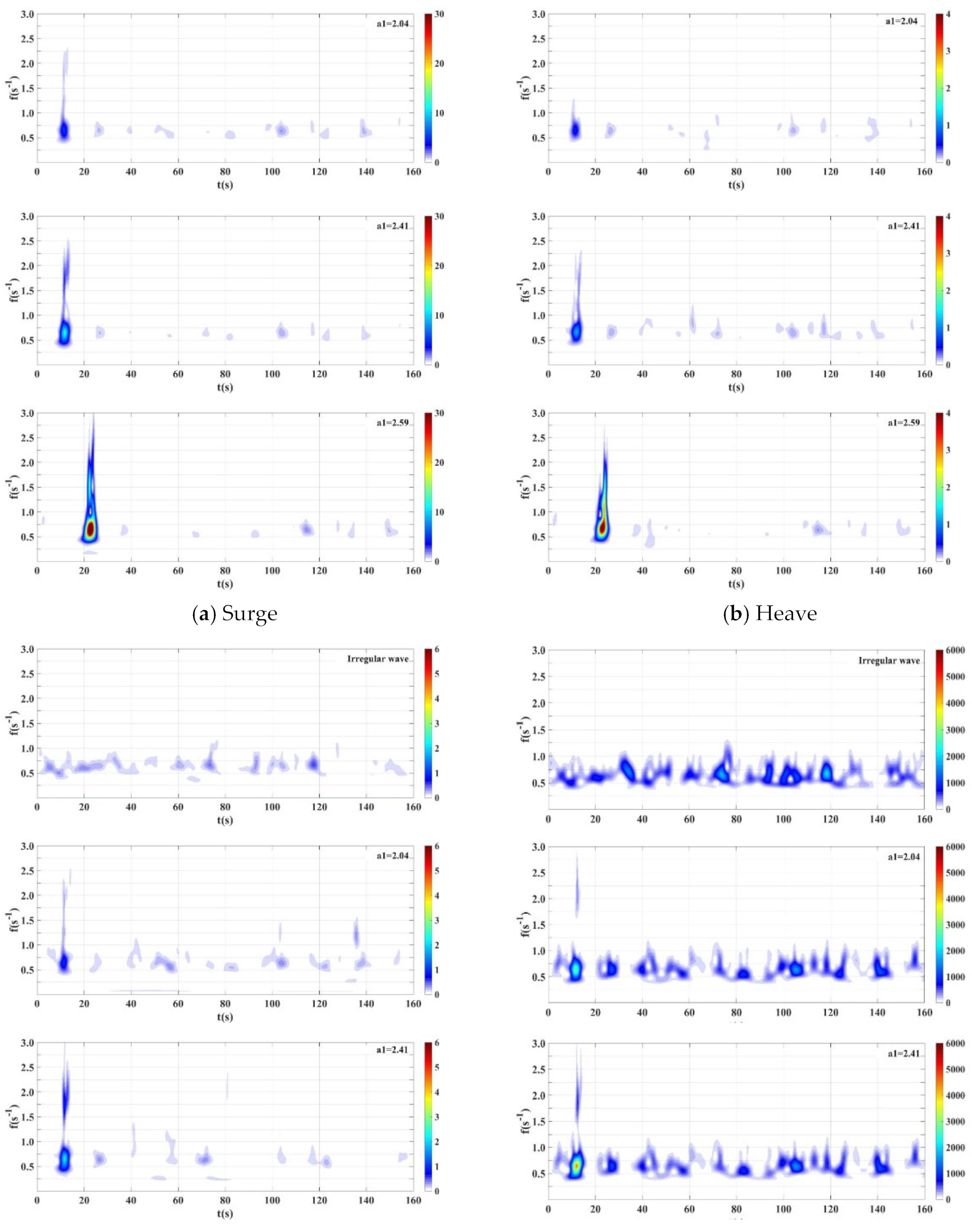
| Parameters | Symbols | Prototype | Unit | Model | Unit |
|---|---|---|---|---|---|
| Length | L | 120.0 | m | 200.0 | cm |
| Diameter | D | 12.0 | m | 20.0 | cm |
| Mass | M | 11232 | t | 52.0 | kg |
| Center of gravity | B | 9.6 | m | 16.0 | cm |
| Center of buoyancy | b0 | 12.0 | m | 10.0 | cm |
| Natural surge period | T0S | 9.90 | s | 1.29 | s |
| Natural heave period | T0H | 10.10 | s | 1.31 | s |
| Natural pitch period | T0P | 4.18 | s | 0.55 | s |
| Buoyancy weight ratio | BWR | 1.20 | - | 1.20 | - |
| Fixed Parameters | H (cm) | T (s) | Wave Length L (m) | Relative Submerged Depth d0/L |
|---|---|---|---|---|
| d = 120 cm d0 = 42 cm d0/d = 0.35 F0 = 13 N | 4.0 | 0.8 | 0.99 | 0.360 |
| 1.0 | 1.56 | 0.231 | ||
| 1.2 | 2.24 | 0.161 | ||
| 1.4 | 3.02 | 0.119 | ||
| 1.6 | 3.84 | 0.094 | ||
| 1.8 | 4.67 | 0.077 | ||
| 2.0 | 5.49 | 0.066 |
| Fixed Parameters | Hs (cm) | TP (s) | Relative Wave Height | Relative Wave Period | Relative Submerged Depth d0/LP | α1 | |||
|---|---|---|---|---|---|---|---|---|---|
| Hs/d | Hs/d0 | TP/T0S | TP/T0H | TP/T0P | |||||
| d = 120 cm d0 = 42 cm d0/d = 0.35 F0 = 13 N | 4.0 | 1.6 | 0.033 | 0.095 | 1.25 | 1.23 | 2.96 | 0.109 | 1.90 |
| 2.04 | |||||||||
| 2.20 | |||||||||
| 2.41 | |||||||||
| 2.51 | |||||||||
| 2.59 | |||||||||
| HS (cm) | TP (s) | HS/d | TP/T0S | α1 | The Time Range for Large Value of Time-Frequency Spectrum | The Frequency Range for Large Value of Time-Frequency Spectrum | The Peak Value of Time-Frequency Spectrum (cm2) | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| t (s) | ∆t (s) | f (Hz) | ∆f (Hz) | Freak Wave | Random Wave | Ratio | |||||
| 4.0 | 1.6 | 0.033 | 1.25 | 1.90 | 9.7~13.3 | 3.6 | 0.48~0.88 | 0.40 | 3.74 | 1.73 | 2.16 |
| 2.04 | 9.6~14.1 | 4.5 | 0.46~0.90 | 0.44 | 5.10 | 1.90 | 2.68 | ||||
| 2.20 | 8.5~13.7 | 5.2 | 0.42~0.98 | 0.52 | 7.68 | 1.88 | 4.09 | ||||
| 2.41 | 8.6~14.8 | 6.2 | 0.38~1.02/1.31~2.12 | 1.45 | 11.46 | 1.86 | 6.16 | ||||
| 2.51 | 8.5~16.2 | 7.7 | 0.37~2.07 | 1.70 | 21.12 | 1.91 | 11.06 | ||||
| 2.59 | 18.3~26.9 | 8.6 | 0.36~2.69 | 2.33 | 42.76 | 1.89 | 22.62 | ||||
| HS (cm) | TP (s) | HS/d | TP/T0S | α1 | The time Range for Large Value of Time-Frequency Spectrum | The Frequency Range for Large Value of Time-Frequency Spectrum | The Peak Value of Time-Frequency Spectrum (cm2) | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| t (s) | ∆t (s) | f (Hz) | ∆f (Hz) | Freak Wave | Random Wave | Ratio | |||||
| 4.0 | 1.6 | 0.033 | 1.23 | 1.90 | 10.2~12.9 | 0.7 | 0.59~0.78 | 0.19 | 0.48 | 0.36 | 1.33 |
| 2.04 | 10.2~13.2 | 3.0 | 0.55~0.79 | 0.24 | 0.58 | 0.39 | 1.49 | ||||
| 2.20 | 9.1~13.6 | 4.5 | 0.52~0.81 | 0.29 | 0.85 | 0.40 | 2.13 | ||||
| 2.41 | 9.8~14.5 | 4.7 | 0.47~0.92 | 0.45 | 1.15 | 0.38 | 3.03 | ||||
| 2.51 | 9.9~15.1 | 5.2 | 0.48~1.29 | 0.81 | 2.70 | 0.41 | 6.59 | ||||
| 2.59 | 19.0~25.9 | 6.9 | 0.40~2.07 | 1.67 | 4.58 | 0.39 | 11.74 | ||||
| HS (cm) | TP (s) | HS/d | TP/T0S | α1 | The Time Range for Large Value of Time-Frequency Spectrum | The Frequency Range for Large Value of Time-Frequency Spectrum | The Peak Value of Time-Frequency Spectrum (cm2) | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| t (s) | ∆t (s) | f (Hz) | ∆f (Hz) | Freak Wave | Random Wave | Ratio | |||||
| 4.0 | 1.6 | 0.033 | 2.96 | 1.90 | 10.2~12.6 | 0.4 | 0.61~0.78 | 0.17 | 0.76 | 0.65 | 1.17 |
| 2.04 | 10.2~12.8 | 0.6 | 0.55~0.78 | 0.23 | 1.22 | 0.71 | 1.72 | ||||
| 2.20 | 8.7~12.9 | 4.2 | 0.49~0.80 | 0.31 | 1.41 | 0.67 | 2.10 | ||||
| 2.41 | 9.6~14.1 | 4.5 | 0.42~0.88/1.55~1.98 | 0.89 | 2.12 | 0.69 | 3.07 | ||||
| 2.51 | 9.6~15.7 | 6.1 | 0.39~0.95/1.35~1.98 | 1.19 | 5.33 | 0.69 | 7.72 | ||||
| 2.59 | 18.6~25.9 | 7.3 | 0.38~2.85 | 2.47 | 8.69 | 0.70 | 12.41 | ||||
| HS (cm) | TP (s) | HS/d | TP/T0S | α1 | The Time Range for Large Value of Time-Frequency Spectrum | The Frequency Range for Large Value of Time-Frequency Spectrum | The Peak Value of Time-Frequency Spectrum (cm2) | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| t (s) | ∆t (s) | f (Hz) | ∆f (Hz) | Freak wave | Random wave | Ratio | |||||
| 4.0 | 1.6 | 0.033 | 1.25 | 1.90 | 10.2~12.5 | 0.3 | 0.55~0.70 | 0.15 | 2437.00 | 1990.31 | 1.22 |
| 2.04 | 10.2~13.0 | 2.8 | 0.54~0.74 | 0.20 | 2844.76 | 1960.63 | 1.45 | ||||
| 2.20 | 9.8~13.5 | 3.7 | 0.51~0.78 | 0.27 | 3443.41 | 1978.33 | 1.74 | ||||
| 2.41 | 10.1~14.1 | 4.0 | 0.47~0.80 | 0.33 | 4396.62 | 1969.57 | 2.23 | ||||
| 2.51 | 9.7~13.8 | 4.1 | 0.47~0.81 | 0.34 | 4892.77 | 1976.15 | 2.48 | ||||
| 2.59 | 19.8~24.3 | 4.5 | 0.44~0.88 | 0.44 | 6203.59 | 1992.67 | 3.11 | ||||
| HS (cm) | TP (s) | α1 | Energy Concentration Degree δE | The Maximum Value of Generalized Energy Spectrum Emax | mE (Generalised Energy Spectrum Area within TEmax~TEmin) | Time Distribution Parameter of Energy Concentration ΔTE | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Freak Wave | Random Wave | Ratio | Freak Wave | Random Wave | Ratio | Freak Wave | Random Wave | Ratio | ||||
| 4.0 | 1.6 | 1.90 | 24.13 | 7.12 | 3.39 | 2.46 | 0.67 | 3.67 | 5.23 | 1.44 | 3.63 | 2.04 |
| 2.04 | 27.15 | 6.95 | 3.91 | 3.05 | 0.68 | 4.49 | 7.58 | 2.01 | 3.77 | 2.53 | ||
| 2.20 | 35.28 | 7.03 | 5.02 | 4.67 | 0.72 | 6.49 | 12.38 | 2.34 | 5.29 | 2.93 | ||
| 2.41 | 48.38 | 6.95 | 6.96 | 6.75 | 0.70 | 9.64 | 18.85 | 2.53 | 7.45 | 3.32 | ||
| 2.51 | 51.88 | 6.39 | 8.12 | 9.92 | 0.68 | 14.59 | 30.56 | 2.70 | 11.32 | 4.01 | ||
| 2.59 | 68.11 | 7.26 | 9.38 | 22.78 | 0.84 | 27.12 | 69.79 | 2.75 | 25.38 | 4.08 | ||
| HS (cm) | TP (s) | α1 | Energy Concentration Degree δE | The Maximum Value of Generalized Energy Spectrum Emax | mE (Generalised Energy Spectrum Area within TEmax~TEmin) | Time Distribution Parameter of Energy Concentration ΔTE | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Freak Wave | Random Wave | Ratio | Freak Wave | Random Wave | Ratio | Freak Wave | Random Wave | Ratio | ||||
| 4.0 | 1.6 | 1.90 | 10.42 | 4.59 | 2.27 | 0.21 | 0.09 | 2.33 | 0.52 | 0.15 | 3.47 | 2.05 |
| 2.04 | 13.31 | 4.83 | 2.76 | 0.24 | 0.10 | 2.40 | 0.66 | 0.18 | 3.67 | 2.23 | ||
| 2.20 | 16.73 | 5.02 | 3.33 | 0.33 | 0.11 | 3.00 | 1.05 | 0.21 | 5.00 | 2.66 | ||
| 2.41 | 25.43 | 5.13 | 4.96 | 0.58 | 0.12 | 4.83 | 1.72 | 0.23 | 7.48 | 2.93 | ||
| 2.51 | 45.12 | 4.96 | 9.10 | 1.29 | 0.12 | 10.75 | 3.86 | 0.29 | 13.31 | 3.59 | ||
| 2.59 | 74.82 | 5.39 | 13.88 | 3.43 | 0.11 | 31.18 | 8.35 | 0.32 | 26.09 | 3.94 | ||
| HS (cm) | TP (s) | α1 | Energy Concentration Degree δE | The Maximum Value of Generalized Energy Spectrum Emax | mE (Generalised Energy Spectrum Area within TEmax~TEmin) | Time Distribution Parameter of Energy Concentration ΔTE | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Freak Wave | Random Wave | Ratio | Freak Wave | Random Wave | Ratio | Freak Wave | Random Wave | Ratio | ||||
| 4.0 | 1.6 | 1.90 | 13.11 | 5.09 | 2.58 | 0.74 | 0.48 | 1.68 | 0.85 | 0.81 | 1.05 | 0.75 |
| 2.04 | 15.35 | 5.05 | 3.04 | 0.88 | 0.48 | 1.83 | 1.02 | 0.86 | 1.19 | 0.78 | ||
| 2.20 | 16.13 | 5.23 | 3.08 | 1.04 | 0.49 | 2.12 | 2.18 | 1.66 | 1.31 | 1.86 | ||
| 2.41 | 22.48 | 5.32 | 4.23 | 1.57 | 0.50 | 3.14 | 3.61 | 1.85 | 1.95 | 2.12 | ||
| 2.51 | 26.40 | 5.03 | 5.25 | 2.24 | 0.49 | 4.57 | 6.06 | 2.17 | 2.79 | 2.81 | ||
| 2.59 | 56.28 | 5.16 | 10.91 | 6.07 | 0.50 | 12.14 | 16.28 | 2.42 | 6.73 | 3.38 | ||
| HS (cm) | TP (s) | α1 | Energy Concentration Degree δE | The Maximum Value of Generalized Energy Spectrum Emax | mE (Generalised Energy Spectrum Area within TEmax~TEmin) | Time Distribution Parameter of Energy Concentration ΔTE | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Freak Wave | Random Wave | Ratio | Freak Wave | Random Wave | Ratio | Freak Wave | Random Wave | Ratio | ||||
| 4.0 | 1.6 | 1.90 | 6.75 | 3.72 | 1.81 | 951.31 | 565.33 | 1.68 | 2040.91 | 1293.70 | 1.58 | 1.6 |
| 2.04 | 7.93 | 3.72 | 2.13 | 1151.1 | 566.27 | 2.03 | 2739.86 | 1492.25 | 1.84 | 1.93 | ||
| 2.20 | 9.63 | 3.72 | 2.59 | 1463.94 | 557.39 | 2.63 | 4077.95 | 1771.43 | 2.30 | 2.48 | ||
| 2.41 | 12.34 | 3.73 | 3.31 | 1892.41 | 562.25 | 3.37 | 5476.09 | 1860.38 | 2.94 | 2.71 | ||
| 2.51 | 13.66 | 3.66 | 3.73 | 2136.23 | 546.27 | 3.91 | 6092.69 | 1891.97 | 3.22 | 2.80 | ||
| 2.59 | 15.23 | 3.73 | 4.08 | 2710.00 | 583.92 | 4.64 | 8924.96 | 1985.69 | 4.49 | 3.10 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pan, W.; Cui, C.; He, M. Experimental Study of the Hydrodynamic Characteristics of a Submerged Floating Tunnel under Freak Wave (II: Time-Frequency Domain Study). J. Mar. Sci. Eng. 2023, 11, 971. https://doi.org/10.3390/jmse11050971
Pan W, Cui C, He M. Experimental Study of the Hydrodynamic Characteristics of a Submerged Floating Tunnel under Freak Wave (II: Time-Frequency Domain Study). Journal of Marine Science and Engineering. 2023; 11(5):971. https://doi.org/10.3390/jmse11050971
Chicago/Turabian StylePan, Wenbo, Cheng Cui, and Meng He. 2023. "Experimental Study of the Hydrodynamic Characteristics of a Submerged Floating Tunnel under Freak Wave (II: Time-Frequency Domain Study)" Journal of Marine Science and Engineering 11, no. 5: 971. https://doi.org/10.3390/jmse11050971
APA StylePan, W., Cui, C., & He, M. (2023). Experimental Study of the Hydrodynamic Characteristics of a Submerged Floating Tunnel under Freak Wave (II: Time-Frequency Domain Study). Journal of Marine Science and Engineering, 11(5), 971. https://doi.org/10.3390/jmse11050971






