Model Predictive Energy-Maximising Tracking Control for a Wavestar-Prototype Wave Energy Converter

Abstract

To date, one of the main challenges in the wave energy field is to achieve energy-maximizing control in order to reduce the levelized cost of energy (LCOE). This paper presents a model predictive velocity tracking control method based on a hierarchical structure for a Wavestar-like deivce in the WEC-SIM benchmark. The first part of the system structure aims to estimate the wave excitation moment (WEM) by using a Kalman filter. Then, an extended Kalman filter (EKF) is chosen to obtain the amplitude and angular frequency of the WEM in order to compute the reference velocity. Following this, a low-level model predictive control (MPC) method is designed to ensure the wave energy converter (WEC) tracks the optimal reference velocity for maximum energy extraction from irregular waves. Two Gaussian Process (GP) models are considered to predict the future wave excitation moment and future reference velocity, which are needed in MPC design. The proposed strategy can give a new vision for energy-maximizing tracking control based on MPC.

1. Introduction

To date, climate changes have become a significant problem and are manifested in different ways. People are starting to realize the emergence of a fossil fuel crisis and the disadvantages of using traditional fossil fuels. Hence, the concept of exploring sustainable and renewable energy has been enhanced. Wave energy shows great potential [1,2] to fulfill the growing energy demand worldwide compared with other renewable resources (wind, solar energy, etc).

Although wave energy takes the needs of commercial promotion and actual deployment into consideration, the technologies involved are still immature and lead to a high levelized cost of energy (LCOE) [3] compared with the other marine renewable energy sources, e.g., compared with wind energy. Hence, lowering the LCOE has been a primary task in the wave energy field. Excluding the reduction of operation and maintenance costs [4] to reduce LCOE, the other elegant way is to achieve energy maximization through a WEC device, attempting to harvest energy from the ocean waves and convert the absorbed mechanical energy into electrical energy [5] using a control system.

For the research target, the point absorber wave energy converter (PAWEC) type of device is popular as it has has a relatively simple structure and can be arranged into an array [6] of suitable size to absorb as much power as possible. For example, there have been numbers of related works in the literature based on a special form of point absorber device known as the Wavestar-prototype WEC [7,8,9,10]. This was selected in an open competition [11] to compare different WEC control systems on a standard benchmark, the WEC-SIM software and experimental tests. This paper focuses on the use of a wavestar-like system to perform energy-maximizing control design [12] based on a very good WEC-SIM numerical model.

For the purpose of energy maximization, a considerable number of control strategies can be found in the literature, such as reactive control [13], model predictive control (MPC) [14], moment-matching based control [15], Spectral/Pseudospectral-based (MPC-like type) control [16], LTI (LiTe-Con) controller [17], etc. The most well known of these is reactive control [18], based on linear resonance theory, and it has been discussed and tested in many references. It is usually necessary to amplify the WEC motion to capture as much wave energy as possible. At first glance, this seems to be because the use of a “complex conjugate” method may violate the WEC linear model assumption of the hydrodynamics, involving many power fluctuations (both positive and negative), and can be limited to application for regular wave conditions, due to its frequency-dependent characteristic. The other choice is MPC [14,16,19], which selects the average absorbed mechanical power as an objective function and maximizes the power by solving an optimization problem. The MPC can reach the optimal solution for energy extraction and deal with system constraints elegantly. This is why the MPC approach has a significant research following. Additionally, an alternative choice of energy-maximizing design is based on a hierarchical structure [20] with a low-level controller, e.g., a robust controller, for optimal reference velocity tracking. This tracking system idea can achieve a near-resonance operation to bring acceptable results for energy maximization production.

On the basis of MPC and the hierarchical structure strategies, this paper combines them and produces a model predictive velocity tracking control approach for maximum energy extraction. As for the second or high level part of the hierarchical structure, the WEM is estimated by a Kalman filter, and reference velocity profile calculation is set in it. On the other hand, the reference velocity computation requires the instantaneous amplitude and frequency of the WEM, which are estimated by the EKF in this paper. Theoretically, the WEM is assumed to be a narrow-band harmonic process and modeled as a single cyclical component based on Harvey’s structural model [21]. Following this, on-line estimation can be performed to obtain the angular amplitude and frequency of WEM by the designed EKF in order to compute the reference velocity. Next, model predictive tracking control is placed in the low-level part of the whole designed structure. The objective function comprises the velocity error signal and control input and is transferred into a quadratic index to reach its minimum with input constraint. However, the future excitation moment and future reference velocity information are required to be predicted and used in the MPC objective function. Usually, an autoregressive model is used for the prediction of the WEM [22]. However, for the real-time forecasting requirement, the AR model needs to be updated, which will increase the prediction time. Here, two GP models are chosen instead to provide the short-term forecasting [23]. The hyperparameters can be preselected before the training process to reduce the prediction time with no need for them to be updated during real-time forecasting. Besides this, since the GP is a kernel-based and nonparametric learning method, it has the advantages of modeling flexibility, as well as prediction with learning smoothness and the use of noise parameters based on a training set.

The remainder of this paper is organized as follows. Section 2 describes the Wavestar-prototype WEC modeling and the overall hierarchical tracking system structure. Section 3 presents the design of a Kalman filter for the WEM estimation and EKF for reference velocity computation. Section 4 shows the design of the model predictive velocity tracking control with GP model for short-term forecasting. Section 5 gives the simulation results and discussions. Finally, Section 6 presents the concluding discussion.

2. Modeling and the Whole System Scheme

This section presents the description of the dynamics of a Wavestar-like device (the scaled 1:20 benchmark) based on the well-known Cummins equation and the expression of the hierarchical tracking control structure. The parameters of the WEC dynamics [19] are provided by Wavestar experiments and a hydrodynamic database (WAMIT computation). The numerical simulation model has been developed on the WEC-SIM simulator and verified in [24].

As for the hierarchical tracking control structure, this was first proposed by [20] and adopted for energy-maximizing controller design. This paper focuses on this strategy and gives a new version of velocity tracking design based on MPC to reach a near resonance condition. The control input constraint can be handled in MPC, which shows an advantage compared with some other control methods.

2.1. WEC Dynamics

The scaled Wavestar-prototype device is a kind of wave-activated body WEC, as shown in Figure 1. A hemispherical float is mechanically connected to an arm that can rotate around a fixed hinge point A [11], which has three independent motions (surge, heave and pitch). At the other side of the arm, a linear motor (power take-off system) is attached on the rotating arm to provide the power take-off force, and it only has one degree of freedom.

In order to reduce the design complexity for estimation and control, the hydrodynamic response of the float-arm can be equivalent to pitch moment only around the fixed hinge point. This means that the linear position and force measurements can be converted to the rotational displacement and moment. Then, the float rotational dynamics at the hinge point A [19] can be treated as the equivalent pitch moment:

$$\begin{array}{ccc}\hfill (J+J_{\infty })\ddot{\theta }\left(t\right)& =& -K_{hs}\theta \left(t\right)-K_v\dot{\theta }\left(t\right)+M_{ex}\left(t\right)-M_{ra}\left(t\right)-M_{PTO}\left(t\right)\hfill \\ \hfill {\dot{r}}_a\left(t\right)& =& A_{ra}{r}_a\left(t\right)+B_{ra}\dot{\theta }\left(t\right)\hfill \\ \hfill M_{ra}\left(t\right)& =& C_{ra}{r}_a\left(t\right)+D_{ra}\dot{\theta }\left(t\right)\hfill \end{array}$$

(1)

where J is the inertia of the float and arm, $J_{\infty }$ is the added inertia, $\ddot{\theta }$ is the rotational angular acceleration of the float, $K_{hs}$ and $K_v$ are the hydrostatic stiffness coefficient and linear damping coefficient respectively, and $M_{ra},M_{ex}and{M}_{PTO}$ are the equivalent radiation moment, the equivalent wave excitation moment and power take-off moment around the hinge point. The radiation moment $M_{ra}={\int }_0^t{h}_r(t-l)\dot{\theta }\left(l\right)dl$ is a convolution integral term, which can dramatically increase computational burden and bring difficulties in estimation and control work design. To overcome these problems, the convolution term can be converted into an order-two linear state space model by using system identification according to Prony’s method according to the realization theory. The internal variable $r_a\left(t\right)$ in the identified order-two state space model does not have physical meaning. $(A_{ra};B_{ra};C_{ra};D_{ra})$ are the state space identified matrices of the convolution term of $M_{ra}$.

Theoretically, the equivalent wave excitation moment around the hinge point based on [19] can be computed as

$$\begin{array}{c}\hfill M_{ex}=-F_{ex,x}sin({\theta }_0+\theta )l_{arm}-F_{ex,z}cos({\theta }_0+\theta )l_{arm}+M_{ex,\theta }\end{array}$$

(2)

where ${\theta }_0$ is the initial angular displacement of the float when it is located at the equilibrium point, $l_{arm}$ is the length of the arm, and $F_{ex,x},F_{ex,z},M_{ex,\theta }$ are the surge, heave and pitch direction components of the wave excitation force acting on the float.

The state space model of the WEC system can be expressed as

$$\begin{array}{ccc}\hfill \dot{x}& =& Ax+Bu+B{M}_{ex}\hfill \\ \hfill y& =& Cx\hfill \end{array}$$

(3)

where $A=\left[\begin{array}{ccc}0& 1& {\mathbf{0}}_{1\times 2}\\ -{\displaystyle \frac{K_{hs}}{J_t}}& -{\displaystyle \frac{K_v+D_{ra}}{J_t}}& -{\displaystyle \frac{C_{ra}}{J_t}}\\ {\mathbf{0}}_{2\times 1}& B_{ra}& A_{ra}\end{array}\right],x=\left[\begin{array}{c}\theta \\ \dot{\theta }\\ r_a\end{array}\right],B=\left[\begin{array}{c}0\\ {\displaystyle \frac{1}{J_t}}\\ {\mathbf{0}}_{2\times 1}\end{array}\right],u=-M_{PTO},C=\left[\begin{array}{ccc}1& 0& {\mathbf{0}}_{1\times 2}\\ 0& 1& {\mathbf{0}}_{1\times 2}\end{array}\right]$.

The state variables $\theta$ and $\dot{\theta }$ are the angular displacement and velocity of the float. $r_a$ is the internal variable of the identified state space model in Equation (1). Concerning the model parameters, $J_t=J+J_{\infty }$ is the total inertia, where ${\mathbf{0}}_{p\times q}$ represents a zero matrix with r rows and q columns.

The electrical energy $E_e$ absorbed by the grid [14] can be defined as

$$\begin{array}{c}\hfill E_e\left(t\right)=-{\int }_t^{t+T}{P}_e\left(r\right)dr=-{\int }_t^{t+T}\mathsf{\Gamma }\left(r\right)P_m\left(r\right)dr\end{array}$$

(4)

where $P_m$ is the absorbed mechanical power by the PTO system, $\mathsf{\Gamma }$ is the conversion efficiency, $P_e$ is the extracted electrical power, and r is the integration variable.

The relationship between $P_e$ and $P_m$ is given below:

$$\begin{array}{c}\hfill P_e\left(t\right)=\mathsf{\Gamma }\left(t\right)P_m\left(t\right)=\mathsf{\Gamma }\left(t\right)M_{PTO}\left(t\right)\dot{\theta }\left(t\right),\left\{\begin{array}{c}\mathsf{\Gamma }\left(t\right)={\mu }_{gen}if{P}_m\left(t\right)\ge 0\\ \mathsf{\Gamma }\left(t\right)={\mu }_{mot}if{P}_m\left(t\right)<0\end{array}\right.\end{array}$$

(5)

where ${\mu }_{gen}$ is the efficiency when the PTO system is assumed to be working in generator mode and ${\mu }_{mot}$ is the motor mode efficiency.

2.2. The Overall Hierarchical Control Structure

For model predictive velocity tracking control design, the proposed hierarchical structure is based on previous work [20] as shown in Figure 2.

The high-level part of the system structure consists of WEM estimation and reference angular velocity generation. The Kalman filter is selected to estimate the WEM, and an EKF is chosen to estimate the instantaneous amplitude and frequency of the WEM. From this, the velocity reference ${\dot{\theta }}_{ref}$ can be calculated.

The low-level part of the control design is based on the MPC, which aims to force the scaled Wavestar-prototype device to track the optimal angular velocity trajectory for the power maximization purpose. Two Gaussian process models are adopted to predict both the future WEM and the future reference velocity, respectively, which are needed in the MPC tracking design.

3. Wave Excitation Moment Estimation and Reference Velocity Computation

For the Wavestar-prototype device, the wave excitation information is a physically unmeasurable quantity, although it is required for optimal control or energy-maximizing control design. The equivalent $M_{ex}$ around the hinge point is an external term (unknown input) of the WEC system and can be estimated by using a Kalman filter. According to the reference velocity calculation, the WEM instantaneous amplitude ${\widehat{A}}_{ex}$ and frequency $\widehat{\omega }$ are required, and they are computed using an EKF.

3.1. Kalman Filter with Random Walk

The discretized system of Equation (3) has the following form:

$$\begin{array}{ccc}\hfill x(k+1)& =& A_{d}x\left(k\right)+B_{d}u\left(k\right)+B_d{M}_{ex}\left(k\right)+{\epsilon }_x\left(k\right)\hfill \\ \hfill y\left(k\right)& =& C_{d}x\left(k\right)+\mu \left(k\right)\hfill \end{array}$$

(6)

where ${\epsilon }_x\left(k\right)$ denotes the unmodeled dynamics and $\mu \left(k\right)$ is the measurement noise. $M_{ex}\left(k\right)$ is considered as an external moment term acting on the WEC float, and it can be treated as an unknown input term of System (6). Then, the discrete time dynamics of the WEM [26] can be considered as

$$\begin{array}{c}\hfill M_{ex}(k+1)=M_{ex}\left(k\right)+{\epsilon }_m\left(k\right)\end{array}$$

(7)

where ${\epsilon }_m\left(k\right)$ is a Gaussian distributed random variable. It means that the next value of WEM will conduct a random step away from the present value after a sampling time, and all moving steps are considered independent. $M_{ex}\left(k\right)$ can be estimated by a Kalman filter when it is being considered as one of the system states. Hence, the augmented system for estimating the WEM is

$$\begin{array}{cc}\hfill \overline{x}(k+1)& =\overline{A}\overline{x}\left(k\right)+\overline{B}u\left(k\right)+\epsilon \left(k\right)\hfill \\ \hfill y\left(k\right)& =\overline{C}\overline{x}\left(k\right)+\mu \left(k\right)\hfill \end{array}$$

(8)

where $\overline{A}=\left[\begin{array}{cc}{A}_d& B_d\\ {\mathbf{0}}_{1\times 4}& 1\end{array}\right],\overline{x}=\left[\begin{array}{c}x\\ M_{ex}\end{array}\right],\overline{B}=\left[\begin{array}{c}{B}_d\\ 0\end{array}\right],\overline{C}=\left[\begin{array}{cc}{C}_d& {\mathbf{0}}_{2\times 1}\end{array}\right],\epsilon \left(k\right)=\left[\begin{array}{c}{\epsilon }_x\left(k\right)\\ {\epsilon }_m\left(k\right)\end{array}\right].$

The dimensions of system matrices are $\overline{A}\in {\mathfrak{R}}^{5\times 5}$, $\overline{B}\in {\mathfrak{R}}^{5\times 1}$, $\overline{C}\in {\mathfrak{R}}^{2\times 5}$. $\epsilon \left(k\right)$ and $\mu \left(k\right)$ are uncorrelated zero-mean white noise sequences with covariance matrices $Q_f$ and $R_f$.

Then, the Kalman filter prediction update equation [26] is

$$\begin{array}{ccc}\hfill \widehat{\overline{x}}\left(k\right|k-1)& =& \overline{A}\widehat{\overline{x}}(k-1|k-1)+\overline{B}u(k-1)\hfill \\ \hfill P_f\left(k\right|k-1)& =& \overline{A}{P}_f(k-1|k-1){\overline{A}}^T+Q_f\hfill \end{array}$$

The Kalman filter correction update equation [26] becomes

$$\begin{array}{ccc}\hfill K_f\left(k\right)& =& P_f\left(k\right|k-1){\overline{C}}^T{(\overline{C}{P}_f\left(k\right|k-1){\overline{C}}^T+R_f)}^{-1}\hfill \\ \hfill \widehat{\overline{x}}\left(k\right|k)& =& \widehat{\overline{x}}\left(k\right|k-1)+K_f\left(k\right)(y\left(k\right)-\overline{C}\widehat{\overline{x}}\left(k\right|k-1))\hfill \\ \hfill P_f\left(k\right|k)& =& (I-K_f\left(k\right)\overline{C})P_f\left(k\right|k-1)\hfill \end{array}$$

Hence, the estimated ${\widehat{M}}_{ex}$ can be obtained from the optimal estimation of state vector $\widehat{\overline{x}}$. Note the following:

$\widehat{\overline{x}}\left(k\right|k-1)$ is a predicted prior state estimate given the observations at time k−1.

$P_f\left(k\right|k-1)$ is a predicted priori covariance matrix given the observations at time k−1.

$\widehat{\overline{x}}\left(k\right|k)$ is an updated posteriori state estimate given the observations at time k.

$P_f\left(k\right|k)$ is an updated posteriori covariance matrix given the observations at time k.

3.2. Extended Kalman Filter

On the basis of the high-level part of the hierarchical strategy in Figure 2, the instantaneous amplitude and frequency of WEM must be obtained in order to compute the reference velocity ${\dot{\theta }}_{ref}$. Hence, an efficient EKF method for the recursive estimation is required. Additionally, it is assumed that the WEM signal is a narrow-band process, and its harmonic model can be expressed as

$$\begin{array}{c}\hfill M_{ex}\left(t\right)=A_{ex}\left(t\right)cos(\omega \left(t\right)·t+\beta \left(t\right))\end{array}$$

(9)

where $A_{ex}\left(t\right),\omega \left(t\right)$ and $\beta \left(t\right)$ are the time-varying amplitude, angular frequency and phase of the WEM signal, respectively. Based on Harvey’s structural model presented in [21], the WEM can be modeled as a single cyclical component:

$$\begin{array}{cc}\hfill \left[\begin{array}{c}\psi (k+1)\\ {\psi }^{*}(k+1)\\ \omega (k+1)\end{array}\right]& =\left[\begin{array}{ccc}cos\left(\omega \left(k\right)T_s\right)& sin\left(\omega \left(k\right)T_s\right)& 0\\ -sin\left(\omega \left(k\right)T_s\right)& cos\left(\omega \left(k\right)T_s\right)& 0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{c}\psi \left(k\right)\\ {\psi }^{*}\left(k\right)\\ \omega \left(k\right)\end{array}\right]+\left[\begin{array}{c}\varsigma \left(k\right)\\ {\varsigma }^{*}\left(k\right)\\ \kappa \left(k\right)\end{array}\right]\hfill \\ \hfill M_{ex}\left(k\right)& =\psi \left(k\right)+\zeta \left(k\right)\hfill \end{array}$$

(10)

where $d_e\left(k\right)={\left[\varsigma \left(k\right){\varsigma }^{*}\left(k\right)\kappa \left(k\right)\right]}^T$ and $\zeta \left(k\right)$ are random process and measurement noise, and $\psi \left(k\right)$ and ${\psi }^{*}\left(k\right)$ are related states of the WEM amplitude and phase. The state vector $x_e\left(k\right)={\left[\begin{array}{c}{x}_{e,1}\left(k\right)x_{e,2}\left(k\right)x_{e,3}\left(k\right)\end{array}\right]}^T={\left[\begin{array}{c}\psi \left(k\right){\psi }^{*}\left(k\right)\omega \left(k\right)\end{array}\right]}^T$ and $x_e\left(k\right)\in {\mathfrak{R}}^{3\times 1}$, corresponding to the sampling time $T_s$.

The non-linear time-varying Model (10) can be formulated as follows:

$$\begin{array}{ccc}\hfill x_e\left(k\right)& =& f(x_e(k-1),d_e(k-1))\hfill \\ \hfill z_e\left(k\right)& =& h(x_e\left(k\right),\zeta \left(k\right))\hfill \end{array}$$

(11)

where the estimated excitation moment ${\widehat{M}}_{ex}$ is treated as the actual measurement $z_e\left(k\right)$. Based on the above definition and without knowing the noise information, the a priori state and measurement from time $k-1$ are

$$\begin{array}{ccc}\hfill {\widehat{x}}_e\left(k\right|k-1)& =& f({\widehat{x}}_e(k-1|k-1),0)\hfill \\ \hfill {\widehat{z}}_e\left(k\right|k-1)& =& h({\widehat{x}}_e\left(k\right|k-1),0)\hfill \end{array}$$

(12)

where ${\widehat{x}}_e\left(k\right|k-1)$ is the estimate of $x_e\left(k\right)$ and ${\widehat{z}}_e\left(k\right|k-1)$ is the estimate of $z_e\left(k\right)$ based on measurements from time $k-1$.

On application of a first-order Taylor series expansion of Equation (12), the linearized system time-varying Jacobian matrix $F\left(k\right)$ [27] is obtained as

$$\begin{array}{cc}\hfill & F\left(k\right)=\frac{\partial f}{\partial x_e}|{\widehat{x}}_e(k-1|k-1)\hfill \\ \hfill & =\left(\begin{array}{ccc}cos\left(\omega \left(k\right)T_s\right)& sin\left(\omega \left(k\right)T_s\right)& T_s(-sin\left(\omega \left(k\right)T_s\right)\psi \left(k\right)+cos\left(\omega \left(k\right)T_s\right){\psi }^{\prime }\left(k\right))\\ -sin\left(\omega \left(k\right)T_s\right)& cos\left(\omega \left(k\right)T_s\right)& T_s(-cos\left(\omega \left(k\right)T_s\right)\psi \left(k\right)-sin\left(\omega \left(k\right)T_s\right){\psi }^{\prime }\left(k\right))\\ 0& 0& 1\end{array}\right)\hfill \end{array}$$

The observed Jacobian matrix is

$$\begin{array}{c}\hfill H\left(k\right)=\frac{\partial h}{\partial x_e}|{\widehat{x}}_e\left(k\right|k-1)\triangleq \left[100\right]\end{array}$$

Thus, the EKF time-update equations are

$$\begin{array}{ccc}\hfill {\widehat{x}}_e\left(k\right|k-1)& =& f({\widehat{x}}_e(k-1|k-1),0)\hfill \\ \hfill P_e\left(k\right|k-1)& =& F\left(k\right)P_e(k-1|k-1)F^T\left(k\right)+Q_e\hfill \end{array}$$

The use of Jacobian matrices $F\left(k\right)$ and $H\left(k\right)$ to perform the model and measurement updates leads to

$$\begin{array}{ccc}\hfill K_e\left(k\right)& =& P_e\left(k\right|k-1)H^T\left(k\right){(H\left(k\right)P_e\left(k\right|k-1)H^T\left(k\right)+R_e)}^{-1}\hfill \\ \hfill {\widehat{x}}_e\left(k\right|k)& =& {\widehat{x}}_e\left(k\right|k-1)+K_e\left(k\right)(z_e\left(k\right)-h({\widehat{x}}_e\left(k\right|k-1),0))\hfill \\ \hfill P_e\left(k\right|k)& =& (I-K_e\left(k\right)H\left(k\right))P_e\left(k\right|k-1)\hfill \end{array}$$

where $Q_e$ and $R_e$ are suitably chosen variance process and measurement noise matrices. After the on-line estimation, the estimated angular amplitude and frequency [21] are

$$\begin{array}{cc}\hfill {\widehat{A}}_{ex}\left(k\right|k)& =\sqrt{{\widehat{x}}_{e,1}{\left(k\right|k)}^2+{\widehat{x}}_{e,2}{\left(k\right|k)}^2}\hfill \\ \hfill \widehat{\omega }\left(k\right|k)& ={\widehat{x}}_{e,3}\left(k\right|k)\hfill \end{array}$$

(13)

Next, consider the forcing of the float to reach a near resonance condition. The reference velocity [20] can then be described as

$$\begin{array}{ccc}\hfill & & {\dot{\theta }}_{ref}\left(t\right)={\displaystyle \frac{1}{T\left(t\right)}}{\widehat{M}}_{ex}\left(t\right)\hfill \end{array}$$

(14)

$$\begin{array}{ccc}\hfill where& & {\displaystyle \frac{1}{T\left(t\right)}}=\left\{\begin{array}{cc}{\displaystyle \frac{1}{2B\left(\omega \right)+2K_v^0}},& if{\displaystyle \frac{\widehat{\omega }{\theta }_{lim}}{{\widehat{A}}_{ex}}}>{\displaystyle \frac{1}{2B\left(\omega \right)+2K_v^{\left(0\right)}}}\\ {\displaystyle \frac{\widehat{\omega }{\theta }_{lim}}{{\widehat{A}}_{ex}}},& otherwise\end{array}\right.\hfill \end{array}$$

(15)

$B\left(\omega \right)$ is the radiation damping coefficient, and $K_v^0$ is the extra viscous damping coefficient. ${\theta }_{lim}$ is the maximum angular displacement within the allowable range. Hence, the reference velocity can be calculated from Equations (14) and (15) since the instantaneous amplitude ${\widehat{A}}_{ex}$ and frequency $\widehat{\omega }$ of the WEM signal have been obtained using the EKF.

4. Model Predictive Tracking Control with Short-Term Forecasting

In general, MPC is often used as an optimal strategy for the purpose of energy-maximizing by setting the average mechanical power as its objective function with control input and physical position constraints [16]. This paper tests the value of MPC in another way by a hierarchical velocity tracking structure based on the scheme in Figure 2. The velocity error signal is considered in the quadratic objective function for the purpose of tracking. In addition, the future WEM and future reference velocity are predicted in the short term by two separate Gaussian Process models. Furthermore, it is desirable to adopt the short-term forecasting of $M_{ex}$ and ${\dot{\theta }}_{ref}$ using uncorrelated Gaussian Process models. The forecasting time needs to be considered carefully, based on a trade-off between prediction accuracy and computation complexity.

4.1. Model Predictive Control

By defining $v=\dot{\theta }$ and with $C_v=\left[0100\right]$, and by considering the angular velocity as the WEC system output, this leads to a discrete-time state space model:

$$\begin{array}{cc}\hfill x(k+1)& =A_{d}x\left(k\right)+B_{d}u\left(k\right)+B_d{\widehat{M}}_{ex}\left(k\right)\hfill \\ \hfill v\left(k\right)& =C_{v}x\left(k\right)\hfill \end{array}$$

(16)

After iterating Model (16) with the prediction horizon N, a prediction model will have the following form:

$$\begin{array}{c}\hfill V_N=S_{av}x\left(k\right)+S_{bv}{u}_N+S_{bv}{M}_{ex,N}\end{array}$$

(17)

with $V_N=\left[\begin{array}{c}v(k+1)\\ v(k+2)\\ \cdots \\ v(k+N)\end{array}\right],S_{av}=\left[\begin{array}{c}{C}_v{A}_d\\ C_v{A}_d^2\\ \cdots \\ C_v{A}_d^N\end{array}\right],u_N=\left[\begin{array}{c}u\left(k\right)\\ u(k+1)\\ \cdots \\ u(k+N-1)\end{array}\right],M_{ex,N}=\left[\begin{array}{c}{\widehat{M}}_{ex}\left(k\right)\\ {\widehat{M}}_{ex}(k+1)\\ \cdots \\ {\widehat{M}}_{ex}(k+N)\end{array}\right],$$S_{bv}=\left[\begin{array}{ccccc}{C}_v{B}_d& 0& 0& \cdots & 0\\ C_v{A}_d{B}_d& C_v{B}_d& 0& \cdots & 0\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ C_v{A}_d^{N-1}{B}_d& C_v{A}_d^{N-2}{B}_d& \cdots & C_v{A}_d{B}_d& C_v{B}_d\end{array}\right]$.

Note that these stacked predictions are used in the objective function of the next optimization problem.

By defining $v_{ref}={\dot{\theta }}_{ref}$, the constrained discrete time optimization problem can be considered as follows:

$$\begin{array}{c}\underset{\begin{array}{c}{V}_N,u_N\\ M_{eN}\end{array}}{min}\sum _{i=1}^N{[v(k+i)-v_{ref}(k+i)]}^T{Q}_m[v(k+i)-v_{ref}(k+i)]+\sum _{i=0}^{N-1}{\left[u(k+i)\right]}^T{R}_{m}u(k+i)\end{array}$$

(18)

$$\begin{array}{c}subjectto\left|u(k+i)\right|\le u_{max}\end{array}$$

(19)

According to Equations (17) and (18), the MPC objective function is selected as

$$\begin{array}{c}\hfill J_m={\displaystyle \frac{1}{2}}{V}_N^T\overline{Q}{V}_N-v_{ref,N}^T\overline{Q}{V}_N+{\displaystyle \frac{1}{2}}{v}_{ref,N}^T\overline{Q}{v}_{ref,N}+{\displaystyle \frac{1}{2}}{u}_N^T\overline{R}{u}_N\end{array}$$

(20)

where $\overline{Q}=\left(\begin{array}{ccc}{Q}_m& 0& 0\\ 0& \ddots & 0\\ 0& 0& Q_m\end{array}\right),\overline{R}=\left(\begin{array}{ccc}{R}_m& 0& 0\\ 0& \ddots & 0\\ 0& 0& R_m\end{array}\right),v_{ref,N}=\left(\begin{array}{c}{v}_{ref}(k+1)\\ ⋮\\ v_{ref}(k+N)\end{array}\right)$.

By substituting Equations (17) into (20), the objective function is transformed into

$$\begin{array}{cc}\hfill J_m=& {\displaystyle \frac{1}{2}}{(S_{av}x\left(k\right)+S_{bv}{u}_N+S_{bv}{M}_{ex,N})}^T\overline{Q}(S_{av}x\left(k\right)+S_{bv}{u}_N+S_{bv}{M}_{ex,N})+{\displaystyle \frac{1}{2}}{u}_N^T\overline{R}{u}_N\hfill \\ & -v_{ref,N}^T\overline{Q}{S}_{av}x\left(k\right)-v_{ref,N}^T\overline{Q}{S}_{bv}{u}_N-v_{ref,N}^T\overline{Q}{S}_{bv}{M}_{ex,N}+{\displaystyle \frac{1}{2}}{v}_{ref,N}^T\overline{Q}{v}_{ref,N}\hfill \end{array}$$

(21)

Considering the velocity tracking and dropping some bias terms, the objective function $J_m$ can be converted into its quadratic form:

$$\begin{array}{cc}\hfill J_m& ={\displaystyle \frac{1}{2}}{u}_N^T{H}_m{u}_N+f_m^T{u}_N\end{array}$$

(22)

where $H_m=S_{bv}^T\overline{Q}{S}_{bv}+\overline{R}$, $f_m^T=x^T\left(k\right)S_{av}^T\overline{Q}{S}_{bv}+M_{ex,N}^T{S}_{bv}^T\overline{Q}{S}_{bv}-v_{ref,N}^T\overline{Q}{v}_{ref,N}$.

Thereby, the velocity tracking problem is transformed into a Quadratic Programming (QP) optimization problem, and the energy-maximizing generation can be achieved when the scaled Wavestar-like device can track the reference angular velocity ${\dot{\theta }}_{ref}$. The qpOASES QP solver [28] is utilized to solve the QP optimization. It is particularly well suited for MPC applications that need fast QP solving rates with high reliability. As for the sequences $M_{ex,N}$ and $v_{ref,N}$, these can be obtained from the GP model to obtain short-term forecasting.

4.2. Gaussian Process Model

To specify the a priori expression of a GP model [29], the mean function $m\left(a\right)$ and covariance function $k(a,a^{*})$ are defined as follows:

$$\begin{array}{ccc}\hfill f\left(a\right)& \sim & \mathcal{GP}(m\left(a\right),k(a,a^{*}))\hfill \\ \hfill m\left(a\right)& =& \mathbb{E}\left[f\right(a\left)\right]\hfill \\ \hfill k(a,a^{*})& =& cov(f\left(a\right),f\left(a^{*}\right))\hfill \end{array}$$

(23)

where $a\in {\Re }^{\mathcal{D}}$ is a vector of the dynamics input with dimension $\mathcal{D}$, and $f\left(a\right)$ and $f\left(a^{*}\right)$ are arbitrary Gaussian scalar variables indexed by a and $a^{*}$.

Next, define a training set $\mathcal{D}=(\mathit{a},\mathbf{z})$, where the matrix $\mathit{a}=[a_1,a_2,\cdots ,a_n]$ contains all input vectors, and $\mathbf{z}=[z_1,z_2,\cdots ,z_n]$ is a corresponding vector with all scalar outputs. Then, a GP posterior model can be determined as

$$\begin{array}{c}\hfill z_i=f\left(a_i\right)+{ϵ}_i{ϵ}_i\sim \mathcal{N}(0,{\sigma }^2)\end{array}$$

(24)

where z is the observed output values, $f\left(a\right)$ is the GP model values, and $ϵ$ is a zero mean white Gaussian noise.

Here, a spectral mixture (SM) kernel is chosen as the covariance function for excitation moment and reference velocity forecasting. The form is given by [30] as

$$\begin{array}{c}\hfill k_{SM}\left(\tau \right)=\sum _{s=1}^S{w}_{s}cos\left(2\pi {\tau }^T{\mu }_s\right)\prod _{o=1}^{O}exp(-2{\pi }^2{\tau }_o^2{v}_s^{\left(o\right)})\end{array}$$

(25)

Regarding the one-dimensional input $O=1$, S is a selected number of the wave frequency components, and $\tau$ is the distance between two arbitrary points $a_i$ and $a_j$. According to the view of wave reconstruction, the parameters of the SM kernel hyperparameter vector $\mathsf{\Theta }={({\mu }_s,w_s,v_s)}^T$ can denote the the amplitude, period and evolutionary-scale of each wave component. This means that this SM kernel [23] can be applied as the covariance function of a GP model for wave forecasting directly owing to its automatic discovery capability.

The hyperparameters of $\mathsf{\Theta }$ in the SM kernel can be calculated by optimizing the marginal likelihood function [29] as

$$\begin{array}{c}\hfill logp\left(\mathbf{z}\right|\mathit{a},\mathsf{\Theta })=-{\displaystyle \frac{1}{2}}log|K+{\sigma }^{2}I|-{\displaystyle \frac{1}{2}}{\mathbf{z}}^T{(K+{\sigma }^{2}I)}^{-1}\mathbf{z}-{\displaystyle \frac{n}{2}}log\left(2\pi \right)\end{array}$$

(26)

Note that the choice of highly suitable initial hyperparameters before the training process can promote the convergence rate of optimization and avoid reaching an unsatisfactory local optimum. After the training process, the posterior joint distribution of the prediction $f^{*}$ with given input vector $\mathit{a}$ has the following form:

$$\begin{array}{c}\hfill \left[\begin{array}{c}{f}^{*}\\ \mathbf{z}\end{array}\right]\sim (\left[\begin{array}{c}m\left({\mathit{a}}^{*}\right)\\ m\left(\mathit{a}\right)\end{array}\right],\left[\begin{array}{cc}k({\mathit{a}}^{*},{\mathit{a}}^{*})& k({\mathit{a}}^{*},\mathit{a})\\ k(\mathit{a},{\mathit{a}}^{*})& K+{\sigma }^{2}I\end{array}\right])\end{array}$$

(27)

with $k({\mathit{a}}^{*},\mathit{a})=k(\mathit{a},{\mathit{a}}^{*})=[k({\mathit{a}}_1,{\mathit{a}}^{*}),\cdots ,k({\mathit{a}}_N,{\mathit{a}}^{*})]$. Then, based on the Joint Gaussian Distribution Theorem, the predicted result about $f^{*}$ can be described as

$$\begin{array}{ccc}\hfill \mu \left(f^{*}\right)& =\hfill & \hfill m\left({\mathit{a}}^{*}\right)+k({\mathit{a}}^{*},\mathit{a}){[K+{\sigma }^{2}I]}^{-1}(\mathbf{z}-m\left(\mathit{a}\right))\\ \hfill \sigma \left(f^{*}\right)& =\hfill & \hfill k({\mathit{a}}^{*},{\mathit{a}}^{*})-k({\mathit{a}}^{*},\mathit{a}){[K+{\sigma }^{2}I]}^{-1}k(\mathit{a},{\mathit{a}}^{*})\end{array}$$

(28)

The Gaussian Process for Machine Learning (GPML) package [29] is applied to design the GP model and perform the training and test prediction work.

5. Results and Discussion

The simulation works are conducted using the open-source software WEC-Sim, developed in Matlab/Simulink using the multi-body dynamics solver Simscape Multibody—refer to WEC-Sim documentation [31] and applications [32,33,34,35,36]. The main contribution focuses on a Kalman filter approach to WEM estimation; in addition to optimal reference computation based on EKF, GP modeling is used for short-term forecasting and velocity tracking through MPC and tested on a WEC-Sim model of the 1:20 scaled Wavestar device in WEC-Sim. The simulation parameters are listed in

Table 1. The simulation parameters.

Parameters	Values
Simulation sampling time $T_s$	0.05 s
Inertia of float and arm J	1.0 kg m${}^2$
Added inertia $J_{\infty }$	0.4805 kg m${}^2$
Hydrostatic coefficient $K_{hs}$	92.33 Nm rad${}^{-1}$
Linear damping coefficient $K_v$	1.8 Nm rad${}^{-1}$s${}^{-1}$
Length of the arm $l_{arm}$	0.54875 m
Efficiency of generator mode ${\mu }_{gen}$	0.7
Efficiency of motor mode ${\mu }_{gen}$	${0.7}^{-1}$
KF coefficient $Q_f$	diag(0.01 0.1 0.01 0.01 200)
KF coefficient $R_f$	diag(0.01; 0.01)
EKF initial state $x_e$	${[1,1,5]}^T$
EKF coefficient $Q_e$	$diag(0.2,0.2,0.001)$
EKF coefficient $R_e$	0.1
Angular displacement limit ${\theta }_{lim}$	0.4 rad
Control limit $u_{max}$	$\pm 12$ Nm
GP coefficient S	12

. A fixed-step size ode8 (Dormand-Prince) solver is selected to conduct the simulation works for the WEC-Sim numerical model in Matlab/Simulink software.

The matrices for the approximation of radiation moment are $A_{ra}=\left[\begin{array}{cc}-13.59& -13.35\\ 8.0& 0\end{array}\right],B_{ra}=\left[\begin{array}{c}8.0\\ 0\end{array}\right],C_{ra}=\left[4.7390.5\right],D_{ra}=-0.1586.$

The JONSWAP (JS) wave Spectrum is adopted to generate three irregular waves: Seastate1, Seastate2 and Seastate3. The significant wave height $H_{m0}$ and peak wave period $T_p$ of irregular waves, MPC prediction horizon $N_p$ and MPC coefficients $Q_m$, $R_m$ are shown in

Table 2. The irregular wave information and MPC coefficients.

Case	${\mathit{H}}_{\mathit{m}0}$	${\mathit{T}}_{\mathit{p}}$	${\mathit{N}}_{\mathit{p}}$	${\mathit{Q}}_{\mathit{m}}$	${\mathit{R}}_{\mathit{m}}$
Seastate1	0.0208	0.988	20	0.5	$2\times {10}^{-3}$
Seastate2	0.0625	1.412	30	0.5	$5\times {10}^{-4}$
Seastate3	0.1042	1.836	40	0.5	$2\times {10}^{-4}$

. The wave peak enhancement factor $\varkappa =1$.

Figure 3 presents the estimated ${\widehat{M}}_{ex}$ from the KF over the time interval 50–75 s. It can be seen that some biases arise in the crests of the estimated WEM due to the WEC-Sim numerical model having some additional static moments and the offset between the center of bouyancy (CoB) and center of gravity (CoG). Additionally, a small lag of about 0.05 s occurs between the estimated ${\widehat{M}}_{ex}$ and the calculated $M_{ex}$. The reason for this lag is that a relatively large sampling time has to be utilized for the requirement of the QP solving time in MPC due to its computational complexity. The sampling time is 0.05 s, which is larger than the most frequently used sampling rate (0.001 s). This means that the KF will not produce the most accurate estimation performance with zero lag, but the estimation performance is acceptable.

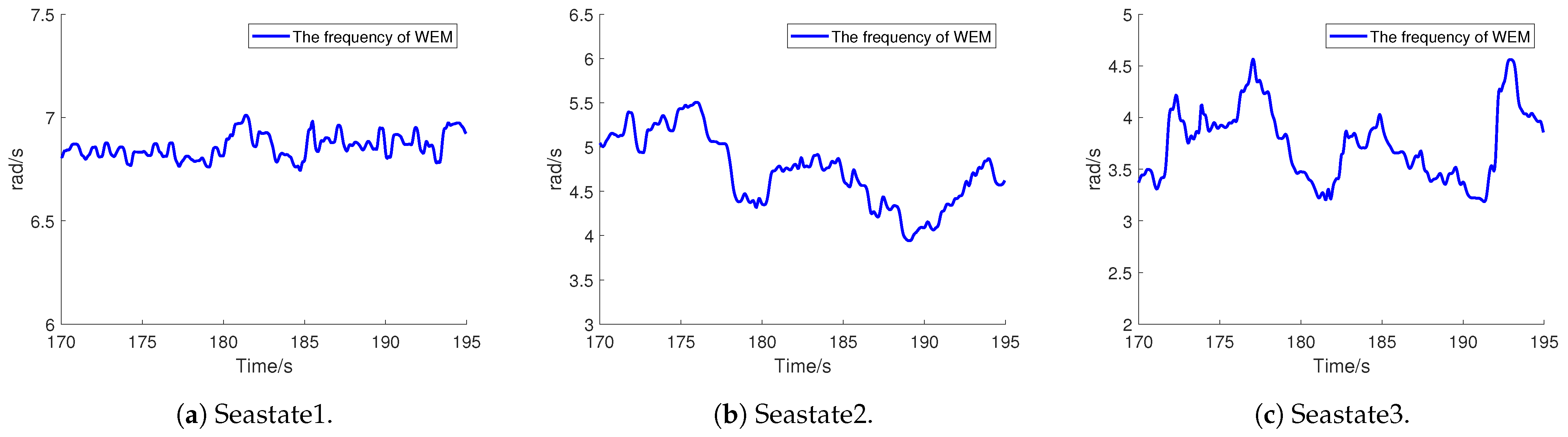
The estimated instantaneous amplitude ${\widehat{A}}_{ex}$ is shown in Figure 4 along with the estimated excitation moment ${\widehat{M}}_{ex}$. The estimated instantaneous frequency $\widehat{\omega }$ is given in Figure 5. The EKF convergence time is usually long, and the initial values need to be chosen reasonably close to the expected values to avoid a long convergence time.

Two GP models are employed to provide the future WEM and velocity information for MPC tracking design. In other words, the predicted future WEM sequence and future reference velocity sequence are used in the MPC objective function. It is clear that, most of the time, the predicted WEM based on the GP model is matched well with the calculated ideal WEM in Figure 6. The GP modeling method shows good learning smoothness and accuracy for WEM prediction. The suitable hyperparameters of the GP model can be preselected before the training process to reduce the prediction time and promote the convergence rate of optimization. There is no need to update the hyperparameters during the real-time forecasting. From Equations (14) and (15), the wave excitation moment ${\widehat{M}}_{ex}$ and reference angular velocity ${\dot{\theta }}_{ref}$ share the same phase but a different amplitude when the tracking control is achieved for the WEC system. Hence, the predicted future reference velocity shows similar trends to the predicted future WEM in Figure 7.

The MPC angular velocity tracking result is shown in Figure 8. To start from the MPC standpoint, the overall tracking performance is good, even if the float velocity shows occasional amplitude differences with the reference velocity. However, the tracking errors between the reference velocity and float velocity are small and acceptable. Most of the time, they share the same phase. The primary role of the reference velocity is to capture the same phase with the estimated ${\widehat{M}}_{ex}$ so as to reach a near resonance condition for energy-maximizing purposes. This means that the WEC system is forced to follow the incident waves by MPC when the tracking mission is obtained. In total, the MPC method lacks some robustness to a certain extent, which is unlike the other robust methods, which can result in very small tracking errors for the WEC system doing the tracking work. However, the MPC has a good advantage in terms of input constraint handling.

The generated instantaneous power and extracted energy through the power take-off system are shown in Figure 9 and Figure 10. It is clear that the proposed MPC tracking approach only causes very few negative power excursions, which is a benefit for the PTO system solving the large bidirectional flow problem and reducing the energy loss during the motor mode.

The PTO moment control input is given in Figure 11. The red lines represent the input maximum limits of $\pm 12$ Nm, showing that the MPC control input satisfies the input constraint conditions. The MPC tracking performance can be improved if the MPC coefficient $R_m$ is decreased, but this can bring a large PTO moment in the control input. Conversely, if a large $R_m$ is adopted and the control input can be small, the MPC tracking performance will certainly decline.

6. Conclusions

This paper concentrates on model predictive velocity tracking control design based on a hierarchical structure to reach energy-maximizing generation for a Wavestar-like device in the WEC-SIM benchmark. The high-level part of the overall structure includes a KF for WEM estimation and an EKF for providing the instantaneous amplitude and frequency of WEM to calculate the optimal reference velocity. Two Gaussian Process models are selected to provide the future information, multiple steps ahead of the reference velocity and wave excitation moment for MPC design with accurate prediction accuracy and good smoothness. The low-level model predictive controller shows good tracking performance with small errors and pushes the WEC system into a near-resonance condition for power maximization extraction. Furthermore, it is shown that the MPC tracking system approach can take the input constraint into consideration as well and generate a low level of negative power, which is beneficial for the PTO system to avoid large bidirectional energy flow. Considering that the KF and MPC still lack robustness to a certain extent, future work may focus on how to design a robust controller under a large sampling time and how to improve the robustness of the designed MPC.