A Multi-Objective Optimization of the Anchor-Last Deployment of the Marine Submersible Buoy System Based on the Particle Swarm Optimization Algorithm
Abstract
:1. Introduction
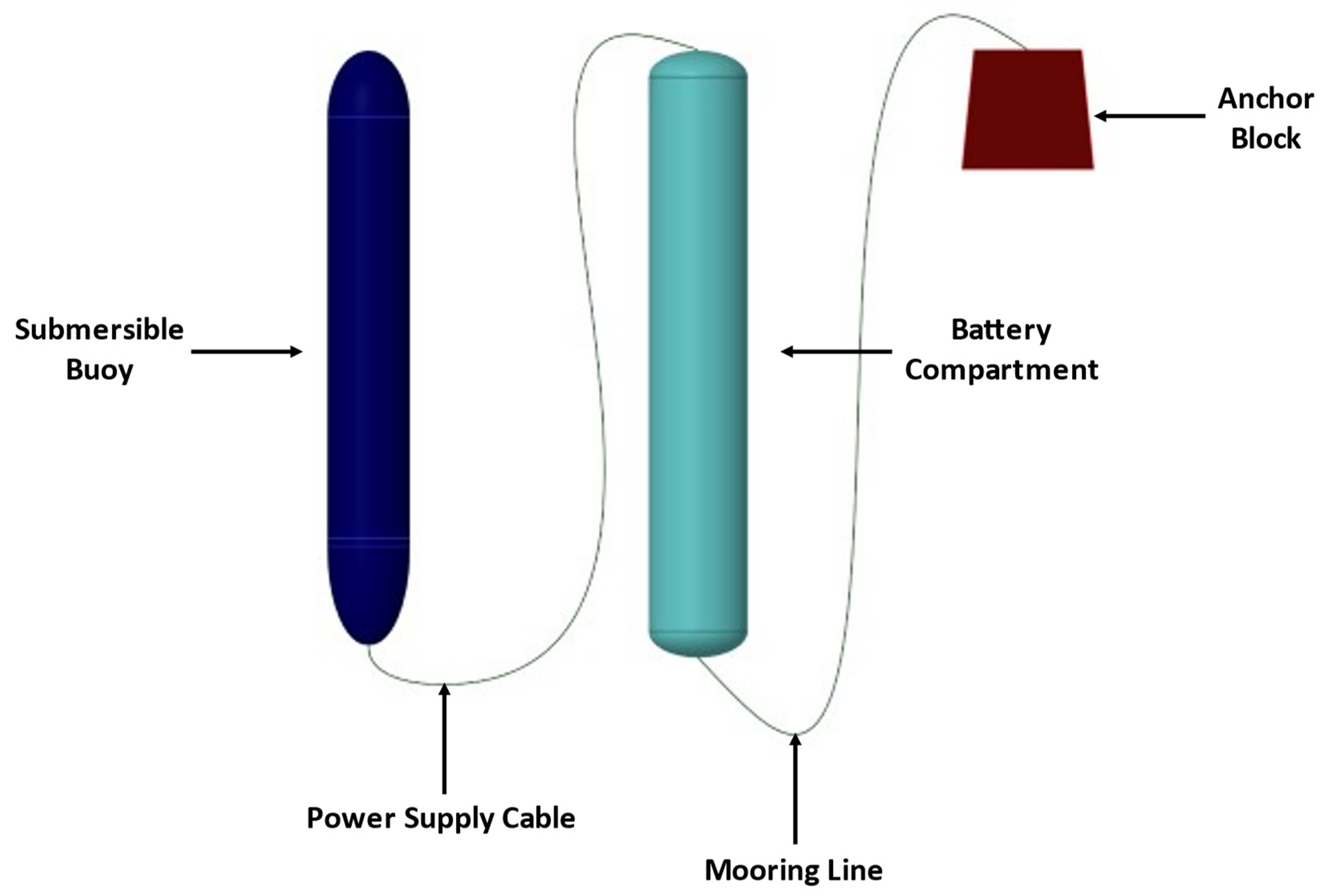
2. Background
3. Hydraulic Resistance Calculation
3.1. Numerical Method
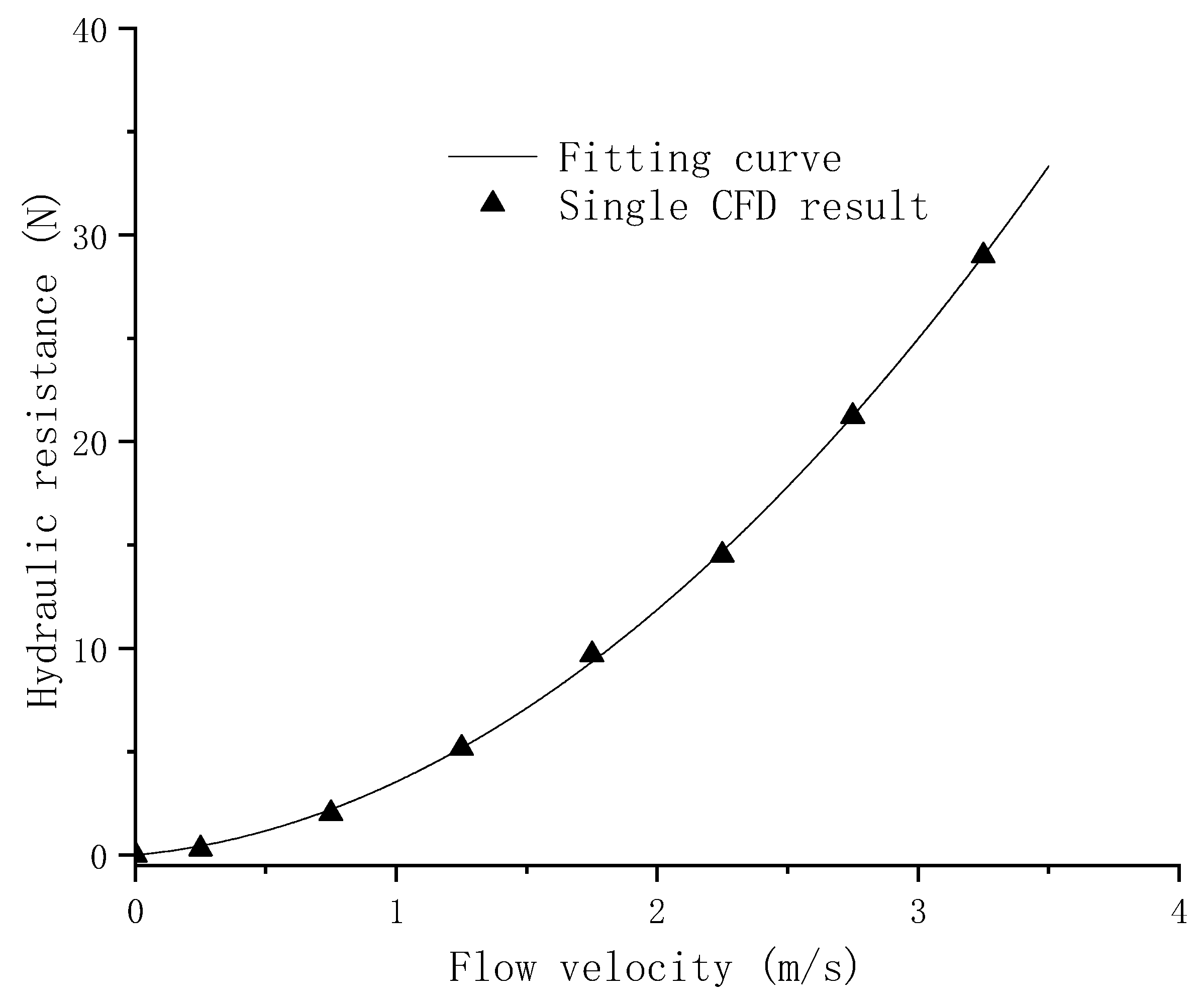
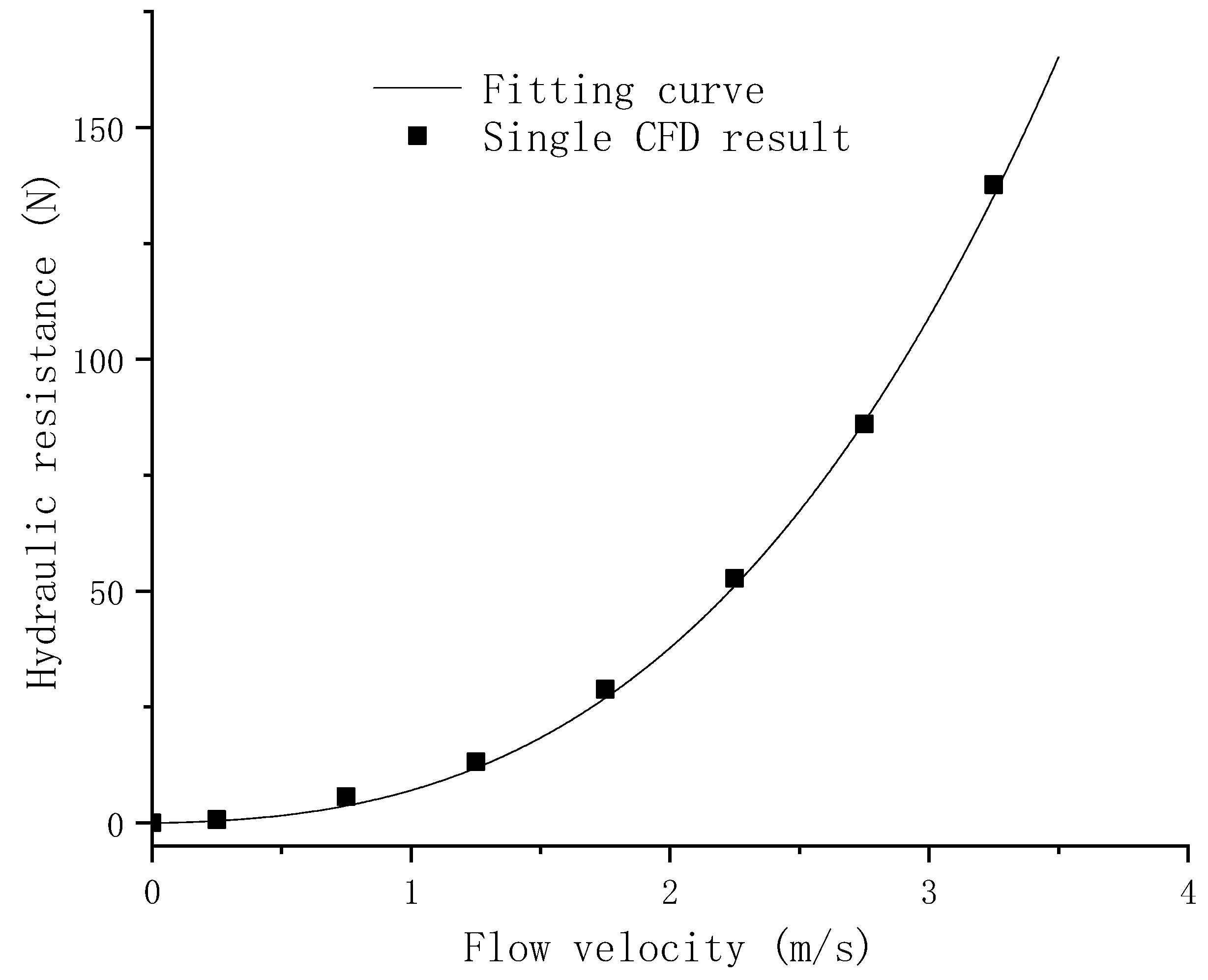
3.2. Numerical Method Verification
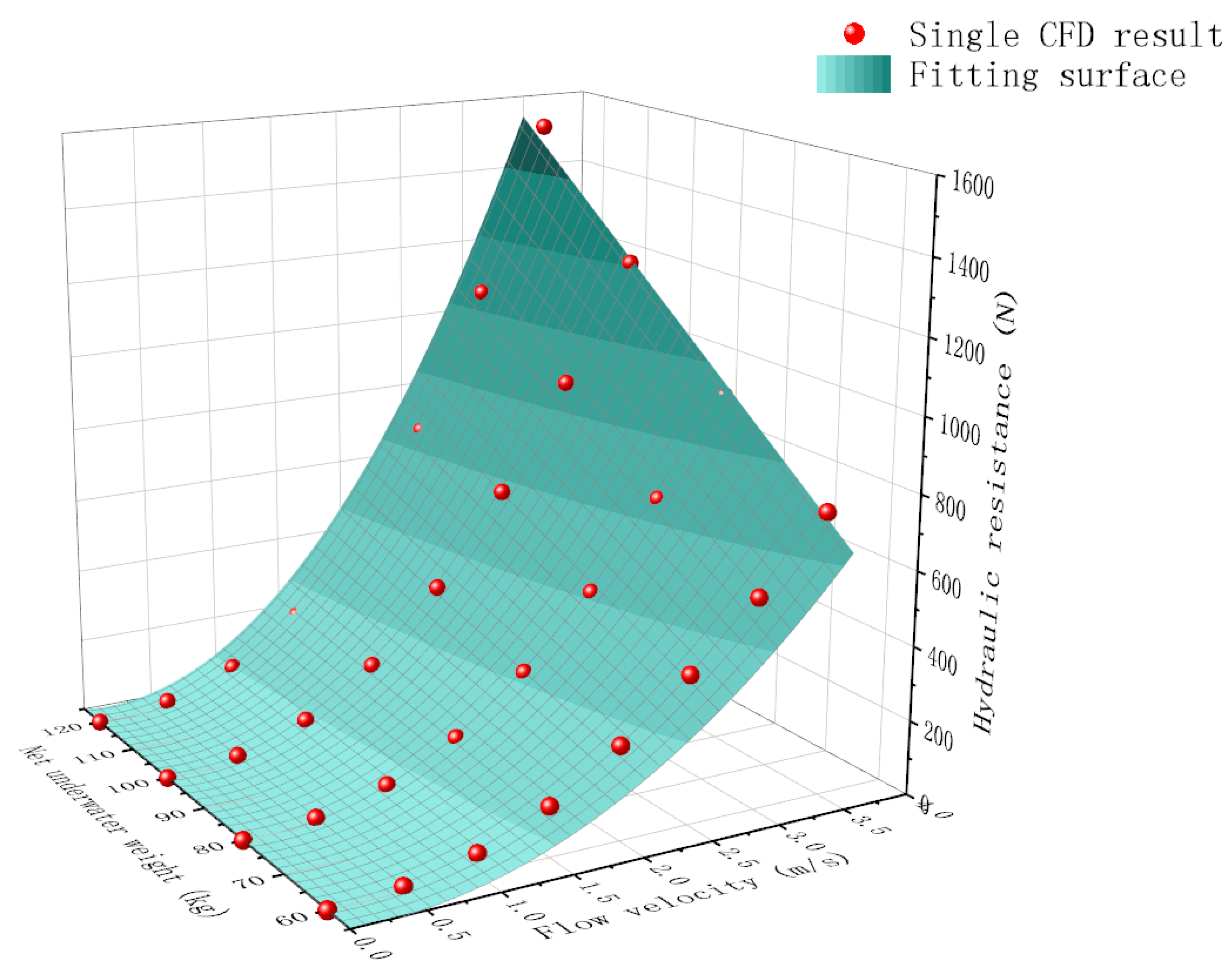
3.3. Hydraulic Resistance of Components in Submersible Buoy System
4. Dynamic Model of the Marine Submersible Buoy System
4.1. Dynamic Equations of Anchor Last Deployment Process
4.2. Velocity Variation of Marine Submersible Buoy
4.3. Tension Variation of Cables in Marine Submersible Buoy
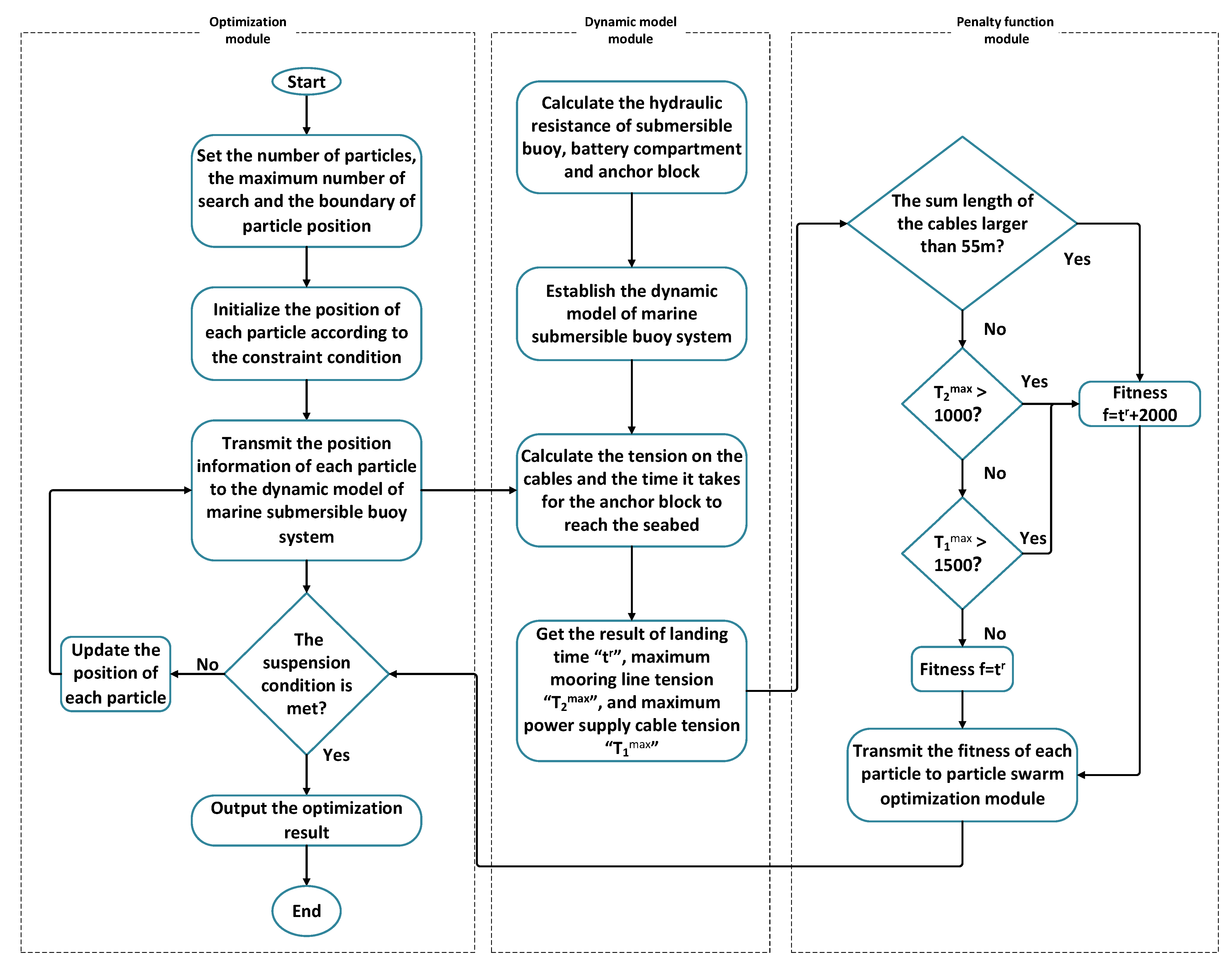
5. Optimization of Marine Submersible Buoy System
5.1. Particle Swarm Optimization
5.2. Optimization Model
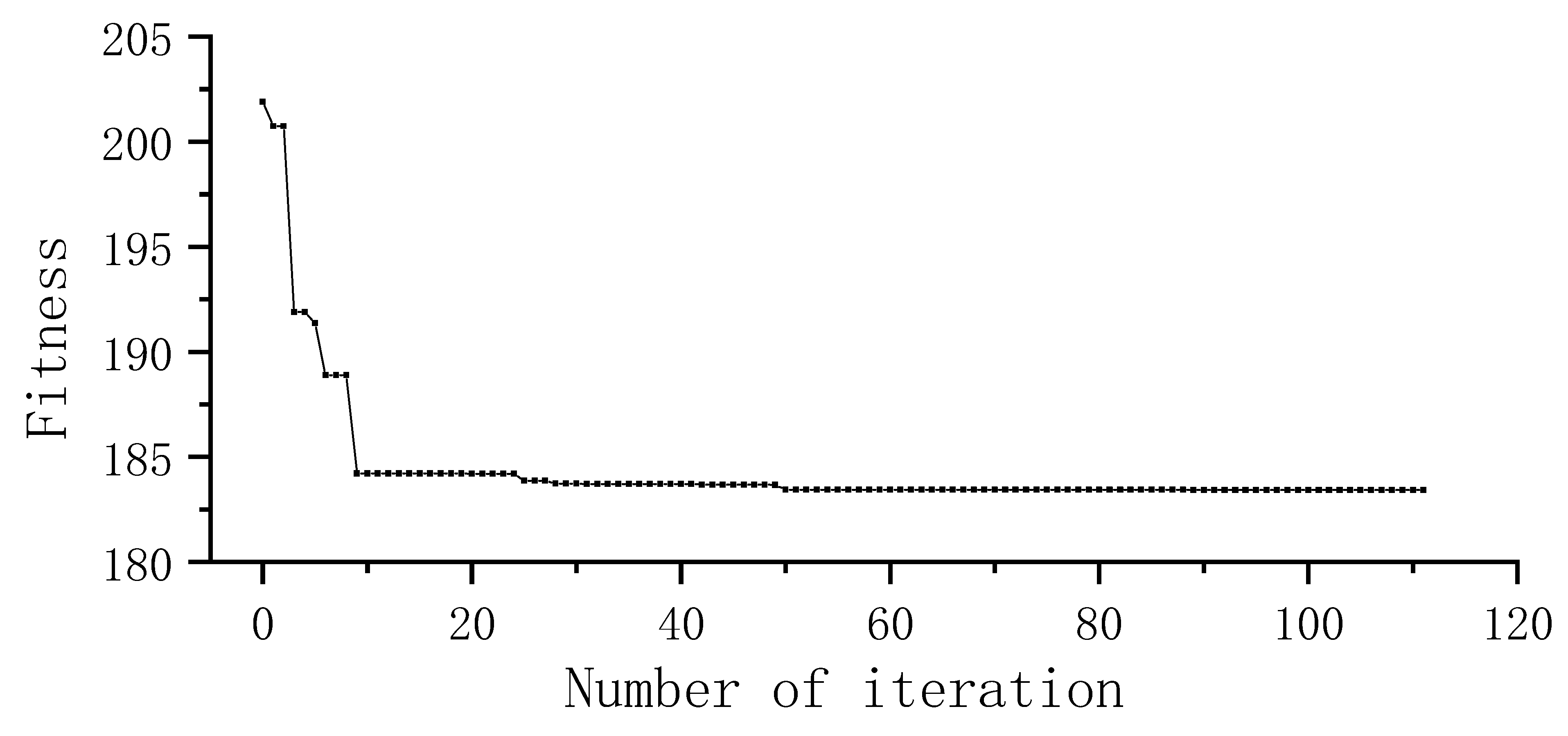
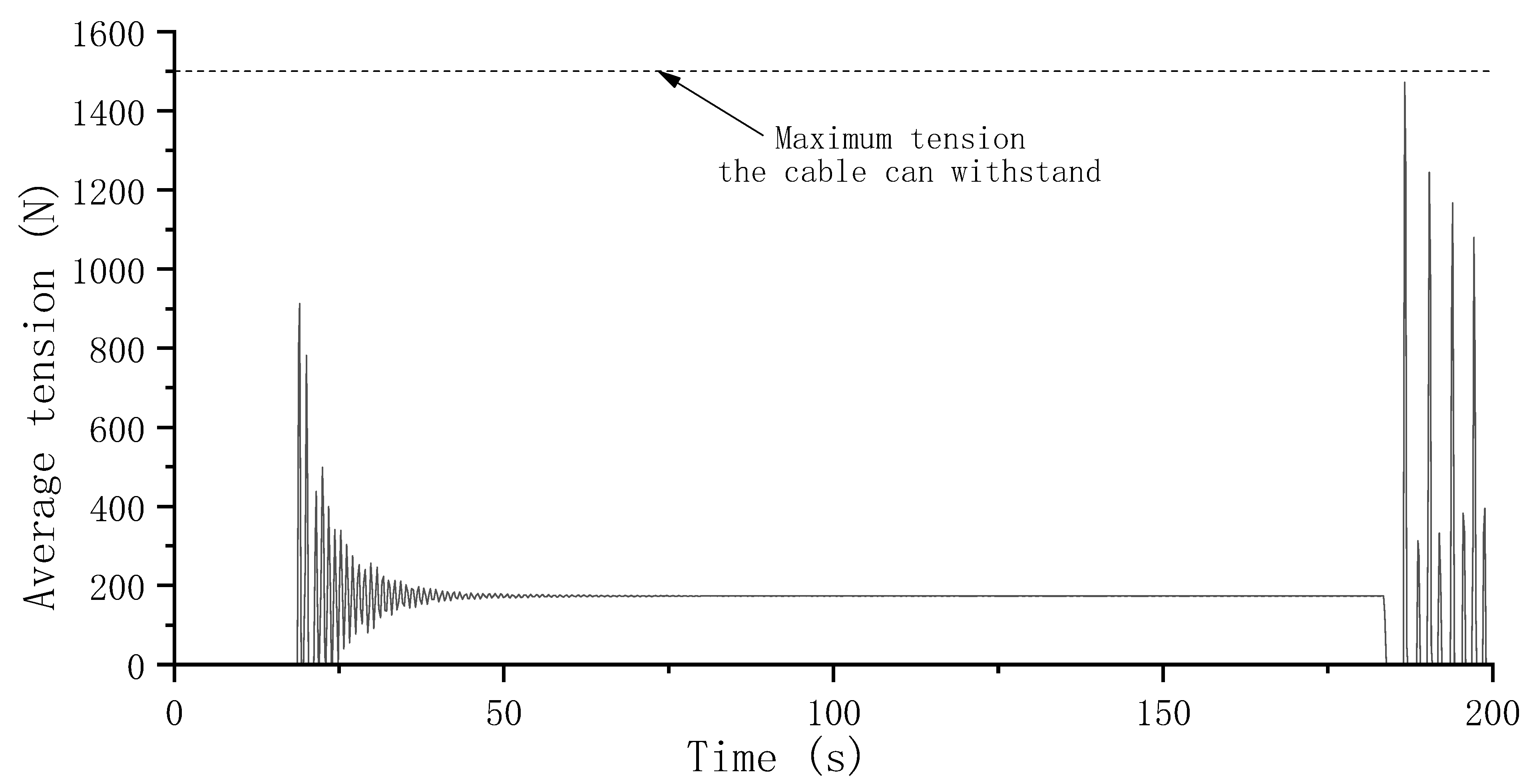
5.3. Optimization Result and Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Da, L.; Wang, C.; Lu, X.; Han, M.; Deng, X. The characteristic analysis of ambient sea noise spectrum based on submersible buoy. Acta Oceanol. Sin. 2014, 36, 54–60. [Google Scholar]
- Feng, S.; Wang, L.; Dong, L.; Li, Q. Design of data-sampling and high-capacity storage system in acoustic submersible buoy application. J. Appl. Acoust. 2014, 33, 81–86. [Google Scholar]
- Xing, Y.; Wang, Z.; Liu, Z.; Xiang, X.; Yu, Y.; Xu, Y. Underwater Acoustics Data Acquisition System Based on Submersible Buoy. Meas. Control Technol. 2015, 34, 28–30,34. [Google Scholar]
- Zhang, H.; Cao, W.; Wu, Z.; Song, X.; Wang, J.; Yan, T. Biofouling on deep-sea submersible buoy systems off Xisha and Dongsha Islands in the northern South China Sea. Int. Biodeterior. Biodegrad. 2015, 104, 92–96. [Google Scholar] [CrossRef]
- Meng, K.; Qin, H.; Zhu, X.; Hou, F. Design and test of a new mobile submersible deep-sea seismic recording system. J. Trop. Oceanogr. 2020, 39, 49–56. [Google Scholar]
- Kennedy, J.; Eberhart, R. Particle Swarm Optimization. In Proceedings of the Icnn95-International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995. [Google Scholar]
- Shul’ga, N.A.; Bezverkhii, A.I. Lagrangian description and numerical analysis of a discrete model of flexible systems. Int. Appl. Mech. 2004, 40, 1398–1404. [Google Scholar] [CrossRef]
- Wang, J.; Luan, X. Shell failure and deformation of the submersible buoy under high pressure condition. Mar. Sci. Bull. 2010, 29, 481–487. [Google Scholar]
- Lai, B.; Zhao, C.; Chen, X.; Tang, Y.; Lin, W. A Novel Structural Form of Semi-Submersible Platform for a Floating Offshore Wind Turbine with Hydrodynamic Performance Analysis. In Applied Mechanics and Materials; Trans Tech Publications Ltd.: Stafa-Zurich, Switzerland, 2014; pp. 109–113. [Google Scholar]
- Qiao, D.; Yan, J.; Ou, J. Effects of Mooring Line with Buoys System on the Global Responses of a Semi-Submersible Platform. Brodogradnja 2014, 65, 79–96. [Google Scholar]
- Qui, Z.; Jia, L.; Qin, Y.; Zhang, S.; Sun, X. Dynamic Modeling and Simulating Analysis of Submersible Buoy System. In Applied Mechanics and Materials; Trans Tech Publications Ltd.: Stafa-Zurich, Switzerland, 2014; pp. 1391–1396. [Google Scholar]
- Tsukada, R.I.; Shiguemoto, D.A.; Morooka, C.K. Numerical Simulation of Vim Response of a Submersible Buoy Using a Semi-Empirical Approach. In Proceedings of the 33rd International Conference on Ocean, Offshore and Arctic Engineering, San Francisco, CA, USA, 8–13 June 2014; Volume 2. [Google Scholar]
- Fontoura, D.V.R.; Tsukada, R.I.; Shiguemoto, D.A. Numerical Simulation of a Submersible Buoy Using a Wake Oscillator Model Calibrated for Vim. In Proceedings of the ASME 34th International Conference on Ocean, Offshore and Arctic Engineering, St. John’s, NL, Canada, 31 May–5 June 2015; Volume 2. [Google Scholar]
- Ji, C.; Yuan, Z. Experimental study of a hybrid mooring system. J. Mar. Sci. Technol. 2015, 20, 213–225. [Google Scholar] [CrossRef] [Green Version]
- Zheng, Z.; Xu, J.; Huang, P.; Wang, L.; Yang, X.; Chang, Z. Dynamics of Anchor Last Deployment of Submersible Buoy System. J. Ocean. Univ. China 2016, 15, 69–77. [Google Scholar] [CrossRef]
- Chen, J.; Hu, Z.; Duan, F. Comparisons of dynamical characteristics of a 5 MW floating wind turbine supported by a spar-buoy and a semi-submersible using model testing methods. J. Renew. Sustain. Energy 2018, 10, 053311. [Google Scholar] [CrossRef] [Green Version]
- Ghafari, H.; Dardel, M. Parametric study of catenary mooring system on the dynamic response of the semi-submersible platform. Ocean. Eng. 2018, 153, 319–332. [Google Scholar] [CrossRef]
- Yan, J.; Qiao, D.; Ou, J. Optimal design and hydrodynamic response analysis of deep water mooring system with submerged buoys. Ships Offshore Struct. 2018, 13, 476–487. [Google Scholar] [CrossRef]
- Yang, Q.; Zheng, Y.; Wang, Z.; Zhang, Y.; Hao, Z. The Influence of Vertical Cable on Flow Field and Acoustic Analysis of a Submersible Buoy System Based on CFD. In Proceedings of the 2019 14th IEEE Conference on Industrial Electronics and Applications (ICIEA), Xi’an, China, 19–21 June 2019; pp. 53–57. [Google Scholar]
- Zhang, Y.; Zheng, Y.; Wang, Z.; Yang, Q.; Hao, Z. Flow Noise Assessment and Analysis of Submersible Buoy Based on FEM/AML Method. In Proceedings of the 2019 14th IEEE Conference on Industrial Electronics and Applications (ICIEA), Xi’an, China, 19–21 June 2019; pp. 1386–1391. [Google Scholar]
- Zhilei, Z.; Peng, M.; Houbing, L.; Kun, H.; Feng, L.; Ge, J. A Low-Power DAQ System with High-Speed Storage for Submersible Buoy. In Proceedings of the 2019 IEEE 2nd International Conference on Electronics Technology (ICET), Chengdu, China, 10–13 May 2019; pp. 400–403. [Google Scholar]
- Touzon, I.; Nava, V.; Gao, Z.; Mendikoa, I.; Petuya, V. Small scale experimental validation of a numerical model of the HarshLab2.0 floating platform coupled with a non-linear lumped mass catenary mooring system. Ocean. Eng. 2020, 200, 107036. [Google Scholar] [CrossRef]
- Chandrasekaran, S.; Uddin, S.A.; Wahab, M. Dynamic Analysis of Semi-submersible Under the Postulated Failure of Restraining System with Buoy. Int. J. Steel Struct. 2021, 21, 118–131. [Google Scholar] [CrossRef]
- Rong, X.; Dou, P.; Chen, J. Time-domain coupling analysis of semi-submersible floating foundation with four buoys for offshore wind turbine and its mooring system. J. Phys. Conf. Ser. 2021, 2005, 012208. [Google Scholar] [CrossRef]
- Amaechi, C.V.; Wang, F.; Ye, J. Experimental Study on Motion Characterisation of CALM Buoy Hose System under Water Waves. J. Mar. Sci. Eng. 2022, 10, 204. [Google Scholar] [CrossRef]
- Amaechi, C.V.; Wang, F.; Ye, J. Numerical studies on CALM buoy motion responses and the effect of buoy geometry cum skirt dimensions with its hydrodynamic waves-current interactions. Ocean. Eng. 2022, 244, 110378. [Google Scholar] [CrossRef]
- Chen, X.; Liu, B.; Le, G. Numerical Simulation Research on the Anchor Last Deployment of Marine Submersible Buoy System Based on VOF Method. J. Mar. Sci. Eng. 2022, 10, 1681. [Google Scholar] [CrossRef]
- Han, D.; Wang, W.; Li, X.; Su, X. Optimization design of multiple tuned mass dampers for semi-submersible floating wind turbine. Ocean. Eng. 2022, 264, 112536. [Google Scholar] [CrossRef]
- Li, M.; Liu, Y.; Liu, Y.; Chen, G.; Tang, Q.; Han, Y.; Wen, Y. Simulative Evaluation of the Underwater Geodetic Network Configuration on Kinematic Positioning Performance. Remote Sens. 2022, 14, 1939. [Google Scholar] [CrossRef]
- Neisi, A.; Ghassemi, H.; Iranmanesh, M.; He, G. Effect of the multi-segment mooring system by buoy and clump weights on the dynamic motions of the floating platform. Ocean. Eng. 2022, 260, 111990. [Google Scholar] [CrossRef]
- Harlow, F.H.; Nakayama, P.I. Turbulence Transport Equations. Phys. Fluids 1967, 10, 2323–2332. [Google Scholar] [CrossRef]
- Gao, T.; Wang, Y.; Pang, Y.; Cao, J. Hull shape optimization for autonomous underwater vehicles using CFD. Eng. Appl. Comput. Fluid Mech. 2016, 10, 601–609. [Google Scholar] [CrossRef] [Green Version]






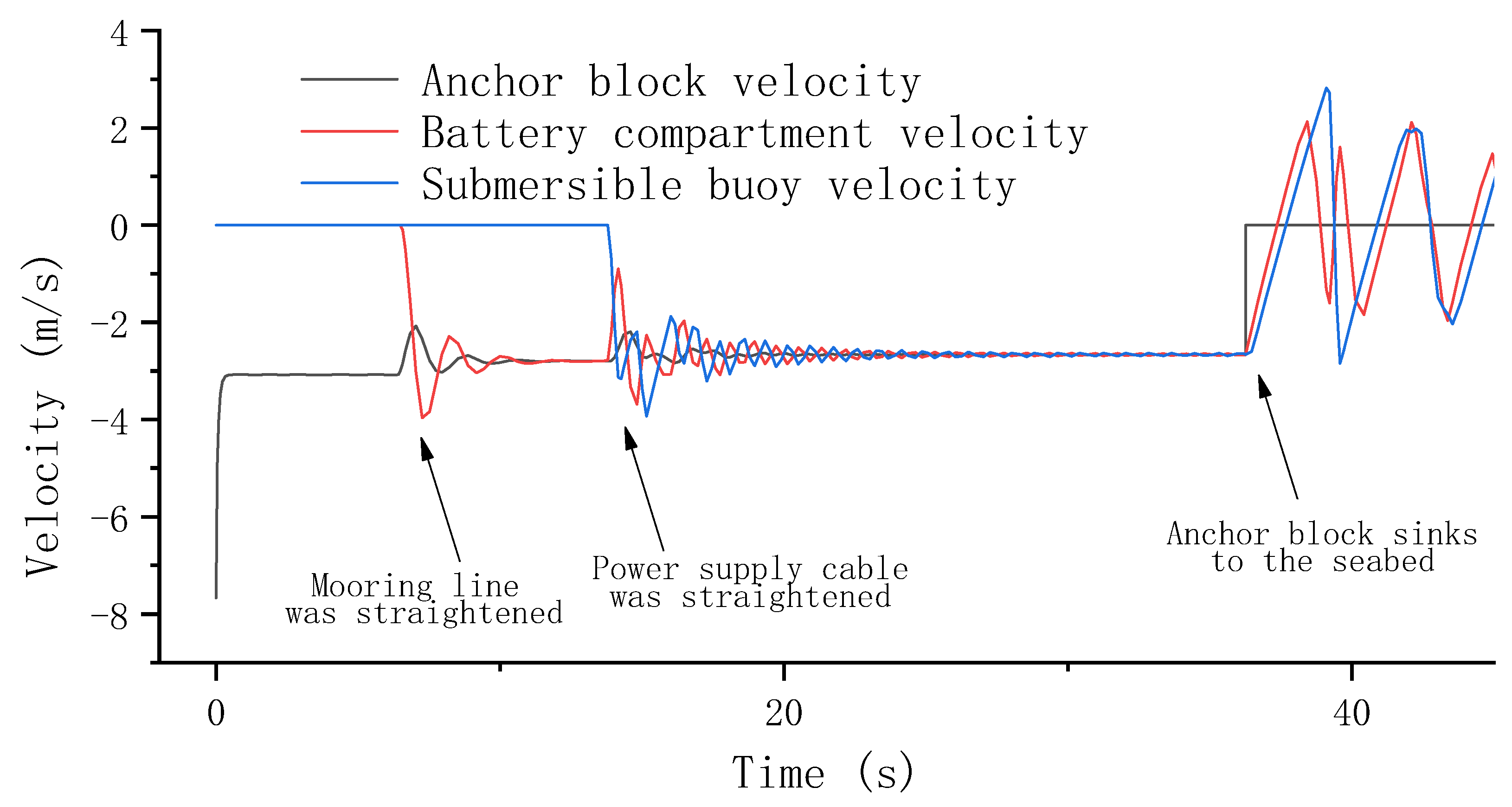
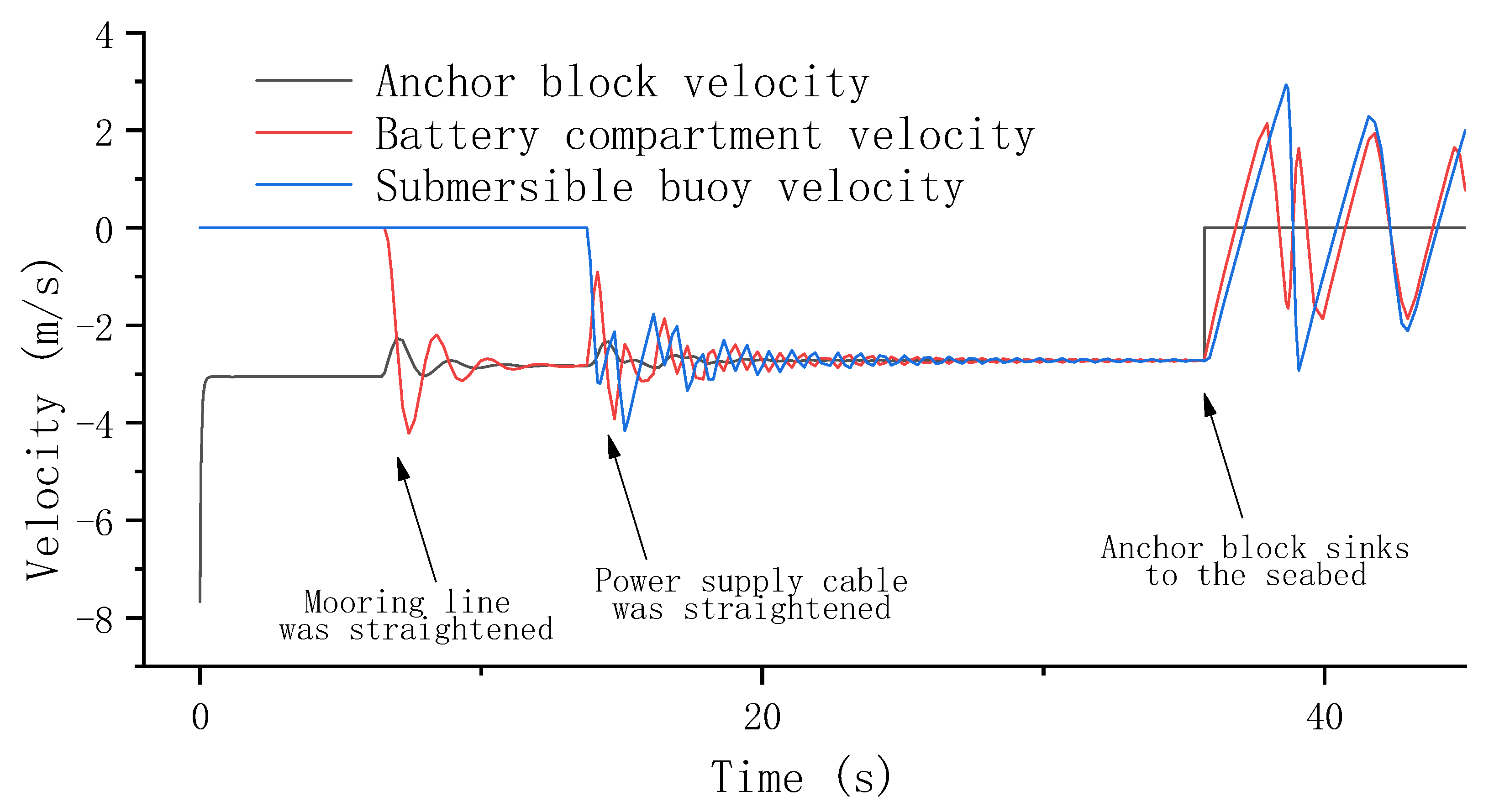
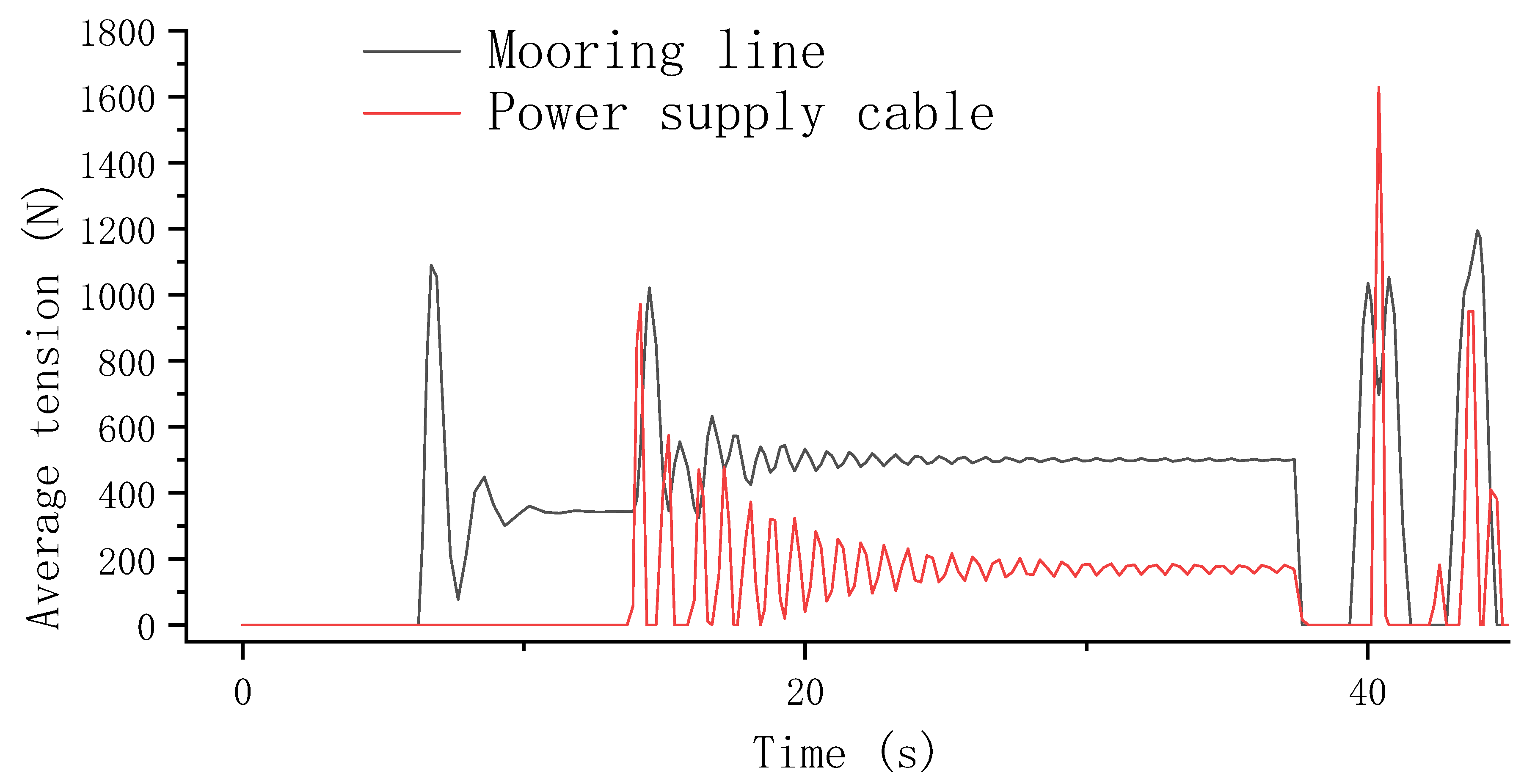

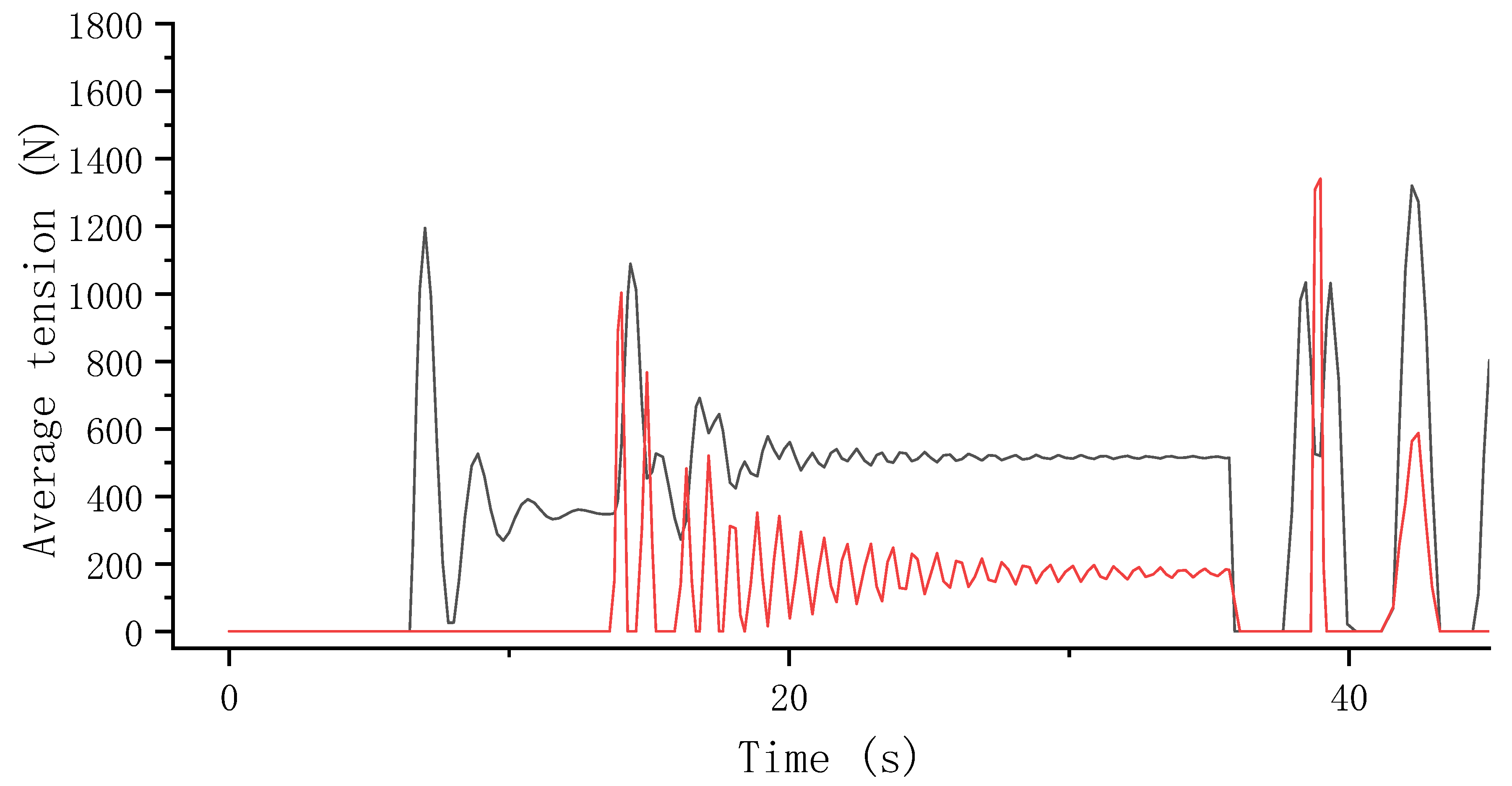

| Component | Added Mass Coefficient | Gravity | Net Buoyancy |
|---|---|---|---|
| Submersible buoy | 0.0991 | 65 kg | 152.88 N |
| Battery compartment | 0.1086 | 100 kg | 257.74 N |
| Cable | Length | Elasticity Modulus | Cross Section Area |
|---|---|---|---|
| Mooring line | 20 m | 1273.2 MPa | 19.6 mm2 |
| Power supply cable | 20 m | 636.6 MPa | 78.5 mm2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, X.; Liu, B.; Le, G. A Multi-Objective Optimization of the Anchor-Last Deployment of the Marine Submersible Buoy System Based on the Particle Swarm Optimization Algorithm. J. Mar. Sci. Eng. 2023, 11, 1305. https://doi.org/10.3390/jmse11071305
Chen X, Liu B, Le G. A Multi-Objective Optimization of the Anchor-Last Deployment of the Marine Submersible Buoy System Based on the Particle Swarm Optimization Algorithm. Journal of Marine Science and Engineering. 2023; 11(7):1305. https://doi.org/10.3390/jmse11071305
Chicago/Turabian StyleChen, Xiaohan, Bing Liu, and Guigao Le. 2023. "A Multi-Objective Optimization of the Anchor-Last Deployment of the Marine Submersible Buoy System Based on the Particle Swarm Optimization Algorithm" Journal of Marine Science and Engineering 11, no. 7: 1305. https://doi.org/10.3390/jmse11071305
APA StyleChen, X., Liu, B., & Le, G. (2023). A Multi-Objective Optimization of the Anchor-Last Deployment of the Marine Submersible Buoy System Based on the Particle Swarm Optimization Algorithm. Journal of Marine Science and Engineering, 11(7), 1305. https://doi.org/10.3390/jmse11071305






