Numerical Investigation on Cavitation Jet in Circular Arc Curve Chamber Self-Excited Oscillation Nozzle
Abstract
:1. Introduction
2. Design of SEON
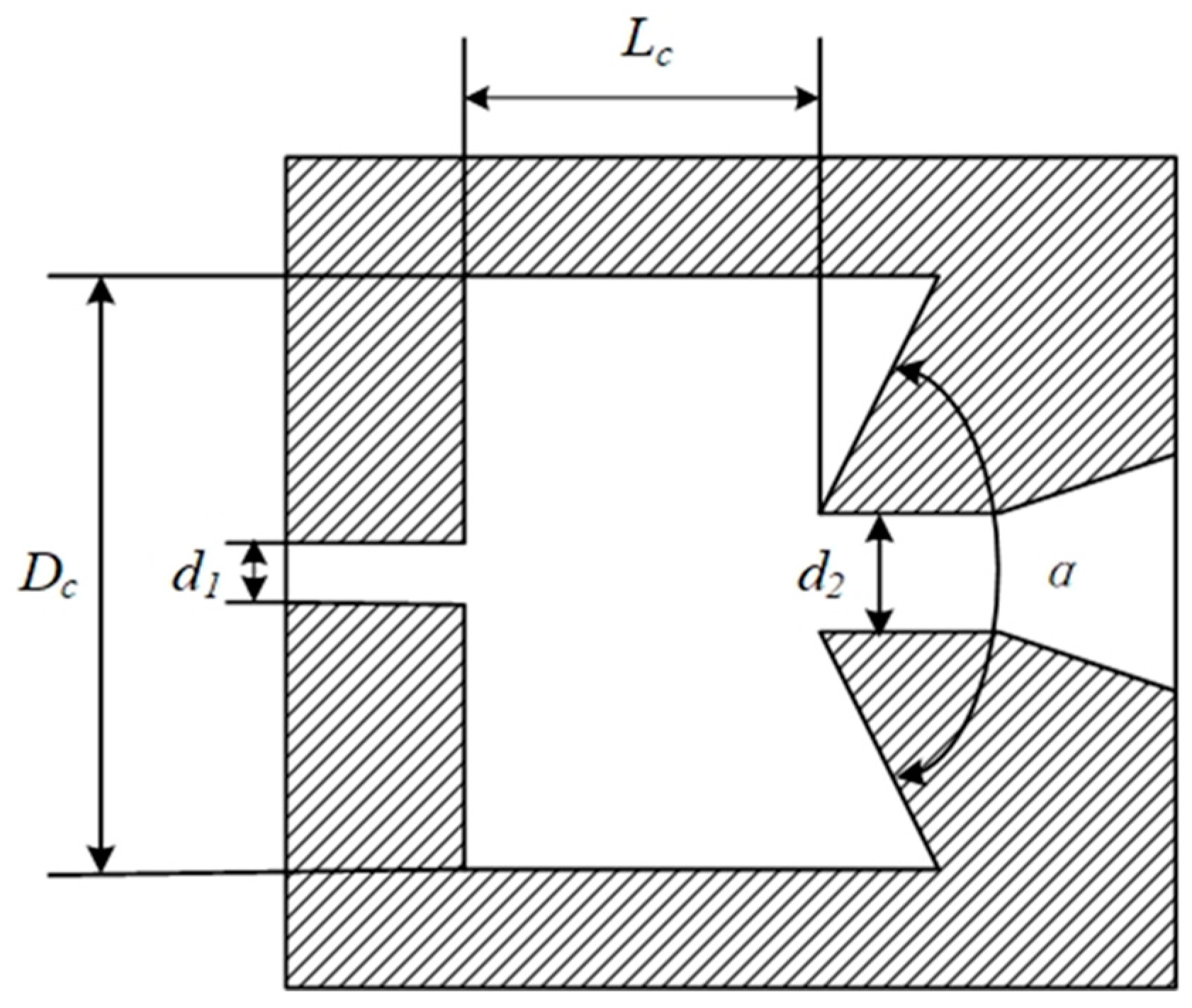
2.1. Design of Broken-Line Chamber SEON
2.2. Design of Circular Arc Curve Chamber SEON
3. Modeling
4. Results and Discussion
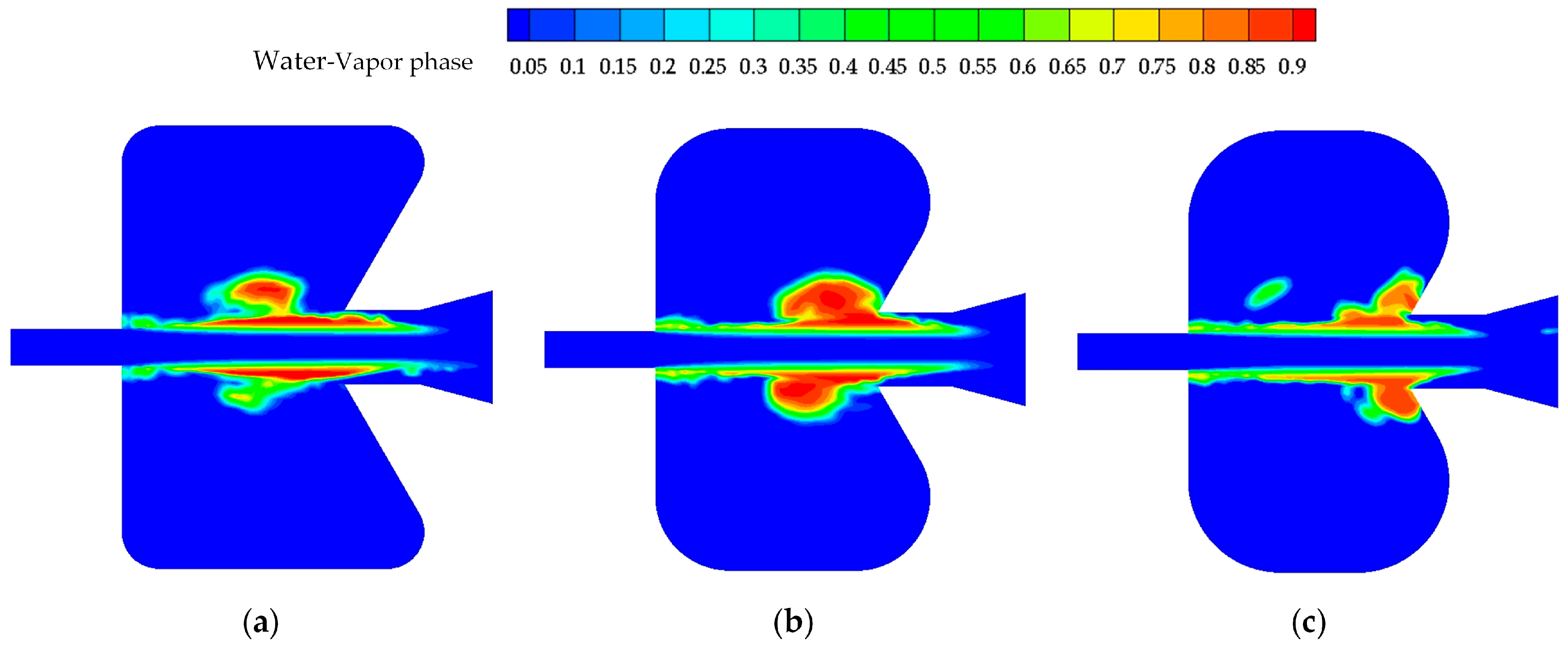
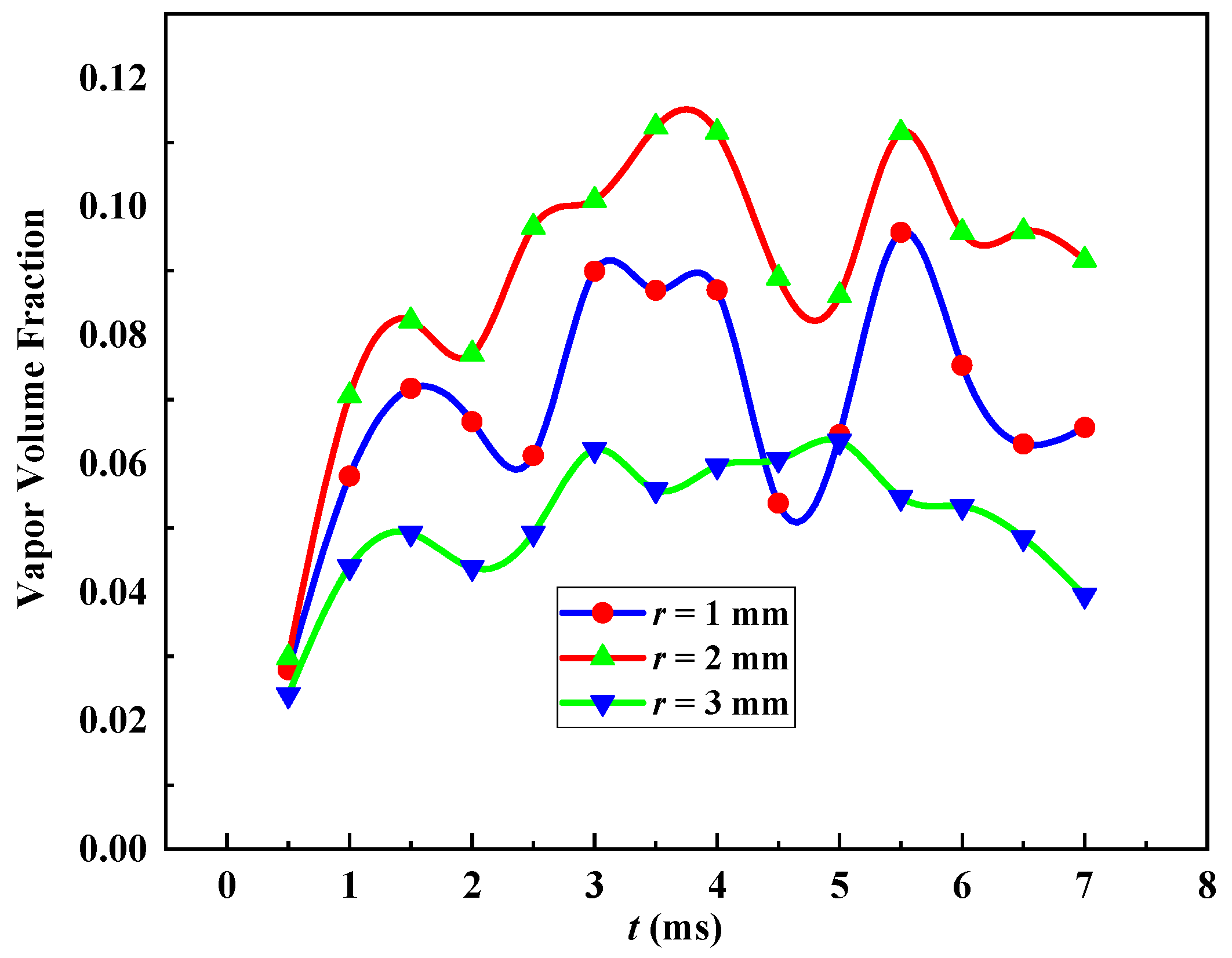
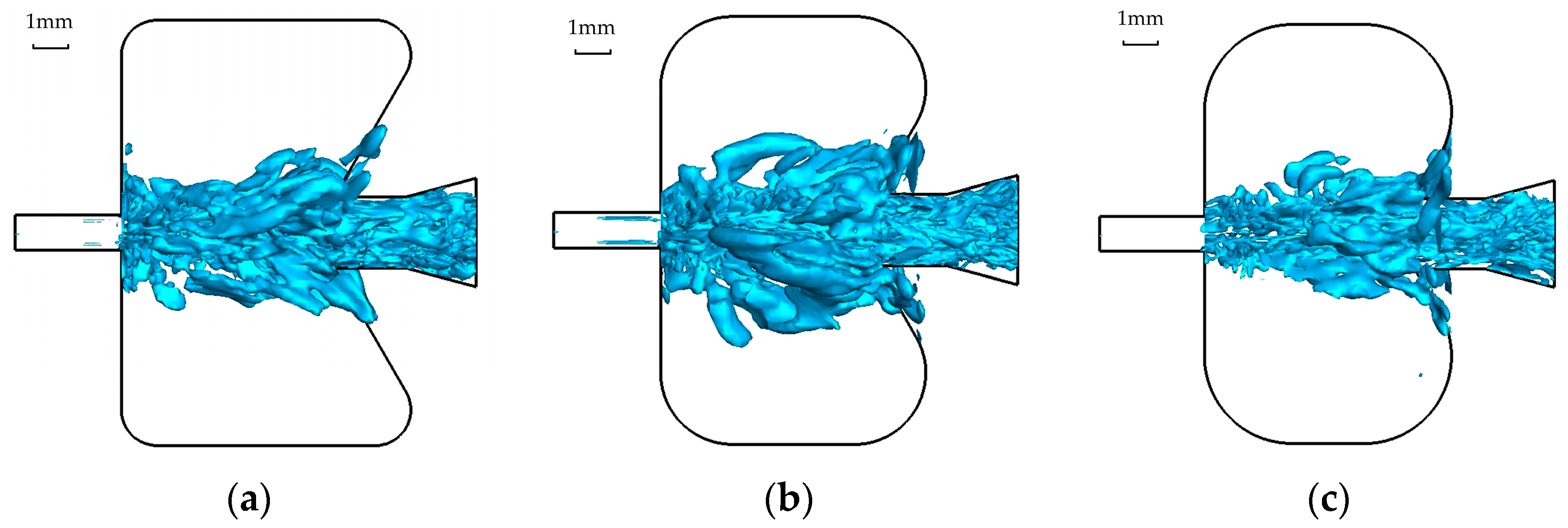
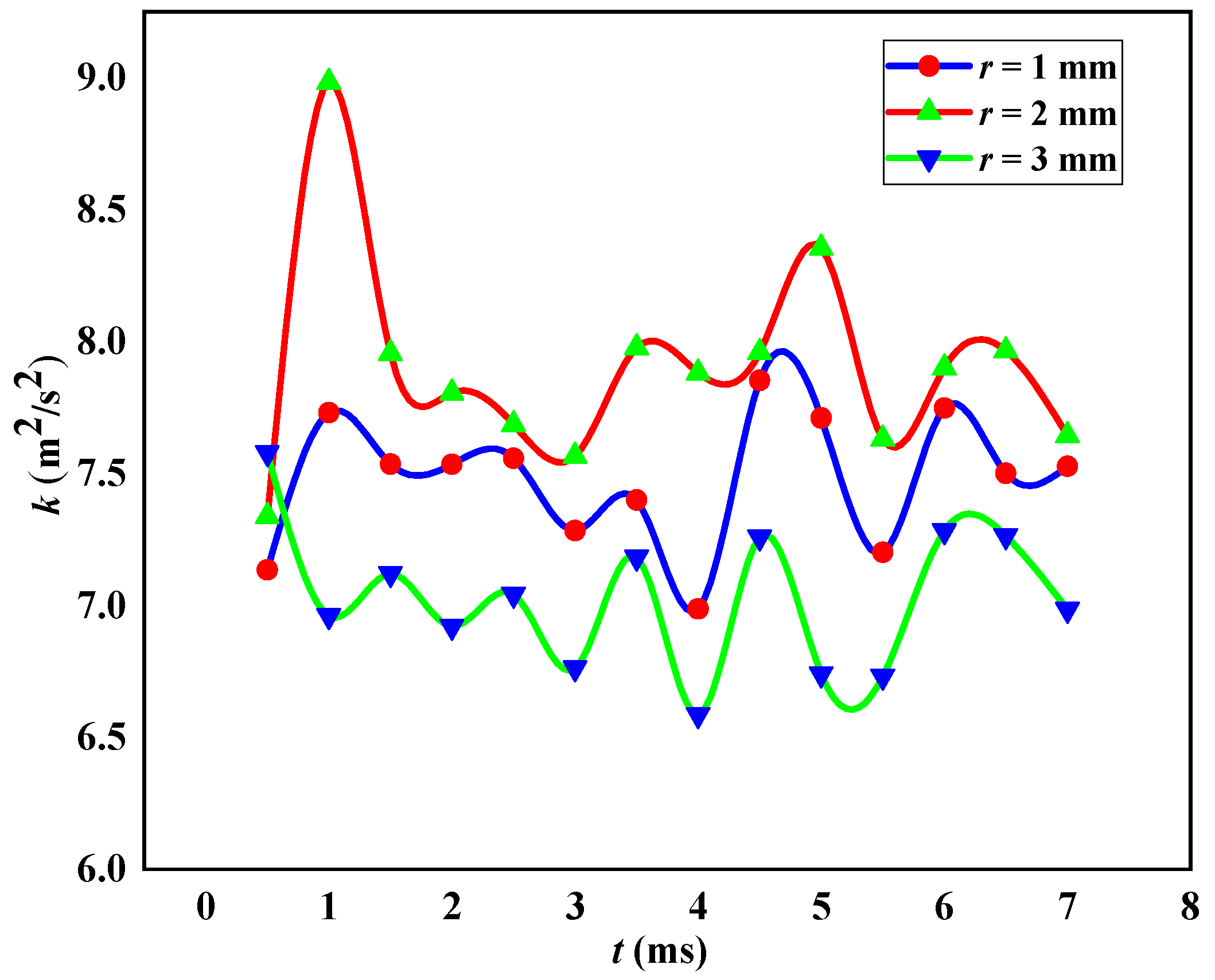
4.1. Effect of Circular Arc Radius on Cavitation Performance of SEON
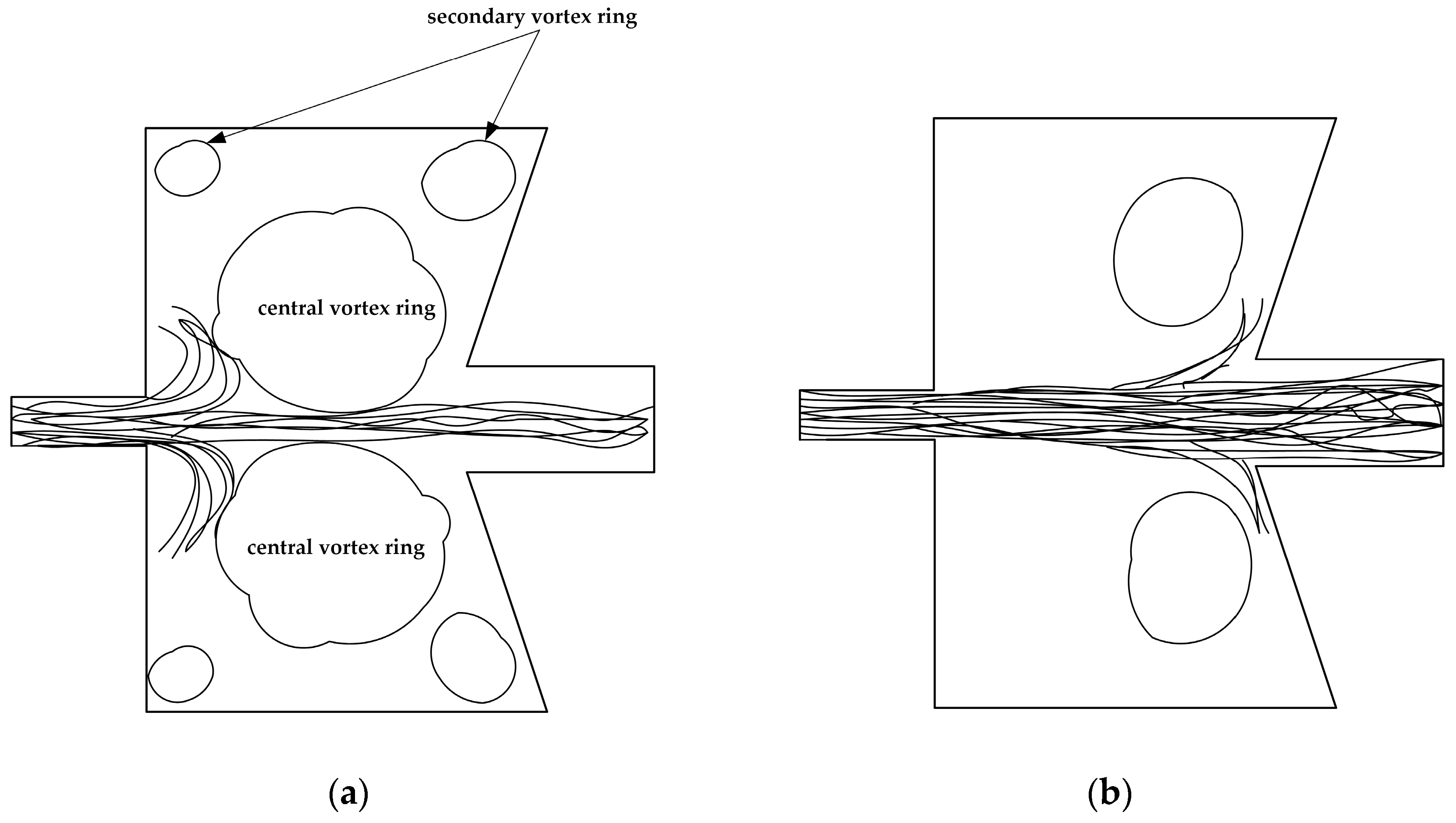
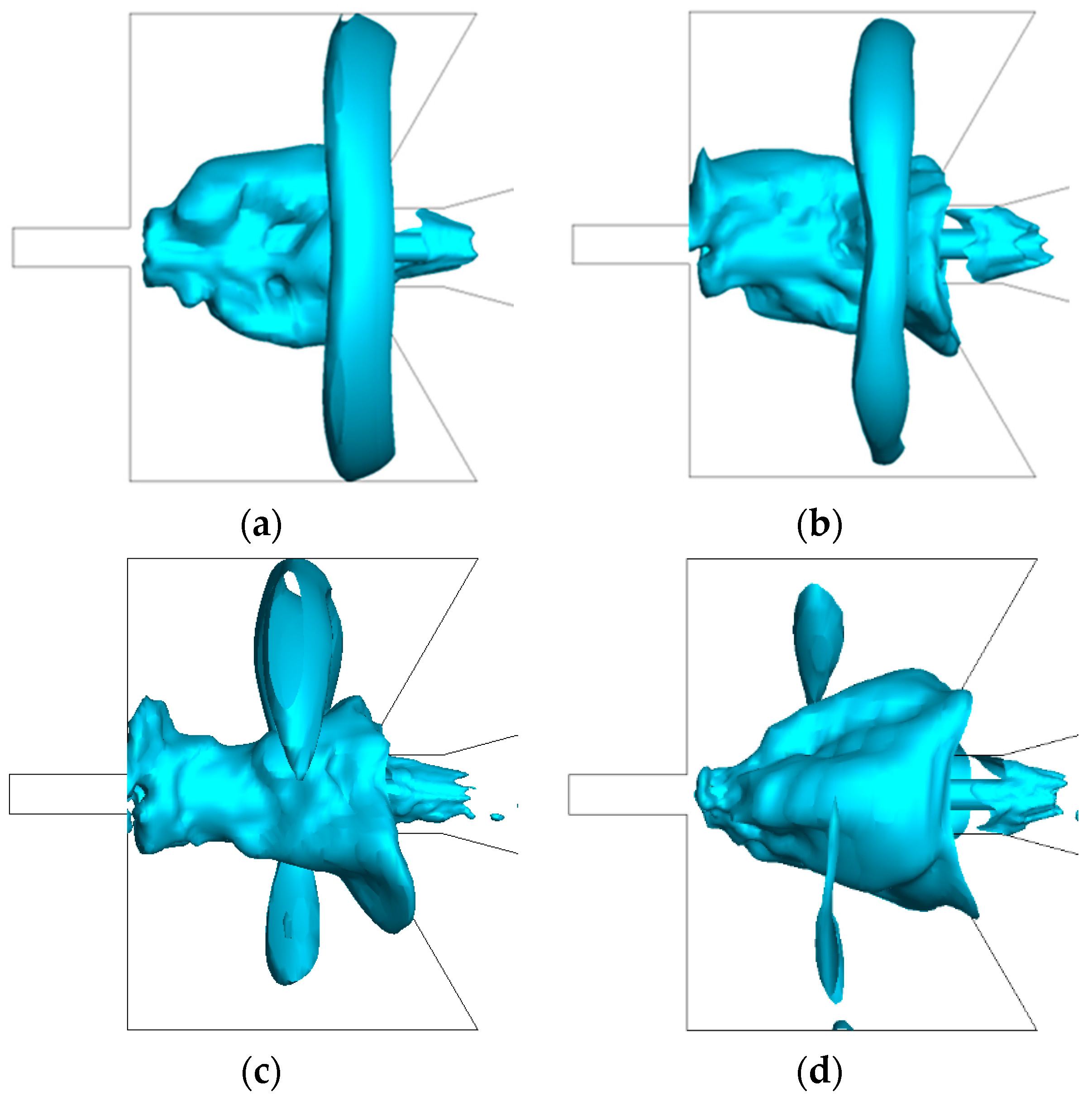
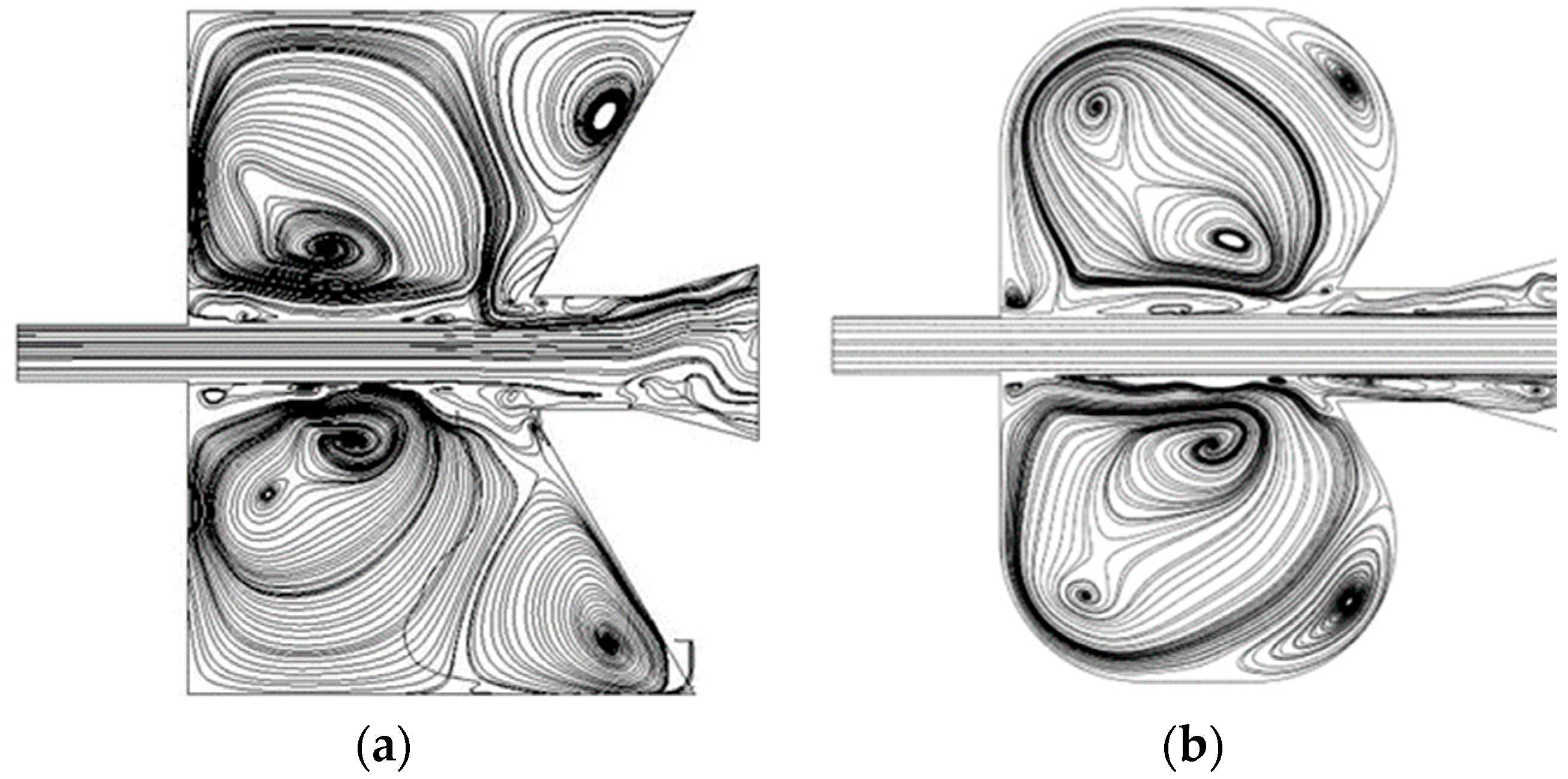
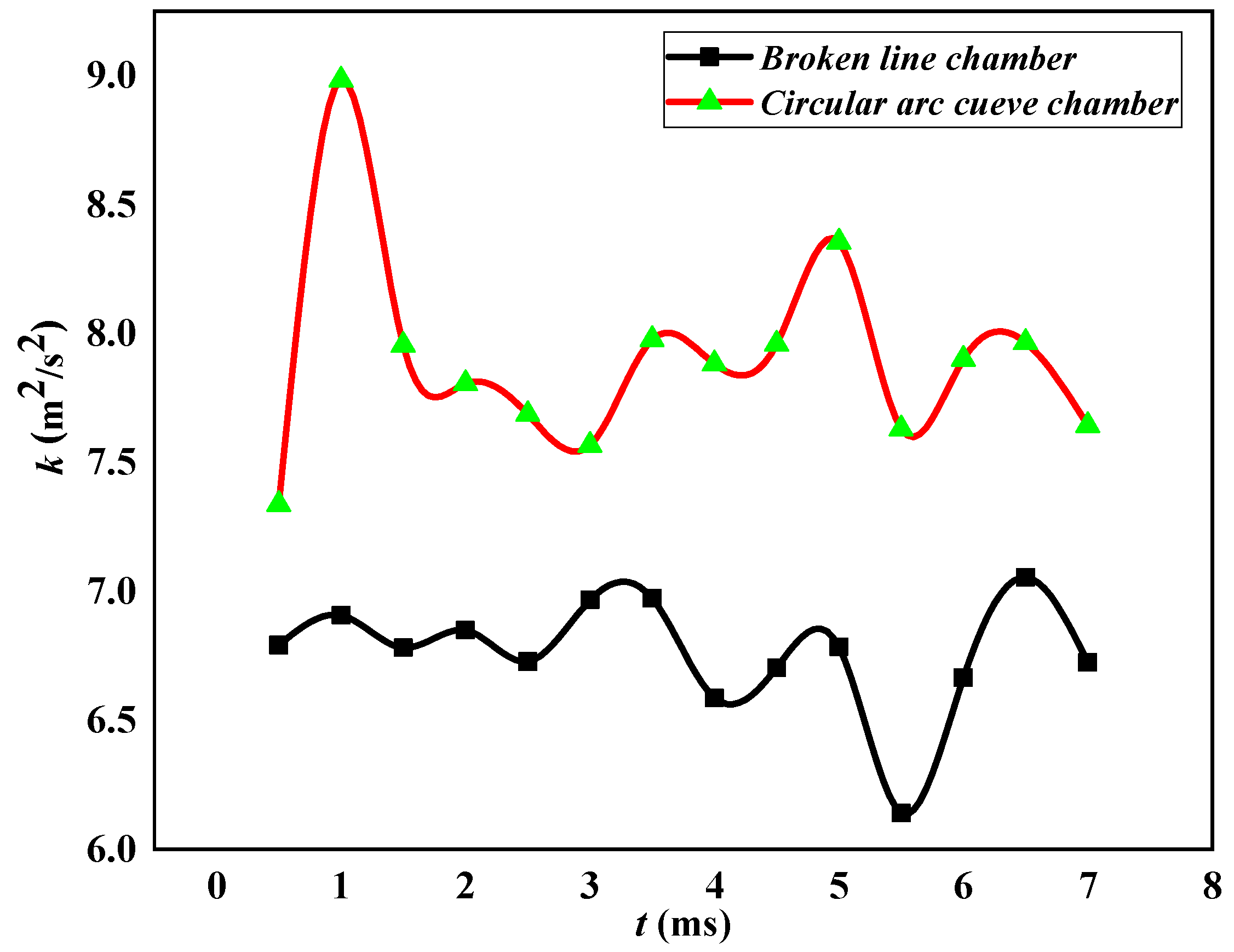
4.2. Comparative Study on Circular Arc Curve Chamber SEON and Broken-Line Chamber SEON
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Cui, L.H.; Ma, F.; Cai, T.F. Investigation of Pressure Oscillation and Cavitation Characteristics for Submerged Self-Resonating Waterjet. Appl. Sci. 2021, 11, 6972. [Google Scholar] [CrossRef]
- Liu, C.T.; Liu, G.; Yan, Z.X. Study on Cleaning Effect of Different Water Flows on the Pulsed Cavitating Jet Nozzle. Shock Vib. 2019, 2019, 1496594. [Google Scholar] [CrossRef]
- Yamauchi, Y.; Soyama, H.; Adachi, Y.; Yamauchi, Y.; Soyama, H.; Adachi, Y.; Sato, K.; Shindo, T.; Oba, R.; Oshima, R.; et al. Suitable Region of High-Speed Submerged Water Jets for Cutting and Peening. JSME Int. J. Ser. B 1995, 38, 31–38. [Google Scholar] [CrossRef] [Green Version]
- Peng, K.; Tian, S.; Li, G.; Huang, Z.; Zhang, Z. Cavitation in water jet under high ambient pressure conditions. Exp. Therm. Fluid Sci. 2017, 89, 9–18. [Google Scholar] [CrossRef]
- Johnson, V.E., Jr.; Chahine, G.L.; Lindenmuth, W.T.; Conn, A.F.; Frederick, G.S.; Giacchino, G.J., Jr. Cavitating and Structured Jets for Mechanical Bits to Increase Drilling Rate—Part I: Theory and Concepts. J. Energy Resour. Technol. 1984, 106, 282–288. [Google Scholar] [CrossRef]
- Liu, W.C.; Kang, Y.; Zhang, M.X.; Wang, X.; Li, D.; Xie, L. Experimental and theoretical analysis on chamber pressure of a self-resonating cavitation waterjet. Ocean Eng. 2018, 151, 33–45. [Google Scholar] [CrossRef]
- Pan, Y.; Ma, F.; Liu, B.S.; Cai, T. Cavitation intensity and erosion pattern of a self-excited cavitating jet. J. Mater. Process. Technol. 2020, 282, 116668. [Google Scholar] [CrossRef]
- Zhou, M.M.; Liu, H.X.; Kang, C.; Wei, X. Resistance of curved surfaces to the cavitation erosion produced through high-pressure submerged waterjet. Wear 2019, 440, 203091. [Google Scholar] [CrossRef]
- Hutli, E.; Nedeljkovic, M.S.; Bonyar, A.; Légrády, D. Experimental study on the influence of geometrical parameters on the cavitation erosion characteristics of high speed submerged jets. Exp. Therm. Fluid Sci. 2017, 80, 281–292. [Google Scholar] [CrossRef] [Green Version]
- Zhong, X.; Dong, J.M.; Liu, M.S.; Meng, R.; Li, S.; Pan, X. Experimental study on ship fouling cleaning by ultrasonic-enhanced submerged cavitation jet: A preliminary study. Ocean Eng. 2022, 258, 111844. [Google Scholar] [CrossRef]
- Peng, C.; Tian, S.C.; Li, G.S. Joint experiments of cavitation jet: High-speed visualization and erosion test. Ocean Eng. 2018, 149, 1–13. [Google Scholar] [CrossRef]
- Watanabe, R.; Yanagisawa, K.; Yamagata, T.; Fujisawa, N. Simultaneous shadowgraph imaging and acceleration pulse measurement of cavitating jet. Wear 2016, 358–359, 72–79. [Google Scholar] [CrossRef]
- Fujisawa, N.; Fujita, Y.; Yanagisawa, K.; Fujisawa, K.; Yamagata, T. Simultaneous observation of cavitation collapse and shock wave formation in cavitating jet. Exp. Therm. Fluid Sci. 2018, 94, 159–167. [Google Scholar] [CrossRef]
- Zhong, X.; Dong, J.M.; Meng, R.X.; Liu, M.; Pan, X. Quantitative Evaluation of Submerged Cavitation Jet Performance Based on Image Processing Method. J. Mar. Sci. Eng. 2022, 10, 1336. [Google Scholar] [CrossRef]
- Peng, C.; Tian, S.C.; Li, G.S. Determination of the shedding frequency of cavitation cloud in a submerged cavitation jet based on high-speed photography images. J. Hydrodyn. 2021, 33, 127–139. [Google Scholar] [CrossRef]
- Petkovšek, M.; Dular, M. Simultaneous observation of cavitation structures and cavitation erosion. Wear 2013, 300, 55–64. [Google Scholar] [CrossRef]
- Soyama, H. High-speed observation of a cavitating jet in air. J. Fluids Eng. Trans. ASME 2005, 127, 1095–1101. [Google Scholar] [CrossRef]
- Cai, T.F.; Pan, Y.; Ma, F. Effects of nozzle lip geometry on the cavitation erosion characteristics of self-excited cavitating waterjet. Exp. Therm. Fluid Sci. 2020, 117, 110137. [Google Scholar] [CrossRef]
- Li, D.; Kang, Y.; Ding, X.L.; Liu, W. Experimental study on the effects of feeding pipe diameter on the cavitation erosion performance of self-resonating cavitating waterjet. Exp. Therm. Fluid Sci. 2017, 82, 314–325. [Google Scholar] [CrossRef]
- Li, Y.J.; Chen, H.S.; Wang, J.D.; Chen, D. Effect of Grooves on Cavitation Around the Body of Revolution. J. Fluids Eng. Trans. ASME 2010, 132, 011301. [Google Scholar] [CrossRef]
- Li, D.; Kang, Y.; Wang, X.C.; Ding, X.; Fang, Z. Effects of nozzle inner surface roughness on the cavitation erosion characteristics of high speed submerged jets. Exp. Therm. Fluid Sci. 2016, 74, 444–452. [Google Scholar] [CrossRef]
- Cai, T.; Pan, Y.; Ma, F.; Xu, P. Effects of Organ-Pipe Chamber Geometry on the Frequency and Erosion Characteristics of the Self-Excited Cavitating Waterjet. Energies 2020, 13, 978. [Google Scholar] [CrossRef] [Green Version]
- Wang, Z.H.; Hu, Y.N.; Chen, S.; Zhou, L.; Xu, W.; Lien, F.S. Investigation of self-excited oscillation chamber cavitation effect with special emphasis on wall shape. Trans. Can. Soc. Mech. Eng. 2020, 44, 244–255. [Google Scholar] [CrossRef]
- Wand, L.Q.; Wang, X.M.; Xu, R.L.; Li, J.Y. Structure-parameter Optimized Study of Self-exicited Oscillation Pulsation-jet Nozzle in Low-press and Amount-flux. Fluid Mach. 2004, 32, 7–10. [Google Scholar] [CrossRef]
- Lai, S.; Liao, Z. The Theory and Experimental Study of the Self-Excited Oscillation Pulsed Jet Nozzle (Pipeline Pulsed Flow Generator). Nat. Resour. 2013, 4, 395–403. [Google Scholar] [CrossRef] [Green Version]
- Yang, Y.; Shi, W.; Tan, L.; Li, W.; Chen, S.; Pan, B. Numerical Research of the Submerged High-Pressure Cavitation Water Jet Based on the RANS-LES Hybrid Model. Shock Vib. 2021, 2021, 6616718. [Google Scholar] [CrossRef]


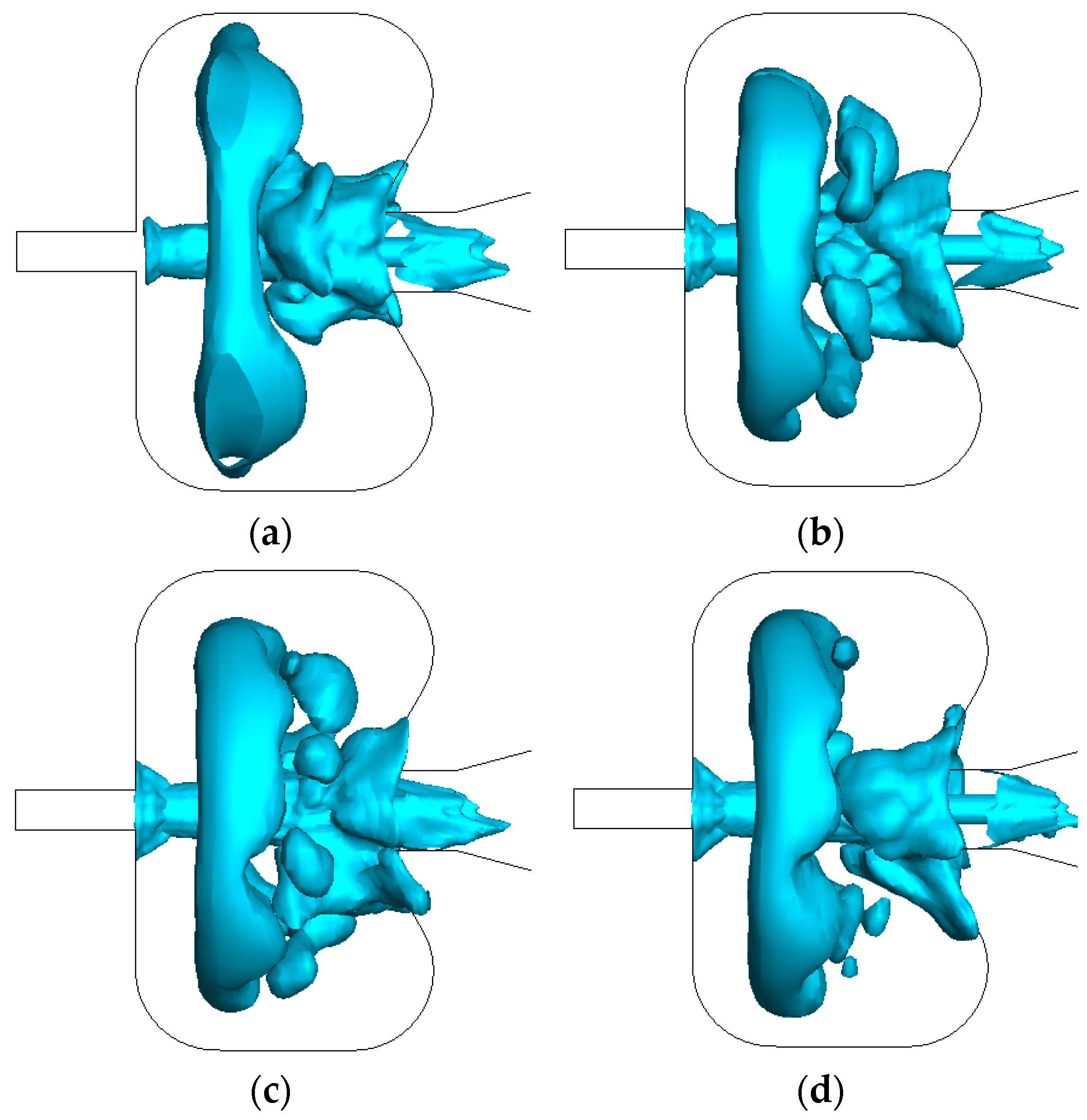


| Dimensionless Parameters | d2/d1 | Dc/d2 | Lc/Dc |
|---|---|---|---|
| Value | 1.6–2.3 | 6.0–9.0 | 0.5–0.7 |
| Structural Parameter | Symbol | Value | Unit |
|---|---|---|---|
| Upper nozzle diameter | d1 | 1 | mm |
| Lower nozzle diameter | d2 | 2 | mm |
| Chamber diameter | Dc | 12 | mm |
| Chamber length | Lc | 6 | mm |
| Collision wall angle | α | 120 | o |
| Grid Number | Velocity (m/s) | Deviation (%) | Pressure (Pa) | Deviation (%) | |
|---|---|---|---|---|---|
| Point A | 462,813 | 200.74 | 20,130,917 | ||
| 504,214 | 200.42 | 0.159 | 20,104,380 | 0.132 | |
| 576,392 | 200.16 | 0.130 | 20,087,306 | 0.085 | |
| 641,547 | 200.12 | 0.019 | 20,076,867 | 0.052 | |
| 799,182 | 200.09 | 0.015 | 20,083,893 | 0.035 | |
| Point B | 462,813 | 200.47 | 20,275,709 | ||
| 504,214 | 200.80 | 0.164 | 20,125,930 | 0.744 | |
| 576,392 | 200.63 | 0.085 | 20,053,343 | 0.362 | |
| 641,547 | 200.56 | 0.036 | 20,077,435 | 0.120 | |
| 799,182 | 200.61 | 0.024 | 20,094,500 | 0.085 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dong, J.; Meng, R.; Chen, J.; Liu, M.; Zhong, X.; Pan, X. Numerical Investigation on Cavitation Jet in Circular Arc Curve Chamber Self-Excited Oscillation Nozzle. J. Mar. Sci. Eng. 2023, 11, 1391. https://doi.org/10.3390/jmse11071391
Dong J, Meng R, Chen J, Liu M, Zhong X, Pan X. Numerical Investigation on Cavitation Jet in Circular Arc Curve Chamber Self-Excited Oscillation Nozzle. Journal of Marine Science and Engineering. 2023; 11(7):1391. https://doi.org/10.3390/jmse11071391
Chicago/Turabian StyleDong, Jingming, Rongxuan Meng, Jing Chen, Mushan Liu, Xiao Zhong, and Xinxiang Pan. 2023. "Numerical Investigation on Cavitation Jet in Circular Arc Curve Chamber Self-Excited Oscillation Nozzle" Journal of Marine Science and Engineering 11, no. 7: 1391. https://doi.org/10.3390/jmse11071391
APA StyleDong, J., Meng, R., Chen, J., Liu, M., Zhong, X., & Pan, X. (2023). Numerical Investigation on Cavitation Jet in Circular Arc Curve Chamber Self-Excited Oscillation Nozzle. Journal of Marine Science and Engineering, 11(7), 1391. https://doi.org/10.3390/jmse11071391






