Numerical Simulation of Improved Gas Production from Oceanic Gas Hydrate Accumulation by Permeability Enhancement Associated with Geomechanical Response
Abstract
:1. Introduction
1.1. Background
1.2. Targeted Accumulation
1.3. Objectives
2. Methodology
2.1. Coupled Numerical Simulators
2.2. Governing Equations
2.2.1. Flows of Fluid and Heat
2.2.2. Geomechanics
2.2.3. The Coupling Method between Geomechanics and Flows of Fluid and Heat
3. Numerical Model
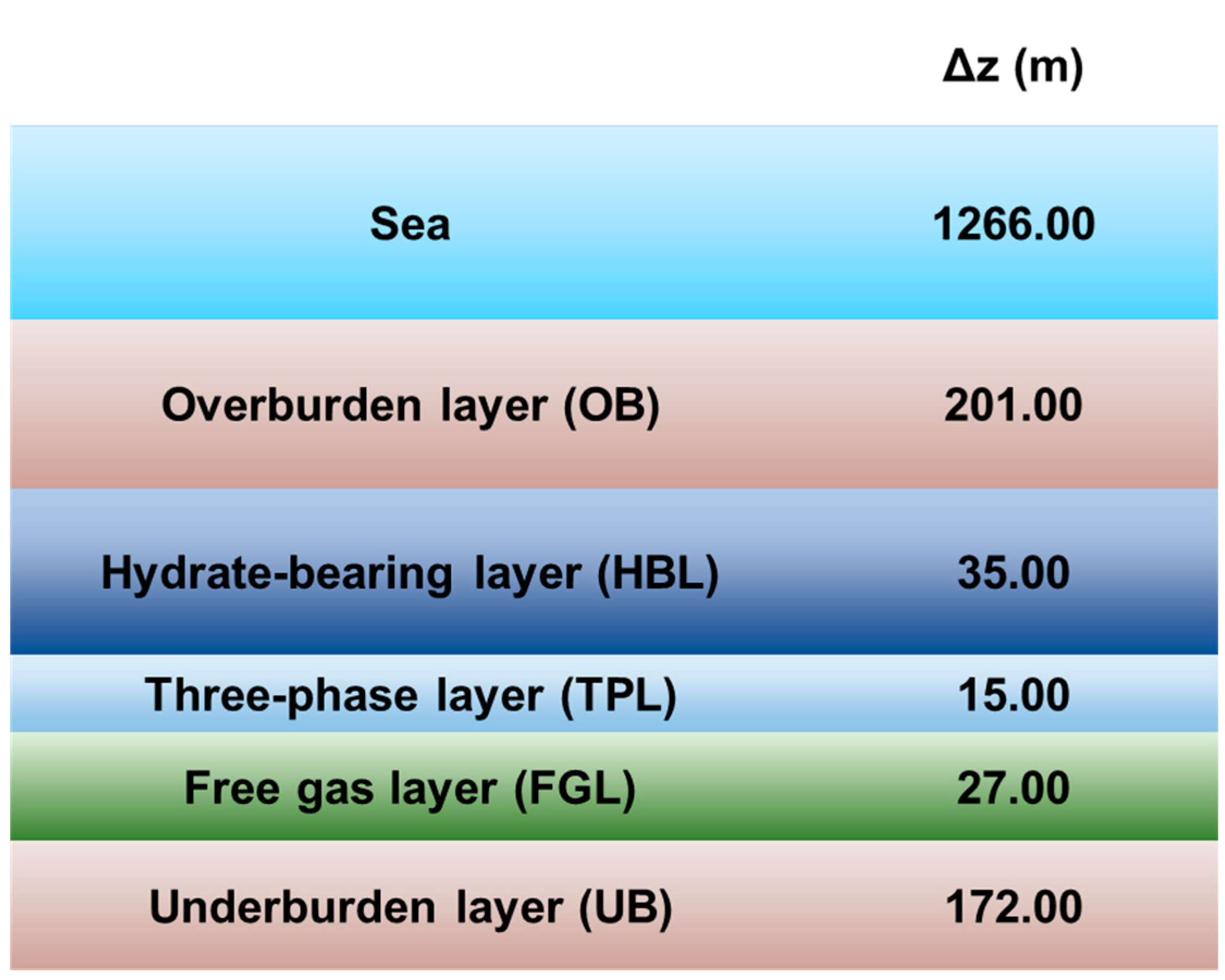
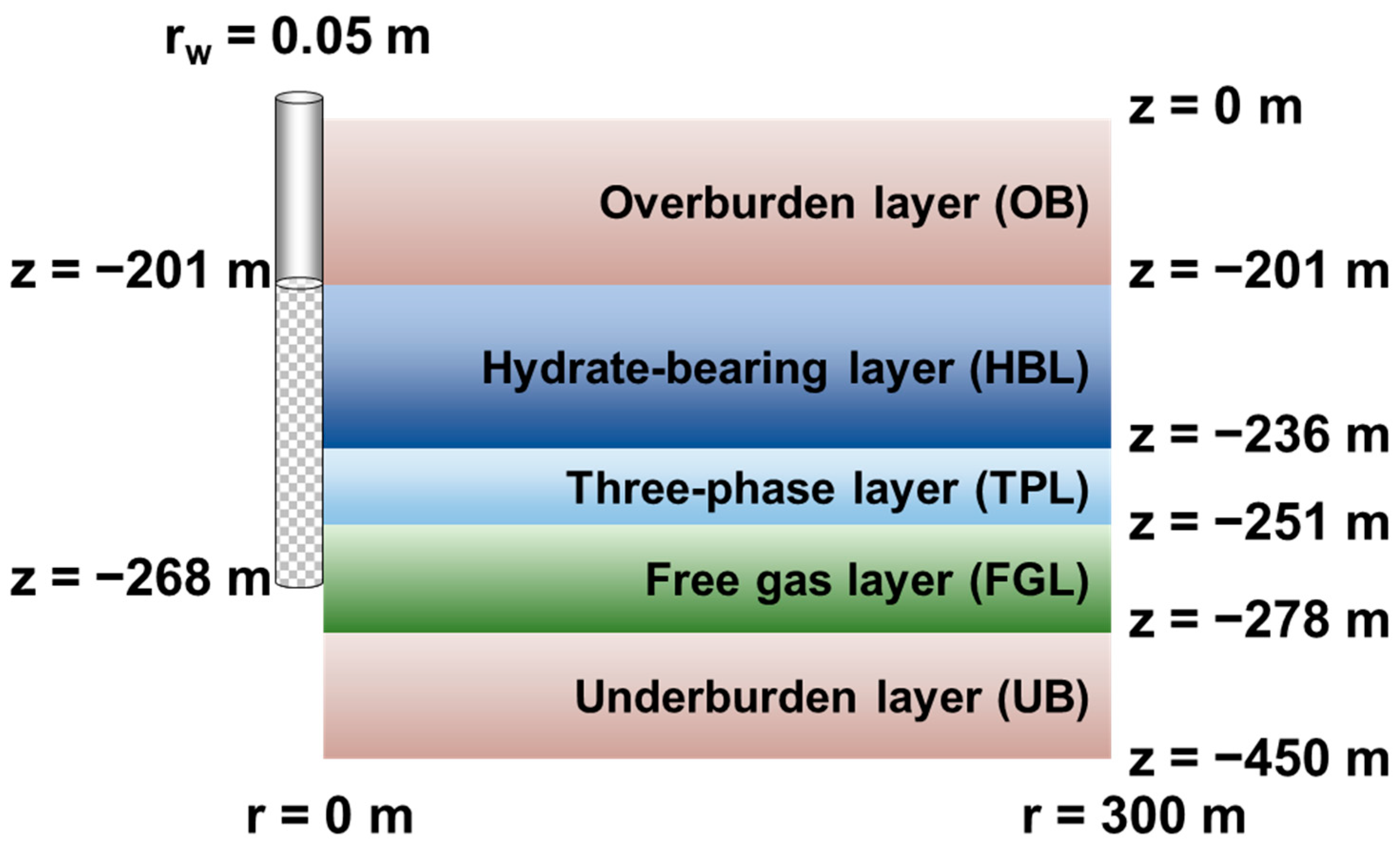
3.1. The Geologic Model
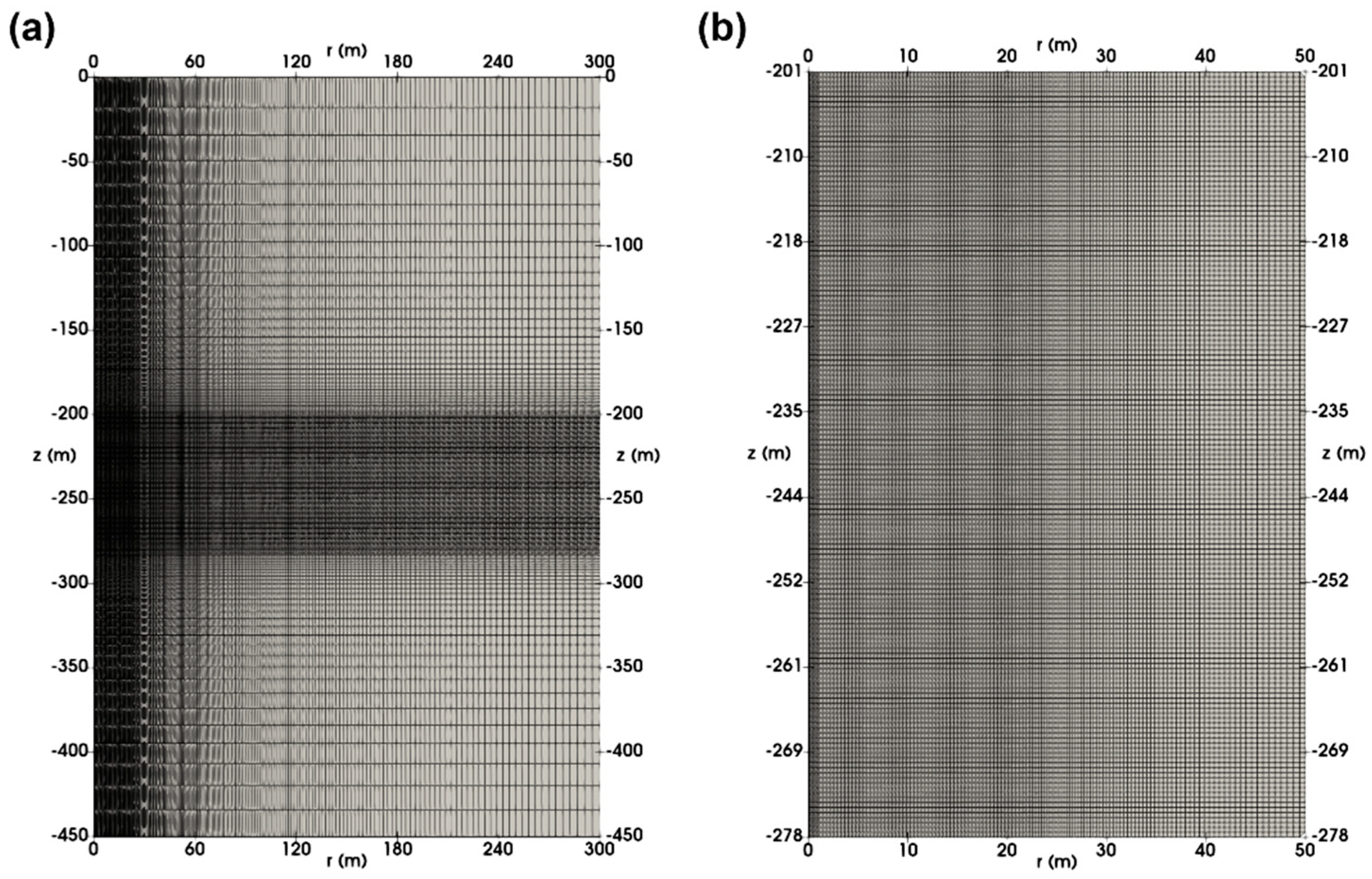
3.2. Domain Discretization
3.3. Well Description
3.4. System Properties
3.5. Initial Conditions
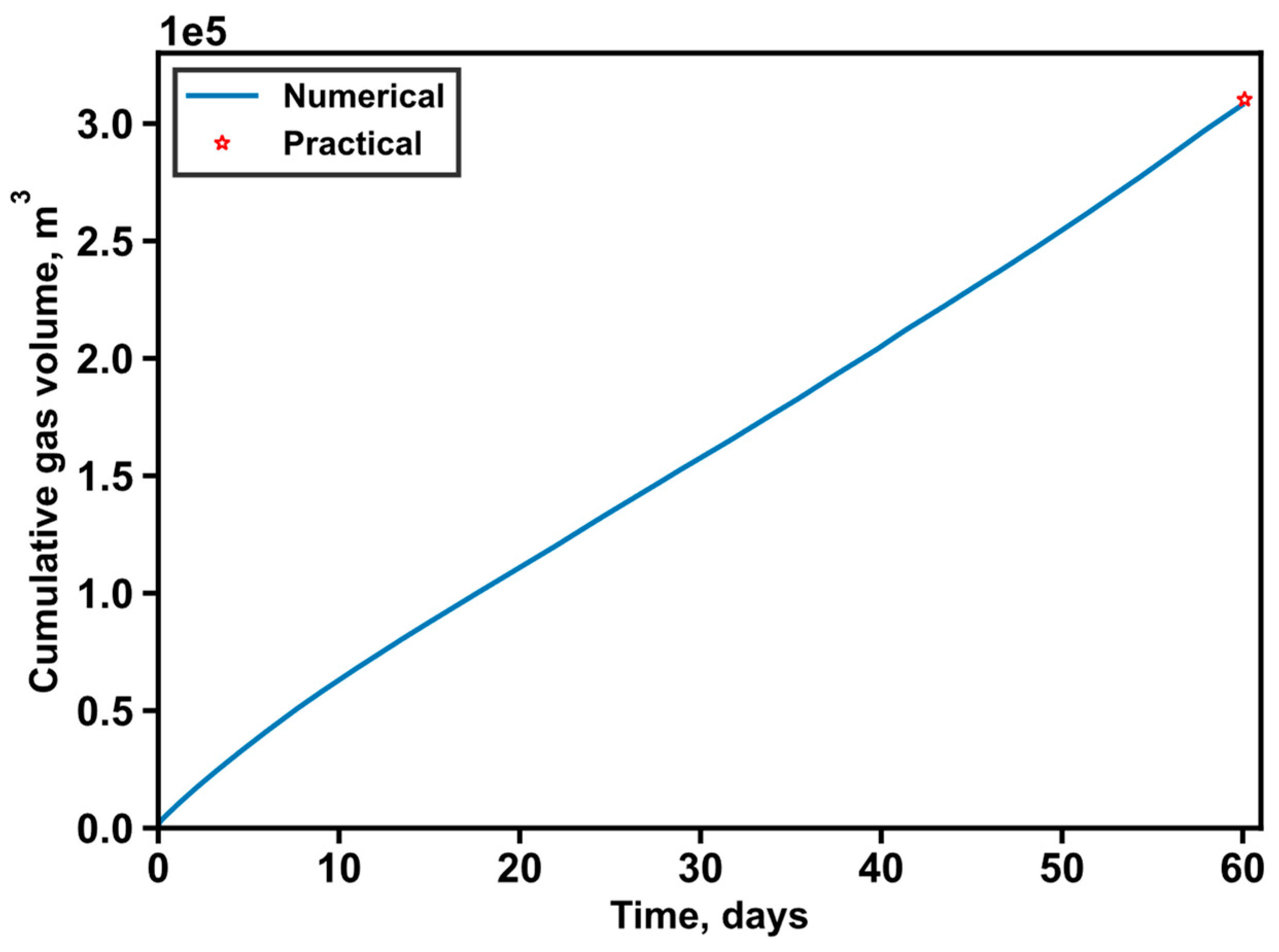
3.6. Model Validation
3.7. Simulations Cases
4. Results and Discussion
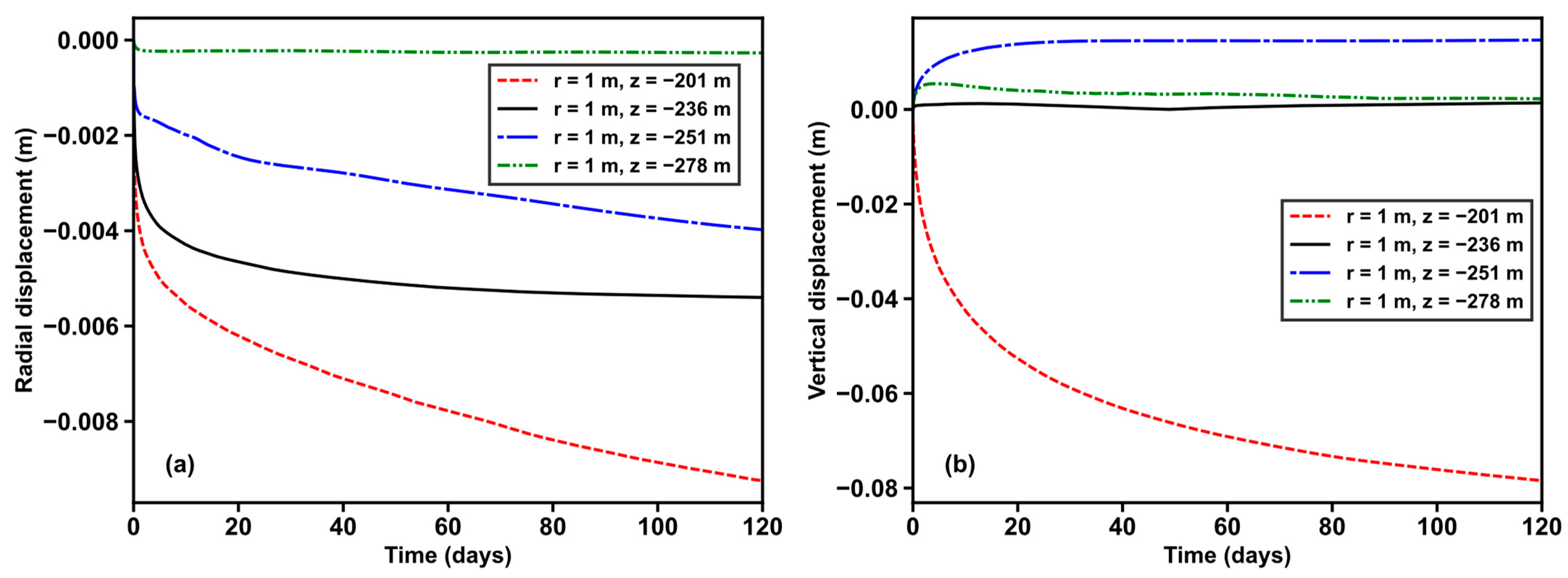
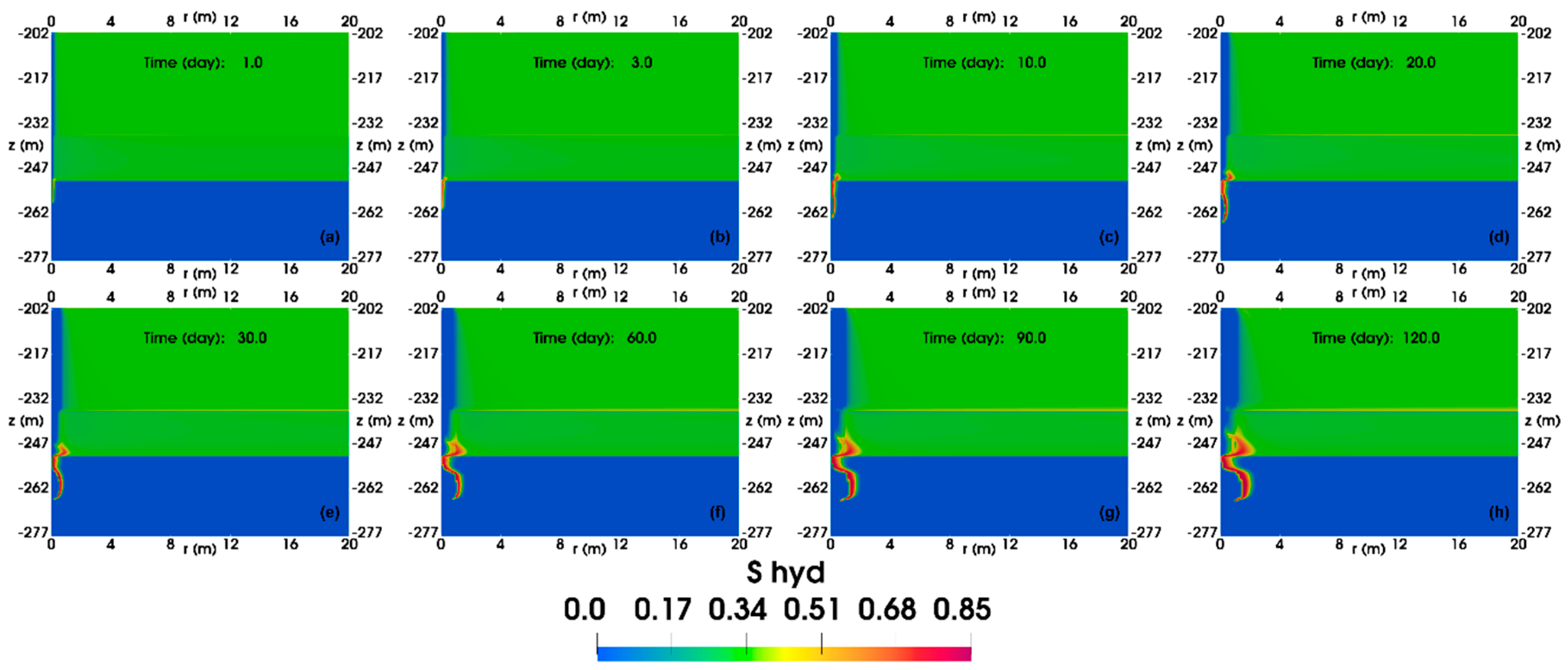
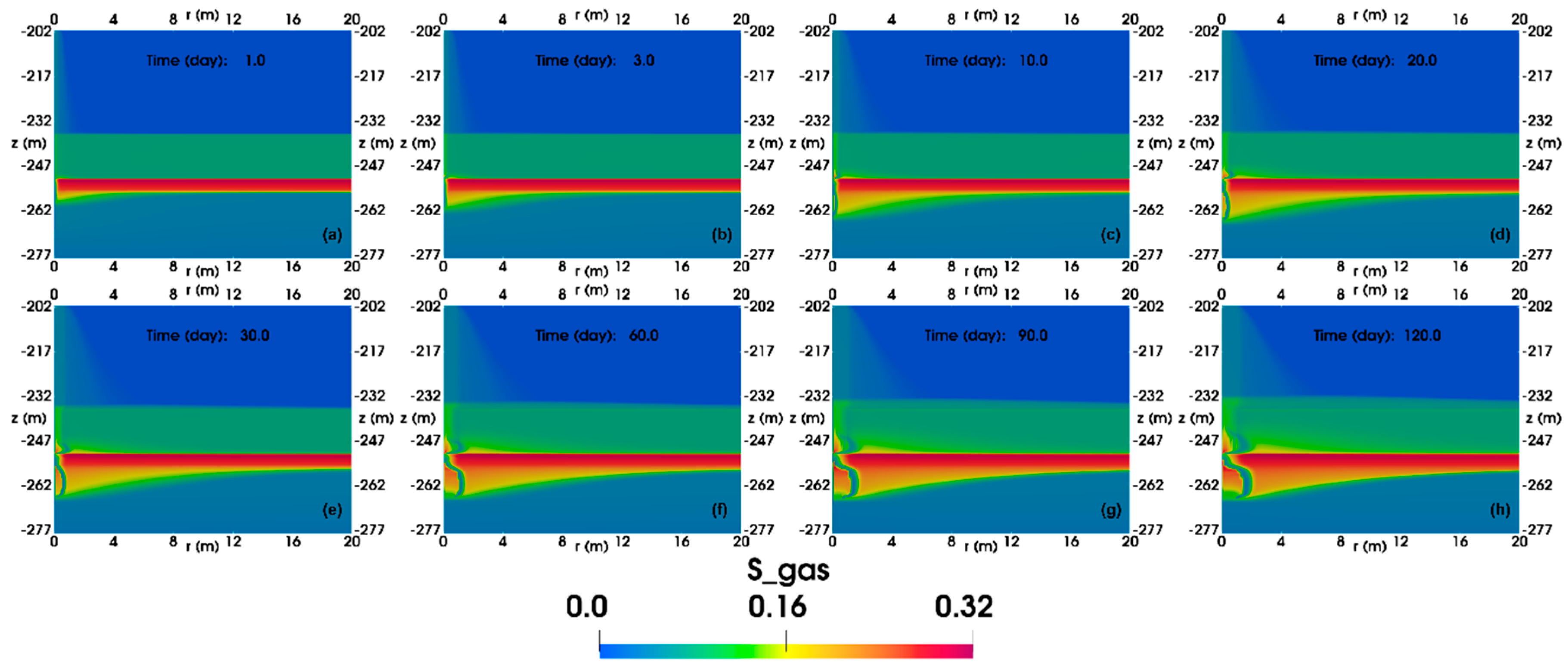
4.1. Base Case
4.1.1. Fluid Production
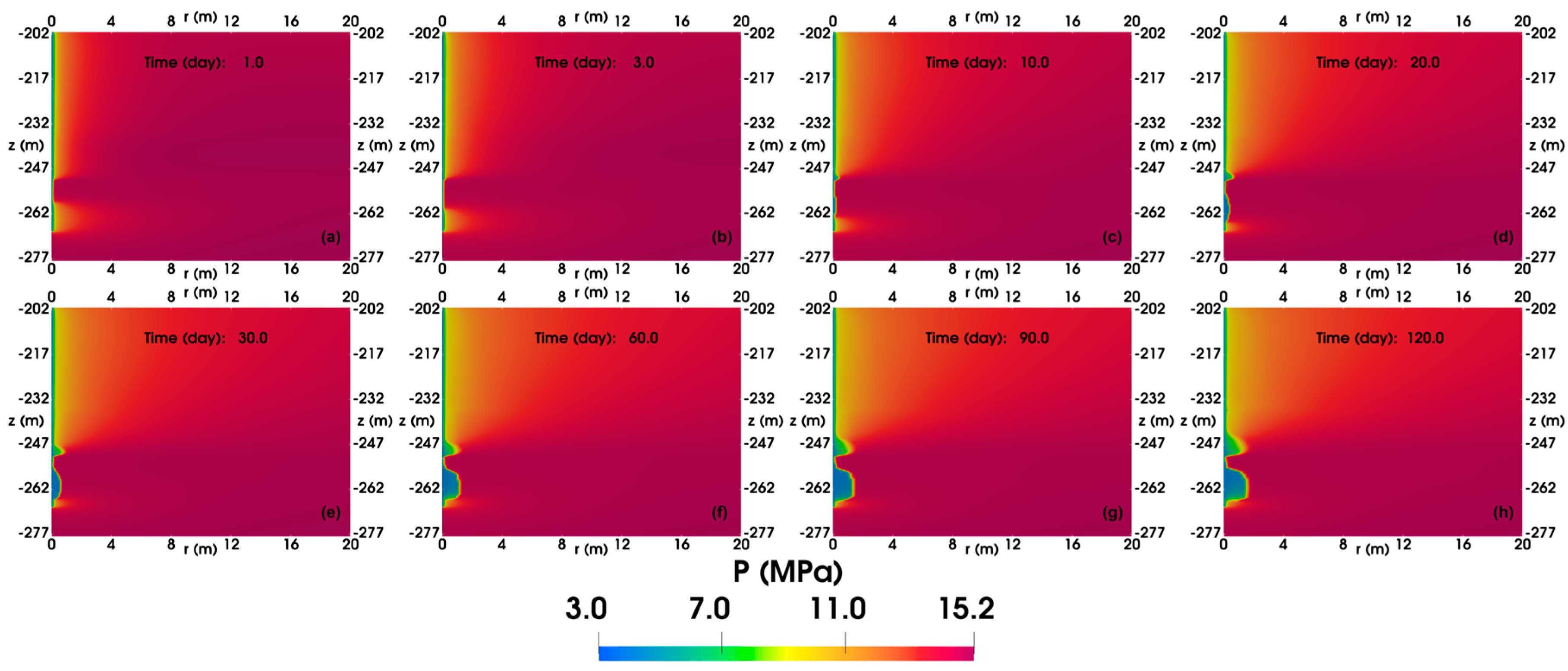
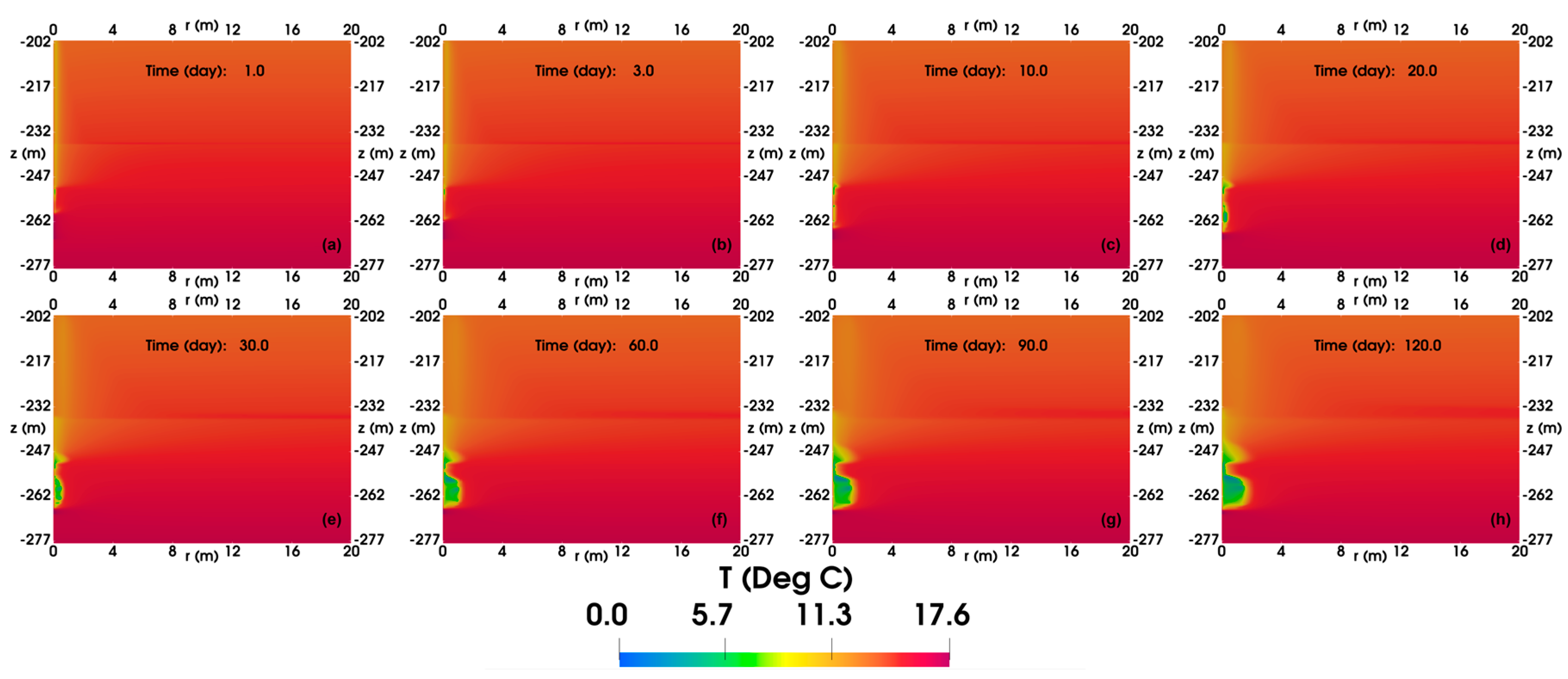
4.1.2. Spatial Distributions
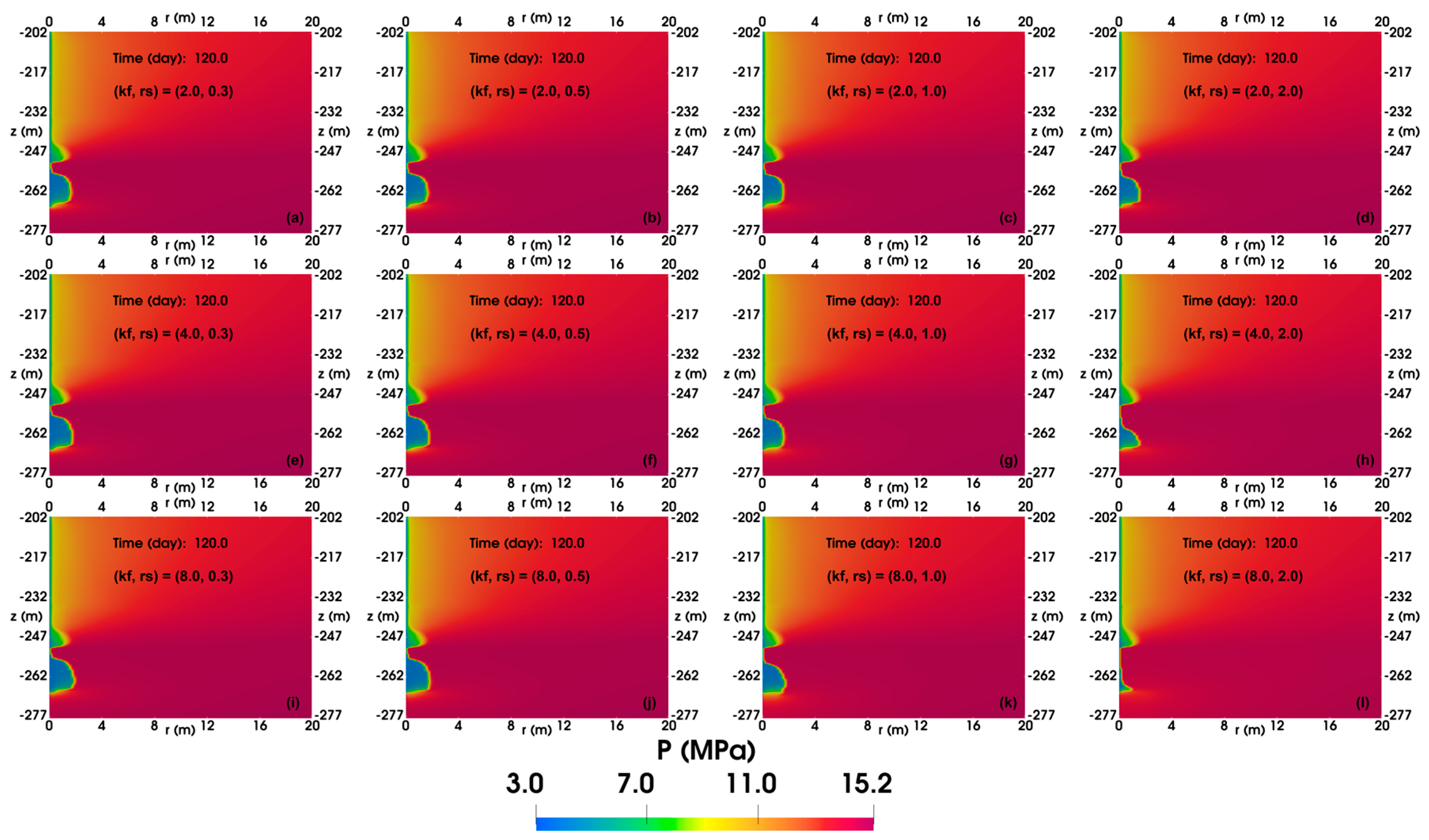
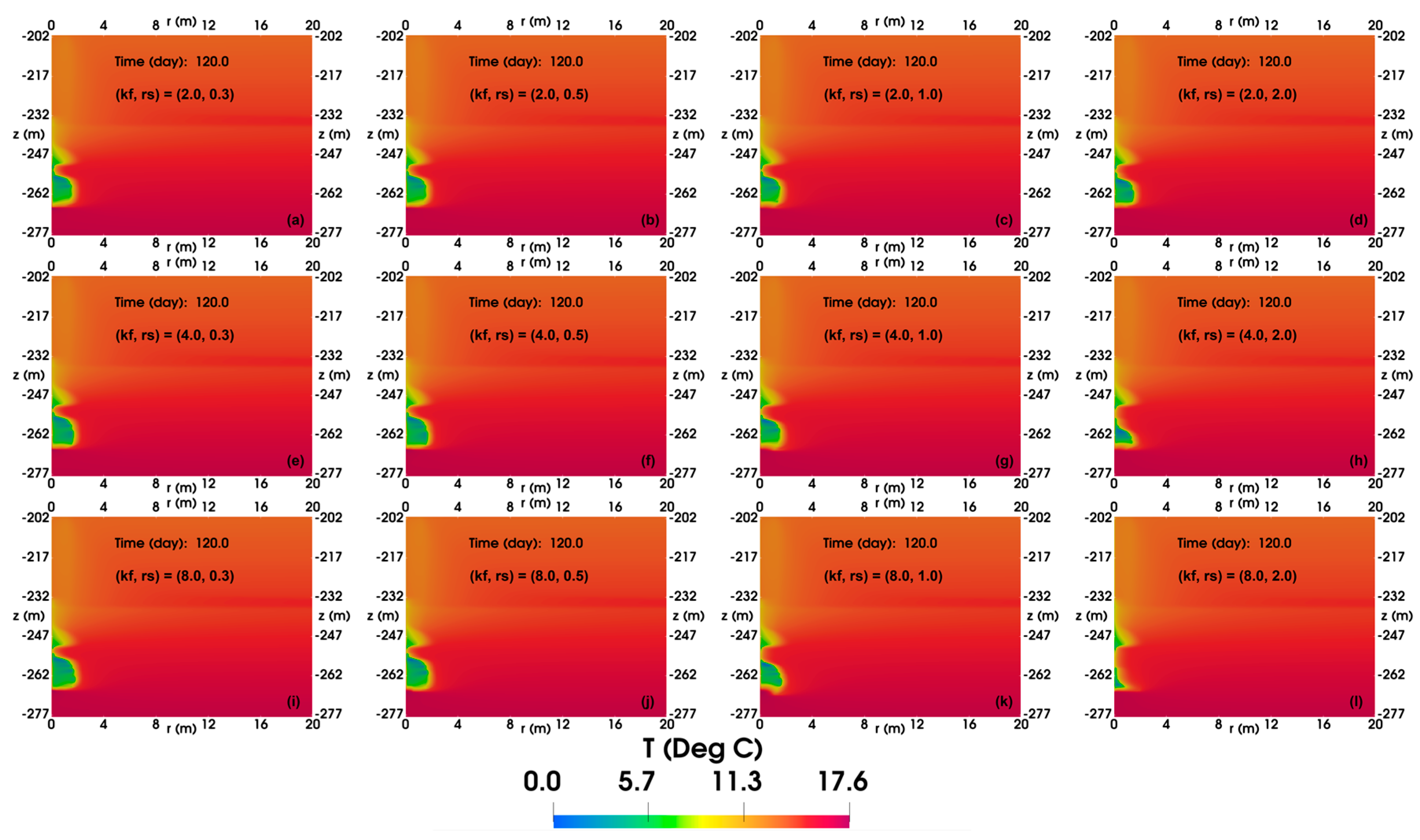
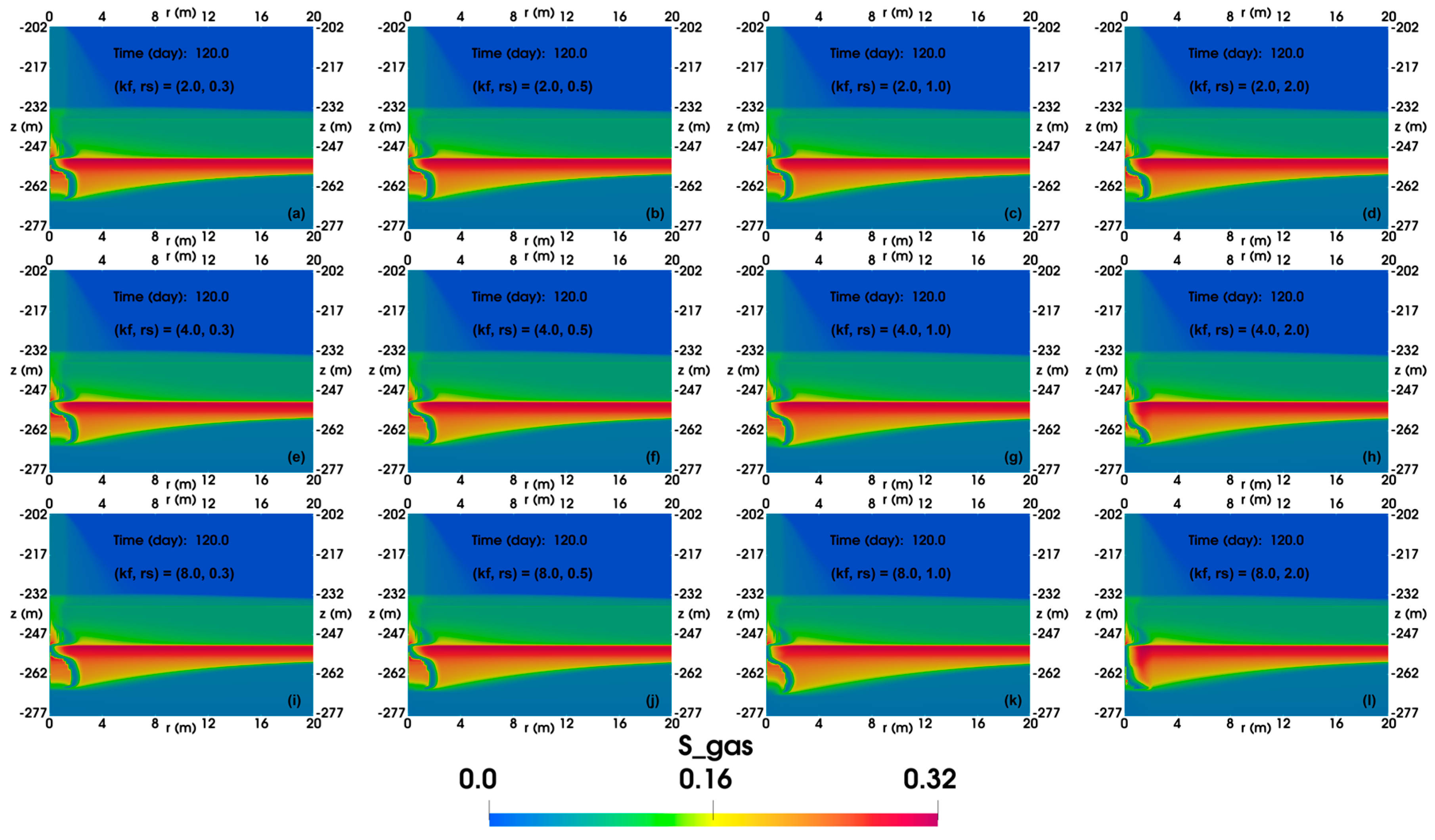
4.2. Effect of Permeability Enhancement
4.2.1. Fluid Production
4.2.2. Spatial Distributions
5. Conclusions
- To evaluate the effectiveness of permeability enhancement considering the geomechanical responses in the Shenhu area, a coupled simulation using pTOUGH+HYDRATE V1.5 and the RGMS (Reservoir Geomechanics Simulator) is implemented.
- Based on the geophysical surveys and analysis of core samples at well SHSC-4 located in the Shenhu area of the northern South China Sea, the established numerical simulation model is accurate, and the simulation results are highly consistent with the trial production data, ensuring the reliability of the outcomes obtained in this study.
- In the base case, the formation and dissociation of gas hydrates in the free gas layer (FGL) alternate, ultimately resulting in a low-temperature region near 0 °C and leading to the cessation of the simulation after 120 days of production. The cumulative gas production reached 6.2 × 105 ST m3.
- In the base case, the FGL contributes the most to gas production, accounting for 72.17% of the cumulative gas production (Vg), followed by the three-phase layer (TPL), accounting for 23.54% of the cumulative gas production, and the hydrate-bearing layer (HBL) contributes the least, accounting for only 4.29% of the cumulative gas production.
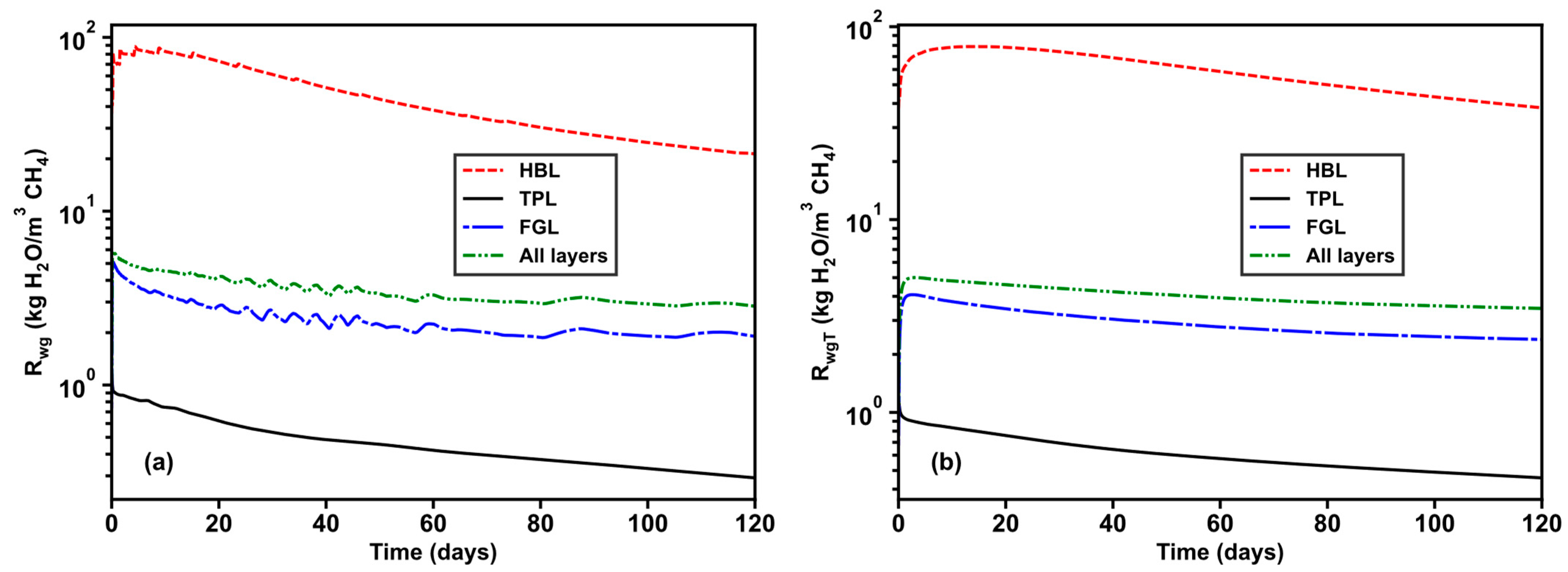
- In the base case, the cumulative water-to-gas ratio (Rwg) from the HBL, TPL, and FGL gradually decreases during the production of gas hydrates. RwgT from the HBL, which contributes the least to gas production, is the highest, with a value several times those from TPL and FGL.
- In the base case, the gas production obtained without permeability enhancement is insufficient for commercial production. Permeability enhancement can be an option used to increase gas production.
- After increasing the permeabilities of the HBL, TPL, and FGL with the same permeability enhancement ratio (fk) and the same simulated radius (rs), the improvement effect of modifying the FGL is the best, with a maximum increase of 87%. The required mass of water separated from a unit of gas is the lowest when applying permeability enhancement in the FGL, with a minimum value of 85% of the original separation mass.
- The results of modifying the FGL show that the higher the degree of permeability enhancement, the deeper the impact of permeability enhancement and the closer the formation and dissociation of gas hydrates are to the wellbore, making it more difficult for gas to be obstructed by the formation of gas hydrates, which is more conducive to production.
- Although permeability enhancement is attempted in this study, it did not extend the production period as the simulation still ends due to low temperature in the FGL. Future research should focus on exploring methods to prevent such low temperatures from occurring in the FGL.
- The results obtained by considering geomechanical responses differ from previous numerical studies that only considered flow and thermal behaviors. This indicates that neglecting geomechanical responses may result in an incorrect natural gas hydrate production scheme. Therefore, future numerical studies should take geomechanical responses into consideration to obtain more realistic results.
- In future work, it is imperative to discover production schemes that effectively mitigate the occurrence of a low-temperature region after 120 days of production, which currently causes disruptions in numerical simulations, thus enabling the extension of the observation period. Moreover, new production schemes combined with permeability enhancement should be explored to facilitate the achievement of production rates that meet the necessary threshold for the commercial exploitation of natural gas hydrates.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Change in the quantity in parentheses | |
| Specific enthalpy of hydrate dissociation/formation (J∙kg−1) | |
| Del operator | |
| CR | Heat capacity of the dry rock (J∙kg−1∙K−1) |
| dA | Differential surface (m2) |
| dV | Differential volume (m3) |
| E | Young’s modulus (Pa) |
| G | Shear modulus (Pa) |
| G0 | Shear modulus when the hydrate saturation is zero (Pa) |
| G1 | Shear modulus when the hydrate saturation is one (Pa) |
| hβ | Specific enthalpy of phase (J∙kg−1) |
| Kdr | Drained bulk modulus (Pa) |
| Kdr0 | Drained modulus when the hydrate saturation is zero (Pa) |
| Kdr1 | Drained modulus when the hydrate saturation is one (Pa) |
| Skeletal grain modulus (Pa) | |
| Radial permeability (m2) | |
| Relative permeability of phase | |
| Vertical permeability (m2) | |
| Composite thermal conductivity of the medium/fluid ensemble (W∙m−1∙K−1) | |
| Formation thermal conductivity under desaturated conditions (W∙m−1∙K−1) | |
| Formation thermal conductivity under fully liquid-saturated conditions (W∙m−1∙K−1) | |
| Thermal conductivity of ice phase (W∙m−1∙K−1) | |
| MA | Cumulative mass of aqueous phase |
| MG | Cumulative mass of gaseous phase |
| Mθ | Heat accumulation term |
| Mκ | Mass accumulation of component κ (kg∙m−3) |
| P | Pressure (Pa) |
| Pt | Average mobile fluid pressure (Pa) |
| Pt,0 | Initial equivalent pore pressure (Pa) |
| Pβ | Pressure of phase (Pa) |
| Qg | Volumetric rate of CH4 well production |
| Qw | Water mass production rate |
| qκ | Source/sink term of component κ (kg∙m−3∙s−1) |
| r | Radial direction |
| Rwg | Instantaneous water-to-gas ratio |
| RwgT | Cumulative water-to-gas ratio |
| Saturation of phase | |
| T | Temperature (K or °C) |
| t | Time (s) |
| ur | Radial displacement (m) |
| uz | Vertical displacement (m) |
| Specific internal energy of phase (J∙kg−1) | |
| Vg | Cumulative volume of CH4 produced at the well |
| Vn | Volume of the subdomain (m3) |
| Mass fraction of component κ in phase | |
| z | Direction along the z-axis |
| Biot’s coefficient | |
| Γn | Surface of subdomain n (m2) |
| γ | Empirical permeability reduction factor |
| εv | Current volumetric strain |
| εv,0 | Initial volumetric strain |
| Viscosity of phase (Pa∙s) | |
| ν | Poisson’s ratio |
| Bulk density (kg∙m−3) | |
| Fluid density (kg∙m−3) | |
| Rock density (kg∙m−3) | |
| Density of phase (kg∙m−3) | |
| Reservoir porosity | |
| Initial porosity | |
| Flux vector of component κ (kg∙m−2∙s−1) | |
| Flux vector of phase (kg∙m−2∙s−1) | |
| Flux vector of component κ in phase (kg∙m−2∙s−1) | |
| g | Gravitational acceleration vector (m∙s−2) |
| k | Absolute permeability tensor (m2) |
| u | Displacement vector (m) |
| Strain tensor | |
| Total stress tensor (Pa) | |
| Effective stress tensor (Pa) |
References
- Sloan, E.D. Fundamental Principles and Applications of Natural Gas Hydrates. Nature 2003, 426, 353–359. [Google Scholar] [CrossRef]
- Chong, Z.R.; Yang, S.H.B.; Babu, P.; Linga, P.; Li, X.-S. Review of Natural Gas Hydrates as an Energy Resource: Prospects and Challenges. Appl. Energy 2016, 162, 1633–1652. [Google Scholar] [CrossRef]
- Makogon, Y.F.; Holditch, S.A.; Makogon, T.Y. Natural Gas-Hydrates—A Potential Energy Source for the 21st Century. J. Pet. Sci. Eng. 2007, 56, 14–31. [Google Scholar] [CrossRef]
- Rutqvist, J.; Moridis, G.J.; Grover, T.; Collett, T. Geomechanical Response of Permafrost-Associated Hydrate Deposits to Depressurization-Induced Gas Production. J. Pet. Sci. Eng. 2009, 67, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Sun, J.; Ning, F.; Li, S.; Zhang, K.; Liu, T.; Zhang, L.; Jiang, G.; Wu, N. Numerical Simulation of Gas Production from Hydrate-Bearing Sediments in the Shenhu Area by Depressurising: The Effect of Burden Permeability. J. Unconv. Oil Gas Resour. 2015, 12, 23–33. [Google Scholar] [CrossRef]
- Yin, Z.; Moridis, G.; Chong, Z.R.; Tan, H.K.; Linga, P. Numerical Analysis of Experiments on Thermally Induced Dissociation of Methane Hydrates in Porous Media. Ind. Eng. Chem. Res. 2018, 57, 5776–5791. [Google Scholar] [CrossRef]
- Li, G.; Li, X.-S.; Tang, L.-G.; Zhang, Y. Experimental Investigation of Production Behavior of Methane Hydrate under Ethylene Glycol Injection in Unconsolidated Sediment. Energy Fuels 2007, 21, 3388–3393. [Google Scholar] [CrossRef]
- Ohgaki, K.; Takano, K.; Sangawa, H.; Matsubara, T.; Nakano, S. Methane Exploitation by Carbon Dioxide from Gas Hydrates—Phase Equilibria for CO2-CH4 Mixed Hydrate System. J. Chem. Eng. Jpn. 1996, 29, 478–483. [Google Scholar] [CrossRef] [Green Version]
- Kvamme, B.; Zhao, J.; Wei, N.; Sun, W.; Saeidi, N.; Pei, J.; Kuznetsova, T. Hydrate Production Philosophy and Thermodynamic Calculations. Energies 2020, 13, 672. [Google Scholar] [CrossRef] [Green Version]
- Kvamme, B. Mechanisms for CH4/CO2 Swapping in Natural Sediments. Fluids 2022, 7, 260. [Google Scholar] [CrossRef]
- Kvamme, B. Thermodynamics and Kinetic Mechanisms for CH4/CO2 Swapping in Natural Sediments. Energy Fuels 2022, 36, 6374–6396. [Google Scholar] [CrossRef]
- Moridis, G.J.; Silpngarmlert, S.; Reagan, M.T.; Collett, T.; Zhang, K. Gas Production from a Cold, Stratigraphically-Bounded Gas Hydrate Deposit at the Mount Elbert Gas Hydrate Stratigraphic Test Well, Alaska North Slope: Implications of Uncertainties. Mar. Pet. Geol. 2011, 28, 517–534. [Google Scholar] [CrossRef]
- Collett, T.S.; Lee, M.W.; Agena, W.F.; Miller, J.J.; Lewis, K.A.; Zyrianova, M.V.; Boswell, R.; Inks, T.L. Permafrost-Associated Natural Gas Hydrate Occurrences on the Alaska North Slope. Mar. Pet. Geol. 2011, 28, 279–294. [Google Scholar] [CrossRef]
- Myshakin, E.M.; Ajayi, T.; Anderson, B.J.; Seol, Y.; Boswell, R. Numerical Simulations of Depressurization-Induced Gas Production from Gas Hydrates Using 3-D Heterogeneous Models of L-Pad, Prudhoe Bay Unit, North Slope Alaska. J. Nat. Gas Sci. Eng. 2016, 35, 1336–1352. [Google Scholar] [CrossRef]
- Anderson, B.J.; Kurihara, M.; White, M.D.; Moridis, G.J.; Wilson, S.J.; Pooladi-Darvish, M.; Gaddipati, M.; Masuda, Y.; Collett, T.S.; Hunter, R.B.; et al. Regional Long-Term Production Modeling from a Single Well Test, Mount Elbert Gas Hydrate Stratigraphic Test Well, Alaska North Slope. Mar. Pet. Geol. 2011, 28, 493–501. [Google Scholar] [CrossRef]
- Moridis, G.J.; Collett, T.S.; Dallimore, S.R.; Satoh, T.; Hancock, S.; Weatherill, B. Numerical Studies of Gas Production from Several CH4 Hydrate Zones at the Mallik Site, Mackenzie Delta, Canada. J. Pet. Sci. Eng. 2004, 43, 219–238. [Google Scholar] [CrossRef] [Green Version]
- Uddin, M.; Wright, F.; Dallimore, S.; Coombe, D. Gas Hydrate Dissociations in Mallik Hydrate Bearing Zones A, B, and C by Depressurization: Effect of Salinity and Hydration Number in Hydrate Dissociation. J. Nat. Gas Sci. Eng. 2014, 21, 40–63. [Google Scholar] [CrossRef]
- Bazaluk, O.; Sai, K.; Lozynskyi, V.; Petlovanyi, M.; Saik, P. Research into Dissociation Zones of Gas Hydrate Deposits with a Heterogeneous Structure in the Black Sea. Energies 2021, 14, 1345. [Google Scholar] [CrossRef]
- Klymenko, V.; Ovetskyi, S.; Martynenko, V.; Vytyaz, O.; Uhrynovskyi, A. An Alternative Method of Methane Production from Deposits of Subaquatic Gas Hydrates. Min. Miner. Depos. 2022, 16, 11–17. [Google Scholar] [CrossRef]
- Lin, J.-S.; Uchida, S.; Myshakin, E.M.; Seol, Y.; Rutqvist, J.; Boswell, R. Assessing the Geomechanical Stability of Interbedded Hydrate-Bearing Sediments under Gas Production by Depressurization at NGHP-02 Site 16. Mar. Pet. Geol. 2019, 108, 648–659. [Google Scholar] [CrossRef] [Green Version]
- Moridis, G.J.; Reagan, M.T.; Queiruga, A.F.; Boswell, R. Evaluation of the Performance of the Oceanic Hydrate Accumulation at Site NGHP-02-09 in the Krishna-Godavari Basin during a Production Test and during Single and Multi-Well Production Scenarios. Mar. Pet. Geol. 2019, 108, 660–696. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.; Moridis, G.J.; Blasingame, T.A. Effect of Geomechanics and of Grid Discretization on the Predictions of Production from Natural Hydrate Deposits and of the Associated Geomechanical System Response. Gas Sci. Eng. 2023, 112, 204942. [Google Scholar] [CrossRef]
- Moridis, G.J.; Kim, J.; Reagan, M.T.; Kim, S.-J. Analysis of Short- and Long-Term System Response During Gas Production from a Gas Hydrate Deposit at the UBGH2-6 Site of the Ulleung Basin in the Korean East Sea. Can. J. Chem. Eng. 2023, 101, 735–763. [Google Scholar] [CrossRef]
- Yu, T.; Guan, G.; Abudula, A.; Yoshida, A.; Wang, D.; Song, Y. Enhanced Gas Recovery from Methane Hydrate Reservoir in the Nankai Trough, Japan. Energy Procedia 2019, 158, 5213–5218. [Google Scholar] [CrossRef]
- Zhu, H.; Xu, T.; Yuan, Y.; Xia, Y.; Xin, X. Numerical Investigation of the Natural Gas Hydrate Production Tests in the Nankai Trough by Incorporating Sand Migration. Appl. Energy 2020, 275, 115384. [Google Scholar] [CrossRef]
- Gu, Y.; Sun, J.; Qin, F.; Ning, F.; Cao, X.; Liu, T.; Qin, S.; Zhang, L.; Jiang, G. Enhancing Gas Recovery from Natural Gas Hydrate Reservoirs in the Eastern Nankai Trough: Deep Depressurization and Underburden Sealing. Energy 2023, 262, 125510. [Google Scholar] [CrossRef]
- Ye, J.; Qin, X.; Xie, W.; Lu, H.; Ma, B.; Qiu, H.; Liang, J.; Lu, J.; Kuang, Z.; Lu, C.; et al. The Second Natural Gas Hydrate Production Test in the South China Sea. China Geol. 2020, 3, 197–209. [Google Scholar] [CrossRef]
- Wu, N.; Li, Y.; Wan, Y.; Sun, J.; Huang, L.; Mao, P. Prospect of Marine Natural Gas Hydrate Stimulation Theory and Technology System. Nat. Gas Ind. B 2021, 8, 173–187. [Google Scholar] [CrossRef]
- Li, J.; Ye, J.; Qin, X.; Qiu, H.; Wu, N.; Lu, H.; Xie, W.; Lu, J.; Peng, F.; Xu, Z.; et al. The First Offshore Natural Gas Hydrate Production Test in South China Sea. China Geol. 2018, 1, 5–16. [Google Scholar] [CrossRef]
- Sun, Y.; Li, B.; Guo, W.; Lü, X.; Zhang, Y.; Li, K.; Wang, P.; Jin, G.; Jia, R.; Qu, L. Comparative Analysis of the Production Trial and Numerical Simulations of Gas Production from Multilayer Hydrate Deposits in the Qilian Mountain Permafrost. J. Nat. Gas Sci. Eng. 2014, 21, 456–466. [Google Scholar] [CrossRef]
- Liu, H.; Zhan, L.; Zhang, J.; Shang, S.; Lu, H. Numerical Investigation on Environmental Effect Associated with Gas-Hydrate Exploitation. Geoenergy Sci. Eng. 2023, 227, 211857. [Google Scholar] [CrossRef]
- Ruppel, C.D.; Kessler, J.D. The Interaction of Climate Change and Methane Hydrates. Rev. Geophys. 2017, 55, 126–168. [Google Scholar] [CrossRef]
- Ruppel, C. Permafrost-Associated Gas Hydrate: Is It Really Approximately 1 % of the Global System? J. Chem. Eng. Data 2015, 60, 429–436. [Google Scholar] [CrossRef]
- Farahani, M.V.; Hassanpouryouzband, A.; Yang, J.; Tohidi, B. Development of a Coupled Geophysical–Geothermal Scheme for Quantification of Hydrates in Gas Hydrate-Bearing Permafrost Sediments. Phys. Chem. Chem. Phys. 2021, 23, 24249–24264. [Google Scholar] [CrossRef] [PubMed]
- Farahani, M.V.; Hassanpouryouzband, A.; Yang, J.; Tohidi, B. Insights into the Climate-Driven Evolution of Gas Hydrate-Bearing Permafrost Sediments: Implications for Prediction of Environmental Impacts and Security of Energy in Cold Regions. RSC Adv. 2021, 11, 14334–14346. [Google Scholar] [CrossRef] [PubMed]
- Wu, S.; Wang, J. On the China′s Successful Gas Production Test from Marine Gas Hydrate Reservoirs. Chin. Sci. Bull. 2018, 63, 2–8. [Google Scholar] [CrossRef] [Green Version]
- Boswell, R.; Collett, T.S. Current Perspectives on Gas Hydrate Resources. Energy Environ. Sci. 2011, 4, 1206–1215. [Google Scholar] [CrossRef]
- Joshi, S.D. Cost/Benefits of Horizontal Wells. In Proceedings of the SPE Western Regional/AAPG Pacific Section Joint Meeting, Long Beach, CA, USA, 19–24 May 2003; p. 2. [Google Scholar] [CrossRef]
- Feng, Y.; Chen, L.; Suzuki, A.; Kogawa, T.; Okajima, J.; Komiya, A.; Maruyama, S. Enhancement of Gas Production from Methane Hydrate Reservoirs by the Combination of Hydraulic Fracturing and Depressurization Method. Energy Convers. Manag. 2019, 184, 194–204. [Google Scholar] [CrossRef]
- Moridis, G. User’s Manual of the TOUGH+ Core Code v1.5: A General-Purpose Simulator of Non-Isothermal Flow and Transport through Porous and Fractured Media; LBNL-6871E.; Lawrence Berkeley National Lab. (LBNL): Berkeley, CA, USA, 2014. [Google Scholar] [CrossRef] [Green Version]
- Chibura, P.E.; Zhang, W.; Luo, A.; Wang, J. A Review on Gas Hydrate Production Feasibility for Permafrost and Marine Hydrates. J. Nat. Gas Sci. Eng. 2022, 100, 104441. [Google Scholar] [CrossRef]
- Sun, X.; Luo, T.; Wang, L.; Wang, H.; Song, Y.; Li, Y. Numerical Simulation of Gas Recovery from a Low-Permeability Hydrate Reservoir by Depressurization. Appl. Energy 2019, 250, 7–18. [Google Scholar] [CrossRef]
- Yuan, Y.; Gong, Y.; Xu, T.; Zhu, H. Multiphase Flow and Geomechanical Responses of Interbedded Hydrate Reservoirs during Depressurization Gas Production for Deepwater Environment. Energy 2023, 262, 125603. [Google Scholar] [CrossRef]
- Zhao, X.; Wang, Z.; Zhao, Y.; Zuo, J.; Li, P.; Liang, W.; Wang, B.; Chen, X.; Lei, H.; Jin, G. Coupled Thermal–Hydrodynamic–Mechanical Numerical Simulation of Natural Gas Hydrate Horizontal Well Depressurization Production: Method and Application in the South China Sea. Nat. Gas Ind. B 2022, 9, 548–560. [Google Scholar] [CrossRef]
- Xia, Y.; Xu, T.; Yuan, Y.; Xin, X.; Zhu, H. Geomechanical Response Induced by Multiphase (Gas/Water) Flow in the Mallik Hydrate Reservoir of Canada. SPE J. 2022, 27, 434–451. [Google Scholar] [CrossRef]
- Zhang, J.; Li, X.; Chen, Z.; Li, Q.; Li, G.; Lv, T. Numerical Simulation of the Improved Gas Production from Low Permeability Hydrate Reservoirs by Using an Enlarged Highly Permeable Well Wall. J. Pet. Sci. Eng. 2019, 183, 106404. [Google Scholar] [CrossRef]
- Li, B.; Ma, X.; Zhang, G.; Guo, W.; Xu, T.; Yuan, Y.; Sun, Y. Enhancement of Gas Production from Natural Gas Hydrate Reservoir by Reservoir Stimulation with the Stratification Split Grouting Foam Mortar Method. J. Nat. Gas Sci. Eng. 2020, 81, 103473. [Google Scholar] [CrossRef]
- Sun, J.; Ning, F.; Liu, T.; Liu, C.; Chen, Q.; Li, Y.; Cao, X.; Mao, P.; Zhang, L.; Jiang, G. Gas Production from a Silty Hydrate Reservoir in the South China Sea Using Hydraulic Fracturing: A Numerical Simulation. Energy Sci. Eng. 2019, 7, 1106–1122. [Google Scholar] [CrossRef] [Green Version]
- Yu, T.; Guan, G.; Wang, D.; Song, Y.; Abudula, A. Numerical Investigation on the Long-Term Gas Production Behavior at the 2017 Shenhu Methane Hydrate Production Site. Appl. Energy 2021, 285, 116466. [Google Scholar] [CrossRef]
- Rutqvist, J.; Moridis, G.J. Numerical Studies on the Geomechanical Stability of Hydrate-Bearing Sediments. SPE J. 2009, 14, 267–282. [Google Scholar] [CrossRef]
- Moridis, G.J.; Kim, J.; Reagan, M.T.; Kim, S.-J. Feasibility of Gas Production from a Gas Hydrate Accumulation at the UBGH2-6 Site of the Ulleung Basin in the Korean East Sea. J. Pet. Sci. Eng. 2013, 108, 180–210. [Google Scholar] [CrossRef]
- Moridis, G.J.J.; Collett, T.S.S.; Pooladi-Darvish, M.; Hancock, S.; Santamarina, C.; Boswell, R.; Kneafsey, T.; Rutqvist, J.; Kowalsky, M.B.B.; Reagan, M.T.T.; et al. Challenges, Uncertainties, and Issues Facing Gas Production from Gas-Hydrate Deposits. SPE Reserv. Eval. Eng. 2011, 14, 76–112. [Google Scholar] [CrossRef] [Green Version]
- Rutqvist, J.; Moridis, G.J.; Grover, T.; Silpngarmlert, S.; Collett, T.S.; Holdich, S.A. Coupled Multiphase Fluid Flow and Wellbore Stability Analysis Associated with Gas Production from Oceanic Hydrate-Bearing Sediments. J. Pet. Sci. Eng. 2012, 92–93, 65–81. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Liang, J.; Zong, X.; Gong, Y.; Wan, T. Differentiated distribution of methane hydrate in the Shenhu area of the northern South China Sea and controlling factors. Mar. Geol. Front. 2015, 31, 24. [Google Scholar]
- Zhang, J.; Moridis, G.J.; Blasingame, T.A. Message Passing Interface (MPI) Parallelization of Iteratively Coupled Fluid Flow and Geomechanics Codes for the Simulation of System Behavior in Hydrate-Bearing Geologic Media. Part 1: Methodology and Validation. SPE Reserv. Eval. Eng. 2022, 25, 600–620. [Google Scholar] [CrossRef]
- Zhang, J.; Moridis, G.J.; Blasingame, T.A. Message Passing Interface (MPI) Parallelization of Iteratively Coupled Fluid Flow and Geomechanics Codes for the Simulation of System Behavior in Hydrate-Bearing Geologic Media. Part 2: Parallel Performance and Application. SPE Reserv. Eval. Eng. 2022, 25, 621–640. [Google Scholar] [CrossRef]
- Narasimhan, T.N.; Witherspoon, P.A. An Integrated Finite Difference Method for Analyzing Fluid Flow in Porous Media. Water Resour. Res. 1976, 12, 57–64. [Google Scholar] [CrossRef] [Green Version]
- Narasimhan, T.N.; Witherspoon, P.A.; Edwards, A.L. Numerical Model for Saturated-Unsaturated Flow in Deformable Porous Media: 2. The Algorithm. Water Resour. Res. 1978, 14, 255–261. [Google Scholar] [CrossRef] [Green Version]
- Kamath, V.A. Study of Heat Transfer Characteristics during Dissociation of Gas Hydrates in Porous Media; University of Pittsburgh: Pittsburgh, PA, USA, 1984. [Google Scholar]
- Kowalsky, M.B.; Moridis, G.J. Comparison of Kinetic and Equilibrium Reaction Models in Simulating Gas Hydrate Behavior in Porous Media. Energy Convers. Manag. 2007, 48, 1850–1863. [Google Scholar] [CrossRef] [Green Version]
- Moridis, G.J. User’s Manual for the Hydrate v1.5 Option of TOUGH+ v1.5: A Code for the Simulation of System Behavior in Hydrate-Bearing Geologic Media; LBNL-6869E; Lawrence Berkeley National Lab. (LBNL): Berkeley, CA, USA, 2014. [Google Scholar] [CrossRef] [Green Version]
- Biot, M.A. General Theory of Three-Dimensional Consolidation. J. Appl. Phys. 1941, 12, 155–164. [Google Scholar] [CrossRef]
- Terzaghi, K.; Peck, R.B.; Mesri, G. Soil Mechanics in Engineering Practice, 3rd ed.; John Wiley & Sons: New York, NY, USA, 1996. [Google Scholar]
- Mcnamee, J.; Gibson, R.E. Displacement functions and linear transforms applied to diffusion through porous elastic media. Q. J. Mech. Appl. Math. 1960, 13, 98–111. [Google Scholar] [CrossRef]
- Mcnamee, J.; Gibson, R.E. Plane strain and axially symmetric problems of the consolidation of a semi-infinite clay stratum. Q. J. Mech. Appl. Math. 1960, 13, 210–227. [Google Scholar] [CrossRef]
- Moridis, G.J.; Reagan, M.T. Strategies for Gas Production from Oceanic Class 3 Hydrate Accumulations. In Proceedings of the Offshore Technology Conference, Houston, Texas, USA, 30 April–3 May 2007. [Google Scholar] [CrossRef] [Green Version]
- Qin, X.; Liang, Q.; Ye, J.; Yang, L.; Qiu, H.; Xie, W.; Liang, J.; Lu, J.; Lu, C.; Lu, H.; et al. The Response of Temperature and Pressure of Hydrate Reservoirs in the First Gas Hydrate Production Test in South China Sea. Appl. Energy 2020, 278, 115649. [Google Scholar] [CrossRef]
- Shang, S.; Gu, L.; Zhan, L.; Qiu, H.; Lu, H. Application of Horizontal Well to Gas Production from a Hydrate Reservoir with Free Gas and High Irreducible Water. J. Nat. Gas Sci. Eng. 2021, 94, 104102. [Google Scholar] [CrossRef]
- Sun, J.; Zhang, L.; Ning, F.; Lei, H.; Liu, T.; Hu, G.; Lu, H.; Lu, J.; Liu, C.; Jiang, G.; et al. Production Potential and Stability of Hydrate-Bearing Sediments at the Site GMGS3-W19 in the South China Sea: A Preliminary Feasibility Study. Mar. Pet. Geol. 2017, 86, 447–473. [Google Scholar] [CrossRef]
- van Genuchten, M.T. A Closed-Form Equation for Predicting the Hydraulic Conductivity of Unsaturated Soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef] [Green Version]
- Rutqvist, J.; Wu, Y.; Tsang, C.; Bodvarsson, G. A Modeling Approach for Analysis of Coupled Multiphase Fluid Flow, Heat Transfer, and Deformation in Fractured Porous Rock. Int. J. Rock Mech. Min. Sci. 2002, 39, 429–442. [Google Scholar] [CrossRef]
- Moridis, G.J.; Kowalsky, M.B.; Pruess, K. Depressurization-Induced Gas Production from Class 1 Hydrate Deposits. SPE Reserv. Eval. Eng. 2007, 10, 458–481. [Google Scholar] [CrossRef]





| Properties, Conditions, Models | Values |
|---|---|
| Initial pressure at the bottom of TPL | 14.93 MPa |
| Initial temperature at the bottom of TPL | 14.82 °C |
| Gas composition | 100% CH4 |
| Initial saturation of HBL | SH = 0.34 |
| Intrinsic permeabilities of HBL | kh = 2.86 × 10−15 m2 = 2.9 mD; kz = kh |
| of HBL | 0.35 |
| Initial saturation of TPL | SH = 0.31, SG = 0.078 |
| Intrinsic permeabilities of TPL | kh = 1.48 × 10−15 m2 = 1.5 mD; kz = kh |
| of TPL | 0.33 |
| Initial saturation of FGL | SG = 0.078 |
| Intrinsic permeabilities of FGL | kh = 7.30 × 10−15 m2 = 7.4 mD; kz = kh |
| of FGL | 0.32 |
| Intrinsic permeabilities of OB | kh = 9.87 × 10−18 m2 = 0.01 mD; kz = kh |
| of OB | 0.10 |
| Intrinsic permeabilities of UB | kh = 9.87 × 10−18 m2 = 0.01 mD; kz = kh |
| of UB | 0.10 |
| Dry thermal conductivity | kθd = 1 W∙m−1∙K−1 |
| Specific heat CR | 1000 J kg−1∙K−1 |
| Grain density ρR | 2650 kg∙m−3 |
| Composite thermal conductivity model [40] | |
| Relative permeability model EPM#2 [40] | ; ; |
| SirA, SirG, n, nG [69] | 0.65; 0.03; 3.50; 2.50 |
| Capillary pressure model [70] | |
| λ, P0, SirA, SmxA of HBLs | 0.45; 104 Pa; 0.65; 1.0 |
| Porosity–permeability relationship [71] | |
| Empirical permeability reduction factor γ [71] | 29.0 |
| Properties | Values |
|---|---|
| Young’s modulus of HBL | E = 200 MPa at SH = 0; E = 1.4 GPa at SH = 1 |
| Young’s modulus of TPL | E = 200 MPa at SH = 0; E = 1.4 GPa at SH = 1 |
| Young’s modulus of FGL | E = 200 MPa |
| Young’s modulus of OB | E = 70 MPa |
| Young’s modulus of UB | E = 200 MPa |
| Poisson’s ratio of HBL | ν = 0.15 |
| Poisson’s ratio of TPL | ν = 0.15 |
| Poisson’s ratio of FGL | ν = 0.45 |
| Poisson’s ratio of OB | ν = 0.45 |
| Poisson’s ratio of UB | ν = 0.45 |
| Biot’s coefficient | α = 0.99 |
| Cumulative Gas Production (ST m3) | ||||||
|---|---|---|---|---|---|---|
| rs (m) | ||||||
| 0.3 | 0.5 | 1 | 2 | |||
| kf | HBL | 2 | 631,851 | 637,193 | 642,373 | 645,883 |
| 4 | 639,688 | 648,514 | 661,047 | 679,954 | ||
| 8 | 646,531 | 657,912 | 677,975 | 711,590 | ||
| TPL | 2 | 641,762 | 648,207 | 657,112 | 667,160 | |
| 4 | 654,888 | 667,240 | 685,330 | 702,448 | ||
| 8 | 660,201 | 676,255 | 698,987 | 706,541 | ||
| FGL | 2 | 687,226 | 696,737 | 714,312 | 731,513 | |
| 4 | 712,884 | 740,743 | 811,315 | 855,335 | ||
| 8 | 758,690 | 788,555 | 924,427 | 1,160,649 | ||
| Vg/Vg,0 | ||||||
|---|---|---|---|---|---|---|
| rs (m) | ||||||
| 0.3 | 0.5 | 1 | 2 | |||
| kf | HBL | 2 | 1.019 | 1.028 | 1.036 | 1.042 |
| 4 | 1.032 | 1.046 | 1.066 | 1.097 | ||
| 8 | 1.043 | 1.061 | 1.094 | 1.148 | ||
| TPL | 2 | 1.035 | 1.046 | 1.060 | 1.076 | |
| 4 | 1.056 | 1.076 | 1.106 | 1.133 | ||
| 8 | 1.065 | 1.091 | 1.128 | 1.140 | ||
| FGL | 2 | 1.109 | 1.124 | 1.152 | 1.180 | |
| 4 | 1.150 | 1.195 | 1.309 | 1.380 | ||
| 8 | 1.224 | 1.272 | 1.491 | 1.872 | ||
| Cumulative Water-to-Gas Ratio (kg H2O/m3 CH4) | ||||||
|---|---|---|---|---|---|---|
| rs (m) | ||||||
| 0.3 | 0.5 | 1 | 2 | |||
| kf | HBL | 2 | 3.599 | 3.624 | 3.676 | 3.760 |
| 4 | 3.683 | 3.739 | 3.834 | 3.939 | ||
| 8 | 3.725 | 3.800 | 3.920 | 4.029 | ||
| TPL | 2 | 3.373 | 3.349 | 3.318 | 3.282 | |
| 4 | 3.325 | 3.283 | 3.226 | 3.172 | ||
| 8 | 3.308 | 3.256 | 3.192 | 3.173 | ||
| FGL | 2 | 3.308 | 3.307 | 3.289 | 3.221 | |
| 4 | 3.294 | 3.268 | 3.159 | 2.969 | ||
| 8 | 3.234 | 3.236 | 3.066 | 2.406 | ||
| RwgT/RwgT,0 | ||||||
|---|---|---|---|---|---|---|
| rs (m) | ||||||
| 0.3 | 0.5 | 1 | 2 | |||
| kf | HBL | 2 | 1.268 | 1.277 | 1.296 | 1.325 |
| 4 | 1.298 | 1.318 | 1.351 | 1.388 | ||
| 8 | 1.313 | 1.339 | 1.382 | 1.420 | ||
| TPL | 2 | 1.189 | 1.180 | 1.169 | 1.157 | |
| 4 | 1.172 | 1.157 | 1.137 | 1.118 | ||
| 8 | 1.166 | 1.148 | 1.125 | 1.118 | ||
| FGL | 2 | 1.166 | 1.165 | 1.159 | 1.135 | |
| 4 | 1.161 | 1.152 | 1.113 | 1.046 | ||
| 8 | 1.140 | 1.140 | 1.080 | 0.848 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, R.; Zhang, J.; Wang, T.; Lu, H. Numerical Simulation of Improved Gas Production from Oceanic Gas Hydrate Accumulation by Permeability Enhancement Associated with Geomechanical Response. J. Mar. Sci. Eng. 2023, 11, 1468. https://doi.org/10.3390/jmse11071468
Wang R, Zhang J, Wang T, Lu H. Numerical Simulation of Improved Gas Production from Oceanic Gas Hydrate Accumulation by Permeability Enhancement Associated with Geomechanical Response. Journal of Marine Science and Engineering. 2023; 11(7):1468. https://doi.org/10.3390/jmse11071468
Chicago/Turabian StyleWang, Rui, Jiecheng Zhang, Tianju Wang, and Hailong Lu. 2023. "Numerical Simulation of Improved Gas Production from Oceanic Gas Hydrate Accumulation by Permeability Enhancement Associated with Geomechanical Response" Journal of Marine Science and Engineering 11, no. 7: 1468. https://doi.org/10.3390/jmse11071468
APA StyleWang, R., Zhang, J., Wang, T., & Lu, H. (2023). Numerical Simulation of Improved Gas Production from Oceanic Gas Hydrate Accumulation by Permeability Enhancement Associated with Geomechanical Response. Journal of Marine Science and Engineering, 11(7), 1468. https://doi.org/10.3390/jmse11071468






